Ultrafast Hyperspectral Transient Absorption Spectroscopy: Application to Single Layer Graphene
Abstract
1. Introduction
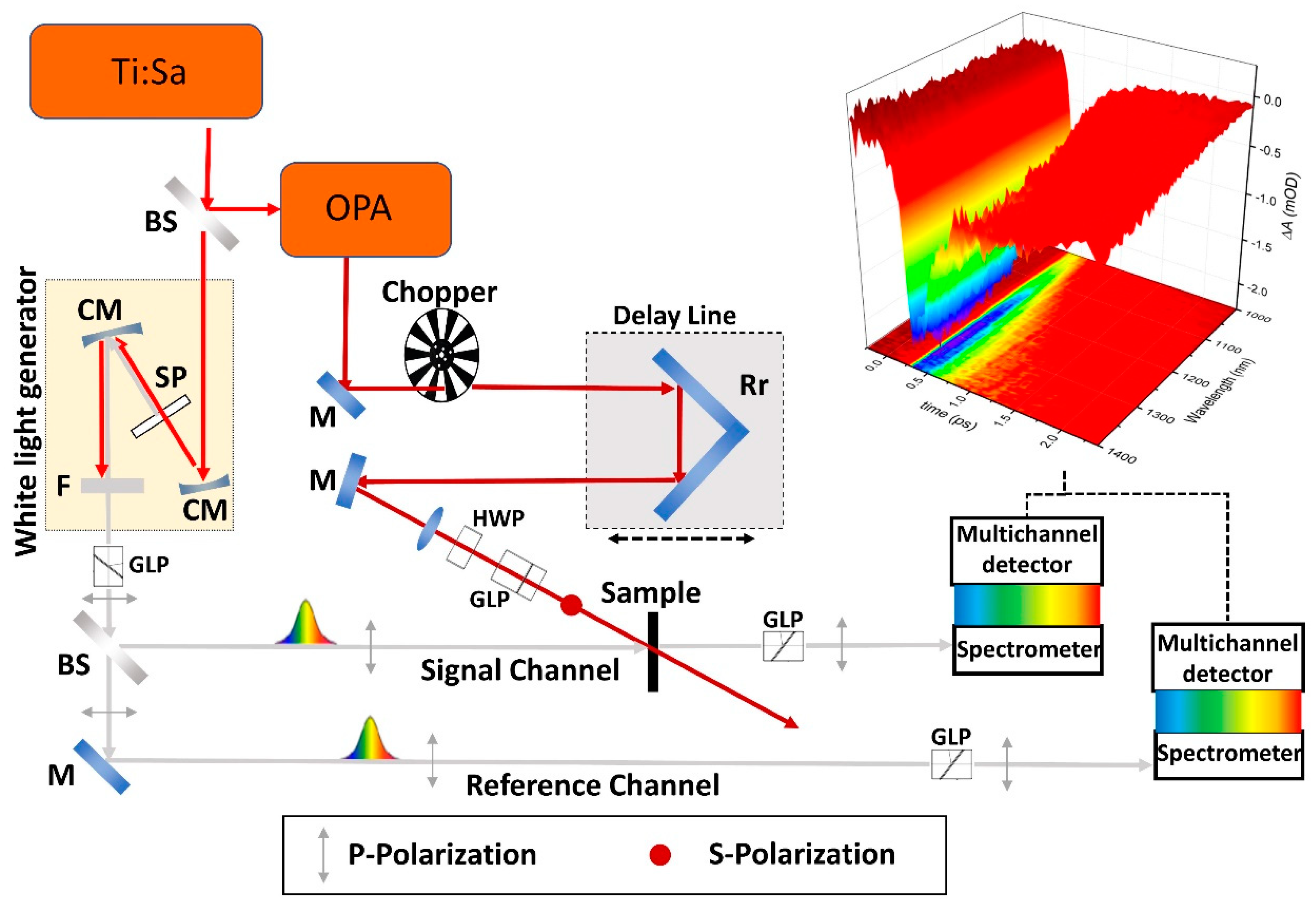
2. Experimental Setup
3. Results
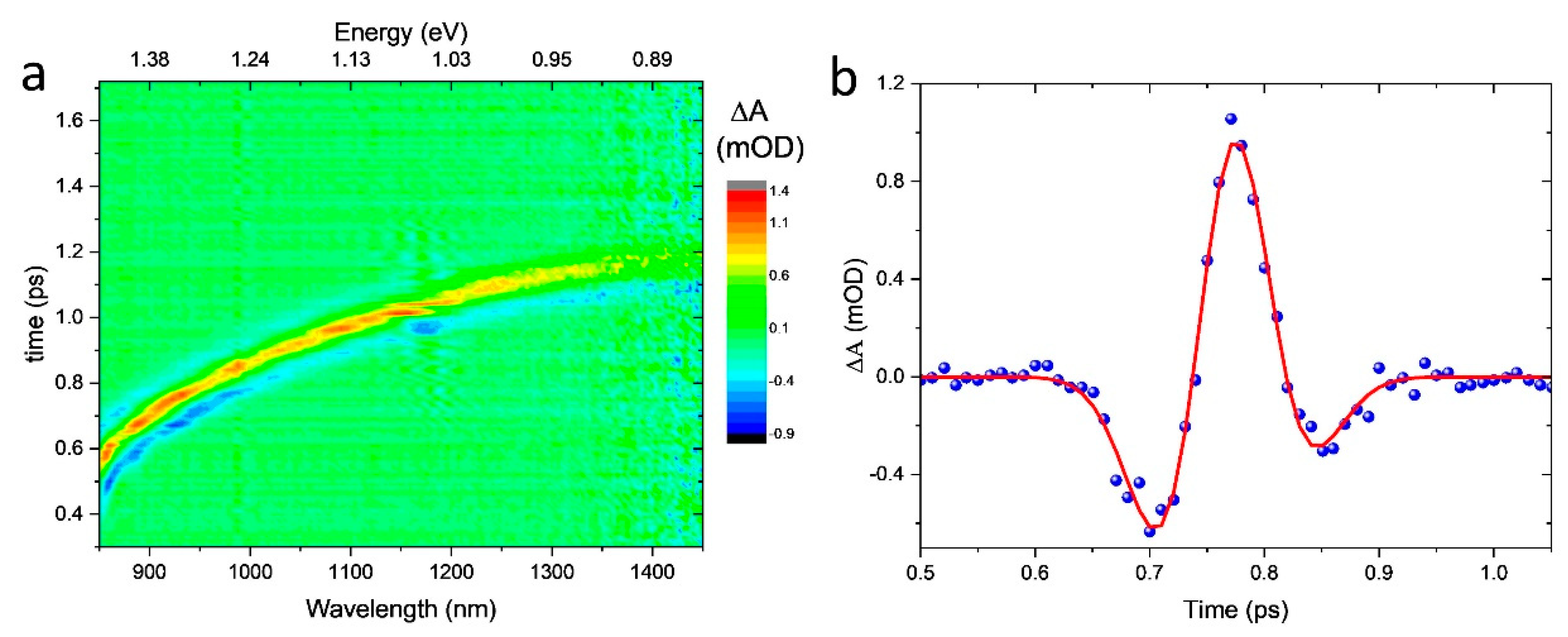
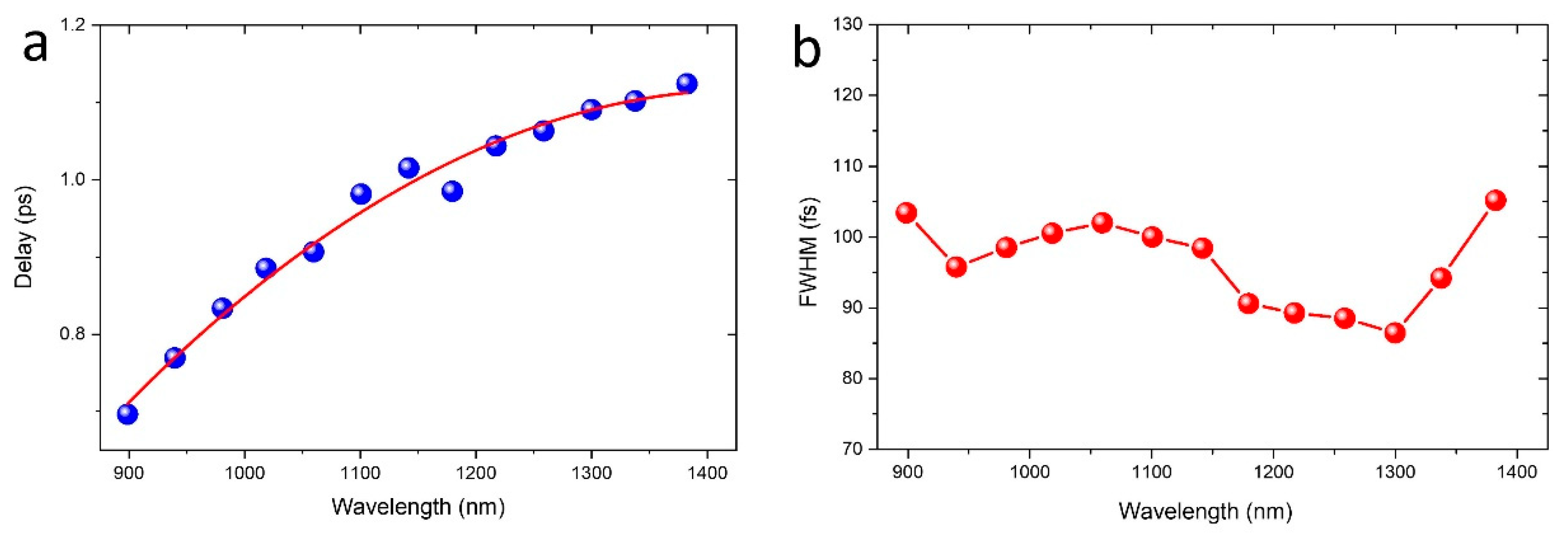
3.1. Chirp Correction and Time Resolution
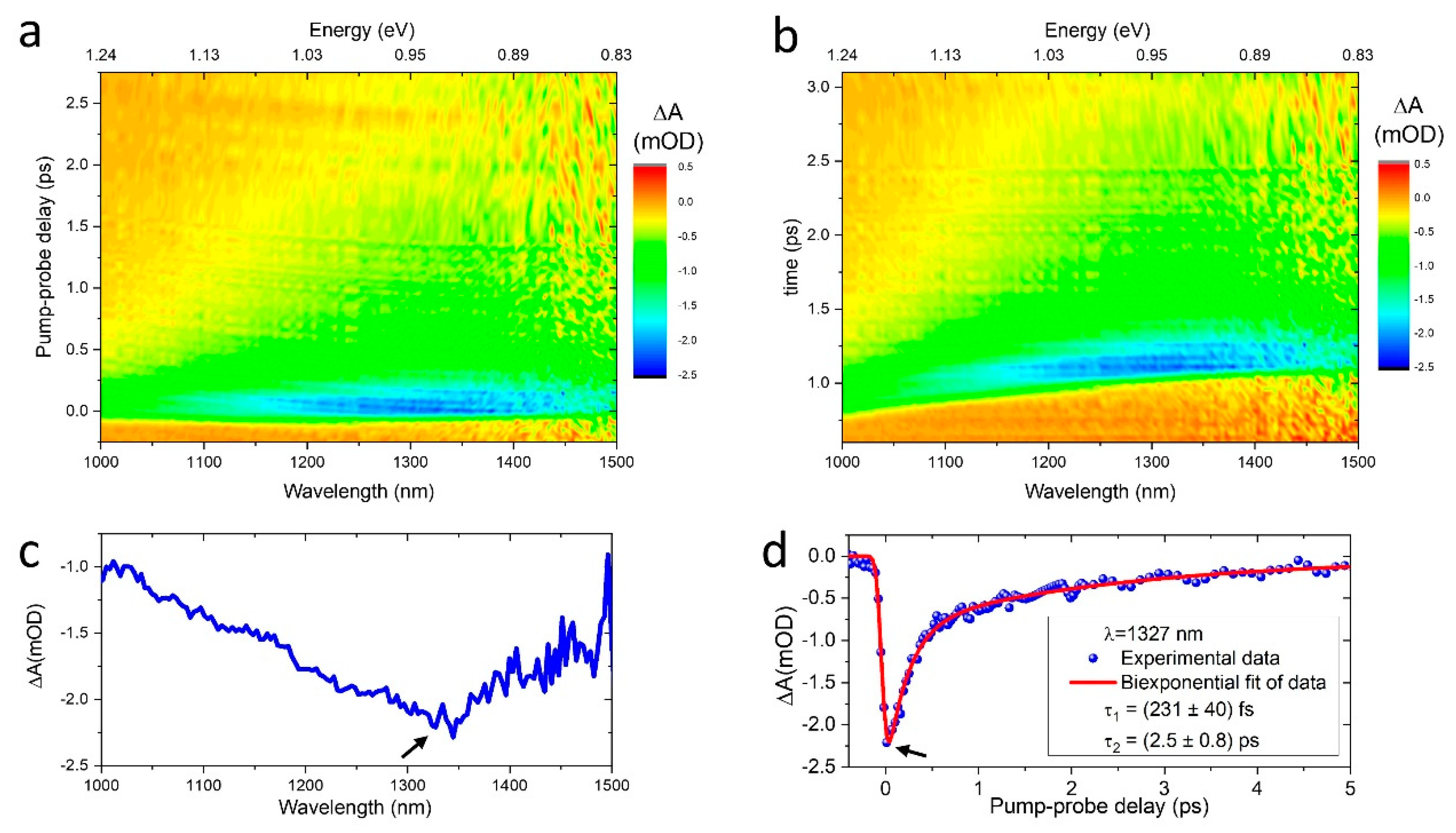
3.2. Ultrafast Carrier Dynamics in 2D Graphene
4. Discussion and Conclusions
Funding
Conflicts of Interest
References
- Kambhampati, P. Unraveling the Structure and Dynamics of Excitons in Semiconductor Quantum Dots. Acc. Chem. Res. 2011, 44, 1–13. [Google Scholar] [CrossRef] [PubMed]
- Sfeir, M.Y.; Qian, H.; Nobusada, K.; Jin, R. Ultrafast Relaxation Dynamics of Rod-Shaped 25-Atom Gold Nanoclusters. J. Phys. Chem. C 2011, 115, 6200–6207. [Google Scholar] [CrossRef]
- Gesuele, F.; Sfeir, M.Y.; Koh, W.-K.; Murray, C.B.; Heinz, T.F.; Wong, C.W. Ultrafast Supercontinuum Spectroscopy of Carrier Multiplication and Biexcitonic Effects in Excited States of PbS Quantum Dots. Nano Lett. 2012, 12, 2658–2664. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Berera, R.; van Grondelle, R.; Kennis, J.T.M. Ultrafast transient absorption spectroscopy: Principles and application to photosynthetic systems. Photosynth. Res. 2009, 101, 105–118. [Google Scholar] [CrossRef] [PubMed]
- Zewail, A.H. Femtochemistry: Atomic-Scale Dynamics of the Chemical Bond. J. Phys. Chem. A 2000, 104, 5660–5694. [Google Scholar] [CrossRef]
- Itri, F.; Monti, D.M.; Della Ventura, B.; Vinciguerra, R.; Chino, M.; Gesuele, F.; Lombardi, A.; Velotta, R.; Altucci, C.; Birolo, L.; et al. Femtosecond UV-laser pulses to unveil protein–protein interactions in living cells. Cell. Mol. Life Sci. 2016, 73, 637–648. [Google Scholar] [CrossRef] [PubMed]
- Auböck, G.; Consani, C.; van Mourik, F.; Chergui, M. Ultrabroadband femtosecond two-dimensional ultraviolet transient absorption. Opt. Lett. 2012, 37, 2337. [Google Scholar] [CrossRef] [PubMed]
- Alfano, R.R. The Supercontinuum Laser Source; Springer: New York, NY, USA, 2016; ISBN 978-1-4939-3324-2. [Google Scholar]
- Vulto, S.I.E.; Kennis, J.T.M.; Streltsov, A.M.; Amesz, J.; Aartsma, T.J. Energy Relaxation within the B850 Absorption Band of the Isolated Light-Harvesting Complex LH2 from Rhodopseudomonas acidophila at Low Temperature. J. Phys. Chem. B 1999, 103, 878–883. [Google Scholar] [CrossRef]
- Savikhin, S.; van Amerongen, H.; Kwa, S.L.; van Grondelle, R.; Struve, W.S. Low-temperature energy transfer in LHC-II trimers from the Chl a/b light-harvesting antenna of photosystem II. Biophys. J. 1994, 66, 1597–1603. [Google Scholar] [CrossRef][Green Version]
- Tkachenko, N.V. Optical Spectroscopy: Methods and Instrumentations; Elsevier: Amsterdam, The Netherlands, 2006; p. 307. ISBN 9780444521262. [Google Scholar]
- Auböck, G.; Consani, C.; Monni, R.; Cannizzo, A.; van Mourik, F.; Chergui, M. Femtosecond pumpsupercontinuum-probe setup with 20 kHz repetition rate. Rev. Sci. Instrum. 2012, 83, 2010–2015. [Google Scholar] [CrossRef]
- Moon, J.A. Optimization of signal-to-noise ratios in pump-probe spectroscopy. Rev. Sci. Instrum. 1993, 64, 1775–1778. [Google Scholar] [CrossRef]
- Dobryakov, A.L.; Kovalenko, S.A.; Weigel, A.; Pérez-Lustres, J.L.; Lange, J.; Müller, A.; Ernsting, N.P. Femtosecond pump/supercontinuum-probe spectroscopy: Optimized setup and signal analysis for single-shot spectral referencing. Rev. Sci. Instrum. 2010, 81, 113106. [Google Scholar] [CrossRef] [PubMed]
- Megerle, U.; Pugliesi, I.; Schriever, C.; Sailer, C.F.; Riedle, E. Sub-50 fs broadband absorption spectroscopy with tunable excitation: Putting the analysis of ultrafast molecular dynamics on solid ground. Appl. Phys. B Lasers Opt. 2009, 96, 215–231. [Google Scholar] [CrossRef]
- Klimov, V.I.; McBranch, D.W. Femtosecond high-sensitivity, chirp-free transient absorption spectroscopy using kilohertz lasers. Opt. Lett. 1998, 23, 277–279. [Google Scholar] [CrossRef] [PubMed]
- Lorenc, M.; Ziolek, M.; Naskrecki, R.; Karolczak, J.; Kubicki, J.; Maciejewski, A. Artifacts in femtosecond transient absorption spectroscopy. Appl. Phys. B Lasers Opt. 2002, 74, 19–27. [Google Scholar] [CrossRef]
- Chachisvilis, M.; Fidder, H.; Sundström, V. Electronic coherence in pseudo two-colour pump-probe spectroscopy. Chem. Phys. Lett. 1995. [Google Scholar] [CrossRef]
- Kang, I.; Smolorz, S.; Krauss, T.; Wise, F.; Aitken, B.; Borrelli, N. Time-domain observation of nuclear contributions to the optical nonlinearities of glasses. Phys. Rev. B Condens. Matter Mater. Phys. 1996, 54, R12641–R12644. [Google Scholar] [CrossRef]
- Valadan, M.; D’Ambrosio, D.; Gesuele, F.; Velotta, R.; Altucci, C. Temporal and spectral characterization of femtosecond deep-UV chirped pulses. Laser Phys. Lett. 2015, 12, 025302. [Google Scholar] [CrossRef]
- Hellwarth, R.; Cherlow, J.; Yang, T.T. Origin and frequency dependence of nonlinear optical susceptibilities of glasses. Phys. Rev. B 1975, 11, 964–967. [Google Scholar] [CrossRef]
- Kovalenko, S.A.; Dobryakov, A.L.; Ruthmann, J.; Ernsting, N.P. Femtosecond spectroscopy of condensed phases with chirped supercontinuum probing. Phys. Rev. A 1999, 59, 2369–2384. [Google Scholar] [CrossRef]
- Trebino, R. Frequency-Resolved Optical Gating: The Measurement of Ultrashort Laser Pulses; Springer US: Boston, MA, USA, 2000; ISBN 978-1-4613-5432-1. [Google Scholar]
- Rasmusson, M.; Tarnovsky, A.N.; Åkesson, E.; Sundström, V. On the use of two-photon absorption for determination of femtosecond pump-probe cross-correlation functions. Chem. Phys. Lett. 2001. [Google Scholar] [CrossRef]
- Dobryakov, A.L.; Pérez Lustres, J.L.; Kovalenko, S.A.; Ernsting, N.P. Femtosecond transient absorption with chirped pump and supercontinuum probe: Perturbative calculation of transient spectra with general lineshape functions, and simplifications. Chem. Phys. 2008, 347, 127–138. [Google Scholar] [CrossRef]
- Descrovi, E.; Ricciardi, C.; Giorgis, F.; Lérondel, G.; Blaize, S.; Pang, C.X.; Bachelot, R.; Royer, P.; Lettieri, S.; Gesuele, F.; et al. Field localization and enhanced Second-Harmonic Generation in silicon-based microcavities. Opt. Express 2007, 15, 4159. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Gesuele, F.; Lettieri, S.; Maddalena, P.; Liscidini, M.; Andreani, L.C.; Ricciardi, C.; Ballarini, V.; Giorgis, F. Band-edge and cavity second harmonic conversion in doubly resonant microcavity. J. Phys. B At. Mol. Opt. Phys. 2007, 40, 727–734. [Google Scholar] [CrossRef]
- Bonaccorso, F.; Colombo, L.; Yu, G.; Stoller, M.; Tozzini, V.; Ferrari, A.C.; Ruoff, R.S.; Pellegrini, V. 2D materials. Graphene, related two-dimensional crystals, and hybrid systems for energy conversion and storage. Science 2015, 347, 1246501. [Google Scholar] [CrossRef] [PubMed]
- Xia, F.; Wang, H.; Xiao, D.; Dubey, M.; Ramasubramaniam, A. Two-dimensional material nanophotonics. Nat. Photonics 2014, 8, 899–907. [Google Scholar] [CrossRef]
- Bhimanapati, G.R.; Lin, Z.; Meunier, V.; Jung, Y.; Cha, J.; Das, S.; Xiao, D.; Son, Y.; Strano, M.S.; Cooper, V.R.; et al. Recent Advances in Two-Dimensional Materials beyond Graphene. ACS Nano 2015, 9, 11509–11539. [Google Scholar] [CrossRef]
- Nivas, J.J.J.; Gesuele, F.; Allahyari, E.; Oscurato, S.L.; Fittipaldi, R.; Vecchione, A.; Bruzzese, R.; Amoruso, S. Effects of ambient air pressure on surface structures produced by ultrashort laser pulse irradiation. Opt. Lett. 2017, 42, 2710. [Google Scholar] [CrossRef] [PubMed]
- Basov, D.N.; Fogler, M.M.; Garcia de Abajo, F.J. Polaritons in van der Waals materials. Science 2016, 354, aag1992. [Google Scholar] [CrossRef]
- Tran, T.T.; Bray, K.; Ford, M.J.; Toth, M.; Aharonovich, I. Quantum emission from hexagonal boron nitride monolayers. Nat. Nanotechnol. 2016, 11, 37–41. [Google Scholar] [CrossRef]
- Geim, A.K.; Novoselov, K.S. The rise of graphene. Nat. Mater. 2007, 6, 183–191. [Google Scholar] [CrossRef] [PubMed]
- Ajayi, O.A.; Anderson, N.C.; Cotlet, M.; Petrone, N.; Gu, T.; Wolcott, A.; Gesuele, F.; Hone, J.; Owen, J.S.; Wong, C.W. Time-resolved energy transfer from single chloride-terminated nanocrystals to graphene. Appl. Phys. Lett. 2014, 104, 171101. [Google Scholar] [CrossRef]
- Geim, A.K.; Grigorieva, I.V. Van der Waals heterostructures. Nature 2013, 499, 419–425. [Google Scholar] [CrossRef]
- Attanzio, A.; Sapelkin, A.; Gesuele, F.; van der Zande, A.; Gillin, W.P.; Zheng, M.; Palma, M. Carbon Nanotube-Quantum Dot Nanohybrids: Coupling with Single-Particle Control in Aqueous Solution. Small 2017, 13, 1603042. [Google Scholar] [CrossRef]
- Hong, X.; Kim, J.; Shi, S.-F.; Zhang, Y.; Jin, C.; Sun, Y.; Tongay, S.; Wu, J.; Zhang, Y.; Wang, F. Ultrafast charge transfer in atomically thin MoS2/WS2 heterostructures. Nat. Nanotechnol. 2014, 9, 1–5. [Google Scholar] [CrossRef] [PubMed]
- Freeley, M.; Attanzio, A.; Cecconello, A.; Amoroso, G.; Clement, P.; Fernandez, G.; Gesuele, F.; Palma, M. Tuning the Coupling in Single-Molecule Heterostructures: DNA-Programmed and Reconfigurable Carbon Nanotube-Based Nanohybrids. Adv. Sci. 2018, 5, 1800596. [Google Scholar] [CrossRef]
- Butler, S.Z.; Hollen, S.M.; Cao, L.; Cui, Y.; Gupta, J.A.; Gutiérrez, H.R.; Heinz, T.F.; Hong, S.S.; Huang, J.; Ismach, A.F. Opportunities in Two-Dimensional Materials Beyond Graphene. ACS Nano 2013, 7, 2898–2926. [Google Scholar] [CrossRef]
- Frisenda, R.; Castellanos-Gomez, A. Robotic assembly of artificial nanomaterials. Nat. Nanotechnol. 2018, 13, 441–442. [Google Scholar] [CrossRef]
- Novoselov, K.S.; Jiang, D.; Schedin, F.; Booth, T.J.; Khotkevich, V.V.; Morozov, S.V.; Geim, A.K. Two-dimensional atomic crystals. Proc. Natl. Acad. Sci. USA 2005, 102, 10451–10453. [Google Scholar] [CrossRef]
- Paton, K.R.; Varrla, E.; Backes, C.; Smith, R.J.; Khan, U.; O’Neill, A.; Boland, C.; Lotya, M.; Istrate, O.M.; King, P.; et al. Scalable production of large quantities of defect-free few-layer graphene by shear exfoliation in liquids. Nat. Mater. 2014, 13, 624–630. [Google Scholar] [CrossRef]
- Kaur, J.; Gravagnuolo, A.M.; Maddalena, P.; Altucci, C.; Giardina, P.; Gesuele, F. Green synthesis of luminescent and defect-free bio-nanosheets of MoS2: Interfacing two dimensional crystals with hydrophobins. RSC Adv. 2017, 7, 22400–22408. [Google Scholar] [CrossRef]
- Li, X.; Cai, W.; An, J.; Kim, S.; Nah, J.; Yang, D.; Piner, R.; Velamakanni, A.; Jung, I.; Tutuc, E.; et al. Large-area synthesis of high-quality and uniform graphene films on copper foils. Science 2009, 324, 1312–1314. [Google Scholar] [CrossRef] [PubMed]
- Li, X.; Magnuson, C.W.; Venugopal, A.; An, J.; Suk, J.W.; Han, B.; Borysiak, M.; Cai, W.; Velamakanni, A.; Zhu, Y.; et al. Graphene Films with Large Domain Size by a Two-Step Chemical Vapor Deposition Process. Nano Lett. 2010, 10, 4328–4334. [Google Scholar] [CrossRef] [PubMed]
- Lettieri, S.; Pallotti, D.K.; Gesuele, F.; Maddalena, P. Unconventional ratiometric-enhanced optical sensing of oxygen by mixed-phase TiO2. Appl. Phys. Lett. 2016, 109, 031905. [Google Scholar] [CrossRef]
- Pallotti, D.K.; Passoni, L.; Gesuele, F.; Maddalena, P.; Di Fonzo, F.; Lettieri, S. Giant O2-Induced Photoluminescence Modulation in Hierarchical Titanium Dioxide Nanostructures. ACS Sens. 2017, 2, 61–68. [Google Scholar] [CrossRef] [PubMed]
- Coscia, U.; Ambrosone, G.; Gesuele, F.; Grossi, V.; Parisi, V.; Schutzmann, S.; Basa, D.K. Laser annealing study of PECVD deposited hydrogenated amorphous silicon carbon alloy films. Appl. Surf. Sci. 2007, 254, 984–988. [Google Scholar] [CrossRef]
- Gesuele, F.; Nivas, J.J.J.; Fittipaldi, R.; Altucci, C.; Bruzzese, R.; Maddalena, P.; Amoruso, S. Analysis of nascent silicon phase-change gratings induced by femtosecond laser irradiation in vacuum. Sci. Rep. 2018, 8, 12498. [Google Scholar] [CrossRef] [PubMed]
- Ferrari, A.C.; Meyer, J.C.; Scardaci, V.; Casiraghi, C.; Lazzeri, M.; Mauri, F.; Piscanec, S.; Jiang, D.; Novoselov, K.S.; Roth, S.; et al. Raman Spectrum of Graphene and Graphene Layers. Phys. Rev. Lett. 2006, 97, 187401. [Google Scholar] [CrossRef]
- Ferrari, A.; Basko, D. Raman spectroscopy as a versatile tool for studying the properties of graphene. Nat. Nanotechnol. 2013, 8, 235–246. [Google Scholar] [CrossRef]
- Gesuele, F.; Pang, C.X.; Leblond, G.; Blaize, S.; Bruyant, A.; Royer, P.; Deturche, R.; Maddalena, P.; Lerondel, G. Towards routine near-field optical characterization of silicon-based photonic structures: An optical mode analysis in integrated waveguides by transmission AFM-based SNOM. Phys. E Low Dimens. Syst. Nanostruct. 2009, 41, 1130–1134. [Google Scholar] [CrossRef]
- Blaize, S.; Gesuele, F.; Stefanon, I.; Bruyant, A.; Lérondel, G.; Royer, P.; Martin, B.; Morand, A.; Benech, P.; Fedeli, J.-M. Real-space observation of spectral degeneracy breaking in a waveguide-coupled disk microresonator. Opt. Lett. 2010, 35, 3168. [Google Scholar] [CrossRef] [PubMed]
- Dawlaty, J.M.; Shivaraman, S.; Chandrashekhar, M.; Rana, F.; Spencer, M.G. Measurement of ultrafast carrier dynamics in epitaxial graphene. Appl. Phys. Lett. 2008, 92, 1–3. [Google Scholar] [CrossRef]
- Obraztsov, P.A.; Rybin, M.G.; Tyurnina, A.V.; Garnov, S.V.; Obraztsova, E.D.; Obraztsov, A.N.; Svirko, Y.P. Broadband light-induced absorbance change in multilayer graphene. Nano Lett. 2011, 11, 1540–1545. [Google Scholar] [CrossRef] [PubMed]
- Winnerl, S.; Mittendorff, M.; König-Otto, J.C.; Schneider, H.; Helm, M.; Winzer, T.; Knorr, A.; Malic, E. Ultrafast Processes in Graphene: From Fundamental Manybody Interactions to Device Applications. Ann. Phys. 2017, 529, 1–12. [Google Scholar] [CrossRef]
- Malic, E.; Winzer, T.; Bobkin, E.; Knorr, A. Microscopic theory of absorption and ultrafast many-particle kinetics in graphene. Phys. Rev. B Condens. Matter Mater. Phys. 2011, 84. [Google Scholar] [CrossRef]
- König-Otto, J.C.; Mittendorff, M.; Winzer, T.; Kadi, F.; Malic, E.; Knorr, A.; Berger, C.; De Heer, W.A.; Pashkin, A.; Schneider, H.; et al. Slow Noncollinear Coulomb Scattering in the Vicinity of the Dirac Point in Graphene. Phys. Rev. Lett. 2016, 117, 1–6. [Google Scholar] [CrossRef] [PubMed]
- Mittendorff, M.; Winzer, T.; Malic, E.; Knorr, A.; Berger, C.; De Heer, W.A.; Schneider, H.; Helm, M.; Winnerl, S. Anisotropy of excitation and relaxation of photogenerated charge carriers in graphene. Nano Lett. 2014, 14, 1504–1507. [Google Scholar] [CrossRef][Green Version]
- George, P.A.; Strait, J.; Dawlaty, J.; Shivaraman, S.; Chandrashekhar, M.; Rana, F.; Spencer, M.G. Ultrafast Optical-Pump Terahertz-Probe Spectroscopy of the Carrier Relaxation and Recombination Dynamics in Epitaxial Graphene. Nano Lett. 2008, 8, 4248–4251. [Google Scholar] [CrossRef]
- Sun, D.; Wu, Z.K.; Divin, C.; Li, X.; Berger, C.; De Heer, W.A.; First, P.N.; Norris, T.B. Ultrafast relaxation of excited dirac fermions in epitaxial graphene using optical differential transmission spectroscopy. Phys. Rev. Lett. 2008, 101, 1–4. [Google Scholar] [CrossRef]
- Brida, D.; Tomadin, A.; Manzoni, C.; Kim, Y.J.; Lombardo, A.; Milana, S.; Nair, R.R.; Novoselov, K.S.; Ferrari, A.C.; Cerullo, G.; et al. Ultrafast collinear scattering and carrier multiplication in graphene. Nat. Commun. 2013, 4, 1987. [Google Scholar] [CrossRef]
- Hwang, E.H.; Hu, B.Y.K.; Das Sarma, S. Inelastic carrier lifetime in graphene. Phys. Rev. B Condens. Matter Mater. Phys. 2007, 76, 1–6. [Google Scholar] [CrossRef]
- Polini, M.; Asgari, R.; Borghi, G.; Barlas, Y.; Pereg-Barnea, T.; MacDonald, A.H. Plasmons and the spectral function of graphene. Phys. Rev. B Condens. Matter Mater. Phys. 2008, 77, 3–6. [Google Scholar] [CrossRef]
- Chirayath, V.A.; Callewaert, V.; Fairchild, A.J.; Chrysler, M.D.; Gladen, R.W.; McDonald, A.D.; Imam, S.K.; Shastry, K.; Koymen, A.R.; Saniz, R.; et al. Auger electron emission initiated by the creation of valence-band holes in graphene by positron annihilation. Nat. Commun. 2017, 8, 1–7. [Google Scholar] [CrossRef] [PubMed]
- Winzer, T.; Malić, E. Impact of Auger processes on carrier dynamics in graphene. Phys. Rev. B Condens. Matter Mater. Phys. 2012, 85, 1–5. [Google Scholar] [CrossRef]
- Winzer, T.; Knorr, A.; Malic, E. Carrier multiplication in graphene. Nano Lett. 2010, 10, 4839–4843. [Google Scholar] [CrossRef] [PubMed]
© 2019 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gesuele, F. Ultrafast Hyperspectral Transient Absorption Spectroscopy: Application to Single Layer Graphene. Photonics 2019, 6, 95. https://doi.org/10.3390/photonics6030095
Gesuele F. Ultrafast Hyperspectral Transient Absorption Spectroscopy: Application to Single Layer Graphene. Photonics. 2019; 6(3):95. https://doi.org/10.3390/photonics6030095
Chicago/Turabian StyleGesuele, Felice. 2019. "Ultrafast Hyperspectral Transient Absorption Spectroscopy: Application to Single Layer Graphene" Photonics 6, no. 3: 95. https://doi.org/10.3390/photonics6030095
APA StyleGesuele, F. (2019). Ultrafast Hyperspectral Transient Absorption Spectroscopy: Application to Single Layer Graphene. Photonics, 6(3), 95. https://doi.org/10.3390/photonics6030095




