Generation of Coherent and Spatially Squeezed States of an Electromagnetic Beam in a Planar Inhomogeneous Dielectric Waveguide

Abstract

We use slow-varying amplitude approximation (SVA) for the wave equation to study both analytically and numerically propagation of an electromagnetic beam in the waveguide structure with parabolic susceptibility spatial dependence. Such a structure is similar to the harmonic oscillator in quantum mechanics. We analyze this structure as a single mode guide and introduce the notion of number of “photons” in the mode. In particular, we pay special attention to the possibility of effective build-up of the coherent and spatially squeezed vacuum states of the mode that can be of interest for a number of practical applications. The way to provide these types of mode excitation is suggested. Several applications for controlling the mode composition of an electromagnetic wave in the parabolic index-gradient waveguide for various frequency ranges are considered.

1. Introduction

To date, a number of hybrid optoelectronic computing devices require transmitting of electromagnetic wave “packets” along waveguide structures from a nanoscale “source” to a nanoscale “receiver” [1,2]. In the areas of integrated photonics and nano-electronics, quite complex multidimensional structures on a chip are available [3,4]. The searches for opportunities to control such an electromagnetic field that carries information between, for example, the chosen quantum bit and the chosen single-photon detector are of particular interest.

In this paper, we demonstrate how the well-known analogy between the propagation of light beams in wave optics and the movement of micro-particles in quantum mechanics can be applied in optimization procedures for elements and systems of optoelectronic computing devices. We especially want to draw attention here to the problem of changing the direction of the Poynting vector of an electromagnetic beam (the “light rotation problem”) at relatively small distances and without significant losses [5]. The spatially varying dielectric constant (susceptibility) in the required waveguide structures can be represented in the framework of our central approach with the spatial distribution of the potential energy for a quantum particle [6,7,8].

A number of operations in photonic and optoelectronic circuits require the ability to “collect” the energy of the electromagnetic field in certain areas of the system. The simplest illustrative examples are the graded-index fibers with a close to parabolic index profile. This form of spatial inhomogeneity for dielectric constants leads to the fact that a Gaussian input beam (somewhat displaced against the center of the fiber core) will oscillate without fully reaching the edges of the core region. This behavior, which allows us to reduce the energy dissipation and distortion of the wave packet shape, is similar to the oscillations of a coherent wave packet in a quantum harmonic oscillator. Today, it is possible not only to put into practice any necessary susceptibility profile due to doping of the dielectric, but also to realize its local control (e.g., by applying voltages to selected electrodes) [9].

The ability to manage the spatial distribution of the energy density at a higher level will increase the efficiency and selectivity of interactions between the elements and parts of a large integrated circuit. We have already demonstrated the methods to control the mode composition of a classical light in a planar graded index waveguide with nanostructured core. The proposed description was based on the analogy with quantum Rabi-type transitions in a rectangular potential well. We have already applied the analysis of the “quantum” behavior of classical electromagnetic waves for the simplest two-mode waveguide and Y-splitter with planar geometry—the basis for optical computing systems [10,11].

In this article, we will move from a consideration of a waveguide with a rectangular susceptibility profile (the case of the extremely non-equidistant spectrum of the Hamiltonian eigenvalues) [10,11] to analysis of the structure with a parabolic profile of the susceptibility $\chi \left(x\right)$. Such a waveguide structure is schematically shown in Figure 1a. The structure with such a susceptibility profile is similar to the quantum harmonic oscillator that is characterized by the equidistant spectrum of eigenstates. As a result, temporal evolution of the quantum state in parabolic potential is rather specific. Among nonstationary states, first of all coherent and squeezed states are of interest. We will see further that such states can be build-up for the classical electromagnetic field in the waveguide with susceptibility modulated along the propagation axis $z$ (see Figure 1b). Special attention will be paid to the studies of the “classical decoherence” of such states in a real waveguide structure.

2. Model and Methods

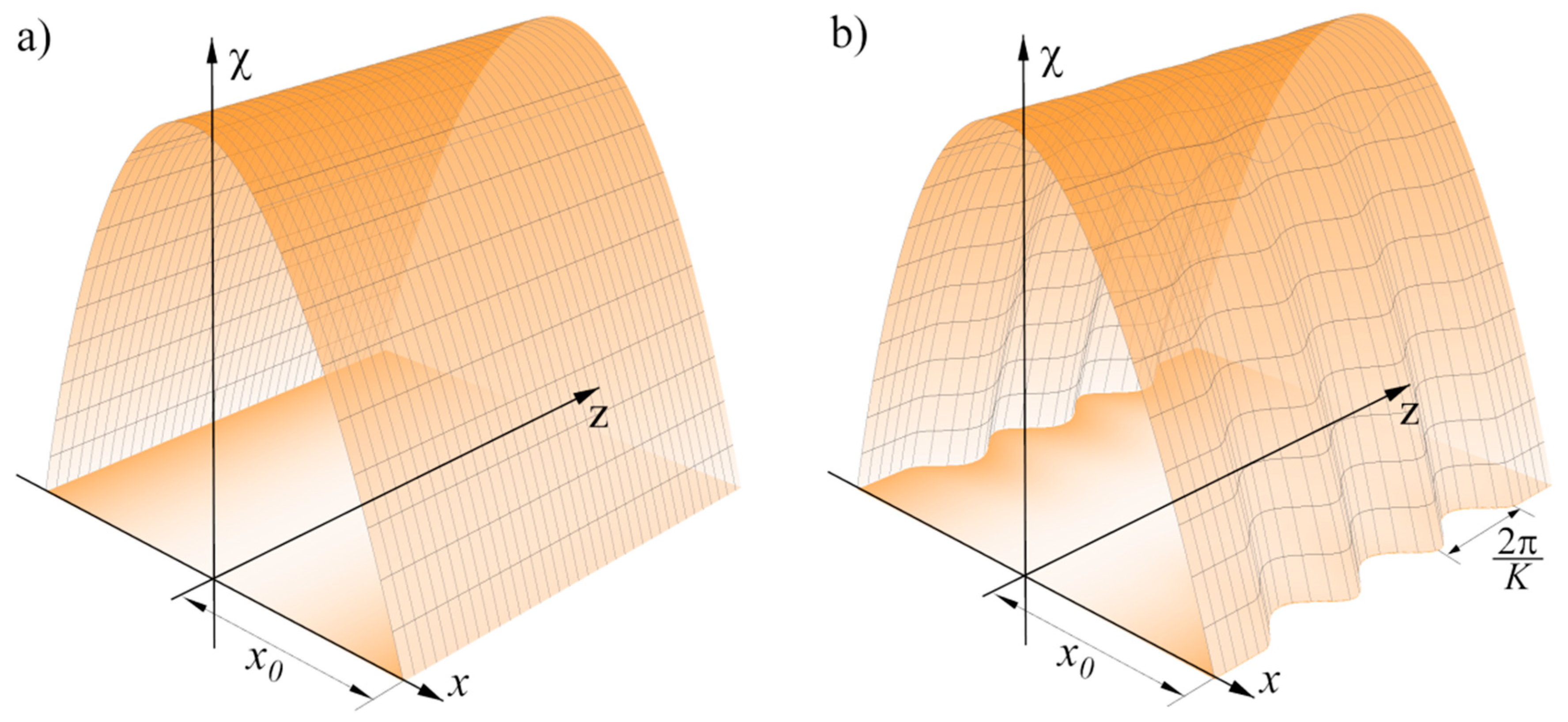
2.1. Optical–Mechanical Analogy and Transverse Spatial Modes of the Beam

It is known that light propagation in modern waveguide structures can be considered often in the frames of slow-varying amplitude (SVA) approximation [12,13], when electric field strength in the wave field of frequency $\omega$ is presented in the form $\mathit{E}\left(\mathit{r},t\right)={\mathit{E}}_0\left(\mathit{r}\right)exp(i\left(kz-\omega t\right))$ with $\left|\nabla E_0\right|<<k{E}_0$ and $k=\omega /\mathrm{c}$, c is the speed of light. For the linearly polarized beam propagating in z-direction (see Figure 1) in a spatially inhomogeneous medium characterized by the susceptibility $\chi \left(\mathit{r}\right)$ ($\left|\nabla \chi \right|<<k\chi$), or permittivity $\epsilon \left(\mathit{r}\right)=1+4\pi \chi \left(\mathit{r}\right)$ one can write the equation for the amplitude ${\mathit{E}}_0\left(\mathit{r}\right)$:

$$ik\frac{\partial {\mathit{E}}_0\left({\mathit{r}}_{\perp },z\right)}{\partial z}=-\frac{1}{2}{\nabla }_{\perp }^2{\mathit{E}}_0\left({\mathit{r}}_{\perp },z\right)+\eta \left({\mathit{r}}_{\perp },z\right){\mathit{E}}_0.$$

(1)

Here ${\mathit{r}}_{\perp }=\left\{x,y\right\}$ are the coordinates perpendicular to the propagation direction, ${\nabla }_{\perp }^2$ is the Laplace operator over these coordinates and $\eta \left({\mathit{r}}_{\perp },z\right)=-2\pi k_{}^2\chi \left({\mathit{r}}_{\perp },z\right)$. Equation (1) is known as the Schroedinger equation in optics and is mathematically identical to the equation for the quantum particle motion in two-dimensional space ${\mathit{r}}_{\perp }=\left\{x,y\right\}$ with variation in time potential field $V\left({\mathit{r}}_{\perp },t\right)$:

$$i\hslash \frac{\partial \psi }{\partial t}=-\frac{{\hslash }^2}{2m}{\nabla }_{\perp }^2\psi \left({\mathit{r}}_{\perp },t\right)+V\left({\mathit{r}}_{\perp },t\right)\psi \left({\mathit{r}}_{\perp },t\right).$$

(2)

The mathematical similarity of Equations (1) and (2) is the basis of the optical–mechanical analogy and can be applied for analysis of different problems both in quantum theory and wave optics. We can see from Equations (1) and (2) that the coordinate z along which the light beam propagates is analogous to the time in quantum theory, while the function $\eta \left({\mathit{r}}_{\perp },z\right)$ determined by the susceptibility of the media has the meaning of an inverted potential $-V\left({\mathit{r}}_{\perp },t\right)$ varying in time. In particular, if the susceptibility of the medium depends on the propagating electric field strength, Equation (1) becomes nonlinear one. Such a nonlinear Schroedinger equation is widely used in nonlinear optics [14,15], for example, to analyze the filamentation phenomenon [16] or multiwave mixing processes in a plasma channel formed by high-intensity laser pulses [17]. The analogy between optics and quantum mechanics becomes even more complete if it is possible to study the propagation of the linear polarized beam in inhomogeneous media, when the electric field can be characterized by the single spatial component [14].

In this paper similar to [7,8,10,11] we restricted ourselves to the situation where the linearly polarized beam propagates along the planar waveguide structure with $\eta =\eta \left(x\right)$ with the electric field vector oriented perpendicular both $x$ and $z$ axes. The spatial periodic modulation of the waveguide structure along the z-direction can cause transitions between transverse field modes with different distributions of the field energy in space [6,7,8]. For example, the Rabi-type oscillations between two lowest transverse field modes in the waveguide with a rectangular profile were analyzed in [10,11].

For the given waveguide profile of susceptibility $\chi \left(x\right)$ the beam structure in the waveguide can be presented in the form

$$E_0\left(x,z\right)={{\displaystyle \sum }}_n{C}_n{R}_n\left(x\right)exp\left(-i\frac{{\lambda }_n^2}{2k}z\right),$$

(3)

where $R_n\left(x\right)$ and ${\lambda }_n$ (cm⁻¹) obey the eigenvalue problem:

$$\left(\frac{d^2}{d{x}^2}+4\pi k^2\chi \left(x\right)+{\lambda }_n^2\right)R_n\left(x\right)=0.$$

(4)

Its solution gives rise to a number of transverse modes of the beam propagating in z-direction. We use the following normalization condition for eigenfunctions $R_n\left(x\right)$:

$${\displaystyle \int }{\left|R_n\left(x\right)\right|}^{2}dx=\frac{E_{tot}^2}{8\pi }a.$$

(5)

Here $E_{tot}$ is the electric field strength in the mode and $a$ is the normalization length. All eigenfunctions $R_n\left(x\right)$ are orthogonal to each other and the decomposition coefficients $C_n$ have the sense of the amplitude of population probability for the n-th transverse waveguide mode. General solution (3) gives the spatial distribution of the electric field during the propagation along the z-axis.

In this paper we analyzed the waveguide with the parabolic profile of the susceptibility $\chi \left(x\right)={\chi }_0\left(x\right)={\rm X}-\alpha {(x/x_0)}^2$ (${\rm X}\ge \alpha >0$, x₀ is the characteristic transverse scale). As it was mentioned above, such a structure provides the possibility of beam focusing to the near $x=0$ region and is similar to the harmonic oscillator potential in quantum theory. In this case the eigenfunctions of the transverse modes are expressed through the Hermitian polynomials $H_n\left(x\right)$:

$$R_n\left(x\right)=\sqrt{\frac{E_{tot}^2}{8\pi }}{N}_n{H}_n\left(x/a\right)exp(-x^2/\left(2a^2\right)),$$

(6)

where $N_n=1/\sqrt{2^{n}n!\sqrt{\pi }}$ is the normalization constant and $a^2=x_0/\sqrt{4\pi k^2\alpha }$. As for the spectrum of the transverse states, it is given by the expression ${\lambda }_n^2=2a^{-2}(n+1/2)-4\pi {\rm X}{k}^2, n=0,\hspace{0.17em}1,\hspace{0.17em}2,\dots$ The specific feature of this spectrum is its equidistant character, i.e., the distance between any two neighboring states is the same. This fact allows us to use the quantum field terminology [18] to state that we have only the transverse mode of the field in our waveguide structure, but this mode has different levels of excitation given by the quantum number $n=0,\hspace{0.17em}1,\hspace{0.17em}2,\dots$. Moreover, the number n can be considered as an amount of “photons” in only the transverse mode. The spatial distribution of the field for the definite number of “photons” is given by Equation (6).

If for the initial instant of time $C_0=1$ and other coefficients are equal zero, we have the beam with the Gaussian profile,

$$R_0\left(x\right)=\sqrt{\frac{E_{tot}^2}{8\pi }}\frac{1}{\sqrt[4]{\pi }}exp(-x^2/\left(2a^2\right)),$$

(7)

propagating along the waveguide. Such a beam represents the ground state of the transverse mode. In general, the spatial distribution and evolution of the beam in the waveguide with a parabolic profile of susceptibility can be very different. Among others, two of them are of the most interest, namely, the coherent spatial state and the spatially squeezed state of the transverse mode.

2.2. Coherent Spatial States of the Beam

We started the discussion from a coherent state [19,20], suggesting the presence of a Poisson distribution over the squared coefficients ${\left|C_n\right|}^2$:

$$w_n={\left|C_n\right|}^2=\frac{{\left|\zeta \right|}^{2n}}{n!}exp(-{\left|\zeta \right|}^2),$$

(8)

where $\zeta$ is the complex number, and the value $\langle n\rangle ={\left|\zeta \right|}^2$ his the “average amount of quanta” in the coherent state. If $\zeta =0$ the coherent state is turning to the ground (“vacuum”) state of the oscillator. For the case $\langle n\rangle >0$ and real $\zeta$ one obtains the transverse spatial oscillations of the beam along the direction of propagation (see Figure 2):

$${\left|E_0\left(x,z\right)\right|}^2~E_{tot}^{2}exp\left(-\frac{\left(x-x_{amp}cos(z/k{a}^2\right){)}^2}{a^2}\right).$$

The amplitude of these oscillations $x_{amp}$ is proportional to $\sqrt{\langle n\rangle }$: $x_{amp}=a\sqrt{\langle n\rangle }$, while the spatial width of the beam is $~a$. Hence if $\langle n\rangle >>1$ the amplitude is much greater than the width and these oscillations of the beam are similar to the classical oscillatory motion.

2.3. Spatially Squeezed Vacuum State of the Beam

Another state of the quantum oscillator which is of importance for practical applications is the spatially squeezed vacuum state [21,22,23]. This state can also be expressed in a Gaussian form, but with a width different from Equation (7):

$$R_{sq}\left(x\right)=\sqrt{\frac{E_{tot}^2}{8\pi }}\frac{1}{\sqrt[4]{\pi {\beta }^2}}exp(-x^2/\left(2a^2{\beta }^2\right)),$$

(9)

where $\beta$ is the squeezing parameter. Such a state is essentially nonclassical as the average over the quantum state electric field strength is equal to zero for any instant of the $z$-coordinate, while “the average amount of quanta” in the squeezed vacuum state is determined by the expression

$$\langle n\rangle =\frac{1}{4}{\left(\beta -1/\beta \right)}^2$$

(10)

and can be large if $\beta >>1$ or $\beta <<1$. Nevertheless, this state is characterized by the oscillations of the width of the beam while its shape is still Gaussian (Figure 3). As for the decomposition Equation (3), only even states have nonzero populations, while for all odd coefficients $C_{2n+1}=0$.

Squeezed states of light are widely investigated nowadays in quantum optics (see, for example, [24,25,26,27] and a lot of references in these papers) where squeezing is analyzed in the frames of secondary quantization of the electromagnetic field mode [18]. Hereafter we mean squeezing in the transverse classical light beam mode in the ordinary (spatial) space.

3. Results

We studied the possibility of exciting the coherent and spatially squeezed vacuum states of the transverse beam mode. Such control was possible if dielectric waveguide parameters depended also on coordinates along the propagation direction [10]. It was supposed that the waveguide susceptibility was slightly modulated over the z-direction. In this case presented the susceptibility of the structure $\chi \left(x,z\right)$ in the form

$$\chi \left(x,z\right)={\chi }_0\left(x\right)+{\chi }_1\left(x,z\right),$$

(11)

where the first term in the right part determined the parabolic dependence of the susceptibility while the second one provided the spatial modulation of the susceptibility of the structure. We supposed that

$${\chi }_1\left(x,z\right)=\delta {\chi }_1\left(x\right)cos(Kz),$$

(12)

with $\left|\delta {\chi }_1\left(x\right)\right|<<\left|{\chi }_0\left(x\right)\right|$ and $K$ was the wave number that determined the spatial period over the z-direction of the structure $z_0=2\pi /K$. Then the additional term in Equation (11) was considered as a perturbation that caused the transitions between transverse states of the beam. Really, by substituting general decomposition Equation (3) to Equation (1) and taking into account that $R_n\left(x\right)$ is the solution of the eigenvalue problem Equation (4), one obtained the following set of equations for the population of the resonator transverse states

$$id{C}_n/dz={{\displaystyle \sum }}_m{C}_m\left(z\right)M_{nm}exp\left(\frac{i}{2k}\left({\lambda }_n^2-{\lambda }_m^2\right)z\right)cos K z.$$

(13)

We supposed that initial beam structure corresponded to the ground oscillator state. Hence, $C_0\left(z=0\right)=1$ and $C_{m\ne 0}\left(z=0\right)=0$ were the initial conditions. Here

$$M_{nm}=\frac{8\pi }{E_{tot}^{2}a}\cdot 2\pi k{\displaystyle \int }{R}_n^{*}\left(x\right)\delta {\chi }_1\left(x\right)R_m(x)dx.$$

(14)

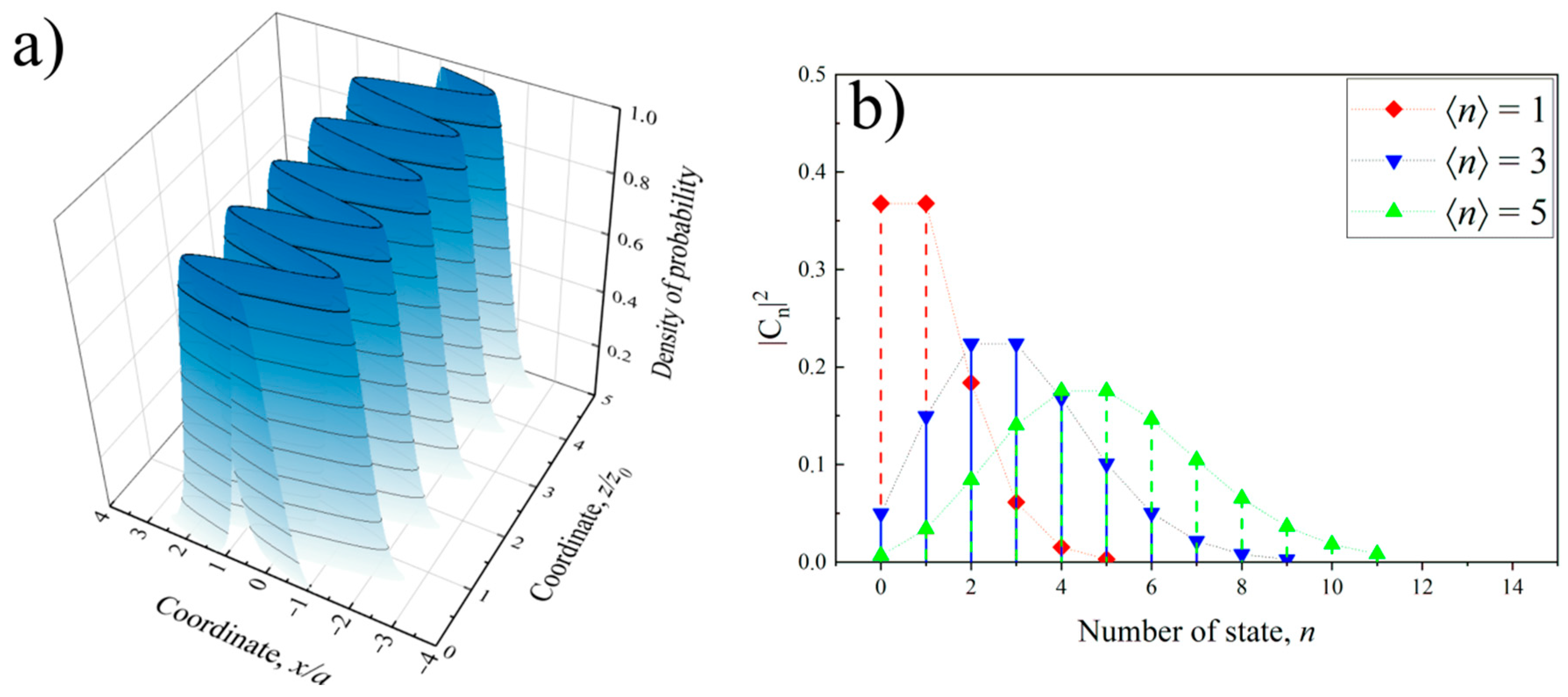
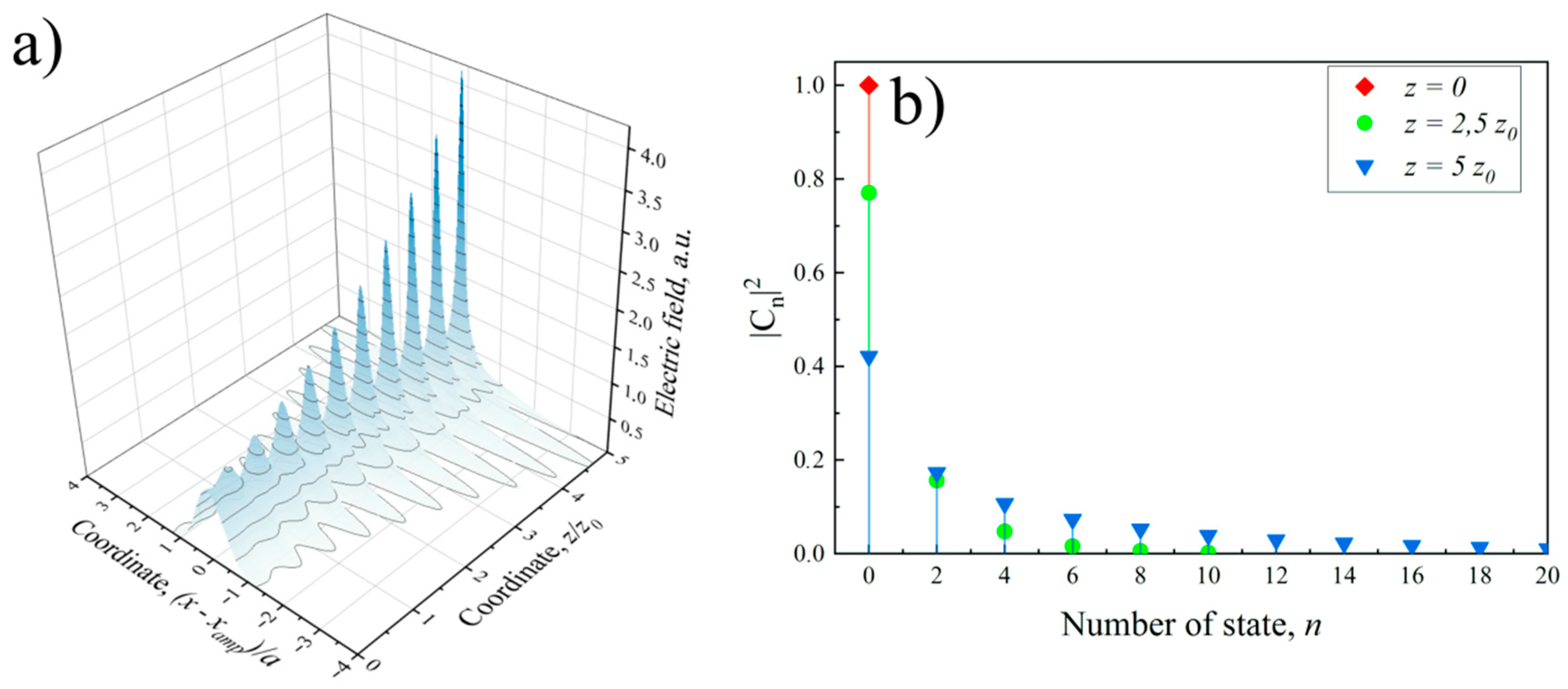
3.1. Excitation of the Transverse Coherent Spatial State of the Beam

We supposed that $\delta {\chi }_1\left(x\right)=\gamma x/x_0$. Then inequation (14) only integrals with $m=n\pm 1$ have nonzero values ($M_{n+1,n}=\frac{2\pi k\gamma a{z}_0}{x_0}\sqrt{\left(n+1\right)/2}={\Theta }_{coh}\sqrt{\left(n+1\right)/2}$), and the set of Equation (13) could be written in the form

$$i{z}_{0}d{C}_n/dz={\Theta }_{coh}\left(C_{n+1}\sqrt{\left(n+1\right)/2}exp\left(-i\frac{z}{k{a}^2}\right)+C_{n-1}\sqrt{n/2}exp\left(i\frac{z}{k{a}^2}\right)\right)cos K z.$$

(15)

If $K=1/k{a}^2$ the resonant term appeared to exist in Equation (15). Then, neglecting the oscillating terms, we rewrote the set of Equation (15) in the form:

$$i{z}_{0}d{C}_n/dz={\Theta }_{coh}\times 0.5\times \left(C_{n+1}\sqrt{\left(n+1\right)/2}+C_{n-1}\sqrt{n/2}\right).$$

(16)

Assuming that initially the system was in the vacuum state ($C_0\left(t=0\right)=1,C_{n\ne 0}\left(t=0\right)=0$) the set of equations had the analytical solution in the form of a Poisson distribution Equation (8) with an “average amount of quanta” $\langle n\rangle ={(\pi k\gamma az/x_0)}^2$. In our situation $\langle n\rangle$ increased along the $z$-coordinate that corresponded to the growing of the amplitude of the transverse oscillation of the beam in the waveguide. The obtained beam oscillations are presented in Figure 4.

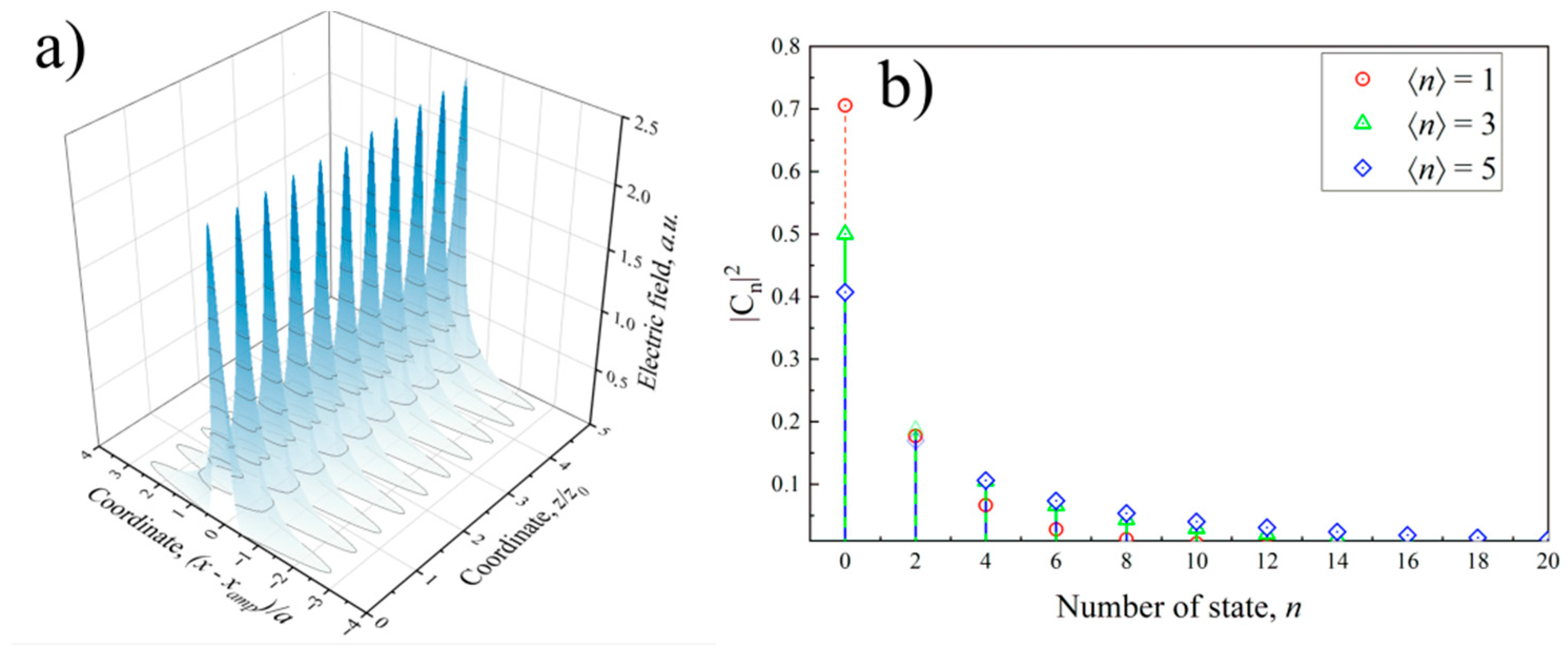
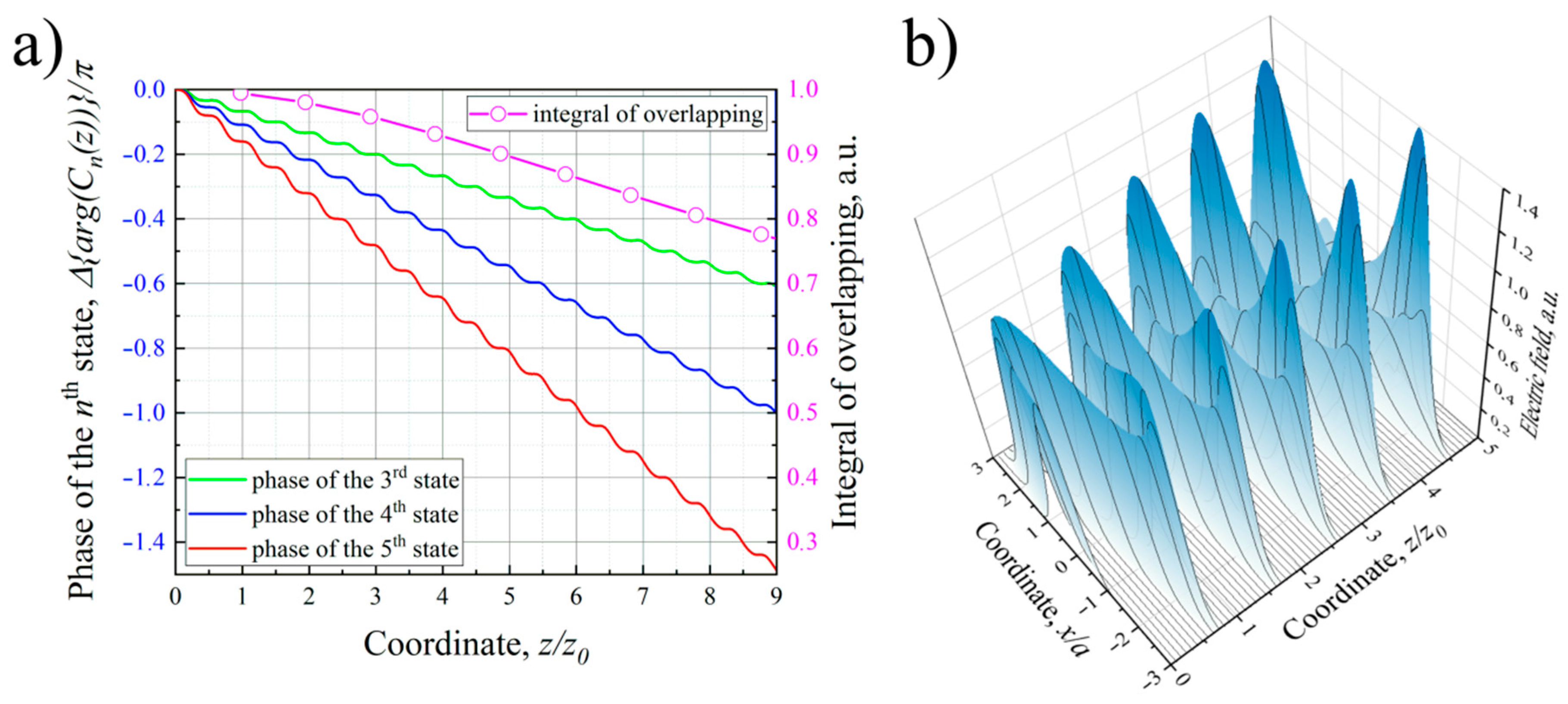
3.2. Excitation of the Spatially Squeezed Vacuum State of the Beam

We excited the spatial squeezed vacuum state of beam propagation in the waveguide. In this case the waveguide was prepared with spatial modulation of the susceptibility other than Equations (11) and (12):

$$\chi \left(x,z\right)={\chi }_0\left(x\right)+{\chi }_2\left(x,z\right)$$

(17)

with ${\chi }_2\left(x,z\right)=\delta {\chi }_2\left(x\right)cos(Kz)$ and $\delta {\chi }_2\left(x\right)={\gamma }_2{(x/x_0)}^2$. In this case from Equation (13) one obtained

$$i{z}_{0}d{C}_n/dz=\left(C_{n+2}{M}_{n+2,n}exp\left(-i\frac{2z}{k{a}^2}\right)+C_n{M}_{nn}+C_{n-2}{M}_{n,n-2}exp\left(i\frac{2z}{k{a}^2}\right)\right)cosKz.$$

(18)

Here $M_{n+2,n}=\frac{2\pi k{\gamma }_2{z}_0}{x_0^2}{a}^2\sqrt{\left(n+2\right)\left(n+1\right)}/2={\Theta }_{sq}\sqrt{\left(n+2\right)\left(n+1\right)}/2$ and $M_{n,n}={\Theta }_2\left(n+1/2\right)$. In this case resonant excitation of transverse beam oscillation was possible if $K$ was twice greater than in Section 3.1, and equal to $K=2/\left(k{a}^2\right)$. Then the set of Equation (18) were simplified and rewritten in the form

$$i{z}_{0}d{C}_n/dz=\frac{{\Theta }_{sq}}{4}\left(\sqrt{\left(n+2\right)\left(n+1\right)}{C}_{n+2}+\sqrt{n\left(n-1\right)}{C}_{n-2}\right).$$

(19)

The numerical solution of the set Equation (19) for the same initial conditions is presented in Figure 5 and visually demonstrates the squeezing: only even states ($C_{2n},\hspace{0.17em}n=1,2,3,\dots$) were populated along the z-direction beam propagation. As a result, the average position of the beam was equal to zero, while its spatial width oscillated along coordinate $z$ with increasing amplitude (see Figure 5). Detailed analysis of the beam structure demonstrated that the beam nevertheless kept its Gaussian form in the transverse direction; the transverse squeezed vacuum state of the beam was excited during its propagation. The dependence of “average amount of quanta” on the coordinate $z$ was found to be the parabolic one: ($\langle n\rangle ~z^2$).

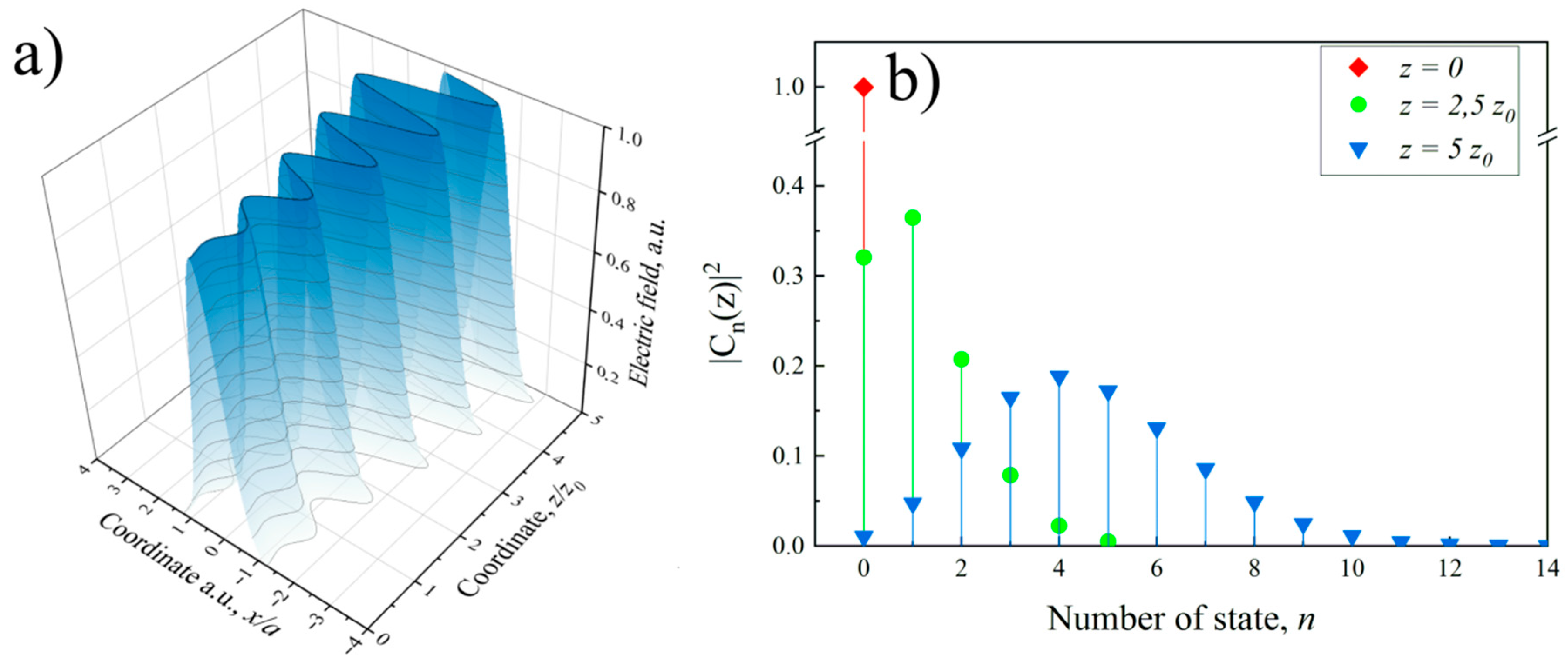
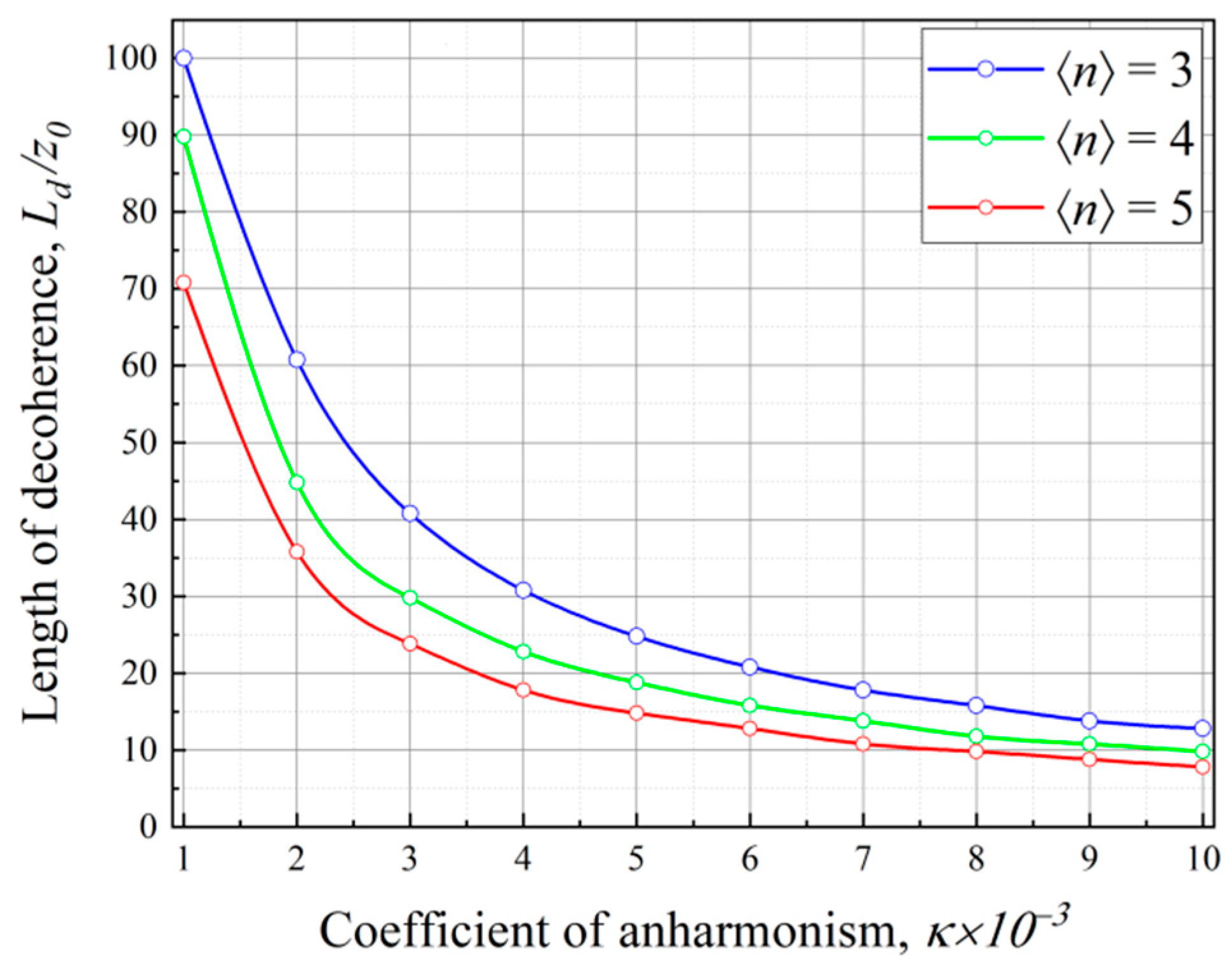
3.3. Decoherence of the Spatial Transverse Beam Structure

In reality, the waveguide has some impurities or/and defects in the structure that result in the decoherence of the beam during its propagation and destruction of the excited transverse coherent or squeezed vacuum state. Below we present the simple model of such “classical decoherence” for the transverse beam state in the non-ideal waveguide. Let us imagine that our waveguide was a non-ideal one and had the susceptibility profile that slightly disturbed the parabolic dependence ${\chi }_0\left(x\right)$:

$$\chi \left(x\right)={\chi }_0\left(x\right)+\Delta \chi \left(x\right),$$

where $\Delta \chi$ was considered as a perturbation. Hence we applied the perturbation theory that was similar to the quantum mechanical one [10,11]. Then one obtained the set of equations for decomposition coefficients $C_n\left(z\right)$:

$$id{C}_n/dz={{\displaystyle \sum }}_m{C}_m\cdot \delta M_{nm}exp\left(\frac{i}{2k}\left({\lambda }_n^2-{\lambda }_m^2\right)z\right).$$

(20)

Here $\delta M_{nm}=\frac{8\pi }{E_0^{2}a}\cdot 2\pi k{\displaystyle \int }{R}_n^{*}\left(x\right)\cdot \Delta \chi \left(x\right)\cdot R_m(x)dx$. In our situation the values $\delta M_{nm}$ did not depend on the longitudinal coordinate, hence all the terms on the right hand of Equation (20) oscillated along the $z$-coordinate except the term with $m=n$. It was this term that contributed dominantly for small perturbations at large distances. Hence, the approximate solution of Equation (20) was

$$C_n\left(z\right)=C_n\left(z=0\right)\times exp(-i\delta M_{nn}z).$$

(21)

It means that for small perturbations only the additional phase shift $\Delta \varphi \left(z\right)=\delta M_{nn}z$ appeared to exist during the beam propagation, while the probabilities $|C_n{|}^2$ did not depend on $z$. Evidently, this dephasing of the amplitude probabilities resulted in destruction of the transverse state of the beam.

The term of disturbance $\Delta \chi \left(x\right)$ that is responsible for the dephasing in reality can have very different structures. For simplicity to be more specific, we assumed that $\Delta \chi =-{\gamma }_4{(x/x_0)}^4$. Then

$$\delta \varphi \left(z\right)=-\kappa \left(z/z_0\right)\frac{3}{2}(n^2+n+1/2),\kappa =\frac{2\pi k{\gamma }_4{a}^4{z}_0}{x_0^4}.$$

(22)

From Equations (21) and (22) we see that the more the number of the state n, the faster the increment of the additional phase shift and the faster the decoherence process. Numerical results for phase shifts were also obtained by solving the set Equation (20) for the initial coherent state with different values of the average amount of quanta $\langle n\rangle$. These data for the given value of the dimensionless parameter (coefficient of anharmonism) $\kappa =0.01$ and average number of quanta $\langle n\rangle =5$ arepresented in Figure 6a and were found to be in agreement with the analytical expression Equation (22). The high-frequency oscillations of phase shift $\Delta \varphi \left(z\right)$ pronounced that Figure 6a resulted from the contribution of non-diagonal elements $M_{nm}$ in Equation (20). The evolution of the spatial transverse structure of the beam for the above given parameters is presented in Figure 6b and clearly demonstrates the beam destruction along the axis of propagation.

We assumed that the length of decoherence $L_d$ was the length for which the additional phase shift was equal to $\pi$ for the state with $n\approx \langle n\rangle$. In reality, states with $n=3÷6$ contributed dominantly to the coherent state with $\langle n\rangle =5$. Then one obtained

$$L_d\approx \frac{2z_0}{\kappa ({\langle n\rangle }^2+\langle n\rangle +\frac{1}{2})}.$$

(23)

For the above parameters the decoherence length was about $9z_0$ and corresponded to the significant change of the wavepacket shape. We also noted that the decoherence length was estimated from the analysis of the $z$-dependence of the integral of overlapping (IO) of the transverse wavepackets moving in perturbed and ideal parabolic waveguides

$$IO\left(z\right)=\frac{8\pi }{E_{tot}^{2}a}{\displaystyle \int }{E}_0^{*}\left(x,z\right)E_0^{\left(coh\right)}\left(x,z\right)dx,$$

(24)

where $E_0\left(x,z\right)$ and $E_0^{\left(coh\right)}\left(x,z\right)$ were transverse wavepackets in the perturbed and ideal waveguides respectively. The dependence $IO\left(z\right)$ for $\langle n\rangle =5$, parameter $\kappa =\frac{2\pi k{\gamma }_4{a}^4{z}_0}{x_0^4}=0.01$ is also presented in Figure 6a. It was found that the phase shift $\Delta \varphi \left(L_d\right)=\pi$ for the state $n\approx \langle n\rangle -1$ corresponded approximately to the $IO\left(L_d\right)~0.8$. Hence, we used this estimation

$$IO\left(L_d\right)=\frac{8\pi }{E_{tot}^{2}a}{\displaystyle \int }{E}_0^{*}\left(x,L_d\right)E_0^{\left(coh\right)}\left(x,L_d\right)dx\approx 0.8,$$

(25)

for the determination of the decoherence length as it was more visual than estimation Equation (23). The results obtained from Equation (25) in dependence of parameter $\kappa$ for different average amount of quanta in the initial transverse coherent state is presented in Figure 7. It was seen that the $L_d~1/\kappa$ as well as the dependence $L_d~{\langle n\rangle }^{-2}$ were approximately valid.

4. Discussion

Is it possible to implement into practice the generation of the coherent and spatially squeezed states described above? For preliminary estimates, we will focus on the features of modern integrated photonic technology (“µm-range”) and radio-photonics (“mm-range”). The choice of a specific frequency range is determined by the spectra of the “sources” connected by the waveguide structure with a parabolic susceptibility profile. In the first case (“µm-range”), we are talking about, for example, “atomic qubits” and atomic-based computing systems. In the second case (“mm-range”), we mean, for example, microwave resonators used for control, read-out, and coupling in systems of artificial atoms based on superconducting heterostructures [28,29].

For the material of the waveguide structure, it is reasonable to put for simplicity ε(x = 0) ≈ 10, $\chi \left(x=0\right)=\left(\epsilon \left(x=0\right)-1\right)/4\pi \approx 0.72$. The inhomogeneous doping of the structure can form the parabolic profile of the waveguide permittivity. Really, taking into account that free charged particle gas contributes negatively to the permittivity of the media, we can estimate the level of the waveguide doping in the near-boundary region at a level of N_d ~ 10¹⁹ cm⁻³, while in the near-axes area the level of doping will be small. Moreover, by applying the external DC voltage to the waveguide boundaries one can control the local level of dopants in the structure volume and create “a force” that causes spatial beam oscillations in the waveguide during its propagation. Assuming that $\chi \left(x=x_0\right)\approx 0$, and hence $X=\chi \left(x=0\right)$ ≈ 0.72, α = X ≈ 0.72, one can get the following set of parameters in the micrometer and mm spatial range for the model under investigation (see

Table 1. Preliminary estimates for waveguide and wave packet parameters for the generation of coherent and spatially squeezed states.

Parameter	µm-Range	mm-Range
k, cm−1	104	10
x0, cm	≈2 × 10−3	≈2
$a=\sqrt{x_0/\sqrt{4\pi k^2\alpha }}$, cm	≈2.5 × 10−4	≈2.5 × 10−1
$K=1/k{a}^2$, cm−1	≈1.6 × 103	≈1.6
$z_0=2\pi /K$, cm	≈3.9 × 10−3	≈3.9
${\Theta }_{coh}=2\pi k\gamma a{z}_0/x_0$	1	1
${\Theta }_{sq}=2\pi k{\gamma }_2{a}^2{z}_0/x_0^2$	0.5	0.5
$\kappa =2\pi k{\gamma }_4{a}^4{z}_0/x_0^4$	0.01	0.01

).

It is clear from the data that for both ranges of parameters the characteristic transverse size of the coherent wave packet $a={\left(x_0/\sqrt{4\pi k^2\alpha }\right)}^{1/2}$ is significantly less than the transverse size of the waveguide x₀. Hence there exist several dozen of eigenstates in the parabolic well. The wave number determines the spatial period over the z-direction for the waveguide susceptibility profile. For example, for $K=1/k{a}^2\approx {10}^4$ cm⁻³ in order to build-up effectively coherent and spatially squeezed states one needs to create electrodes at the waveguide boundaries in order to control the local concentration in the near boundary waveguide volume of dopants with a spatial resolution of 1 μm. For reasonable accuracy in creating of the susceptibility profile, the decoherence length is several times greater than the length at which the coherent and spatially squeezed states are swung effectively. This means that in perspective the considered pumping of energy into the transverse mode and compression in space of electromagnetic beams directly in the waveguide can be used in transmitting signals from a nanoscale source to a nanoscale radiation receiver.

A simplified scheme of the possible application for the transition of an electromagnetic wave beam from both the elements Q₁ and Q₂ to the element Q₃ is presented in Figure 8. Let the “sources” Q₁ and Q₂ be designed so that the emitted beams are localized in the central part of the waveguide (the number of “photons” in the transverse mode, n, is zero), which allows one to minimize undesired dissipation and absorption. Then, in order to send these “signals” to the Q₃ element, one needs to swing the discussed coherent state in the “active area”, as shown in the Figure 8. Thus, the effects considered in the article can be used to create an optical analogue of the “adder”-element. It should be emphasized that by rearranging (or disabling) in situ the controlling DC fields in the “active area”, one can either swing the oscillations of a coherent state with a different spatial period along the Oz axis, or keep the original state, localized in the center of the waveguide. Moreover, it is possible to excite the spatially squeezed vacuum states in order to realize the optical prototype of the “splitter” element, as shown in Figure 8 (here the element Q₃ is the “source” and the elements Q₄ and Q₅ are the “receivers”). For complex systems of integrated and microwave photonics, the considered concept may be of interest due to the possibility of rotating beams of electromagnetic waves at small distances and with small losses.

All the above estimations were performed while neglecting the losses of the energy of the beam. In reality, losses due to different types of impurities and inhomogeneities obviously exist, as well as losses resulting from the high level of the dopant concentration. The last will be of importance first of all for the high excitation level of the transverse mode when the beam in the guide oscillates with the amplitude of order of its size $~x_0$. Further, we plan to improve the model and introduce the spatially non-uniform absorption that will allow analysis of the losses in the waveguide in dependence on the degree of transverse mode excitation more precisely.