Overcoming Challenges in Large-Core SI-POF-Based System-Level Modeling and Simulation
Abstract
1. Introduction
2. POF Modeling Challenges
3. Component Modeling
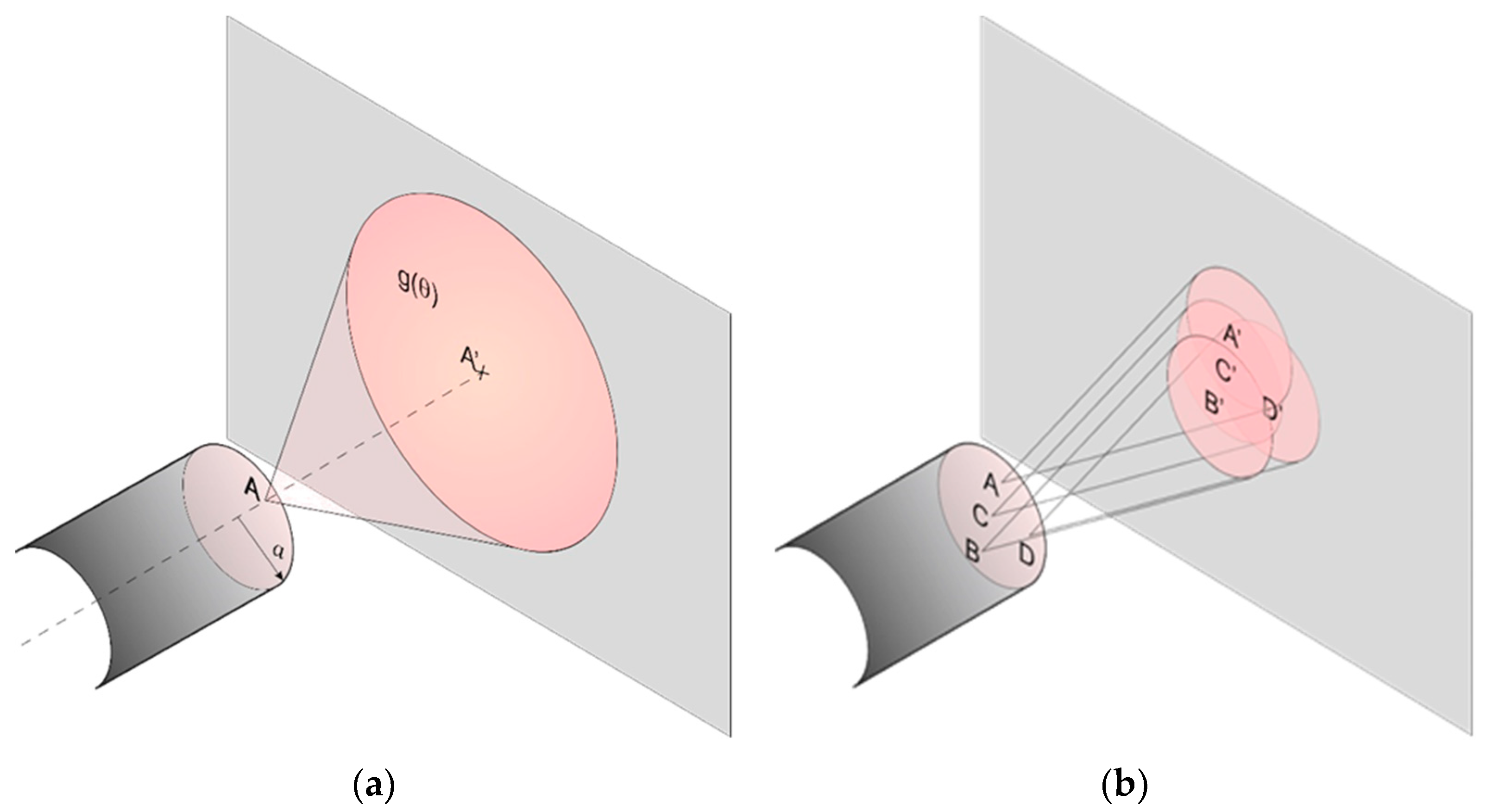
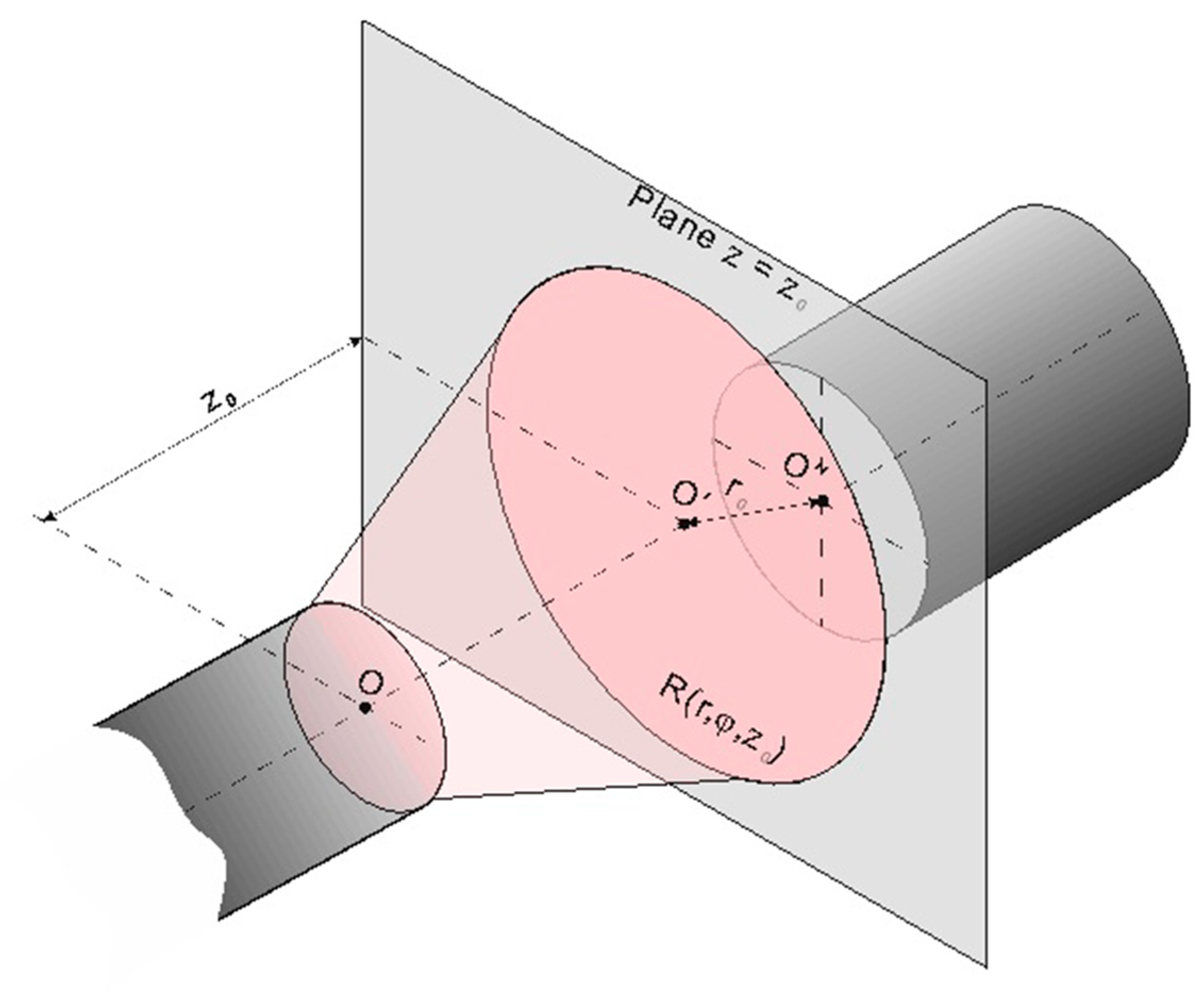
3.1. SI-POF Modeling
3.2. Transmitter Modeling
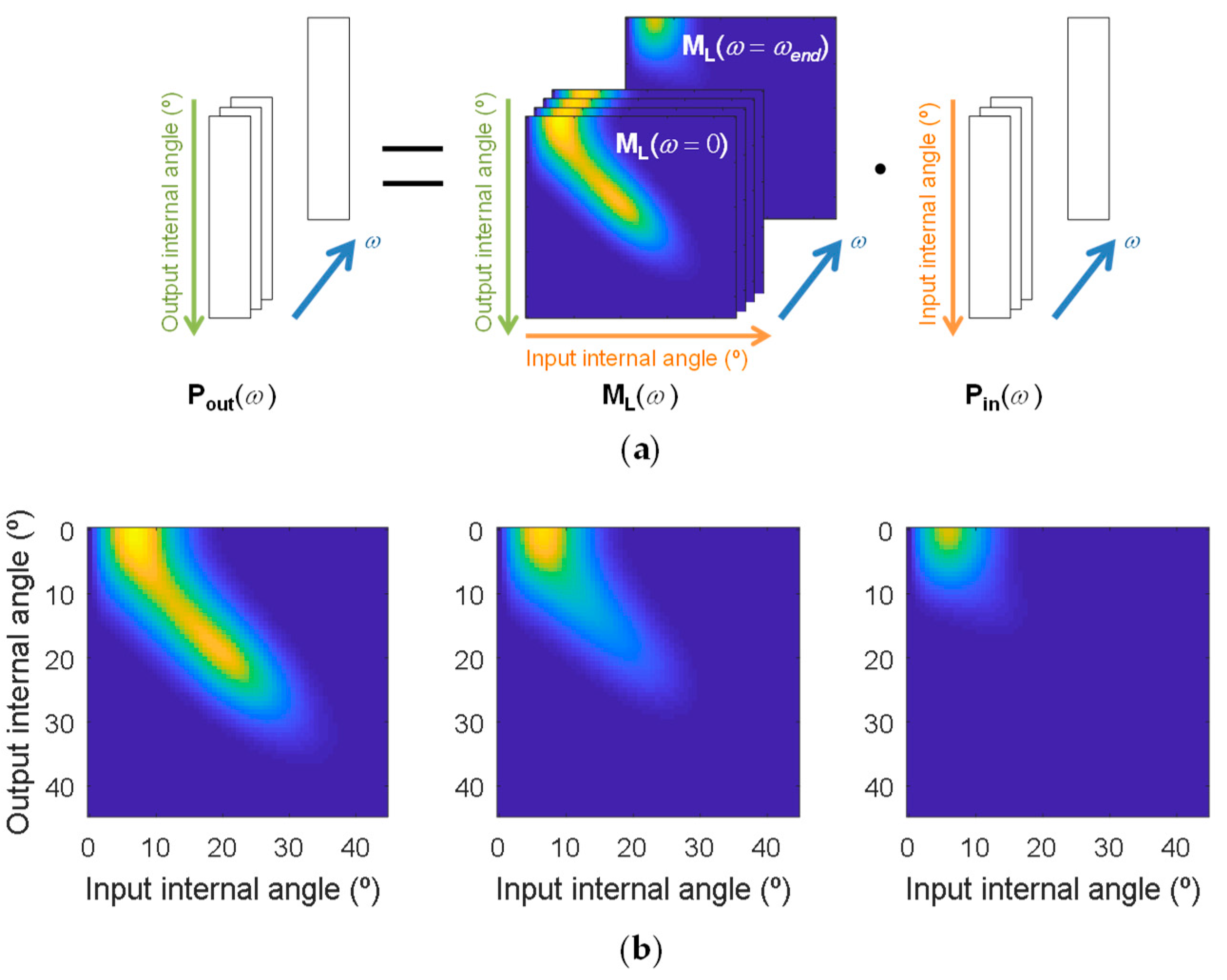
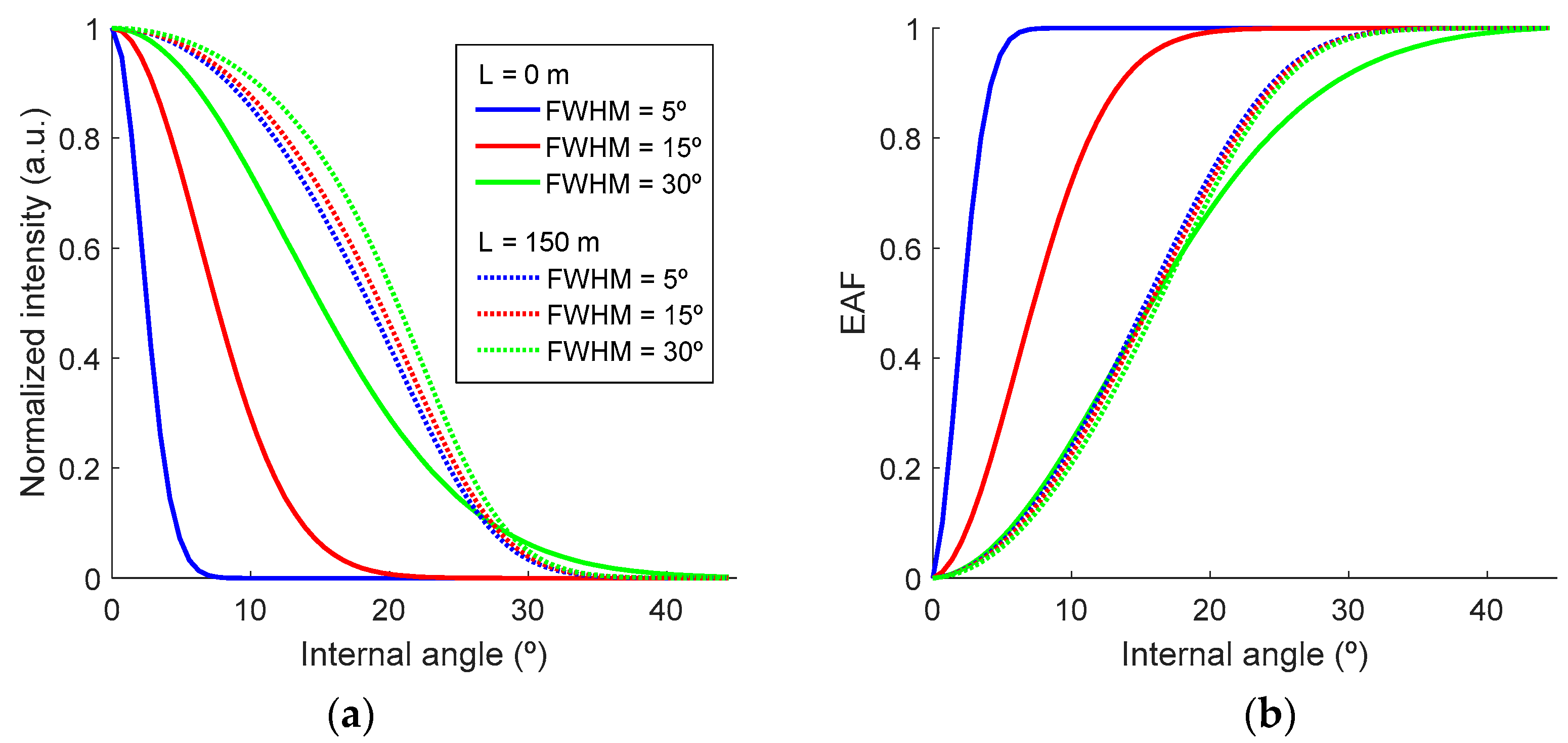
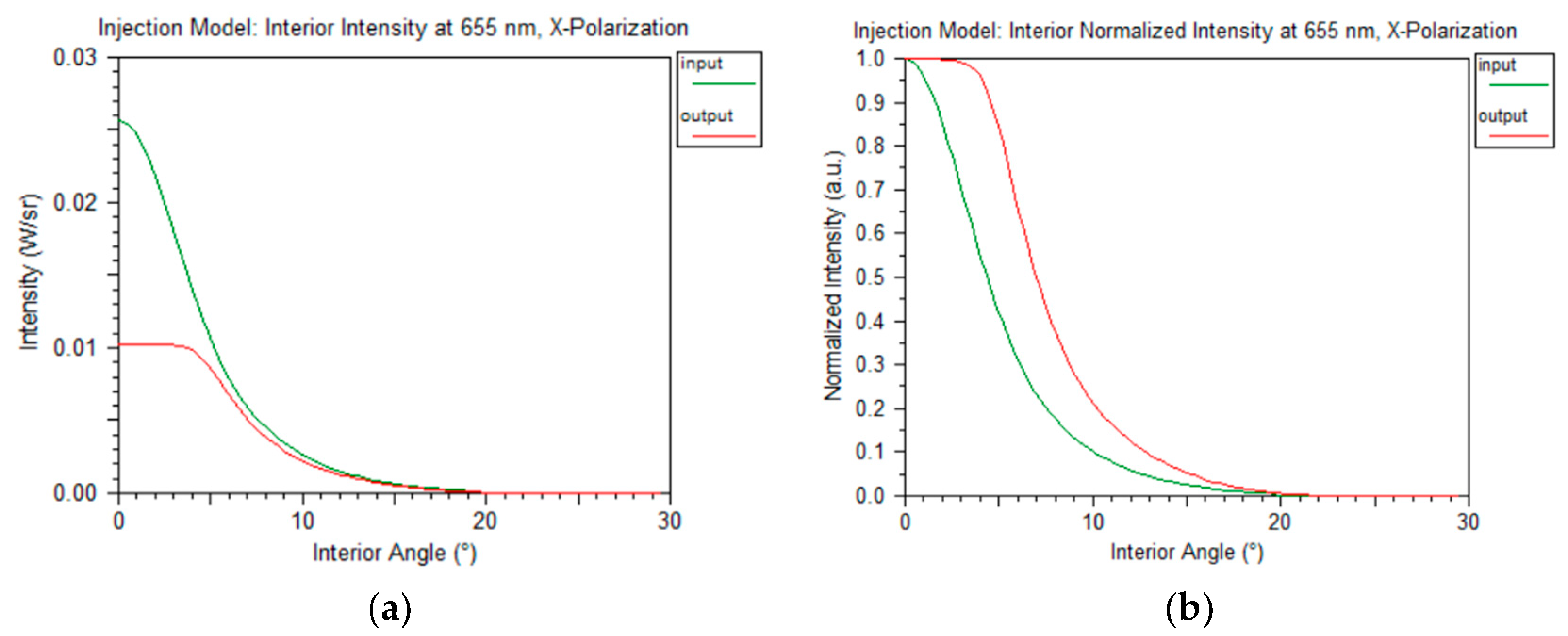
3.3. SI-POF Injection
3.4. Connector Modeling
3.5. Fiber Bends
3.6. Detector Coupling
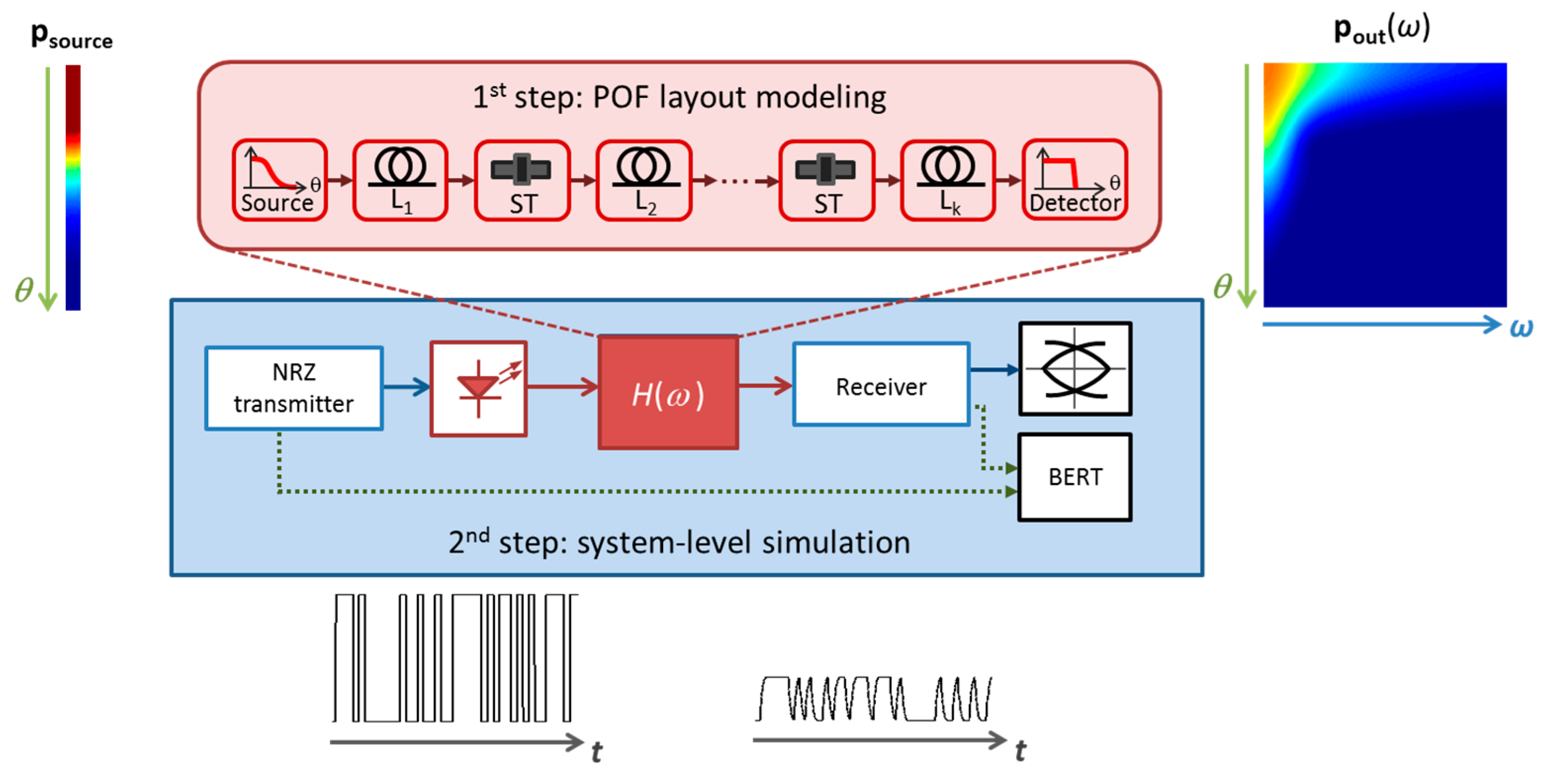
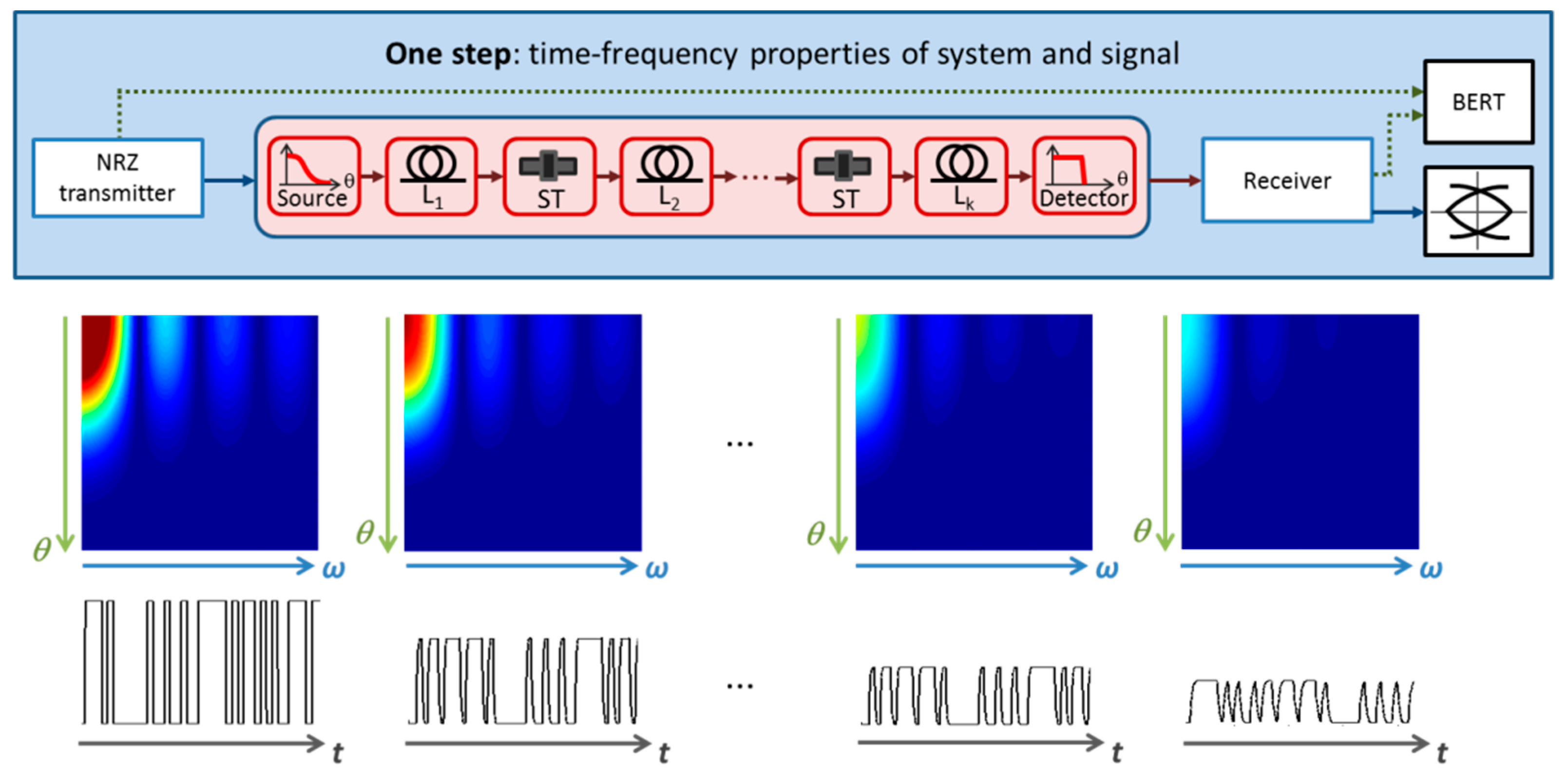
4. System Level Modeling: Two-Step and One-Step Approaches
5. Commercial Software
5.1. MATLAB/Simulink
5.2. ModeSYS
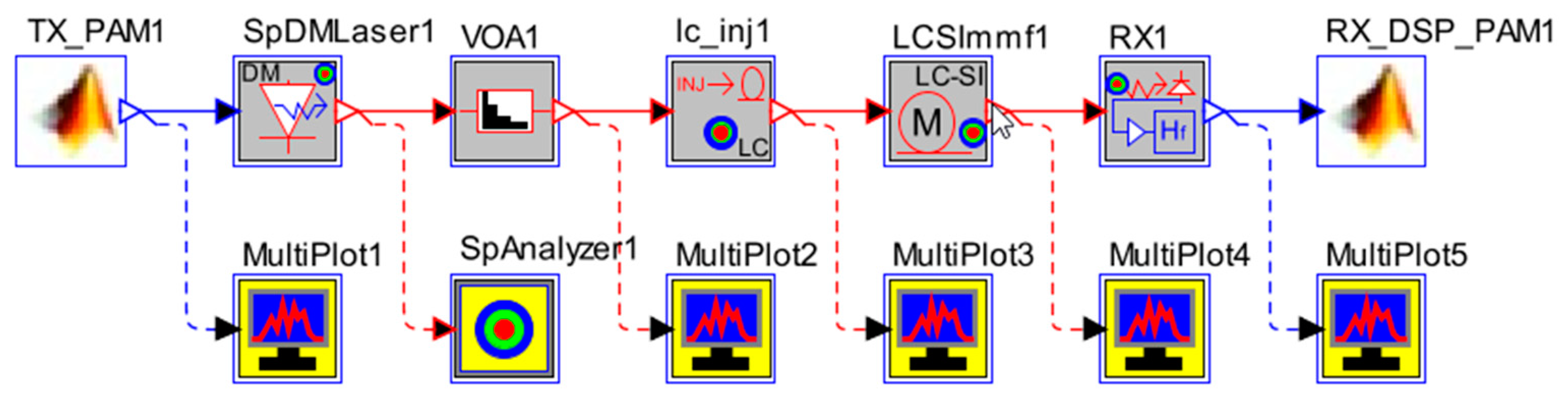
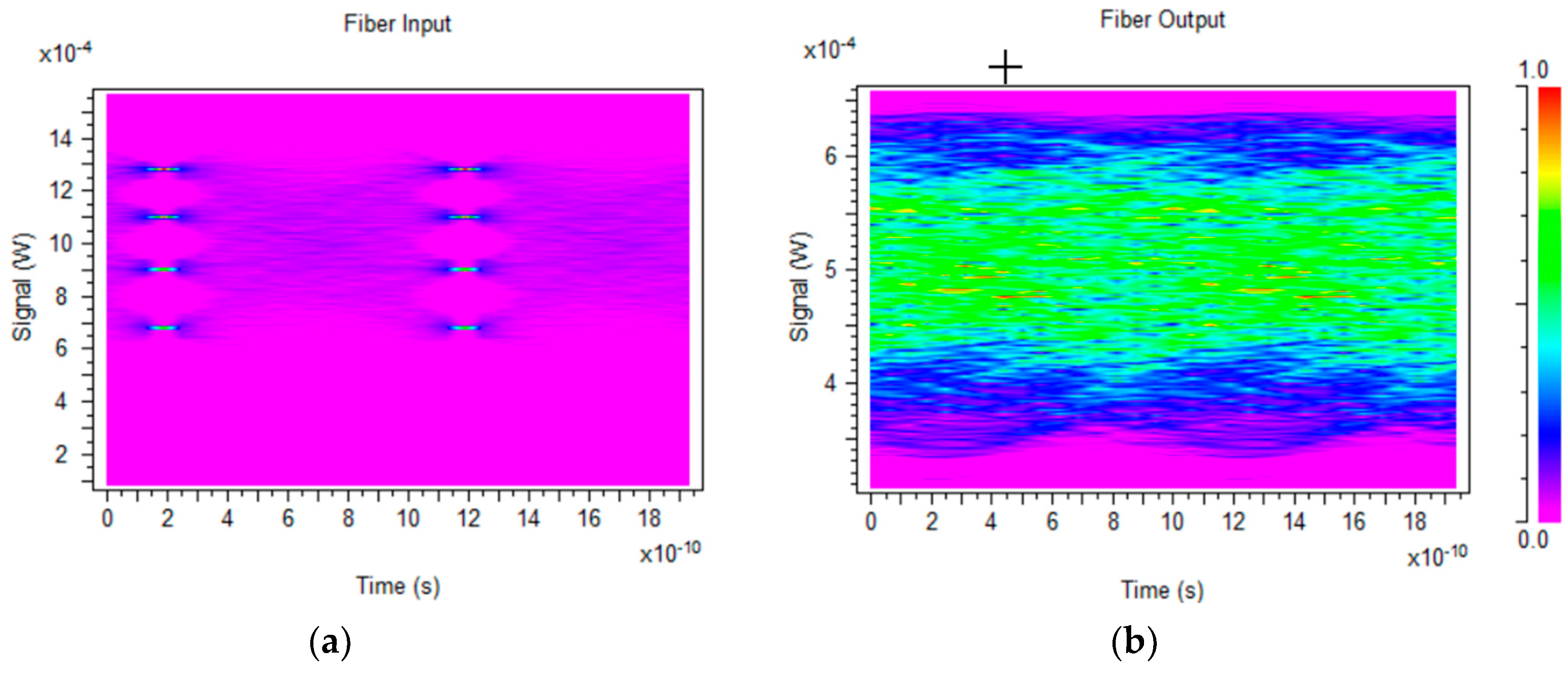
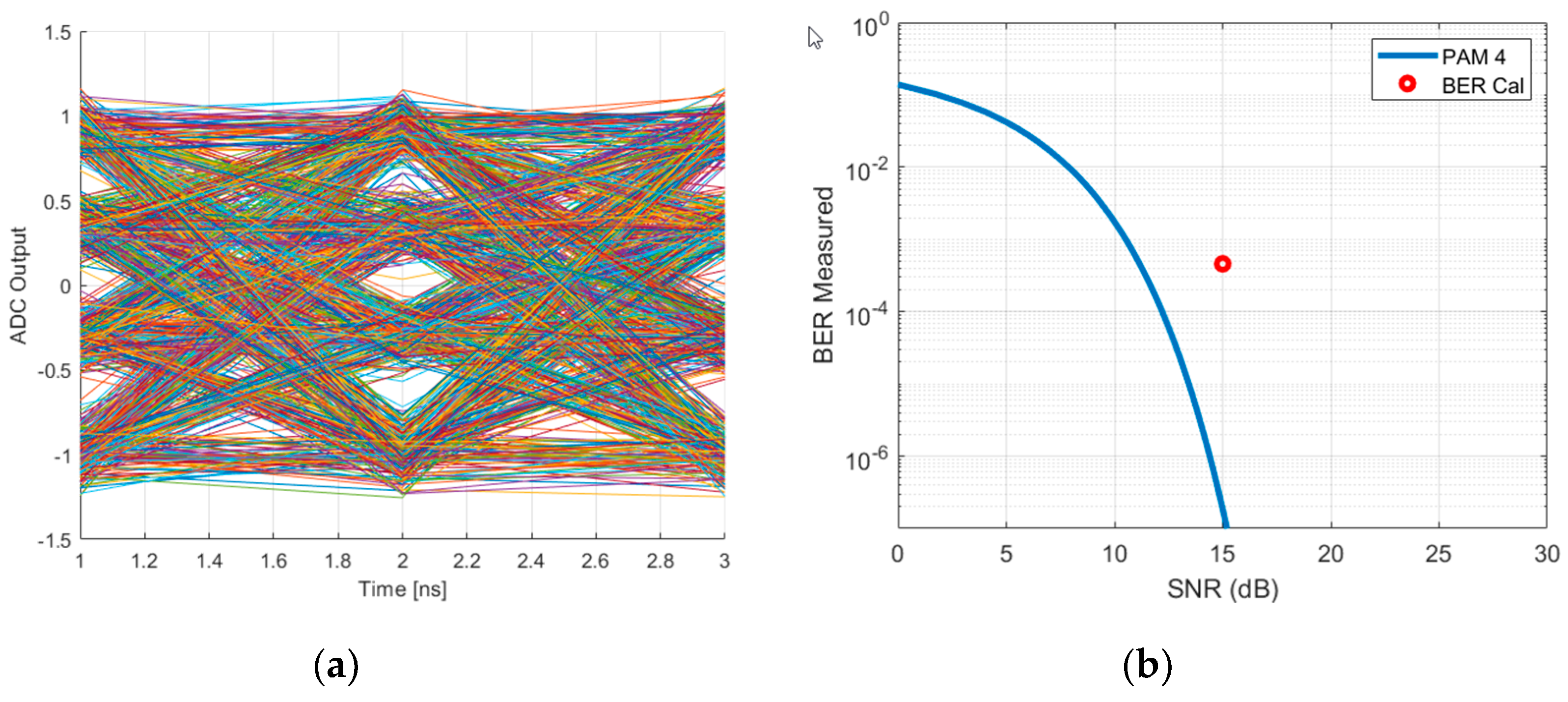
6. System Level Simulation Example: PAM-4 Transmission over Large-Core Plastic Optical Fiber
7. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Losada, M.A.; Mateo, J. Short Range (in-building) Systems and Networks: A Chance for Plastic Optical Fibers. In WDM Systems and Networks. Modeling, Simulation, Design and Engineering; Antoniades, N., Ellinas, G., Roudas, I., Eds.; Springer: New York, NY, USA, 2012; pp. 301–323. [Google Scholar]
- Nespola, A.; Abrate, S.; Gaudino, R.; Zerna, C.; Offenbeck, B.; Weber, N. High-Speed Communications Over Polymer Optical Fibers for In-Building Cabling and Home Networking. IEEE Photonics J. 2010, 2, 347–358. [Google Scholar] [CrossRef]
- Grzemba, A. MOST: The Automotive Multimedia Network; Franzis Verlag: Munich, Germany, 2011; ISBN 9783645650618. [Google Scholar]
- Truong, T.K. Commercial airplane fibre optics: Needs, opportunities, challenges. In Proceedings of the 19th International Conference on Plastic Optic Fibres and Application, Tokyo, Japan, 19–21 October 2010; p. DN2-1–M. [Google Scholar]
- Lee, S.C.J.; Breyer, F.; Randel, S.; van den Boom, H.P.A.; Koonen, A.M.J. High-speed transmission over multimode fiber using discrete multitone modulation. J. Opt. Netw. 2008, 7, 183–196. [Google Scholar]
- Breyer, F.; Lee, S.C.J.; Randel, S.; Hanik, N. Comparison of OOK- and PAM-4 Modulation for 10 Gbit/s Transmission over up to 300 m Polymer Optical Fiber. In Proceedings of the OFC/NFOEC 2008—2008 Conference on Optical Fiber Communication/National Fiber Optic Engineers Conference, San Diego, CA, USA, 24–28 February 2008; IEEE: Piscataway, NJ, USA, 2008; p. OWB5. [Google Scholar]
- Zeolla, D.; Nespola, A.; Gaudino, R. Comparison of different modulation formats for 1-Gb/s SI-POF transmission systems. IEEE Photonics Technol. Lett. 2011, 23, 950–952. [Google Scholar] [CrossRef]
- Loquai, S.; Kruglov, R.; Ziemann, O.; Vinogradov, J.; Bunge, C.-A. 10 Gbit/s over 25 m Plastic Optical Fiber as a Way for Extremely Low-Cost Optical Interconnection. In Proceedings of the Optical Fiber Communication Conference, San Diego, CA, USA, 21–25 March 2010; OSA: Washington, DC, USA, 2010; p. OWA6. [Google Scholar]
- Loquai, S.; Kruglov, R.; Schmauss, B.; Bunge, C.-A.; Winkler, F.; Ziemann, O.; Hartl, E.; Kupfer, T. Comparison of Modulation Schemes for 10.7 Gb/s Transmission Over Large-Core 1 mm PMMA Polymer Optical Fiber. J. Light. Technol. 2013, 31, 2170–2176. [Google Scholar] [CrossRef]
- Ziemann, O.; Krauser, J.; Zamzowr, P.E.; Daum, W. Application of Polymer Optical and Glass Fibers. In POF Handbook: Optical Short Range Transmission Systems, 2nd ed.; Springer: Berlin/Heidelberg, Germany, 2008. [Google Scholar]
- Koike, K.; Koike, Y. Design of Low-Loss Graded-Index Plastic Optical Fiber Based on Partially Fluorinated Methacrylate Polymer. J. Light. Technol. 2009, 27, 41–46. [Google Scholar] [CrossRef]
- Polley, A.; Kim, J.H.; Decker, P.J.; Ralph, S.E. Statistical Study of Graded-Index Perfluorinated Plastic Optical Fiber. J. Light. Technol. 2011, 29, 305–315. [Google Scholar]
- Technologies | Perfluorinated GI-POF. Available online: https://chromisfiber.com/technology/why-perfluorinated-gi-pof/ (accessed on 16 June 2019).
- Aldabaldetreku, G.; Zubia, J.; Durana, G.; Arrue, J. Numerical Implementation of the Ray-Tracing Method in the Propagation of Light Through Multimode Optical Fiber. In POF Modelling: Theory, Measurements and Application; Bunge, C.A., Poisel, H., Eds.; Verlag Books on Demand GmbH: Norderstedt, Germany, 2007. [Google Scholar]
- Berganza, A.; Aldabaldetreku, G.; Zubia, J.; Durana, G.; Arrue, J. Misalignment Losses in Step-Index Multicore Plastic Optical Fibers. J. Light. Technol. 2013, 31, 2177–2183. [Google Scholar] [CrossRef]
- Berganza, A.; Aldabaldetreku, G.; Zubia, J.; Durana, G. Ray-tracing analysis of crosstalk in multi-core polymer optical fibers. Opt. Express 2010, 18, 22446–22461. [Google Scholar] [CrossRef]
- Arrue, J.; Aldabaldetreku, G.; Durana, G.; Zubia, J.; Garces, I.; Jimenez, F. Design of mode scramblers for step-index and graded-index plastic optical fibers. J. Light. Technol. 2005, 23, 1253–1260. [Google Scholar] [CrossRef]
- Arrue, J.; Kalymnios, D.; Zubia, J.; Fuster, G. Light power behaviour when bending plastic optical fibres. IEE Proc. Optoelectron. 1998, 145, 313–318. [Google Scholar] [CrossRef]
- Appelt, V.; Bunge, C.; Kruglov, R.; Surkova, G.; Poisel, H.; Zadorin, A. Determination of Mode Coupling Matrix Used by Split-Step Algorithm. In POF Modelling: Theory, Measurements and Application; Bunge, C.A., Poisel, H., Eds.; Verlag Books on Demand GmbH: Norderstedt, Germany, 2007. [Google Scholar]
- Gloge, D. Optical Power Flow in Multimode Fibers. Bell Syst. Tech. J. 1972, 51, 1767–1783. [Google Scholar] [CrossRef]
- Breyer, F.; Hanik, N.; Lee, S.; Randel, S. Getting the Impulse Respose of SI-POF by solving the Time-Dependent Power-Flow Equation Using the Crank-Nicholson Scheme. In POF Modelling: Theory, Measurements and Application; Bunge, C.A., Poisel, H., Eds.; Verlag Books on Demand GmbH: Norderstedt, Germany, 2007. [Google Scholar]
- Djordjevich, A.; Savovic, S. Investigation of mode coupling in step index plastic optical fibers using the power flow equation. IEEE Photonics Technol. Lett. 2000, 12, 1489–1491. [Google Scholar] [CrossRef]
- Mateo, J.; Losada, M.A.; Garcés, I.; Zubia, J. Global characterization of optical power propagation in step-index plastic optical fibers. Opt. Express 2006, 14, 9028–9035. [Google Scholar] [CrossRef]
- Stepniak, G.; Siuzdak, J. Modeling of transmission characteristics in step-index polymer optical fiber using the matrix exponential method. Appl. Opt. 2018, 57, 9203–9207. [Google Scholar] [CrossRef]
- Jiang, G.; Shi, R.F.; Garito, A.F. Mode coupling and equilibrium mode distribution conditions in plastic optical fibers. IEEE Photonics Technol. Lett. 1997, 9, 1128–1130. [Google Scholar] [CrossRef]
- Zubia, J.; Durana, G.; Aldabaldetreku, G.; Arrue, J.; Losada, M.A.; Lopez-Higuera, M. New method to calculate mode conversion coefficients in si multimode optical fibers. J. Light. Technol. 2003, 21, 776–781. [Google Scholar] [CrossRef]
- Rousseau, M.; Jeunhomme, L. Numerical Solution of the Coupled-Power Equation in Step-Index Optical Fibers. IEEE Trans. Microw. Theory Tech. 1977, 25, 577–585. [Google Scholar] [CrossRef]
- Djordjevich, A.; Savović, S. Numerical solution of the power flow equation in step-index plastic optical fibers. J. Opt. Soc. Am. B 2004, 21, 1437–1438. [Google Scholar] [CrossRef]
- Mateo, J.; Losada, M.A.; Zubia, J. Frequency response in step index plastic optical fibers obtained from the generalized power flow equation. Opt. Express 2009, 17, 2850–2860. [Google Scholar] [CrossRef]
- Esteban, A.; Losada, M.A.; Mateo, J.; Antoniades, N.; López, A.; Zubia, J. Effects of connectors in si-pofs transmission properties studied in a matrix propagation framework. In Proceedings of the 20th International Conference on Plastic Optical Fibres and Applications, Bilbao, Spain, 14–16 September 2011; pp. 341–346. [Google Scholar]
- Losada, M.A.; Mateo, J.; Martínez-Muro, J.J. Assessment of the impact of localized disturbances on SI-POF transmission using a matrix propagation model. J. Opt. 2011, 13, 055406. [Google Scholar] [CrossRef]
- Losada, M.A.; López, A.; Mateo, J. Attenuation and diffusion produced by small-radius curvatures in POFs. Opt. Express 2016, 24, 15710. [Google Scholar] [CrossRef]
- ModeSYSTM–Multimode Optical Communication Systems. Available online: https://www.synopsys.com/optical-solutions/rsoft/system-network-modesys.html (accessed on 15 June 2019).
- Richards, D.H.; Losada, M.A.; Antoniades, N.; Lopez, A.; Mateo, J.; Jiang, X.; Madamopoulos, N. Modeling Methodology for Engineering SI-POF and Connectors in an Avionics System. J. Light. Technol. 2013, 31, 468–475. [Google Scholar] [CrossRef]
- Lopez, A.; Jiang, X.; Losada, M.A.; Mateo, J.; Richards, D.; Madamopoulos, N.; Antoniades, N. Temperature sensitivity of POF links for avionics applications. In Proceedings of the 2017 19th International Conference on Transparent Optical Networks (ICTON), Girona, Spain, 2–6 July 2017; IEEE: Piscataway, NJ, USA, 2017. [Google Scholar]
- Pujols, N.; Losada, M.Á.; Mateo, J.; López, A.; Richards, D. A POF Model for Short Fiber Segments in Avionics Applications. In Proceedings of the 2016 18th International Conference on Transparent Optical Networks (ICTON), Trento, Italy, 10–14 July 2016; IEEE: Piscataway, NJ, USA, 2016. [Google Scholar]
- Raptis, N.; Grivas, E.; Pikasis, E.; Syvridis, D. Space-time block code based MIMO encoding for large core step index plastic optical fiber transmission systems. Opt. Express 2011, 19, 10336–10350. [Google Scholar] [CrossRef]
- Lopez, A.; Losada, A.; Mateo, J.; Zubia, J. On the Variability of Launching and Detection in POF Transmission Systems. In Proceedings of the 2018 20th International Conference on Transparent Optical Networks (ICTON), Bucharest, Romania, 1–5 July 2018; IEEE: Piscataway, NJ, USA, 2018. [Google Scholar]
- Werzinger, S.; Bunge, C.A.; Loquai, S.; Ziemann, O. An Analytic Connector Loss Model for Step-Index Polymer Optical Fiber Links. J. Light. Technol. 2013, 31, 2769–2776. [Google Scholar] [CrossRef]
- Werzinger, S.; Bunge, C.A. Statistical analysis of intrinsic and extrinsic coupling losses for step-index polymer optical fibers. Opt. Express 2015, 23, 22318–22329. [Google Scholar] [CrossRef]
- IEEE 802.3bv-2017—IEEE Standard for Ethernet Amendment 9: Physical Layer Specifications and Management Parameters for 1000 Mb/s Operation Over Plastic Optical Fiber. Available online: https://standards.ieee.org/standard/802_3bv-2017.html (accessed on 13 June 2019).
- Mena, P.V.; Ghillino, E.; Richards, D.; Hyuga, S.; Nakai, M.; Kagami, M.; Scarmozzino, R. Using system simulation to evaluate design choices for automotive ethernet over plastic optical fiber. In Proceedings of the SPIE 10560, Metro and Data Center Optical Networks and Short-Reach Links, San Francisco, CA, USA, 30–31 January 2018; Glick, M., Srivastava, A.K., Akasaka, Y., Eds.; SPIE: Bellingham, WA, USA, 2018; Volume 10560, p. 17. [Google Scholar]
- Lopez, A.; Losada, A.; Richards, D.; Mateo, J.; Jiang, X.; Antoniades, N. Statistical Approach for Modeling Connectors in SI-POF Avionics Systems. In Proceedings of the 2019 International Conference of Transparent Optical Networks (ICTON), Angers, France, 9–13 July 2019. [Google Scholar]
- Cherian, S.; Spangenberg, H.; Caspary, R. Investigation on Harsh Environmental Effects on polymer Fiber Optic link for Aircraft Systems; Kazemi, A.A., Kress, B.C., Mendoza, E.A., Eds.; International Society for Optics and Photonics: Bellingham, WA, USA, 2014; Volume 9202, p. 92020I. [Google Scholar]
- Poisel, H. Optical fibers for adverse environments. In Proceedings of the 12th International. Conference on Plastic Optical. Fibers, Seattle, WA, USA, 14–17 September 2003; pp. 10–15. [Google Scholar]
- Chen, L.W.; Lu, W.H.; Chen, Y.C. An investigation into power attenuations in deformed polymer optical fibers under high temperature conditions. Opt. Commun. 2009, 282, 1135–1140. [Google Scholar] [CrossRef]
- Savovic, S.; Djordjevich, A. Mode Coupling in Plastic-Clad Silica Fibers and Organic Glass-Clad PMMA Fibers. J. Light. Technol. 2014, 32, 1290–1294. [Google Scholar] [CrossRef]
- Tao, R.; Hayashi, T.; Kagami, M.; Kobayashi, S.; Yasukawa, M.; Yang, H.; Robinson, D.; Baghsiahi, H.; Fernández, F.A.; Selviah, D.R. Equilibrium modal power distribution measurement of step-index hard plastic cladding and graded-index silica multimode fibers. In Proceedings of the SPIE 9368, Optical Interconnects XV, San Francisco, CA, USA, 9–11 February 2015; Schröder, H., Chen, R.T., Eds.; SPIE: Bellingham, WA, USA, 2015; p. 93680N. [Google Scholar]
- Losada, M.A.; Mateo, J.; Serena, L. Analysis of Propagation Properties of Step Index Plastic Optical Fibers At Non-Stationary Conditions. In Proceedings of the 16th International Conference on Plastic Optical Fibres and Applications, Turin, Italy, 10–12 September 2007; pp. 299–302. [Google Scholar]
- Mateo, J.; Losada, M.A.; Antoniades, N.; Richards, D.; Lopez, A.; Zubia, J. Connector misalignment matrix model. In Proceedings of the 21st International Conference on Plastic Optical Fibres and Applications, Atlanta GA, USA, 10–12 September 2012; pp. 90–95. [Google Scholar]
- Mateo, J.; Losada, M.A.; López, A. POF misalignment model based on the calculation of the radiation pattern using the Hankel transform. Opt. Express 2015, 23, 8061–8072. [Google Scholar] [CrossRef]
- Gloge, D. Impulse Response of Clad Optical Multimode Fibers. Bell Syst. Tech. J. 1973, 52, 801–816. [Google Scholar] [CrossRef]
- Yevick, D.; Stoltz, B. Effect of mode coupling on the total pulse response of perturbed optical fibers. Appl. Opt. 1983, 22, 1010–1015. [Google Scholar] [CrossRef]
- Stoltz, B.; Yevick, D. Influence of mode coupling on differential mode delay. Appl. Opt. 1983, 22, 2349–2355. [Google Scholar] [CrossRef]
- Press, W.H.; Teukolsky, S.A.; Vetterling, W.T.; Flannery, B.P. Numerical Recipes in C: The Art of Scientific Computing; Cambridge University Press: Cambridge, UK, 1992; ISBN 9780521431088. [Google Scholar]
- Antoniades, N.; Losada, M.A.; Mateo, J.; Richards, D.; Truong, T.K.; Jiang, X.; Madamopoulos, N. Modeling and characterization of si-pof and connectors for use in an avionics system. In Proceedings of the 20th International Conference on Plastic Optical Fibres and Applications, Bilboa, Spain, 14–16 September 2011; pp. 105–110. [Google Scholar]
- MATLAB—MathWorks—MATLAB & Simulink. Available online: https://www.mathworks.com/products/matlab.html (accessed on 14 June 2019).
- OptSim—OptSim Product Overview | RSoft Products. Available online: https://www.synopsys.com/optical-solutions/rsoft/system-network-optsim.html (accessed on 14 June 2019).
- Lopez, A.; Losada, M.A.; Mateo, J.J. Simulation framework for POF-based communication systems. In Proceedings of the 2015 17th International Conference on Transparent Optical Networks (ICTON), Budapest, Hungary, 5–9 July 2015; IEEE: Piscataway, NJ, USA, 2015; Volume 2015, p. Mo.D5.4. [Google Scholar]
- Alcoceba, A.; Lopez, A.; Losada, M.A.A.; Mateo, J.; Vazquez, C.; López, A.; Losada, M.A.A.; Mateo, J.; Vázquez, C. Building a Simulation Framework for POF Data Links. In Proceedings of the 24th International Conference on Plastic Optical Fibers, Nuremberg, Germany, 22–24 September 2015. [Google Scholar]
- Simulink—Simulation and Model-Based Design—MATLAB & Simulink. Available online: https://www.mathworks.com/products/simulink.html (accessed on 15 June 2019).
- Bosco, G.; Curri, V.; Carena, A.; Poggiolini, P.; Forghieri, F. On the Performance of Nyquist-WDM Terabit Superchannels Based on PM-BPSK, PM-QPSK, PM-8QAM or PM-16QAM Subcarriers. J. Light. Technol. 2011, 29, 53–61. [Google Scholar] [CrossRef]
- Kruglov, R.; Loquai, S.; Bunge, C.-A.; Schueppert, M.; Vinogradov, J.; Ziemann, O. Comparison of PAM and CAP Modulation Schemes for Data Transmission Over SI-POF. IEEE Photonics Technol. Lett. 2013, 25, 2293–2296. [Google Scholar] [CrossRef]
- Kruglov, R.; Vinogradov, J.; Loquai, S.; Ziemann, O.; Bunge, C.-A.; Hager, T.; Strauss, U. 21.4 Gb/s Discrete Multitone Transmission over 50-m SI-POF employing 6-channel WDM. In Proceedings of the Optical Fiber Communication Conference, San Francisco, CA, USA, 9–13 March 2014; OSA: Washington, DC, USA, 2014; p. Th2A.2. [Google Scholar]
- Erkilinc, M.S.; Thakur, M.P.; Pachnicke, S.; Griesser, H.; Mitchell, J.; Thomsen, B.C.; Bayvel, P.; Killey, R.I. Spectrally Efficient WDM Nyquist Pulse-Shaped Subcarrier Modulation Using a Dual-Drive Mach–Zehnder Modulator and Direct Detection. J. Light. Technol. 2016, 34, 1158–1165. [Google Scholar] [CrossRef]
- Karinou, F.; Prodaniuc, C.; Stojanovic, N.; Ortsiefer, M.; Daly, A.; Hohenleitner, R.; Kogel, B.; Neumeyr, C. Directly PAM-4 Modulated 1530-nm VCSEL Enabling 56 Gb/s/λ Data-Center Interconnects. IEEE Photonics Technol. Lett. 2015, 27, 1872–1875. [Google Scholar] [CrossRef]
- Yekani, A.; Chagnon, M.; Park, C.S.; Poulin, M.; Plant, D.V.; Rusch, L.A. Experimental comparison of PAM vs. DMT using an O-band silicon photonic modulator at different propagation distances. In Proceedings of the 2015 European Conference on Optical Communication (ECOC), Valencia, Spain, 27 September–1 October 2015. [Google Scholar]

© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Richards, D.; Lopez, A.; Losada, M.A.; Mena, P.V.; Ghillino, E.; Mateo, J.; Antoniades, N.; Jiang, X. Overcoming Challenges in Large-Core SI-POF-Based System-Level Modeling and Simulation. Photonics 2019, 6, 88. https://doi.org/10.3390/photonics6030088
Richards D, Lopez A, Losada MA, Mena PV, Ghillino E, Mateo J, Antoniades N, Jiang X. Overcoming Challenges in Large-Core SI-POF-Based System-Level Modeling and Simulation. Photonics. 2019; 6(3):88. https://doi.org/10.3390/photonics6030088
Chicago/Turabian StyleRichards, Dwight, Alicia Lopez, M. Angeles Losada, Pablo V. Mena, Enrico Ghillino, Javier Mateo, N. Antoniades, and Xin Jiang. 2019. "Overcoming Challenges in Large-Core SI-POF-Based System-Level Modeling and Simulation" Photonics 6, no. 3: 88. https://doi.org/10.3390/photonics6030088
APA StyleRichards, D., Lopez, A., Losada, M. A., Mena, P. V., Ghillino, E., Mateo, J., Antoniades, N., & Jiang, X. (2019). Overcoming Challenges in Large-Core SI-POF-Based System-Level Modeling and Simulation. Photonics, 6(3), 88. https://doi.org/10.3390/photonics6030088




