Doubly Orthogonal Wavelet Packets for Multi-Users Indoor Visible Light Communication Systems
Abstract
1. Introduction
- Tackle the problem of low modulation bandwidth of LED with the aid of advanced modulation and MA scheme
- Design a VLC system depending upon DWT-MC-CDMA technique that will enjoy the benefits of both OFDM and CDMA, and eliminates the ISI effects without employing CP, which is necessary for DFT-MC-CDMA
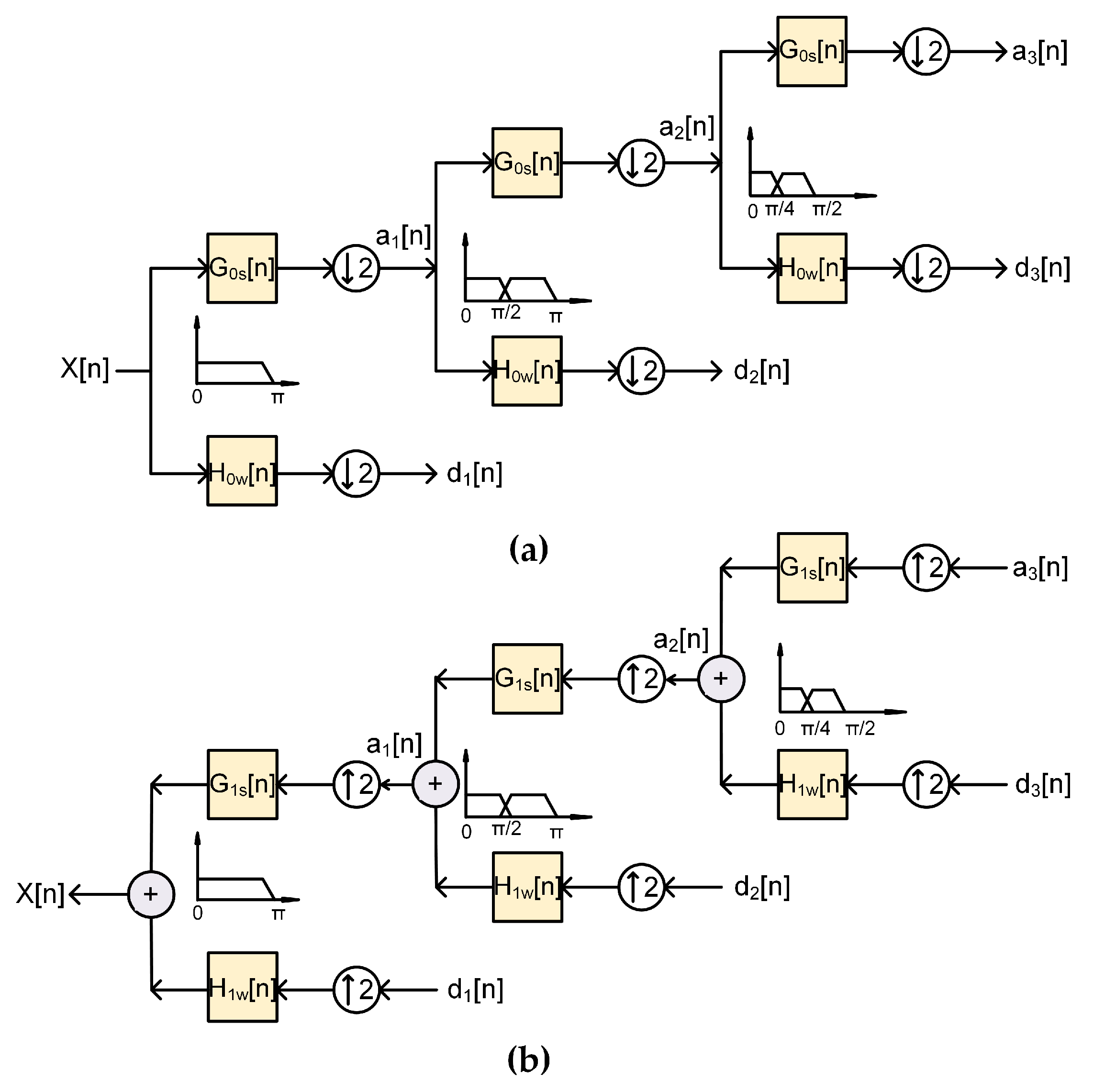
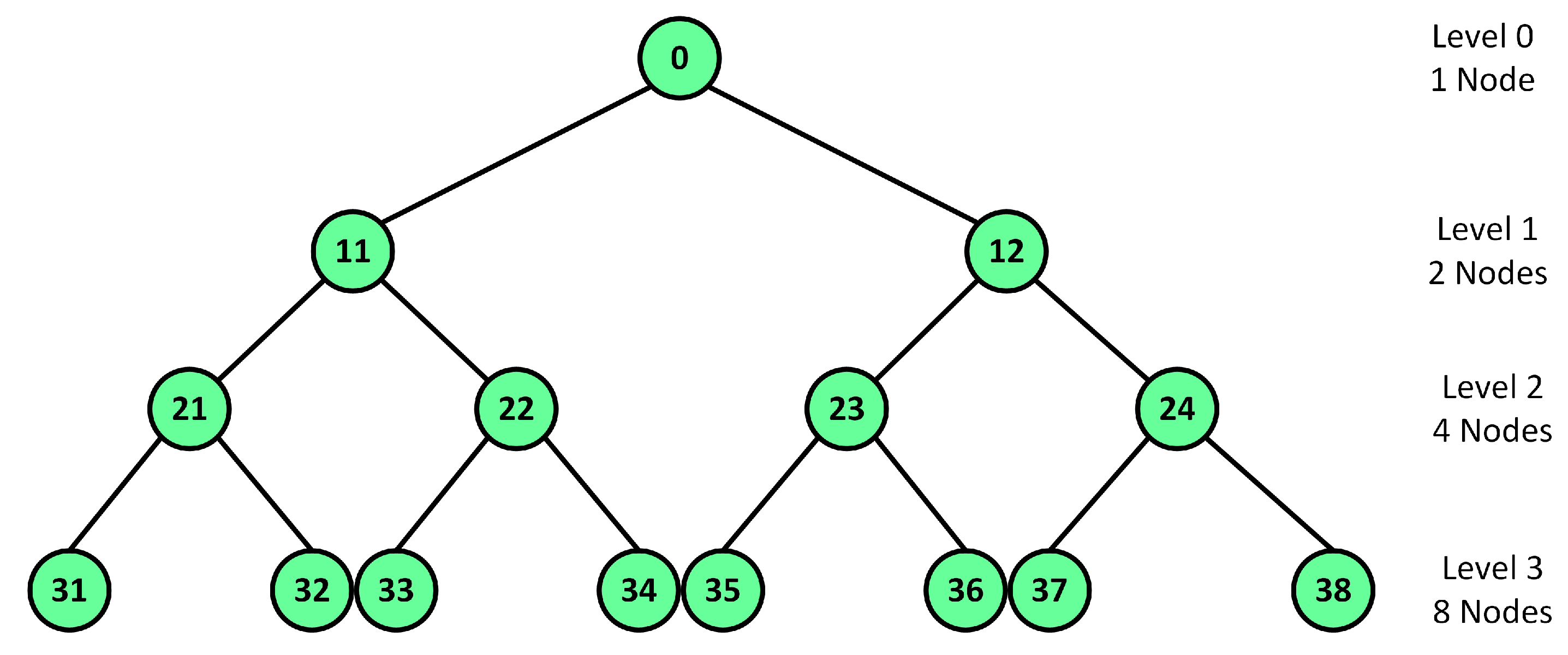
- Provide a brief overview of the generation of DOWP signature waveforms
- Examine the cross-correlation attributes of DOWP signature waveforms and compared it with traditional spreading waveforms
- Investigate the MAI eliminating capability of two sub-optimum linear detectors (ZF and MMSE)
- Evaluate the effectiveness of DOWP-based DWT-MC-CDMA system for multi-users while considering the line-of-sight (LoS) and non-line-of-sight (NLoS) scenarios
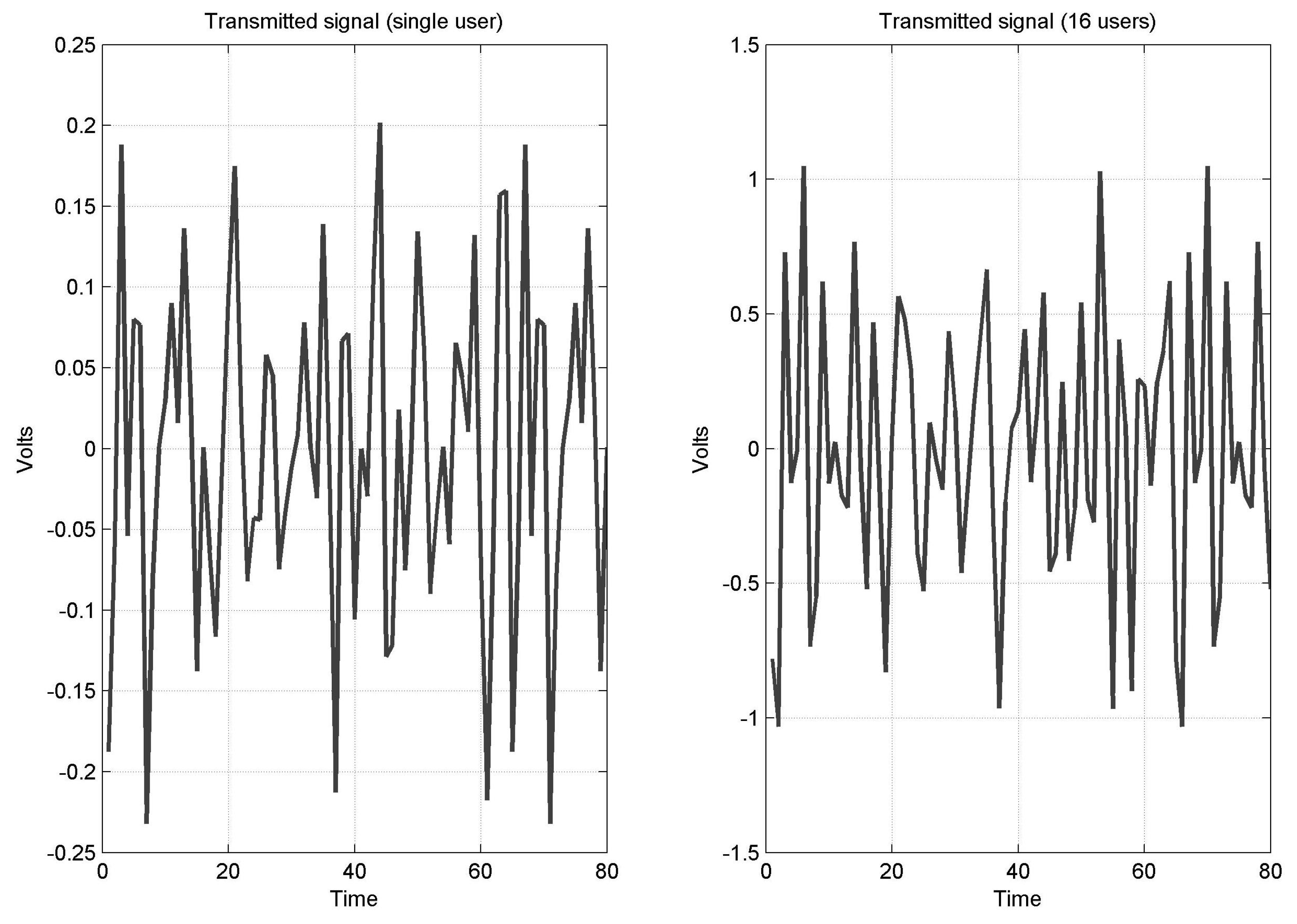
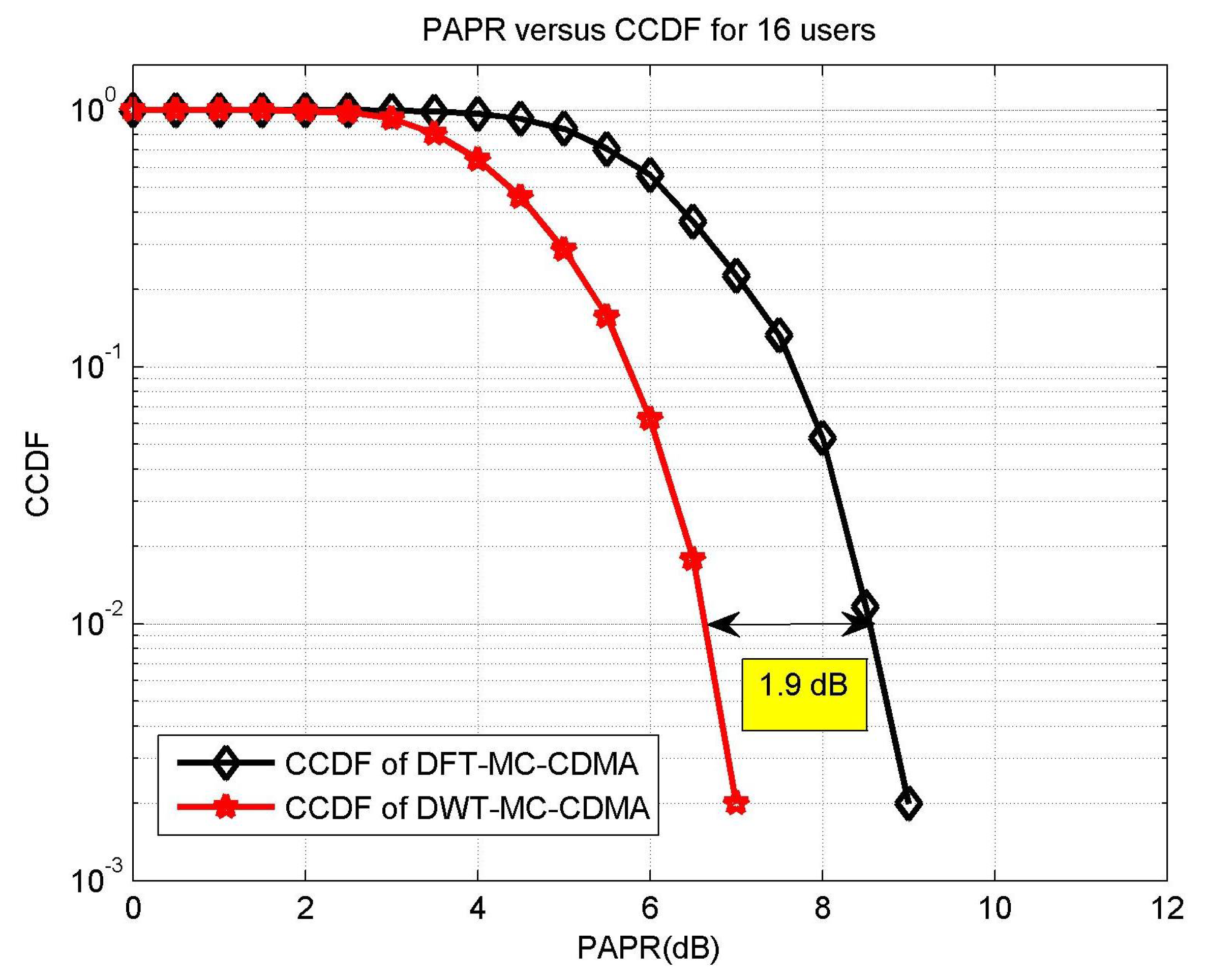
- Study the PAPR reduction ability of DWT-MC-CDMA system using the CCDF graphs
2. Analytical System Modeling
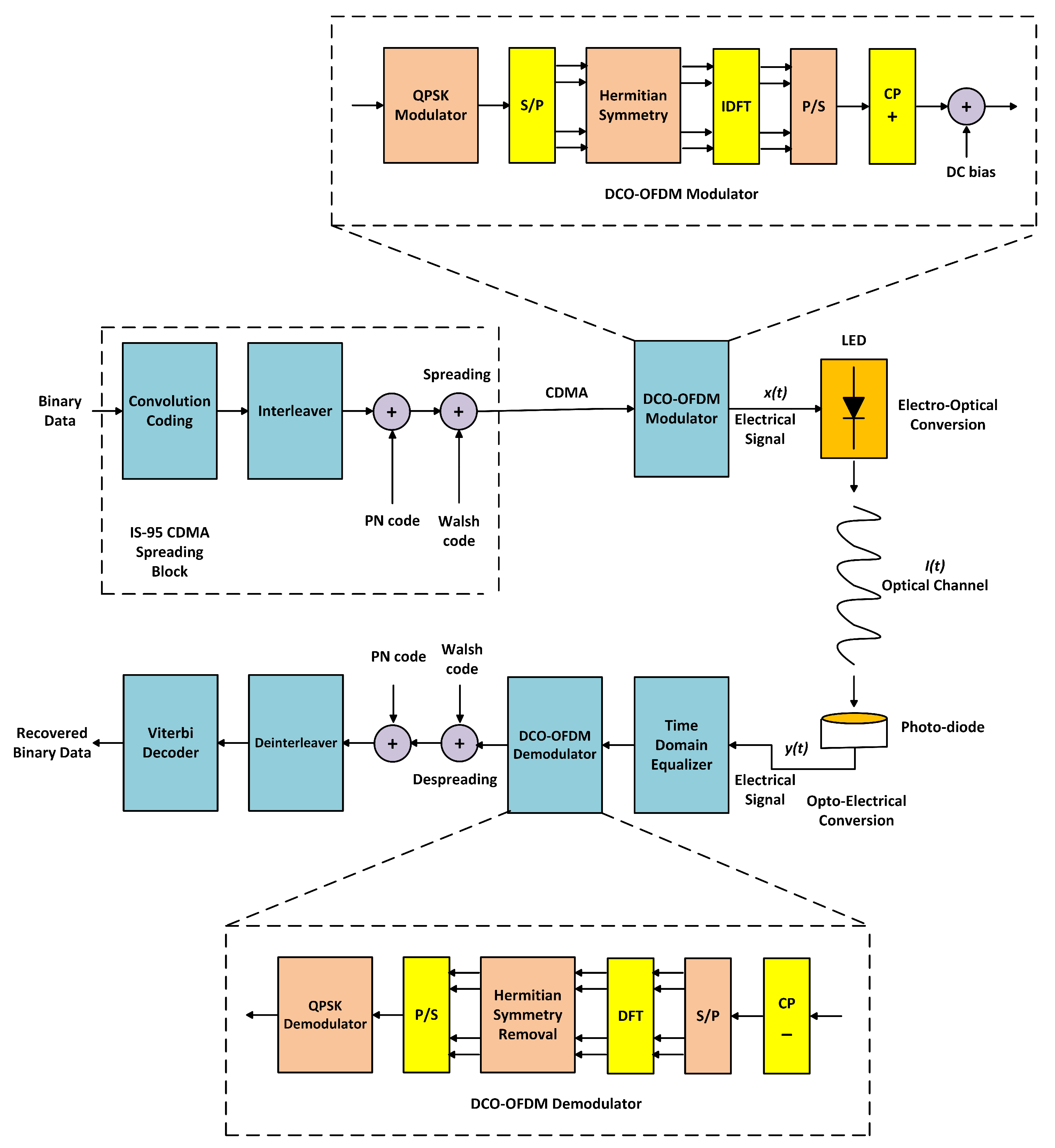
2.1. DFT Based Hybrid Multi-Carrier CDMA
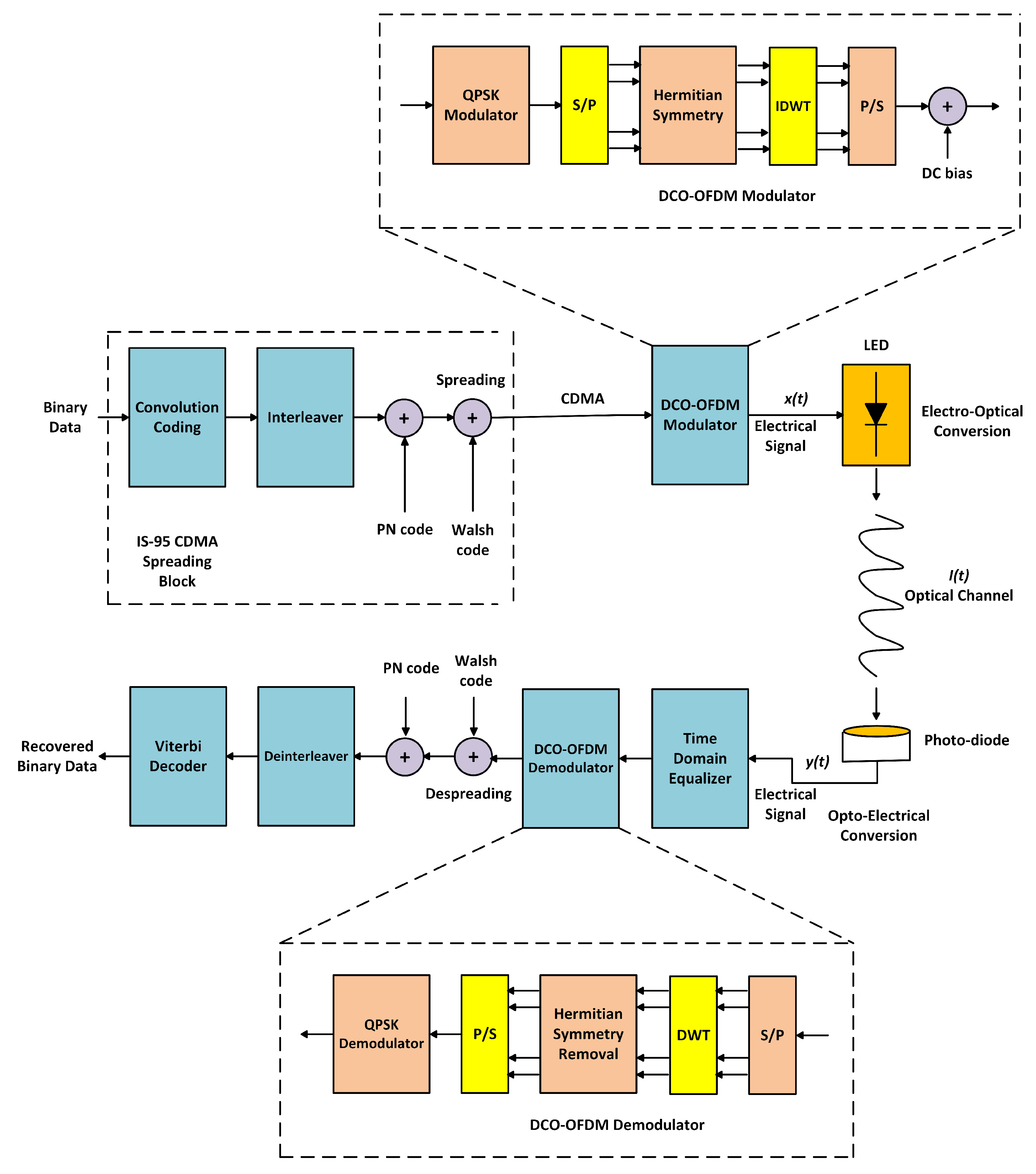
2.2. DWT Based Hybrid Multi-Carrier CDMA
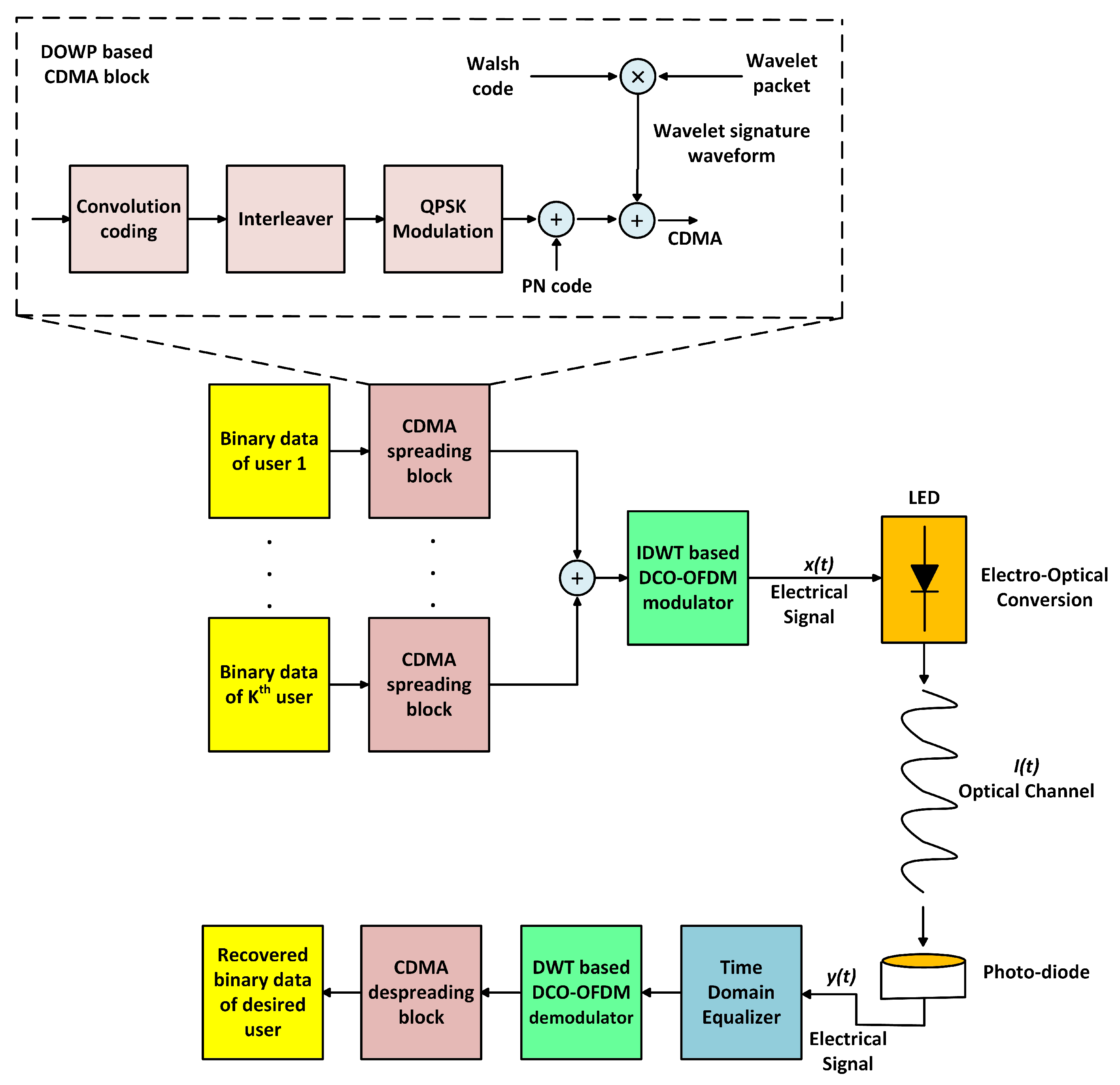
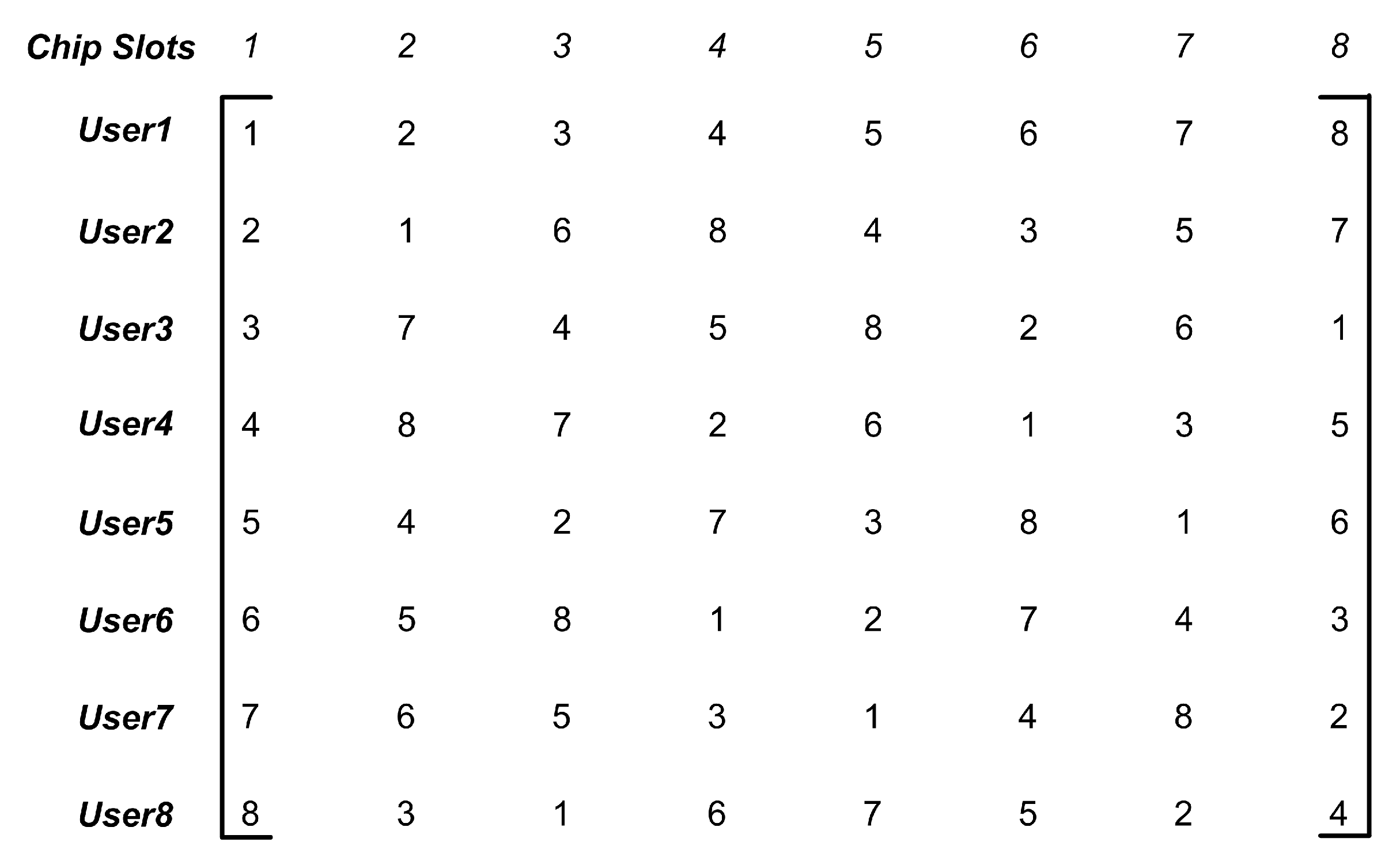
2.3. DOWP Based Multi-Users Hybrid MC-CDMA System
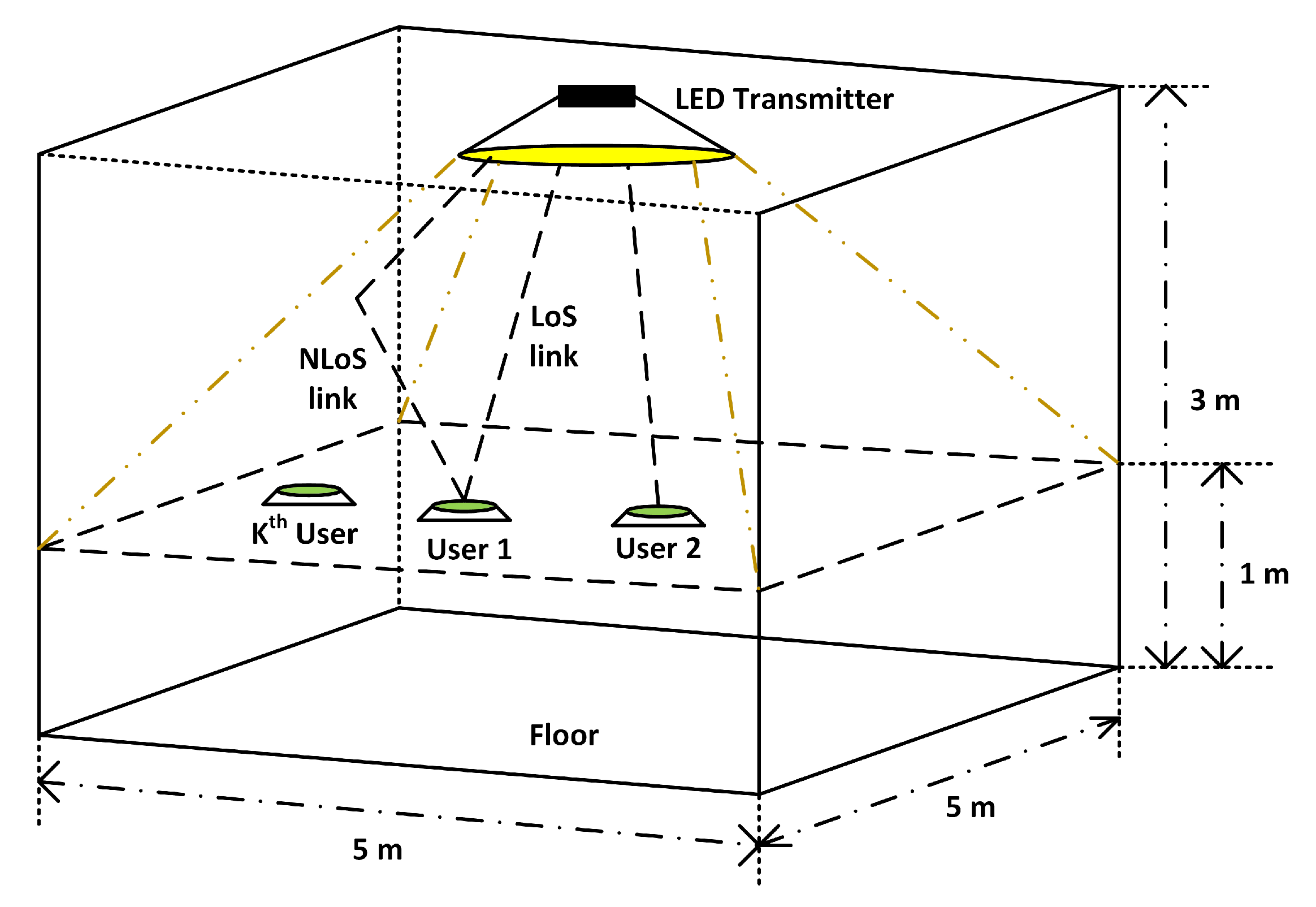
3. VLC Channel Model for Multi-Users Communication
4. Multi-User Detection Techniques
4.1. Zero Forcing (ZF) Based Multi-User Detection
4.2. MMSE Based Multi-User Detection
5. Simulations Outcomes and Analysis
5.1. Simulation Setup
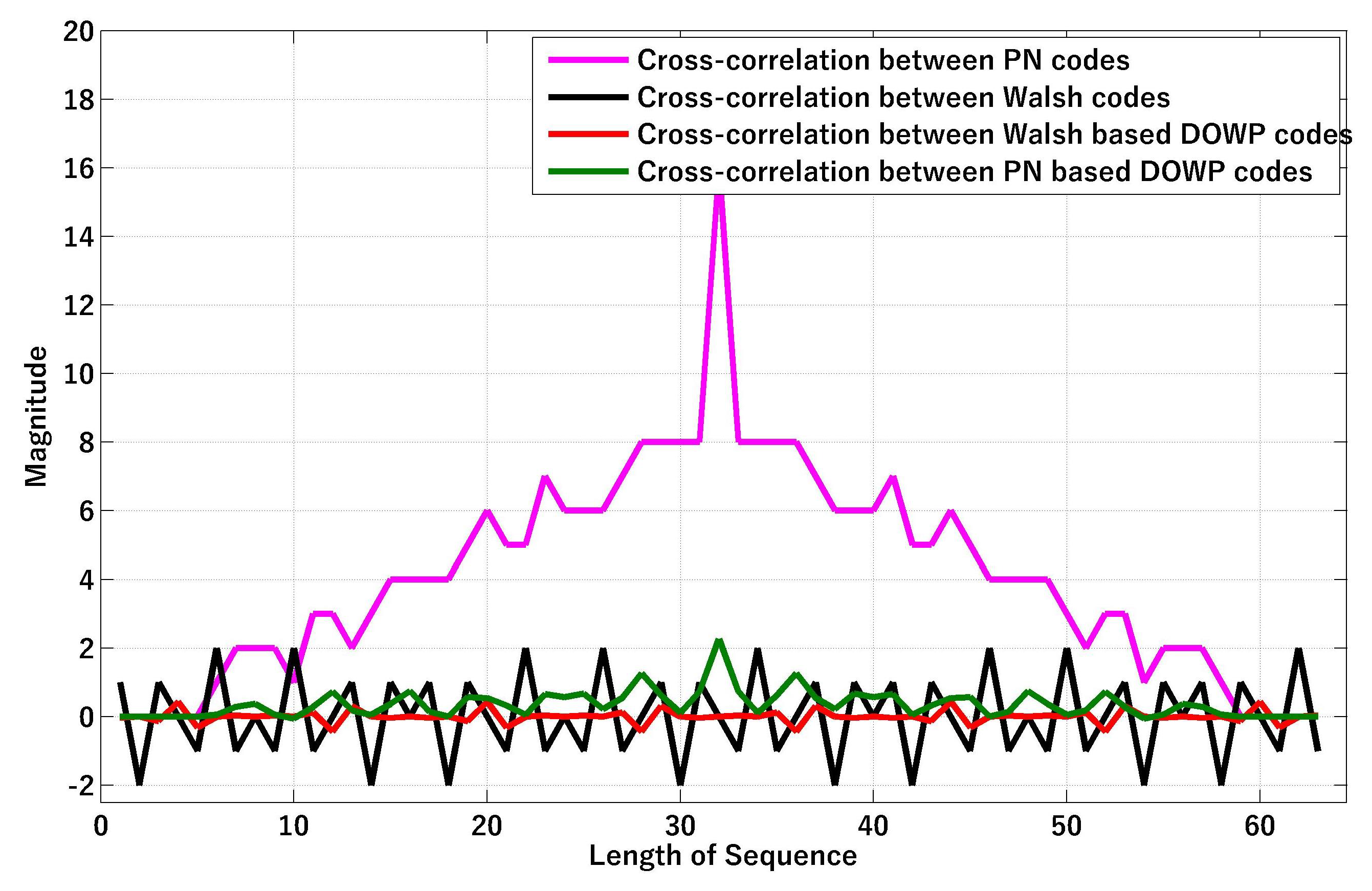
5.2. Cross-Correlation Results for DOWP
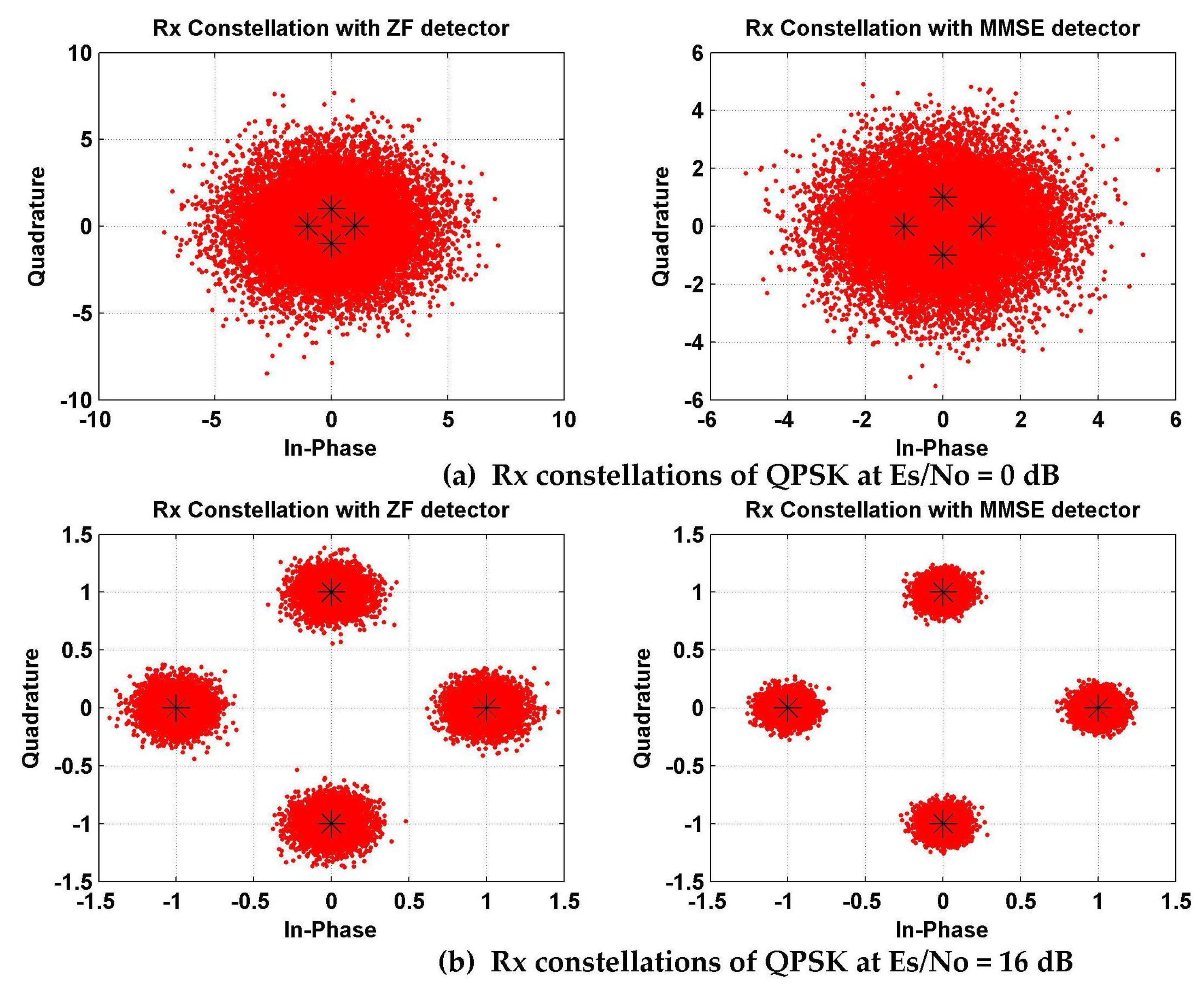
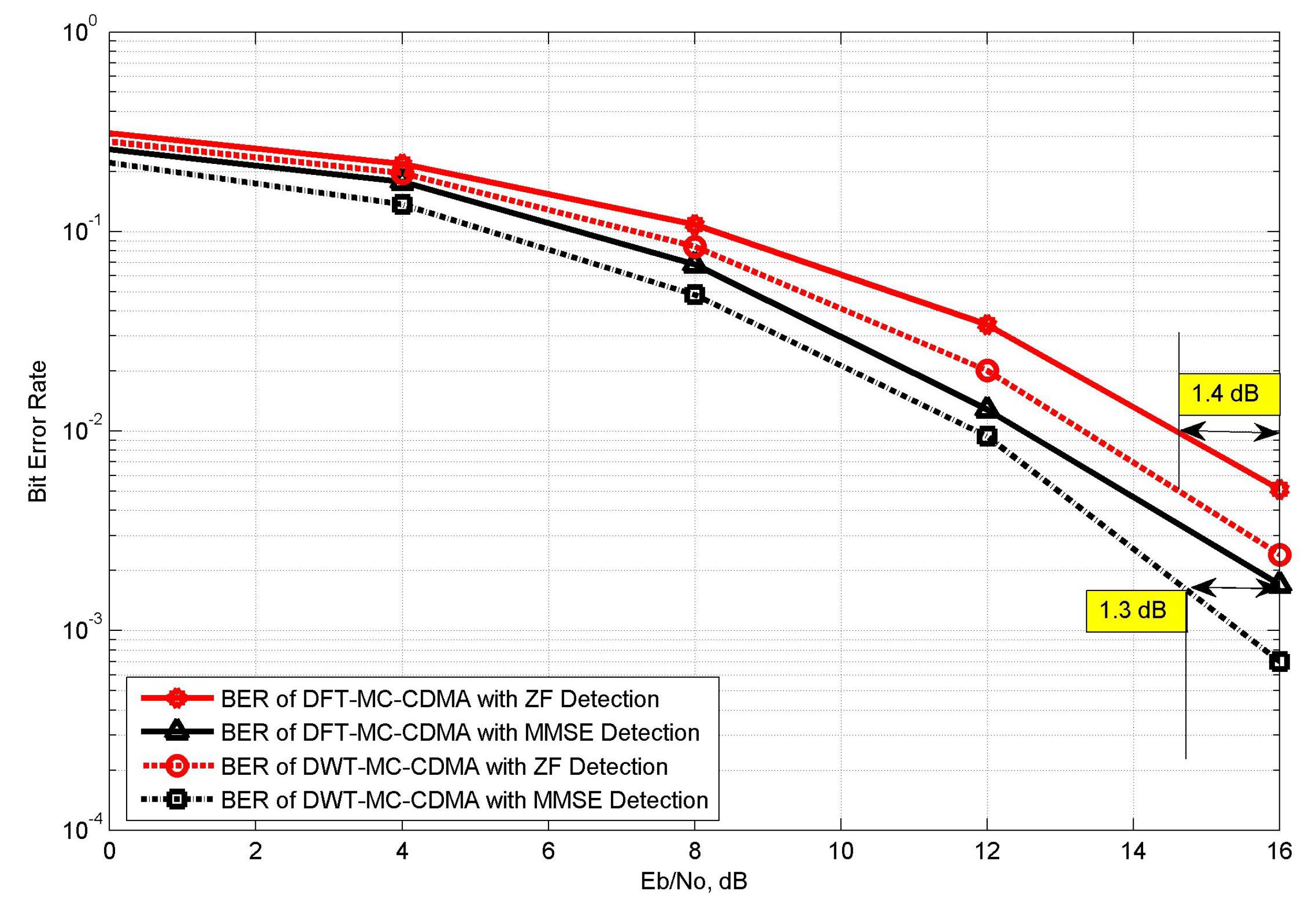
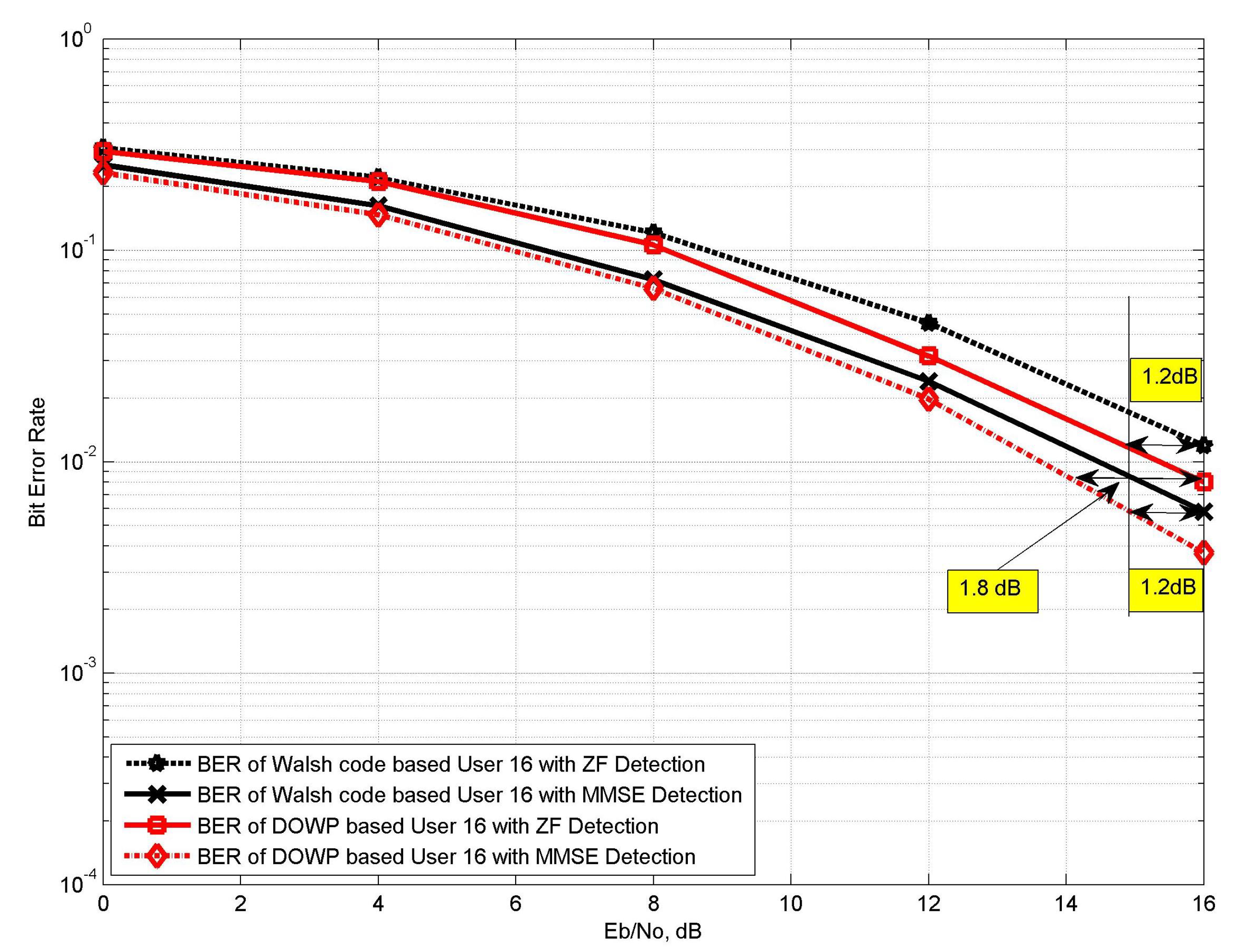
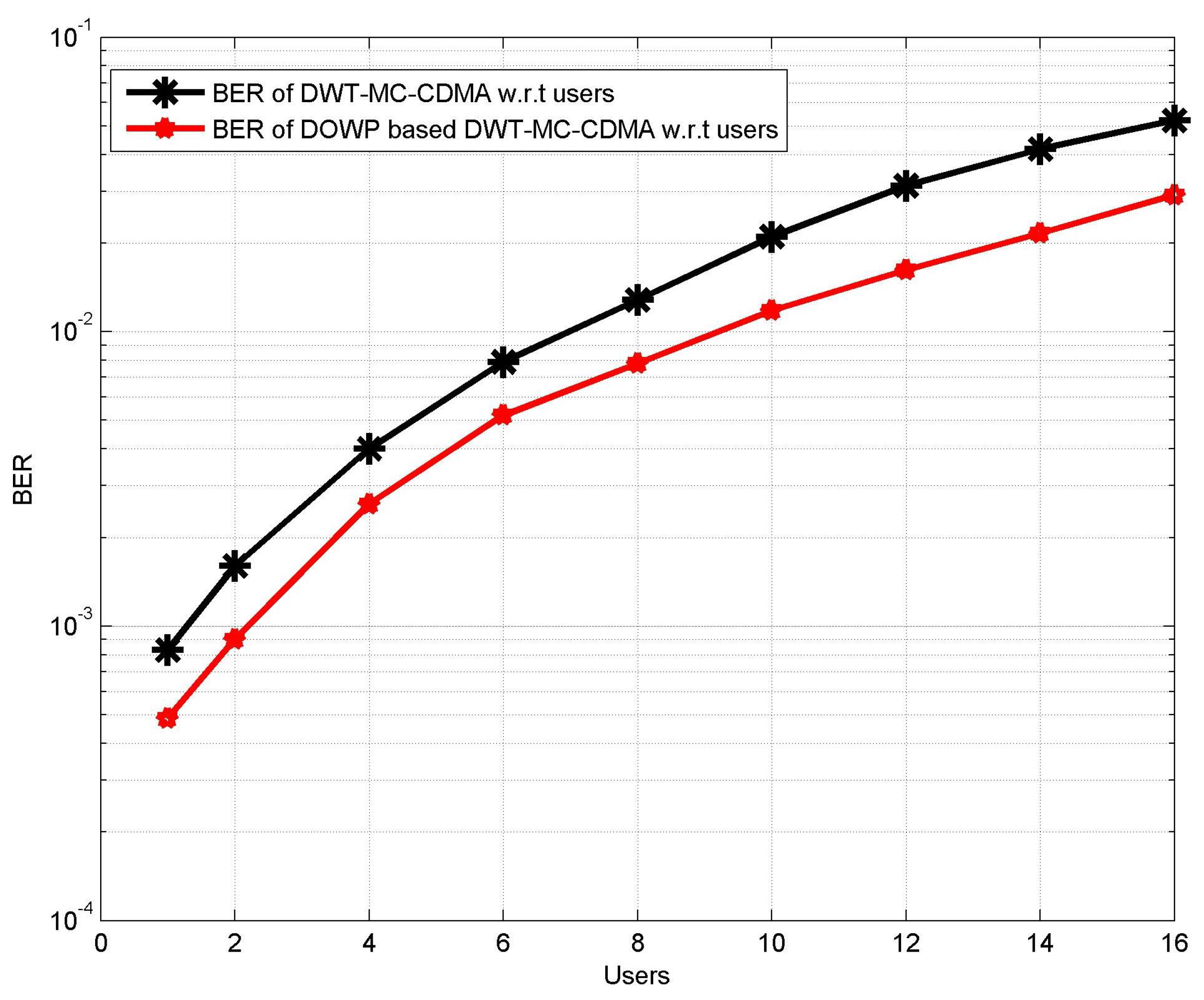
5.3. BER Performance Analysis of Proposed VLC System
5.4. CCDF Based Effectiveness of DWT-MC-CDMA System
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Martínez-Ciro, R.A.; López-Giraldo, F.E.; Betancur-Perez, A.F.; Luna-Rivera, J.M. Design and Implementation of a Multi-Colour Visible Light Communication System Based on a Light-to-Frequency Receiver. Photonics 2019, 6, 42. [Google Scholar] [CrossRef]
- Zvanovec, S.; Chvojka, P.; Haigh, P.A.; Ghassemlooy, Z. Visible light communications towards 5G. Radioengineering 2015, 24, 1–9. [Google Scholar] [CrossRef]
- Sarbazi, E.; Uysal, M. PHY layer performance evaluation of the IEEE 802.15. 7 visible light communication standard. In Proceedings of the 2013 2nd International Workshop on Optical Wireless Communications (IWOW), Newcastle upon Tyne, UK, 21 October 2013; pp. 35–39. [Google Scholar] [CrossRef]
- Ji, R.; Wang, S.; Liu, Q.; Lu, W. High-Speed Visible Light Communications: Enabling Technologies and State of the Art. Appl. Sci. 2018, 8, 589. [Google Scholar] [CrossRef]
- Elgala, H.; Mesleh, R.; Haas, H. Indoor optical wireless communication: Potential and state-of-the-art. IEEE Commun. Mag. 2011, 49. [Google Scholar] [CrossRef]
- Khadr, M.H.; Abd El Aziz, A.; Fayed, H.A.; Aly, M. Bandwidth and BER Improvement Employing a Pre-Equalization Circuit with White LED Arrays in a MISO VLC System. Appl. Sci. 2019, 9, 986. [Google Scholar] [CrossRef]
- Jovicic, A.; Li, J.; Richardson, T. Visible light communication: Opportunities, challenges and the path to market. IEEE Commun. Mag. 2013, 51, 26–32. [Google Scholar] [CrossRef]
- Boucouvalas, A.; Chatzimisios, P.; Ghassemlooy, Z.; Uysal, M.; Yiannopoulos, K. Standards for indoor optical wireless communications. IEEE Commun. Mag. 2015, 53, 24–31. [Google Scholar] [CrossRef]
- Pathak, P.H.; Feng, X.; Hu, P.; Mohapatra, P. Visible light communication, networking, and sensing: A survey, potential and challenges. IEEE Commun. Surv. Tutor. 2015, 17, 2047–2077. [Google Scholar] [CrossRef]
- Martinek, R.; Danys, L.; Jaros, R. Visible Light Communication System Based on Software Defined Radio: Performance Study of Intelligent Transportation and Indoor Applications. Electronics 2019, 8, 433. [Google Scholar] [CrossRef]
- Bawazir, S.S.; Sofotasios, P.C.; Muhaidat, S.; Al-Hammadi, Y.; Karagiannidis, G.K. Multiple Access for Visible Light Communications: Research Challenges and Future Trends. IEEE Access 2018, 6, 26167–26174. [Google Scholar] [CrossRef]
- Elgala, H.; Mesleh, R.; Haas, H.; Pricope, B. OFDM visible light wireless communication based on white LEDs. In Proceedings of the 2007 IEEE 65th Vehicular Technology Conference—VTC2007-Spring, Dublin, Ireland, 22–25 April 2007; pp. 2185–2189. [Google Scholar] [CrossRef]
- Guzmán, B.G.; Jiménez, V.P.G.; Aguayo-Torres, M.C.; Haas, H.; Hanzo, L. Downlink Performance of Optical OFDM in Outdoor Visible Light Communication. IEEE Access 2018, 6, 76854–76866. [Google Scholar] [CrossRef]
- Haigh, P.A.; Ghassemlooy, Z.; Rajbhandari, S.; Papakonstantinou, I.; Popoola, W. Visible light communications: 170 Mb/s using an artificial neural network equalizer in a low bandwidth white light configuration. J. Lightwave Technol. 2014, 32, 1807–1813. [Google Scholar] [CrossRef]
- Basnayaka, D.A.; Haas, H. Hybrid RF and VLC systems: Improving user data rate performance of VLC systems. In Proceedings of the 2015 IEEE 81st Vehicular Technology Conference (VTC Spring), Glasgow, UK, 11–14 May 2015; pp. 1–5. [Google Scholar] [CrossRef]
- Yoo, J.H.; Jung, S.Y. Multi-coded variable PPM with level cutting for high data rate visible light communications. In Proceedings of the 2012 18th Asia-Pacific Conference on Communications (APCC), Jeju Island, Korea, 15–17 October 2012; pp. 703–708. [Google Scholar] [CrossRef]
- Narmanlioglu, O.; Kizilirmak, R.C.; Uysal, M. Performance of OFDM-based adaptive visible light communications. In Proceedings of the 2016 IEEE 10th International Conference on Application of Information and Communication Technologies (AICT), Baku, Azerbaijan, 12–14 October 2016; pp. 1–4. [Google Scholar] [CrossRef]
- Wu, L.; Zhang, Z.; Dang, J.; Liu, H. Adaptive modulation schemes for visible light communications. J. Lightwave Technol. 2014, 33, 117–125. [Google Scholar] [CrossRef]
- Berenguer, P.W.; Jungnickel, V.; Fischer, J.K. The benefit of frequency-selective rate adaptation for optical wireless communications. In Proceedings of the 2016 10th International Symposium on Communication Systems, Networks and Digital Signal Processing (CSNDSP), Prague, Czech Republic, 20–22 July 2016; pp. 1–6. [Google Scholar] [CrossRef]
- Fath, T.; Haas, H. Performance comparison of MIMO techniques for optical wireless communications in indoor environments. IEEE Trans. Commun. 2012, 61, 733–742. [Google Scholar] [CrossRef]
- Sung, J.Y.; Yeh, C.H.; Chow, C.W.; Lin, W.F.; Liu, Y. Orthogonal frequency-division multiplexing access (OFDMA) based wireless visible light communication (VLC) system. Opt. Commun. 2015, 355, 261–268. [Google Scholar] [CrossRef]
- Wang, Q.; Wang, Z.; Dai, L. Multiuser MIMO-OFDM for visible light communications. IEEE Photonics J. 2015, 7, 1–11. [Google Scholar] [CrossRef]
- Al-Ahmadi, S.; Maraqa, O.; Uysal, M.; Sait, S.M. Multi-user visible light communications: State-of-the-art and future directions. IEEE Access 2018, 6, 70555–70571. [Google Scholar] [CrossRef]
- Tsonev, D.; Islim, M.S.; Haas, H. OFDM-based visible light communications. In Optical Wireless Communications; Springer: Cham, Switzerland, 2016; pp. 255–298. [Google Scholar] [CrossRef]
- Armstrong, J. OFDM for optical communications. J. Lightwave Technol. 2009, 27, 189–204. [Google Scholar] [CrossRef]
- Dissanayake, S.D.; Armstrong, J. Comparison of aco-ofdm, dco-ofdm and ado-ofdm in im/dd systems. J. Lightwave Technol. 2013, 31, 1063–1072. [Google Scholar] [CrossRef]
- Giacoumidis, E.; Tsokanos, A.; Mouchos, C.; Zardas, G.; Alves, C.; Wei, J.; Tang, J.; Gosset, C.; Jaouen, Y.; Tomkos, I. Extensive comparisons of optical fast-OFDM and conventional optical OFDM for local and access networks. J. Opt. Commun. Netw. 2012, 4, 724–733. [Google Scholar] [CrossRef]
- Wang, Z.; Wang, Q.; Huang, W.; Xu, Z. Visible Light Communications: Modulation and Signal Processing; John Wiley & Sons: Hoboken, NJ, USA, 2017. [Google Scholar]
- Wang, P.; Xiao, J.; Li, P. Comparison of orthogonal and non-orthogonal approaches to future wireless cellular systems. IEEE Veh. Technol. Mag. 2006, 1, 4–11. [Google Scholar] [CrossRef]
- Marshoud, H.; Sofotasios, P.C.; Muhaidat, S.; Karagiannidis, G.K. Multi-user techniques in visible light communications: A survey. In Proceedings of the 2016 International Conference on Advanced Communication Systems and Information Security (ACOSIS), Marrakesh, Morocco, 17–19 October 2016; pp. 1–6. [Google Scholar] [CrossRef]
- Kazemi, H.; Haas, H. Downlink cooperation with fractional frequency reuse in DCO-OFDMA optical attocell networks. In Proceedings of the 2016 IEEE International Conference on Communications (ICC), Kuala Lumpur, Malaysia, 22–27 May 2016; pp. 1–6. [Google Scholar] [CrossRef]
- Lin, B.; Tang, X.; Yang, H.; Ghassemlooy, Z.; Zhang, S.; Li, Y.; Lin, C. Experimental demonstration of IFDMA for uplink visible light communication. IEEE Photonics Technol. Lett. 2016, 28, 2218–2220. [Google Scholar] [CrossRef]
- Brannstrom, F.; Aulin, T.M.; Rasmussen, L.K. Iterative detectors for trellis-code multiple-access. IEEE Trans. Commun. 2002, 50, 1478–1485. [Google Scholar] [CrossRef]
- Gilhousen, K.S.; Jacobs, I.M.; Padovani, R.; Viterbi, A.J.; Weaver, L.A.; Wheatley, C.E. On the capacity of a cellular CDMA system. IEEE Trans. Veh. Technol. 1991, 40, 303–312. [Google Scholar] [CrossRef]
- Dang, J.; Zhang, Z. Comparison of optical OFDM-IDMA and optical OFDMA for uplink visible light communications. In Proceedings of the 2012 International Conference on Wireless Communications and Signal Processing (WCSP), Huangshan, China, 25–27 October 2012; pp. 1–6. [Google Scholar] [CrossRef]
- Noshad, M.; Brandt-Pearce, M. High-speed visible light indoor networks based on optical orthogonal codes and combinatorial designs. In Proceedings of the 2013 IEEE Global Communications Conference (GLOBECOM), Atlanta, GA, USA, 9–13 December 2013; pp. 2436–2441. [Google Scholar] [CrossRef]
- Guerra-Medina, M.F.; Rojas-Guillama, B.; González, O.; Martín-González, J.A.; Poves, E.; López-Hernández, F.J. Experimental optical code-division multiple access system for visible light communications. In Proceedings of the 2011 Wireless Telecommunications Symposium (WTS), New York, NY, USA, 13–15 April 2011; pp. 1–6. [Google Scholar] [CrossRef]
- Guerra-Medina, M.; Gonzalez, O.; Rojas-Guillama, B.; Martin-Gonzalez, J.; Delgado, F.; Rabadan, J. Ethernet-OCDMA system for multi-user visible light communications. Electron. Lett. 2012, 48, 227–228. [Google Scholar] [CrossRef]
- Shoreh, M.H.; Fallahpour, A.; Salehi, J.A. Design concepts and performance analysis of multicarrier CDMA for indoor visible light communications. J. Opt. Commun. Netw. 2015, 7, 554–562. [Google Scholar] [CrossRef]
- Hara, S.; Prasad, R. Overview of multicarrier CDMA. IEEE Commun. Mag. 1997, 35, 126–133. [Google Scholar] [CrossRef]
- Baig, S.; Asif, H.M.; Umer, T.; Mumtaz, S.; Shafiq, M.; Choi, J.G. High Data Rate Discrete Wavelet Transform-Based PLC-VLC Design for 5G Communication Systems. IEEE Access 2018, 6, 52490–52499. [Google Scholar] [CrossRef]
- Wu, Z.Y.; Gao, Y.L.; Wang, Z.K.; You, C.; Yang, C.; Luo, C.; Wang, J. Optimized DFT-spread OFDM based visible light communications with multiple lighting sources. Opt. Express 2017, 25, 26468–26482. [Google Scholar] [CrossRef]
- Chen, Y.; Yang, C.; Yang, Q.; Liu, W.; Li, C.; Zhang, D. Wavelet transform-OFDM in indoor visible light communication. In Optical Fiber Communication Conference; Optical Society of America: Washington, DC, USA, 2015. [Google Scholar]
- Bulakci, O.; Schuster, M.; Bunge, C.A.; Spinnler, B.; Hanik, N. Wavelet transform based optical OFDM. In Proceedings of the 2009 Conference on Optical Fiber Communication—Incudes Post Deadline Papers, San Diego, CA, USA, 22–26 March 2009; pp. 1–3. [Google Scholar] [CrossRef]
- Zhang, H.; Fan, H.H.; Lindsey, A. Over-loaded DS-CDMA system waveform design using doubly orthogonal wavelet packets. In Proceedings of the IEEE 54th Vehicular Technology Conference—VTC Fall 2001. Proceedings (Cat. No.01CH37211), Atlantic City, NJ, USA, 7–11 October 2001; Volume 2, pp. 1025–1029. [Google Scholar] [CrossRef]
- Hetling, K.; Medley, M.; Saulnier, G.; Das, P. A PR-QMF (wavelet) based spread spectrum communications system. In Proceedings of the Military Communications Conference (MILCOM’94)—Conference Record, Fort Monmouth, NJ, USA, 2–5 October 1994; pp. 760–764. [Google Scholar] [CrossRef]
- Hetling, K.; Saulnier, G.; Das, P. Spreading codes for wireless spread spectrum communications. In Proceedings of the ICC/SUPERCOMM ’96—International Conference on Communications, Dallas, TX, USA, 23–27 June 1996; Volume 1, pp. 68–72. [Google Scholar] [CrossRef]
- Learned, R.E.; Willsky, A.S.; Boroson, D.M. Low complexity optimal joint detection for oversaturated multiple access communications. IEEE Trans. Signal Process. 1997, 45, 113–123. [Google Scholar] [CrossRef]
- Lindsey, A.R. Wavelet packet modulation for orthogonally multiplexed communication. IEEE Trans. Signal Process. 1997, 45, 1336–1339. [Google Scholar] [CrossRef]
- Sklar, B. Digital Communications; Prentice Hall: Upper Saddle River, NJ, USA, 2001; Volume 2. [Google Scholar]
- Sandberg, S.D.; Tzannes, M.A. Overlapped discrete multitone modulation for high speed copper wire communications. IEEE J. Sel. Areas Commun. 1995, 13, 1571–1585. [Google Scholar] [CrossRef]
- Mallat, S. A Wavelet Tour of Signal Processing; Elsevier: Amsterdam, The Netherlands, 1999. [Google Scholar]
- Croisier, A. Perfect channel splitting by use of interpolation/decimation/tree decomposition techniques. In Proceedings of the International Symposium on Information Circuis and Systems, Patras, Greece, 17–21 June 1976. [Google Scholar] [CrossRef]
- Vaidyanathan, P.P. Multirate Systems and Filter Banks; Pearson Education: New Delhi, India, 1993. [Google Scholar]
- Esteban, D.; Galand, C. Application of quadrature mirror filters to split band voice coding schemes. In Proceedings of the IEEE International Conference on Acoustics, Speech, and Signal Processing (ICASSP’77), Hartford, CT, USA, 9–11 May 1977; Volume 2, pp. 191–195. [Google Scholar] [CrossRef]
- Agrawal, S.; Sahu, O. Two-channel quadrature mirror filter bank: An overview. ISRN Signal Process. 2013, 2013. [Google Scholar] [CrossRef]
- Khan, A.; Arif, A.; Nawaz, T.; Baig, S. Walsh Hadamard transform based transceiver design for SC-FDMA with discrete wavelet transform. China Commun. 2017, 14, 193–206. [Google Scholar] [CrossRef]
- Pratama, Y.S.M.; Choi, K.W. Bandwidth Aggregation Protocol and Throughput-Optimal Scheduler for Hybrid RF and Visible Light Communication Systems. IEEE Access 2018, 6, 32173–32187. [Google Scholar] [CrossRef]
- Sewaiwar, A.; Tiwari, S.V.; Chung, Y.H. Smart LED allocation scheme for efficient multiuser visible light communication networks. Opt. Express 2015, 23, 13015–13024. [Google Scholar] [CrossRef] [PubMed]
- Niaz, M.T.; Imdad, F.; Kim, H.S. Power Consumption Efficiency Evaluation of Multi-User Full-Duplex Visible Light Communication Systems for Smart Home Technologies. Energies 2017, 10, 254. [Google Scholar] [CrossRef]
- Marin-Garcia, I.; Guerra, V.; Perez-Jimenez, R. Study and validation of eavesdropping scenarios over a visible light communication channel. Sensors 2017, 17, 2687. [Google Scholar] [CrossRef]
- Yu, Z.; Baxley, R.J.; Zhou, G.T. Multi-user MISO broadcasting for indoor visible light communication. In Proceedings of the International Conference on Acoustics, Speech and Signal Processing (ICASSP), Vancouver, BC, Canada, 26–31 May 2013; pp. 4849–4853. [Google Scholar] [CrossRef]
- Sifaou, H.; Kammoun, A.; Park, K.H.; Alouini, M.S. Robust Transceivers Design for Multi-Stream Multi-User MIMO Visible Light Communication. IEEE Access 2017, 5, 26387–26399. [Google Scholar] [CrossRef]
- Chen, C.; Basnayaka, D.A.; Wu, X.; Haas, H. Efficient Analytical Calculation of Non-Line-of-Sight Channel Impulse Response in Visible Light Communications. J. Lightwave Technol. 2018, 36, 1666–1682. [Google Scholar] [CrossRef]
- Assabir, A.; Elmhamdi, J.; Hammouch, A.; Belhaf, L.; Akherraz, A. The effects of the field of view and reflections on the optical wireless channel. In Proceedings of the International Conference on Electrical and Information Technologies (ICEIT), Rabat, Morocco, 15–18 November 2017; pp. 1–5. [Google Scholar] [CrossRef]
- Bykhovsky, D.; Arnon, S. Multiple access resource allocation in visible light communication systems. J. Lightwave Technol. 2014, 32, 1594–1600. [Google Scholar] [CrossRef]
- Ghassemlooy, Z.; Popoola, W.; Rajbhandari, S. Optical Wireless Communications: System and Channel Modelling With Matlab®; CRC Press: Boca Raton, FL, USA, 2012. [Google Scholar]
- Do, T.H.; Yoo, M. Received power and SNR optimization for visible light communication system. In Proceedings of the 4th International Conference on Ubiquitous and Future Networks (ICUFN), Phuket, Thailand, 4–6 July 2012; pp. 6–7. [Google Scholar] [CrossRef]
- Ganjian, T.; Baghersalimi, G.; Ghassemlooy, Z. Performance evaluation of the received power based on the transmitter position in a visible light communications system. In Proceedings of the Iranian Conference on Electrical Engineering (ICEE), Tehran, Iran, 2–4 May 2017; pp. 1763–1768. [Google Scholar] [CrossRef]
- Hou, Y.; Xiao, S.; Zheng, H.; Hu, W. Multiple access scheme based on block encoding time division multiplexing in an indoor positioning system using visible light. J. Opt. Commun. Netw. 2015, 7, 489–495. [Google Scholar] [CrossRef]
- Komine, T.; Nakagawa, M. Fundamental analysis for visible-light communication system using LED lights. IEEE Trans. Consum. Electron. 2004, 50, 100–107. [Google Scholar] [CrossRef]
- Wang, X.; Lu, W.S.; Antoniou, A. Multiuser detection for multiple-access communications using wavelet-packet transforms. In Proceedings of the Pacific Rim Conference on Communications, Computers and Signal Processing (PACRIM), 10 Years Networking the Pacific Rim, 1987–1997, Victoria, BC, Canada, 20–22 August 1997; Volume 2, pp. 607–610. [Google Scholar] [CrossRef]
- Kühn, V.; Böhnke, R.; Kammeyer, K.D. Multi-user detection in multicarrier-CDMA systems. e&i Elektrotechnik und Informationstechnik 2002, 119, 395–402. [Google Scholar] [CrossRef]
- Moshavi, S. Multi-user detection for DS-CDMA communications. IEEE Commun. Mag. 1996, 34, 124–136. [Google Scholar] [CrossRef]
- Verdii, S. Minimum probability of error for asynchronous Gaussian multiple-access channels. IEEE Trans. Inf. Theory 1986, 32, 85–96. [Google Scholar] [CrossRef]
- Klein, A.; Kaleh, G.K.; Baier, P.W. Zero forcing and minimum mean-square-error equalization for multiuser detection in code-division multiple-access channels. IEEE Trans. Veh. Technol. 1996, 45, 276–287. [Google Scholar] [CrossRef]
- Ueng, F.B.; Wang, H.F.; Chang, R.; Jeng, L.D. Zero forcing and minimum mean square error equalization for OFDM-CDMA multiuser detection in multipath fading channels. In Proceedings of the International Symposium on Intelligent Signal Processing and Communications, Tottori, Japan, 12–15 December 2006; pp. 505–509. [Google Scholar] [CrossRef]
- Poor, H.V.; Verdú, S. Probability of error in MMSE multiuser detection. IEEE Trans. Inf. Theory 1997, 43, 858–871. [Google Scholar] [CrossRef]
- Uzmi, Z.A. Simplified Multiuser Detection for CDMA Systems. Ph.D. Thesis, Stanford University, Stanford, CA, USA, 2002. [Google Scholar]
- Kailath, T.; Sayed, A.H.; Hassibi, B. Linear Estimation; Number Book; Prentice Hall: Upper Saddle River, NJ, USA, 2000. [Google Scholar]
- LUXEON. DS103 LUXEON M Product Datasheet-Lumileds. 2015. Available online: https://www.lumileds.com/uploads/354/DS103-pdf (accessed on 29 March 2019).
- Photonics, H. Si PIN Photodiode. 2017. Available online: https://www.hamamatsu.com/resources/pdf/ssd/s6801_etc_kpin1046e.pdf (accessed on 29 March 2019).
| Parameters | Value |
|---|---|
| Size with lens | 14 mm |
| Effective photosensitive area | 150 mm |
| Cut-off frequency | 50 MHz |
| Responsivity | 0.63 A/W ( = 850 nm) |
| FOV | |
| Operating temperature | C |
| Spectral response range | 320–1060 nm |
| Parameters | DFT-MC-CDMA | DWT-MC-CDMA |
|---|---|---|
| Number of active users | 16 | 16 |
| Number of Data Bits | 184 | 184 |
| Nominal data rate | 9.6 Kbps | 9.6 Kbps |
| Chip rate | 1.2288 Mcps | 1.2288 Mcps |
| Channel coding | Convolution coding with rate | Convolution coding with rate |
| Spreading code | 64-bit Walsh code | 64-bit Walsh code |
| Modulation | QPSK | QPSK |
| Samples per sub-carrier | 64 | 64 |
| CP | thportion of signal | Not required |
| Channel | LoS + NLoS VLC Channel | LoS + NLoS VLC Channel |
| Noise | Shot Noise Modeled as AWGN | Shot Noise Modeled as AWGN |
| Detection Technique | ZF and MMSE | ZF and MMSE |
| Channel Decoder | Viterbi Decoder | Viterbi Decoder |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Khalid, A.; Asif, H.M.; Kostromitin, K.I.; Al-Otaibi, S.; Saidul Huq, K.M.; Rodriguez, J. Doubly Orthogonal Wavelet Packets for Multi-Users Indoor Visible Light Communication Systems. Photonics 2019, 6, 85. https://doi.org/10.3390/photonics6030085
Khalid A, Asif HM, Kostromitin KI, Al-Otaibi S, Saidul Huq KM, Rodriguez J. Doubly Orthogonal Wavelet Packets for Multi-Users Indoor Visible Light Communication Systems. Photonics. 2019; 6(3):85. https://doi.org/10.3390/photonics6030085
Chicago/Turabian StyleKhalid, Arslan, Hafiz Muhammad Asif, Konstantin I. Kostromitin, Sattam Al-Otaibi, Kazi Mohammed Saidul Huq, and Jonathan Rodriguez. 2019. "Doubly Orthogonal Wavelet Packets for Multi-Users Indoor Visible Light Communication Systems" Photonics 6, no. 3: 85. https://doi.org/10.3390/photonics6030085
APA StyleKhalid, A., Asif, H. M., Kostromitin, K. I., Al-Otaibi, S., Saidul Huq, K. M., & Rodriguez, J. (2019). Doubly Orthogonal Wavelet Packets for Multi-Users Indoor Visible Light Communication Systems. Photonics, 6(3), 85. https://doi.org/10.3390/photonics6030085





