Generation of Coherent and Spatially Squeezed States of an Electromagnetic Beam in a Planar Inhomogeneous Dielectric Waveguide
Abstract
1. Introduction
2. Model and Methods
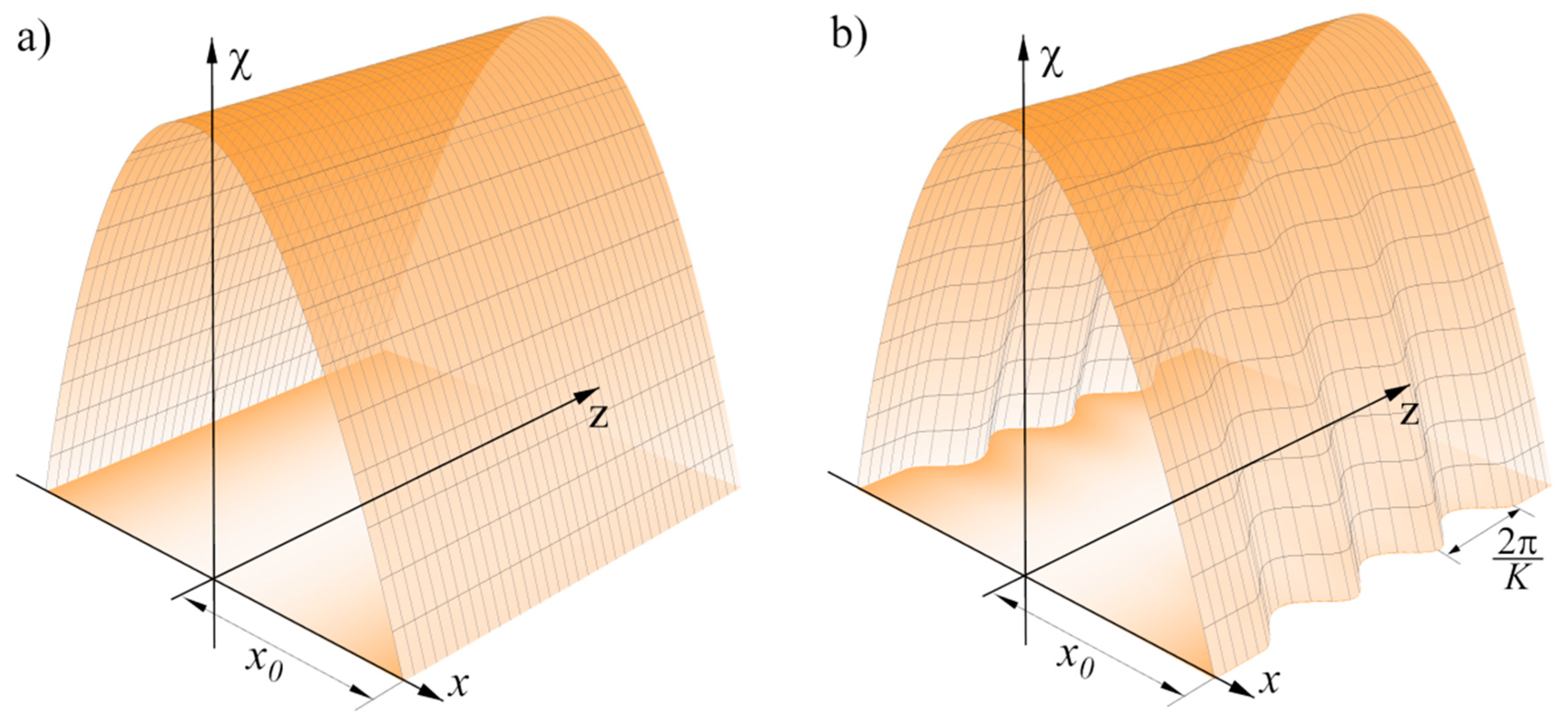
2.1. Optical–Mechanical Analogy and Transverse Spatial Modes of the Beam
2.2. Coherent Spatial States of the Beam
2.3. Spatially Squeezed Vacuum State of the Beam
3. Results
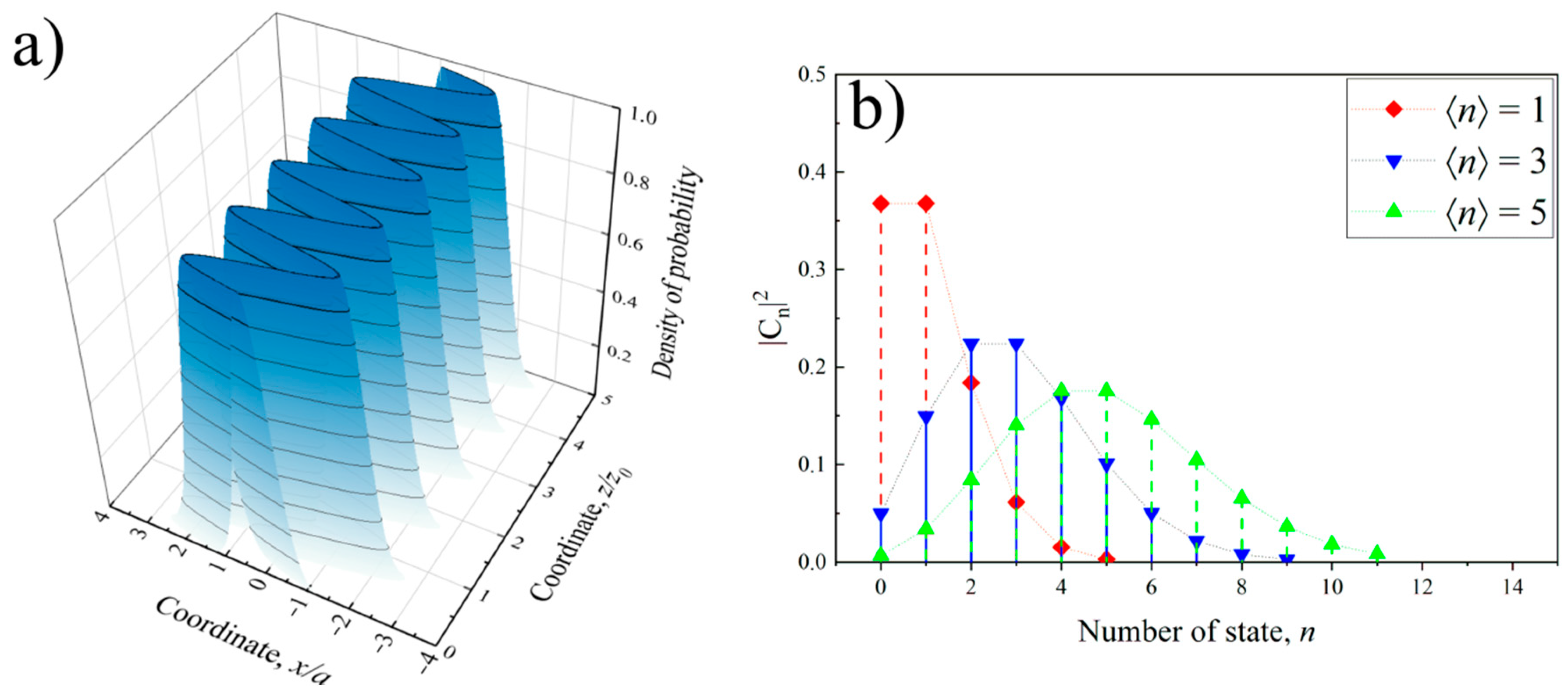
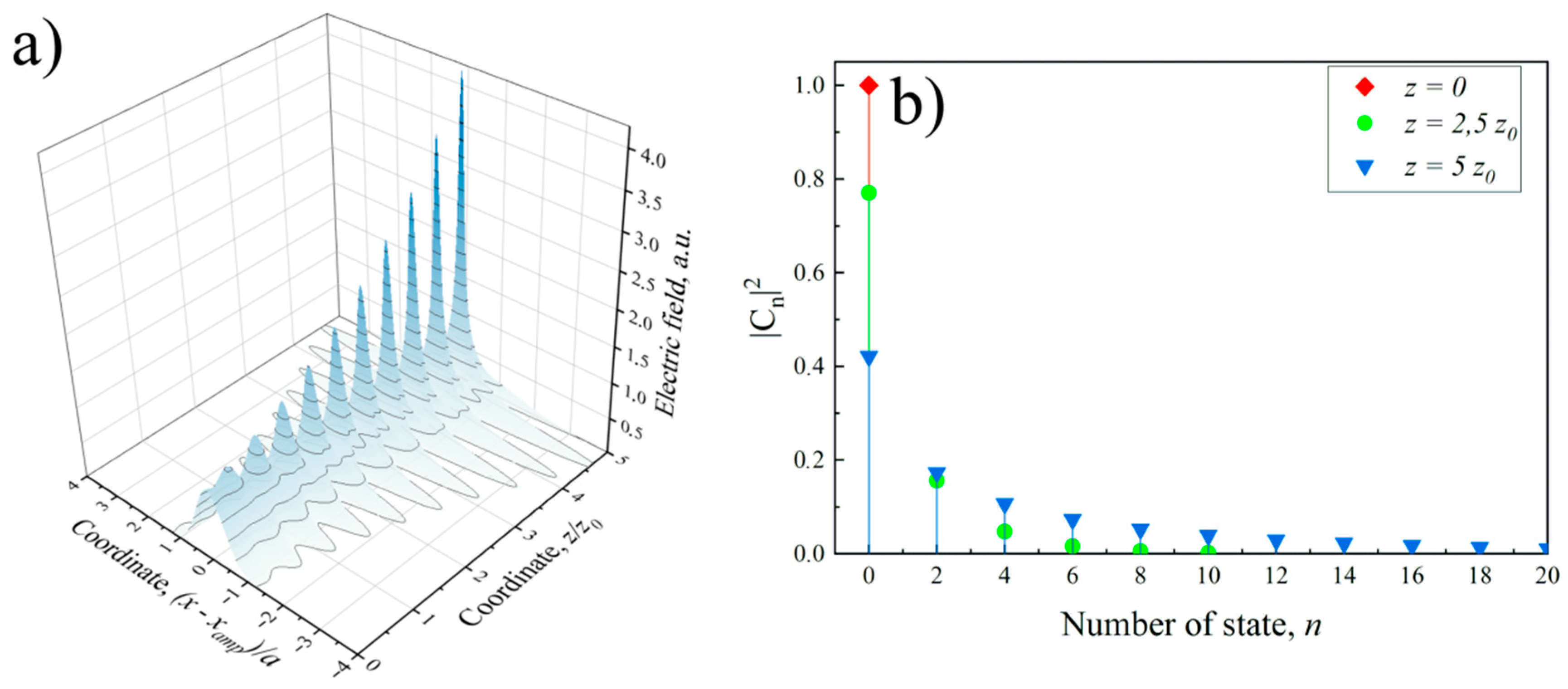
3.1. Excitation of the Transverse Coherent Spatial State of the Beam
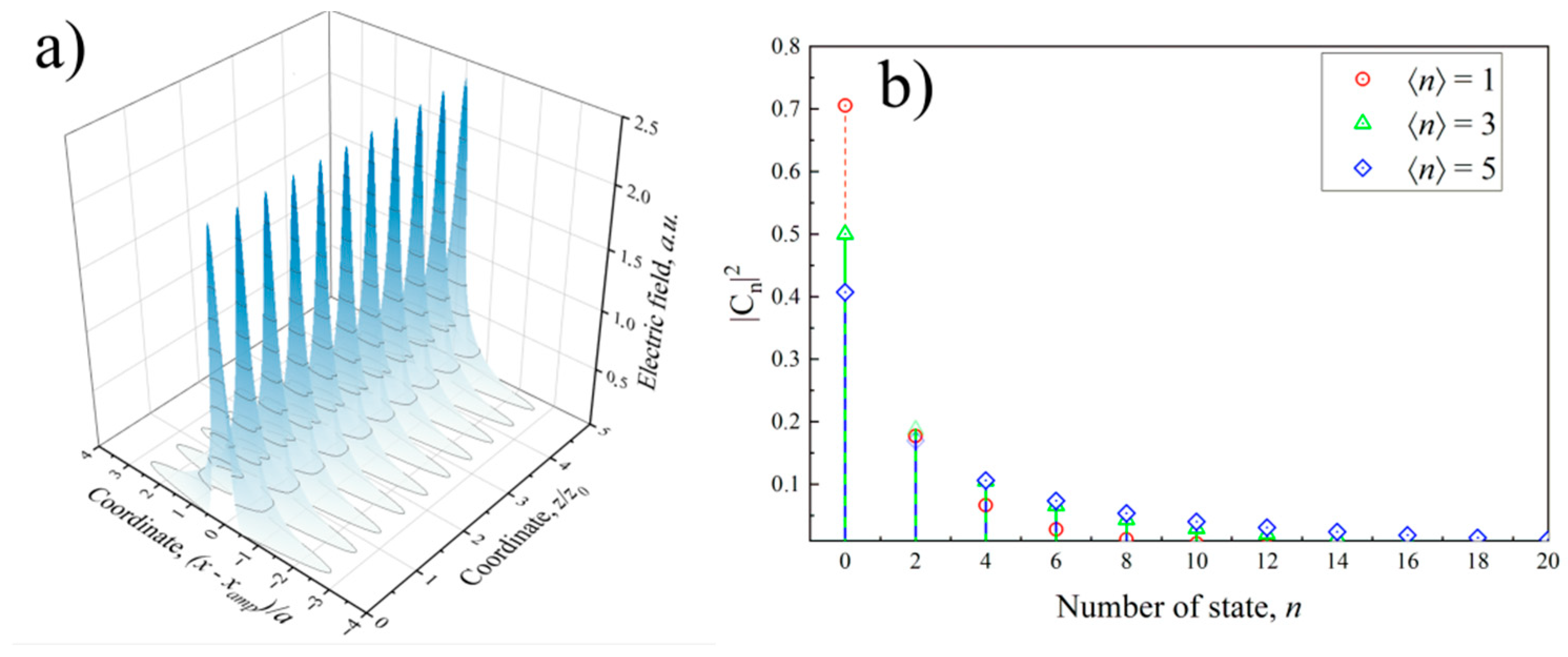
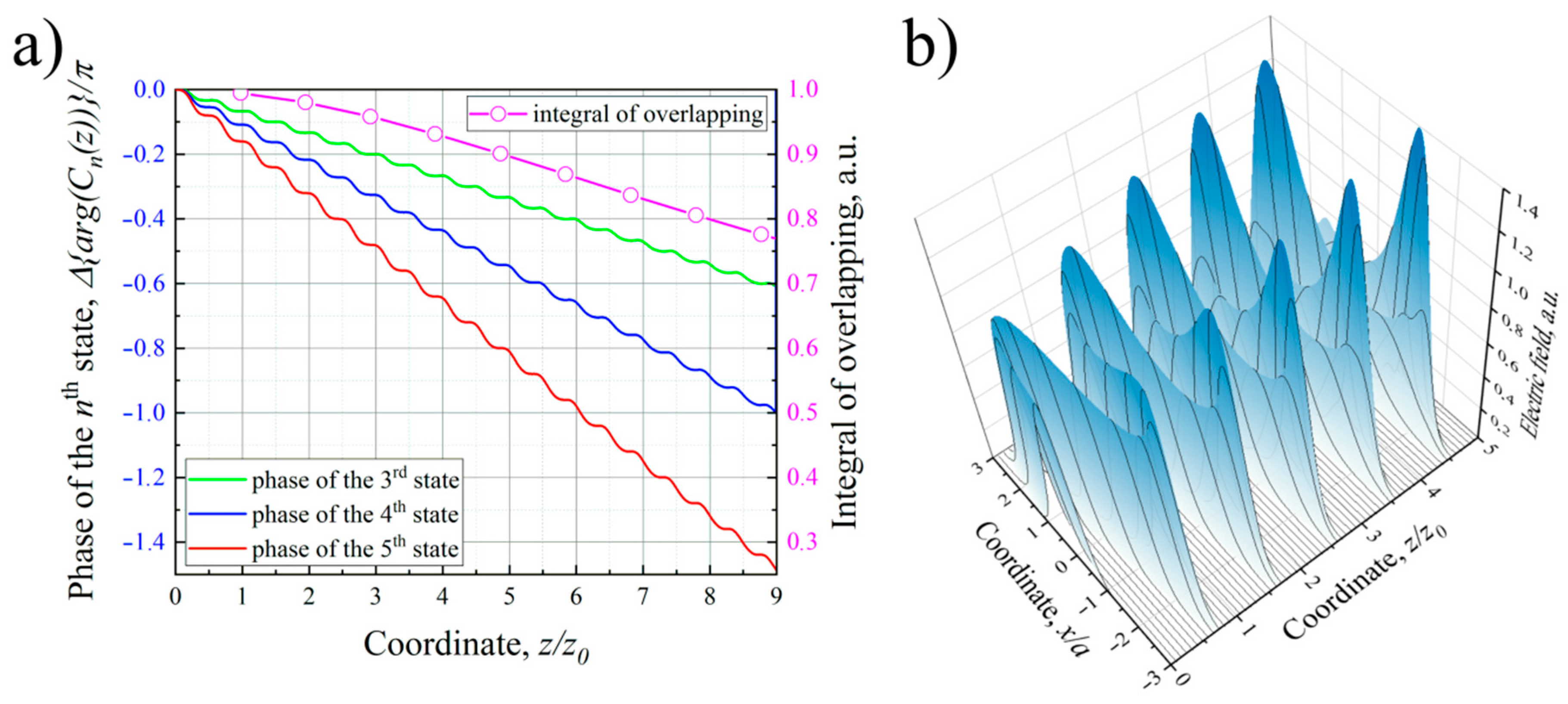
3.2. Excitation of the Spatially Squeezed Vacuum State of the Beam
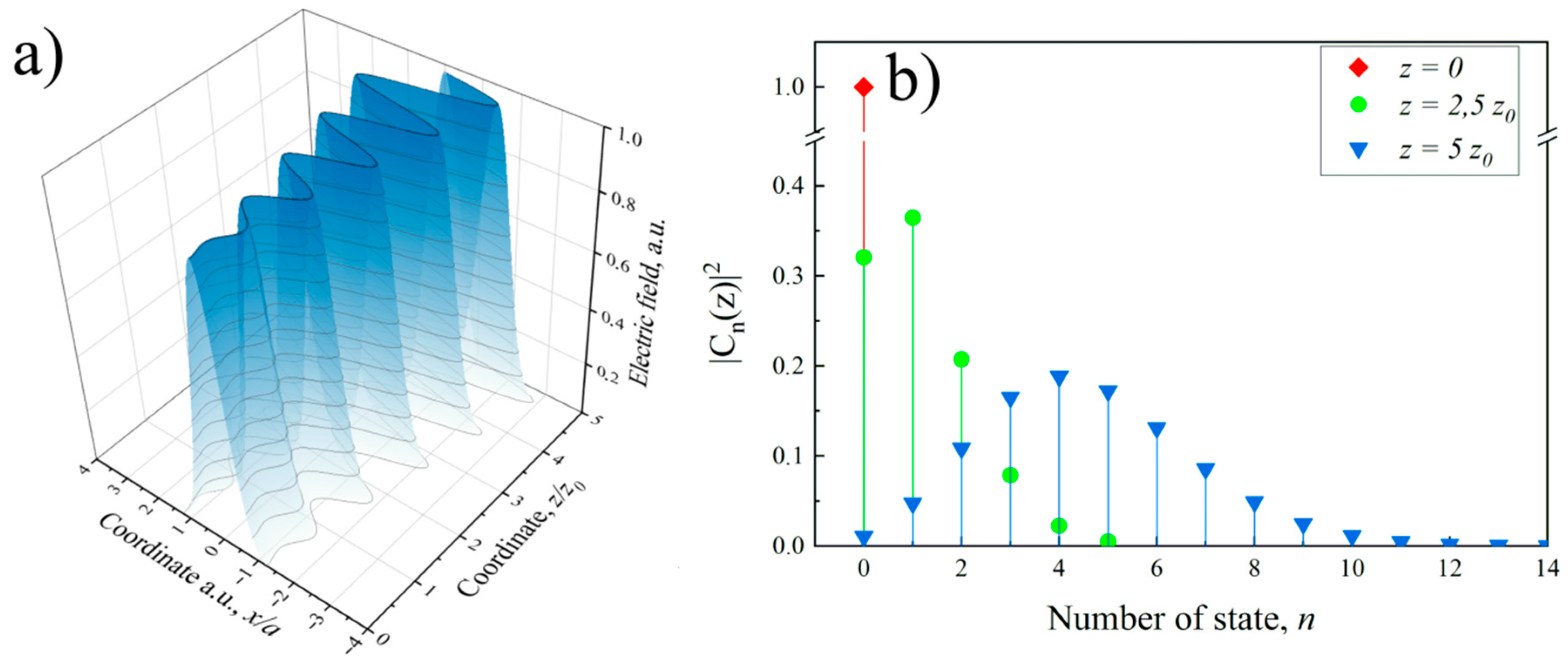
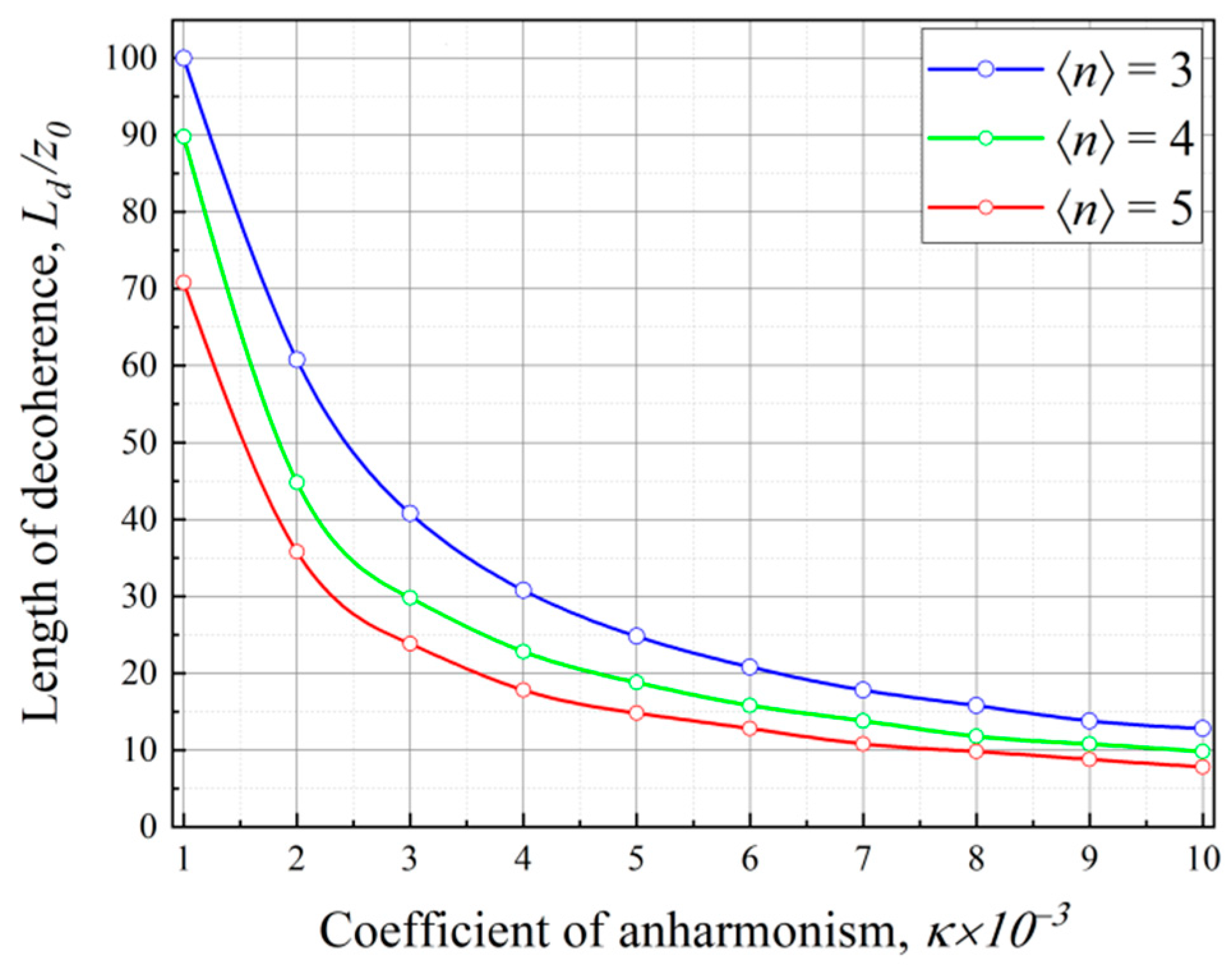
3.3. Decoherence of the Spatial Transverse Beam Structure
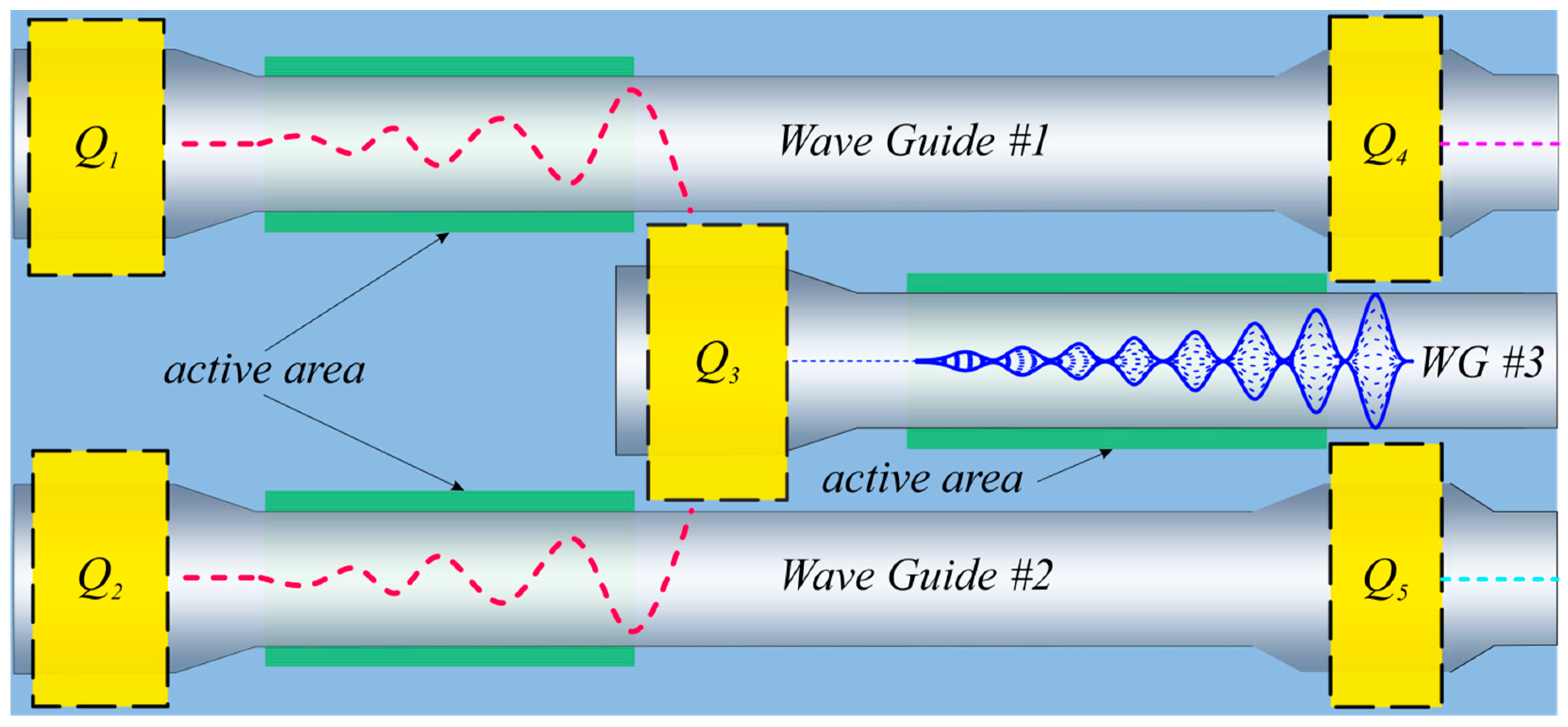
4. Discussion
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Debnath, S.; Linke, N.M.; Figgatt, C.; Landsman, K.A.; Wright, K.; Monroe, C. Demonstration of a small programmable quantum computer with atomic qubits. Nature 2016, 536, 63–66. [Google Scholar] [CrossRef] [PubMed]
- Pokharel, B.; Anand, N.; Fortman, B.; Lidar, D.A. Demonstration of fidelity improvement using dynamical decoupling with superconducting qubits. Phys. Rev. Lett. 2018, 121, 220502. [Google Scholar] [CrossRef] [PubMed]
- Shvartsburg, A.B. Tunneling of electromagnetic waves: Paradoxes and prospects. Phys. Uspekhi 2007, 50, 37–51. [Google Scholar] [CrossRef]
- Bogdanov, S.; Shalaginov, M.Y.; Boltasseva, A.; Shalaev, V.M. Material platforms for integrated quantum photonics. Opt. Mater. Express 2017, 7, 111–132. [Google Scholar] [CrossRef]
- Majumder, A.; Shen, B.; Polson, R.; Menon, R. Ultra-compact polarization rotation in integrated silicon photonics using digital metamaterials. Opt. Express 2017, 25, 19721–19731. [Google Scholar] [CrossRef] [PubMed]
- Lee, K.S.; Erdogan, T. Fiber mode coupling in transmissive and reflective tilted fiber gratings. Appl. Opt. 2000, 39, 1394–1404. [Google Scholar] [CrossRef]
- Kartashov, Y.V.; Vysloukh, V.A.; Torner, L. Resonant mode oscillations in modulated waveguiding structures. Phys. Rev. Lett. 2007, 99, 233903. [Google Scholar] [CrossRef] [PubMed]
- Zhang, X.; Ye, F.; Kartashov, Y.V.; Chen, X. Rabi oscillations and stimulated mode conversion on the subwavelength scale. Opt. Express 2015, 23, 6731–6737. [Google Scholar] [CrossRef]
- Anuszkiewicz, A.; Kasztelanic, R.; Filipkowski, A.; Stepniewski, G.; Stefaniuk, T.; Siwicki, B.; Pysz, D.; Klimczak, M.; Buczynski, R. Fused silica optical fibers with graded index nanostructured core. Sci. Rep. 2019, 8, 12329. [Google Scholar] [CrossRef]
- Bogatskaya, A.V.; Klenov, N.V.; Tereshonok, M.V.; Popov, A.M. “Quantum effects” for classical light in modern waveguide circuits. Laser Phys. Lett. 2019, 16, 056006. [Google Scholar] [CrossRef]
- Bogatskaya, A.V.; Klenov, N.V.; Popov, A.M.; Rakhimov, A.T. “Coherent Transitions” and Rabi-type Oscillations between Spatial Modes of Classical Light. In Proceedings of the 7th International Conference on Photonics, Optics and Laser Technology, Prague, Czech Republic, 25–27 February 2019; pp. 97–101. [Google Scholar] [CrossRef]
- Leontovich, M.A.; Fock, V.A. The solution of the problem for electromagnetic waves diffraction near the Earth by the parabolic equation method. ZhETF 1946, 16, 557. (In Russian) [Google Scholar]
- Akhmanov, S.A. Khokhlov’s method in the theory of nonlinear waves. Phys. Uspekhi 1986, 29, 589–606. [Google Scholar]
- Bergé, L.; Skupin, S.; Nuter, R.; Kasparian, J.; Wolf, J.-P. Ultrashort filaments of light in weakly ionized, optically transparent media. Rep. Prog. Phys. 2007, 70, 1633. [Google Scholar] [CrossRef]
- Couairon, A.; Mysyrowicz, A. Femtosecond filamentation in transparent media. Phys. Rep. 2007, 441, 47–189. [Google Scholar] [CrossRef]
- Chekalin, S.V.; Kandidov, V.P. From self-focusing light beams to femtosecond laser pulse filamentation. Phys. Uspekhi 2013, 56, 123. [Google Scholar] [CrossRef]
- Zheltikov, A.M. The Raman effect in femto- and attosecond physics. Phys. Uspekhi 2011, 54, 29. [Google Scholar] [CrossRef]
- Scully, M.O.; Zubairy, M.S. Quantum Optics; Cambridge University Press: Cambridge, UK, 1997. [Google Scholar]
- Sсhrodinger, E. Der stetige Ubergang von der Mikro-zur Makromechanik. Naturwissenschaften 1926, 14, 664–666. (In German) [Google Scholar] [CrossRef]
- Glauber, R.J. Photon correlations. Phys. Rev. Lett. 1963, 10, 84. [Google Scholar] [CrossRef]
- Stoler, D. Equivalence classes of minimum uncertainty packets. Phys. Rev. D 1970, 1, 3217. [Google Scholar] [CrossRef]
- Slusher, R.E.; Holleberg, L.W.; Yurke, B.; Mertz, J.C.; Valleys, J.F. Observation of Squeezed States Generated by Four-Wave Mixing in an Optical Cavity. Phys. Rev. Lett. 1985, 55, 2409. [Google Scholar] [CrossRef]
- Wu, L.-A.; Kimble, H.J.; Hall, J.H.; Huifa, W. Generation of Squeezed States by Parametric Down Conversion. Phys. Rev. Lett. 1986, 57, 2520. [Google Scholar] [CrossRef]
- Janszky, J.; Yushin, Y. Amplification of squeezed light and multiphoton processes. Phys. Lett. A 1989, 137, 451–452. [Google Scholar] [CrossRef]
- Spasibko, K.Y.; Iskhakov, T.S.; Chekhova, M.V. Spectral properties of high-gain parametric down-conversion. Opt. Express 2012, 20, 7507–7515. [Google Scholar] [CrossRef]
- Agafonov, I.N.; Chekhova, M.V.; Leuchs, G. Two-color bright squeezed vacuum. Phys. Rev. A 2010, 82, 011801. [Google Scholar] [CrossRef]
- Bogatskaya, A.V.; Popov, A.M. Dynamics of an atomic system in a strong non-classical electromagnetic field. Laser Phys. 2013, 23, 07530. [Google Scholar] [CrossRef]
- Gu, X.; Kockum, A.F.; Miranowic, A.; Liu, Y.; Nori, F. Microwave photonics with superconducting quantum circuits. Phys. Rep. 2017, 718–719, 1–102. [Google Scholar] [CrossRef]
- Klenov, N.V.; Kuznetsov, A.V.; Soloviev, I.I.; Bakurski, S.V.; Tikhonova, O.V. Magnetic reversal dynamics of a quantum system on a picosecond timescale. Beilstein J. Nanotechnol. 2015, 6, 1946. [Google Scholar] [CrossRef]
| Parameter | µm-Range | mm-Range |
|---|---|---|
| k, cm−1 | 104 | 10 |
| x0, cm | ≈2 × 10−3 | ≈2 |
| , cm | ≈2.5 × 10−4 | ≈2.5 × 10−1 |
| , cm−1 | ≈1.6 × 103 | ≈1.6 |
| , cm | ≈3.9 × 10−3 | ≈3.9 |
| 1 | 1 | |
| 0.5 | 0.5 | |
| 0.01 | 0.01 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bogatskaya, A.; Schegolev, A.; Klenov, N.; Popov, A. Generation of Coherent and Spatially Squeezed States of an Electromagnetic Beam in a Planar Inhomogeneous Dielectric Waveguide. Photonics 2019, 6, 84. https://doi.org/10.3390/photonics6030084
Bogatskaya A, Schegolev A, Klenov N, Popov A. Generation of Coherent and Spatially Squeezed States of an Electromagnetic Beam in a Planar Inhomogeneous Dielectric Waveguide. Photonics. 2019; 6(3):84. https://doi.org/10.3390/photonics6030084
Chicago/Turabian StyleBogatskaya, Anna, Andrey Schegolev, Nikolay Klenov, and Alexander Popov. 2019. "Generation of Coherent and Spatially Squeezed States of an Electromagnetic Beam in a Planar Inhomogeneous Dielectric Waveguide" Photonics 6, no. 3: 84. https://doi.org/10.3390/photonics6030084
APA StyleBogatskaya, A., Schegolev, A., Klenov, N., & Popov, A. (2019). Generation of Coherent and Spatially Squeezed States of an Electromagnetic Beam in a Planar Inhomogeneous Dielectric Waveguide. Photonics, 6(3), 84. https://doi.org/10.3390/photonics6030084





