Abstract
Mid-infrared optical frequency comb generation in whispering gallery mode microresonators attracts significant interest. Chalcogenide glass microresonators are good candidates for operating in the mid-infrared range. We present the first theoretical analysis of optical frequency comb generation in As2S3 microbubble resonators in the 3–4 μm range. The regime of dissipative soliton plus dispersive wave generation is simulated numerically in the frame of the Lugiato–Lefever equation. Using microbubble geometry allows controlling of the zero-dispersion wavelength and the obtaining of anomalous dispersion needed for soliton generation at the pump wavelength of 3.5 μm, whereas the zero-dispersion wavelength of the analyzed As2S3 glass is ~4.8 μm. It is shown that, for the optimized characteristics of microbubble resonators, optical frequency combs with a spectral width of more than 700 nm (at the level of −30 dB) can be obtained with the low pump power of 10 mW.
1. Introduction
Broadband mid-infrared light sources have many applications in biomedicine, defense, environment monitoring, and sensing. There are several concepts of mid-infrared coherent optical sources, such as solid-state lasers, optical parametric oscillators and amplifiers, semiconductor lasers, fiber lasers, and laser systems based on frequency conversion in different nonlinear media (see, for example, [1,2,3,4,5,6,7,8,9]). Mid-infrared optical frequency comb generation in whispering gallery mode (WGM) microresonators also attracts significant interest. For example, broadband mid-infrared optical frequency combs have been demonstrated in silicon nitride [10], silicon microresonators [11], and crystalline calcium fluoride and magnesium fluoride resonators [12]. WGM glass microresonators for comb generation are developed in the visible and near-infrared ranges [13,14,15,16] but not in the range beyond 2 μm. We previously studied near-infrared optical frequency comb generation in the dissipative soliton regime in silica and germanosilicate solid microspheres pumped at 1.55 μm or at 2 μm [17]. Such microresonators cannot be used in the mid-infrared due to high optical losses [18]. However, we believe that the mid-infrared soliton regime may be implemented in microresonators with a more complicated design (such as a microbubble) on the basis of special glasses. Chalcogenide glass microresonators are good candidates for this target. Chalcogenide glasses have high chemical stability, low optical losses, resistance to atmospheric moisture, a transparency band up to ~10 μm (up to ~20 μm for individual compositions), and high linear and nonlinear refractive indices [19,20,21,22]. Chalcogenide microresonators have been demonstrated in the literature [23,24,25,26], but we have no information about generation of optical frequency combs in them.
Here, for the first time to the best of our knowledge, we investigate theoretically the possibility of using chalcogenide glass microresonators for mid-infrared optical frequency comb generation in the regime of the dissipative soliton plus dispersive waves (DW) [27]. This regime requires small anomalous dispersion at the pump wavelength λp, which should be located near the zero-dispersion wavelength (ZDW) [27,28]. We consider the microbubble geometry of As2S3 microresonators aimed at controlling dispersion. It is known that for microbubbles, ZDW can be both red-shifted and blue-shifted [16,29], whereas for solid microspheres, ZDW for fundamental WGMs is red-shifted [17,30]. We assume continuous wave (CW) pump at 3.5 μm, so ZDW of microbubbles should be blue-shifted by ~1.4 μm from the ZDW of As2S3 glass, which is ~4.8 μm [18]. Such ZDW shift is possible by the corresponding choice of resonator radius and wall thickness. We believe that an Er-doped fluoride CW fiber laser at ~3.5 μm [4,31,32] or an optical parametric generator may be used as a pump source. Other widespread chalcogenide glasses, such as As2Se3 or Te-based ones, have ZDW > 7.4 μm [2,18], so it may be difficult to shift their ZDW in the range <3.5 μm.
2. Materials and Methods
A scheme of the microbubble resonator with radius R and wall thickness b as well as the considered system for mid-infrared optical frequency comb generation are shown in Figure 1. The eigenfrequencies of the WGM microbubble can be found from the numerical solution of the characteristic equation, which is obtained on the basis of Maxwell’s equations. For transverse electric (TE) modes of bubble-like resonators, the characteristic equation takes on the following form [33],
where the refractive index n of the As2S3 microbubble wall is defined by the Sellmeier equation
with constants B1 = 1.8983678, B2 = 1.9222979, B3 = 0.8765134, B4 = 0.1188704, B5 = 0.9569903, C1 = 0.0225 μm2, C2 = 0.0625 μm2, C3 = 0.1225 μm2, C4 = 0.2025 μm2, C5 = 750 μm2 [34], and the coefficient Nl
with z1 = k(R−b) and z2 = nk(R−b); k = 2π/λl is the wavenumber in vacuum; λl is the resonance wavelength; νl = c/λl is the eigenfrequency; c is the speed of light; l is the mode index; ψl(z) = zJl(z) and χl(z) = zYl(z) are the spherical Riccati–Bessel and spherical Riccati–Neumann functions, and Jl(z) and Yl(z) are the spherical Bessel functions of the first and second kind, respectively,
where jl(z) and yl(z) are the standard Bessel functions of the first and second kind, respectively. The derivatives in Equations (1) and (3) can be expressed by
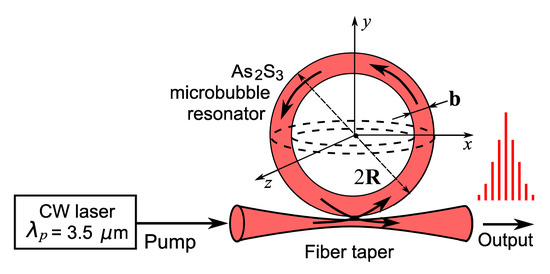
Figure 1.
Scheme of the considered system.
Here we consider only the fundamental TE WGMs with q = 1, q is the index characterizing the number of mode nodes in the radial direction. It is known that when coupling an electromagnetic wave through a fiber taper, the HE11 fiber mode effectively excites the TE modes of the microresonators [35]. We assume this technique of WGM excitation (see Figure 1).
The roots of the characteristic Equation (1) and the corresponding eigenfrequencies νl are found by a homemade numerical code. The frequency dependence of the refractive index is taken into account iteratively. The coefficient of quadratic dispersion β2 with allowance for the material and geometric contributions is calculated by the formula,
where
The nonlinear Kerr coefficients γ of microresonators are estimated by the formula:
Here, n2 = 2·10−18 m2/W [19] is the nonlinear refractive index and the effective WGM volume Veff is determined as follows,
where ε is the electric field of WGM. The explicit expression for ε is very cumbersome, therefore it is not given here but can be found in the paper [33].
The dynamics of the formation of mid-infrared optical frequency combs in As2S3s microbubble resonators is modeled using the Lugiato–Lefever equation [27,36],
where E(t, τ) is the complex envelope of the intracavity field, t and τ are the slow and fast times, tR = 2πRn/c is the microresonator roundtrip time, t = M·tR, M is the microresonator roundtrip number, δ0 is the frequency detuning of the pump field Ein from the nearest resonance, θ is the coupling coefficient, βk is the dispersion coefficient of the k-th order, α = (2π)2R/(Qλp) is the loss coefficient as the sum of intrinsic and coupling losses.
For the numerical simulation of the frequency comb dynamics in the frame of Equation (11), we developed a homemade software using the split-step Fourier method (SSFM) with the fast Fourier transform [37].
3. Results
First of all, we calculated the dispersion of As2S3 spherical microbubble resonators for different geometrical parameters. The ZDW of microbubbles as a function of b and R is shown in Figure 2a.
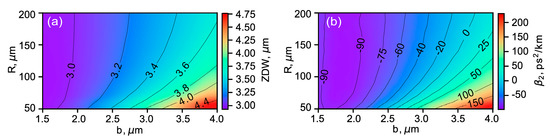
Figure 2.
Zero-dispersion wavelength as a function of thickness and radius of a microbubble (a). Dispersion as a function of thickness and radius of a microbubble calculated at λp = 3.5 μm (b).
One can see that for reasonable values of 1.5 μm < b < 4 μm and 50 μm < R < 200 μm, ZDW can be tuned in a wavelength range wider than 3–4.4 μm. Indeed, we can find geometrical parameters providing anomalous dispersion at the considered pump wavelengths of 3.5 μm. The value of β2 as a function of b and R simulated at λp = 3.5 μm is shown in Figure 2b. Further, we chose the combinations of b and R, ensuring small anomalous dispersion at the pump wavelengths needed for dissipative soliton and DW generation. The functions β2(λ) are plotted in Figure 3.
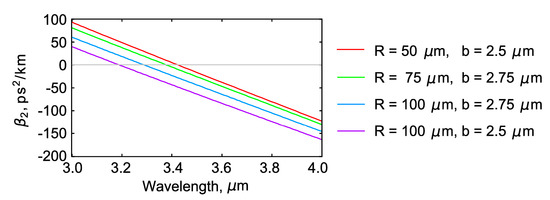
Figure 3.
Dispersion as a function of wavelength.
Next, we calculated the effective WGM volumes by Equation (10) at the central wavelengths of 3.5 μm as functions of the wall thickness and radius (see Figure 4a). WGMs are well-localized in the wall, so the effective volumes are relatively small. After that, the nonlinear Kerr coefficients defined by Equation (9) were estimated for the same geometrical parameters of microbubbles (see Figure 4b). The nonlinear coefficients can be as high as a few hundred (W·km)−1. Such giant values are due to small WGM volumes and the high nonlinear refractive index (n2 of As2S3 glass is ~200–300 times higher than n2 of MgF2 and CaF2 crystals used for mid-infrared frequency comb generation [12] and ~100–200 times higher than n2 of silica glass) [18,19]. Note that for silica microspheres, typical values of the nonlinear Kerr coefficient in the near-infrared are of order a few (W·km)−1 [15,17].
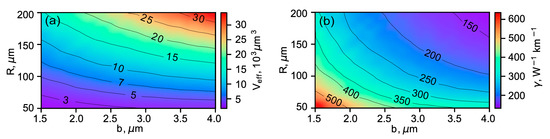
Figure 4.
Effective volume of fundamental WGM (a) and nonlinear coefficient (b) as functions of thickness and radius of a microbubble calculated at λp = 3.5 μm.
Further, we simulated generation of optical frequency combs, taking into account the calculated dispersion and nonlinear Kerr coefficients shown in Figure 3 and Figure 4b, respectively. We took the following values of parameters: The pump power |Ein|2 = 10 mW and Q = 106. The spectra and the corresponding temporal distributions of intracavity intensities are plotted in Figure 5. The microresonators with b = 2.5 μm, R = 50 μm and b = 2.75 μm, R = 75 μm have ZDWs near 3.4 μm and small anomalous dispersion at λp = 3.5 μm: −16 ps2/km and −21 ps2/km, respectively, which is desirable for generation of optical frequency combs with wide spectra. The widest spectra spanning more than 700 nm at the level of −30 dB were obtained in these microbubbles. The corresponding pulse duration is shorter than 100 fs. The spectra broaden so much that a substantial part of their blue wings falls into the normal dispersion region and acts as a source of phase-matched radiation, also known as Cherenkov radiation or DW [27,28]. In the time domain, the short-wavelength DW is located on the trailing edge of the dissipative soliton [17,27,28], which is also shown in Figure 5. Note that the phenomenon of the emission of phase-matched linear DW by perturbed solitons was also studied for optical fibers [38,39,40,41]. For R = 100 μm and b = 2.5 or 2.75 μm, then ZDW < 3.3 μm, only dissipative solitons are generated and there is no DW (see Figure 5, the second and the fourth rows). In these cases, their spectra spanning of about 300 nm at the level of −30 dB are obtained. The corresponding pulse duration is about 200 fs and the repetition rate is about 200 GHz.
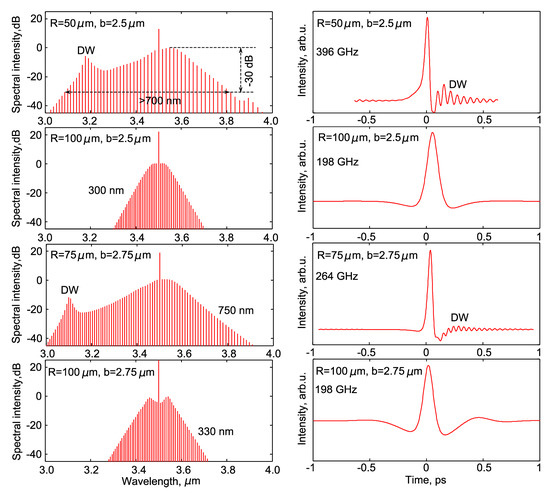
Figure 5.
Spectra of optical frequency combs (left) and temporal intensity distributions (right). DW is dispersive waves.
4. Discussion and Conclusions
In the presented work, we performed numerical analysis of the possibility of using chalcogenide As2S3 glass microbubble resonators for mid-infrared optical frequency comb generation with CW pump at 3.5 μm. We believe that an Er-doped fluoride fiber laser or an optical parametric generator may be used as a pump source. Special attention was paid to the study of the dispersion and nonlinearity of such microresonators. We showed that for reasonable values of radius and wall thickness, ZDW can be blue-shifted by more than 1.8 μm from the ZDW of As2S3 glass, which is ~4.8 μm. The thinner the wall, the higher the geometrical contribution to the dispersion is. The Kerr nonlinear coefficient can be as high as a few hundred (W·km)−1. The thinner the wall and the smaller the radius, the higher the nonlinear coefficient is.
The formation of optical frequency combs was modeled in the frame of the Lugiato–Lefever equation using a SSFM-based homemade computer code. We considered the regime of the dissipative soliton plus DW generation. Small anomalous dispersion is desirable for comb generation with a wide spectrum (>700 nm at the level of −30 dB). The optimal ZDW of microresonators is about 3.4 μm, for which spectra expand in the anomalous and normal dispersion regions. For ZDW < 3.3 μm, the spectral evolution is observed in the anomalous dispersion region, and the short-wavelength wing does not reach the phase-matching point for DW generation. For ZDW > 3.4 μm, the soliton radiates the significant part of its energy to the short-wavelength DW. Thus, the soliton energy decreases, which limits long-wavelength spectral broadening.
As2S3 glass has a large Kerr nonlinearity, so the pump power for comb generation is as low as ~10 mW, which can be profitable for some tasks. We believe that As2S3 glass is a very promising material for developing microbubble resonators for operating in the 3–4 μm range. Such microresonators can play a significant role in many sensing applications due to many absorption lines of chemical compounds in this spectral range. Note that CW laser sources at different wavelengths in the 3–4 μm range may be used for comb generation in the analyzed regime. Figure 2a demonstrating ZDW as a function of the wall thickness and radius may help to design As2S3 microbubble resonators for a certain pump wavelength.
Other widespread chalcogenide glasses, such as As2Se3 or Te-based ones, are also interesting for investigation. However, they have ZDW > 7.4 μm [2,18]. We estimate that for the fundamental TE WGM, As2Se3 microbubble resonators have ZDW > 4 μm for reasonable values of b ≥ 1.5 μm and R ≥ 50 μm, for example, ZDW = 4.5 μm for an As2Se3 microbubble resonator with b = 2.5 μm and R = 50 μm. Therefore, implementation of the considered regime of comb generation in As2Se3 or Te-based glass microbubble resonators requires CW laser pump at longer wavelengths.
Author Contributions
Conceptualization, E.A.A. and A.V.A.; methodology, E.A.A.; software, validation, and formal analysis, E.A.A., M.P.M. and A.A.S.; writing—original draft preparation, E.A.A.; writing—review and editing, E.A.A., M.P.M., A.A.S., and A.V.A.; visualization, E.A.A. and M.P.M.; supervision, E.A.A.; project administration, E.A.A.; funding acquisition, E.A.A.
Funding
This research was funded by the Russian Science Foundation, grant number 18-72-00176.
Conflicts of Interest
The authors declare no conflict of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript, or in the decision to publish the results.
References
- Sorokina, I.T.; Vodopyanov, K.L. (Eds.) Solid-State Mid-Infrared Laser Sources; Springer Science & Business Media: Berlin, Germany, 2003. [Google Scholar]
- Petersen, C.R.; Møller, U.; Kubat, I.; Zhou, B.; Dupont, S.; Ramsay, J.; Benson, T.; Sujecki, S.; Abdel-Moneim, N.; Tang, Z.; et al. Mid-infrared supercontinuum covering the 1.4–13.3 μm molecular fingerprint region using ultra-high NA chalcogenide step-index fibre. Nat. Photonics 2014, 8, 830–834. [Google Scholar] [CrossRef]
- Soboń, G.; Martynkien, T.; Mergo, P.; Rutkowski, L.; Foltynowicz, A. High-power frequency comb source tunable from 2.7 to 4.2 μm based on difference frequency generation pumped by an Yb-doped fiber laser. Opt. Lett. 2017, 42, 1748–1751. [Google Scholar] [CrossRef] [PubMed]
- Henderson-Sapir, O.; Munch, J.; Ottaway, D.J. Mid-infrared fiber lasers at and beyond 3.5 μm using dual-wavelength pumping. Opt. Lett. 2014, 39, 493–496. [Google Scholar] [CrossRef] [PubMed]
- Mitrofanov, A.V.; Voronin, A.A.; Mitryukovskiy, S.I.; Sidorov-Biryukov, D.A.; Pugžlys, A.; Andriukaitis, G.; Flöry, T.; Stepanov, E.A.; Fedotov, A.B.; Baltuška, A.; et al. Mid-infrared-to-mid-ultraviolet supercontinuum enhanced by third-to-fifteenth odd harmonics. Opt. Lett. 2015, 40, 2068–2071. [Google Scholar] [CrossRef] [PubMed]
- Sójka, L.; Pajewski, L.; Popenda, M.; Beres-Pawlik, E.; Lamrini, S.; Markowski, K.; Osuch, T.; Benson, T.M.; Seddon, A.B.; Sujecki, S. Experimental investigation of mid-infrared laser action from Dy3+ doped fluorozirconate fiber. IEEE Photonics Technol. Lett. 2018, 30, 1083–1086. [Google Scholar] [CrossRef]
- Sujecki, S.; Sojka, L.; Seddon, A.; Benson, T.; Barney, E.; Falconi, M.; Prudenzano, F.; Marciniak, M.; Baghdasaryan, H.; Peterka, P.; et al. Comparative modeling of infrared fiber lasers. Photonics 2018, 5, 48. [Google Scholar] [CrossRef]
- Silaev, A.A.; Kostin, V.A.; Laryushin, I.D.; Vvedenskii, N.V. Ionization mechanism of the generation of tunable ultrashort pulses in the mid-infrared range. JETP Lett. 2018, 107, 151–156. [Google Scholar] [CrossRef]
- Anashkina, E.A. Design and numerical modeling of broadband mid-IR rare-earth-doped chalcogenide fiber amplifiers. IEEE Photon. Technol. Lett. 2018, 30, 1190–1193. [Google Scholar] [CrossRef]
- Luke, K.; Okawachi, Y.; Lamont, M.R.E.; Gaeta, A.L.; Lipson, M. Broadband mid-infrared frequency comb generation in a Si3N4 microresonator. Opt. Lett. 2015, 40, 4823–4826. [Google Scholar] [CrossRef] [PubMed]
- Yu, M.; Okawachi, Y.; Griffith, A.G.; Lipson, M.; Gaeta, A.L. Mode-locked mid-infrared frequency combs in a silicon microresonator. Optica 2016, 3, 854–860. [Google Scholar] [CrossRef]
- Savchenkov, A.; Ilchenko, V.S.; Di Teodoro, F.; Belden, P.M.; Lotshaw, W.T.; Matsko, A.B.; Maleki, L. Generation of Kerr combs centered at 4.5 μm in crystalline microresonators pumped with quantum-cascade lasers. Opt. Lett. 2015, 40, 3468–3471. [Google Scholar] [CrossRef]
- Strekalov, D.V.; Marquardt, C.; Matsko, A.B.; Schwefel, H.G.; Leuchs, G. Nonlinear and quantum optics with whispering gallery resonators. J. Opt. 2016, 18, 123002. [Google Scholar] [CrossRef]
- Sumetsky, M. Optical bottle microresonators. Prog. Quantum Electron. 2019, 64, 1–30. [Google Scholar] [CrossRef]
- Webb, K.E.; Erkintalo, M.; Coen, S.; Murdoch, S.G. Experimental observation of coherent cavity soliton frequency combs in silica microspheres. Opt. Lett. 2016, 41, 4613–4616. [Google Scholar] [CrossRef] [PubMed]
- Yang, Y.; Jiang, X.; Kasumie, S.; Zhao, G.; Xu, L.; Ward, J.M.; Yang, L.; Chormaic, S.N. Four-wave mixing parametric oscillation and frequency comb generation at visible wavelengths in a silica microbubble resonator. Opt. Lett. 2016, 41, 5266–5269. [Google Scholar] [CrossRef]
- Anashkina, E.A.; Sorokin, A.A.; Marisova, M.P.; Andrianov, A.V. Development and numerical simulation of spherical microresonators based on SiO2–GeO2 germanosilicate glasses for generation of optical frequency combs. Quantum Electron. 2019, 49, 371–376. [Google Scholar] [CrossRef]
- Tao, G.; Ebendorff-Heidepriem, H.; Stolyarov, A.M.; Danto, S.; Badding, J.V.; Fink, Y.; Ballato, J.; Abouraddy, A.F. Infrared fibers. Adv. Opt. Photonics 2015, 7, 379–458. [Google Scholar] [CrossRef]
- Eggleton, B.J.; Luther-Davies, B.; Richardson, K. Chalcogenide photonics. Nat. Photonics 2011, 5, 141–148. [Google Scholar] [CrossRef]
- Romanova, E.; Kuzyutkina, Y.; Shiryaev, V.; Abdel-Moneim, N.; Furniss, D.; Benson, T.; Seddon, A.; Guizard, S. Measurement of non-linear optical coefficients of chalcogenide glasses near the fundamental absorption band edge. J. Non-Cryst. Solids 2018, 480, 13–17. [Google Scholar] [CrossRef]
- Anashkina, E.A.; Shiryaev, V.S.; Snopatin, G.E.; Muraviev, S.V.; Kim, A.V. On the possibility of mid-IR supercontinuum generation in As-Se-Te/As-S core/clad fibers with all-fiber femtosecond pump source. J. Non-Cryst. Solids 2018, 480, 38–42. [Google Scholar] [CrossRef]
- Anashkina, E.A.; Shiryaev, V.S.; Koptev, M.Y.; Stepanov, B.S.; Muravyev, S.V. Development of As-Se tapered suspended-core fibers for ultra-broadband mid-IR wavelength conversion. J. Non-Cryst. Solids 2018, 480, 43–50. [Google Scholar] [CrossRef]
- Yang, K.; Dai, S.; Wu, Y.; Nie, Q. Fabrication and characterization of Ge–Ga–Sb–S glass microsphere lasers operating at ~1.9 μm. Chin. Phys. B 2018, 27, 117701. [Google Scholar] [CrossRef]
- Grillet, C.; Bian, S.N.; Magi, E.C.; Eggleton, B.J. Fiber taper coupling to chalcogenide microsphere modes. Appl. Phys. Lett. 2008, 92, 171109. [Google Scholar] [CrossRef]
- Wang, P.; Murugan, G.S.; Brambilla, G.; Ding, M.; Semenova, Y.; Wu, Q.; Farrell, G. Chalcogenide microsphere fabricated from fiber tapers using contact with a high-temperature ceramic surface. IEEE Photon. Technol. Lett. 2012, 24, 1103–1105. [Google Scholar] [CrossRef]
- Romanova, E.A.; Zhivotkov, D.S.; Ristic, D.; Ivanda, M.; Shiryaev, V.S. Design of optical microresonators for fiber-optic sensor networks transparent in Mid-IR. In Proceedings of the 2017 Progress in Electromagnetics Research Symposium-Spring (PIERS), St. Petersburg, Russia, 22–25 May 2017; pp. 291–295. [Google Scholar]
- Brasch, V.; Geiselmann, M.; Herr, T.; Lihachev, G.; Pfeiffer, M.H.; Gorodetsky, M.L.; Kippenberg, T.J. Photonic chip–based optical frequency comb using soliton Cherenkov radiation. Science 2016, 351, 357–360. [Google Scholar] [CrossRef]
- Cherenkov, A.V.; Lobanov, V.E.; Gorodetsky, M.L. Dissipative Kerr solitons and Cherenkov radiation in optical microresonators with third-order dispersion. Phys. Rev. A 2017, 95, 033810. [Google Scholar] [CrossRef]
- Riesen, N.; Zhang, W.Q.; Monro, T.M. Dispersion analysis of whispering gallery mode microbubble resonators. Opt. Express 2016, 24, 8832–8847. [Google Scholar] [CrossRef] [PubMed]
- Riesen, N.; Vahid, S.A.; François, A.; Monro, T.M. Material candidates for optical frequency comb generation in microspheres. Opt. Express 2015, 23, 14784–14795. [Google Scholar] [CrossRef]
- Fortin, V.; Maes, F.; Bernier, M.; Bah, S.T.; D’Auteuil, M.; Vallée, R. Watt-level erbium-doped all-fiber laser at 3.44 μm. Opt. Lett. 2016, 41, 559–562. [Google Scholar] [CrossRef] [PubMed]
- Qin, Z.; Hai, T.; Xie, G.; Ma, J.; Yuan, P.; Qian, L.; Li, L.; Zhao, L.; Shen, D. Black phosphorus Q-switched and mode-locked mid-infrared Er:ZBLAN fiber laser at 3.5 μm wavelength. Opt. Express 2018, 26, 8224–8231. [Google Scholar] [CrossRef]
- Teraoka, I.; Arnold, S. Whispering-gallery modes in a microsphere coated with a high-refractive index layer: Polarization-dependent sensitivity enhancement of the resonance-shift sensor and TE-TM resonance matching. J. Opt. Soc. Am. B 2007, 24, 653–659. [Google Scholar] [CrossRef]
- Chaudhari, C.; Suzuki, T.; Ohishi, Y. Design of zero chromatic dispersion chalcogenide As2S3 glass nanofibers. J. Lightw. Technol. 2009, 27, 2095–2099. [Google Scholar] [CrossRef]
- Gorodetsky, M.L.; Ilchenko, V.S. Optical microsphere resonators: Optimal coupling to high-Q whispering-gallery modes. J. Opt. Soc. Am. B 1999, 16, 147–154. [Google Scholar] [CrossRef]
- Lugiato, L.A.; Lefever, R. Spatial dissipative structures in passive optical systems. Phys. Rev. Lett. 1987, 58, 2209–2211. [Google Scholar] [CrossRef]
- Agrawal, G.P. Nonlinear Fiber Optics; Academic Press: Cambridge, MA, USA, 2013. [Google Scholar]
- Wai, P.K.A.; Menyuk, C.R.; Lee, Y.C.; Chen, H.H. Nonlinear pulse propagation in the neighborhood of the zero-dispersion wavelength of monomode optical fibers. Opt. Lett. 1986, 11, 464–466. [Google Scholar] [CrossRef] [PubMed]
- Skryabin, D.V.; Luan, F.; Knight, J.C.; Russell, P.S.J. Soliton self-frequency shift cancellation in photonic crystal fibers. Science 2003, 301, 1705–1708. [Google Scholar] [CrossRef] [PubMed]
- Andrianov, A.; Anashkina, E.; Muravyev, S.; Kim, A. All-fiber design of hybrid Er-doped laser/Yb-doped amplifier system for high-power ultrashort pulse generation. Opt. Lett. 2010, 35, 3805–3807. [Google Scholar] [CrossRef]
- Kotov, L.V.; Koptev, M.Y.; Anashkina, E.A.; Muravyev, S.V.; Andrianov, A.V.; Bubnov, M.M.; Ignat’ev, A.D.; Lipatov, D.S.; Gur’yanov, A.N.; Likhachev, M.E.; et al. Submicrojoule femtosecond erbium-doped fibre laser for the generation of dispersive waves at submicron wavelengths. Quantum Electron. 2014, 44, 458–464. [Google Scholar] [CrossRef]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).