Photonic Crystal Circular Defect (CirD) Laser †
Abstract
:1. Introduction
2. Design of Cird Lasers for Inter-Chip or Intra-Chip Optical Interconnects
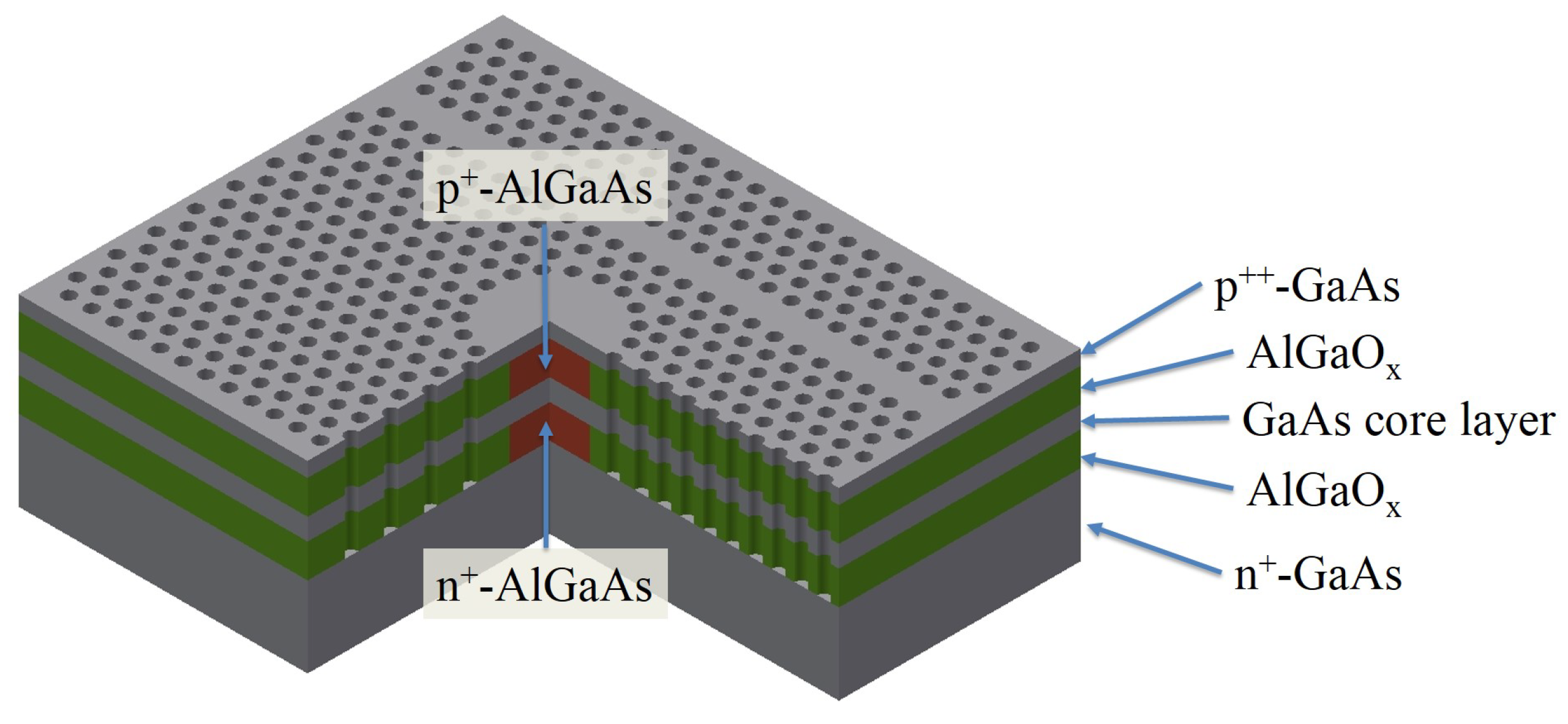
2.1. Cird Laser Structure
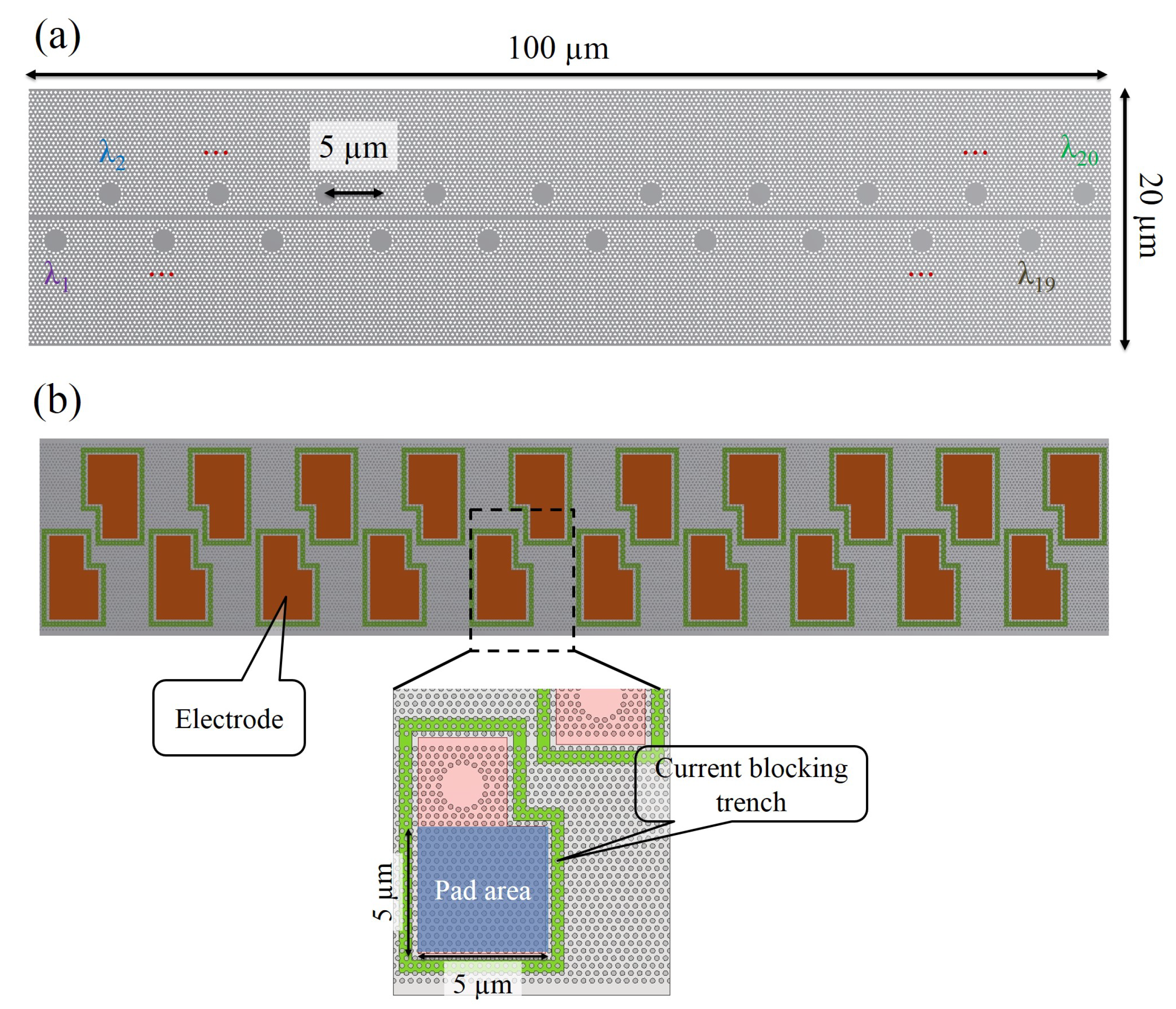
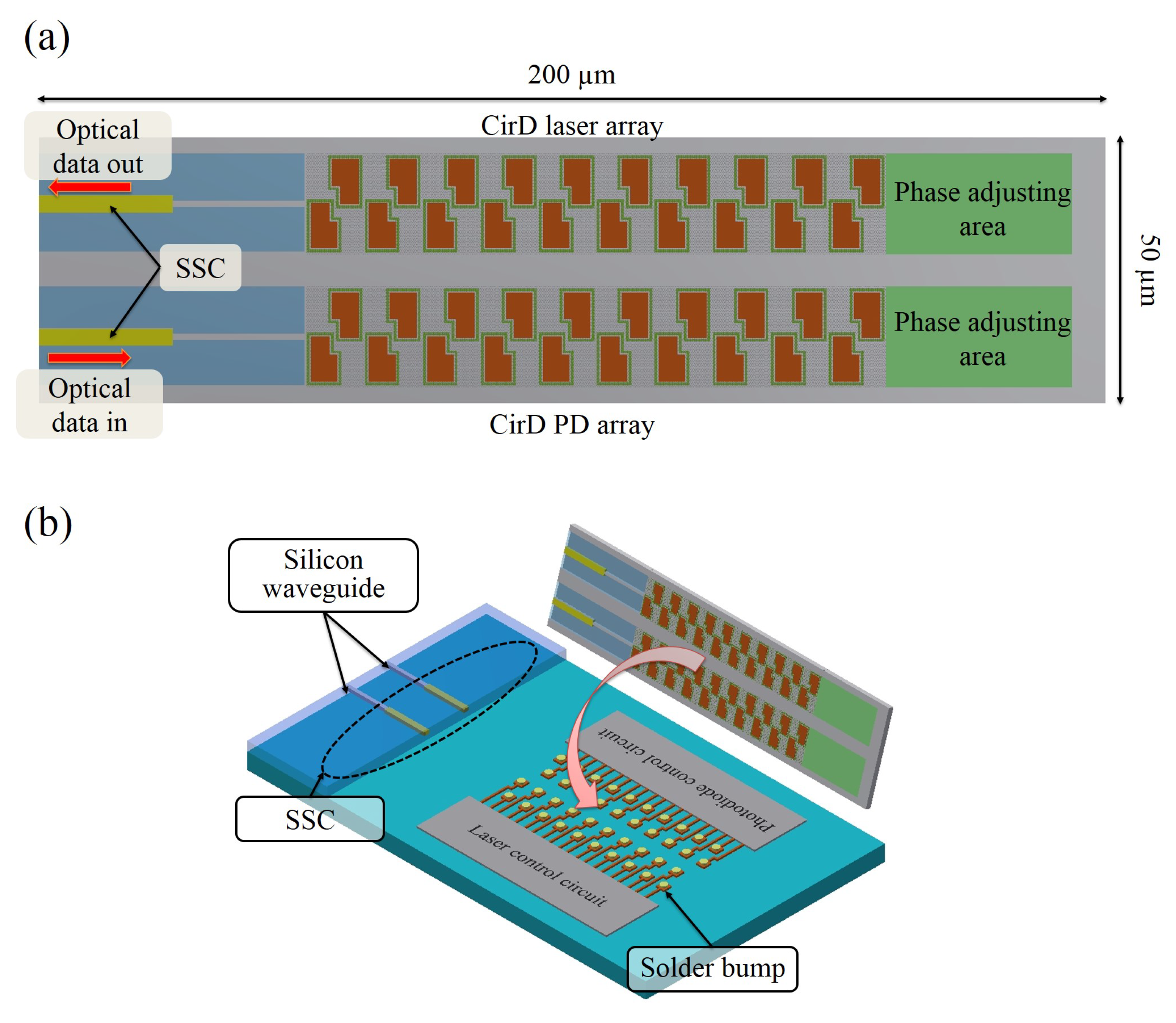
2.2. Monolithic Optical Module Architecture
3. Numerical Analysis of Cird Lasers
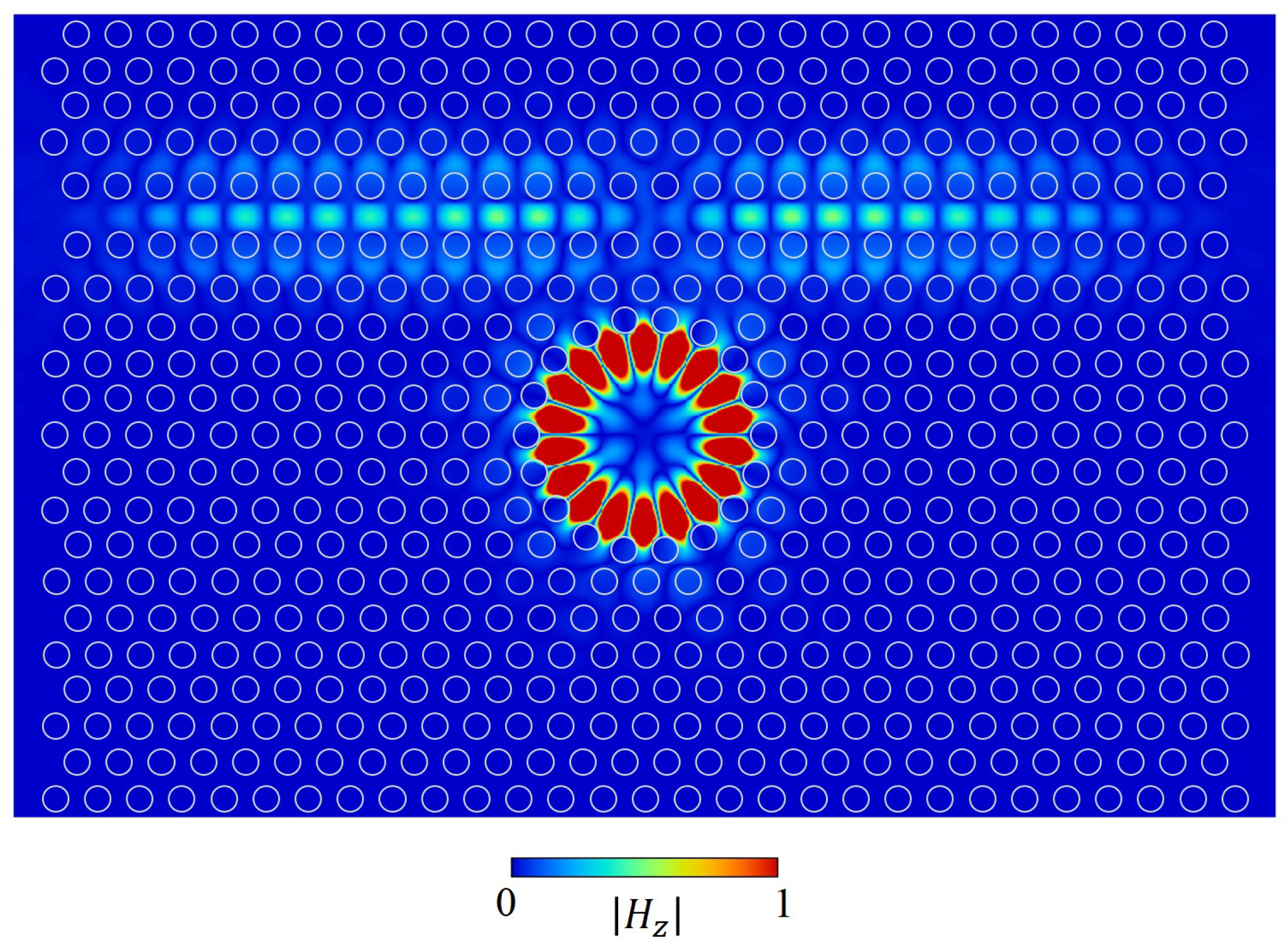
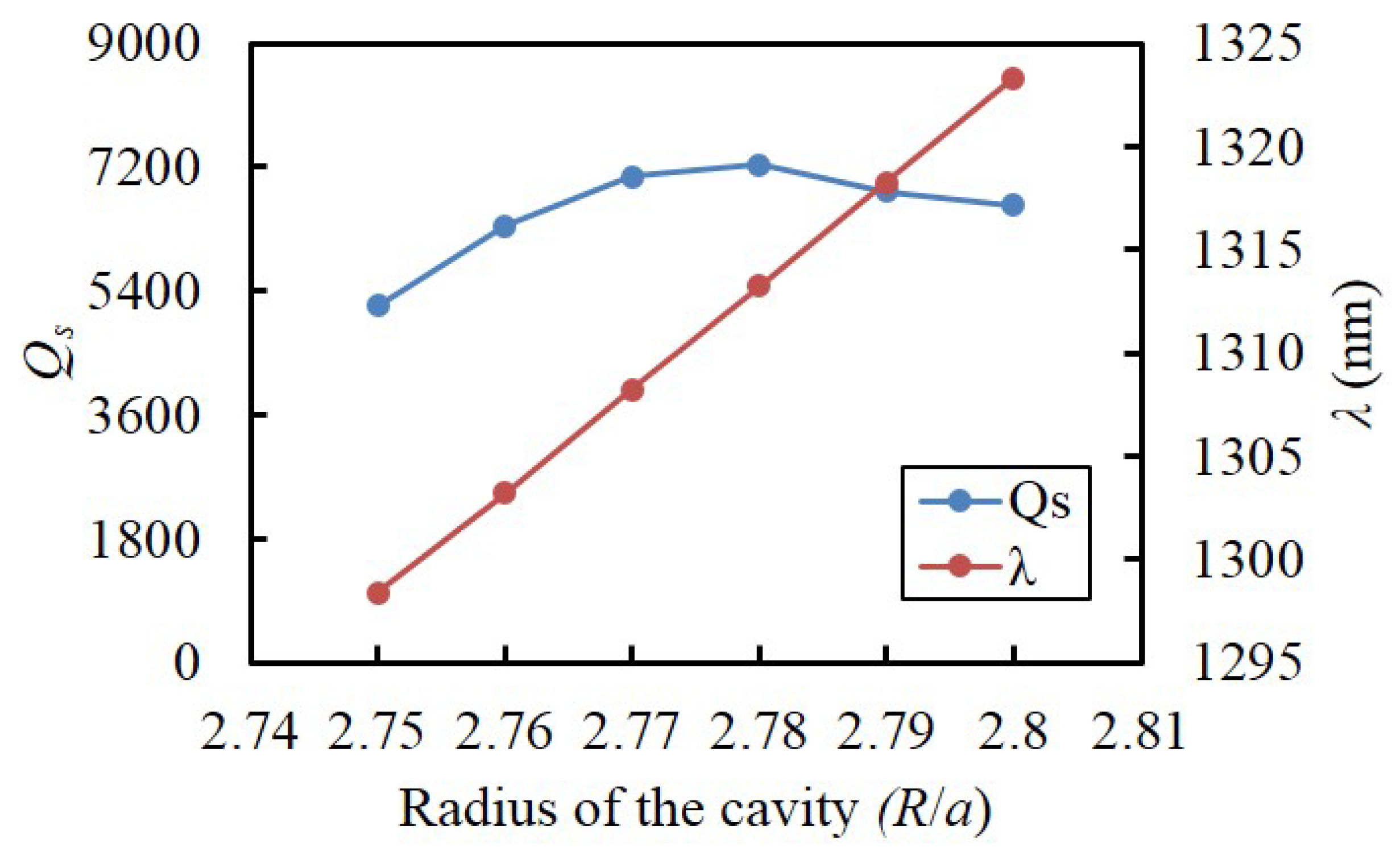
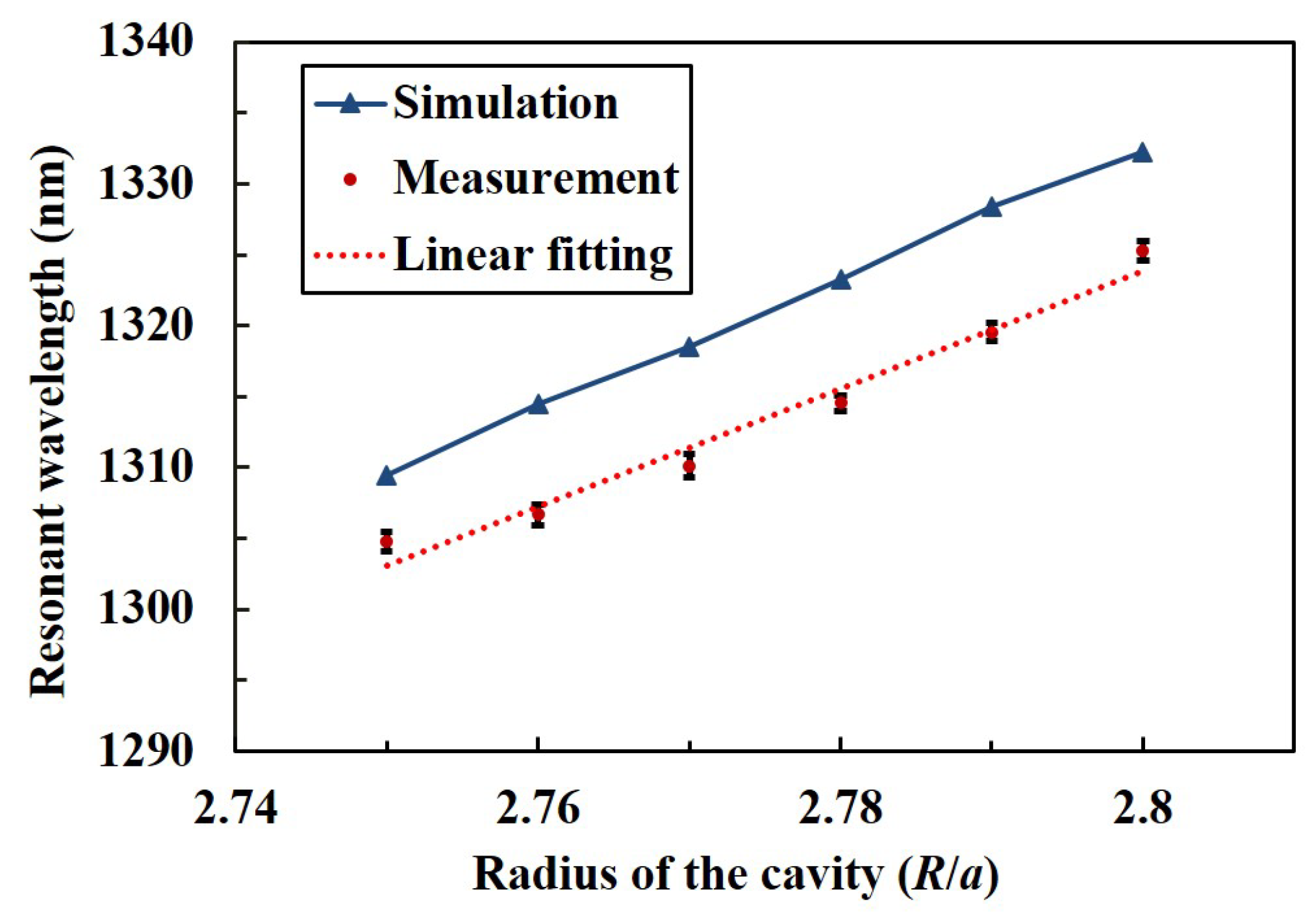
3.1. Resonant Wavelength and Quality Factory
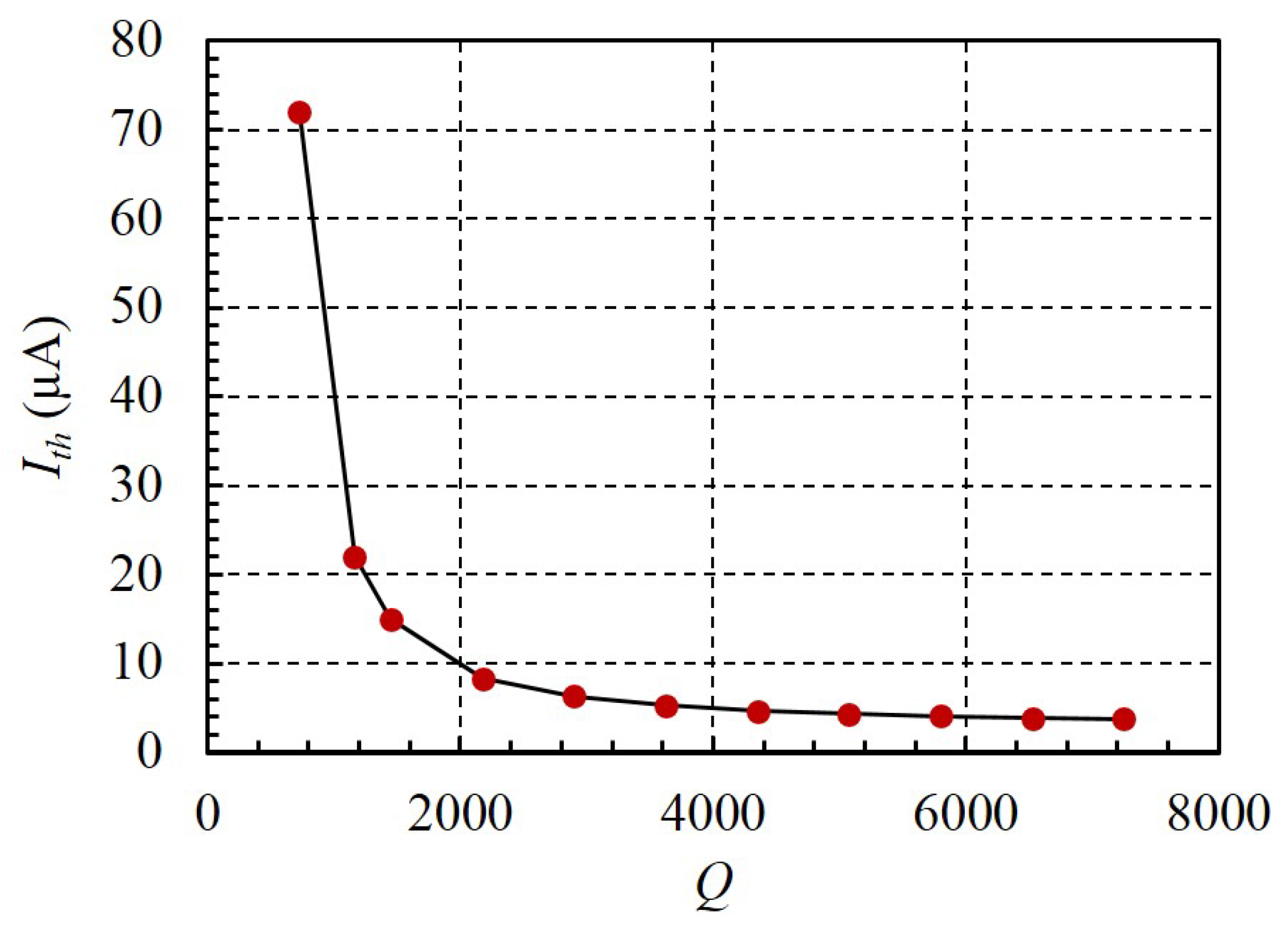
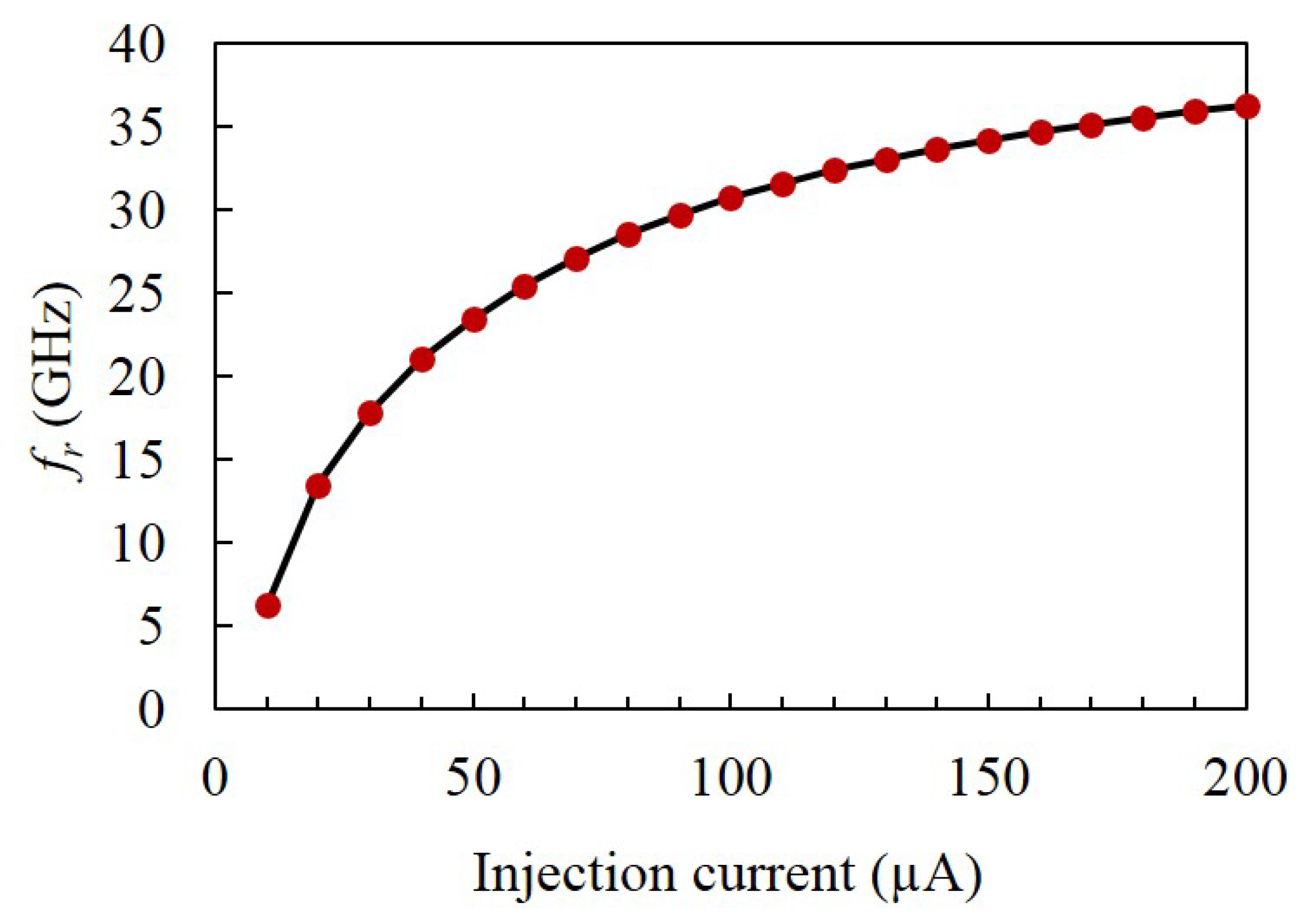
3.2. Lasing Characteristics
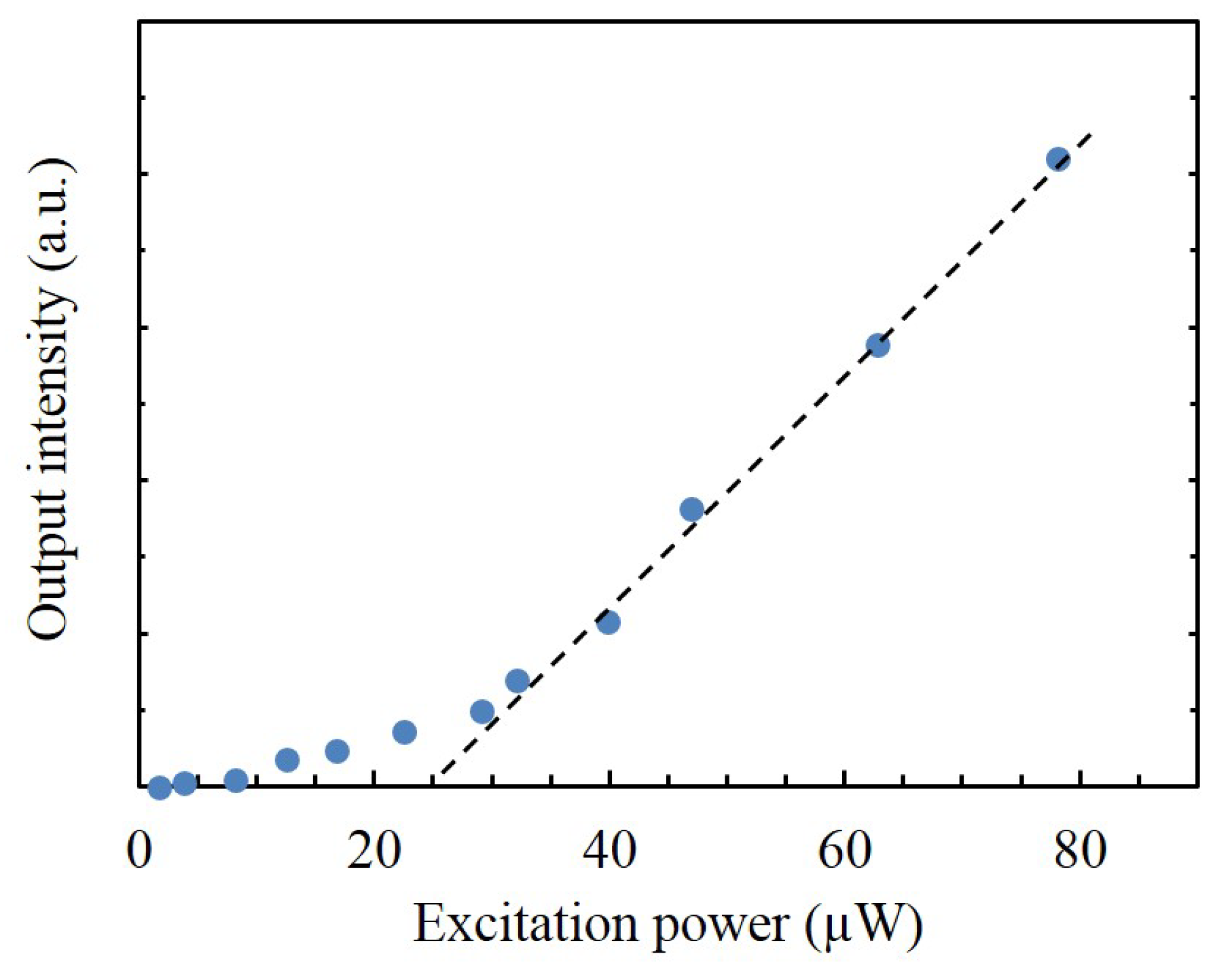
4. Experimental Demonstration of Wavelength Tuning of Cird Lasers
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Young, I.A.; Mohammed, E.; Liao, J.T.; Kern, A.M.; Palermo, S.; Block, B.A.; Reshotko, M.R.; Chang, P.L. Optical I/O technology for tera-scale computing. IEEE J. Solid-State Circuits 2010, 45, 235–248. [Google Scholar] [CrossRef]
- Miller, S.E. Integrated optics: An introduction. Bell Syst. Tech. J. 1969, 48, 2059–2069. [Google Scholar] [CrossRef]
- Kim, G.; Park, J.W.; Kim, I.G.; Kim, S.; Kim, S.; Lee, J.M.; Park, G.S.; Joo, J.; Jang, K.S.; Oh, J.H.; et al. Low-voltage high-performance silicon photonic devices and photonic integrated circuits operating up to 30 Gb/s. Opt. Express 2011, 19, 26936–26947. [Google Scholar] [CrossRef] [PubMed]
- Zheng, X.; Luo, Y.; Lexau, J.; Liu, F.; Li, G.; Thacker, H.D.; Shubin, I.; Yao, J.; Ho, R.; Cunningham, J.E.; et al. 2-pJ/bit (on-chip) 10-Gb/s digital CMOS silicon photonic link. IEEE Photonics Technol. Lett. 2012, 24, 1260–1262. [Google Scholar] [CrossRef]
- Urino, Y.; Usuki, T.; Fujikata, J.; Ishizaka, M.; Yamada, K.; Horikawa, T.; Nakamura, T.; Arakawa, Y. High-density and wide-bandwidth optical interconnects with silicon optical interposers. Photonics Res. 2014, 2, A1–A7. [Google Scholar] [CrossRef]
- Arakawa, Y.; Nakamura, T.; Urino, Y.; Fujita, T. Silicon photonics for next generation system integration platform. IEEE Commun. Mag. 2013, 51, 72–77. [Google Scholar] [CrossRef]
- Fujitsu, NEDO and PETRA DevelopWorld’s Highest Transmission Density Optical Transceiver and High-Speed Energy Efficient Optical Modulator Technology. Available online: http://www.fujitsu.com/global/about/resources/news/press-releases/2017/0919-03.html (accessed on 25 March 2019).
- Kondow, M.; Zhang, X.; Morifuji, M. Proposal of high-density light source with 10 Pbps/cm2 for intra-chip optical-interconnections. In Proceedings of the Collaborative Collaborative Conference on 3D & Materials Research (CC3DMR 2015), Busan, Korea, 15–19 June 2015. Tu-212-1. [Google Scholar]
- Vlasov, Y.A.; McNab, S.J. Losses in single-mode silicon-on-insulator strip waveguides and bends. Opt. Express 2004, 12, 1622–1631. [Google Scholar] [CrossRef]
- Bogaerts, W.; Baets, R.; Dumon, P.; Wiaux, V.; Beckx, S.; Taillaert, D.; Luyssaert, B.; Van Campenhout, J.; Bienstman, P.; Van Thourhout, D. Nanophotonic waveguides in silicon-on-insulator fabricated with CMOS technology. J. Lightware Technol. 2005, 23, 401–412. [Google Scholar]
- Xu, Q.; Schmidt, B.; Pradhan, S.; Lipson, M. Micrometre-scale silicon electro-optic modulator. Nature 2005, 435, 325. [Google Scholar] [CrossRef]
- Huang, Z.; Carey, J.E.; Liu, M.; Guo, X.; Mazur, E.; Campbell, J.C. Microstructured silicon photodetector. Appl. Phys. Lett. 2006, 89, 033506. [Google Scholar] [CrossRef]
- Liu, A.Y.; Bowers, J. Photonic Integration with Epitaxial III–V on Silicon. IEEE J. Sel. Top. Quantum Electron. 2018, 24, 1–12. [Google Scholar] [CrossRef]
- Yablonovitch, E. Inhibited spontaneous emission in solid-state physics and electronics. Phys. Rev. Lett. 1987, 58, 2059. [Google Scholar] [CrossRef] [PubMed]
- Akahane, Y.; Asano, T.; Song, B.S.; Noda, S. High-Q photonic nanocavity in a two-dimensional photonic crystal. Nature 2003, 425, 944. [Google Scholar] [CrossRef] [PubMed]
- O’Brien, J.; Kuang, W.; Cao, J.-R.; Shih, M.-H.; Lee, P.-T.; Bagheri, M.; Mock, A.; Marshall, W.K. Photonic crystal microcavity lasers. J. Phys. D Appl. Phys. 2007, 40, 2671. [Google Scholar] [CrossRef]
- Nomura, M.; Kumagai, N.; Iwamoto, S.; Ota, Y.; Arakawa, Y. Photonic crystal nanocavity laser with a single quantum dot gain. Opt. Express 2009, 17, 15975–15982. [Google Scholar] [CrossRef] [PubMed]
- Takeda, K.; Sato, T.; Shinya, A.; Nozaki, K.; Kobayashi, W.; Taniyama, H.; Notomi, M.; Hasebe, K.; Kakitsuka, T.; Matsuo, S. Few-fJ/bit data transmissions using directly modulated lambda-scale embedded active region photonic-crystal lasers. Nat. Photonics 2013, 7, 569. [Google Scholar] [CrossRef]
- Kuramochi, E.; Nozaki, K.; Shinya, A.; Takeda, K.; Sato, T.; Matsuo, S.; Taniyama, H.; Sumikura, H.; Notomi, M. Large-scale integration of wavelength-addressable all-optical memories on a photonic crystal chip. Nat. Photonics 2014, 8, 474. [Google Scholar] [CrossRef]
- Matsuo, S.; Sato, T.; Takeda, K.; Shinya, A.; Nozaki, K.; Kuramochi, E.; Taniyama, H.; Notomi, M.; Fujii, T.; Hasebe, K.; et al. Photonic crystal lasers using wavelength-scale embedded active region. J. Phys. D Appl. Phys. 2013, 47, 023001. [Google Scholar] [CrossRef]
- Nozaki, K.; Matsuo, S.; Takeda, K.; Fujii, T.; Ono, M.; Shakoor, A.; Kuramochi, E.; Notomi, M. Sub-fF-capacitance photonic-crystal photodetector towards fJ/bit on-chip receiver. IEICE Trans. Electron. 2017, 100, 750–758. [Google Scholar] [CrossRef]
- Nishi, H.; Takeda, K.; Fujii, T.; Kuramochi, E.; Shinya, A.; Notomi, M.; Tsuchizawa, T.; Kakitsuka, T.; Matsuo, S. Low-Operating Energy Heterogeneously Integrated Photonic-Crystal Laser on Si Waveguide. In Proceedings of the IEEE International Semiconductor Laser Conference (ISLC), Santa Fe, NM, USA, 16–19 September 2018; pp. 1–2. [Google Scholar]
- Fujii, T.; Takeda, K.; Diamantopoulos, N.P.; Kanno, E.; Hasebe, K.; Nishi, H.; Nakao, R.; Kakitsuka, T.; Matsuo, S. Heterogeneously integrated membrane lasers on Si substrate for low operating energy optical links. IEEE J. Sel. Top. Quantum Electron. 2018, 24, 1–8. [Google Scholar] [CrossRef]
- Morifuji, M.; Nakaya, Y.; Mitamura, T.; Kondow, M. Novel design of current driven photonic crystal laser diode. IEEE Photonics Technol. Lett. 2009, 21, 513–515. [Google Scholar] [CrossRef]
- Zhang, X.; Hino, T.; Kasamatsu, S.; Suga, S.; He, E.; Xiong, Y.; Morifuji, M.; Kajii, H.; Maruta, A.; Kondow, M. 1.3 μm lasing of circular defect cavity photonic crystal laser with an AlOx cladding layer. IEICE Electron. Express 2017, 14, 20170664. [Google Scholar] [CrossRef]
- Xiong, Y.; Umeda, T.; Zhang, X.; Morifuji, M.; Kajii, H.; Maruta, A.; Kondow, M. Photonic Crystal Circular-Defect Microcavity Laser Designed for Wavelength Division Multiplexing. IEEE J. Sel. Top. Quantum Electron. 2018, 24, 1–7. [Google Scholar] [CrossRef]
- Faraon, A.; Waks, E.; Englund, D.; Fushman, I.; Vučković, J. Efficient photonic crystal cavity-waveguide couplers. Appl. Phys. Lett. 2007, 90, 073102. [Google Scholar] [CrossRef]
- Network Source of Refractive Indexes of the Materials Used in the Model. Available online: https://refractiveindex.info/ (accessed on 25 March 2019).
- Nozaki, K.; Baba, T. Carrier and photon analyses of photonic microlasers by two-dimensional rate equations. IEEE J. Sel. Areas Commun. 2005, 23, 1411–1417. [Google Scholar] [CrossRef]
- Bowers, J.; Hemenway, B.; Gnauck, A.; Wilt, D. High-speed InGaAsP constricted-mesa lasers. IEEE J. Quantum Electron. 1986, 22, 833–844. [Google Scholar] [CrossRef]
- Zhang, X.; Takeuchi, K.; Cong, X.; Xiong, Y.; Morifuji, M.; Maruta, A.; Kajii, H.; Kondow, M. Dry etching of deep air holes in GaAs/AlGaAs-based epi-wafer having InAs quantum dots for fabrication of photonic crystal laser. Jpn. J. Appl. Phys. 2017, 56, 126501. [Google Scholar] [CrossRef]
- Björk, G.; Karlsson, A.; Yamamoto, Y. On the linewidth of microcavity lasers. Appl. Phys. Lett. 1992, 60, 304–306. [Google Scholar] [CrossRef]


| Parameters | Value |
|---|---|
| Thickness of GaAs contact layer | 180 nm |
| Thickness of AlGaAs/AlGaOx cladding layers | 500 nm |
| Thickness of GaAs core layer | 220 nm |
| Lattice constant a | 360 nm |
| Radius of air holes | 0.3 a |
| AlGaOx width | 0.8 a |
| Refractive index of GaAs | 3.400 |
| Refractive index of AlGaAs | 2.924 |
| Refractive index of AlOx | 1.761 |
| Refractive index of air | 1.000 |
| Symbol | Parameters | Value |
|---|---|---|
| Confinement factor at the vertical direction | 0.07 | |
| Gain coefficient | 10 m | |
| Transparent carrier density | 10 m | |
| D | Carrier diffusion constant (out side of the air holes) | 2 × 10 m2/s |
| Carrier lifetime | 1 ns | |
| Group velocity | 8.82 × 10 m/s | |
| V | Carrier injection area volume | 2.23 × 10 m |
| Effective modal area | 3.52 × 10 m2 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xiong, Y.; Ye, H.; Umeda, T.; Mizoguchi, S.; Morifuji, M.; Kajii, H.; Maruta, A.; Kondow, M. Photonic Crystal Circular Defect (CirD) Laser. Photonics 2019, 6, 54. https://doi.org/10.3390/photonics6020054
Xiong Y, Ye H, Umeda T, Mizoguchi S, Morifuji M, Kajii H, Maruta A, Kondow M. Photonic Crystal Circular Defect (CirD) Laser. Photonics. 2019; 6(2):54. https://doi.org/10.3390/photonics6020054
Chicago/Turabian StyleXiong, Yifan, Hanqiao Ye, Takuma Umeda, Shun Mizoguchi, Masato Morifuji, Hirotake Kajii, Akihiro Maruta, and Masahiko Kondow. 2019. "Photonic Crystal Circular Defect (CirD) Laser" Photonics 6, no. 2: 54. https://doi.org/10.3390/photonics6020054
APA StyleXiong, Y., Ye, H., Umeda, T., Mizoguchi, S., Morifuji, M., Kajii, H., Maruta, A., & Kondow, M. (2019). Photonic Crystal Circular Defect (CirD) Laser. Photonics, 6(2), 54. https://doi.org/10.3390/photonics6020054





