A Modified Design of a Hexagonal Circular Photonic Crystal Fiber with Large Negative Dispersion Properties and Ultrahigh Birefringence for Optical Broadband Communication
Abstract
1. Introduction
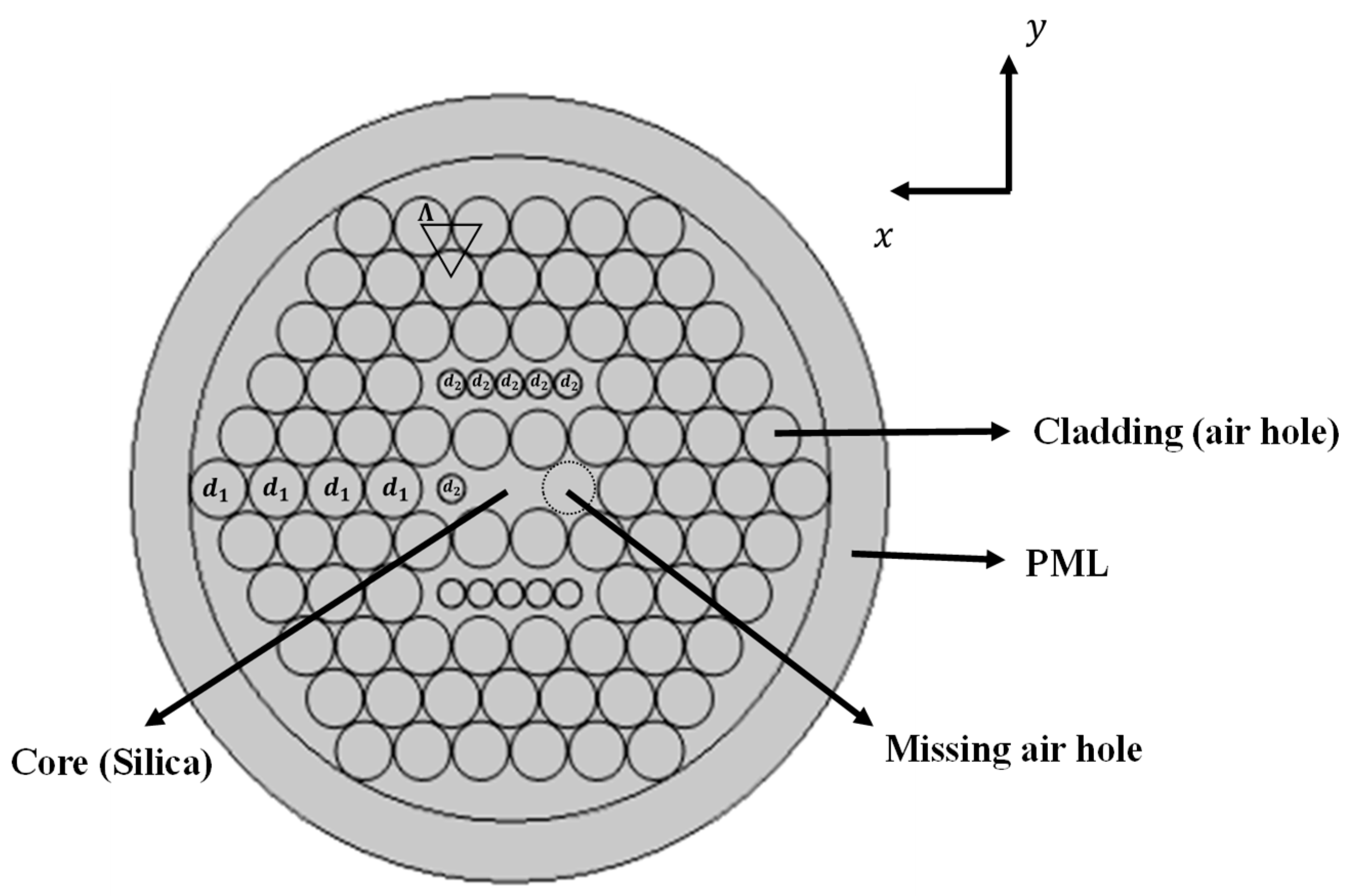
2. Design Structure of the Proposed HC-PCF
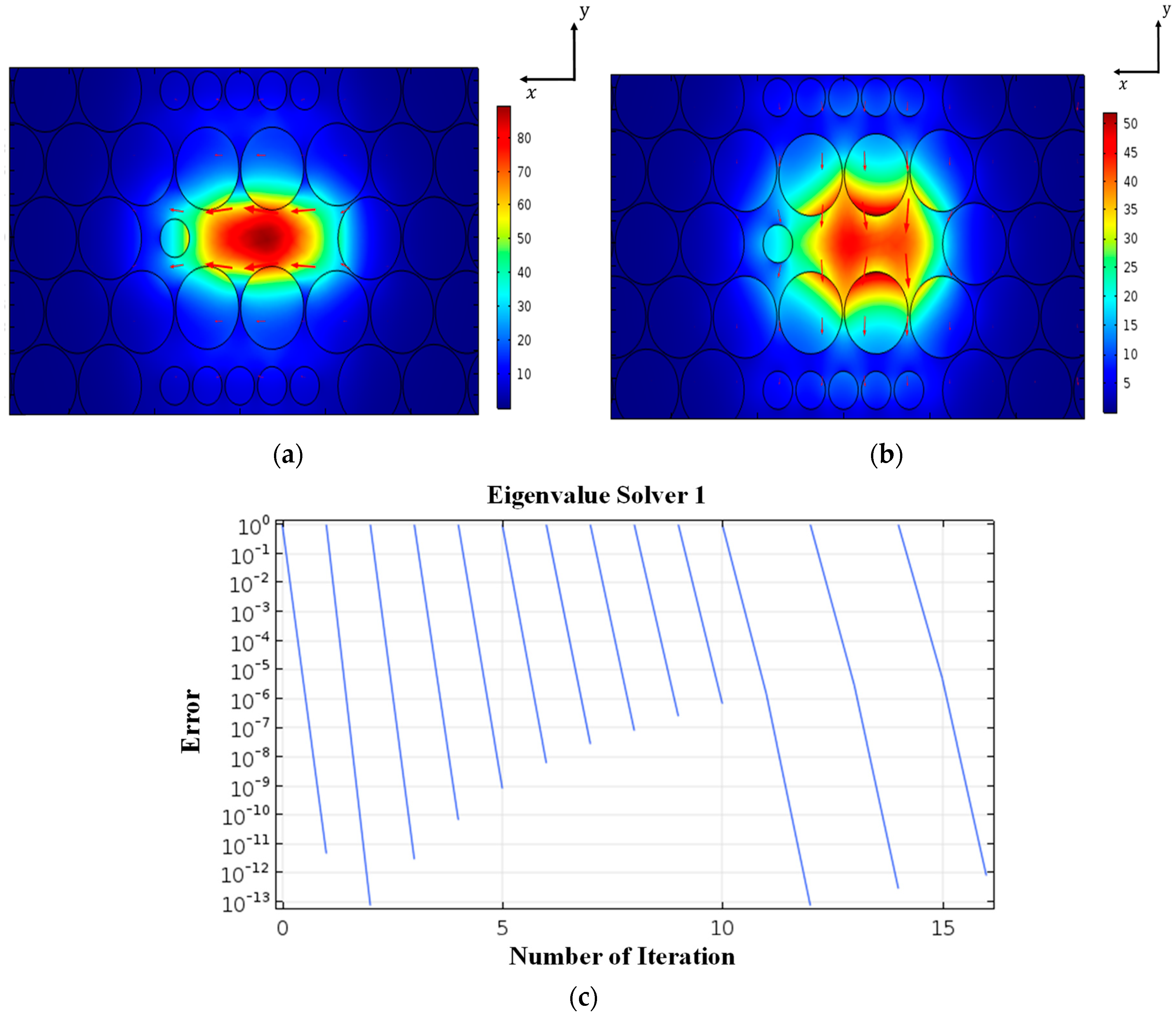
3. Numerical Method
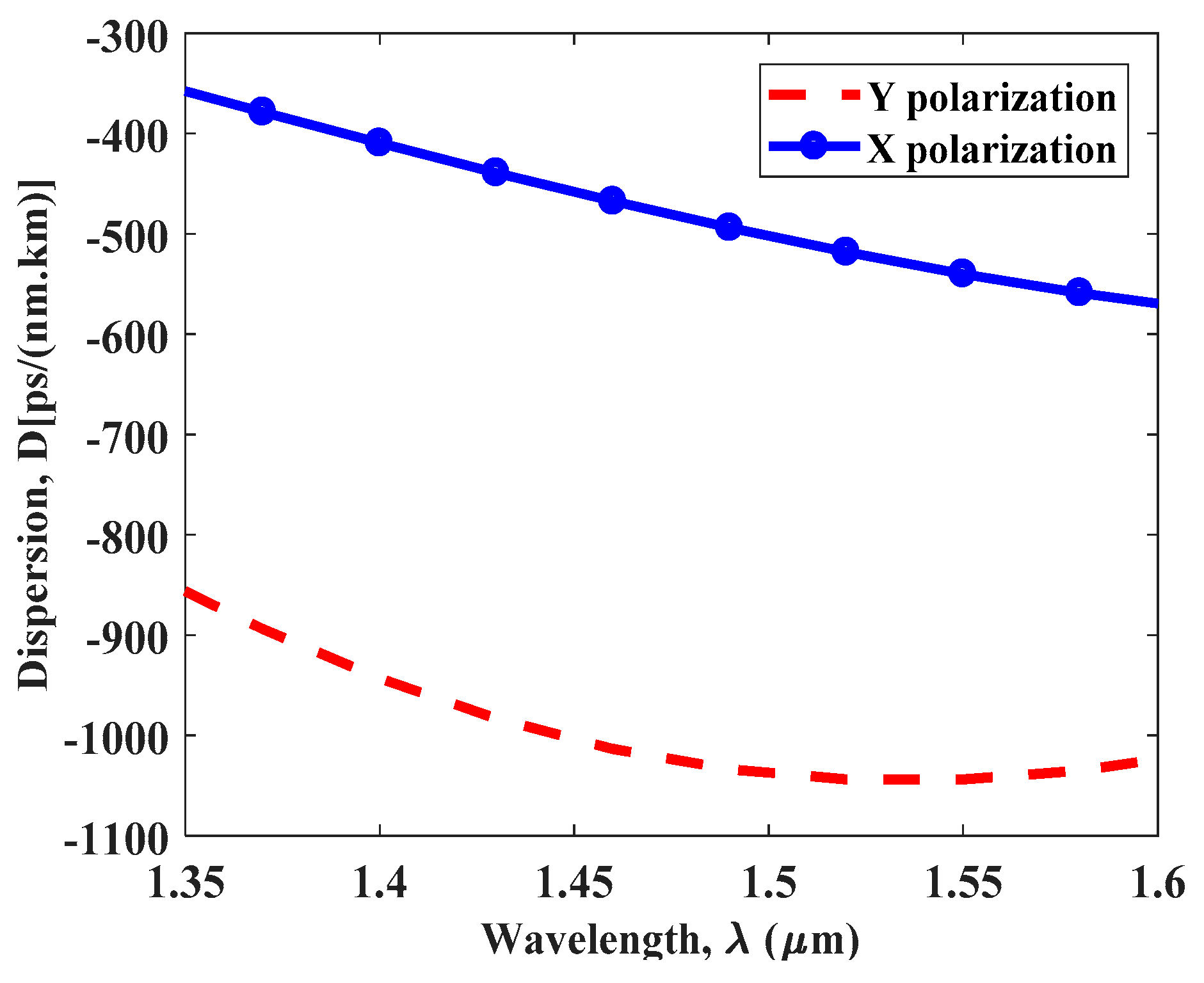
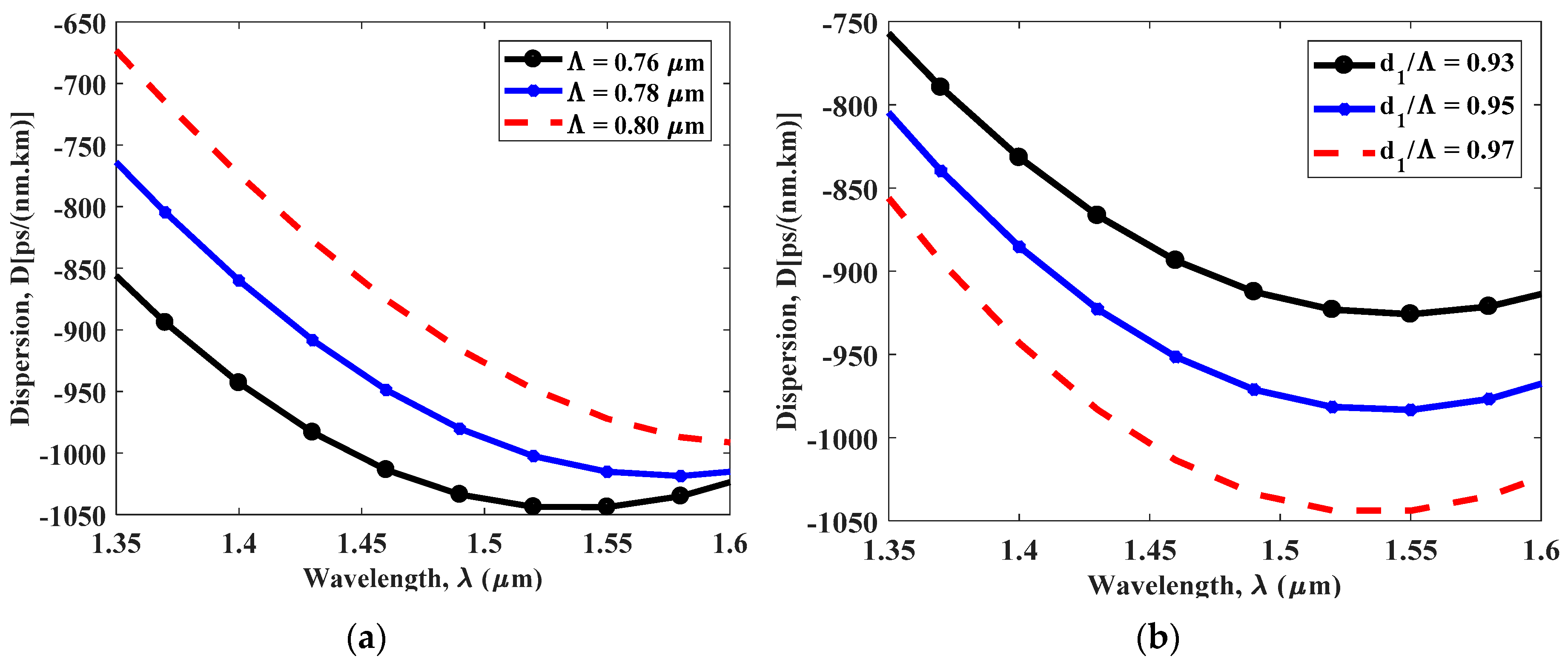
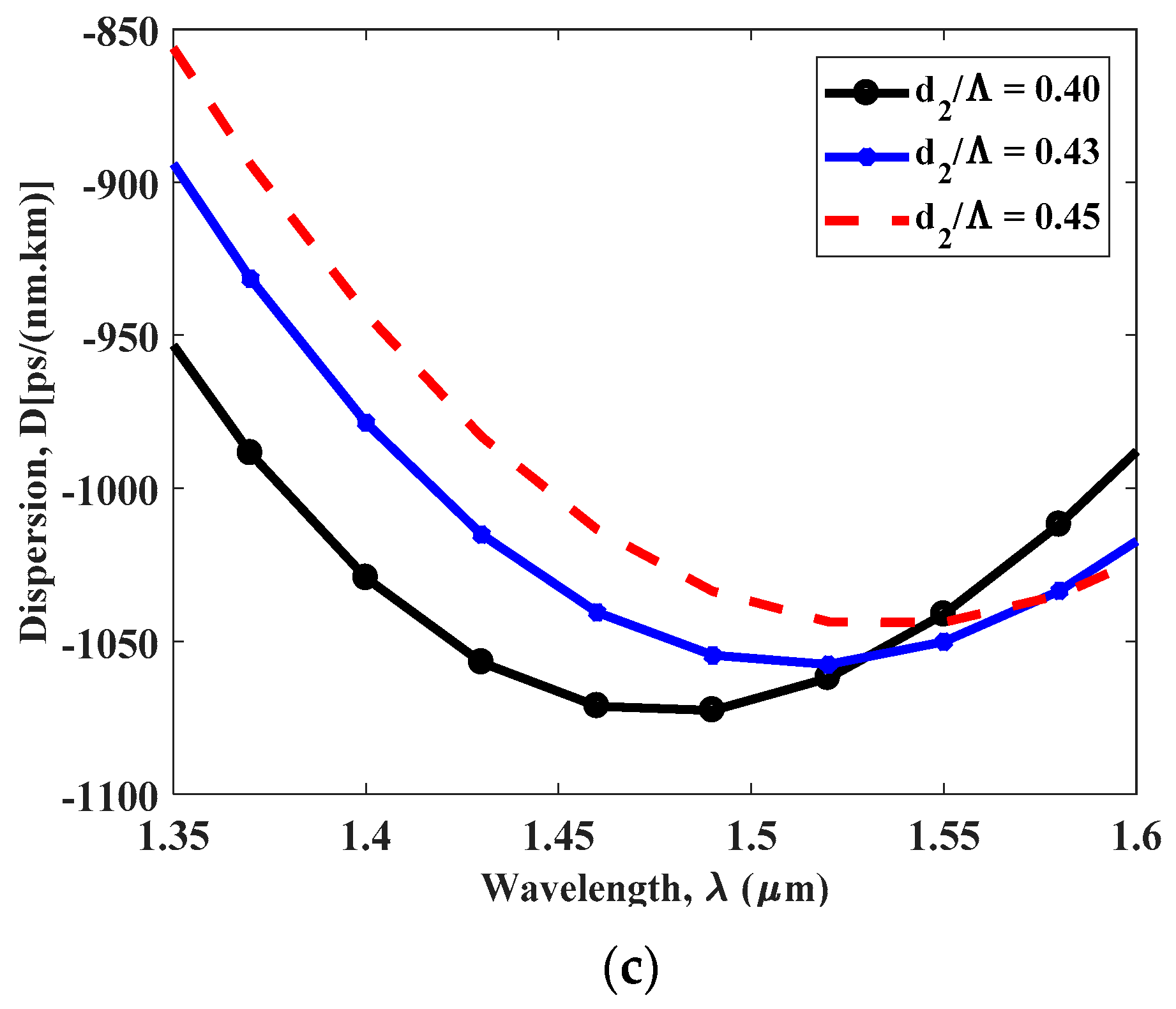
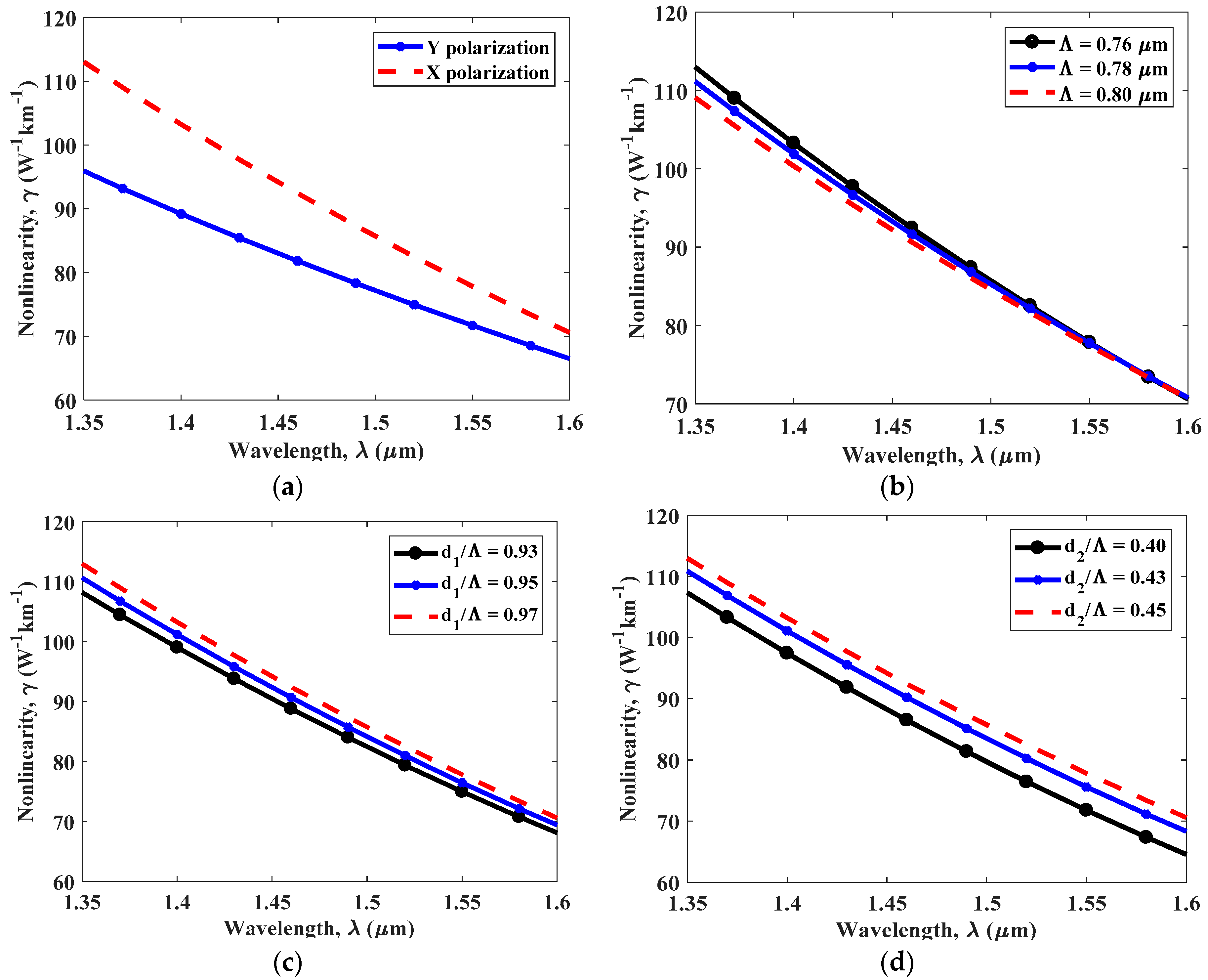
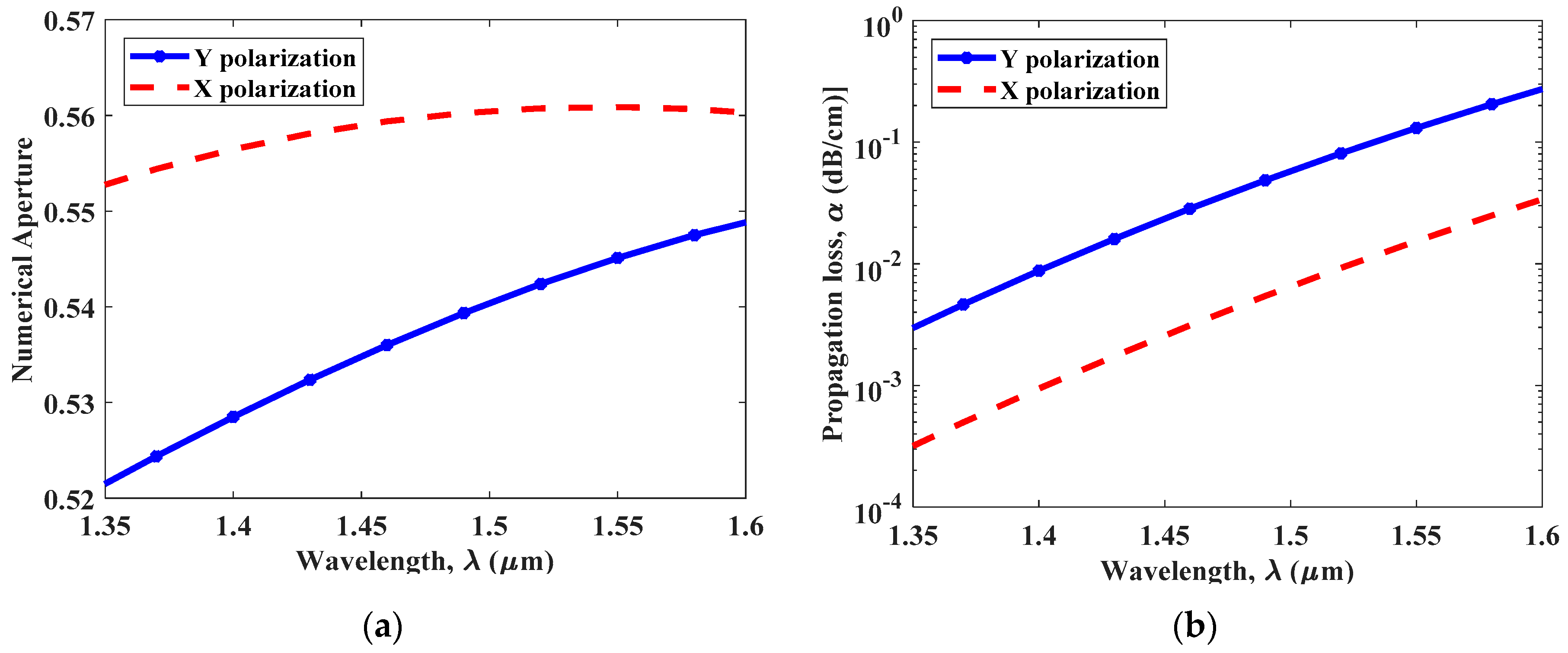
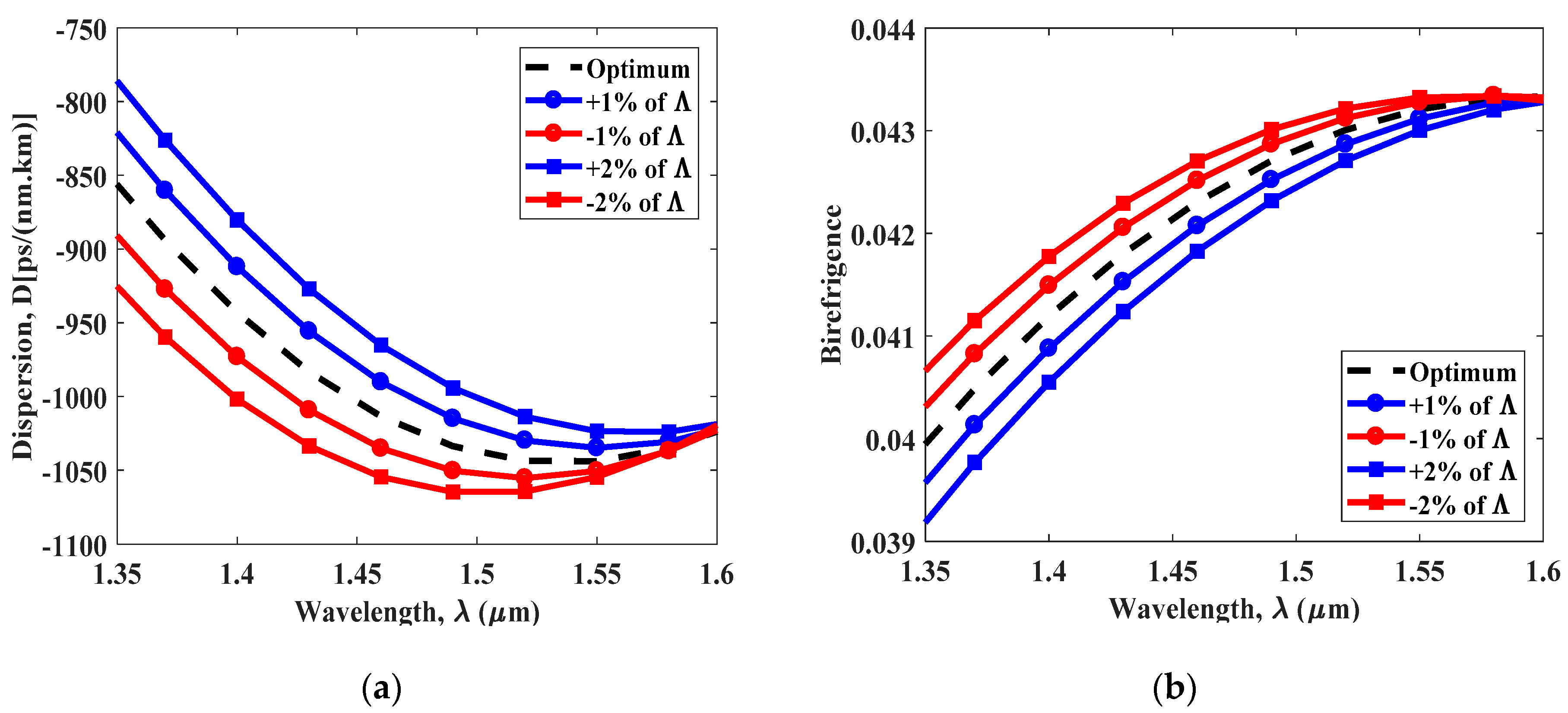
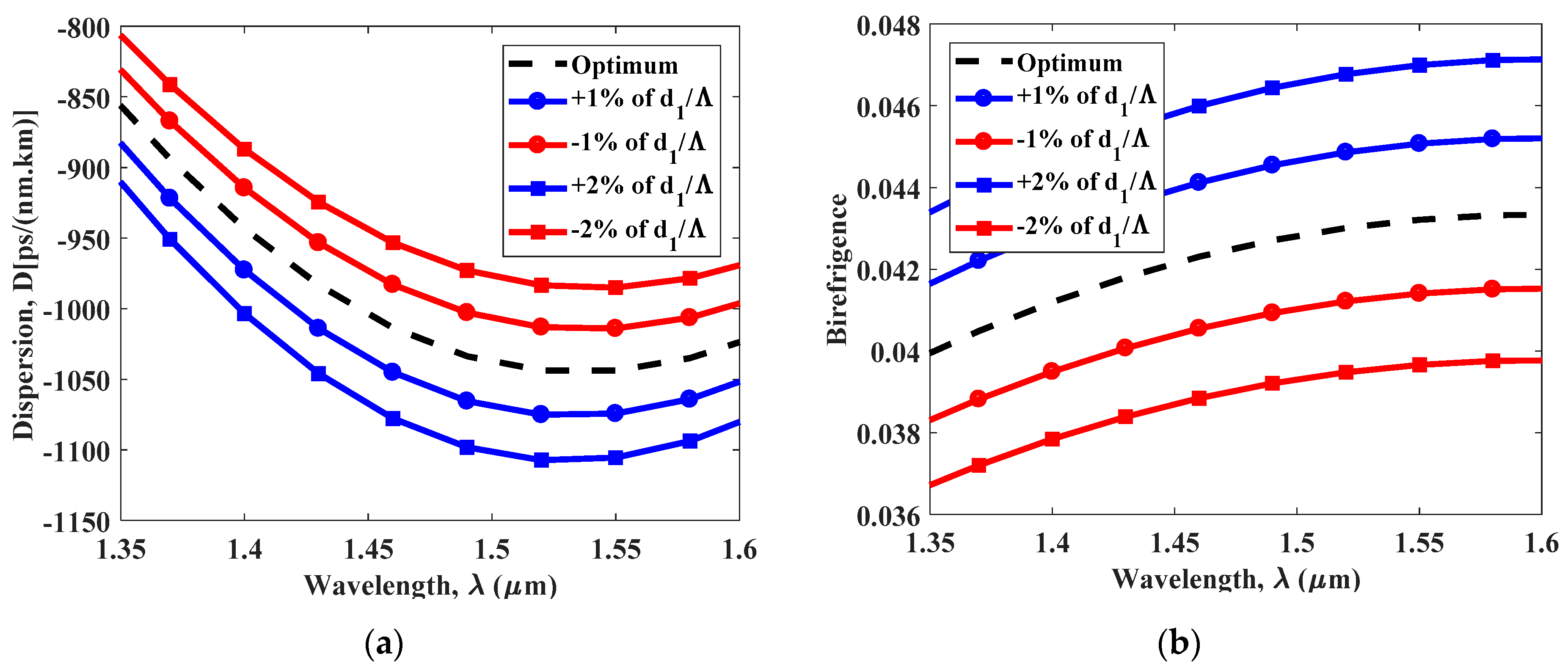
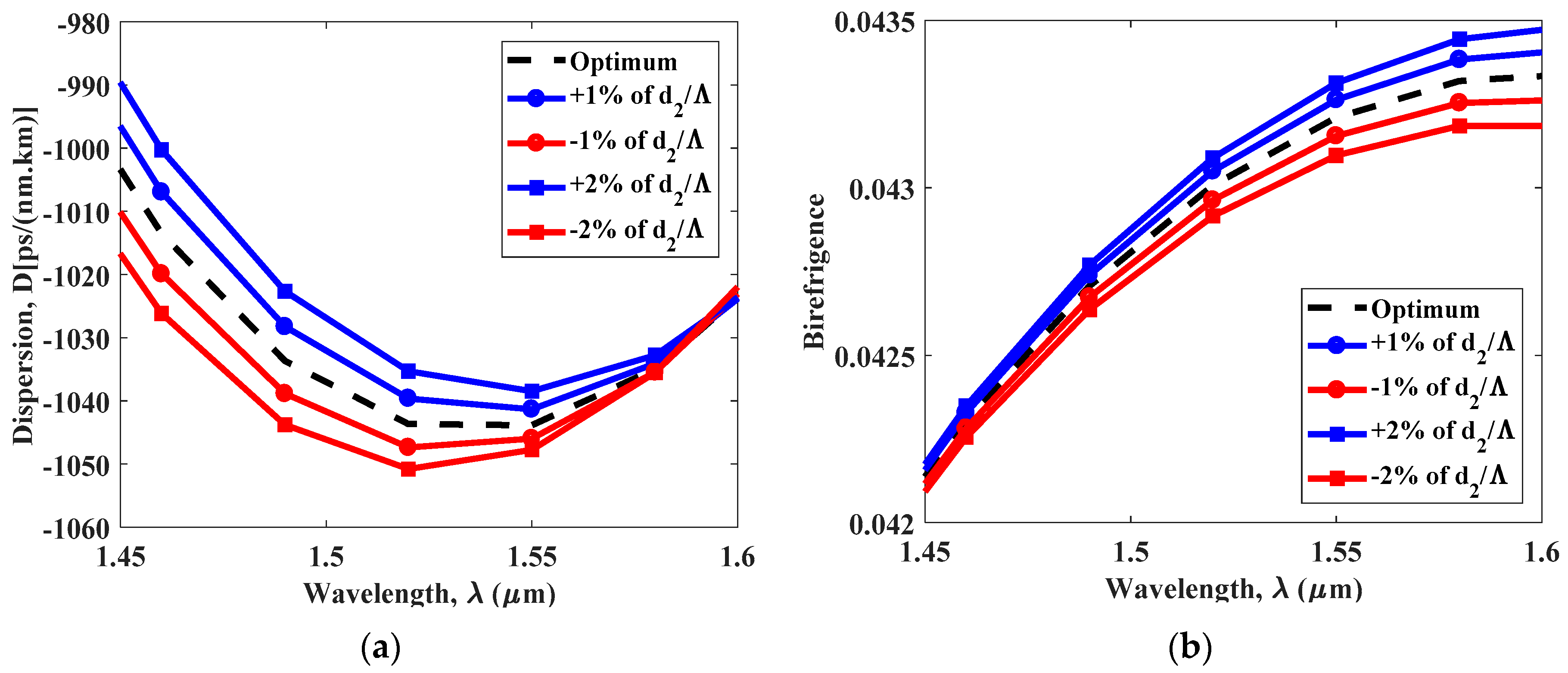
4. Simulation Result and Discussion
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Broeng, J.; Mogilevstev, D.; Barkou, S.E.; Bjarklev, A. Photonic Crystal Fibers: A New Class of Optical Waveguides. Opt. Fiber Technol. 1999, 5, 305–330. [Google Scholar] [CrossRef]
- Zheltikov, A.M. Holey fibers. Physics-Uspekhi 2000, 43, 1125–1136. [Google Scholar] [CrossRef]
- Knight, J.C. Photonic crystal fibres. Nature 2003, 424, 847–851. [Google Scholar] [CrossRef] [PubMed]
- Kubota, H.; Kawanishi, S.; Koyanagi, S.; Tanaka, M.; Yamaguchi, S. Absolutely Single Polarization Photonic Crystal Fiber. IEEE Photonics Technol. Lett. 2004, 16, 182–184. [Google Scholar] [CrossRef]
- Dadabayev, R.; Shabairou, N.; Zalevsky, Z.; Malka, D. A visible light RGB wavelength demultiplexer based on silicon-nitride multicore PCF. Opt. Laser Technol. 2019, 111, 411–416. [Google Scholar] [CrossRef]
- Medhat, M.; El-Zaiat, S.Y. Interferometric determination of the birefringence dispersion of anisotropic materials. Opt. Commun. 1997, 141, 145–149. [Google Scholar] [CrossRef]
- Varshney, S.K.; Saitoh, K.; Saitoh, N.; Tsuchida, Y.; Koshiba, M.; Sinha, R.K. Strategies for realizing photonic crystal fiber bandpass filters. Opt. Express 2008, 16, 9459–9467. [Google Scholar] [CrossRef] [PubMed]
- Florous, N.; Saitoh, K.; Koshiba, M. A novel approach for designing photonic crystal fiber splitters with polarization-independent propagation characteristics. Opt. Express 2005, 13, 7365–7373. [Google Scholar] [CrossRef] [PubMed]
- Grüner-nielsen, L.; Wandel, M.; Kristensen, P.; Jørgensen, C.; Jørgensen, L.V.; Edvold, B.; Pálsdóttir, B.; Jakobsen, D. Dispersion-Compensating Fibers. J. Lightw. Technol. 2005, 23, 3566–3579. [Google Scholar] [CrossRef]
- Saitoh, K.; Koshiba, M.; Hasegawa, T.; Sasaoka, E. Chromatic dispersion control in photonic crystal fibers: Application to ultra-flattened dispersion. Opt. Express 2003, 11, 843. [Google Scholar] [CrossRef] [PubMed]
- Kaijage, S.F.; Namihira, Y.; Hai, N.H.; Begum, F.; Razzak, S.M.A.; Kinjo, T.; Miyagi, K.; Zou, N. Broadband dispersion compensating octagonal photonic crystal fiber for optical communication applications. Jpn. J. Appl. Phys. 2009, 48, 0524011–0524018. [Google Scholar] [CrossRef]
- Selim Habib, M.; Mejbaul Haque, M.; Samiul Habib, M.; Hasan, M.I.; Shaifur Rahman, M.; Razzak, S.M.A. Polarization maintaining holey fibers for residual dispersion compensation over S + C + L wavelength bands. Optik (Stuttg.) 2014, 125, 911–915. [Google Scholar] [CrossRef]
- Samiul Habib, M.; Nasim, K.M.; Selim Habib, M.; Imran Hasan, M.; Ahmad, R. Relative dispersion slope matched dispersion compensating highly birefringent spiral microstructure optical fibers using defected core. Opt. Eng. 2013, 52, 096110. [Google Scholar] [CrossRef]
- Mejbaul Haque, M.; Shaifur Rahman, M.; Samiul Habib, M.; Razzak, S.M.A. Design and characterization of single mode circular photonic crystal fiber for broadband dispersion compensation. Optik (Stuttg.) 2014, 125, 2608–2611. [Google Scholar] [CrossRef]
- Yue, Y.; Kai, G.; Wang, Z.; Sun, T.; Jin, L.; Lu, Y.; Zhang, C.; Liu, J.; Li, Y.; Liu, Y.; et al. Highly birefringent elliptical-hole photonic crystal fiber with squeezed hexagonal lattice. Opt. Lett. 2007, 32, 469–471. [Google Scholar] [CrossRef]
- Steel, M.J.; Osgood, R.M. Elliptical-hole photonic crystal fibers. Opt. Lett. 2001, 26, 229. [Google Scholar] [CrossRef] [PubMed]
- Blanch, A.O.; Knight, J.C.; Wadsworth, W.J.; Arriaga, J.; Mangan, B.J.; Birks, T.A.; Russell, P.S.J. Highly birefringent photonic crystal fibers. Opt. Lett. 2000, 25, 1325–1327. [Google Scholar] [CrossRef]
- Chaudhuri, P.R.; Paulose, V.; Zhao, C.; Lu, C. Near-elliptic core polarization-maintaining photonic crystal fiber: Modeling birefringence characteristics and realization. IEEE Photonics Technol. Lett. 2004, 16, 1301–1303. [Google Scholar] [CrossRef]
- Wang, W.; Yang, B.; Song, H.; Fan, Y. Investigation of high birefringence and negative dispersion photonic crystal fiber with hybrid crystal lattice. Optik (Stuttg.) 2013, 124, 2901–2903. [Google Scholar] [CrossRef]
- Rashid, M.M.; Anower, M.S.; Hasan, M.R.; Tabassum, N. Hexagonal shaped core dodecagonal PCF with high birefringence and nonlinear coefficient. In Proceedings of the 2017 International Conference on Electrical, Computer and Communication Engineering (ECCE), Cox’s Bazar, Bangladesh, 16–18 February 2017; pp. 447–450. [Google Scholar]
- Agrawal, A.; Kejalakshmy, N.; Chen, J.; Rahman, B.M.A.; Grattan, K.T.V. Golden spiral photonic crystal fiber: Polarization and dispersion properties. Opt. Lett. 2008, 33, 2716. [Google Scholar] [CrossRef] [PubMed]
- Agrawal, A.; Kejalakshmy, N.; Rahman, B.M.A.; Grattan, K.T.V. Polarization and dispersion properties of elliptical hole golden spiral photonic crystal fiber. Appl. Phys. B Lasers Opt. 2010, 99, 717–726. [Google Scholar] [CrossRef]
- Revathi, S.; Inbathini, S.R.; Saifudeen, R.A. Highly nonlinear and birefringent spiral photonic crystal fiber. Adv. Optoelectron. 2014. [Google Scholar] [CrossRef]
- Knight, J.C.; Birks, T.; Russell, P.S.J.; Atkin, D. All-silica single-mode optical fiber with photonic crystal cladding. Opt. Lett. 1996, 21, 1547–1549. [Google Scholar] [CrossRef] [PubMed]
- Pysz, D.; Kujawa, I.; Stepien, R.; Klimczak, M.; Filipkowski, A.; Franczyk, M.; Kociszewski, L.; Buzniak, J.; Harasny, K.; Buczynski, R. Stack and draw fabrication of soft glass microstructured fiber optics. Bull. Pol. Acad. Sci. Tech. Sci. 2014, 62, 667–682. [Google Scholar] [CrossRef]
- Biswas, S.; Islam, S.; Islam, M.; Mia, M.; Sayem, S.; Ahmed, F. Design of an Ultrahigh Birefringence Photonic Crystal Fiber with Large Nonlinearity Using All Circular Air Holes for a Fiber-Optic Transmission System. Photonics 2018, 5, 26. [Google Scholar] [CrossRef]
- Malitson, I.H. Interspecimen Comparison of the Refractive Index of Fused Silica. J. Opt. Soc. Am. 1965, 55, 1205–1208. [Google Scholar] [CrossRef]
- Islam, M.I.; Ahmed, K.; Sen, S.; Paul, B.K.; Islam, M.S.; Chowdhury, S.; Hasan, M.R.; Uddin, M.S.; Asaduzzaman, S.; Bahar, A.N. Proposed square lattice photonic crystal fiber for extremely high nonlinearity, birefringence and ultra-high negative dispersion compensation. J. Opt. Commun. 2017. [Google Scholar] [CrossRef]
- Islam Md, A. Broadband Dispersion Compensation of Single Mode Fiber by using Modified Decagonal Photonic Crystal Fiber having High Birefringence. J. Lasers Opt. Photonics 2015, 2, 123. [Google Scholar] [CrossRef]
- Paul, B.K.; Ahmed, K. Si7N3 material filled novel heptagonal photonic crystal fiber for laser applications. Ceram. Int. 2019, 45, 1215–1218. [Google Scholar] [CrossRef]
- Islam, M.I.; Khatun, M.; Ahmed, K. Ultra-high negative dispersion compensating square lattice based single mode photonic crystal fiber with high nonlinearity. Opt. Rev. 2017, 24, 147–155. [Google Scholar] [CrossRef]
- Ghosh, D.; Bose, S.; Roy, S.; Bhadra, S.K. Design and Fabrication of Microstructured Optical Fibers with Optimized Core Suspension for Enhanced Supercontinuum Generation. J. Lightw. Technol. 2015, 33, 4156–4162. [Google Scholar] [CrossRef]
- Bise, R.T.; Trevor, D.J. Sol-gel derived microstructured fiber: Fabrication and characterization. In Proceedings of the OFC/NFOEC Technical Digest. Optical Fiber Communication Conference, Anaheim, CA, USA, 6–11 March 2005; Volume 3. [Google Scholar]
- Liu, Z.; Wu, C.; Vincent Tse, M.-L.; Lu, C.; Tam, H.-Y. Ultrahigh birefringence index-guiding photonic crystal fiber and its application for pressure and temperature discrimination. Opt. Lett. 2013, 38, 1385. [Google Scholar] [CrossRef] [PubMed]
- Hasan, M.R.; Islam, M.A.; Rifat, A.A.; Hasan, M.I. A single-mode highly birefringent dispersion-compensating photonic crystal fiber using hybrid cladding. J. Mod. Opt. 2017, 64, 218–225. [Google Scholar] [CrossRef]
- Hasan, M.I.; Habib, M.S.; Razzak, S.M.A. An elliptical-shaped core residual dispersion compensating octagonal photonic crystal fiber. IEEE Photonics Technol. Lett. 2014, 26, 2047–2050. [Google Scholar] [CrossRef]
- Haque, M.M.; Rahman, M.S.; Habib, M.S.; Habib, M.S. A single mode hybrid cladding circular photonic crystal fiber dispersion compensation and sensing applications. Photonics Nanostruct.-Fundam. Appl. 2015, 14, 63–70. [Google Scholar] [CrossRef]

| Prior Reference | Air Hole Shape | Dispersion , ps/nm.km | Birefringence |
|---|---|---|---|
| [26] | Circular | ||
| [31] | Circular and elliptical | - | |
| [35] | Circular | ||
| [36] | Circular and elliptical | ||
| [37] | Circular and elliptical | ||
| Proposed HC-PCF | Circular |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Biswas, S.K.; Arfin, R.; Habib, A.B.; Amir, S.B.; Zahir, Z.B.; Islam, M.R.; Hussain, M.S. A Modified Design of a Hexagonal Circular Photonic Crystal Fiber with Large Negative Dispersion Properties and Ultrahigh Birefringence for Optical Broadband Communication. Photonics 2019, 6, 19. https://doi.org/10.3390/photonics6010019
Biswas SK, Arfin R, Habib AB, Amir SB, Zahir ZB, Islam MR, Hussain MS. A Modified Design of a Hexagonal Circular Photonic Crystal Fiber with Large Negative Dispersion Properties and Ultrahigh Birefringence for Optical Broadband Communication. Photonics. 2019; 6(1):19. https://doi.org/10.3390/photonics6010019
Chicago/Turabian StyleBiswas, Shovasis Kumar, Rishad Arfin, Ashfia Binte Habib, Syed Bin Amir, Zunayeed Bin Zahir, Mohammad Rezaul Islam, and Md. Shahriar Hussain. 2019. "A Modified Design of a Hexagonal Circular Photonic Crystal Fiber with Large Negative Dispersion Properties and Ultrahigh Birefringence for Optical Broadband Communication" Photonics 6, no. 1: 19. https://doi.org/10.3390/photonics6010019
APA StyleBiswas, S. K., Arfin, R., Habib, A. B., Amir, S. B., Zahir, Z. B., Islam, M. R., & Hussain, M. S. (2019). A Modified Design of a Hexagonal Circular Photonic Crystal Fiber with Large Negative Dispersion Properties and Ultrahigh Birefringence for Optical Broadband Communication. Photonics, 6(1), 19. https://doi.org/10.3390/photonics6010019





