Super-Oscillatory Metalens at Terahertz for Enhanced Focusing with Reduced Side Lobes

Abstract

In this paper, we design and numerically demonstrate an ultra-thin super-oscillatory metalens with a resolution below the diffraction limit. The zones of the lens are implemented using metasurface concepts with hexagonal unit cells. This way, the transparency and, hence, efficiency is optimized, compared to the conventional transparent–opaque zoning approach that introduces, inevitably, a high reflection in the opaque regions. Furthermore, a novel two-step optimization technique, based on evolutionary algorithms, is developed to reduce the side lobes and boost the intensity at the focus. After the design process, we demonstrate that the metalens is able to generate a focal spot of 0.46λ₀ (1.4 times below the resolution limit) at the design focal length of 10λ₀ with reduced side lobes (the side lobe level being approximately −11 dB). The metalens is optimized at 0.327 THz, and has been validated with numerical simulations.

1. Introduction

For any conventional imaging instrument, the fine features of an object are permanently lost in the image, due to the diffraction of light. Small details scatter light mostly into evanescent waves that exponentially decay away from the object and, thus, cannot be captured by the device [1]. To overcome this diffraction limit, novel concepts have been proposed in the last years, such as metamaterials and metasurfaces [2,3,4], dielectric particles [5,6,7], and solid immersion lenses [8], to name a few. Within this realm, super-oscillatory devices have demonstrated their potential in imaging applications with an improved spatial resolution.

Super-oscillations were first introduced at the end of the last century to describe a phenomenon in which a band-limited signal can contain localized field variations with oscillations faster than those of the highest Fourier components of their spectrum [9], as explained in Appendix A.1 below. In optics, the term super-oscillation refers to a near-destructive interference with fast phase variations and high local momenta in a small intensity region [10]. Recently, this phenomenon has been applied to improve the performance of imaging systems by implementing super-oscillatory lenses (SOLs) with subwavelength spatial resolution, defeating the diffraction limit [2,10,11,12,13,14,15,16].

Traditionally, SOLs are planar, multi-annular, and radial focusing devices composed of alternating transparent and opaque concentric rings, usually designed applying optimization techniques, such as genetic algorithms and vector designs [11,12,13]. The optical super-oscillation is controlled by tailoring the interference between the diffracted beams produced by each annular aperture [14]. The main drawback of this procedure is that it gives rise to high amplitude side lobes that reduce the intensity of the subwavelength focal spot generated at the output [10]. Moreover, despite the fact that there is no physical limit regarding the size of the focal spot along the transversal axes, it has been demonstrated that the efficiency of a SOL is dramatically reduced as the resolution is increased [15].

Since they were introduced several years ago, metamaterials (and metasurfaces as their 2D version) have opened new avenues to synthesize and control wave propagation. Metamaterials have been demonstrated within a wide spectral range, from microwaves to optical frequencies, influencing other fields, like acoustics and mechanics, and giving rise to exciting applications. In particular, the field of lenses has greatly benefited from the introduction of metamaterials and metasurfaces since the beginning of the topic and, nowadays, a high variety of focusing devices with exotic performance have been demonstrated [17,18,19,20].

Inspired by the features of metamaterials and metasurfaces, in this work, we propose and demonstrate, both analytically and numerically, a binary SOL designed by alternating semitransparent concentric rings filled with two different metamaterial unit cells. Three objectives are pursued: (i) enhancement of the efficiency by reducing the reflection at the input and, therefore, increase the amplitude at the focus; (ii) reducing the side lobes; and (iii) keeping a narrow focal spot below the diffraction limit, taken as 0.65λ₀ with λ₀ as the operation wavelength, considering the Rayleigh criterion—see [1] and Appendix A.2 in this manuscript. To accomplish this, an advanced version of the binary particle swarm optimization (BPSO) algorithm, based on [21], is developed (described in detail in Appendix A.3). The designed SOL is then implemented using only two different unit cells at the operation frequency of f₀ = 0.327 THz (λ₀ = 917 µm). An increased amplitude of the focal spot and reduced side lobes are obtained with the proposed structure, compared to conventional SOLs based on opaque–transparent zones, without affecting its performance in terms of the subwavelength resolution of the focal spot, with a width of 0.44λ₀ and 0.50λ₀ along the x and y axis, respectively.

In this way, we continue the path started in the last few years to improve the SOL performance by implementing new algorithms or combining them with metasurface concepts. In fact, very recently, a new algorithm to design super-oscillatory devices able to optimize the main-side lobe intensity ratio has been reported, obtaining resolutions between 0.50λ₀ and 0.25λ₀ [22]. Compared with this work, our algorithm is more complex, but can develop solutions with a similar resolution, providing, simultaneously, the actual geometry that fulfills the prescribed field distribution profile. In [23], broadband imaging with a resolution approximately 0.64 times the Rayleigh criterion in the visible range was obtained using metasurface unit cells. However, the phase difference between the zones was fixed at π rad, deterring the transmittance and overall efficiency. It is noteworthy that our lens shows a comparable resolution, but with a higher transmittance efficiency. In [24], a new class of super-oscillation waveform was proposed to obtain lower side lobes, as low as 15 dB below the main spot, at the expense of having a diffraction-limited focus. Our work, in contrast, shows higher side lobes (11 dB below the main beam), but the main spot is not diffraction limited.

As can be seen from this brief state-of-the-art review, one key aspect to obtain a practical super-oscillatory device is the ability of obtaining a subdiffraction main focus with high intensity, while keeping low side lobes. This work tries to summarize all these aspects, combining the use of metasurfaces to get higher the efficiency and a smart design process to obtain, at the same time, the desired field profile with low side lobes.

2. Design and Analytical Results

As mentioned in the introduction, to create different optical paths for the even and odd zones, two different unit cells are used; see schematic in Figure 1a. Both are hexagonal ring slots with side length L_hex carved on a copper metallic film with conductivity σ = 5.8 × 10⁷ S/m and thickness h_m = 0.6 µm (0.65 × 10⁻³λ₀), laying on a polypropylene slab with relative permittivity ɛ_r = 2.25 and thickness h_d = 35 µm (0.038λ₀). Note that, for simplicity, we used the DC nominal conductivity of copper, although, in the terahertz band, this nominal value is usually lower due to granularity, etc.

Before engineering the unit cells for the even and odd zones, a preliminary analytical study is carried out using the Huygens–Fresnel principle, considering homogeneous isotropic materials for the different regions of a cylindrical SOL, while imposing a focal length (FL) value of 10λ₀. From these results (shown in Appendix A.4), it is found that a phase difference of at least π/6 rad between even and odd zones is necessary for the BPSO algorithm to converge and generate the focal spot at the design FL. In addition, since our aim is to increase the amplitude at the focus, both unit cells must be carefully engineered to ensure a high transmittance at the operation frequency. To achieve this, both the magnitude and phase of the transmission coefficient must be adjusted by varying the geometrical parameters of the unit cell. For simplicity, here, only the external radius of the hexagonal slot (α) is modified, as we found that tuning this parameter is enough to achieve a satisfactory performance.

The design is done using the frequency domain solver of the commercial software CST Microwave Studio^®. Unit cell boundary conditions are applied on the transverse plane and open boundaries along z (see coordinate axis in Figure 1a). The structure is illuminated with the fundamental TE₀₀ mode of a Floquet port, which corresponds to a vertically polarized plane wave (E_y), considering only normal incidence. With this setup, the contour maps of the magnitude and phase of the transmission coefficient as a function of α and frequency are calculated and shown in Figure 1b,c, respectively. As observed, the phase of the unit cells can be tuned from −π/2 to π/2 rad within the spectral range under study. Note that the phase excursion does not cover the complete −π to π rad range, as required in a graded index lens design for instance. To increase the phase excursion, one could either increase the frequency range or change the unit cell such that this requirement is fulfilled. However, this is not an issue in the proposed SOL that only requires two unit cells with a small phase difference of π/6 between them. Hence, from these results, we can determine the slot width of each unit cell, taking into account the two design conditions mentioned above, to get the highest possible transmittance and a phase difference larger than π/6 rad at the design frequency of f₀ = 0.327 THz (highlighted with a vertical dashed gray line in Figure 1b,c). The selected unit cells correspond to the designs with α₁ = 60 µm (0.065λ₀) and α₂ = 20 µm (0.022λ₀), which have a relatively high transmission coefficient of 0.8 and a phase of 0.12π and 0.28π, respectively, resulting in a phase difference of 0.16π, fulfilling both requirements. Both solutions have been highlighted with horizontal dashed gray lines in Figure 1b,c.

Once the unit cells have been selected, the SOL design is carried out by implementing a modified BPSO algorithm [6] (see Appendix A.3 for a description of the method and the parameters involved). In our calculations, we consider the following constants: V_max = 6, as suggested in [25], to set a limit and prevent further exploration after the population has converged; c₁ = c₂ = 2, to give equal weight to the social and the cognitive components; and w ∈ [0.4, 0.6], considering a time-varying inertial weight starting from 0.6, and decreasing proportionally after each iteration. The maximum number of iterations is set to 2000. In addition, a swarm of 100 particles is considered, each of them being a vector with 72 components. In order to reduce the computational burden, a cylindrical lens is first designed, and its near-field distribution at the operation frequency is calculated analytically with the Huygens–Fresnel approximation [19,20]. Isotropic point sources, with magnitude and phase taken from the selected unit cells, are placed at each of the 72 positions with a separation of 350 µm (0.381λ₀).

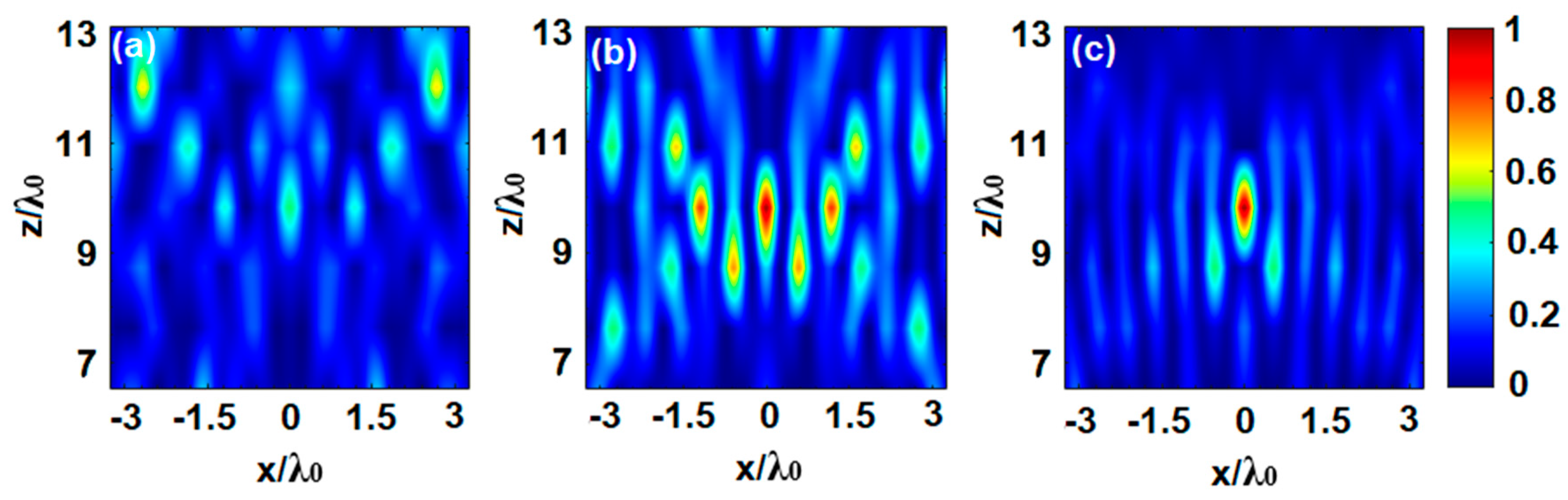
The optimization of the SOL is done in two steps; see Figure 2. In a first stage, an adapted weighted sinc is used as the goal function to get the desired profile of the target power distribution along the x-axis at z = FL = 10λ₀, starting with a random unit cell distribution [13]. The highest weight in the goal function is given to the focal spot. This makes the variance much bigger there than elsewhere, and the optimizer tries to reduce it, quickly developing a focus at the desired point, as shown in Figure 2b. The second step consists in reducing the power distribution of the side lobes with a new weighted exponential goal function. Another optimization process is launched using particles derived from the best combination found in the first step, and varying, then, one position between two consecutive particles. After applying this two-step process, the found global best solution is 111122222111122211221122212211221221221121121121121121121221221211211212, where “1” and “2” stand for unit cells of type 1 and 2 (α₁ and α₂), respectively. This vector is the unit cell distribution along the x-axis, from the center of the lens to its rightmost edge (the left-hand side is obtained by simply mirroring the array, making use of the lens symmetry). Thus, after this procedure, the cylindrical metalens has a total length along the transversal x axis of D ≈ 54λ₀.

The analytical normalized power distribution, obtained by applying the Huygens–Fresnel technique to the solution derived from our algorithm, is shown in Figure 2c. As observed there, a clear focus appears at FL = 9.816λ₀, very near the designed value of FL = 10λ₀. From the power distribution along the x-axis at z = FL, depicted in Figure 3a, we see that the value of full width at half-maximum (FWHM, defined as the distance at which the power distribution has been reduced to half its maximum) in the transversal x direction is FWHM_x = 0.36λ₀, which is well below the diffraction limit (0.65λ₀).

In the next step, we implement a spherical lens by simply applying rotation symmetry to the cylindrical lens solution, obtaining radial zones. As before, we compute, first, the near-field distribution with the Huygens–Fresnel approach. The normalized power profile along both x- and y-axes at FL is represented in Figure 3b (both curves are identical). The focus, in this case, appears at FL = 9.16λ₀, and has a FWHM = 0.46λ₀ both along x and y directions, also below the diffraction limit.

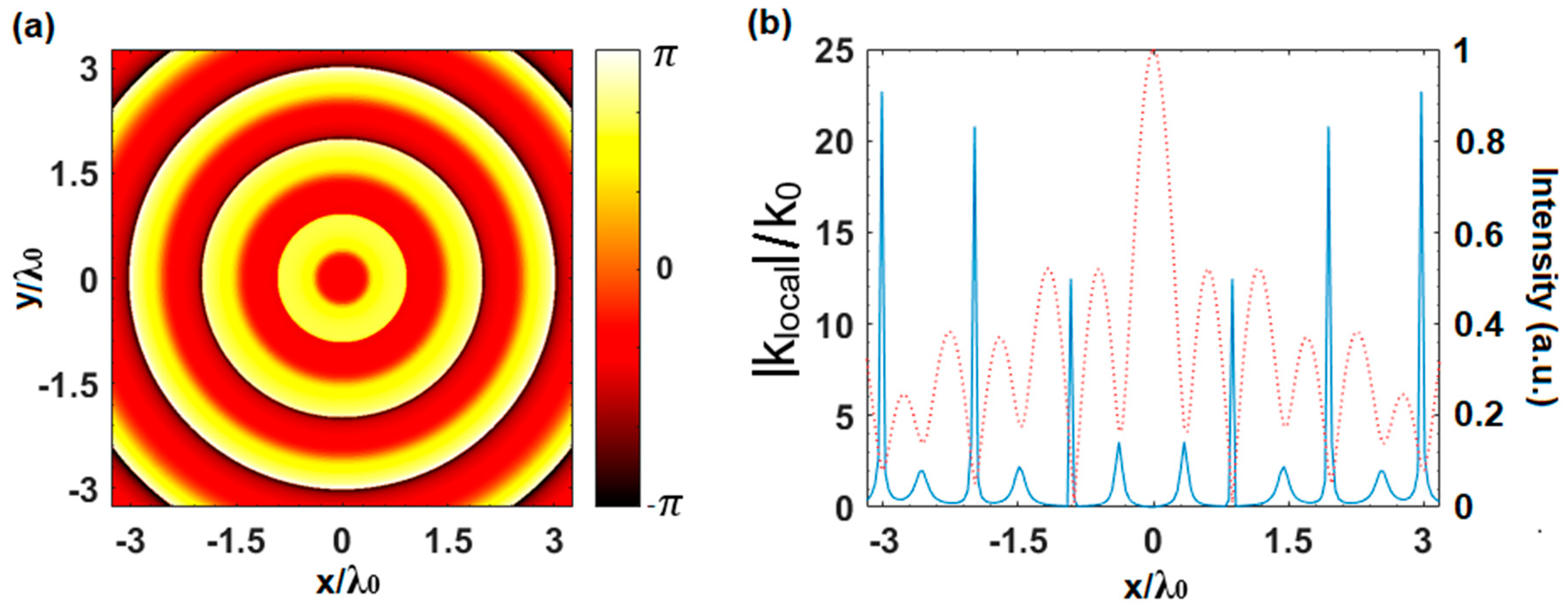
To verify that the focal spot generated in the spherical lens is, indeed, super-oscillatory, we analyze the behavior of the local wavenumber, k_local. According to the definition of super-oscillation [14], k_local is equal to the phase gradient (k_local = ∇Ψ), where Ψ is computed as Ψ = arg{E(r₀)·E(r_i)}, the function arg{a} represents the argument of a complex number a, and E(r₀)·E(r_i) is the scalar product of the electric field vector at points r₀ and r_i; r₀ is the reference point with coordinates (0, 0, FL), and r_i has coordinates (x, y, FL). In the super-oscillatory region, k_local should be larger than the highest wavenumber component (k₀ = 2π/λ₀, in free space). We use the center of the lens as a reference point to calculate the phase of the electric field along the x-axis at the focus (z = FL). As shown in Figure 4, there are regions where the phase rapidly oscillates, and k_local is much larger than k₀, demonstrating that the operation is based on super-oscillations. Moreover, these regions correspond to the electric field intensity minima, which is also a characteristic of super-oscillatory devices.

3. Simulation Results

The transient solver of commercial software CST Microwave Studio^® is used to evaluate the performance of the full metalens. The center of each unit cell is placed at the coordinates of the source points obtained in the Huygens–Fresnel analysis. A schematic of the final design is shown in Figure 1d,e. The lens is illuminated using a plane wave under normal incidence assuming open boundary conditions in all directions. Moreover, magnetic and electric symmetries are applied on the yz-plane and xz-plane, respectively. A fine hexahedral mesh is used, with smallest and largest mesh cells of 17.8 μm (≈0.019λ₀) and 60 μm (≈0.07λ₀), respectively.

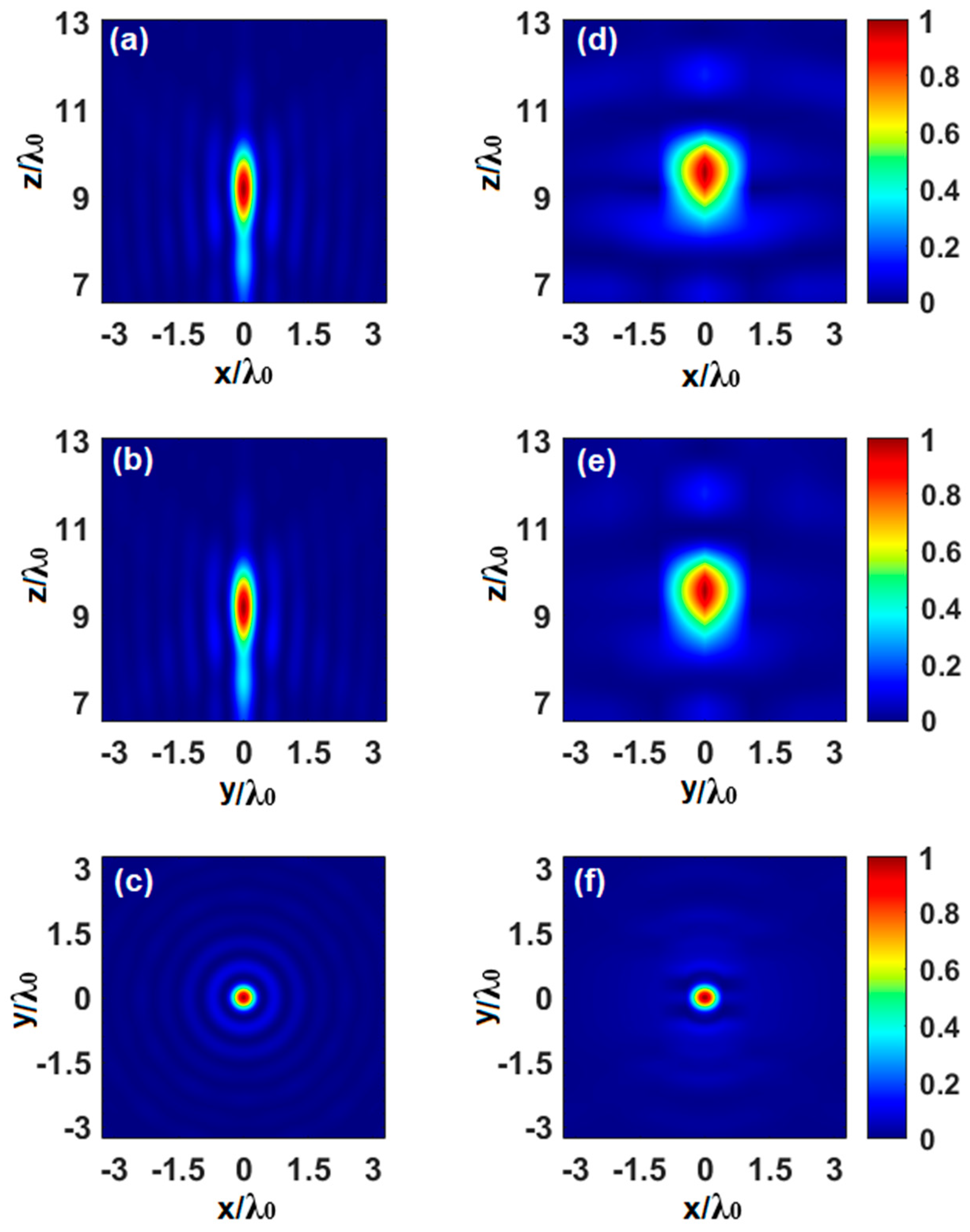
The simulation results of the power distribution on the E-plane (yz), H-plane (xz), and xy-plane (at z = FL), for the designed SOL at the operation frequency of 0.327 THz, are shown in Figure 5 (right column), along with the analytical results of the spherical lens obtained with the Huygens–Fresnel method (left column). As observed, the agreement between both results is qualitatively good, although there are some differences, probably due to the simplifications assumed in the analytical models to speed up the analysis.

To better compare these results, a summary of the metalenses’ performance is shown in

Table 1. Summary of the focusing properties of the studied SOL.

	Cylindrical SOL (Analytical)	Spherical SOL (Analytical)	Spherical SOL (Simulation)
FL	10λ0	9.16λ0	9.56λ0
FWHMx	0.36λ0	0.46λ0	0.44λ0
FWHMy	-	0.46λ0	0.5λ0
Enhancement	-	18.4 dB	16.6 dB
Ellipticity	-	1	0.88
Depth of Focus	1.14λ0	1.28λ0	1.51λ0

. There, the values of the cylindrical SOL are also included for completeness. For the simulated spherical SOL, the subwavelength focal spot is numerically found at a distance of 8.77 mm (9.56λ₀), which is near the designed value (10λ₀) with a transversal resolution of FWHM_x = 0.44λ₀ and FWHM_y = 0.5λ₀ along the x- and y-axis, respectively. Note that these values are below the diffraction limit (0.65λ₀). Low side lobes are obtained in all cases, with a magnitude of the highest side lobe approximately 10% below of the main lobe in the simulated SOL. With respect to the depth of focus (DOF, defined as the distance along the z-axis where the power distribution has decayed half its maximum from the FL), the simulated spherical SOL shows a bigger value than the analytical spherical SOL (1.51λ₀ and 1.28λ₀, respectively). This is an expected result because of the higher accuracy of the numerical analysis, done using the physical unit cells (taken from Figure 1). To compare, further, the focusing performance, the power enhancement (defined as the power amplitude at the FL with and without the SOL) is smaller in the numerical simulation. This can be explained by considering that, in contrast to the analytical calculation, in the simulated model, both material loss and diffraction effects are considered. Finally, it can be noted that the focus ellipticity (defined as the ratio between FWHM_x and FWHM_y) is very close to unity in both spherical lenses, which means an almost spherical focal spot in the xy plane.

4. Conclusions

In this work, we have engineered and evaluated, both analytically and numerically, a THz binary super-oscillatory metalens, with the aim to improve the magnitude of the focal spot and achieve, at the same time, a reduction of its side lobes. As a result, an ultrathin metalens with thickness around 0.04λ₀ has been demonstrated at 0.327 THz. A new algorithm, based on a two-step variation of the BPSO, has been developed to enhance the intensity at the focus, and mitigate the side lobe level. The solution obtained shows super-resolution with reduced side lobes and a large enhancement while allowing a spherical focus, with ellipticity close to unity. Both the analytically and numerically calculated spherical lens create a subwavelength focal spot near the prescribed FL, sharper than 0.5λ₀, beating the Rayleigh diffraction limit (0.65λ₀). Moreover, there are no significant side lobes (around 10% of the central peak power), with a power enhancement at the FL of more than 16 dB.