LCoS SLM Study and Its Application in Wavelength Selective Switch
Abstract
:1. Introduction
2. Analysis on LCoS for the WSS System
2.1. Response Time
2.2. Crosstalk
2.2.1. Device Level Crosstalk
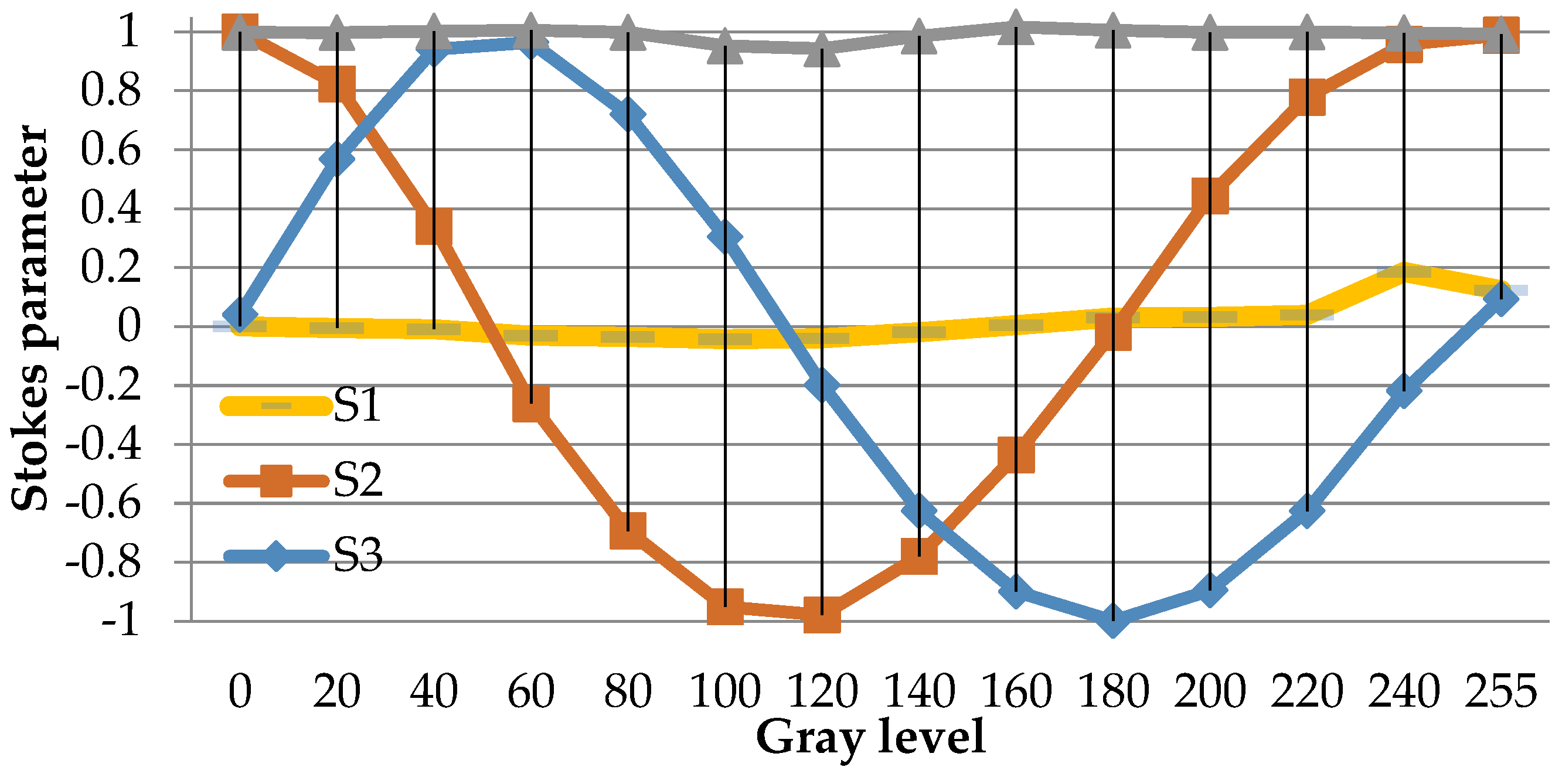
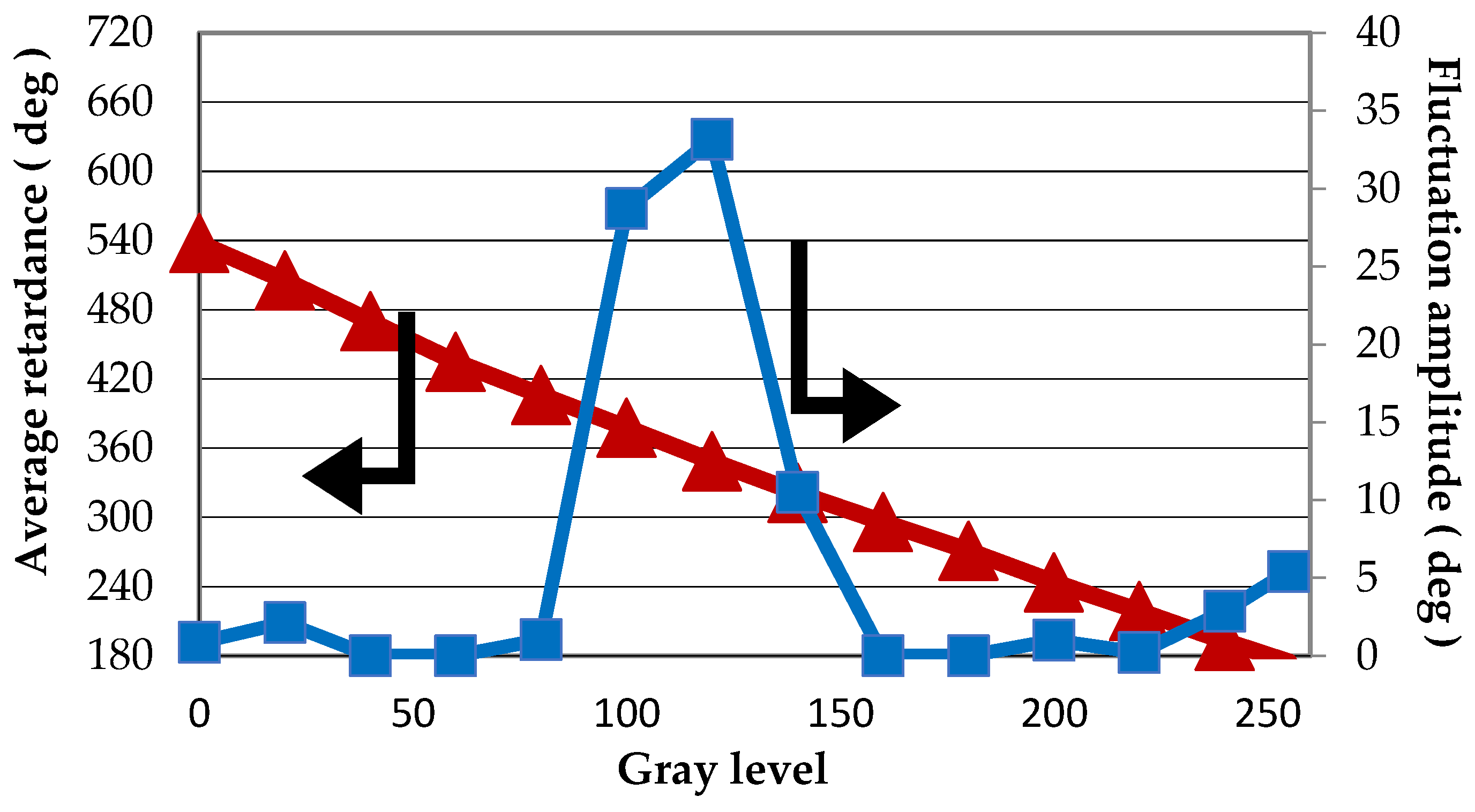
Phase Flicker
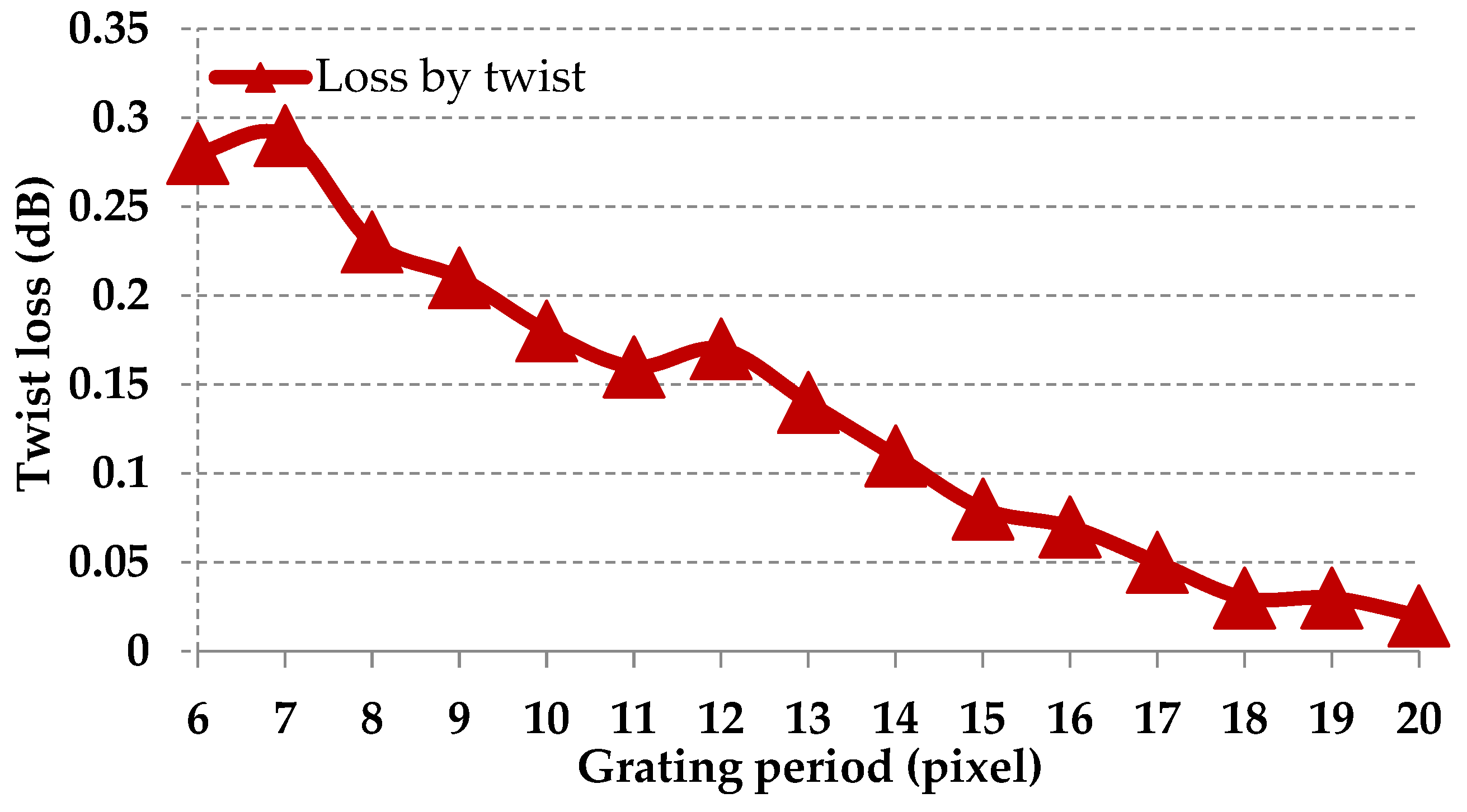
Fringing Field Effect
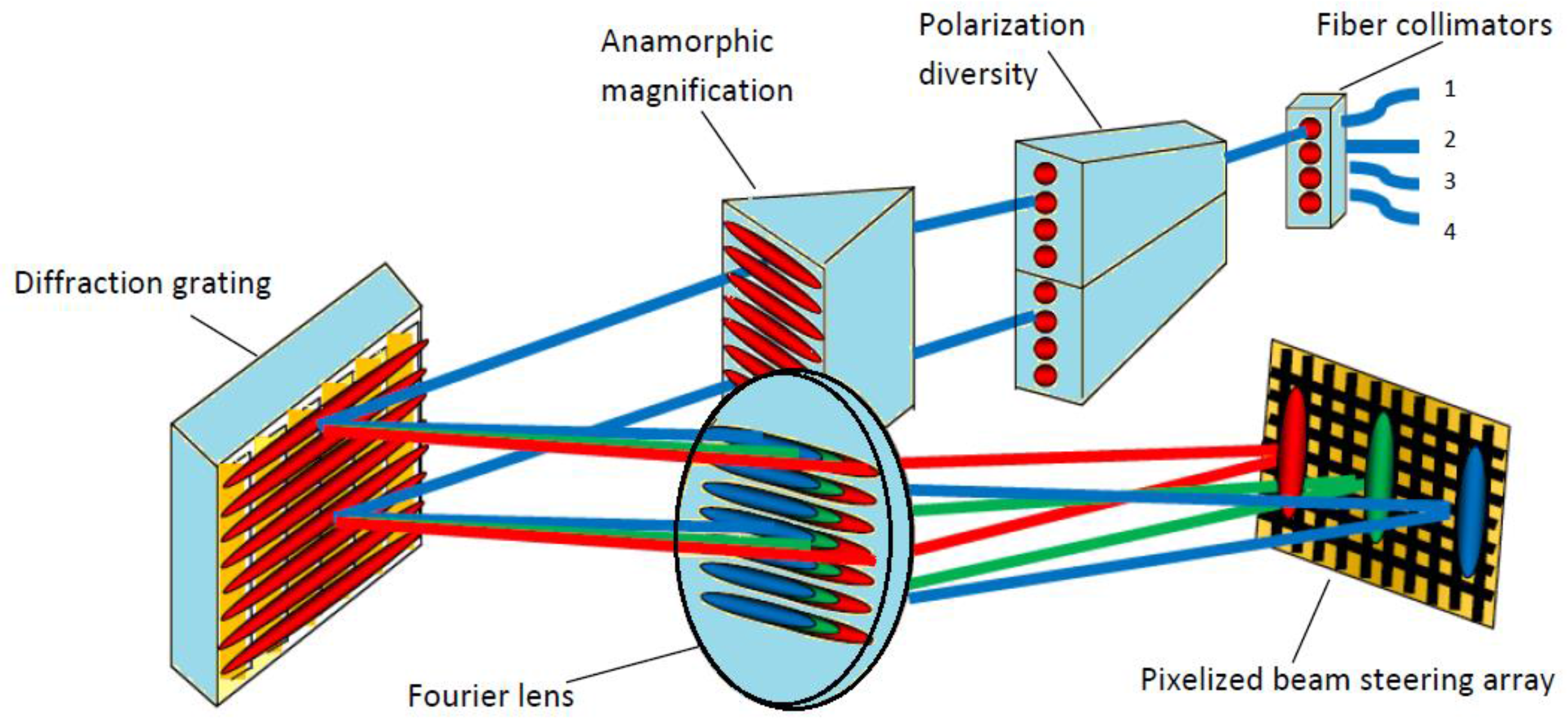
2.2.2. System Level Crosstalk
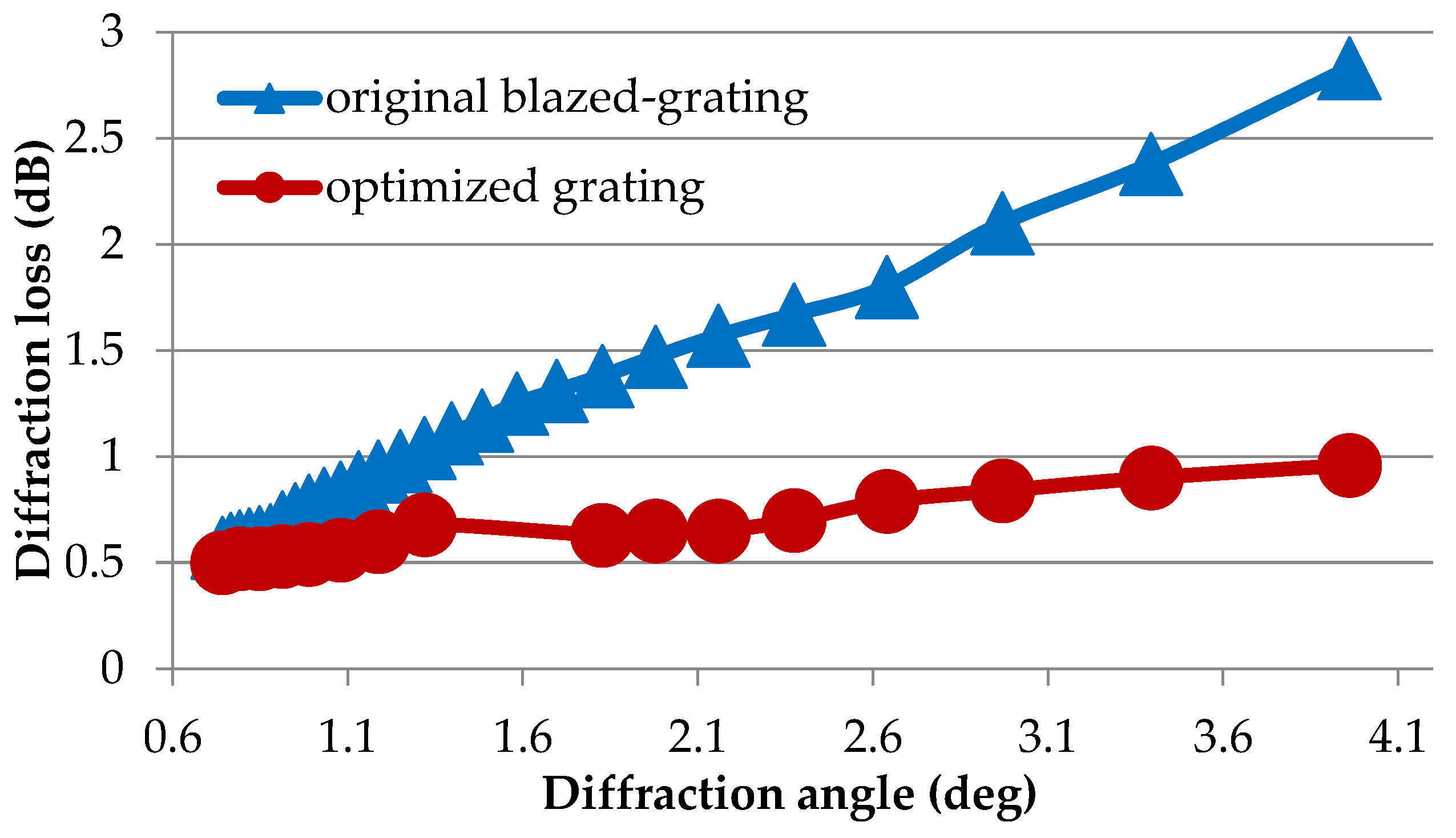
2.3. Insertion Loss
3. The Trend of LCoS Device for Future WSS Module
3.1. Faster LCoS Response for Faster WSS Switching
3.2. Higher Reflectivity of the LCoS Front Cover Plate for Lower WSS Loss
3.3. Smaller LCoS Pixel Size for Higher Number of WSS Ports Counts
4. Discussion and Conclusions
Acknowledgment
Author Contributions
Conflicts of Interest
References
- Bleha, W.P.; Lei, L.A. Advances in liquid crystal on silicon (LCoS) spatial light modulator technology. SPIE Def. Secur. Sens. Int. Soc. Opt. Photonics 2013. [Google Scholar] [CrossRef]
- Hermerschmidt, A.; Lazarev, G.; Rozhkov, O.V. LC-based Phase-modulating Spatial Light Modulators. In Proceedings of the Digital Holography and Three-Dimensional Imaging, Seattle, WA, USA, 13–17 July 2014. [Google Scholar]
- Turunen, J.; Wyrowski, F. (Eds.) Diffractive Optics for Industrial and Commercial Applications; John Wiley & Sons: Hoboken, NJ, USA, 1997. [Google Scholar]
- Coufal, H.; Psaltis, D.; Sincerbox, G. Holographic Data Storage. In Springer Series in Optical Sciences; Springer: Berlin/Heidelberg, Germany, 2000; Volume 76. [Google Scholar]
- Osten, W.; Kohler, C.; Liesener, J. Evaluation and application of spatial light modulators for optical metrology. Opt. Pura Apl. 2005, 38, 71–81. [Google Scholar]
- Roelens, M.A.; Frisken, S.; Bolger, J.A.; Abakoumov, D.; Baxter, G.; Poole, S.; Eggleton, B.J. Dispersion trimming in a reconfigurable wavelength selective switch. J. Light. Technol. 2008, 26, 73–78. [Google Scholar] [CrossRef]
- Salsi, M.; Koebele, C.; Sperti, D.; Tran, P.; Mardoyan, H.; Brindel, P.; Bigo, S.; Boutin, A.; Verluise, F.; Sillard, P. Mode-Divison Multiplexing of 2100 Gb/s Channels Using an LCOS-Based Spatial Modulator. J. Light. Technol. 2012, 30, 618–623. [Google Scholar] [CrossRef]
- Solís-Prosser, M.; Arias, A.; Varga, J.; Rebón, L.; Ledesma, S.; Iemmi, C.; Neves, L. Preparing arbitrary pure states of spatial qudits with a single phase-only spatial light modulator. Opt. Lett. 2013, 38, 4762–4765. [Google Scholar] [CrossRef] [PubMed]
- Schröder, J.; Roelens, M.A.; Du, L.B.; Lowery, A.J.; Eggleton, B.J. LCOS based waveshaper technology for optical signal processing and performance monitoring. In Proceedings of the 17th Opto-Electronics and Communications Conference (OECC), Busan, Korea, 2–6 July 2012. [Google Scholar]
- Wu, S.T.; Yang, D.K. Reflective Liquid Crystal Displays; John Wiley & Sons Inc.: Chichester, UK, 2005. [Google Scholar]
- Davey, N.C.T.; Chrstmas, J.; Chu, D.; Crossland, B. The Applications and Technology for Phase-Only Liquid Crystal on Silicon Devices. J. Disp. Technol. 2011, 7, 112–119. [Google Scholar]
- Keyworth, B.P. ROADM subsystems and technologies. In Proceedings of the Optical Fiber Communication Conference and Exposition (OFC/NFOEC), Anaheim, CA, USA, 6-11 March .2005; pp. 1–4. [Google Scholar]
- Strasser, T.A.; Wagener, J.L. Wavelength-Selective Switches for ROADM Applications. IEEE J. Sel. Top. Quantum Electron. 2010, 16, 1150–1157. [Google Scholar]
- De Hennin, S.; Wall, P.; Moffat, S.H.; Keyworth, B.P.; Colbourne, P.D. Addressing Manufacturability and Reliability of MEMS-based WSS. In Proceedings of the OFC/NFOE Conference on Optical Fiber Communication and the National Fiber Optic Engineers Conference, Anaheim, CA, USA, 25–29 March 2007. [Google Scholar]
- Chu, T.; Yamada, H.; Ishida, S.; Arakawa, Y. Compact 1 × N thermo-optic switches based on silicon photonic wire waveguides. Opt. Express 2005, 13, 10109–10114. [Google Scholar] [CrossRef] [PubMed]
- Cheng, Q.; Wonfor, A.; Penty, R.V.; White, I.H. Scalable, low-energy hybrid photonic space switch. J. Light. Technol. 2013, 31, 3077–3084. [Google Scholar] [CrossRef]
- Shiraiwa, M.; Furukawa, H.; Miyazawa, T.; Awaji, Y.; Wada, N. High-Speed Wavelength Resource Reconfiguration System Concurrently Establishing/Removing Multi-wavelength Signals. IEEE Photonics J. 2016, 8, 1–7. [Google Scholar]
- Frisken, S.; Baxter, G.; Abakoumov, D.; Zhou, H.; Clarke, I.; Poole, S. Flexible and grid-less wavelength selective switch using LCOS technology. In Proceedings of the Optical Fiber Communication Conference and Exposition (OFC/NFOEC), Los Angeles, CA, USA, 6–10 March 2011; pp. 1–3. [Google Scholar]
- Finisar Application Note, Group Delay Ripple Compensation. Available online: https://www.finisar.com/sites/default/files/resources/an_waveshaper_group_delay_ripple_compensation.pdf (accessed on 23 March 2017).
- Pulikkaseril, C.; Stewart, L.A.; Roelens, M.A.F.; Baxter, G.W.; Poole, S.; Frisken, S. Spectral Modeling of Channel Band Shapes in Wavelength Selective Switches. Opt. Express 2011, 19, 8458–8470. [Google Scholar] [CrossRef] [PubMed]
- He, J.; Norwood, R.A.; Brandt-Pearce, M.; Djordjevic, I.B.; Cvijetic, M.; Subramaniam, S.; Himmelhuber, R.; Reynolds, C.; Blanche, P.; Lynn, B.; et al. A survey on recent advances in optical communications. Comput. Electr. Eng. 2014, 40, 216–240. [Google Scholar]
- Collings, N.; Davey, T.; Christmas, J.; Chu, D.P.; Crossland, B. The applications and technology of phase-only liquid crystal on silicon devices. J. Disp. Technol. 2011, 7, 112–119. [Google Scholar]
- Wilkinson, T.D.; Henderson, C.D.; Leyva, D.G.; Crossland, W.A. Phase modulation with the next generation of liquid crystal over silicon technology. J. Mater. Chem. 2006, 16, 3359–3365. [Google Scholar] [CrossRef]
- Zhang, P.; Tan, Y.; Liu, W.; Chen, W. Methods for optical pahse retardation measurement: A review. Sci. China Technol. Sci. 2013, 56, 1155–1164. [Google Scholar] [CrossRef]
- Zhang, Z.C.; Yang, H.N.; Robertson, B.; Redmond, M.; Pivnenko, M.; Collings, N.; Crossland, W.A.; Chu, D. Diffraction based phase compensation method for phase-only liquid crystal on silicon devices in operation. Appl. Opt. 2012, 51, 3837–3846. [Google Scholar] [PubMed]
- Engstrom, D.; Persson, M.; Bengtsson, J.; Goksor, M. Calibration of spatial light modulators suffering from spatially varying phase response. Opt. Express 2013, 21, 16086–16103. [Google Scholar] [PubMed]
- Reichelt, S. Spatially resolved phase-response calibration of liquid-crystal-based spatial light modulators. Appl. Opt. 2013, 52, 2610–2618. [Google Scholar] [CrossRef] [PubMed]
- Bone, M.; Coates, D.; Crossland, W.; Gunn, P.; Ross, P. Ferroelectric liquid crystal display capable of video line address times. Displays 1987, 8, 115–118. [Google Scholar] [CrossRef]
- Handschy, M.; Johnson, K.; Moddel, G.; Pagano-Stauffer, L. Electro-optic applications of ferroelectric liquid crystals to optical computing. Ferroelectrics 1988, 85, 279–289. [Google Scholar] [CrossRef]
- Grigory, L.; Andreas, H.; Sven, K.; Osten, S. 1. LCOS Spatial Light Modulators: Trends and Applications. In Optical Imaging & Metrology Advanced Technologies; John Wiley & Sons: Hoboken, NJ, USA, 2012; pp. 1–29. [Google Scholar]
- Stamm, S.; Riethoven, J.J.; Le Texier, V.; Gopalakrishnan, C.; Kumanduri, V.; Tang, Y.; Barbosa-Morais, N.L.; Thanaraj, T.A. ASD: A bioinformatics resource on alternative slicing. Nucleic Acids Res. 2006, 34, D46–D55. [Google Scholar] [PubMed]
- McKnight, D.J.; Vass, D.G.; Sillitto, R.M. Development of a spatial light modulator: A randomly addressed liquid crystal over nMOS array. Appl. Opt. 1989, 28, 4757–4762. [Google Scholar] [CrossRef] [PubMed]
- Soref, R.A.; Rafuse, M.J. Electrically controlled birefringence of thin nematic films. J. Appl. Phys. 1972, 43, 2029–2037. [Google Scholar] [CrossRef]
- Labrunie, G.; Robert, J. Transient behavior of the electrically controlled birefringence in a nematic liquid crystal. J. Appl. Phys. 1973, 44, 4869–4874. [Google Scholar]
- Armitage, D.; Kinell, D.K. Miniature spatial light modulators. Proc. SPIE 1990, 1296, 158–165. [Google Scholar]
- Buckley, E. Holographic laser projection. J. Disp. Technol. 2011, 7, 135–140. [Google Scholar]
- Dasgupta, P.; Das, M.K.; Das, B. Physical properties of three liquid crystals with negative dielectric anisotropy from X-ray diffraction and optical birefringence measurements. Mol. Cryst. Liq. Cryst. 2011, 540, 154–161. [Google Scholar]
- Cotter, L.K.; Drabik, T.J.; Dillon, R.J.; Handschy, M.A. Ferroelectric-liquid-crystal/silicon-integrated circuit spatial light modulator. Opt. Lett. 1990, 15, 291–293. [Google Scholar] [PubMed]
- Armitage, D.; Kinell, D.K. Liquid crystal integrated silicon spatial light modulator. Appl. Opt. 1992, 31, 3945–3949. [Google Scholar] [CrossRef] [PubMed]
- Wang, H.; Nie, X.; Wu, T.X.; Wu, S.T. Cell gap effect on the dynamics of liquid crystal phase modulators. Mol. Cryst. Liq. Cryst. 2005. [Google Scholar] [CrossRef]
- Hyman, R.M.; Lorenz, A.; Morris, S.M.; Wilkinson, T.D. Polarization-independent phase modulation using a blue-phase liquid crystal over silicon device. Appl. Opt. 2014, 53, 6925–6929. [Google Scholar] [CrossRef] [PubMed]
- Leyva, D.G.; Robertson, B.; Henderson, C.J.; Wilkinson, T.D.; O’Brien, D.C.; Faulkner, G. Cross-talk analysis in a telecentric adaptive free-space optical relay based on a spatial light modulator. Appl. Opt. 2006, 45, 63–75. [Google Scholar]
- Yang, H.; Robertson, B.; Chu, D. Transient crosstalk in LCOS based WSS and a method to suppress the crosstalk levels. In Proceedings of the Optical Fiber Communication Conference and Exposition and the National Fiber Optic Engineers Conference (OFC/NFOEC), Anaheim, CA, USA, 17–21 March 2013. [Google Scholar]
- Yang, H.; Robertson, B.; Yu, D.; Zhang, Z.; Chu, D. Origin of transient crosstalk and its reduction in phase-only LCOS wavelength selective switches. J. Light. Technol. 2013, 31, 3822–3829. [Google Scholar] [CrossRef]
- Kaminow, I.; Li, T.; Willner, A.E. Technology and application of liquid crystal on silicon (LCoS) in telecommunications. In Optical Fiber Telecommunications Volume VIA: Components and Subsystems; Academic Press: New York, NY, USA, 2013. [Google Scholar]
- HOLOEYEs SLMs. Available online: www.holoeye.com (accessed on 20 March 2017).
- Noguchi, K.; Sakano, T.; Matsumoto, T. A rearrangeable multichannel free-space optical switch based on multistage network configuration. J. Light. Technol. 1991, 9, 1726–1732. [Google Scholar] [CrossRef]
- Mora, M.C.; Minguez, A.M.; Horche, P.R. Design of equalized ROADMs devices with flexible bandwidth based on LCoS technology. In Proceedings of the 19th European Conference on Networks and Optical Communications-(NOC), Milano, Italy, 4–6 June 2014; pp. 41–46. [Google Scholar]
- Hermerschmidt, A.; Osten, S.; Krüger, S.; Blümel, T. Wave front generation using a phase-only modulating liquid-crystal-based micro-display with HDTV resolution. In Proceedings of the International Congress on Optics and Optoelectronics, International Society for Optics and Photonics, Prague, Czech Republic, 16 April 2007. [Google Scholar]
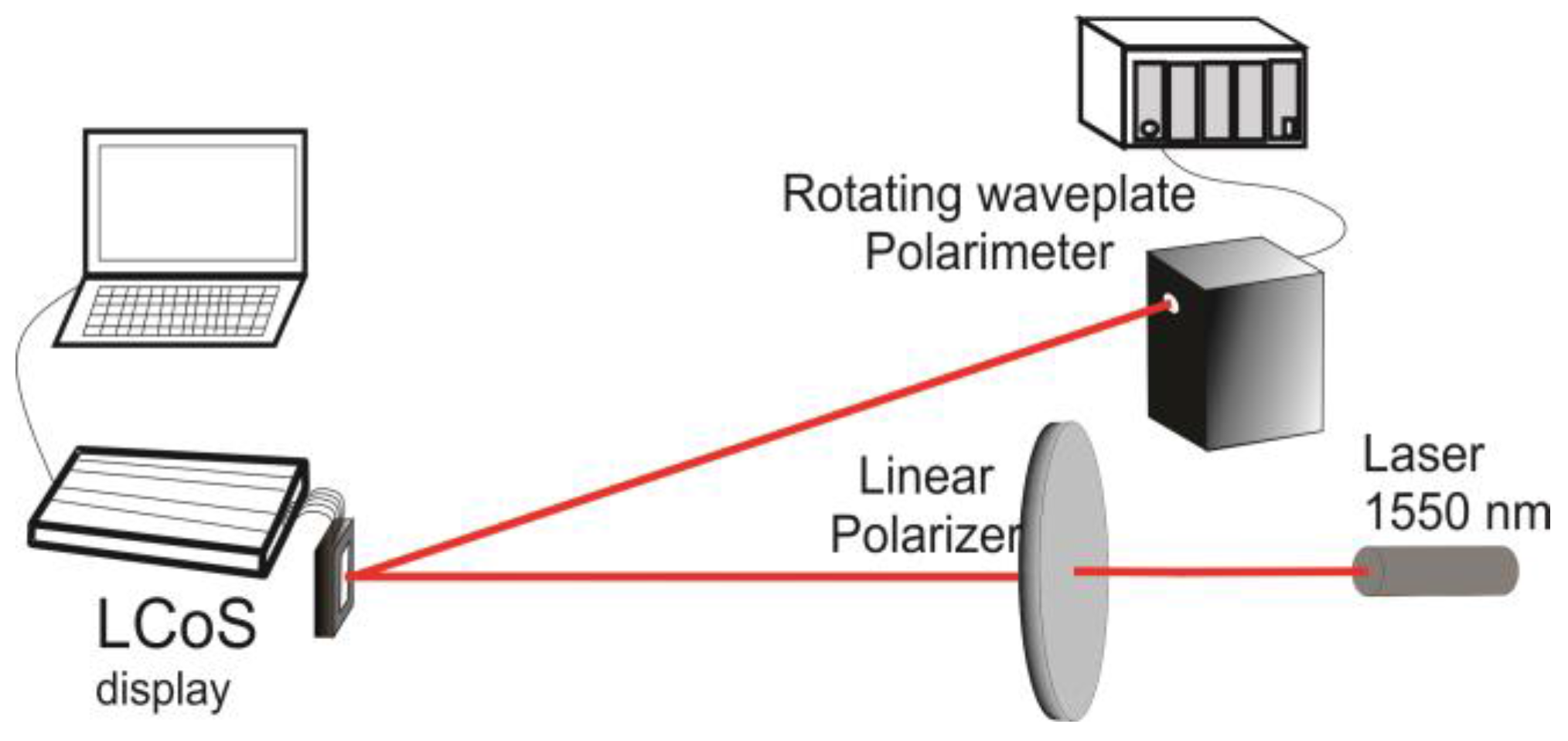
- Martínez, F.J.; Márquez, A.; Gallego, S.; Ortuño, M.; Francés, J.; Pascual, I.; Beléndez, A. Predictive capability of average Stokes polarimetry for simulation of phase multilevel elements onto LCoS devices. Appl. Opt. 2015, 54, 1379–1386. [Google Scholar] [CrossRef] [PubMed]
- Martínez, F.J.; Márquez, A.; Gallego, S.; Francés, J.; Pascual, I.; Beléndez, A. Extended linear polarimeter to measure retardance and flicker: Application to liquid crystal on silicon devices in two working geometries. Opt. Eng. 2014, 53, 014105. [Google Scholar]
- Martínez, F.J.; Márquez, A.; Gallego, S.; Francés, J.; Pascual, I.; Beléndez, A. Retardance and flicker modeling and characterization of electro-optic linear retarders by averaged Stokes polarimetry. Opt. Lett. 2014, 39, 1011–1014. [Google Scholar] [CrossRef] [PubMed]
- Martínez, F.J.; Márquez, A.; Gallego, S.; Ortuño, M.; Francés, J.; Beléndez, A.; Pascual, I. Averaged Stokes polarimetry applied to evaluate retardance and flicker in PA-LCoS devices. Opt. Express 2014, 22, 15064–15074. [Google Scholar] [PubMed]
- García-Márquez, J.; López, V.; González-Vega, A.; Noé, E. Flicker minimization in an LCoS spatial light modulator. Opt. Express 2012, 20, 8431–8441. [Google Scholar] [CrossRef] [PubMed]
- Apter, B.; Efron, U.; Bahat-Treidel, E. On the fringing-field effect in liquid-crystal beam-steering devices. Appl. Opt. 2004, 43, 11–19. [Google Scholar] [PubMed]
- Efron, U.; Apter, B.; Bahat-Treidel, E. Fringing-field effect in liquid-crystal beam-steering devices: An approximate analytical model. J. Opt. Soc. Am. A Opt. Image Sci. Vis. 2004, 21, 1996–2008. [Google Scholar] [PubMed]
- Lu, T.; Pivnenko, M.; Robertson, B.; Chu, D. Pixel-level fringing-effect model to describe the phase profile and diffraction efficiency of a liquid crystal on silicon device. Appl. Opt. 2015, 54, 5903–5910. [Google Scholar] [CrossRef] [PubMed]
- Dames, M.P.; Dowling, R.J.; McKee, P.; Wood, D. Efficient optical elements to generate intensity weighted spot arrays: Design and fabrication. Appl. Opt. 1991, 30, 2685–2691. [Google Scholar] [PubMed]
- Broomfield, S.; Neil, M.; Paige, E.; Yang, G. Programmable binary phase-only optical device based on ferroelectric liquid crystal SLM. Electron. Lett. 1992, 28, 26–28. [Google Scholar] [CrossRef]
- Gerchberg, R.W. A practical algorithm for the determination of phase from image and diffraction plane pictures. Optik 1972, 35, 237. [Google Scholar]
- Lingel, C.; Haist, T.; Osten, W. Optimizing the diffraction efficiency of SLM-based holography with respect to the fringing field effect. Appl. Opt. 2013, 52, 6877–6883. [Google Scholar] [PubMed]
- Wang, X.; Wang, B.; Pouch, J.; Miranda, F.; Fisch, M.; Anderson, J.E.; Sergan, V.; Bos, P.J. Liquid crystal on silicon (LCOS) wavefront corrector and beam steerer. In Proceedings of the Optical Science and Technology, SPIE’s 48th Annual Meeting, International Society for Optics and Photonic, San Diego, CA, USA, 3 August 2003; pp. 139–146. [Google Scholar]
- Wang, X.; Wang, B.; Bos, P.J.; McManamon, P.F.; Pouch, J.J.; Miranda, F.A.; Anderson, J.E. Modeling and design of an optimized liquid-crystal optical phased array. J. Appl. Phys. 2005, 98, 073101. [Google Scholar]
- Hällstig, E.; Stigwall, J.; Martin, T.; Sjöqvist, L.; Lindgren, M. Fringing fields in a liquid crystal spatial light modulator for beam steering. J. Mod. Opt. 2004, 51, 1233–1247. [Google Scholar] [CrossRef]
- Sinefeld, D.; Marom, D.M. Insertion Loss and Crosstalk Analysis of a Fiber Switch Based on a Pixelized Phase Modulator. J. Light. Technol. 2011, 29, 69–77. [Google Scholar]
- Stockley, J.E.; Subacius, D.; Serati, S.A. Influence of the inter-pixel region in liquid crystal diffraction gratings. In Proceedings of the Liquid Crystal Materials, Devices, and Applications VII, San Jose, CA, USA, 23 January 1999; pp. 127–136. [Google Scholar]
- Guo, Z.; Yan, J.; Xing, Y.; Zheng, Y.; Li, Q. A Novel Three Electrodes Structure LCoS with Low Fringing Field Effect. In SID Symposium Digest of Technical Papers; Wiley Online Library: Hoboken, NJ, USA, 2016; pp. 183–184. [Google Scholar]
- Yang, H.; Robertson, B.; Chu, D. Crosstalk reduction in holographic wavelength selective switches based on phase-only LCOS devices. In Proceedings of the Optical Fiber Communications Conference and Exhibition (OFC), San Francisco, CA, USA, 9–13 March 2014. [Google Scholar]
- Robertson, B.; Yang, H.; Redmond, M.M.; Collings, N.; Liu, J.; Jeziorska-Chapman, A.M.; Moore, J.R.; Zhang, Z.; Crossland, W.A.; Wonfor, A.; et al. The use of wavefront encoding to reduce crosstalk in a multicasting fiber telecom switch. In Proceedings of the Optical Fiber Communication Conference and Exposition (OFC/NFOEC), 2012 and the National Fiber Optic Engineers Conference, Los Angeles, CA, USA, 4–8 March 2012. [Google Scholar]
- Robertson, B.; Zhang, Z.; Yang, H.; Redmond, M.M.; Collings, N.; Liu, J.; Lin, R.; Jeziorska-Chapman, A.M.; Moore, J.R.; Crossland, W.A.; et al. Reduction of crosstalk in a colourless multicasting LCOS-based wavelength selective switch by the application of wavefront encoding. SPIE OPTO Int. Soc. Opt. Photonics 2012. [Google Scholar] [CrossRef]
- Tan, K.L.; Warr, S.T.; Manolis, I.G.; Wilkinson, T.D.; Redmond, M.M.; Crossland, W.A.; Mears, R.J.; Robertson, B. Dynamic holography for optical interconnections. II. Routing holograms with predictable location and intensity of each diffraction order. J. Opt. Soc. Am. A 2001, 18, 205–215. [Google Scholar] [CrossRef]
- Robertson, B.; Zhang, Z.; Redmond, M.M.; Collings, N.; Liu, J.; Lin, R.; Jeziorska-Chapman, A.M.; Moore, J.R.; Crossland, W.A.; Chu, D. Use of wavefront encoding in optical interconnects and fiber switches for cross talk mitigation. Appl. Opt. 2012, 51, 659–668. [Google Scholar] [PubMed]
- Parker, M.C.; Cohen, A.D.; Mears, R.J. Dynamic digital holographic wavelength filtering. J. Light. Technol. 1998, 16, 1259–1270. [Google Scholar]
- Fontaine, N.K.; Chen, H.; Ercan, B.; Ryf, R.; Labroille, G.; Barre, N.; Jian, P.; Morizur, J.F.; Neilson, D.T. Wavelength selective switch with optimal steering element utilization. In Proceedings of the Optical Fiber Communications Conference and Exhibition (OFC), Anaheim, CA, USA, 20–22 March 2016. [Google Scholar]
- Yang, H.; Robertson, B.; Wilkinson, P.; Chu, D. Small phase pattern 2D beam steering and a single LCOS design of 40 1 × 12 stacked wavelength selective switches. Opt. Express 2016, 24, 12240–12253. [Google Scholar] [CrossRef] [PubMed]
- He, Z.; Nose, T.; Sato, S. Diffraction and polarization properties of a liquid crystal grating. Jpn. J. Appl. Phys. 1996, 35, 3529–3530. [Google Scholar]
- Harris, S.R. Polarization effects in nematic liquid crystal optical phased arrays. Proc. SPIE 2003, 5213, 26–39. [Google Scholar] [CrossRef]
- Baxter, G.; Frisken, S.; Abakoumov, D.; Zhou, H.; Clarke, I.; Bartos, A.; Poole, S. Highly programmable wavelength selective switch based on liquid crystal on silicon switching elements. In Proceedings of the Optical Fiber Communication Conference and National Fiber Optic Engineers Conference, Anaheim, CA, USA, 5–10 March 2006. [Google Scholar]
- Frisken, S. Advances in liquid crystal on silicon wavelength selective switching. In Proceedings of the Optical Fiber Communication Conference, Optical Society of America, Anaheim, CA, USA, 25 March 2007. [Google Scholar]
- Zong, L.; Zhao, H.; Feng, Z.; Yan, Y. Low-cost, degree-expandable and contention-free ROADM architecture based on M × N WSS. In Proceedings of the Optical Fiber Communications Conference and Exhibition (OFC), Anaheim, CA, USA, 20–22 March 2016. [Google Scholar]
- Zong, L.; Zhao, H.; Yan, Y.; Feng, Z. Demonstration of quasi-contentionless flexible ROADM based on a multiport WXC. J. Opt. Commun. Netw. 2016, 8, A141–A151. [Google Scholar]
- Zong, L.; Zhao, H.; Feng, Z.; Yan, Y. 8 × 8 Flexible Wavelength Cross-Connect for CDC ROADM Application. IEEE Photonics Technol. Lett. 2015, 27, 2603–2606. [Google Scholar]
- Yang, H.; Robertson, B.; Wilkinson, P.; Chu, D. Stacked wavelength selective switch design for low-cost CDC ROADMs. In Proceedings of the OptoElectronics and Communications Conference (OECC) Held Jointly with 2016 International Conference on Photonics in Switching (PS), Niigata, Japan, 3–7 July 2016. [Google Scholar]
- Marom, D.M.; Colbourne, P.D.; D’Errico, A.; Fontaine, N.K.; Ikuma, Y.; Proietti, R.; Zong, L.; Rivas-Moscoso, J.M.; Tomkos, I. Survey of Photonic Switching Architectures and Technologies in Support of Spatially and Spectrally Flexible Optical Networking [Invited]. J. Opt. Commun. Netw. 2017, 9, 1–26. [Google Scholar]
- Marom, D.M.; Sinefeld, D. Beyond wavelength-selective channel switches: Trends in support of flexible/elastic optical networks. In Proceedings of the 14th International Conference on Transparent Optical Networks (ICTON), Coventry, UK, 2–5 July 2012. [Google Scholar]
- Uetsuka, H.; Namiki, S.; Sasaki, K. N × N Wavelength Selective Switches. In Proceedings of the OptoElectronics and Communications Conference (OECC) Held jointly with 2016 International Conference on Photonics in Switching (PS), Niigata, Japan, 3–7 July 2016; pp. 1–3. [Google Scholar]
- Suzuki, K.; Nakajima, M.; Yamaguchi, K.; Takashi, G.; Ikuma, Y.; Shikama, K.; Ishii, Y.; Itoh, M.; Fukutoku, M.; Hashimoto, T.; et al. Wavelength selective switch for multi-core fiber based space division multiplexed network with core-by-core switching capability. In Proceedings of the 2016 21st OptoElectronics and Communications Conference (OECC) held jointly with 2016 International Conference on Photonics in Switching (PS), Niigata, Japan, 3–7 July 2016. [Google Scholar]
- Rao, L.; He, S.; Wu, S.-T. Blue-phase liquid crystals for reflective projection displays. J. Disp. Technol. 2012, 8, 555–558. [Google Scholar]
- Yan, J.; Li, Y.; Wu, S. High-efficiency and fast-response tunable phase grating using a blue phase liquid crystal. Opt. Lett. 2011, 36, 1404–1406. [Google Scholar] [CrossRef] [PubMed]
- Zhu, J.; Lu, J.; Qiang, J.; Zhong, E.; Ye, Z.; He, Z.; Guo, X.; Dong, C.; Su, Y.; Shieh, H.D. 1D/2D switchable grating based on field-induced polymer stabilized blue phase liquid crystal. J. Appl. Phys. 2012, 111, 033101. [Google Scholar] [CrossRef]
- Chen, H.; Tan, G.; Huang, Y.; Weng, Y.; Choi, T.H.; Yoon, T.H.; Wu, S.T. A Low Voltage Liquid Crystal Phase Grating with Switchable Diffraction Angles. Sci. Rep. 2017, 7, 39923. [Google Scholar] [CrossRef] [PubMed]
- Earnshaw, M.; Cappuzzo, M.; Chen, E.; Gomez, L.; Griffin, A.; Laskowski, E.; Wong-Foy, A. Highly-integrated planar lightwave circuit wavelength selective switch. Electron. Lett. 2003, 39, 1397–1398. [Google Scholar]
- Gu, X.; Seno, K.; Tanobe, H.; Koyama, F. Wavelength selective switch with high angular dispersion element based on Bragg reflector waveguide. In Proceedings of the 2013 18th Micro-optics Conference (MOC), Meguro, Japan, 27–30 October 2013. [Google Scholar]
- Iwama, M.; Takahashi, M.; Kimura, M.; Uchida, Y.; Hasegawa, J.; Kawahara, R.; Kagi, N. LCOS-based Flexible Grid 1 × 40 Wavelength Selective Switch Using Planar Lightwave Circuit as Spot Size Converter. In Proceedings of the Optical Fiber Communication Conference, Los Angeles, CA, USA, 22–26 March 2015. [Google Scholar]
- Iwama, M.; Takahashi, M.; Uchida, Y.; Kimura, M.; Kawahara, R.; Matsushita, S.-I.; Mukaihara, T. Low loss 1 × 93 wavelength selective switch using PLC-based spot size converter. In Proceedings of the European Conference of Optical Communication (ECOC), Valencia, Spain, 27 September–1 October 2015. [Google Scholar]
| Various Types of Electro-Optic LC Structures | Pros and Cons |
|---|---|
| Twisted nematic (TN) configuration | Complicated precise phase level representation in phase-only hologram due to coupled amplitude and phase |
| VAN configuration | Slow response time; High threshold voltage |
| Zero-twisted ECB | Delayed response time in relaxation; Suitable for phase-only light modulation |
| Optical compensated birefringence (OCB) | Faster response; Smaller phase modulation depth compared with ECB or TN; Higher curing temperature degrades the reflectivity of aluminum surface |
| Surface-stabilized ferroelectric LC (SSFLC) | Low light usage efficiency [38]; Large quantization noise [39] |
| Definition | Physical Phenomenon | Compensation Method | |
|---|---|---|---|
| Device level crosstalk | Crosstalk induced by the LCoS’ physical effects | Phase flicker Fringing field effect | Voltage optimization method |
| System level crosstalk | Crosstalk induced by other features of WSS system | Output fiber position, Lens aperture, Field spot on the LCoS, Grating pitch, Shape of pulse | Computer Generated Hologram(CGH), Wavefront encoding, Pulse shaping, Filtering out higher orders |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, M.; Zong, L.; Mao, L.; Marquez, A.; Ye, Y.; Zhao, H.; Vaquero Caballero, F.J. LCoS SLM Study and Its Application in Wavelength Selective Switch. Photonics 2017, 4, 22. https://doi.org/10.3390/photonics4020022
Wang M, Zong L, Mao L, Marquez A, Ye Y, Zhao H, Vaquero Caballero FJ. LCoS SLM Study and Its Application in Wavelength Selective Switch. Photonics. 2017; 4(2):22. https://doi.org/10.3390/photonics4020022
Chicago/Turabian StyleWang, Mi, Liangjia Zong, Lei Mao, Andres Marquez, Yabin Ye, Han Zhao, and Francisco Javier Vaquero Caballero. 2017. "LCoS SLM Study and Its Application in Wavelength Selective Switch" Photonics 4, no. 2: 22. https://doi.org/10.3390/photonics4020022
APA StyleWang, M., Zong, L., Mao, L., Marquez, A., Ye, Y., Zhao, H., & Vaquero Caballero, F. J. (2017). LCoS SLM Study and Its Application in Wavelength Selective Switch. Photonics, 4(2), 22. https://doi.org/10.3390/photonics4020022





