Abstract
Elastic optical networks (EONs) based on orthogonal frequency-division multiplexing (OFDM) are considered a promising solution for the next optical network’s generation. These networks make it possible to choose an adequate portion of the available spectrum to satisfy the requested capacity. In this paper, we consider the impact of spectrum fragmentation along the optical single/multipath routing transmission on the efficiency of the EONs. This involves reducing the fragmentation effects by dynamically updating and controlling the minimum bandwidth allocation granularity (). We adopt linear and nonlinear dynamic mechanisms, which are denoted as LDA and NLDA, respectively, to choose proper bandwidth granularities that are proportional to the optical link/path bandwidth fragmentation status. In order to avoid either splitting the capacity request over many routing paths, which would increase the management complexity, or encouraging single path transmission, the proposed schemes aim to choose a proper bandwidth allocation granularity () for a predefined set of suggested values. Simulation results show that varying the bandwidth granularity based on the optical path fragmentation status can offer an improved performance over fixed granularity with respect to the bandwidth blocking probability, the number of path splitting actions, the throughput, and the differential delay constraint issue in terms of: the network bandwidth utilization and multipath distribution.
1. Introduction
The current optical transport network based on wavelength optical networks (OTN-WDM) suffers from serious limitations because of the expected capacity crunch in the physical capacity of the current optical fibers [1,2,3]. Moreover, in addition to the dramatic increase in the network services for new generations of bandwidth consuming applications (in the presence of fixed rate and the rigid frequency grid of the wavelength-routed optical networks 50 GHz), the mismatch of granularity between the cooperative layers (Client-layer & WDM-layer) results a degradation of the efficiency of the spectral utilization over the current OTN [4]. Usually, most of the service requests are provided with more than the necessary spectral resources, due to the mismatch of granularity. In order to tackle these limitations, a new generation of flexible or Elastic Optical Networks (EONs) need to be adopted [5].
The concept of EON was first presented in [6], in which the operators manage the OTNs by adaptively allocating spectral resources. In EONs, the principle of optical orthogonal frequency-division multiplexing (O-OFDM) has been considered a promising technique for the optical network future because of its helpful characteristics [7], and a possible implementation of elastic networking. Using OFDM for EON offers a finer granularity mechanism, which makes it possible to slice off the right amount of available spectrum resources to save more resources in order to serve other clients [8]. In this technique, all subcarriers are overlapping in the frequency domain, where each frequency subcarrier represents the smallest frequency slot (FS) that can be sliced from the available bandwidth [9].
The problem of routing and wavelength assignment (RWA), in a conventional optical network, has been changed to routing and spectrum allocation (RSA), which is also extended to be routing, modulation, and spectrum allocation (RMSA). Both RSA and RMSA are considered NP-hard problems [10,11]. To achieve an optimum solution and reduce the complexity, this problem can be separated into two sub-problems: routing and spectrum allocation [12].
Various RSA mechanisms over EONs have been investigated as single path and multipath routing [10,13,14]. For instance, in [13], a novel approach including an RSA algorithm was proposed, based on a distance adaptive modulation technique. A BW-efficient RMSA has also been considered, where the lowest required number of available contiguous slots on the shortest path is allocated to accommodate the light path request. In [14], Zuqing et al. presented a HSMR-OPC (hybrid single-/multi-path routing using online path computation). Fixed bandwidth allocation granularities () are used in their algorithms. Their results showed that choosing an appropriate value of the BW allocation granularity () is an important parameter that the operator can control, in order to reduce the number of rejected service requests.
Although, the EON is considered a promising solution for conventional rigid optical network limitations, a serious fragmentation problem arises. After some time, the spectrum on the optical links/paths will be fragmented because of the non-uniform spectrum usage [15], which results in the degradation of the spectrum utilization, a decrease in the spectrum efficiency that would achieve elasticity benefits, and an increase in the blocking probability. Minimizing fragmentation and defragmentation methods is considered a serious challenge in RSA problems, as well as when considering RMSA.
In addition, spectrum fragmentation makes it very difficult to control the spectrum allocation. Fragmentation is a purely unwanted random process that leaves many resources unused and reduces the spectrum efficiency. Choosing a proper bandwidth allocation granularity () for multipath provisioning is considered one of the most important parameters to mitigate the tradeoff between management complexity and blocking probability (BP).
In this paper, we aim to reduce the fragmentation’s problem effect by dynamically controlling and updating the bandwidth granularity () of each candidate optical path in a single and multipath provisioning routing mechanism. A tradeoff between management complexities (multipath routing) and reducing the blocking probability (single path routing) has been taken into account. The details of this work are described in the next sections.
2. Dynamic Minimum Bandwidth Allocation Granularity and Fragmentation
2.1. Dynamic Minimum Bandwidth Allocation Granularity
The minimum spectrum that can be assigned over an optical path represents the minimum bandwidth allocation granularity (). That is to say, the optical path is only considered an acceptable candidate path if it has at least the granularity size of the predefined bandwidth. The is defined as a block of slots which is an optical spectrum of contiguous subcarriers. In EONs, these subcarrier frequency slots (FSs) should meet the spectrum contiguity, spectrum continuity, and non-overlapping constraints along the requested optical paths.
In our presented model, we refer to as a variable size of the minimum bandwidth that could be assigned, based on the spectrum availability and the fragmentation status over the candidate optical path. Hybrid single/multipath routing (HSMR) is activated to choose a proper optical path(s) by either assigning a single path or splitting the request among multipath paths. To avoid service request blocking, the is updated dynamically, to make sure that each fragmented spectrum can be utilized efficiently. At the same time, the service request capacity is not split over many paths: , where C denotes the total requested capacity and Ci is the sub-capacity that can be assigned for an optical candidate path. Assigning a small bandwidth granularity, for example = 1, at the transponders to meet the minimum required unit of slots, would lead to a spreading out of the requested capacity over many paths. This would increase the management complexity at the receiver side. On the contrary, selecting a large value would lead to a single path transmission scenario, which would increase the blocking probability.
In terms of fragmentation, a high fragmentation ratio (γ) over an optical path would reduce the probability of finding an adequate number of continuous subcarrier slots that obey the routing constraints. Meanwhile, the low fragmentation ratio would increase the probability of finding more of the consecutive subcarriers.
2.2. Fragmentation
In an operational network, as the time passes, some of the light path requests will depart as soon as their life time is finished, and new requests will arrive and will need to be accommodated. The available spectrum would be highly fragmented in the case of highly dynamic service provisioning. Each one of the new arrivals will need a certain amount of spectrum in the form of contiguous and continuous frequency slots (FSs); otherwise, it will be rejected (blocked).
The connection arrivals and disconnections are a purely random process, which means that the spectrum distribution over the optical paths is also random. This randomness of the fragmentation makes it hard to determine the optimum value of the best BW allocation granularity. However, due to the fragmentation over optical links/paths, the non-aligned or isolated contiguous subcarriers in the spectrum domain of EON, are considered useless resources. To increase the spectrum utilization in the network, the network’s operator is also able to utilize the fragmentation status over the network.
Bandwidth fragmentation assessment has been widely investigated in literature, generally in terms of the bandwidth blocking probability (BBP) [14,16,17,18,19]. Prior research aims at reducing the fragmentation effect by either proposing spectral defragmentation algorithms, or managing the demand’s connections over the network. For instance, in [14], the results illustrated the importance of choosing a proper BW allocation granularity (), which impacts both the blocking BBP and the number of path splitting actions per request. In [16], simulations and mathematical modeling showed that there is a strong relationship between the bandwidth fragmentation and the bandwidth allocation granularity (). Other researchers have attempted to calculate the bandwidth fragmentation ratio (γ), which has been formulated in various research papers, such as [18]. In [18], a link, a path, and network utilization entropy (UE_path) for assessing resource fragmentation were proposed, as indicated in Equation (4).
To mitigate the fragmentation’s effect along the optical link (e) and the candidate optical path (Pi), which belongs to the main sets E and P, respectively, we need to optimize the spectrum utilization and the spectrum efficiency by taking into account the following objective:
Minimizing the equation above, based on routing constraints, requires managing the bandwidth granularity () to allocate a proper spectrum along the optical routing path. We believe that serving the network with certain bandwidth granularities needs to be managed carefully in terms of the optical path fragmentation status.
In this work, we focus on the role of granularity () that can be considered, in general, as a control parameter for increasing the spectral efficiency, thereby reducing the blocking opportunity, the number of path splitting occurrences, and other networks’ parameters.
3. Proposed Mechanism
3.1. Dynamic BW Granularity Adaptation Mechanisms
We propose two algorithms in order to adaptively change the minimum BW granularity (). Both of these factors depend on the currently available spectrum and the fragmentation status over the optical candidate’s path (Pi). The first is the linear dynamic adaptation mechanism denoted as LDA; meanwhile, the other is a non-linear dynamic adaptation granularity, denoted as NDA. To evaluate the performances, we adopted the following two equations:
Non-Linear adaptation (m ≥ 2):
Linear Adaptation (m = 1):
In Equation (2), m represents the mth order of the curve, m ≥ 2, see Figure 1. Increasing m results in maintaining a slow adaptation for a low fragmentation ratio (γ). Because the fragmentation ratio is usually small at this early stage, it is not necessary to assign a small granularity or activate the multipath provisioning, which reduces the management complexity. This factor would be left to the operator to determine, based on the network specifications. We used m = 2 for evaluation purposes. In order to reduce the unlimited choices of NDA(i) and LDA(i), we constrained the range of into five integer values, which are {1,2,3,4,5}, as indicated in [14,20,21]. In Equations (2) and (3), stands for the fragmentation ratio over the optical path Pi. The fragmentation ratio is calculated by the path utilization entropy in [18], using the following equation:
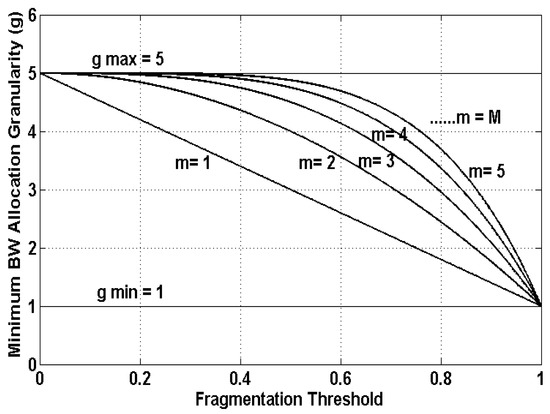
Figure 1.
Dynamic minimum BW granularity () selection based on the fragmentation ratio ().
N is the number of total frequency slots in link e, and . i represents the candidate path among the P possible paths in multipath provisioning for a light path request LR(s, d, C), where Pi P and P = {P1, P2, …, Pi}.
We used the HSMR-OPC/-FPS (Hybrid Single/Multipath Routing-Online Path Computation-First Path Set) schemes that are proposed in [14] to investigate our suggested adaptation mechanisms. The requested capacity (C) of the light path request (LR) splits over multiple paths if no one path can accommodate the requested capacity. The distributed sub-capacities should satisfy the following equation:
Each requires contiguous slots for each Pi candidate path. In terms of NS, NG (guard band), and the slot’s bandwidth as a function of the modulation level format, the can be rewritten as follows:
where represents the digital modulation level format of the optical transmission reach, which is given as follows:
The maximum number of paths of the set P is limited by, max (number of candidates Pi) ≤ ; however, k is the k-shortest fiber optical path between the source (s) and the destination (d). To reduce the complexity of the computations and to make this approach feasible in practice, we limited to be the five shortest candidate paths. This complexity includes checking the k-shortest path, the subcarrier slots (FS), and the fiber links (E), so that the computational complexity of applying the algorithm is in O(|k|·|FS|·|E|).
The network topologies have been represented by graph (G) of , where, V, E, B, and D are the node set, the fiber link set, the bandwidth, and the length of e (where e belongs to E set), respectively. While the network is operational and updated after each operation, the G topology is converted to a new virtual auxiliary topology In , any link that doesn’t have the minimum bandwidth granularity () will be omitted. Each link in will be re-weighted as follows:
where α is a modulation constant and is the spectrum usage with respect to the total spectrum. These parameters were defined as mentioned in [14]:
where represents the maximum modulation level format, Sum(be) is the spectrum usage over the link e, and B is the total bandwidth. In our research, the minimum available = 1 over any link should be 1, in order to remain in the updated auxiliary graph.
3.2. Routing and Spectrum Allocation Constraints
3.2.1. Contiguousness of Spectrum Constraint
The allocated subcarrier slots (FSs) for the whole demand in a single path transmission or for part of the demand in a multipath transmission, need to be located beside each other on the candidate optical path (s). To ensure that this occurs, is defined as a binary variable which equals 1 if the of the link e of the path (Pi) is used, and otherwise equals 0. Te is defined as an integer variable representing the number of an available free spectrum (gaps). To make sure that the link has at least one free available slot, we determine the total number of gaps along the e, using the following equation:
If Te ≥ 1, then based on the counted gaps and their locations over the link (e), a mask We is created, and this can be defined as follows:
Then, we create another mask Wp,i for a candidate path. Wp,i is used to determine the spectrum pattern over the candidate path depending on the We and includes the location of the gaps along the optical path. Following this, the locations of the proper consecutive spectrums are identified. We and Wp,i are used to define the spectrum locations, in addition to preventing the spectrum from overlapping.
3.2.2. Continuity of Spectrum Constraint
There is no frequency conversion or regeneration over the network. Each allocated frequency for any service demand over the link (e) should be allocated over the same locations and over all the links that belong to the assigned optical path. Each allocated frequency will not be released until the expiration of the service time. To guarantee spectrum continuity, we used the following equations:
3.2.3. Spectrum Non-Overlapping Constraint
It is critical to ensure that there are assigned subcarrier slots over a physical link (e), where and e work as part of the assigned optical path (p), which can’t be assigned to another spectrum optical path, even though the latter would share the same physical link e. Therefore, we applied the same idea that is mentioned in [14] in order to avoid overlapping, as follows:
where represents the AND operator and sum is used to calculate the sum of all the elements.
3.2.4. Differential Delay Constraint
The differential delay issue during multipath provisioning is due to the nature of fiber optics, in which the transmitted signals experience a differential delay effect [22]. We investigated the NDA under the presence and the absence of the differential delay issue.
DD is the differential delay and τ is a threshold which represents the propagation delay time delay between Pj(t) and Pi(t), respectively, where DD can be calculated as follows:
Equation (18) represents the propagation delay in terms of the path’s lengths. r1 stands for a propagation delay in μs/km, which is considered 5 μs/km as mentioned in different works, such as [23,24]. The delay that is caused by the equipment is beyond the scope of this work.
3.3. Network Topologies and Simulation Parameters of the Test Networks.
To test the performance of our approaches for dynamic bandwidth granularity adaptations, NSFNET and US backbone network topologies are used, as shown in Figure 2a,b. These topologies have been employed as a test bed by other works, such as in [14,20,21]. NSFNET has 14 stations indexed from 1 to 14 with 22 links, and the US backbone network has 24 stations, from 1 to 24 with 43 links.
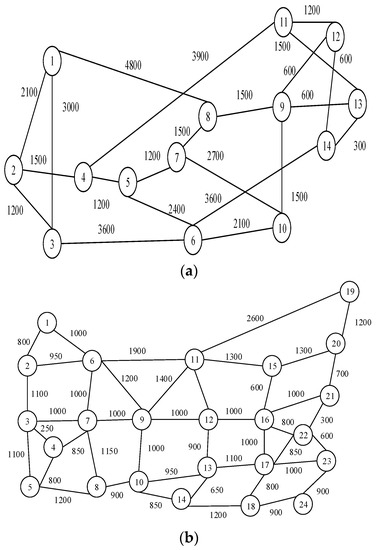
Figure 2.
Topologies used in simulation. (a) NSFNET; (b) US BACKBONE.
These network topologies have been represented by the . The light path request is represented by , where s, d, C, and Δt are the source, the destination, the capacity, and the service time, respectively. The arrivals of rate λ requests that the per time units are generated by Poisson processes. The service time Δt of each request followed the negative exponential distribution with mean μ) time units [25], and the traffic load in Erlangs can be considered as (λ* μ).
We propose heuristic algorithms for on-line path computations in Algorithms 1 and 2, respectively. The algorithms show the procedures of the proposed dynamic adaptation schemes. Algorithm 1 proposes the dynamic adaptation mechanism where we can use either the LDA or NDA granularity that is given by Equations (2) and (3). Table 1 shows the parameters which have been used in the simulations.

Table 1.
The parameters which have been used in the simulation.
Algorithm 2 is considered an extension of Algorithm 1, where the differential delay constraint is activated. Algorithm 3 is used for fixed path calculations. We use these algorithms to investigate the adaptation’s effect on the overall network performance, mainly in terms of BBP and other parameters such as network fragmentation, throughput, the distribution of path splitting per request, and bandwidth network utilization.
| Algorithm 1: Proposed Dynamic Adaptation Mechanism Using Online Path Computation. |
| Input: ), . Output: Single or HSMR for LR 1. receive the incoming service request ; 2. while the network is operational. Update to be a virtual auxiliary topology using (Equation (9)); 3. sort the calculated k-shortest routing path from s to d in G\ based on 4. for all candidate paths do 5. choose the modulation level Mi for real distance, using (Equation (8)); 6. calculate UE_path (γi) for each path using (Equation (4)); 7. determine the NDA(i) using (Equation (2)); 8. for all consecutive slots with size ≥ NDA(i) do 9. use (Equation (6)) to allocate capacity Ci as in (Equation (5)); 10. if C is satisfied in Equation (5) 11. break for-loops in step 4 and step 8; 12. end if 13. end for 14. end for 15. if then 16. assign the request as blocked request; 17. end if 18. end while |
| Algorithm 2: Multipath Assignment Under Differential Delay Adaptation Constraint. |
| Input: , and a differential delay threshold (τ) Output: All candidate paths that satisfy τ. Condition: no available single short path 1. while the network is operational do 2. for to K, do 3. sort all available paths in ascending order of 4. delay in new path set P 5. end for 6. for do 7. If , using (Equation (18)) then 8. as paths can be assigned 9. end if 10. end for 11. use (Equation (6)) to allocate capacity Ci as in (Equation (5)); 12. If 13. assign the request as blocked request 14. end if 15. end while |
| Algorithm 3: Proposed Dynamic Adaptation Mechanism Using Fixed Path Computation |
| Input: . Output: Single or HSMR for LR 1. for all that ask for service do 2. find k-shortest routing path and Implement a set of path P 3. end 4. while the network is operational. Update 5. sort the calculated k-shortest routing path from s to d based on ; 6. for all candidate paths do 7. choose the modulation level for real distance, using (Equation (8)); 8. calculate UE_path (γi) for each path using (Equation (4)); 9. determine the the NDA(i), using (Equation (2)); 10. for all consecutive slots with size ≥ NDA(i), do 11. use (Equation (5)) to allocate capacity as in (Equation (6)); 12. if C is satisfied in (Equation (5)) 13. break for-loops in step 4 and step 8; 14. end if 15. end for 16. end for 17. If then assign the request as blocked request; 18. end if 19. end while |
4. Validation and Numerical Simulation Results
To evaluate the dynamic granularity adaptation performance of both LDA(i) and NDA(i) under some of the network’s parameters, we pursued the online path computation of a hybrid single/multipath routing, based on dynamic RMSA (HSMR-OPC). We also used fixed path sets with dynamic RMSA, using HSMR-FPS-LSoSHF (LSoSHF: Largest slots-over-square-of-hops first) to investigate the number of path splitting occurrences per request. We simulated the spectrum allocation policy for max = 5 and min = 1, which are static values. Our adaptation mechanisms are embedded, and the multipath provisioning part is activated when there is no single path that can accommodate the light path request LR(s, d, C). Figure 3 shows that the bandwidth blocking probability is significantly improved by using a dynamic BW granularity adaptation for both test beds, compared to using a fixed max = 5 and, therefore, approaches that of min = 1.
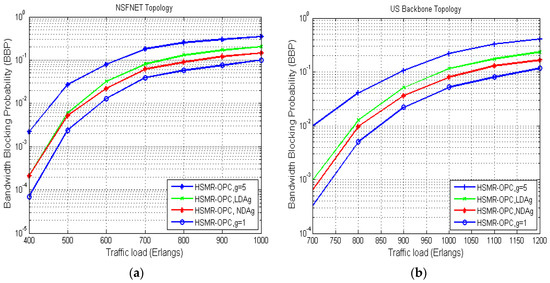
Figure 3.
Bandwidth blocking probability varying with load in (a) NSFNET and (b) US Backbone.
Figure 4 illustrates the simulation results with respect to the average throughput. The HSMR-RMSA-OPC of = 1, 5, LDA, and NDA, are presented. The average throughput of the LDA and NDA are enhanced, compared to the fixed minimum granularity; = 1. It is evident that LDA and NDA show improvement for all traffic loads in terms of traffic throughput. The average throughput is greatly improved for NDA compared to max = 5. This improvement, of about 5 Tb/s, is beneficial for the performance of optical networks.
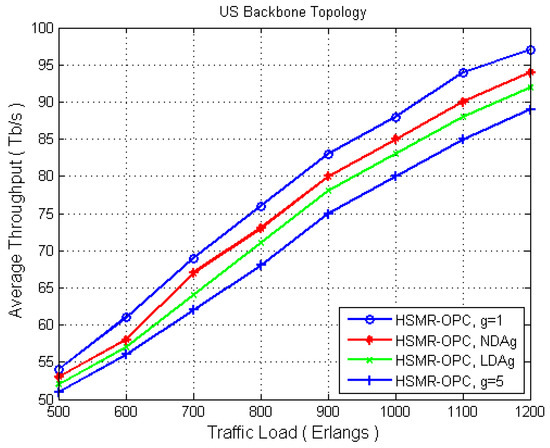
Figure 4.
Average throughput vs. varying load in US Backbone.
In terms of path splitting, as in Figure 5, NDA offers an improvement for the distribution percentage when compared to min = 1. Simulation data shows that 80% of the total requests are still served by a single routing path by using the NDA, compared to 75% using min = 1 and 93% for max = 5. The largest number of path splitting occurrences per request for max = 5, NDA, and min = 1 are 5, 6, and 12, consecutively. The simulation results showed that using a larger BW allocation granularity of (i.e., = 5) forces the HSMR scheme to become a single path routing scenario, which explains the increase in BBP.
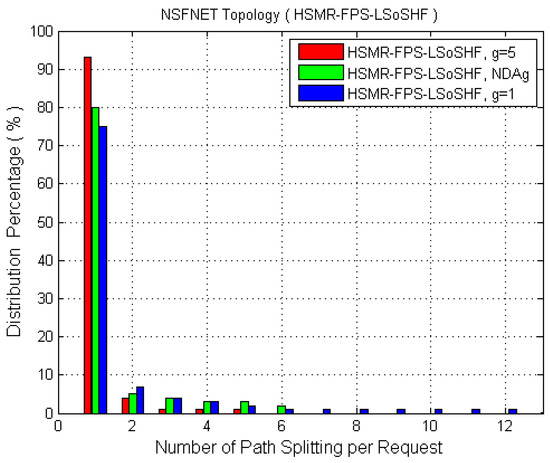
Figure 5.
Distribution in percentage vs. number of path splitting per request.
Figure 6 presents the simulation results on the average network bandwidth utilization as a function of traffic load in Erlangs for HSMR-OPC-NDA with/without differential delay constraint (DD), fixed bandwidth granularity (MP-FFSA with = 5) with DD, and the single path first fit spectrum allocation (SP-FFSA). It can be seen that NDA without the DD scheme achieves the best network bandwidth utilization compared to the others. However, in spite of a 10% reduction (on average) in utilization (at high traffic load) occurring when adding the DD constraint, NDA is also able to maintain a higher utilization than both MP-FFSA and SP-FFSA.
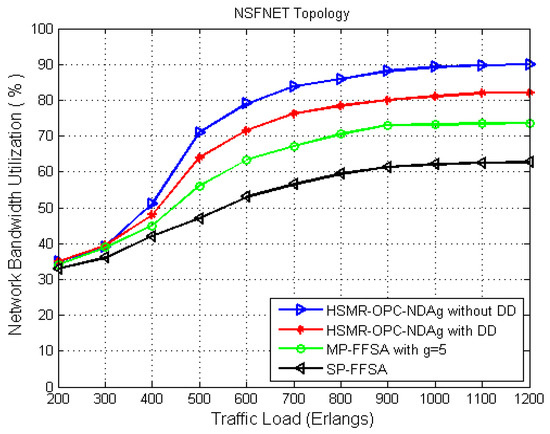
Figure 6.
Network Bandwidth Utilization.
Also, it is clear that at traffic loads less than 300 Erlangs, there is no noticeable differentiation among the schemes, possibly because there are a lot of gaps which reflect the spectrum availability along the links and the paths. At 1000 Erlangs, NDA achieves values that are 12.5% and 30% better than MP-FFSA and SP-FFSA, respectively.
Figure 7 shows a multipath distribution based on path-difference using NDA with DD, as a function of a traffic load for different differential delay constraints. The path distance differences were considered as up to 1000 km, 2000 km, and 3000 km, which are 0 ms, 5 ms, and 10 ms, respectively. For example, at a traffic load of 1000 Erlangs, 87% of the multipath routing is served by zero differential delays. In [26], well-controlled management is achieved within 3000 km or within 15 ms; meanwhile, the NDA achieves a better result under a well-controlled management within 2000 km or within 10 ms.
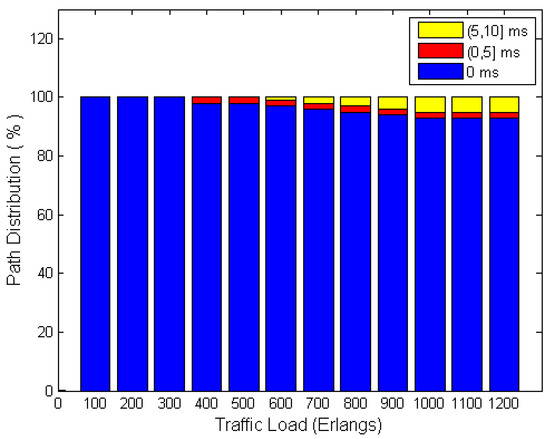
Figure 7.
Multipath distribution based on path-distance difference using NDA.
The BBP for NDA and other schemes with or without DD constraints are shown in Figure 8. It can be noticed that employing the DD increased the BBP.
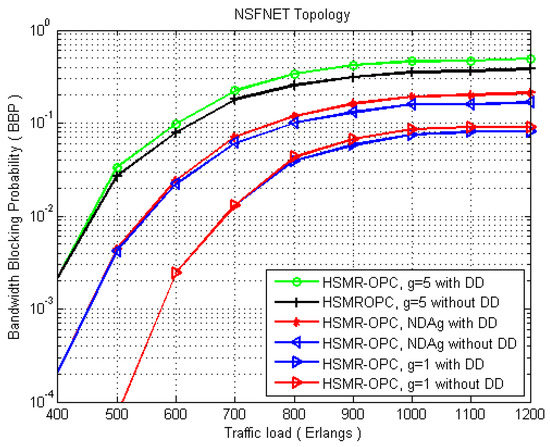
Figure 8.
Bandwidth blocking probability with/without differential delay constraint.
When the load traffic increases, the BBP also rises. Table 2 illustrates the percentage increase with and without DD constraints for different traffic loads. With or without the fixed = 1 and = 5, the BBP increases by about 8% and 23% on average. Meanwhile, the NDA with or without the DD constraint increases by around 14%.

Table 2.
Percentage increase in BBP for with/without DD constraints.
Comparisons for a traffic load of 1000 Erlangs using the simulation results show that NDA with DD is about 21% higher than NDA without DD, as well as 14% and 29.5% for = 1 and = 5, respectively. For = 1, there is no significant differentiation for traffic loads less than 800 Erlangs. The last column shows the calculated average for each bandwidth granularity mechanism = 1, NDA, and = 5.
5. Conclusions
In sum, dynamic BW allocation granularity adaptation mechanisms, denoted as LDA and NDA, were proposed and defined. The performance of these schemes was tested and validated using MATLAB simulation software. They were investigated under dynamic path algorithms to show the effect of granularity adaptation on the EON’s performance metrics, specifically the BBP performance. The simulation results show that LDA and NDA schemes allow a better performance than using a fixed minimum BW allocation granularity scheme that employs fixed granularities such as = 1 and = 5. A fixed-path selection (FPS) algorithm was also investigated to show the NDA effect on the path splitting per request. The dynamic adaptation reduces the number of path splitting occurrences per request, compared to the scheme that uses the smallest fixed granularity ( = 1).
Differential delay effects on the multipath service provisioning were also discussed. The simulation results showed that the adaptation of NDA offers an improved performance in terms of the “distribution of the path-distance differences”, compared to a single path service.
For future analysis, it would be a good idea to improve these mechanisms by taking into account other network metrics. A promising step towards realizing a fully-optimized BW allocation is considering defragmentation optimization and differential delay during multipath provisioning.
Author Contributions
We introduce the concept of “bandwidth allocation granularity adaptation” linear and nonlinear adaptation mechanisms for multipath provisioning in elastic optical OFDM networks. Simulation results show that granularity adaptation improves bandwidth blocking probability, throughput, the number of path splitting per request, and distribution of the path-distance differences.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Willner, A.; Li, T.; Kaminow, I. Optical Fiber Telecommunications; Academic Press: Oxford, UK, 2013. [Google Scholar]
- Essiambre, R.; Kramer, G.; Winzer, P.J.; Foschini, G.J.; Goebel, B. Capacity Limits of Optical Fiber Networks. J. Light. Technol. 2010, 28, 662–701. [Google Scholar] [CrossRef]
- Berthold, J.; Saleh, A.A.M.; Blair, L.; Simmons, J.M. Optical Networking: Past, Present, and, Future. J. Light. Technol. 2008, 26, 1104–1118. [Google Scholar] [CrossRef]
- Gertel, O.; Jinno, M.; Loard, A.; Yoo, B. Elastic optical networking: A new dawn for the optical layer? IEEE Commun. Mag. 2012, 50, s12–s20. [Google Scholar] [CrossRef]
- Jinno, M.; Ohara, T.; Sone, Y.; Hirano, A.; Ishida, O.; Tomizawa, M. Introducing Elasticity and Adaptation into the Optical Domain Toward more Efficient and Scalable Optical Transport Networks. In Proceedings of the 2010 ITU-T Kaleidoscope: Beyond the Internet?—Innovations for Future Networks and Services, Pune, India, 13–15 December 2010; pp. 1–7. [Google Scholar]
- Jinno, M.; Takara, H.; Kozicki, B.; Tsukishima, Y.; Sone, Y.; Matsuoka, S. Spectrum-efficient and scalable elastic optical path network: Architecture, benefits, and enabling technologies. IEEE Commun. Mag. 2009, 47, 66–73. [Google Scholar]
- Hwang, T.; Yang, C.; Wu, G.; Li, S.; Li, G.Y. OFDM and Its Wireless Applications: A Survey. IEEE Trans. Veh. Technol. Soc. 2009, 58, 1673–1694. [Google Scholar] [CrossRef]
- Christodoulopoulo, K.; Tomkos, I.; Varvarigos, E. Elastic Bandwidth Allocation in Flexible OFDM-Based Optical Networks. J. Light. Technol. 2011, 29, 1354–1366. [Google Scholar] [CrossRef]
- Zhang, G.; DeLeenheer, M.; Morea, A.; Mukherjee, B. A Survey on OFDM-Based Elastic Core Optical Networking. IEEE Commun. Surv. Tutor. 2013, 15, 65–87. [Google Scholar] [CrossRef]
- Chatterjee, B.C.; Sarma, N.; Oki, E. Routing and Spectrum Allocation in Elastic Optical Networks: A Tutorial. IEEE Commun. Surv. Tutor. 2015, 17, 1776–1800. [Google Scholar] [CrossRef]
- Zang, H. WDM Mesh Networks: Management and Survivability; Kluwer Academic Publishers: Norwell, MA, USA, 2003. [Google Scholar]
- Christodoulopoulo, K.; Tomkos, I.; Varvarigos, E. Routing and Spectrum Allocation in OFDM-Based Optical Networks with Elastic Bandwidth Allocation. In Proceedings of the 2010 IEEE Global Telecommunications Conference GLOBECOM 2010, Miami, FL, USA, 6 –10 December 2010; pp. 1–6. [Google Scholar]
- Jinno, M.; Kozicki, B.; Takara, H.; Watanabe, A.; Sone, Y.; Tanaka, T.; Hirano, A. Distance-Adaptive Spectrum Resource Allocation in Spectrum-Sliced Elastic Optical Path Network. IEEE Commun. Mag. 2010, 48, 138–145. [Google Scholar] [CrossRef]
- Zhu, Z.; Lu, W.; Zhang, L.; Ansari, N. Dynamic Service Provisioning in Elastic Optical Networks with Hybrid Single-/Multiple-Path Routing. J. Light. Technol. 2013, 31, 15–22. [Google Scholar] [CrossRef]
- Khodashenas, P.S.; Comellas, J.; Spadaro, S.; Perelló, J.; Junyent, G. Using spectrum fragmentation to better allocate time-varying connections in elastic optical networks. IEEE/OSA J. Opt. Commun. Net. 2014, 6, 433–440. [Google Scholar] [CrossRef]
- Shi, J.W.; Zhu, Z.; Zhang, M.; Ansari, N. On the effect of Bandwidth Fragmentation on Blocking Probability in Elastic Optical Networks. IEEE Trans. Commun. 2013, 16, 2970–2978. [Google Scholar]
- Wen, K.; Yin, Y.; Geisler, D.J.; Chang, S.; Yoo, S.J.B. Dynamic on-demand Light path provisioning using spectral defragmentation in flexible bandwidth networks. In Proceedings of the 2011 37th European Conference and Exhibition on Optical Communication (ECOC), Geneva, Switzerland, 18–22 September 2011; pp. 1–3. [Google Scholar]
- Xi, W.; Zhang, Q.; Kim, I.; Palacharla, P.; Sekiya, M. Utilization Entropy for Assessing Resource Fragmentation in Optical Networks. In Proceedings of the 2012 and the National Fiber Optic Engineers Conference Optical Fiber Communication Conference and Exposition (OFC/NFOEC), Los Angeles, CA, USA, 4–8 March 2012; pp. 1–3. [Google Scholar]
- Zhang, M.; Lu, W.; Zhu, Z.; Yin, Y.; Yoo, S.J.B. Planning and provisioning of elastic O-OFDM networks with fragmentation- aware routing and spectrum assignment (RSA) algorithms. In Proceedings of the 2012 Asia Communications and Photonics Conference (ACP), Guangzhou, China, 7–10 November 2012; pp. 1–3. [Google Scholar]
- Al-Tarawneh, L.; Taebi, S. Dynamic adaptation of bandwidth granularity for multipath routing in elastic optical OFDM networks. In Proceedings of the 2015 Conference on Lasers and Electro-Optics (CLEO), San Jose, CA, USA, 10–15 May 2015; pp. 1–2. [Google Scholar]
- Al-Tarawneh, L.; Taebi, S. Linear dynamic adaptation of the BW granularity allocation for elastic optical OFDM networks. In Proceedings of the 2015 International Symposium on Performance Evaluation of Computer and Telecommunication Systems (SPECTS), Chicago, IL, USA, 26–29 July 2015; pp. 1–7. [Google Scholar]
- Tibuleac, S.; Filer, M. Transmission Impairments in DWDM Ne- works with Reconfigurable Optical Add-Drop Multiplexers. J. Light. Technol. 2013, 28, 557–598. [Google Scholar] [CrossRef]
- Huang, S.; Rai, S.; Mukherjee, B. Survivable Differential Delay Aware Multi-Service over SONET/SDH networks with virtual concatenation. In Proceedings of the Optical Fiber Communication and the National Fiber Optic Engineers Conference, Anaheim, CA, USA, 25–29 March 2007; pp. 25–29. [Google Scholar]
- Barlow, G. Traffic Delay in Ethernet over SONET/SDH. Available online: http://www.innocor.com/pdf_files/delay_inEos.pdf (accessed on 27 May 2016).
- Brady, J.F. Traffic Generation Concepts Random Arrivals. Available online: http://www.perfdynamics.com/Classes/Materials/BradyTraffic.pdf (accessed on 18 April 2016).
- Lu, W.; Zhou, X.; Zhang, M.; Zhu, Z. Dynamic Multi-Path Service Provisioning under Differential Delay Constraint in Elastic Optical Networks. IEEE Commun. Lett. 2013, 17, 158–161. [Google Scholar] [CrossRef]
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).