Ultrafast Laser Pulses for Structuring Materials at Micro/Nano Scale: From Waveguides to Superhydrophobic Surfaces
Abstract
:1. Introduction: Fundaments of Femtosecond-Laser Material Processing
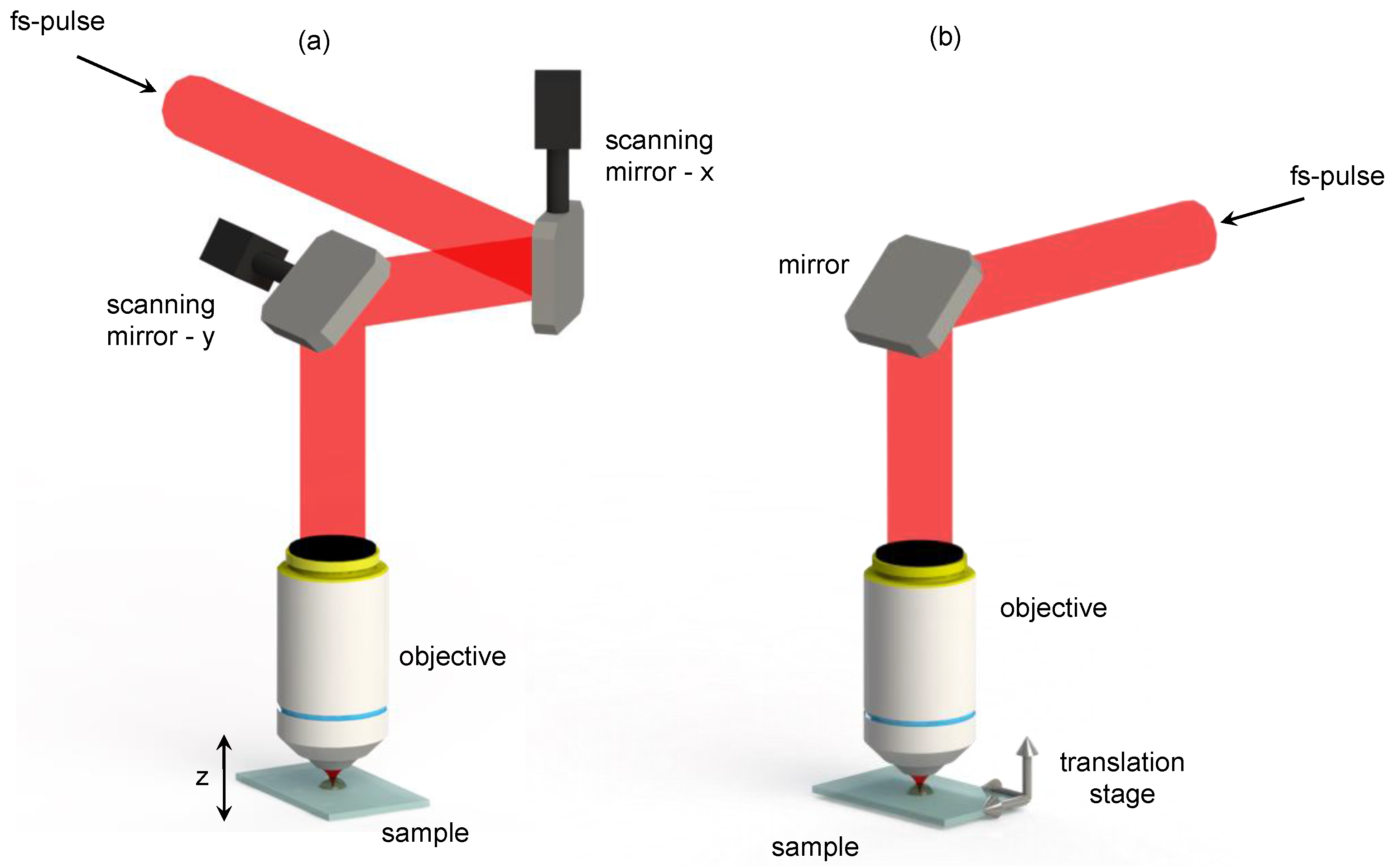
2. Experimental Aspects of fs-Laser Material Processing
3. Fs-Laser Processing of Distinct Materials
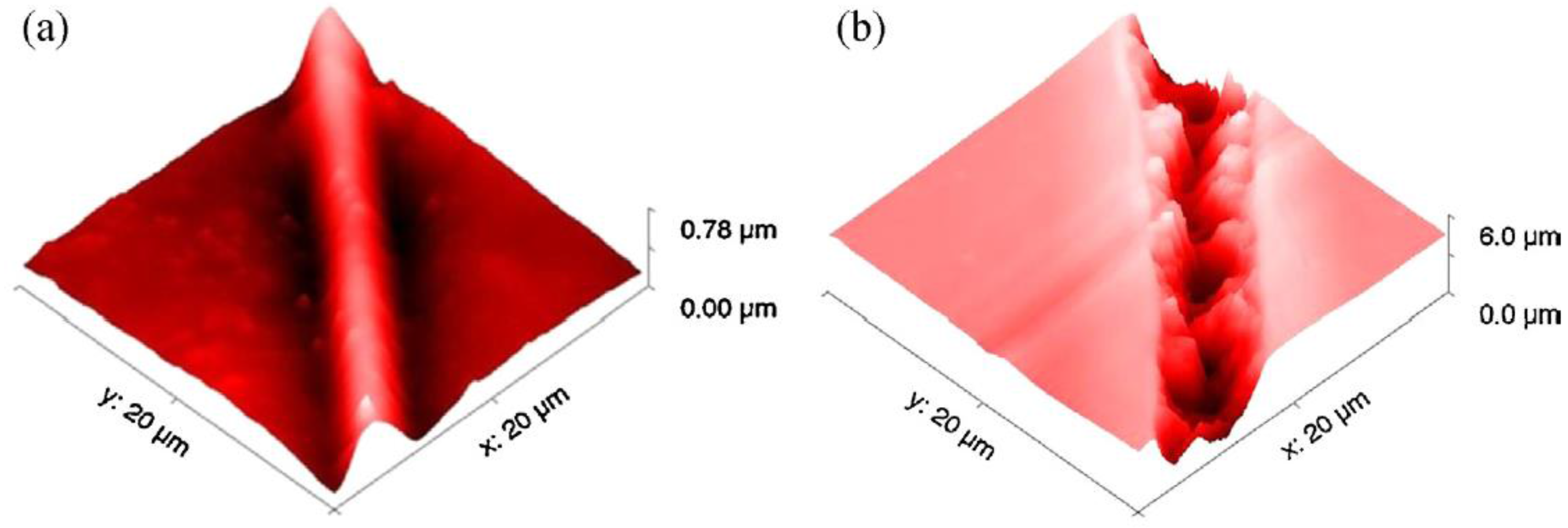
3.1. Optical Waveguides in Polymers
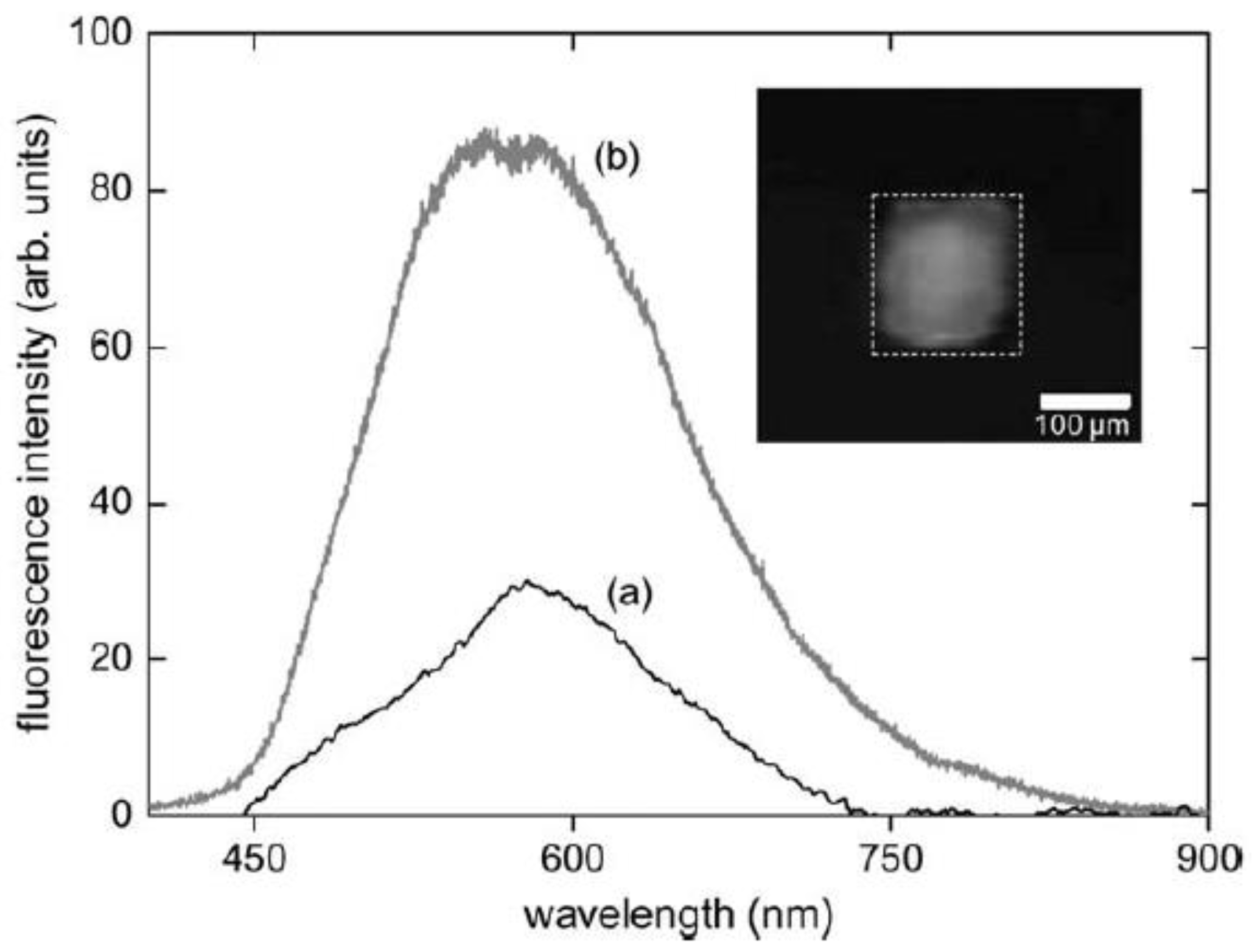
3.2. Fluorescent Polymeric Structures
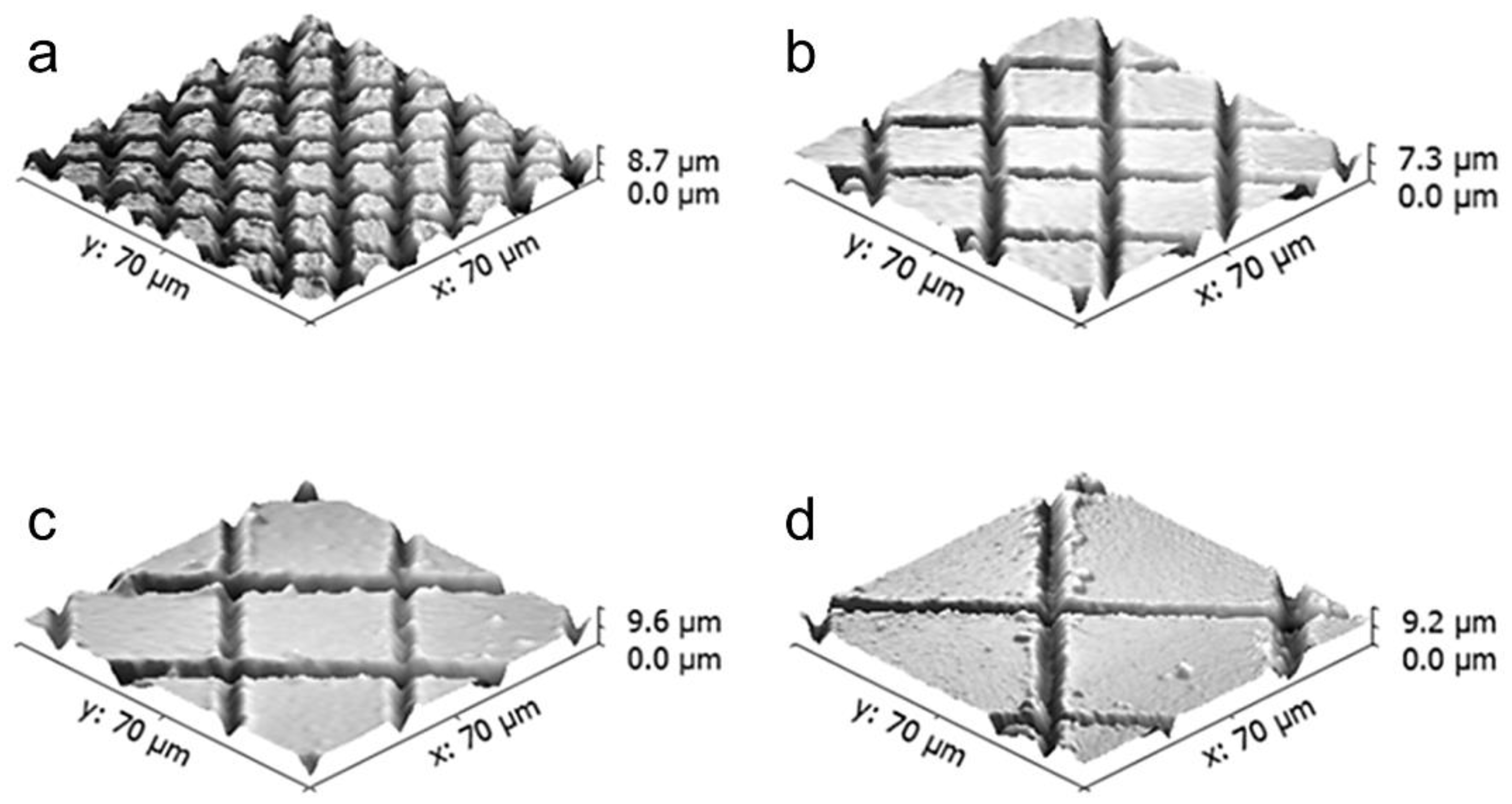
3.3. Superhydrophobic Polymeric Surfaces
3.4. Superhydrophobic Metallic Surfaces
3.5. Optical Waveguides
3.5.1. Optical Waveguides in Glasses
3.5.2. Optical Waveguides in Glasses Containing Metal Nanoparticles
3.6. Gold Ablation for Designing Microelectrodes
3.7. Micromachining Silicon Surfaces
4. Summary
Acknowledgments
Conflicts of Interest
References
- Davis, K.M.; Miura, K.; Sugimoto, N.; Hirao, K. Writing waveguides in glass with a femtosecond laser. Opt. Lett. 1996, 21, 1729–1731. [Google Scholar] [CrossRef] [PubMed]
- Sikorski, Y.; Said, A.A.; Bado, P.; Maynard, R.; Florea, C.; Winick, K.A. Optical waveguide amplifier in Nd-doped glass written with near-IR femtosecond laser pulses. Electron. Lett. 2000, 36, 226–227. [Google Scholar] [CrossRef]
- Florea, C.; Winick, K.A. Fabrication and characterization of photonic devices directly written in glass using femtosecond laser pulses. J. Lightwave Technol. 2003, 21, 246–253. [Google Scholar] [CrossRef]
- Chichkov, B.N.; Momma, C.; Nolte, S.; von Alvensleben, F.; Tunnermann, A. Femtosecond, picosecond and nanosecond laser ablation of solids. Appl. Phys. A Mater. Sci. Process. 1996, 63, 109–115. [Google Scholar] [CrossRef]
- Anisimov, S.I.; Kapeliov, B.L.; Perelman, T.L. Electron-emission from surface of metals induced by ultrashort laser pulses. Zhurnal Eksperimentalnoi Teoreticheskoi Fiziki 1974, 66, 776–781. [Google Scholar]
- Nolte, S.; Momma, C.; Jacobs, H.; Tunnermann, A.; Chichkov, B.N.; Wellegehausen, B.; Welling, H. Ablation of metals by ultrashort laser pulses. J. Opt. Soc. Am. B Opt. Phys. 1997, 14, 2716–2722. [Google Scholar] [CrossRef]
- Momma, C.; Nolte, S.; Chichkov, B.N.; von Alvensleben, F.; Tunnermann, A. Precise laser ablation with ultrashort pulses. Appl. Surf. Sci. 1997, 109, 15–19. [Google Scholar] [CrossRef]
- Keldysh, L.V. Ionization in field of a strong electromagnetic wave. Sov. Phys. JETP-Ussr 1965, 20, 1307. [Google Scholar]
- Schaffer, C.B.; Brodeur, A.; Mazur, E. Laser-induced breakdown and damage in bulk transparent materials induced by tightly focused femtosecond laser pulses. Meas. Sci. Technol. 2001, 12, 1784–1794. [Google Scholar] [CrossRef]
- Stuart, B.C.; Feit, M.D.; Herman, S.; Rubenchik, A.M.; Shore, B.W.; Perry, M.D. Nanosecond-to-femtosecond laser-induced breakdown in dielectrics. Phys. Rev. B 1996, 53, 1749–1761. [Google Scholar] [CrossRef]
- Zayarny, D.A.; Ionin, A.A.; Kudryashov, S.I.; Saraeva, I.N.; Startseva, E.D.; Khmelnitskii, R.A. Nonlinear absorption mechanisms during femtosecond laser surface ablation of silica glass. JETP Lett. 2016, 103, 309–312. [Google Scholar] [CrossRef]
- Gamaly, E.G.; Juodkazis, S.; Nishimura, K.; Misawa, H.; Luther-Davies, B. Laser-matter interaction in the bulk of a transparent solid: Confined microexplosion and void formation. Phys. Rev. B 2006, 73, 214101. [Google Scholar] [CrossRef]
- Bulgakova, N.M.; Bulgakov, A.V. Pulsed laser ablation of solids: Transition from normal vaporization to phase explosion. Appl. Phys. A Mater. Sci. Process. 2001, 73, 199–208. [Google Scholar] [CrossRef]
- Nolte, S.; Will, M.; Burghoff, J.; Tuennermann, A. Femtosecond waveguide writing: A new avenue to three-dimensional integrated optics. Appl. Phys. A Mater. Sci. Process. 2003, 77, 109–111. [Google Scholar] [CrossRef]
- Sun, H.B.; Xu, Y.; Juodkazis, S.; Sun, K.; Watanabe, M.; Matsuo, S.; Misawa, H.; Nishii, J. Arbitrary-lattice photonic crystals created by multiphoton microfabrication. Opt. Lett. 2001, 26, 325–327. [Google Scholar] [CrossRef] [PubMed]
- Li, R.Z.; Peng, R.; Kihm, K.D.; Bai, S.; Bridges, D.; Tumuluri, U.; Wu, Z.; Zhang, T.; Compagnini, G.; Feng, Z.; et al. High-rate in-plane micro-supercapacitors scribed onto photo paper using in situ femtolaser-reduced graphene oxide/Au nanoparticle microelectrodes. Energy Environ. Sci. 2016, 9, 1458–1467. [Google Scholar] [CrossRef]
- Zheng, C.; Hu, A.M.; Kihm, K.D.; Ma, Q.; Li, R.Z.; Chen, T.; Duley, W.W. Femtosecond Laser Fabrication of Cavity Microball Lens (CMBL) inside a PMMA substrate for super-wide angle imaging. Small 2015, 11, 3007–3016. [Google Scholar] [CrossRef] [PubMed]
- Cheng, C.; Wang, S.T.; Wu, J.N.; Yu, Y.C.; Li, R.Z.; Eda, S.; Chen, J.G.; Feng, G.Y.; Lawrie, B.; Hu, A.M. Bisphenol A Sensors on Polyimide Fabricated by Laser Direct Writing for Onsite River Water Monitoring at Attomolar Concentration. ACS Appl. Mater. Interfaces 2016, 8, 17784–17792. [Google Scholar] [CrossRef] [PubMed]
- Miura, K.; Qiu, J.R.; Inouye, H.; Mitsuyu, T.; Hirao, K. Photowritten optical waveguides in various glasses with ultrashort pulse laser. Appl. Phys. Lett. 1997, 71, 3329–3331. [Google Scholar] [CrossRef]
- Chan, J.W.; Huser, T.; Risbud, S.; Krol, D.M. Structural changes in fused silica after exposure to focused femtosecond laser pulses. Opt. Lett. 2001, 26, 1726–1728. [Google Scholar] [CrossRef] [PubMed]
- Chan, J.W.; Huser, T.R.; Risbud, S.H.; Krol, D.M. Modification of the fused silica glass network associated with waveguide fabrication using femtosecond laser pulses. Appl. Phys. A Mater. Sci. Process. 2003, 76, 367–372. [Google Scholar] [CrossRef]
- Chan, J.W.; Huser, T.R.; Risbud, S.H.; Hayden, J.S.; Krol, D.M. Waveguide fabrication in phosphate glasses using femtosecond laser pulses. Appl. Phys. Lett. 2003, 82, 2371–2373. [Google Scholar] [CrossRef]
- Burakov, I.M.; Bulgakova, N.M.; Stoian, R.; Mermillod-Blondin, A.; Audouard, E.; Rosenfeld, A.; Husakou, A.; Hertel, I.V. Spatial distribution of refractive index variations induced in bulk fused silica by single ultrashort and short laser pulses. J. Appl. Phys. 2007, 101. [Google Scholar] [CrossRef]
- Glezer, E.N.; Milosavljevic, M.; Huang, L.; Finlay, R.J.; Her, T.H.; Callan, J.P.; Mazur, E. Three-dimensional optical storage inside transparent materials. Opt. Lett. 1996, 21, 2023–2025. [Google Scholar] [CrossRef] [PubMed]
- Glezer, E.N.; Mazur, E. Ultrafast-laser driven micro-explosions in transparent materials. Appl. Phys. Lett. 1997, 71, 882–884. [Google Scholar] [CrossRef]
- Schaffer, C.B.; Jamison, A.O.; Mazur, E. Morphology of femtosecond laser-induced structural changes in bulk transparent materials. Appl. Phys. Lett. 2004, 84, 1441–1443. [Google Scholar] [CrossRef]
- Qiu, J.R.; Miura, K.; Hirao, K. Three-dimensional optical memory using glasses as a recording medium through a multi-photon absorption process. Jpn. J. Appl. Phys. Part 1 1998, 37, 2263–2266. [Google Scholar] [CrossRef]
- Gorelik, T.; Will, M.; Nolte, S.; Tuennermann, A.; Glatzel, U. Transmission electron microscopy studies of femtosecond laser induced modifications in quartz. Appl. Phys. A Mater. Sci. Process. 2003, 76, 309–311. [Google Scholar] [CrossRef]
- Itoh, K.; Watanabe, W.; Nolte, S.; Schaffer, C.B. Ultrafast processes for bulk modification of transparent materials. MRS Bull. 2006, 31, 620–625. [Google Scholar] [CrossRef]
- Watanabe, W.; Li, Y.; Itoh, K. INVITED Ultrafast laser micro-processing of transparent material. Opt. Laser Technol. 2016, 78, 52–61. [Google Scholar] [CrossRef]
- Tan, D.Z.; Sharafudeen, K.N.; Yue, Y.Z.; Qiu, J.R. Femtosecond laser induced phenomena in transparent solid materials: Fundamentals and applications. Prog. Mater. Sci. 2016, 76, 154–228. [Google Scholar] [CrossRef]
- Nolte, S.; Chichkov, B.N.; Welling, H.; Shani, Y.; Lieberman, K.; Terkel, H. Nanostructuring with spatially localized femtosecond laser pulses. Opt. Lett. 1999, 24, 914–916. [Google Scholar] [CrossRef] [PubMed]
- Schaffer, C.B.; Brodeur, A.; Garcia, J.F.; Mazur, E. Micromachining bulk glass by use of femtosecond laser pulses with nanojoule energy. Opt. Lett. 2001, 26, 93–95. [Google Scholar] [CrossRef] [PubMed]
- Wolfe, D.B.; Ashcom, J.B.; Hwang, J.C.; Schaffer, C.B.; Mazur, E.; Whitesides, G.M. Customization of poly(dimethylsiloxane) stamps by micromachining using a femtosecond-pulsed laser. Adv. Mater. 2003, 15, 62–65. [Google Scholar] [CrossRef]
- Qiu, J.R.; Jiang, X.W.; Zhu, C.S.; Shirai, M.; Si, J.; Jiang, N.; Hirao, K. Manipulation of gold nanoparticles inside transparent materials. Angew. Chem. Int. Ed. 2004, 43, 2230–2234. [Google Scholar] [CrossRef] [PubMed]
- Almeida, J.M.P.; Ferreira, P.H.D.; Manzani, D.; Napoli, M.; Ribeiro, S.J.L.; Mendonca, C.R. Metallic nanoparticles grown in the core of femtosecond laser micromachined waveguides. J. Appl. Phys. 2014, 115. [Google Scholar] [CrossRef]
- Mendonca, C.R.; Cerami, L.R.; Shih, T.; Tilghman, R.W.; Baldacchini, T.; Mazur, E. Femtosecond laser waveguide micromachining of PMMA films with azoaromatic chromophores. Opt. Express 2008, 16, 200–206. [Google Scholar] [CrossRef] [PubMed]
- Liu, X.; Du, D.; Mourou, G. Laser ablation and micromachining with ultrashort laser pulses. IEEE J. Quantum Electron. 1997, 33, 1706–1716. [Google Scholar] [CrossRef]
- Gattass, R.R.; Mazur, E. Femtosecond laser micromachining in transparent materials. Nat. Photonics 2008, 2, 219–225. [Google Scholar] [CrossRef]
- Almeida, J.M.P.; De Boni, L.; Hernandes, A.C.; Mendonca, C.R. Third-order nonlinear spectra and optical limiting of lead oxifluoroborate glasses. Opt. Express 2011, 19, 17220–17225. [Google Scholar] [CrossRef] [PubMed]
- Jenness, N.J.; Wu, Y.Q.; Clark, R.L. Fabrication of three-dimensional electrospun microstructures using phase modulated femtosecond laser pulses. Mater. Lett. 2012, 66, 360–363. [Google Scholar] [CrossRef]
- Silvennoinen, M.; Kaakkunen, J.; Paivasaari, K.; Vahimaa, P. Parallel femtosecond laser ablation with individually controlled intensity. Opt. Express 2014, 22, 2603–2608. [Google Scholar] [CrossRef] [PubMed]
- Torres-Peiro, S.; Gonzalez-Ausejo, J.; Mendoza-Yero, O.; Minguez-Vega, G.; Andres, P.; Lancis, J. Parallel laser micromachining based on diffractive optical elements with dispersion compensated femtosecond pulses. Opt. Express 2013, 21, 31830–31836. [Google Scholar] [CrossRef] [PubMed]
- Lasagni, A.; Yuan, D.J.; Shao, P.; Das, S. Fabrication of periodic microstructures in pentaerythritol triacrylate through femtosecond laser interference two-photon. polymerization. Adv. Eng. Mater. 2009, 11, 595–599. [Google Scholar] [CrossRef]
- Kondo, T.; Matsuo, S.; Juodkazis, S.; Misawa, H. Femtosecond laser interference technique with diffractive beam splitter for fabrication of three-dimensional photonic crystals. Appl. Phys. Lett. 2001, 79, 725–727. [Google Scholar] [CrossRef]
- Kondo, T.; Matsuo, S.; Juodkazis, S.; Mizeikis, V.; Misawa, H. Multiphoton fabrication of periodic structures by multibeam interference of femtosecond pulses. Appl. Phys. Lett. 2003, 82, 2758–2760. [Google Scholar] [CrossRef]
- Sun, H.B.; Kawata, S. Two-photon photopolymerization and 3D lithographic microfabrication. In NMR—3D Analysis—Photopolymerization; Springer-Verlag Berlim: Berlin, Germany, 2004; pp. 169–273. [Google Scholar]
- Hell, S.W.; Wichmann, J. Breaking the diffraction resolution limit by stimulated-emission—Stimulated-emission-depletion fluorescence microscopy. Opt. Lett. 1994, 19, 780–782. [Google Scholar] [CrossRef] [PubMed]
- Elmeranta, M.; Vicidomini, G.; Duocastella, M.; Diaspro, A.; de Miguel, G. Characterization of nanostructures fabricated with two-beam DLW lithography using STED microscopy. Opt. Mater. Express 2016, 6, 3169–3179. [Google Scholar] [CrossRef]
- Fischer, J.; Wegener, M. Three-dimensional direct laser writing inspired by stimulated-emission-depletion microscopy Invited. Opt. Mater. Express 2011, 1, 614–624. [Google Scholar] [CrossRef]
- Ferreira, P.H.D.; Stefanutti, R.; Pavinatto, F.J.; Mendonca, C.R. Femtosecond laser fabrication of waveguides in DR13-doped PMMA. Opt. Commun. 2014, 318, 53–56. [Google Scholar] [CrossRef]
- Patzold, W.M.; Reinhardt, C.; Demircan, A.; Morgner, U. Cascaded-focus laser writing of low-loss waveguides in polymers. Opt. Lett. 2016, 41, 1269–1272. [Google Scholar] [CrossRef] [PubMed]
- Kelb, C.; Patzold, W.M.; Morgner, U.; Rahlves, M.; Reithmeier, E.; Roth, B. Characterization of femtosecond laser written gratings in PMMA using a phase-retrieval approach. Opt. Mater. Express 2016, 6, 3202–3209. [Google Scholar] [CrossRef]
- Bajpai, M.; Srivastava, R.; Kamalasanan, M.N.; Tiwari, R.S.; Chand, S. Charge transport and microstructure in PFO:MEH-PPV polymer blend thin films. Synth. Met. 2010, 160, 1740–1744. [Google Scholar] [CrossRef]
- Si, J.H.; Qiu, J.R.; Zhai, J.F.; Shen, Y.Q.; Hirao, K. Photoinduced permanent gratings inside bulk azodye-doped polymers by the coherent field of a femtosecond laser. Appl. Phys. Lett. 2002, 80, 359–361. [Google Scholar] [CrossRef]
- Estevam-Alves, R.; Ferreira, P.H.D.; Almeida, G.F.B.; Sousa, W.S.; Mendonca, C.R. Microfabrication of electroluminescent polymer for devices construction. Appl. Surf. Sci. 2014, 314, 633–637. [Google Scholar] [CrossRef]
- Oliveira, S.L.; Correa, D.S.; De Boni, L.; Misoguti, L.; Zilio, S.C.; Mendonca, C.R. Two-photon absorption cross-section spectrum of a pi-conjugated polymer obtained using the white-light continuum Z-scan technique. Appl. Phys. Lett. 2006, 88. [Google Scholar] [CrossRef]
- Ferreira, P.H.D.; Silva, D.L.; Misoguti, L.; Mendonca, C.R. MEH-PPV photobleaching control by femtosecond pulse shaping. Phys. Status Solidi A Appl. Mater. Sci. 2009, 206, 126–130. [Google Scholar] [CrossRef]
- Otuka, A.J.G.; Almeida, J.M.P.; Tribuzi, V.; Cardoso, M.R.; Hernandes, A.C.; Correa, D.S.; Mendonca, C.R. Femtosecond Lasers for Processing Glassy and Polymeric Materials. Mater. Res.-Ibero-Am. J. Mater. 2014, 17, 352–358. [Google Scholar] [CrossRef]
- Correa, D.S.; De Boni, L.; Otuka, A.J.G.; Tribuzi, V.; Mendonca, C.R. Two-Photon Polymerization Fabrication of Doped Microstructures, in Polymerization; Gomes, A.D.S., Ed.; Intech: Rijeka, Croatia, 2012; pp. 333–356. [Google Scholar]
- Shukla, S.; Vidal, X.; Furlani, E.P.; Swihart, M.T.; Kim, K.T.; Yoon, Y.K.; Urbas, A.; Prasad, P.N. Subwavelength Direct Laser Patterning of Conductive Gold Nanostructures by Simultaneous Photopolymerization and Photoreduction. ACS Nano 2010, 5, 1947–1957. [Google Scholar] [CrossRef] [PubMed]
- Kuo, W.S.; Lien, C.H.; Cho, K.C.; Chang, C.Y.; Lin, C.Y.; Huang, L.L.H.; Campagnola, P.J.; Dong, C.Y.; Chen, S.J. Multiphoton fabrication of freeform polymer microstructures with gold nanorods. Opt. Express 2010, 18, 27550–27559. [Google Scholar] [CrossRef] [PubMed]
- Maruo, S.; Fourkas, J.T. Recent progress in multiphoton microfabrication. Laser Photonics Rev. 2008, 2, 100–111. [Google Scholar] [CrossRef]
- Haske, W.; Chen, V.W.; Hales, J.M.; Dong, W.T.; Barlow, S.; Marder, S.R.; Perry, J.W. 65 nm feature sizes using visible wavelength 3-D multiphoton lithography. Opt. Express 2007, 15, 3426–3436. [Google Scholar] [CrossRef] [PubMed]
- Fonseca, R.D.; Correa, D.S.; Paris, E.C.; Tribuzi, V.; Dev, A.; Voss, T.; Aoki, P.H.B.; Constantino, C.J.L.; Mendonca, C.R. Fabrication of Zinc Oxide Nanowires/Polymer Composites by Two-Photon. Polymerization. J. Polym. Sci. Part. B Polym. Phys. 2014, 52, 333–337. [Google Scholar] [CrossRef]
- De Miguel, G.; Vicidomini, G.; Duocastella, M.; Diaspro, A. Selective fluorescence functionalization of dye-doped polymerized structures fabricated by direct laser writing (DLW) lithography. Nanoscale 2015, 7, 20164–20170. [Google Scholar] [CrossRef] [PubMed]
- Furstner, R.; Barthlott, W.; Neinhuis, C.; Walzel, P. Wetting and self-cleaning properties of artificial superhydrophobic surfaces. Langmuir 2005, 21, 956–961. [Google Scholar] [CrossRef] [PubMed]
- Wang, S.D.; Lin, B.J.; Hsieh, C.C.; Lin, C.C. Application of superhydrophobic sol gel on canvas. Appl. Surf. Sci. 2014, 307, 101–108. [Google Scholar] [CrossRef]
- Zhu, J.; Hsu, C.-M.; Yu, Z.; Fan, S.; Cui, Y. Nanodome Solar Cells with Efficient Light Management and Self-Cleaning. Nano Lett. 2010, 10, 1979–1984. [Google Scholar] [CrossRef] [PubMed]
- Cardoso, M.R.; Tribuzi, V.; Balogh, D.T.; Misoguti, L.; Mendonca, C.R. Laser microstructuring of azopolymers via surface relief gratings: Controlling hydrophobicity. J. Optoelectron. Adv. Mater. 2010, 12, 745–748. [Google Scholar]
- Jiang, Z.L.; Fang, S.Y.; Wang, C.S.; Wang, H.P.; Ji, C.C. Durable polyorganosiloxane superhydrophobic films with a hierarchical structure by sol-gel and heat treatment method. Appl. Surf. Sci. 2016, 390, 993–1001. [Google Scholar] [CrossRef]
- Guan, W.-S.; Huang, H.-X.; Chen, A.-F. Tuning 3D topography on biomimetic surface for efficient self-cleaning and microfluidic manipulation. J. Micromech. Microeng. 2015, 25, 35001–35009. [Google Scholar] [CrossRef]
- Jin, K.J.; Cremaldi, J.C.; Erickson, J.S.; Tian, Y.; Israelachvili, J.N.; Pesika, N.S. Biomimetic Bidirectional Switchable Adhesive Inspired by the Gecko. Adv. Funct. Mater. 2014, 24, 574–579. [Google Scholar] [CrossRef]
- Baldacchini, T.; Carey, J.E.; Zhou, M.; Mazur, E. Superhydrophobic surfaces prepared by microstructuring of silicon using a femtosecond laser. Langmuir 2006, 22, 4917–4919. [Google Scholar] [CrossRef] [PubMed]
- Blossey, R. Self-cleaning surfaces—Virtual realities. Nat. Mater. 2003, 2, 301–306. [Google Scholar] [CrossRef] [PubMed]
- Neinhuis, C.; Barthlott, W. Characterization and distribution of water-repellent, self-cleaning plant surfaces. Ann. Bot. 1997, 79, 667–677. [Google Scholar] [CrossRef]
- Tuteja, A.; Choi, W.; Ma, M.L.; Mabry, J.M.; Mazzella, S.A.; Rutledge, G.C.; McKinley, G.H.; Cohen, R.E. Designing superoleophobic surfaces. Science 2007, 318, 1618–1622. [Google Scholar] [CrossRef] [PubMed]
- Yan, Y.Y.; Gao, N.; Barthlott, W. Mimicking natural superhydrophobic surfaces and grasping the wetting process: A review on recent progress in preparing superhydrophobic surfaces. Adv. Colloid Interface Sci. 2011, 169, 80–105. [Google Scholar] [CrossRef] [PubMed]
- Sun, T.; Feng, L.; Gao, X.; Jiang, L. Bioinspired surfaces with special wettability. Accounts Chem. Res. 2006, 39, 487. [Google Scholar] [CrossRef]
- Chen, F.; Zhang, D.; Yang, Q.; Yong, J.; Du, G.; Si, J.; Yun, F.; Hou, X. Bioinspired Wetting Surface via Laser Microfabrication. ACS Appl. Mater. Interfaces 2013, 5, 6777–6792. [Google Scholar] [CrossRef] [PubMed]
- Oner, D.; McCarthy, T.J. Ultrahydrophobic surfaces. Effects of topography length scales on wettability. Langmuir 2000, 16, 7777–7782. [Google Scholar] [CrossRef]
- Wu, W.; Zhu, Q.; Qing, F.; Han, C.C. Water Repellency on a Fluorine-Containing Polyurethane Surface: Toward Understanding the Surface Self-Cleaning Effect. Langmuir 2009, 25, 17–20. [Google Scholar] [CrossRef] [PubMed]
- Barberoglou, M.; Zorba, V.; Stratakis, E.; Spanakis, E.; Tzanetakis, P.; Anastasiadis, S.H.; Fotakis, C. Bio-inspired water repellent surfaces produced by ultrafast laser structuring of silicon. Appl. Surf. Sci. 2009, 255, 5425–5429. [Google Scholar] [CrossRef]
- Otten, A.; Herminghaus, S. How plants keep dry: A physicist’s point of view. Langmuir 2004, 20, 2405–2408. [Google Scholar] [CrossRef] [PubMed]
- Vogelaar, L.; Lammertink, R.G.H.; Wessling, M. Superhydrophobic surfaces having two-fold adjustable roughness prepared in a single step. Langmuir 2006, 22, 3125–3130. [Google Scholar] [CrossRef] [PubMed]
- Patankar, N.A. Mimicking the lotus effect: Influence of double roughness structures and slender pillars. Langmuir 2004, 20, 8209–8213. [Google Scholar] [CrossRef] [PubMed]
- Jin, M.H.; Feng, X.J.; Xi, J.M.; Zhai, J.; Cho, K.W.; Feng, L.; Jiang, L. Super-hydrophobic PDMS surface with ultra-low adhesive force. Macromol. Rapid Commun. 2005, 26, 1805–1809. [Google Scholar] [CrossRef]
- Cortese, B.; D’Amone, S.; Manca, M.; Viola, I.; Cingolani, R.; Gigli, G. Superhydrophobicity due to the hierarchical scale roughness of PDMS surfaces. Langmuir 2008, 24, 2712–2718. [Google Scholar] [CrossRef] [PubMed]
- Feng, L.; Li, S.H.; Li, Y.S.; Li, H.J.; Zhang, L.J.; Zhai, J.; Song, Y.L.; Liu, B.Q.; Jiang, L.; Zhu, D.B. Super-hydrophobic surfaces: From natural to artificial. Adv. Mater. 2002, 14, 1857–1860. [Google Scholar] [CrossRef]
- Yang, Y.-L.; Hsu, C.-C.; Chang, T.-L.; Kuo, L.-S.; Chen, P.-H. Study on wetting properties of periodical nanopatterns by a combinative technique of photolithography and laser interference lithography. Appl. Surf. Sci. 2010, 256, 3683–3687. [Google Scholar] [CrossRef]
- Wu, B.; Zhou, M.; Li, J.; Ye, X.; Li, G.; Cai, L. Superhydrophobic surfaces fabricated by microstructuring of stainless steel using a femtosecond laser. Appl. Surf. Sci. 2009, 256, 61–66. [Google Scholar] [CrossRef]
- Cardoso, M.R.; Martins, R.J.; Dev, A.; Voss, T.; Mendonca, C.R. Highly hydrophobic hierarchical nanomicro roughness polymer surface created by stamping and laser micromachining. J. Appl. Polym. Sci. 2015, 132, 4. [Google Scholar] [CrossRef]
- Bonse, J.; Rosenfeld, A.; Krueger, J. Femtosecond laser-induced periodic surface structures: Recent approaches to explain their sub-wavelength periodicities. In Proceedings of the Lat 2010: International Conference on Lasers, Applications, and Technologies, Kazan, Russia, 7 February 2011.
- Cassie, A.B.D.; Baxter, S. Wettability of porous surfaces. Trans. Faraday Soc. 1944, 40, 0546–0550. [Google Scholar] [CrossRef]
- Zorba, V.; Persano, L.; Pisignano, D.; Athanassiou, A.; Stratakis, E.; Cingolani, R.; Tzanetakis, P.; Fotakis, C. Making silicon hydrophobic: Wettability control by two-lengthscale simultaneous patterning with femtosecond laser irradiation. Nanotechnology 2006, 17, 3234–3238. [Google Scholar] [CrossRef]
- Kietzig, A.-M.; Hatzikiriakos, S.G.; Englezos, P. Patterned Superhydrophobic Metallic Surfaces. Langmuir 2009, 25, 4821–4827. [Google Scholar] [CrossRef] [PubMed]
- Li, B.J.; Li, H.; Huang, L.J.; Ren, N.F.; Kong, X. Femtosecond pulsed laser textured titanium surfaces with stable superhydrophilicity and superhydrophobicity. Appl. Surf. Sci. 2016, 389, 585–593. [Google Scholar] [CrossRef]
- Tien, A.C.; Backus, S.; Kapteyn, H.; Murnane, M.; Mourou, G. Short-pulse laser damage in transparent materials as a function of pulse duration. Phys. Rev. Lett. 1999, 82, 3883–3886. [Google Scholar] [CrossRef]
- Almeida, J.M.P.; Fonseca, R.D.; De Boni, L.; Diniz, A.R.S.; Hernandes, A.C.; Ferreira, P.H.D.; Mendonca, C.R. Waveguides and nonlinear index of refraction of borate glass doped with transition metals. Opt. Mater. 2015, 42, 522–525. [Google Scholar] [CrossRef]
- Will, M.; Nolte, S.; Chichkov, B.N.; Tunnermann, A. Optical properties of waveguides fabricated in fused silica by femtosecond laser pulses. Appl. Opt. 2002, 41, 4360–4364. [Google Scholar] [CrossRef] [PubMed]
- Veiko, V.P.; Kudryashov, S.I.; Sergeev, M.M.; Zakoldaev, R.A.; Danilov, P.A.; Ionin, A.A.; Antropova, T.V.; Anfimova, I.N. Femtosecond laser-induced stress-free ultra-densification inside porous glass. Laser Phys. Lett. 2016, 13, 055901. [Google Scholar] [CrossRef]
- Osellame, R.; Taccheo, S.; Marangoni, M.; Ramponi, R.; Laporta, P.; Polli, D.; De Silvestri, S.; Cerullo, G. Femtosecond writing of active optical waveguides with astigmatically shaped beams. J. Opt. Soc. Am. B-Opt. Phys. 2003, 20, 1559–1567. [Google Scholar] [CrossRef]
- Ams, M.; Marshall, G.D.; Spence, D.J.; Withford, M.J. Slit beam shaping method for femtosecond laser direct-write fabrication of symmetric waveguides in bulk glasses. Opt. Express 2005, 13, 5676–5681. [Google Scholar] [CrossRef] [PubMed]
- Cheng, Y.; Sugioka, K.; Midorikawa, K.; Masuda, M.; Toyoda, K.; Kawachi, M.; Shihoyama, K. Control. of the cross-sectional shape of a hollow microchannel embedded in photostructurable glass by use of a femtosecond laser. Opt. Lett. 2003, 28, 55–57. [Google Scholar] [CrossRef] [PubMed]
- Eaton, S.; Zhang, H.; Herman, P.; Yoshino, F.; Shah, L.; Bovatsek, J.; Arai, A. Heat accumulation effects in femtosecond laser-written waveguides with variable repetition rate. Opt. Express 2005, 13, 4708–4716. [Google Scholar] [CrossRef] [PubMed]
- Schaffer, C.B.; Garcia, J.F.; Mazur, E. Bulk heating of transparent materials using a high-repetition-rate femtosecond laser. Appl. Phys. A Mater. Sci. Process. 2003, 76, 351–354. [Google Scholar] [CrossRef]
- Almeida, J.M.P.; De Boni, L.; Avansi, W.; Ribeiro, C.; Longo, E.; Hernandes, A.C.; Mendonca, C.R. Generation of copper nanoparticles induced by fs-laser irradiation in borosilicate glass. Opt. Express 2012, 20, 15106–15113. [Google Scholar] [CrossRef] [PubMed]
- Coelho, J.M.P.; Silva, C.; Ruivo, A.; Matos, A.P. Infrared Nanosecond Laser Radiation in the Creation of Gold and Copper Nanoparticles. Mater. Sci. Forum 2013, 730, 915–919. [Google Scholar]
- Almeida, J.M.P.; Tribuzi, V.; Fonseca, R.D.; Otuka, A.J.G.; Ferreira, P.H.D.; Mastelaro, V.R.; Brajato, P.; Hernandes, A.C.; Dev, A.; Voss, T.; et al. Femtosecond laser processing of glassy and polymeric matrices containing metals and semiconductor nanostructures. Opt. Mater. 2013, 35, 2643–2648. [Google Scholar] [CrossRef]
- Marquestaut, N.; Petit, Y.; Royon, A.; Mounaix, P.; Cardinal, T.; Canioni, L. Three-dimensional silver nanoparticle formation using femtosecond laser irradiation in phosphate glasses: Analogy with photography. Adv. Funct. Mater. 2014, 24, 5824–5832. [Google Scholar] [CrossRef]
- Sekhar, H.; Kiran, P.P.; Rao, D.N. Structural, linear and enhanced third-order nonlinear optical properties of Bi12SiO20 nanocrystals. Mater. Chem. Phys. 2011, 130, 113–120. [Google Scholar] [CrossRef]
- Smolorz, S.; Kang, I.; Wise, F.; Aitken, B.G.; Borrelli, N.F. Studies of optical non-linearities of chalcogenide and heavy-metal oxide glasses. J. Non-Cryst. Solids 1999, 256, 310–317. [Google Scholar] [CrossRef]
- Dai, Y.; Yu, G.; He, M.; Ma, H.; Yan, X.; Ma, G. High repetition rate femtosecond laser irradiation-induced elements redistribution in Ag-doped glass. Appl. Phys. B-Lasers Opt. 2011, 103, 663–667. [Google Scholar] [CrossRef]
- Miura, K.; Qiu, J.R.; Mitsuyu, T.; Hirao, K. Space-selective growth of frequency-conversion crystals in glasses with ultrashort infrared laser pulses. Opt. Lett. 2000, 25, 408–410. [Google Scholar] [CrossRef] [PubMed]
- Stone, A.; Jain, H.; Dierolf, V.; Sakakura, M.; Shimotsuma, Y.; Miura, K.; Hirao, K.; Lapointe, J.; Kashyap, R. Direct laser-writing of ferroelectric single-crystal waveguide architectures in glass for 3D integrated optics. Sci. Rep. 2015, 5, 10391. [Google Scholar] [CrossRef] [PubMed]
- Almeida, J.M.P.; Almeida, G.F.B.; Hernandes, A.C.; Mendonca, C.R. Architecture of lead oxide microcrystals in glass: A laser and etching based method. CrystEngComm 2016, 18, 5959–5964. [Google Scholar] [CrossRef]
- Demetriou, G.; Berube, J.P.; Vallee, R.; Messaddeq, Y.; Petersen, C.R.; Jain, D.; Bang, O.; Craig, C.; Hewak, D.W.; Kar, A.K. Refractive index and dispersion control of ultrafast laser inscribed waveguides in gallium lanthanum sulphide for near and mid-infrared applications. Opt. Express 2016, 24, 6350–6358. [Google Scholar] [CrossRef] [PubMed]
- Caulier, O.; Masselin, P.; Bychkov, E.; Le Coq, D. INVITED Tailoring the morphology of photowritten buried waveguides by helical trajectory in As2S3 glass. Opt. Laser Technol. 2016, 78, 56–61. [Google Scholar] [CrossRef]
- Masselin, P.; Bychkov, E.; Le Coq, D. Direct laser writing of a low-loss waveguide with independent control over the transverse dimension and the refractive index contrast between the core and the cladding. Opt. Lett. 2016, 41, 3507–3510. [Google Scholar] [CrossRef] [PubMed]
- Almeida, J.M.P.; Barbano, E.C.; Arnold, C.B.; Misoguti, L.; Mendonça, C.R. Nonlinear optical waveguides in As2S3-Ag2S chalcogenide glass thin films. Opt. Mater. Express 2017, 7, 93–99. [Google Scholar] [CrossRef]
- Riul, A.; de Sousa, H.C.; Malmegrim, R.R.; dos Santos, D.S.; Carvalho, A.; Fonseca, F.J.; Oliveira, O.N.; Mattoso, L.H.C. Wine classification by taste sensors made from ultra-thin films and using neural networks. Sens. Actuators B Chem. 2004, 98, 77–82. [Google Scholar] [CrossRef]
- Legin, A.; Rudnitskaya, A.; Vlasov, Y.; Di Natale, C.; Davide, F.; D’Amico, A. Tasting of beverages using an electronic tongue. Sens. Actuators B Chem. 1997, 44, 291–296. [Google Scholar] [CrossRef]
- Bueno, L.; Paixao, T.R.L.C. A copper interdigitated electrode and chemometrical tools used for the discrimination of the adulteration of ethanol fuel with water. Talanta 2011, 87, 210–215. [Google Scholar] [CrossRef] [PubMed]
- Kirsanov, D.; Legin, E.; Zagrebin, A.; Ignatieva, N.; Rybakin, V.; Legin, A. Mimicking Daphnia magna bioassay performance by an electronic tongue for urban water quality control. Anal. Chim. Acta 2014, 824, 64–70. [Google Scholar] [CrossRef] [PubMed]
- Kudryashov, S.I.; Ionin, A.A. Multi-scale fluence-dependent dynamics of front-side femtosecond laser heating, melting and ablation of thin supported aluminum film. Int. J. Heat Mass Transf. 2016, 99, 383–390. [Google Scholar] [CrossRef]
- Manzoli, A.; de Almeida, G.F.B.; Filho, J.A.; Mattoso, L.H.C.; Riul, A., Jr.; Mendonca, C.R.; Correa, D.S. Femtosecond laser ablation of gold interdigitated electrodes for electronic tongues. Opt. Laser Technol. 2015, 69, 148–153. [Google Scholar] [CrossRef]
- Wang, A.D.; Jiang, L.; Li, X.W.; Liu, Y.; Dong, X.Z.; Qu, L.T.; Duan, X.M.; Lu, Y.F. Mask-free patterning of high.-conductivity metal. nanowires in open air by spatially modulated femtosecond laser pulses. Adv. Mater. 2015, 27, 6238–6243. [Google Scholar] [CrossRef] [PubMed]
- Riul, A., Jr.; Dantas, C.A.R.; Miyazaki, C.M.; Oliveira, O.N., Jr. Recent advances in electronic tongues. Analyst 2010, 135, 2481–2495. [Google Scholar] [CrossRef] [PubMed]
- Martin, J.I.; Nogues, J.; Liu, K.; Vicent, J.L.; Schuller, I.K. Ordered magnetic nanostructures: Fabrication and properties. J. Magn. Magn. Mater. 2003, 256, 449–501. [Google Scholar] [CrossRef]
- Mijatovic, D.; Eijkel, J.C.T.; van den Berg, A. Technologies for nanofluidic systems: Top-down vs. bottom-up—A review. Lab. Chip 2005, 5, 492–500. [Google Scholar] [CrossRef] [PubMed]
- Wu, C.; Crouch, C.H.; Zhao, L.; Carey, J.E.; Younkin, R.; Levinson, J.A.; Mazur, E.; Farrell, R.M.; Gothoskar, P.; Karger, A. Near-unity below-band-gap absorption by microstructured silicon. Appl. Phys. Lett. 2001, 78, 1850–1852. [Google Scholar] [CrossRef]
- Carey, J.E.; Crouch, C.H.; Shen, M.Y.; Mazur, E. Visible and near-infrared responsivity of femtosecond-laser microstructured silicon photodiodes. Opt. Lett. 2005, 30, 1773–1775. [Google Scholar] [CrossRef] [PubMed]
- Huang, Z.H.; Carey, J.E.; Liu, M.G.; Guo, X.Y.; Mazur, E.; Campbell, J.C. Microstructured silicon photodetector. Appl. Phys. Lett. 2006, 89. [Google Scholar] [CrossRef]
- Iyengar, V.V.; Nayak, B.K.; Gupta, M.C. Optical properties of silicon light trapping structures for photovoltaics. Sol. Energy Mater. Sol. Cells 2010, 94, 2251–2257. [Google Scholar] [CrossRef]
- Nayak, B.K.; Iyengar, V.V.; Gupta, M.C. Efficient light trapping in silicon solar cells by ultrafast-laser-induced self-assembled micro/nano structures. Prog. Photovolt. 2011, 19, 631–639. [Google Scholar] [CrossRef]
- Almeida, G.F.B.; Cardoso, M.R.; Aoki, P.H.B.; Lima, J.J.D., Jr.; Costa, L.D.F.; Rodrigues, C.A.; Constantino, C.J.L.; Mendonca, C.R. Surface morphology and structural modification induced by femtosecond pulses in hydrogenated amorphous silicon films. J. Nanosci. Nanotechnol. 2015, 15, 2495–2500. [Google Scholar] [CrossRef] [PubMed]
- Her, T.H.; Finlay, R.J.; Wu, C.; Mazur, E. Femtosecond laser-induced formation of spikes on silicon. Appl. Phys. A Mater. Sci. Process. 2000, 70, 383–385. [Google Scholar] [CrossRef]
- Crouch, C.H.; Carey, J.E.; Warrender, J.M.; Aziz, M.J.; Mazur, E.; Genin, F.Y. Comparison of structure and properties of femtosecond and nanosecond laser-structured silicon. Appl. Phys. Lett. 2004, 84, 1850–1852. [Google Scholar] [CrossRef]
- Korchagina, T.T.; Gutakovsky, A.K.; Fedina, L.I.; Neklyudova, M.A.; Volodin, V.A. Crystallization of amorphous Si nanoclusters in SiOx films using femtosecond laser pulse annealings. J. Nanosci. Nanotechnol. 2012, 12, 8694–8699. [Google Scholar] [CrossRef] [PubMed]
- Belik, V.P.; Vasyutinskii, O.S.; Kukin, A.V.; Petrov, M.A.; Popov, R.S.; Terukov, E.I. Crystallization of amorphous hydrogenated silicon (a-Si:H) films under irradiation with femtosecond laser pulses. Tech. Phys. Lett. 2016, 42, 788–791. [Google Scholar] [CrossRef]
- Costa, L.D.; Rodrigues, C.A.; de Souza, N.C.; Oliveira, O.N. Statistical characterization of morphological features of layer-by-layer polymer films by image analysis. J. Nanosci. Nanotechnol. 2003, 3, 257–261. [Google Scholar] [CrossRef]
- Liu, X.B. Industrial applications of ultrahigh precision short-pulse laser processing. In Proceedings of Processing in Microelectronics and Photonics IV, San Jose, CA, USA, 22 January 2005.
- Iga, Y.; Ishizuka, T.; Watanabe, W.; Itoh, K.; Li, Y.; Nishii, J. Characterization of micro-channels fabricated by in-water ablation of femtosecond laser pulses. Jpn. J. Appl. Phys. Part 1 2004, 43, 4207–4211. [Google Scholar] [CrossRef]
- Hnatovsky, C.; Taylor, R.S.; Simova, E.; Bhardwaj, V.R.; Rayner, D.M.; Corkum, P.B. Polarization-selective etching in femtosecond laser-assisted microfluidic channel fabrication in fused silica. Opt. Lett. 2005, 30, 1867–1869. [Google Scholar] [CrossRef] [PubMed]
- Ho, S.; Herman, P.R.; Aitchison, J.S. Single- and multi-scan femtosecond laser writing for selective chemical etching of cross section patternable glass micro-channels. Appl. Phys. A Mater. Sci. Process. 2012, 106, 5–13. [Google Scholar] [CrossRef]
- Cheng, G.H.; Wang, Y.S.; Liu, Q.; Zhao, W.; Chen, G.F. Study of three-dimensional storage by parallel writing in PMMA with femtosecond laser pulses. Acta Phys. Sin. 2004, 53, 436–440. [Google Scholar]
- Streltsov, A.M.; Borrelli, N.F. Fabrication and analysis of a directional coupler written in glass by nanojoule femtosecond laser pulses. Opt. Lett. 2001, 26, 42–43. [Google Scholar] [CrossRef] [PubMed]
- Minoshima, K.; Kowalevicz, A.M.; Ippen, E.P.; Fujimoto, J.G. Fabrication of coupled mode photonic devices in glass by nonlinear femtosecond laser materials processing. Opt. Express 2002, 10, 645–652. [Google Scholar] [CrossRef] [PubMed]
- Taccheo, S.; Della Valle, G.; Osellame, R.; Cerullo, G.; Chiodo, N.; Laporta, P.; Svelto, O.; Killi, A.; Morgner, U.; Lederer, M.; et al. Er: Yb-doped waveguide laser fabricated by femtosecond laser pulses. Opt. Lett. 2004, 29, 2626–2628. [Google Scholar] [CrossRef] [PubMed]









© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license ( http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Correa, D.S.; Almeida, J.M.P.; Almeida, G.F.B.; Cardoso, M.R.; De Boni, L.; Mendonça, C.R. Ultrafast Laser Pulses for Structuring Materials at Micro/Nano Scale: From Waveguides to Superhydrophobic Surfaces. Photonics 2017, 4, 8. https://doi.org/10.3390/photonics4010008
Correa DS, Almeida JMP, Almeida GFB, Cardoso MR, De Boni L, Mendonça CR. Ultrafast Laser Pulses for Structuring Materials at Micro/Nano Scale: From Waveguides to Superhydrophobic Surfaces. Photonics. 2017; 4(1):8. https://doi.org/10.3390/photonics4010008
Chicago/Turabian StyleCorrea, Daniel S., Juliana M. P. Almeida, Gustavo F. B. Almeida, Marcos R. Cardoso, Leonardo De Boni, and Cleber R. Mendonça. 2017. "Ultrafast Laser Pulses for Structuring Materials at Micro/Nano Scale: From Waveguides to Superhydrophobic Surfaces" Photonics 4, no. 1: 8. https://doi.org/10.3390/photonics4010008
APA StyleCorrea, D. S., Almeida, J. M. P., Almeida, G. F. B., Cardoso, M. R., De Boni, L., & Mendonça, C. R. (2017). Ultrafast Laser Pulses for Structuring Materials at Micro/Nano Scale: From Waveguides to Superhydrophobic Surfaces. Photonics, 4(1), 8. https://doi.org/10.3390/photonics4010008





