Development of Sub 10 fs Visible-NIR, UV, and DUV Pulses and Their Applications to Ultrafast Spectroscopy
Abstract
:1. Generation of Ultrashort Laser Pulse
1.1. Basics of Nonlinear Optical Processes
1.1.1. Nonlinear Optical Processes and Nonlinear Susceptibilities
(i) Case I: NLO Processes Involving Only Virtual States
(ii) Case II: NLO Processes Involving Only Real States
1.1.2. Optical Parametric Amplification (OPA)
1.2. Visible Ultrashort Pulse Generation by Non-Collinear Optical Parametric Amplification
2. Spectroscopic Application of the Ultrashort Laser Pulses
2.1. Ultrafast Time-Resolved Spectroscopy Using Visible Pulses
2.1.1. Fastscan Time-Resolved Transient Absorption Spectroscopy System
2.1.2. Ultrafast Electronic and Vibrational Dynamics Measured Using Visible Pulse
2.2. UV and DUV Pulse Generation and Spectroscopy
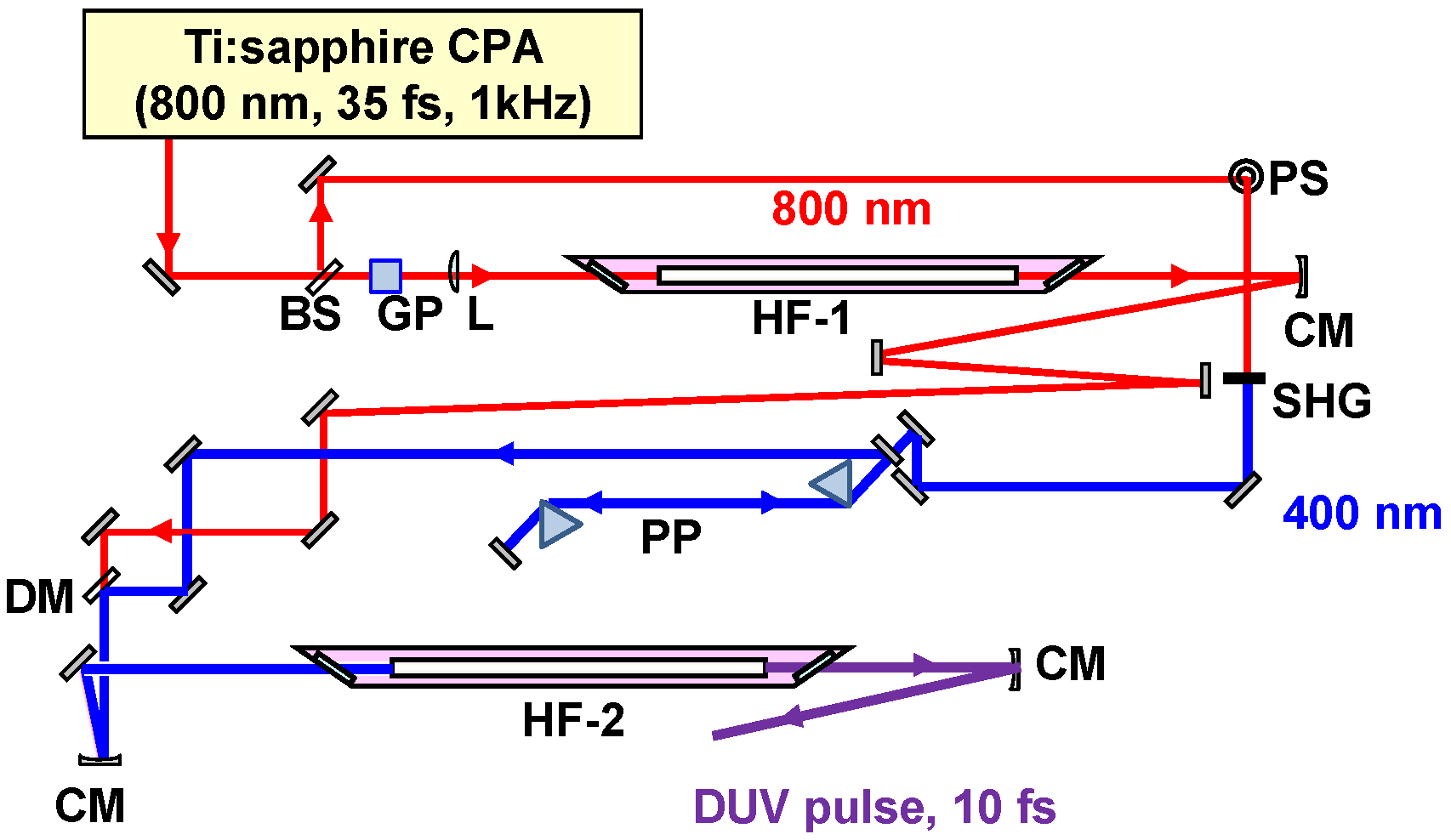
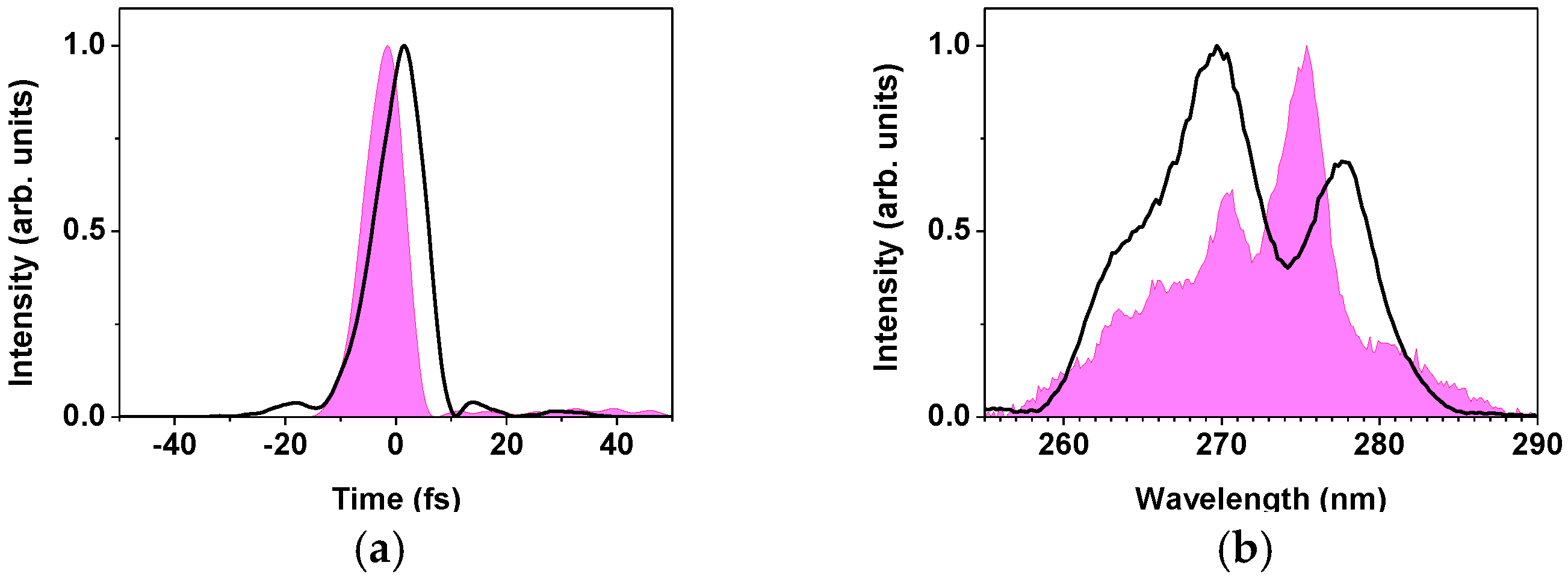
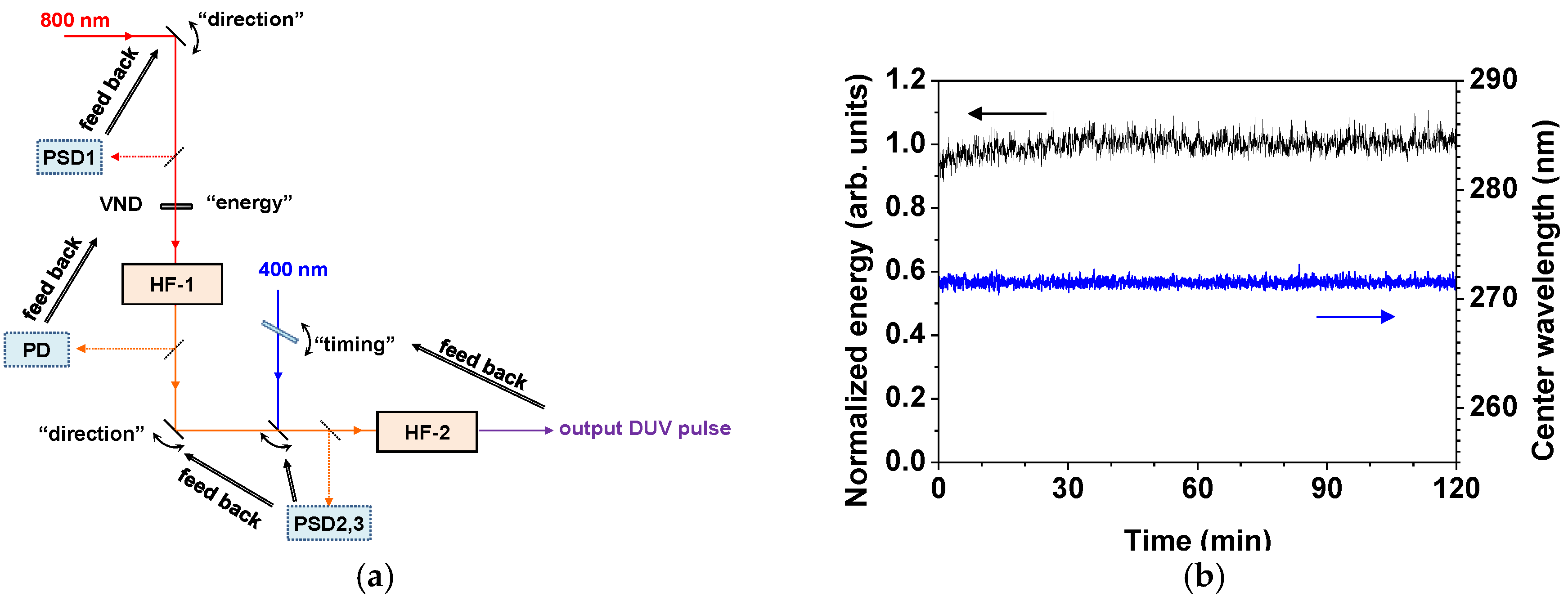
2.2.1. Sub-10-fs Deep-Ultraviolet Light Source
2.2.2. Stabilization of the Light Source
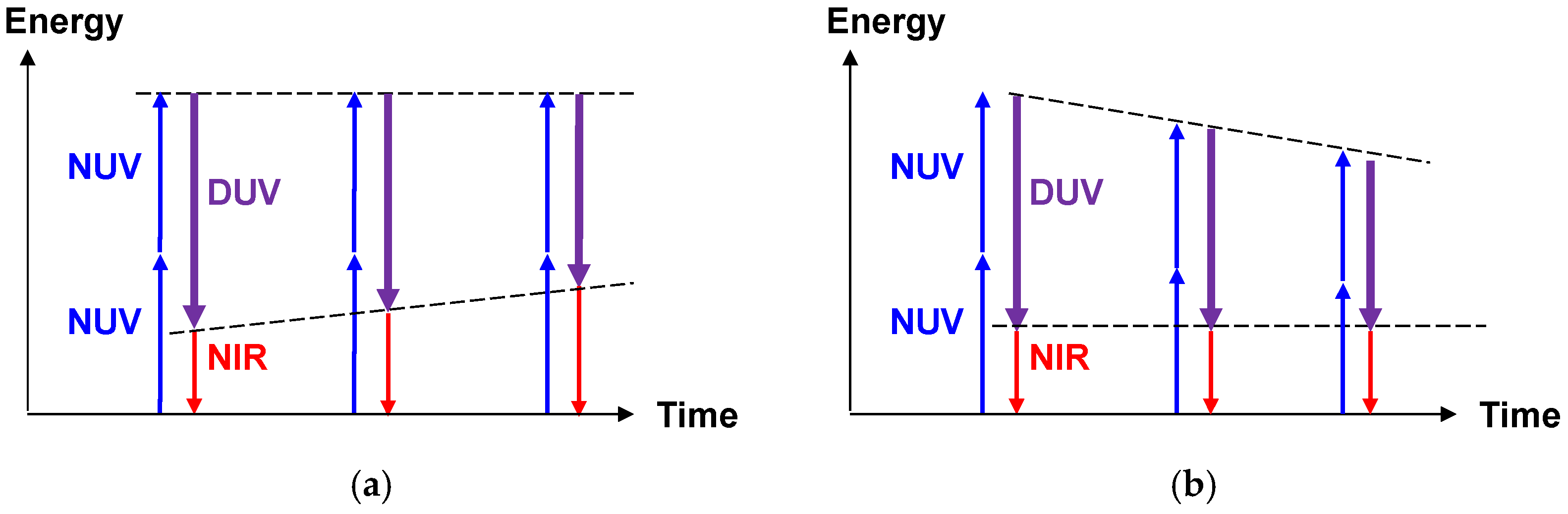
2.2.3. Spectroscopic Applications of the Light Source
Author Contributions
Conflicts of Interest
References
- Norrish, R.G.W.; Porter, G. Chemical reactions produced by very high light intensities. Nature 1949, 164, 658. [Google Scholar] [CrossRef]
- Maiman, T.H. Stimulated Optical Radiation in Ruby. Nature 1960, 187, 493–494. [Google Scholar] [CrossRef]
- Lamb, W.E. Theory of an optical maser. Phys. Rev. 1964, 134, A1429–A1450. [Google Scholar] [CrossRef]
- Polanyi, J.C.; Zewail, A.H. Direct Observation of the Transition State. Acc. Chem. Res. 1995, 28, 119–132. [Google Scholar] [CrossRef]
- Chosrowjan, H.; Mataga, N.; Shibata, Y.; Tachibanaki, S.; Kandori, H.; Shichida, Y.; Okada, T.; Kouyama, T. Rhodopsin Emission in Real Time: A New Aspect of the Primary Event in Vision. J. Am. Chem. Soc. 1998, 120, 9706–9707. [Google Scholar] [CrossRef]
- Pellegrino, F. Ultrafast energy transfer processes in photosynthetic systems probed by picosecond fluorescence spectroscopy. Opt. Eng. 1983, 22, 508–520. [Google Scholar] [CrossRef]
- Boyer, A.; Déry, M.; Selles, P.; Arbour, C.; Boucher, F. Colour discrimination by forward and reverse photocurrents in bacteriorhodopsin-based photosensor. Biosens. Bioelectron. 1995, 10, 415–422. [Google Scholar] [CrossRef]
- Hellingwerf, K.J.; Hendriks, J.; Gensch, T. On the Configurational and Conformational Changes in Photoactive Yellow Protein that Leads to Signal Generation in Ectothiorhodospira halophila. J. Biol. Phys. 2002, 28, 395–412. [Google Scholar] [CrossRef] [PubMed]
- Imamoto, Y.; Kataoka, M. Structure and photoreaction of photoactive yellow protein, a structural prototype of the PAS domain superfamily. Photochem. Photobiol. 2007, 83, 40–49. [Google Scholar] [CrossRef] [PubMed]
- Kuhnert, L. A new optical photochemical memory device in a light-sensitive chemical active medium. Nature 1986, 319, 393–394. [Google Scholar] [CrossRef]
- Ikeda, T.; Horiuchi, S.; Karanjit, D.B.; Kurihara, S.; Tazuke, S. Photochemical Image Storage in Polymer Liquid Crystals. Chem. Lett. 1988, 17, 1679–1682. [Google Scholar] [CrossRef]
- Korolev, N.E.; Mokienko, I.Y.; Poletimov, A.E.; Shcheulin, A.S. Optical storage material based on doped fluoride crystals. Phys. Status Solidi 1991, 127, 327–333. [Google Scholar] [CrossRef]
- De Waele, V.; Schmidhammer, U.; Mrozek, T.; Daub, J.; Riedle, E. Ultrafast bidirectional dihydroazulene/vinylheptafulvene (DHA/VHF) molecular switches: Photochemical ring closure of vinylheptafulvene proven by a two-pulse experiment. J. Am. Chem. Soc. 2002, 124, 2438–2439. [Google Scholar] [CrossRef] [PubMed]
- Hulin, D.; Mysyrowicz, A.; Antonetti, A.; Migus, A.; Masselink, W.T.; Morkoç, H.; Gibbs, H.M.; Peyghambarian, N. Ultrafast all-optical gate with subpicosecond ON and OFF response time. Appl. Phys. Lett. 1986, 49, 749. [Google Scholar] [CrossRef]
- Eichmann, G.; Li, Y.; Alfano, R.R. Optical binary coded ternary arithmetic and logic. Appl. Opt. 1986, 25, 3113. [Google Scholar] [CrossRef] [PubMed]
- Wilhelm, T.; Piel, J.; Riedle, E. Sub-20-fs pulses tunable across the visible from a blue-pumped single-pass noncollinear parametric converter. Opt. Lett. 1997, 22, 1494. [Google Scholar] [CrossRef] [PubMed]
- Cerullo, G.; Nisoli, M.; Stagira, S.; De Silvestri, S. Sub-8-fs pulses from an ultrabroadband optical parametric amplifier in the visible. Opt. Lett. 1998, 23, 1283–1285. [Google Scholar] [CrossRef] [PubMed]
- Kobayashi, T.; Shirakawa, A. Tunable visible and near-infrared pulse generator in a 5 fs regime. Appl. Phys. B Lasers Opt. 2000, 70, S239–S246. [Google Scholar] [CrossRef]
- Yabushita, A.; Lee, Y.-H.; Kobayashi, T. Development of a multiplex fast-scan system for ultrafast time-resolved spectroscopy. Rev. Sci. Instrum. 2010, 81, 63110. [Google Scholar] [CrossRef] [PubMed]
- Yabushita, A.; Kao, C.-H.; Lee, Y.-H.; Kobayashi, T. Development and demonstration of table-top synchronized fast-scan femtosecond time-resolved spectroscopy system by single-shot scan photo detector array. Jpn. J. Appl. Phys. 2015, 54, 072401. [Google Scholar] [CrossRef]
- Baum, P.; Lochbrunner, S.; Riedle, E. Tunable sub-10-fs ultraviolet pulses generated by achromatic frequency doubling. Opt. Lett. 2004, 29, 1686–1688. [Google Scholar] [CrossRef] [PubMed]
- Durfee, C.G.; Backus, S.; Kapteyn, H.C.; Murnane, M.M. Intense 8-fs pulse generation in the deep ultraviolet. Opt. Lett. 1999, 24, 697–699. [Google Scholar] [CrossRef] [PubMed]
- Trushin, S.A.; Kosma, K.; Fuß, W.; Schmid, W.E. Sub-10-fs supercontinuum radiation generated by filamentation of few-cycle 800 nm pulses in argon. Opt. Lett. 2007, 32, 2432–2434. [Google Scholar] [CrossRef] [PubMed]
- Graf, U.; Fieß, M.; Schultze, M.; Kienberger, R.; Krausz, F.; Goulielmakis, E. Intense few-cycle light pulses in the deep ultraviolet. Opt. Express 2008, 16, 18956–18963. [Google Scholar] [CrossRef] [PubMed]
- Reiter, F.; Graf, U.; Schultze, M.; Schweinberger, W.; Schröder, H.; Karpowicz, N.; Azzeer, A.M.; Kienberger, R.; Krausz, F.; Goulielmakis, E. Generation of sub-3 fs pulses in the deep ultraviolet. Opt. Lett. 2010, 35, 2248–2250. [Google Scholar] [CrossRef] [PubMed]
- Kida, Y.; Liu, J.; Teramoto, T.; Kobayashi, T. Sub-10 fs deep-ultraviolet pulses generated by chirped-pulse four-wave mixing. Opt. Lett. 2010, 35, 1807–1809. [Google Scholar] [CrossRef] [PubMed]
- Kosma, K.; Trushin, S.A.; Fuß, W.; Schmid, W.E. Cyclohexadiene ring opening observed with 13 fs resolution: Coherent oscillations confirm the reaction path. Phys. Chem. Chem. Phys. 2009, 11, 172–181. [Google Scholar] [CrossRef] [PubMed]
- Kobayashi, T.; Kida, Y. Ultrafast spectroscopy with sub-10 fs deep-ultraviolet pulses. Phys. Chem. Chem. Phys. 2012, 14, 6200–6210. [Google Scholar] [CrossRef] [PubMed]
- Kida, Y.; Liu, J.; Kobayashi, T. Single 10-fs deep-ultraviolet pulses generated by broadband four-wave mixing and high-order dispersion compensation. Appl. Phys. B 2011, 105, 675–679. [Google Scholar] [CrossRef]
- Wojtkiewicz, J.; Durfee, C.G. Hollow-fiber OP-CPA for energetic ultrafast ultraviolet pulse generation. In Proceedings of the Conference on Lasers and Electro-Optics, Long Beach, CA, USA, 19–22 May 2002; pp. 423–424.
- Wojtkiewicz, J.; Hudek, K.; Durfee, C.C. Chirped-pulse frequency conversion of ultrafast pulses to the deep-UV. In Proceedings of the Conference on Lasers and Electro-Optics, Baltimore, MD, USA, 22 May 2005; pp. 186–188.
- Tzankov, P.; Steinkellner, O.; Zheng, J.; Husakou, A.; Herrmann, J.; Freyer, W.; Petrov, V.; Noack, F. Generation and Compression of Femtosecond Pulses in the Vacuum Ultraviolet by Chirped-Pulse Four-Wave Difference-Frequency Mixing. In Proceedings of the Conference on Lasers and Electro-Optics, Anaheim, CA, USA, 25–29 March 2006.
- Liu, J.; Kobayashi, T. Generation of sub-20-fs multicolor laser pulses using cascaded four-wave mixing with chirped incident pulses. Opt. Lett. 2009, 34, 2402–2404. [Google Scholar] [CrossRef] [PubMed]
- Fork, R.L.; Cruz, C.H.B.; Becker, P.C.; Shank, C.V. Compression of optical pulses to six femtoseconds by using cubic phase compensation. Opt. Lett. 1987, 12, 483–485. [Google Scholar] [CrossRef] [PubMed]
- Nisoli, M.; de Silvestri, S.; Svelto, O. Generation of high energy 10 fs pulses by a new pulse compression technique. Appl. Phys. Lett. 1996, 68, 2793. [Google Scholar] [CrossRef]
- Cavalieri, A.L.; Goulielmakis, E.; Horvath, B.; Helml, W.; Schultze, M.; Fieß, M.; Pervak, V.; Veisz, L.; Yakovlev, V.S.; Uiberacker, M.; et al. Intense 1.5-cycle near infrared laser waveforms and their use for the generation of ultra-broadband soft-x-ray harmonic continua. New J. Phys. 2007, 9, 242. [Google Scholar] [CrossRef]
- Kida, Y.; Kobayashi, T. Generation of sub-10 fs ultraviolet Gaussian pulses. J. Opt. Soc. Am. B 2010, 28, 139–148. [Google Scholar] [CrossRef]
- Kida, Y.; Okamura, K.; Liu, J.; Kobayashi, T. Sub-10-fs deep-ultraviolet light source with stable power and spectrum. Appl. Opt. 2012, 51, 6403–6410. [Google Scholar] [CrossRef] [PubMed]
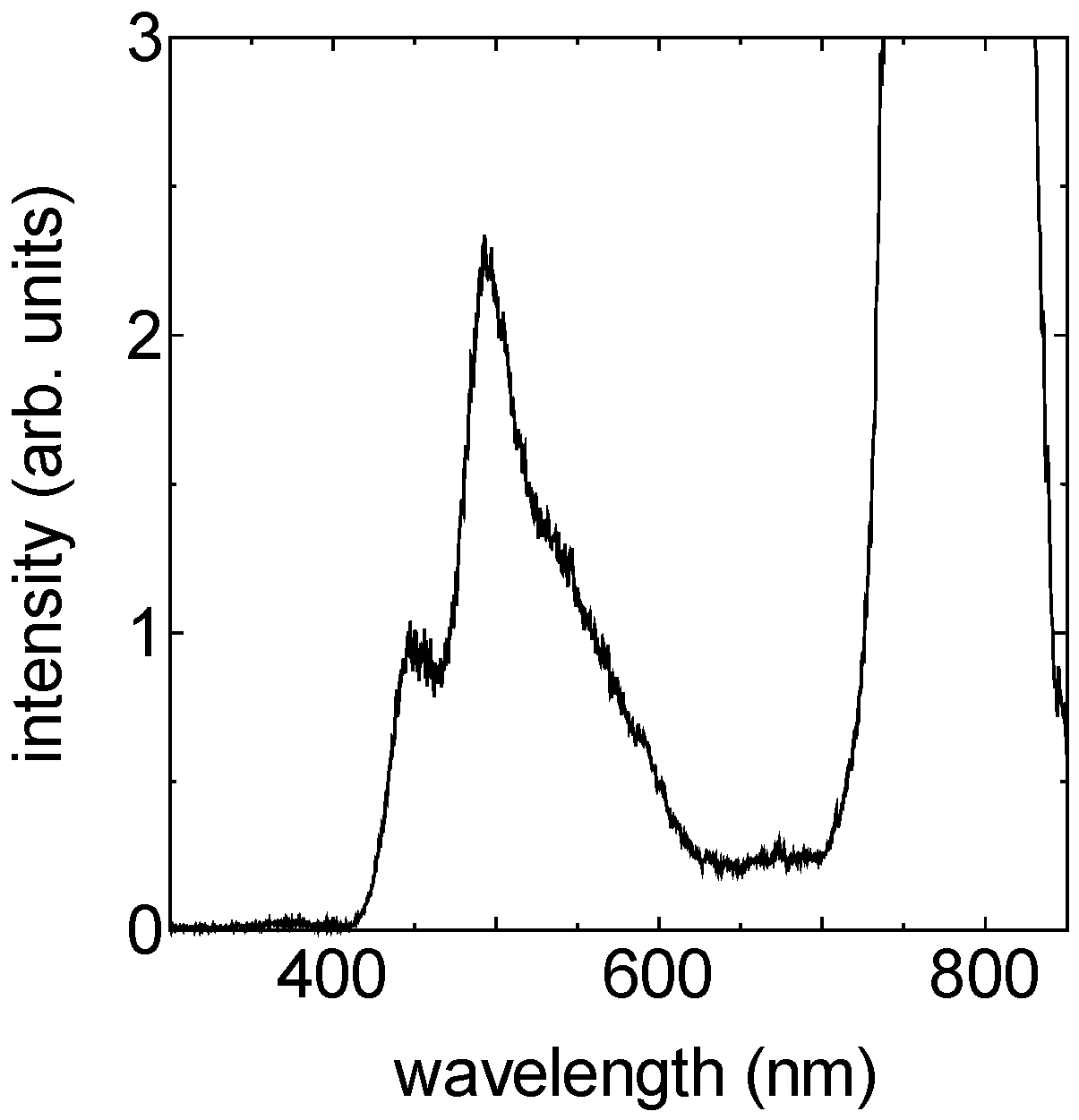
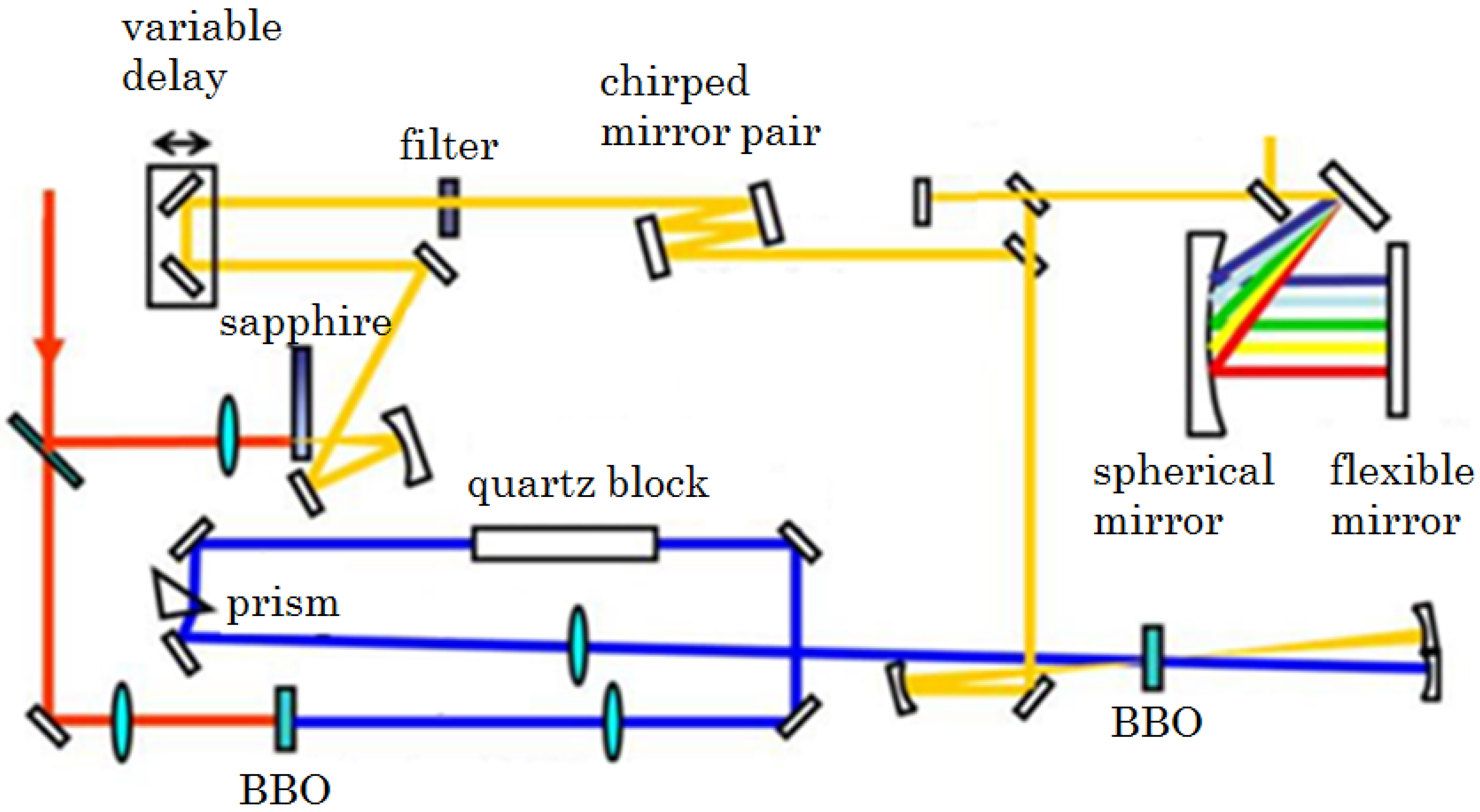
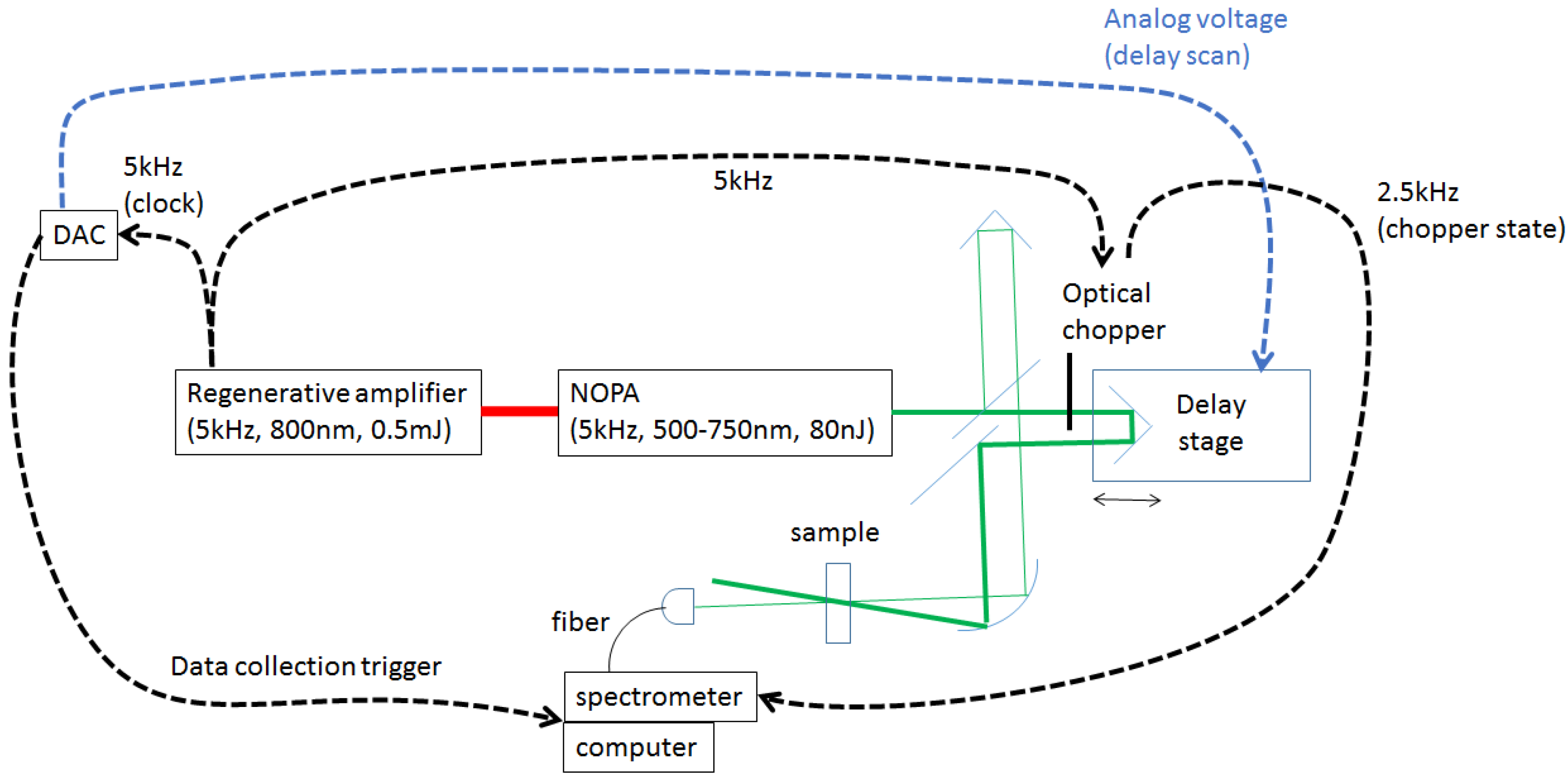
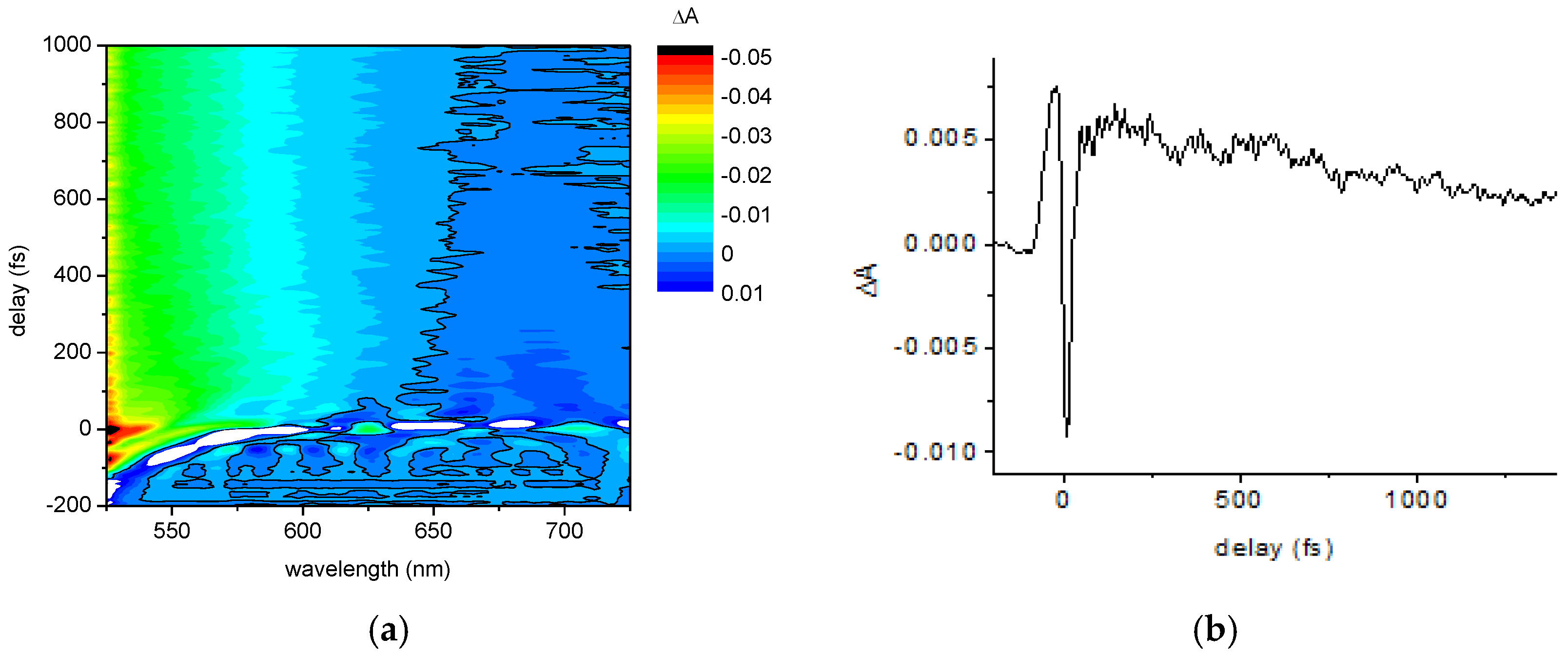
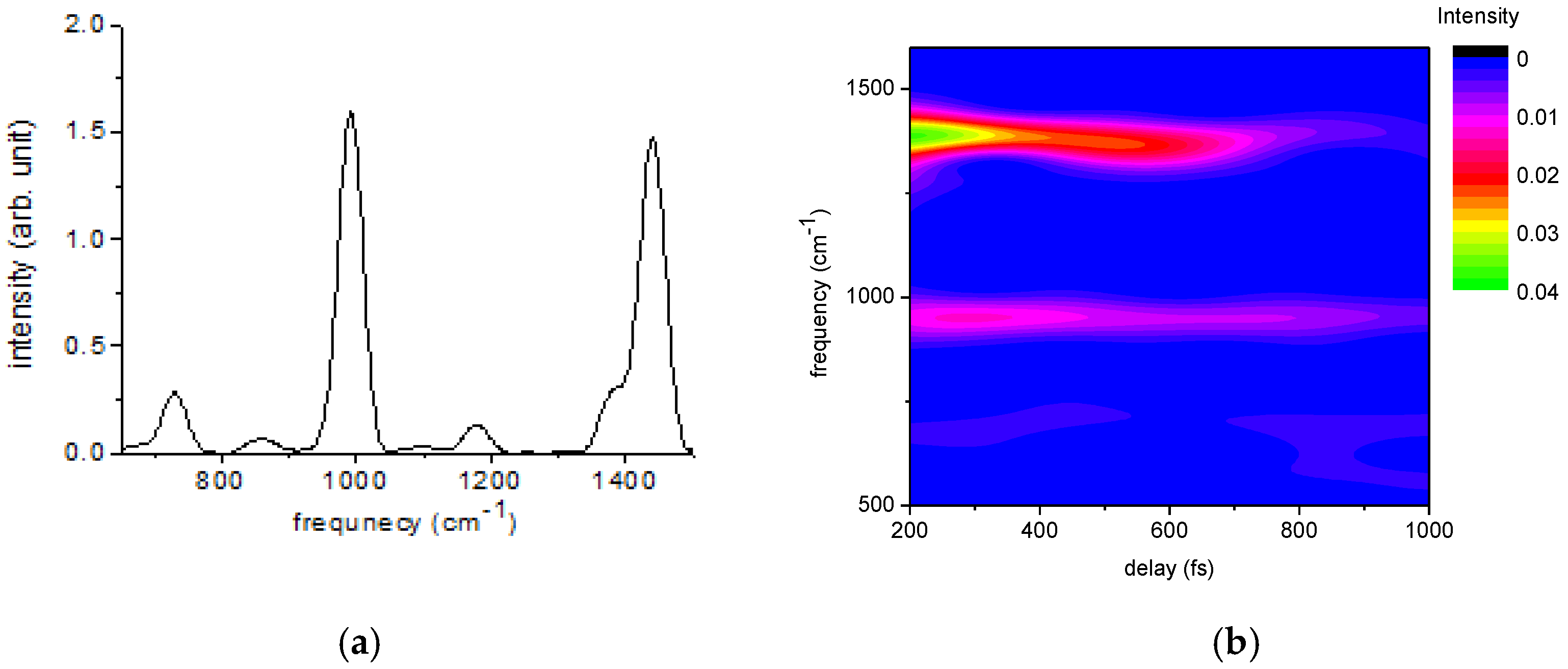
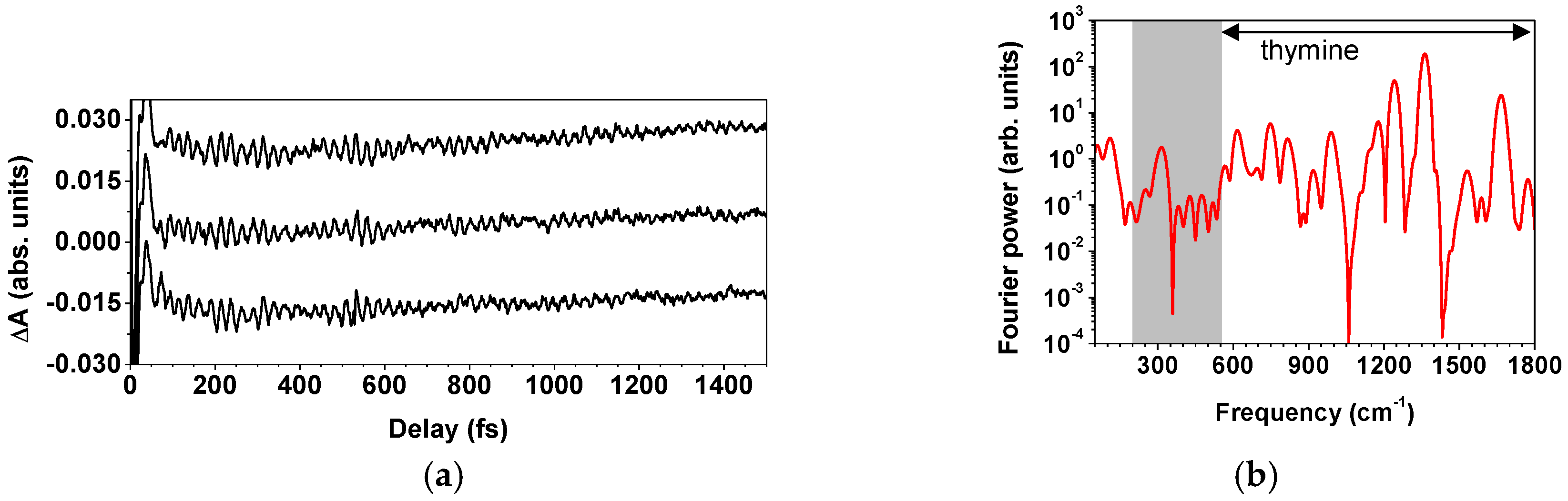
| Frequency (cm−1) | Amplitude | Lifetime (fs) | Origin |
|---|---|---|---|
| 1439 | 37 | 527 | P3HT |
| 991 | 15 | 2117 | benzene |
| 1378 | 11 | 875 | P3HT |
| 1174 | 3 | 3705 | benzene |
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kobayashi, T.; Yabushita, A.; Kida, Y. Development of Sub 10 fs Visible-NIR, UV, and DUV Pulses and Their Applications to Ultrafast Spectroscopy. Photonics 2016, 3, 64. https://doi.org/10.3390/photonics3040064
Kobayashi T, Yabushita A, Kida Y. Development of Sub 10 fs Visible-NIR, UV, and DUV Pulses and Their Applications to Ultrafast Spectroscopy. Photonics. 2016; 3(4):64. https://doi.org/10.3390/photonics3040064
Chicago/Turabian StyleKobayashi, Takayoshi, Atsushi Yabushita, and Yuichiro Kida. 2016. "Development of Sub 10 fs Visible-NIR, UV, and DUV Pulses and Their Applications to Ultrafast Spectroscopy" Photonics 3, no. 4: 64. https://doi.org/10.3390/photonics3040064
APA StyleKobayashi, T., Yabushita, A., & Kida, Y. (2016). Development of Sub 10 fs Visible-NIR, UV, and DUV Pulses and Their Applications to Ultrafast Spectroscopy. Photonics, 3(4), 64. https://doi.org/10.3390/photonics3040064







