XUV Transient Absorption Spectroscopy: Probing Laser-Perturbed Dipole Polarization in Single Atom, Macroscopic, and Molecular Regimes
Abstract
:1. Introduction
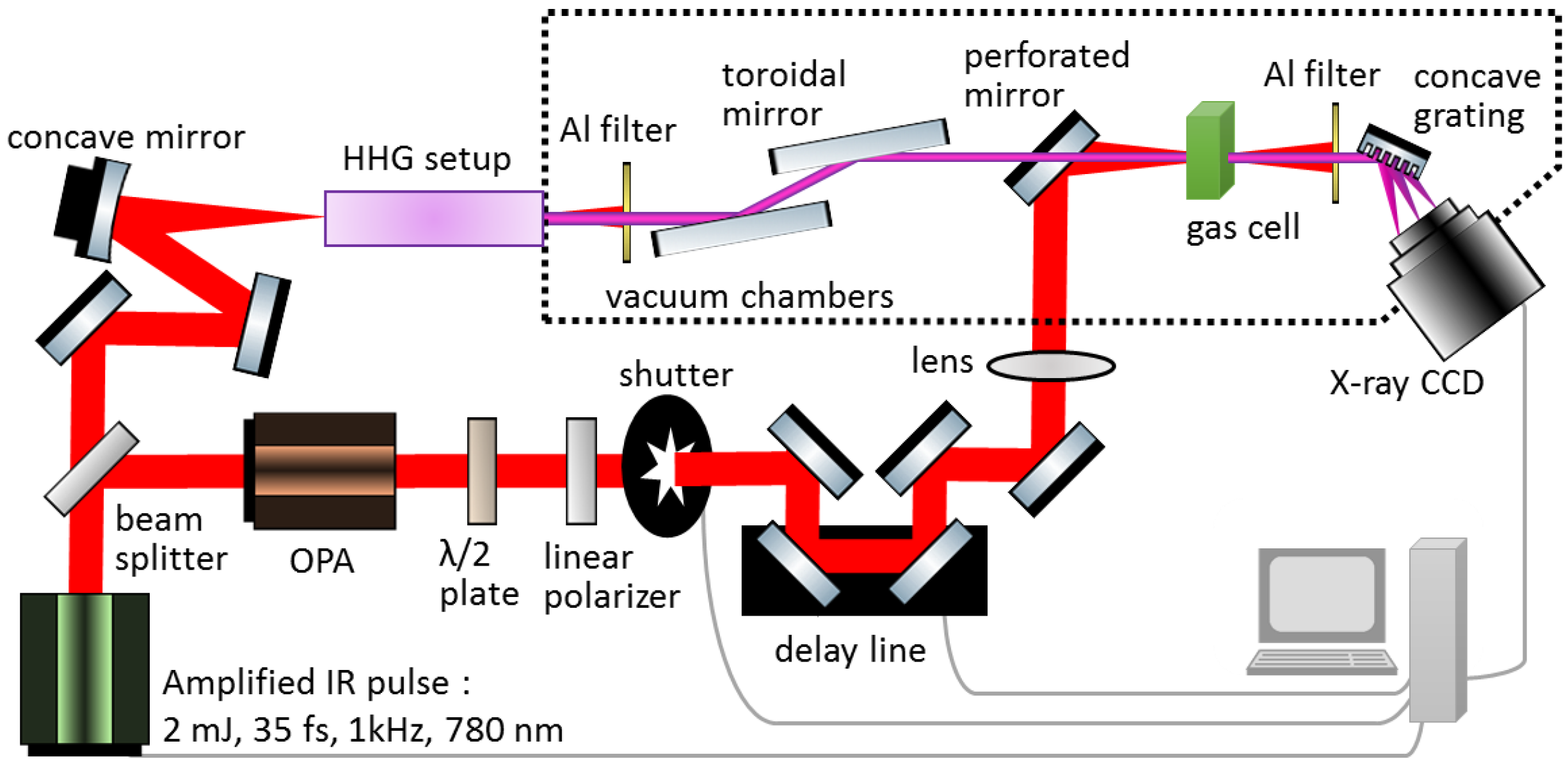
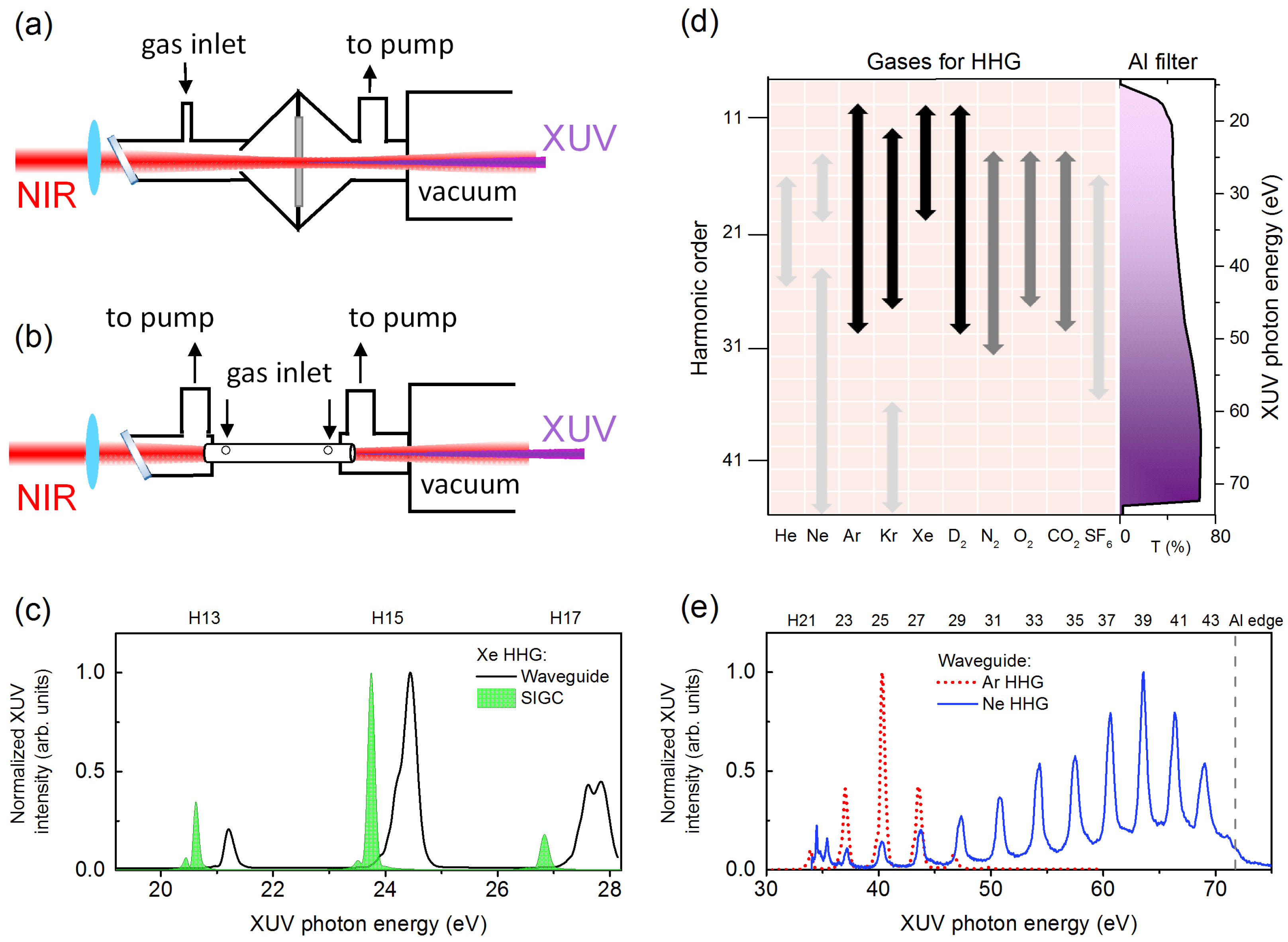
2. Experimental Methods
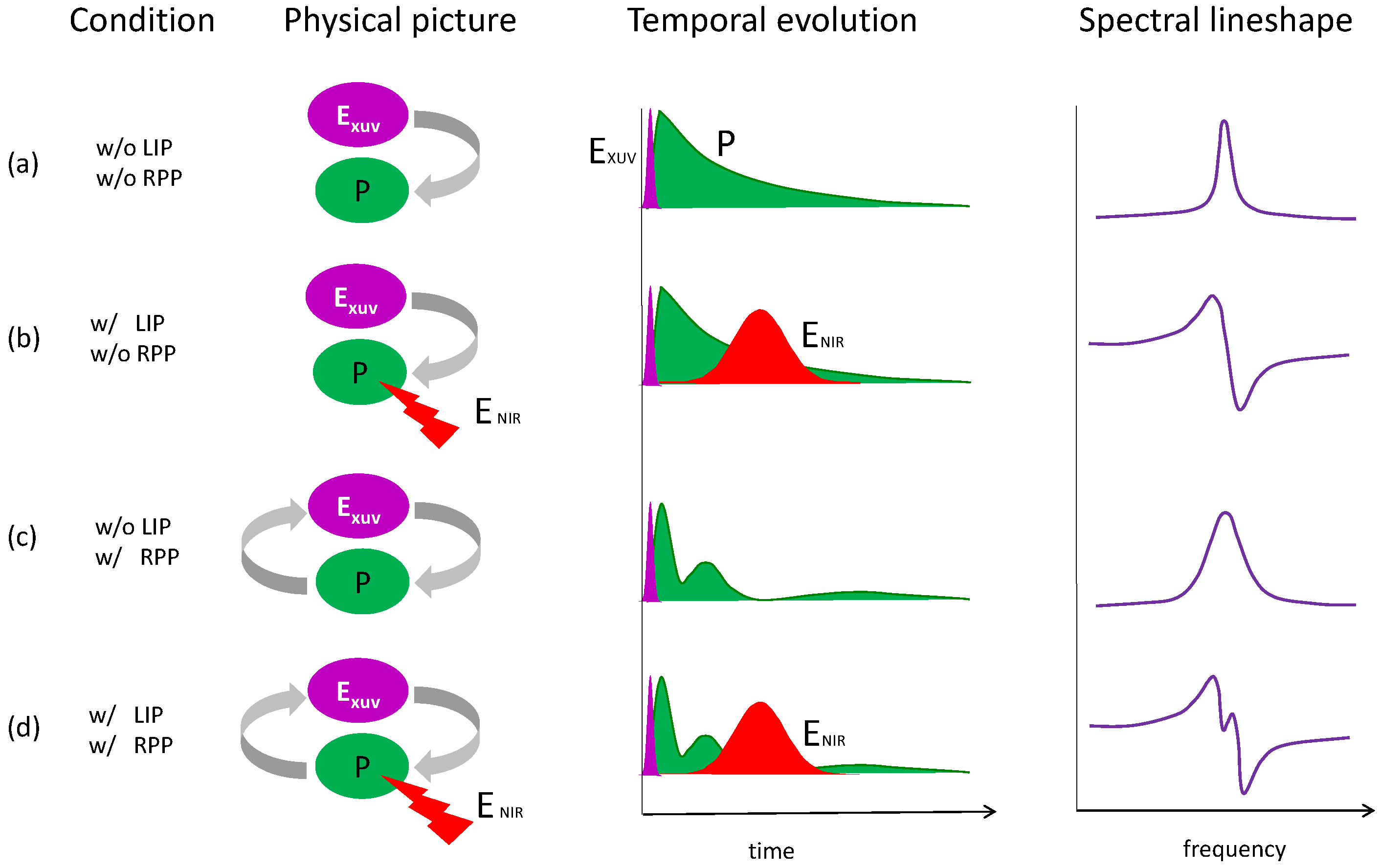
3. Laser Modification of Dipole Polarization in Helium: Temporal and Spectral Properties
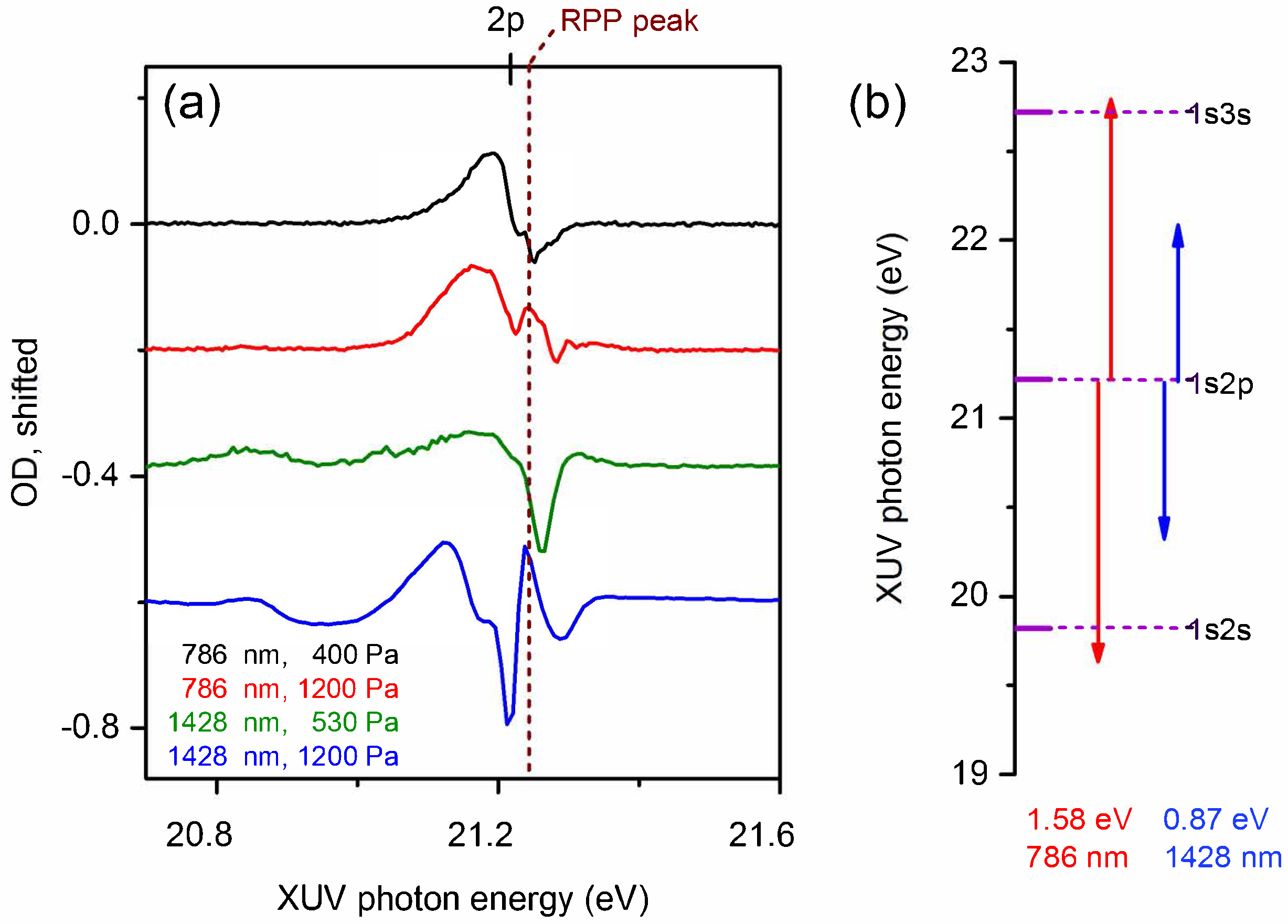
4. Laser Modification of Dipole Polarization in Helium: Pressure and Wavelength Dependence
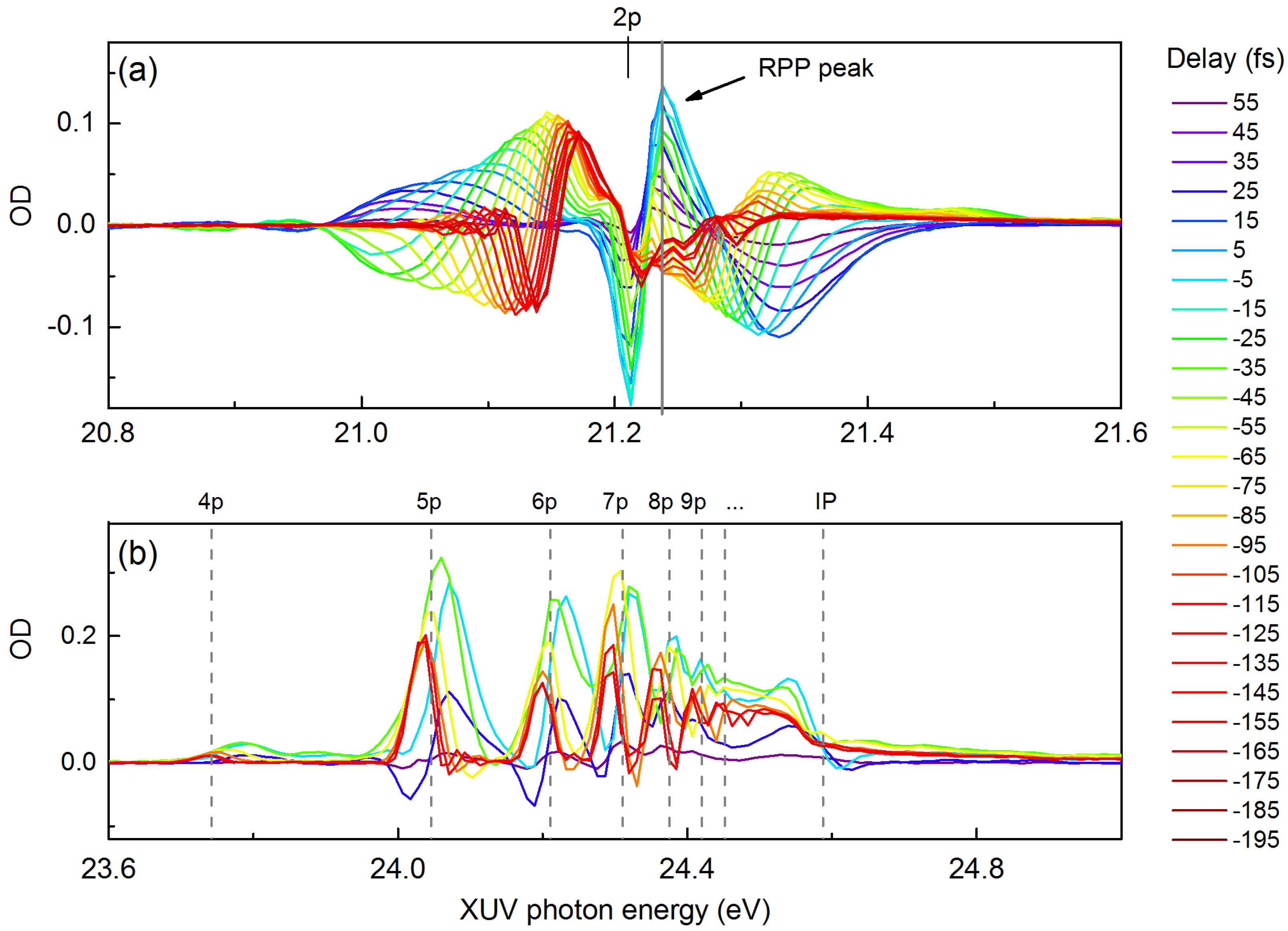
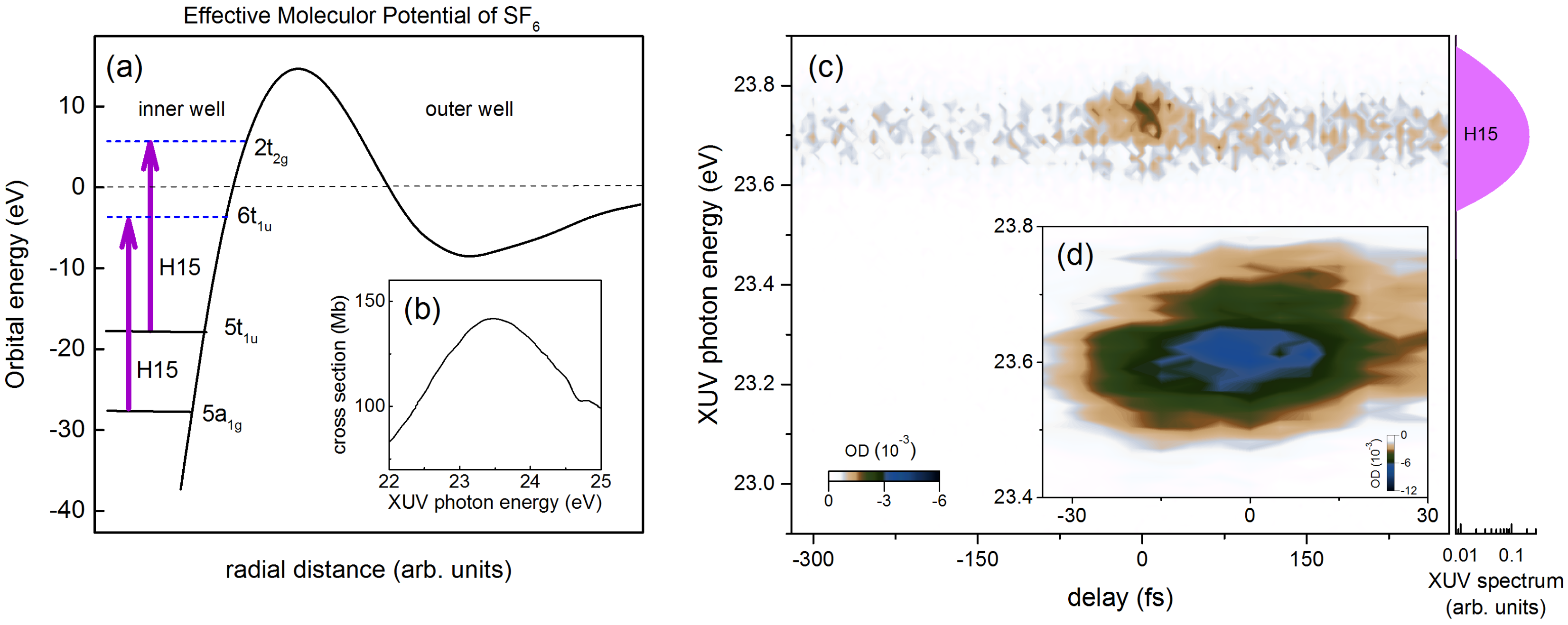
5. Probing Dipole Polarization in a Polyatomic SF Molecule
6. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
Abbreviations
| APTs | attosecond pulse trains |
| ATAS | attosecond transient absorption spectroscopy |
| FID | free-induction decay |
| FWHM | full width at half maximum |
| H13 | 13th harmonics |
| H15 | 15th harmonics |
| H17 | 17th harmonics |
| HHG | high-harmonic generation |
| LICS | laser-induced continuum structure |
| LIP | laser-induced phase |
| NIR | near infrared |
| OD | optical density |
| OPA | optical parametric amplifier |
| SIGC | semi-infinite gas cell |
| RPP | resonant pulse propagation |
| XUV | extreme ultraviolet |
References
- Sarovar, M.; Ishizaki, A.; Fleming, G.R.; Whaley, K.B. Quantum entanglement in photosynthetic light-harvesting complexes. Nat. Phys. 2010, 6, 462–467. [Google Scholar] [CrossRef]
- Presti, D.; Delbrück, M. Photoreceptors for biosynthesis, energy storage and vision. Plant Cell Environ. 1978, 1, 81–100. [Google Scholar] [CrossRef]
- Li, B.; Zhao, J.; Onda, K.; Jordan, K.D.; Yang, J.; Petek, H. Ultrafast interfacial proton-coupled electron transfer. Science 2006, 311, 1436–1440. [Google Scholar] [CrossRef] [PubMed]
- Belsley, M. Ultrafast spectroscopy: Quantum information and wavepackets, by Joel Yuen-Zhou, Jacob J. Krich, Ivan Kassal, Allan S. Johnson and Alán Aspuru-Guzik: Scope: Monograph. Level: Postgraduate, early career researcher, researcher, specialist. Contemp. Phys. 2016, 57, 281–282. [Google Scholar] [CrossRef]
- Reid, D.T.; Heyl, C.M.; Thomson, R.R.; Trebino, R.; Steinmeyer, G.; Fielding, H.H.; Holzwarth, R.; Zhang, Z.; Del’Haye, P.; Südmeyer, T.; et al. Roadmap on ultrafast optics. J. Opt. 2016, 18, 093006. [Google Scholar] [CrossRef]
- Miao, J.; Ishikawa, T.; Robinson, I.K.; Murnane, M.M. Beyond crystallography: Diffractive imaging using coherent X-ray light sources. Science 2015, 348, 530–535. [Google Scholar] [CrossRef] [PubMed]
- Krause, J.L.; Schafer, K.J.; Kulander, K.C. High-order harmonic generation from atoms and ions in the high intensity regime. Phys. Rev. Lett. 1992, 68, 3535. [Google Scholar] [CrossRef] [PubMed]
- Corkum, P.B. Plasma perspective on strong field multiphoton ionization. Phys. Rev. Lett. 1993, 71, 1994. [Google Scholar] [CrossRef] [PubMed]
- Chini, M.; Zhao, B.; Wang, H.; Cheng, Y.; Hu, S.; Chang, Z. Subcycle ac stark shift of helium excited states probed with isolated attosecond pulses. Phys. Rev. Lett. 2012, 109, 073601. [Google Scholar] [CrossRef] [PubMed]
- Chen, S.; Bell, M.J.; Beck, A.R.; Mashiko, H.; Wu, M.; Pfeiffer, A.N.; Gaarde, M.B.; Neumark, D.M.; Leone, S.R.; Schafer, K.J. Light-induced states in attosecond transient absorption spectra of laser-dressed helium. Phys. Rev. A 2012, 86, 063408. [Google Scholar] [CrossRef]
- Loh, Z.H.; Greene, C.H.; Leone, S.R. Femtosecond induced transparency and absorption in the extreme ultraviolet by coherent coupling of the He 2s2p (1 Po) and 2p 2 (1 Se) double excitation states with 800 nm light. Chem. Phys. 2008, 350, 7–13. [Google Scholar] [CrossRef]
- Holler, M.; Schapper, F.; Gallmann, L.; Keller, U. Attosecond electron wave-packet interference observed by transient absorption. Phys. Rev. Lett. 2011, 106, 123601. [Google Scholar] [CrossRef]
- Ott, C.; Kaldun, A.; Raith, P.; Meyer, K.; Laux, M.; Evers, J.; Keitel, C.H.; Greene, C.H.; Pfeifer, T. Lorentz meets Fano in spectral line shapes: a universal phase and its laser control. Science 2013, 340, 716–720. [Google Scholar] [CrossRef] [PubMed]
- Liao, C.T.; Sandhu, A.; Camp, S.; Schafer, K.J.; Gaarde, M.B. Beyond the single-atom response in absorption line shapes: probing a dense, laser-dressed helium gas with attosecond pulse trains. Phys. Rev. Lett. 2015, 114, 143002. [Google Scholar] [CrossRef] [PubMed]
- Papadogiannis, N.; Kalpouzos, C.; Goulielmakis, E.; Nersisyan, G.; Charalambidis, D.; Augé, F.; Weihe, F.; Balcou, P. Kilohertz extreme-ultraviolet light source based on femtosecond high-order harmonic generation from noble gases. Appl. Phys. B 2001, 73, 687–692. [Google Scholar] [CrossRef]
- Paul, P.M.; Toma, E.; Breger, P.; Mullot, G.; Augé, F.; Balcou, P.; Muller, H.; Agostini, P. Observation of a train of attosecond pulses from high harmonic generation. Science 2001, 292, 1689–1692. [Google Scholar] [CrossRef] [PubMed]
- Durfee, C.G., III; Rundquist, A.R.; Backus, S.; Herne, C.; Murnane, M.M.; Kapteyn, H.C. Phase matching of high-order harmonics in hollow waveguides. Phys. Rev. Lett. 1999, 83, 2187. [Google Scholar] [CrossRef]
- Rundquist, A.; Durfee, C.G.; Chang, Z.; Herne, C.; Backus, S.; Murnane, M.M.; Kapteyn, H.C. Phase-matched generation of coherent soft X-rays. Science 1998, 280, 1412–1415. [Google Scholar] [CrossRef] [PubMed]
- Henke, B.L.; Gullikson, E.M.; Davis, J.C. X-ray interactions: Photoabsorption, scattering, transmission, and reflection at E = 50–30,000 eV, Z = 1–92. Atom. Data Nuclear Data Tables 1993, 54, 181–342. [Google Scholar] [CrossRef]
- Winterfeldt, C.; Spielmann, C.; Gerber, G. Colloquium: Optimal control of high-harmonic generation. Rev. Mod. Phys. 2008, 80, 117. [Google Scholar] [CrossRef]
- Schultz, T.; Vrakking, M. Attosecond and XUV Spectroscopy: Ultrafast Dynamics and Spectroscopy; John Wiley & Sons: Somerset, NJ, USA, 2013. [Google Scholar]
- Gaarde, M.B.; Buth, C.; Tate, J.L.; Schafer, K.J. Transient absorption and reshaping of ultrafast XUV light by laser-dressed helium. Phys. Rev. A 2011, 83, 013419. [Google Scholar] [CrossRef]
- Wu, M.; Chen, S.; Camp, S.; Schafer, K.J.; Gaarde, M.B. Theory of strong-field attosecond transient absorption. J. Phys. B Atom. Mol. Opt. Phys. 2016, 49, 062003. [Google Scholar] [CrossRef]
- Chen, S.; Wu, M.; Gaarde, M.B.; Schafer, K.J. Laser-imposed phase in resonant absorption of an isolated attosecond pulse. Phys. Rev. A 2013, 88, 033409. [Google Scholar] [CrossRef]
- Armstrong, L., Jr.; Beers, B.L.; Feneuille, S. Resonant multiphoton ionization via the Fano autoionization formalism. Phys. Rev. A 1975, 12, 1903. [Google Scholar] [CrossRef]
- Heller, Y.I.; Popov, A. Parametric generation and absorption of tunable vacuum-ultraviolet radiation controlled by laser-induced autoionizing-like resonances in the continuum. Opt. Commun. 1976, 18, 449–451. [Google Scholar] [CrossRef]
- Knight, P.L.; Lauder, M.; Dalton, B.J. Laser-induced continuum structure. Phys. Rep. 1990, 190, 1–61. [Google Scholar] [CrossRef]
- Liao, C.T.; Sandhu, A.; Camp, S.; Schafer, K.J.; Gaarde, M.B. Attosecond transient absorption in dense gases: Exploring the interplay between resonant pulse propagation and laser-induced line-shape control. Phys. Rev. A 2016, 93, 033405. [Google Scholar] [CrossRef]
- Crisp, M.D. Propagation of small-area pulses of coherent light through a resonant medium. Phys. Rev. A 1970, 1, 1604. [Google Scholar] [CrossRef]
- Shivaram, N.; Timmers, H.; Tong, X.M.; Sandhu, A. Attosecond-resolved evolution of a laser-dressed helium atom: interfering excitation paths and quantum phases. Phys. Rev. Lett. 2012, 108, 193002. [Google Scholar] [CrossRef] [PubMed]
- Cheng, Y.; Chini, M.; Wang, X.; Gonzalez-Castrillo, A.; Palacios, A.; Argenti, L.; Martin, F.; Chang, Z. Reconstruction of an excited-state molecular wave packet with attosecond transient absorption spectroscopy. Phys. Rev. A 2016, 94, 023403. [Google Scholar] [CrossRef]
- Warrick, E.R.; Cao, W.; Neumark, D.M.; Leone, S.R. Probing the Dynamics of Rydberg and Valence States of Molecular Nitrogen with Attosecond Transient Absorption Spectroscopy. J. Phys. Chem. A 2016, 120, 3165–3174. [Google Scholar] [CrossRef] [PubMed]
- Liao, C.T.; Li, X.; Haxton, D.J.; Rescigno, T.N.; Lucchese, R.R.; McCurdy, C.W.; Sandhu, A. Probing autoionizing states of molecular oxygen with XUV transient absorption: Electronic symmetry dependent lineshapes and laser induced modification. ArXiv 2016. [Google Scholar]
- Ferré, A.; Staedter, D.; Burgy, F.; Dagan, M.; Descamps, D.; Dudovich, N.; Petit, S.; Soifer, H.; Blanchet, V.; Mairesse, Y. High-order harmonic transient grating spectroscopy of SF6 molecular vibrations. J. Phys. B Atom. Mol. Opt. Phys. 2014, 47, 124023. [Google Scholar] [CrossRef]
- Wagner, N.L.; Wüest, A.; Christov, I.P.; Popmintchev, T.; Zhou, X.; Murnane, M.M.; Kapteyn, H.C. Monitoring molecular dynamics using coherent electrons from high harmonic generation. Proc. Natl. Acad. Sci. USA 2006, 103, 13279–13285. [Google Scholar] [CrossRef] [PubMed]
- Pertot, Y.; Schmidt, C.; Matthews, M.; Chauvet, A.; Huppert, M.; Svoboda, V.; von Conta, A.; Tehlar, A.; Baykusheva, D.; Wolf, J.P.; et al. Time-resolved X-ray absorption spectroscopy with a water window high-harmonic source. Science 2017, 355, 264–267. [Google Scholar] [CrossRef] [PubMed]
- Mitsuke, K.; Suzuki, S.; Imamura, T.; Koyano, I. Negative-ion mass spectrometric study of ion-pair formation in the vacuum ultraviolet. III. J. Chem. Phys. 1990, 93, 8717–8724. [Google Scholar] [CrossRef]
- Gustafsson, T. Partial photoionization cross sections of SF6 between 20 and 54 eV: An interpretation of the photoelectron spectrum. Phys. Rev. A 1978, 18, 1481–1489. [Google Scholar] [CrossRef]
- Dehmer, J.L.; Parr, A.C.; Wallace, S.; Dill, D. Photoelectron branching ratios and angular distributions for the valence levels of SF6 in the range 16 ≤ hν ≤ 30 eV. Phys. Rev. A 1982, 26, 3283–3292. [Google Scholar] [CrossRef]
- Nefedov, V. Quasistationary states in X-ray absorption spectra of chemical compounds. J. Struct. Chem. 1970, 11, 272–276. [Google Scholar] [CrossRef]
- Holland, D.; Shaw, D.; Hopkirk, A.; MacDonald, M.; McSweeney, S. A study of the absolute photoabsorption cross section and the photoionization quantum efficiency of sulphur hexafluoride from the ionization threshold to 420 A. J. Phys. B Atom. Mol. Opt. Phys. 1992, 25, 4823. [Google Scholar] [CrossRef]
- Sze, K.; Brion, C. Inner-shell and valence-shell electronic excitation of SF6, SeF6 and TeF6 by high energy electron impact: An investigation of potential barrier effects. Chem. Phys. 1990, 140, 439–472. [Google Scholar] [CrossRef]
- Ferrett, T.; Lindle, D.; Heimann, P.; Piancastelli, M.; Kobrin, P.; Kerkhoff, H.; Becker, U.; Brewer, W.; Shirley, D. Shape-resonant and many-electron effects in the S 2p photoionization of SF6. J. Chem. Phys. 1988, 89, 4726–4736. [Google Scholar] [CrossRef]
- Nakamatsu, H.; Mukoyama, T.; Adachi, H. Theoretical X-ray absorption spectra of SF6 and H2S. J. Chem Phys. 1991, 95, 3167–3174. [Google Scholar] [CrossRef]

© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license ( http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liao, C.-T.; Sandhu, A. XUV Transient Absorption Spectroscopy: Probing Laser-Perturbed Dipole Polarization in Single Atom, Macroscopic, and Molecular Regimes. Photonics 2017, 4, 17. https://doi.org/10.3390/photonics4010017
Liao C-T, Sandhu A. XUV Transient Absorption Spectroscopy: Probing Laser-Perturbed Dipole Polarization in Single Atom, Macroscopic, and Molecular Regimes. Photonics. 2017; 4(1):17. https://doi.org/10.3390/photonics4010017
Chicago/Turabian StyleLiao, Chen-Ting, and Arvinder Sandhu. 2017. "XUV Transient Absorption Spectroscopy: Probing Laser-Perturbed Dipole Polarization in Single Atom, Macroscopic, and Molecular Regimes" Photonics 4, no. 1: 17. https://doi.org/10.3390/photonics4010017
APA StyleLiao, C.-T., & Sandhu, A. (2017). XUV Transient Absorption Spectroscopy: Probing Laser-Perturbed Dipole Polarization in Single Atom, Macroscopic, and Molecular Regimes. Photonics, 4(1), 17. https://doi.org/10.3390/photonics4010017




