Multi-Scale Simulation for Transient Absorption Spectroscopy under Intense Few-Cycle Pulse Laser
Abstract
:1. Introduction
2. Materials and Methods
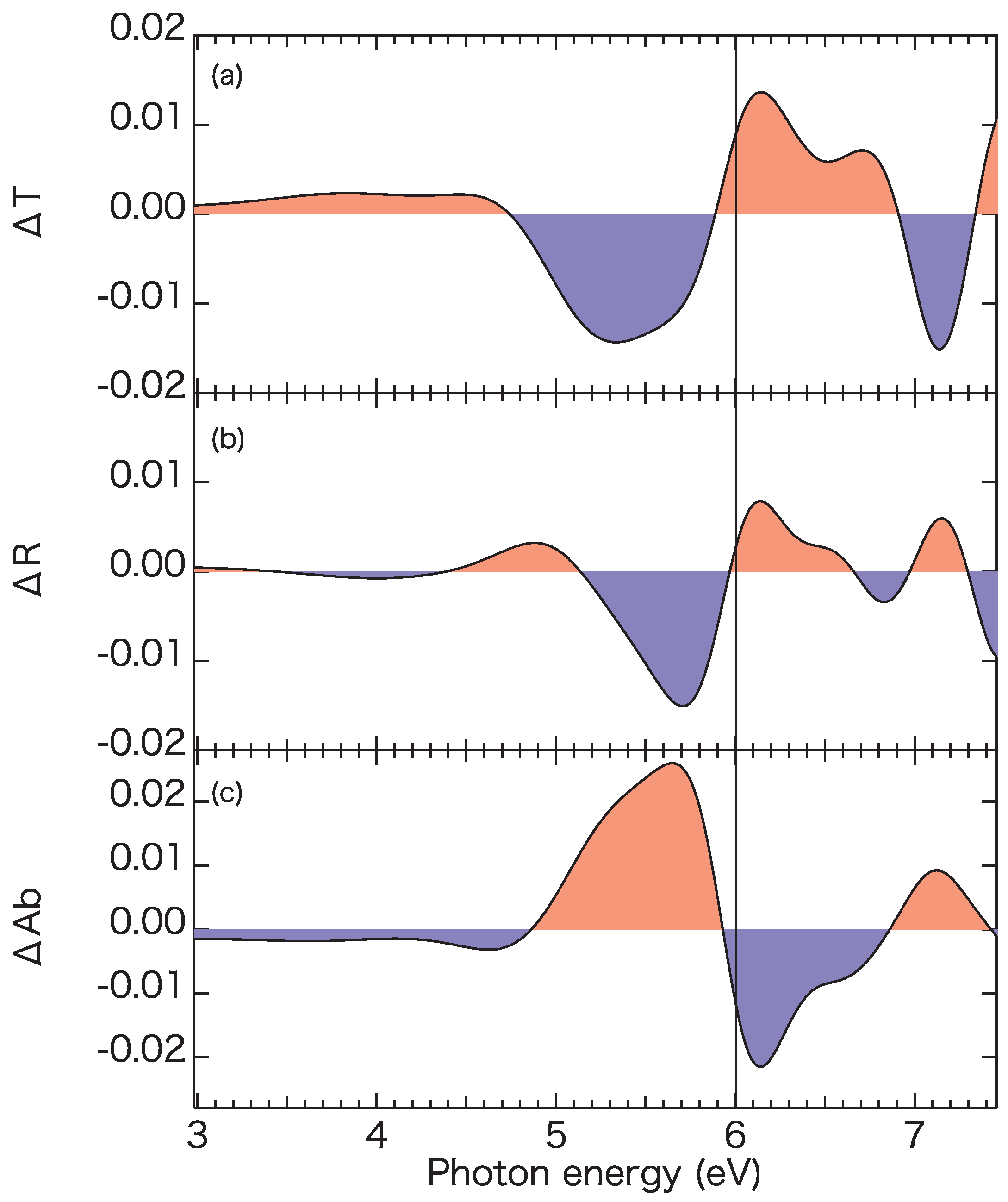
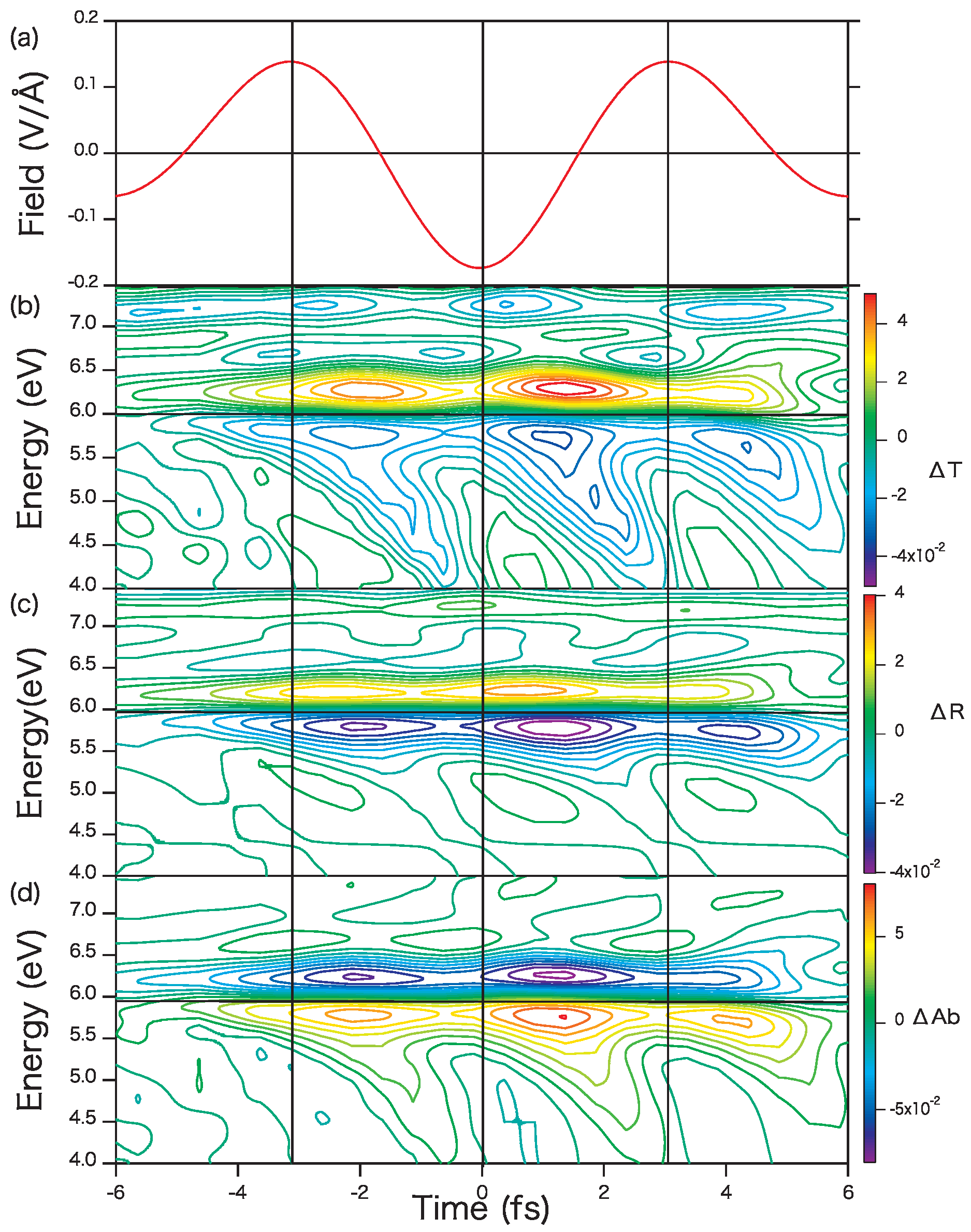
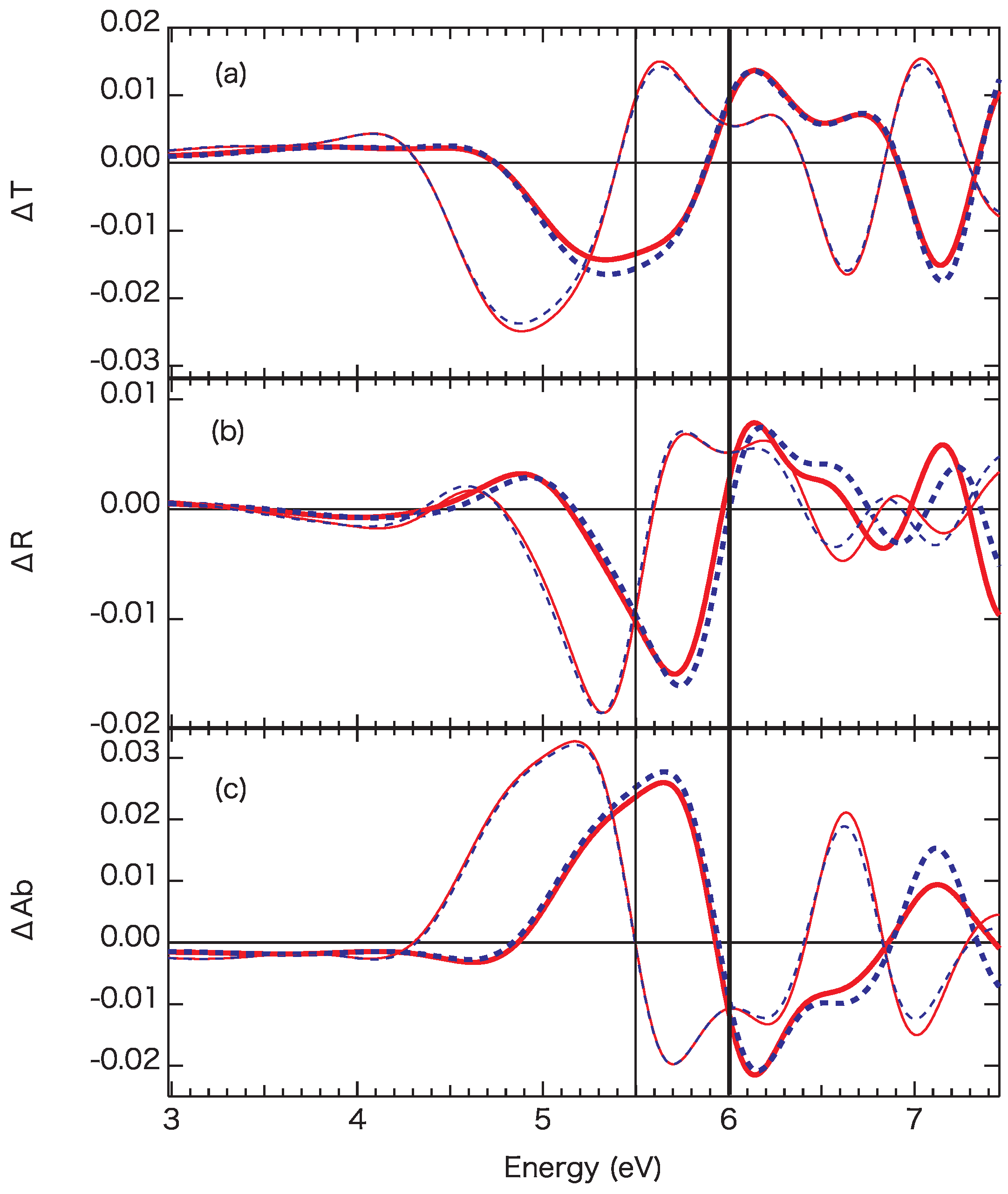
3. Numerical Results and Discussion
4. Conclusions
Acknowledgments
Conflicts of Interest
References
- Zhao, K.; Zhang, Q.; Chini, M.; Wu, Y.; Wang, X.; Chang, Z. Tailoring a 67 attosecond pulse through advantageous phase-mismatch. Opt. Lett. 2012, 37, 3891–3893. [Google Scholar] [CrossRef] [PubMed]
- Hentschel, M.; Kienberger, R.; Spielmann, C.; Reider, G.A.; Milosevic, N.; Brabec, T.; Corkum, P.; Heinzmann, U.; Drescher, M.; Krausz, F. Attosecond metrogy. Nature 2001, 414, 509–513. [Google Scholar] [CrossRef] [PubMed]
- Hirori, H.; Doi, A.; Blanchard, F.; Tanaka, K. Single-cycle terahertz pulses with amplitudes exceeding 1 MV/cm generated by optical rectification in LiNbO3. Appl. Phys. Lett. 2011, 98, 091106. [Google Scholar] [CrossRef]
- Chin, H.A.; Calderon, G.O.; Kono, J. Extreme Midinfrared Nonlinear Optics in Semiconductors. Phys. Rev. Lett. 2001, 86, 3292–3295. [Google Scholar] [CrossRef] [PubMed]
- Hirori, H.; Shinokita, K.; Shirai, M.; Tani, S.; Kadoya, Y.; Tanaka, K. Extraordinary carrier multiplication gated by a picosecond electric field pulse. Nat. Commun. 2011, 2, 594. [Google Scholar] [CrossRef] [PubMed]
- Schiffrin, A.; Paasch-Colberg, T.; Karpowicz, N.; Apalkov, V.; Gerster, D.; Mühlbrandt, S.; Korbman, M.; Reichert, J.; Schultze, M.; Holzner, S.; et al. Optical-filed-induced current in dielectrics. Nature 2013, 493, 70–73. [Google Scholar] [CrossRef] [PubMed]
- Schultze, M.; Bothschafter, E.M.; Sommer, A.; Holzner, S.; Schweinberger, W.; Fiess, M.; Hofstetter, M.; Kienberger, R.; Apalkov, V.; Yakovlev, V.S.; et al. Controlling dielectrics with the electric field of light. Nature 2013, 493, 75–82. [Google Scholar] [CrossRef] [PubMed]
- Nobelli, F.; Fausti, D.; Giusti, F.; Parmigiani, F.; Hoffmann, M. Mixed regime of light-matter interaction revealed by phase sensitive measurements of the dynamical Franz-Keldysh effect. Sci. Rep. 2013, 3, 1227. [Google Scholar]
- Schultze, M.; Ramasesha, K.; Pemmaraju, C.D.; Sato, S.A.; Whitmore, D.; Gandman, A.; Prell, J.S.; Borja, L.J.; Prendergast, D.; Yabana, K.; et al. Attosecond band-gap dynamics in silicon. Science 2014, 346, 1348–1352. [Google Scholar] [CrossRef] [PubMed]
- Franz, W. Einfluß eines elektrischen Feldes auf eine optische Absorptionskante. Z. Naturforsch. A 1958, 13, 484–489. [Google Scholar] [CrossRef]
- Keldysh, V.L. Behaviour of Non-Metallic Crystals in Strong Electric Fields. Sov. Phys. JETP 1958, 6, 763–770. [Google Scholar]
- Tharmalingam, K. Optical Absorption in the Presence of a Uniform Field. Phys. Rev. 1963, 130, 2204–2206. [Google Scholar] [CrossRef]
- Seraphin, O.B.; Hess, B.R. Franz-Keldysh Effect above the Fundamental Edge in Germanium. Phys. Rev. Lett. 1965, 14, 138–140. [Google Scholar] [CrossRef]
- Nahory, E.R.; Shay, L.J. Reflectance Modulation by the Surface Field in GaAs. Phys. Rev. Lett. 1968, 21, 1569–1571. [Google Scholar] [CrossRef]
- Shen, H.; Dutta, M. Franz-Keldysh oscillations in modulation spectroscopy. J. Appl. Phys. 1995, 78, 2151–2176. [Google Scholar] [CrossRef]
- Wahlstrand, K.J.; Sipe, E.J. Independent-particle theory of the Franz-Keldysh effect including interband coupling: Application to calculation of electroabsorption in GaAs. Phys. Rev. B 2010, 82, 075206. [Google Scholar] [CrossRef]
- Duque-Gomez, F.; Sipe, E.J. The Franz-Keldysh effect revisited: Electroabsorption including interband coupling and excitonic effects. J. Phys. Chem. Solids 2015, 76, 138–152. [Google Scholar] [CrossRef]
- Yacoby, Y. High-frequency Franz-Keldysh Effect. Phys. Rev. 1968, 169, 610–619. [Google Scholar] [CrossRef]
- Jauho, A.P.; Johnsen, K. Dynamical Franz-Keldysh effect. Phys. Rev. Lett. 1996, 76, 4576–4579. [Google Scholar] [CrossRef] [PubMed]
- Nordstrom, B.K.; Johnsen, K.; Allen, S.J.; Jauho, A.-P.; Birnir, B.; Kono, J.; Noda, T.; Akiyama, H.; Sakaki, H. Excitonic Dynamical Franz-Keldysh Effect. Phys. Rev. Lett. 1998, 81, 457–460. [Google Scholar] [CrossRef]
- Srivastava, A.; Srivastava, R.; Wang, J.; Kono, J. Laser-Induced Above-Band-Gap Transparency in GaAs. Phys. Rev. Lett. 2004, 93, 157401. [Google Scholar] [CrossRef] [PubMed]
- Mizumoto, Y.; Kayanuma, Y.; Srivastava, A.; Kono, J.; Chin, H.A. Dressed-band theory for semiconductors in a high-intensity infrared laser field. Phys. Rev. B 2006, 74, 045216. [Google Scholar] [CrossRef]
- Ghimire, S.; DiChiara, D.A.; Sistrunk, E.; Szafruga, B.U.; Agostini, P.; DiMauro, F.L.; Reis, A.D. Redshift in the Optical Absorption of ZnO Single Crystals in the Presence of an Intense Midinfrared Laser Field. Phys. Rev. Lett. 2011, 107, 167407. [Google Scholar] [CrossRef] [PubMed]
- Otobe, T.; Shinohara, Y.; Sato, A.S.; Yabana, K. Femtosecond time-resolved dynamical Franz-Keldysh effect. Phys. Rev. B 2016, 93, 045124. [Google Scholar] [CrossRef]
- Otobe, T. Time-resolved dynamical Franz-Keldysh effect produced by an elliptically polarized laser. Phys. Rev. B 2016, 94, 165152. [Google Scholar] [CrossRef]
- Lucchini, M.; Sato, A.S.; Ludwig, A.; Herrmann, J.; Volkov, M.; Kasmi, L.; Shinohara, Y.; Yabana, K.; Gallmann, L.; Keller, U. Attosecond dynamical Franz-Keldsh effect in polycrystalline diamond. Science 2016, 353, 916–919. [Google Scholar] [CrossRef] [PubMed]
- Hirori, H.; Uchida, K.; Tanaka, K.; Otobe, T.; Mochizuki, T.; Kim, C.; Yoshita, M.; Akiyama, H.; Pfeiffer, L.N.; West, K.W. Time-resolved observation of dynamical Franz-Keldysh effect under coherent multi-cycle terahertz pulses. In Proceedings of the JSAP-OSA Joint Symposia 2015, Nagoya, Japan, 13–16 September 2015.
- Otobe, T.; Yamagiwa, M.; Iwata, J.-I.; Yabana, K.; Nakatsukasa, T.; Bertsch, F.G. First-principles electron dynamics simulation for optical breakdown of dielectrics under an intense laser field. Phys. Rev. B 2008, 77, 165104. [Google Scholar] [CrossRef]
- Bertsch, F.G.; Iwata, J.-I.; Rubio, A.; Yabana, K. Real-space, real-time method for the dielectric function. Phys. Rev. B 2000, 62, 7998–8002. [Google Scholar] [CrossRef]
- Yabana, K.; Sugiyama, T.; Shinohara, Y.; Otobe, T.; Bertsch, F.G. Time-dependent density functional theory for strong electromagnetic field in crystalline solids. Phys. Rev. B 2012, 85, 045134. [Google Scholar] [CrossRef]
- Sato, A.S.; Yabana, K.; Shinohara, Y.; Otobe, T.; Lee, K.-M.; Bertsch, F.G. Time-dependent density functional theory of high-intensity short-pulse laser irradiation on insulators. Phys. Rev. B 2015, 92, 205413. [Google Scholar] [CrossRef]
- Perdew, P.J.; Wang, Y. Accurate and simple analytic representation of the electron-gas correlation energy. Phys. Rev. B 1992, 45, 13244–13249. [Google Scholar] [CrossRef]
- Becke, D.A.; Johnson, R.E. A simple effective potential for exchange. J. Chem. Phys. 2006, 124, 221101. [Google Scholar] [CrossRef] [PubMed]
- Tran, F.; Blaha, P. Accurate Band Gaps of Semiconductors and Insulators with a Semilocal Exchange-Correlation Potential. Phys. Rev. Lett. 2009, 102, 226401. [Google Scholar] [CrossRef] [PubMed]
- Troullier, N.; Martins, L.J. Efficient pseudopotentials for plane-wave calculations. Phys. Rev. B 1991, 43, 1993–2006. [Google Scholar] [CrossRef]
- Kleinman, L.; Bylander, M.D. Efficacious Form for Model Pseudopotentials. Phys. Rev. Lett. 1982, 48, 1425–1428. [Google Scholar] [CrossRef]


© 2016 by the author; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Otobe, T. Multi-Scale Simulation for Transient Absorption Spectroscopy under Intense Few-Cycle Pulse Laser. Photonics 2016, 3, 63. https://doi.org/10.3390/photonics3040063
Otobe T. Multi-Scale Simulation for Transient Absorption Spectroscopy under Intense Few-Cycle Pulse Laser. Photonics. 2016; 3(4):63. https://doi.org/10.3390/photonics3040063
Chicago/Turabian StyleOtobe, Tomohito. 2016. "Multi-Scale Simulation for Transient Absorption Spectroscopy under Intense Few-Cycle Pulse Laser" Photonics 3, no. 4: 63. https://doi.org/10.3390/photonics3040063
APA StyleOtobe, T. (2016). Multi-Scale Simulation for Transient Absorption Spectroscopy under Intense Few-Cycle Pulse Laser. Photonics, 3(4), 63. https://doi.org/10.3390/photonics3040063




