1. Introduction
Highly sensitive optical fiber sensors have been used in many areas due to the advantages, including compactness, all-fiber structure, immunity to electro-magnetic irradiation, waterproofness, and so on [
1,
2]. Among those fiber sensors, wavelength-interrogated sensors are intrinsically based on the measurement of the wavelength drift to extract the sensing signal, such as fiber Bragg grating (FBG) sensors for strain and temperature sensing. With the change of strain or temperature, the refractive index or the grating period varies, and thus, the resonant wavelength shifts. Usually, for a conventional silica FBG sensor operated around a 1550-nm wavelength, the change of 1 με (με = microstrain) leads to the wavelength shift of about 1 pm, and thus, the strain sensitivity is about 1 pm/με. Under the same circumstance, the temperature sensitivity is about 13 pm/°C [
3,
4,
5]. Therefore, FBGs are very sensitive sensors for strain and temperature sensing, and thus, they have been used for high precision measurements in broad areas.
On the other hand, to obtain a high precision measurement, the resolution of the interrogator is equally important. One can take an optical spectrum analyzer (OSA) as an interrogator for FBG sensors. With a high resolution up to 20 pm (YOKOGAWA AQ6370D), the measured strain and temperature resolution are only ~20 με and ~1.5 °C for FBG sensors with 1-pm/με strain sensitivity and 13-pm/°C temperature sensitivity, respectively. Such a kind of measurement resolution is far beyond the requirements for applications like crustal deformation measurement, rock structure monitoring, ocean water observation, circumstance monitoring for mines, special science inspections, and so on. For example, an ultrahigh sensitivity sensor is needed to measure the strain of the crustal deformation induced by the tides at the shores, which is at the scale of nano-ε (ε = strain) [
6,
7,
8]. To measure such a small amount of strain, one needs to use a very sophisticated system to interrogate the FBG sensors [
9]. Such a nanoscale amount of strain is totally invisible for the 20-pm resolution OSA based on the conventional FBG sensor. Therefore, it would be of great significance if one can enhance the sensitivity of the sensor, which, on the other hand, will directly reduce the required resolution of the interrogator.
The intrinsic sensitivity of the sensor is decided by the material and structure of the sensor. Thus, in order to improve the sensitivity, pre-processing of the sensor is usually needed [
10,
11,
12,
13,
14]. By tapering the FBG or fabricating FBG over nanofiber, an improved strain sensitivity of 2.5 pm/με has been obtained [
15]. By fabricating FBG over polymer fiber, a temperature sensitivity of 360 pm/°C has been achieved [
12,
13]. The disadvantages of pre-processing are the effectiveness and reliability. The pre-processing usually increases the instability and complexity, which weakens the key advantage of the FBG sensor. Thus, it is more preferable to use post-processing techniques to enhance the sensitivity, such as four wave mixing (FWM)-based optical signal processing, which is also the main topic of this review paper.
Recently, degenerated FWM for frequency chirp magnification (FCM) has been utilized to improve the frequency sweeping bandwidth and, consequently, to improve the spatial resolution of an optical frequency domain reflectometer [
16,
17]. Meanwhile, FWM-based FCM has also been used to enhance the sensitivity of a conventional FBG sensor [
18]. Without changing the sensor head, the sensitivity can be magnified by a factor of five based on single-stage high-order FWM. Further improvement has been realized by using high-order and cascaded FWM, and 7.6-pm/με strain sensitivity for a conventional FBG has been obtained, which has been magnified by a factor of six [
19,
20]. The continuous wave of the FWM pump limits the FWM efficiency, and thus, it is quite difficult to further improve the sensitivity. There are several methods to improve the FWM efficiency. One of them is using pump pulse modulation to increase the peak power. Another is using optimized highly nonlinear fiber (HNLF) with a larger nonlinear coefficient and a smaller dispersion/dispersion slope, so that phase matching can be easily achieved and optical parametric amplification (OPA) can be induced.
In this paper, we demonstrated FWM-based optical signal processing for the sensitivity enhancement of FBG sensors. Degenerated FWM, cascaded two-stage FWM and pump-pulsed FWM with OPA are experimentally studied and comprehensively reviewed. Assisted by OPA and high-order FWM, record performances of 13.3-pm/με strain sensitivity and 141.2-pm/°C temperature sensitivity for silica FBG sensors are obtained, respectively.
This paper is an extended and comprehensive review study of our recent progress, and it is organized as follows. In
Section 2, the general principle of degenerated FWM for enhancing the FBG sensitivity is introduced, and single-stage FWM for the strain sensitivity enhancement is briefly investigated. In
Section 3, cascaded and two-stage FWM for obtaining six-times enhanced sensitivity is presented. In
Section 4, the use of pump pulse modulation and OPA for obtaining ~14-times enhanced sensitivity is studied.
2. Degenerated FWM for Sensitivity Enhancement
To enhance the sensitivity of a fiber sensor by FWM, one needs to use wavelength interrogation for the fiber sensor, so that the sensing signal can be interpreted by the wavelength drifting. FBG sensors are intrinsically interrogated by the Bragg wavelength. Particularly, an FBG laser can be constructed with the FBG as the sensor head, and the lasing wavelength drifting can thus be used for wavelength interrogation. Then, sensitivity enhancement of the FBG sensor can be realized by using the FBG laser as the FWM pump to implement a system for all-optical frequency chirp magnification.
In degenerated FWM, the generated first-order idler has an electrical field
Ei described by [
21]:
where
ωp, ϕp and
Ap are respectively the angular frequency, phase and amplitude for the pump.
ωs,
ϕs and
As are respectively the angular frequency, phase and amplitude for the signal. Additionally,
c is a constant related to FWM efficiency. Thus, after the FWM, the pump, signal and first-order idler have a phase relationship and a frequency relationship respectively governed by
ϕi–1 = 2
ϕp –
ϕs and
ωi–1 = 2
ωp –
ωs. Consider a pump with a frequency chirp of
δω; the obtained idler would have a frequency of
2(ωp + δω) – ωs. Therefore, the phase and frequency chirp of the first-order idler can be doubled compared with that of the pump [
22]. In a high order FWM process, the frequency for the
k-th order idler would be:
ωi–k = (
k + 1)(
ωp +
δω) –
kωs. Then, one can significantly magnify the frequency chirp along with the increase of the idler order. Consider the wavelength drift as one kind of frequency chirp; one can obtain a magnified wavelength drift.
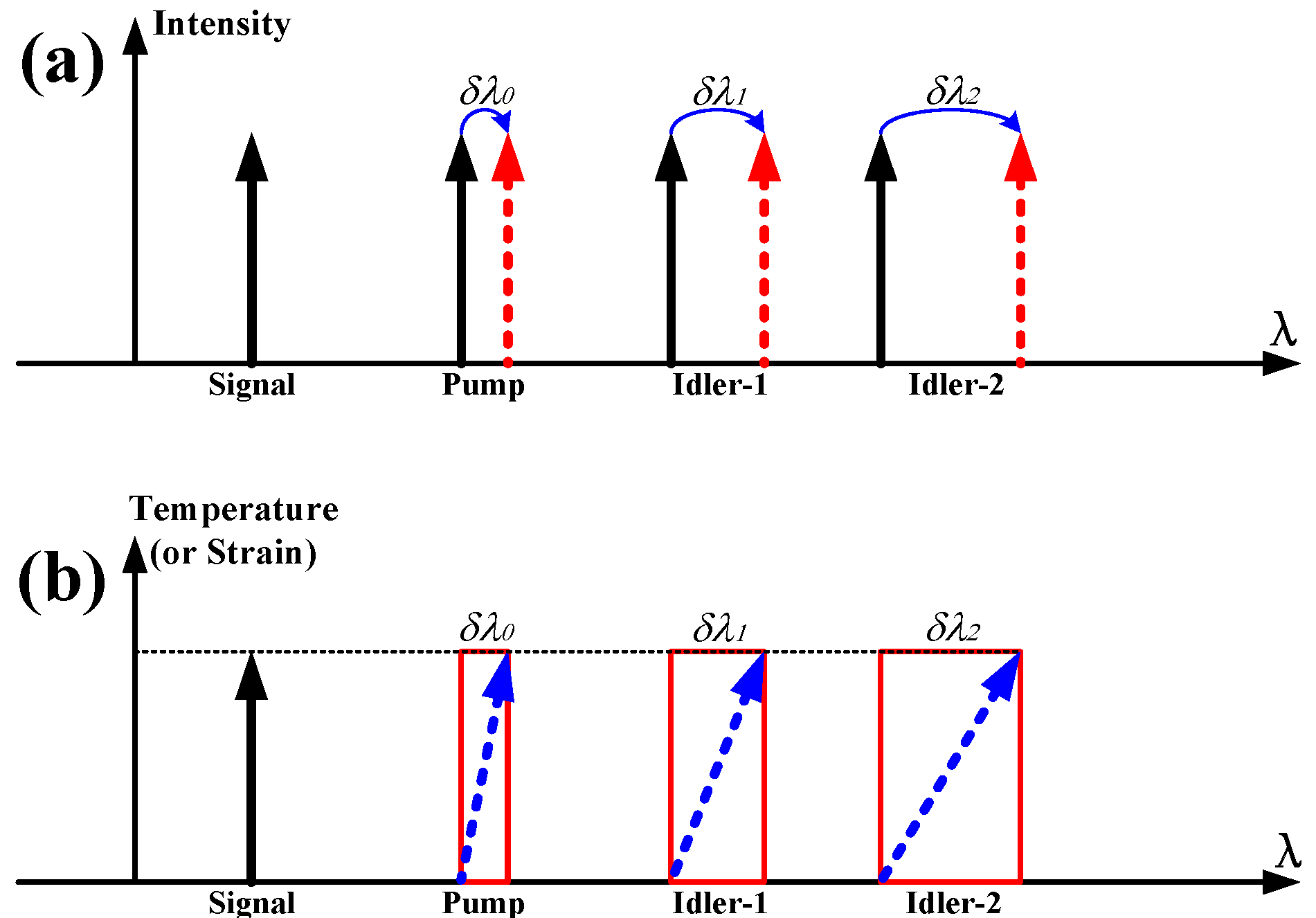
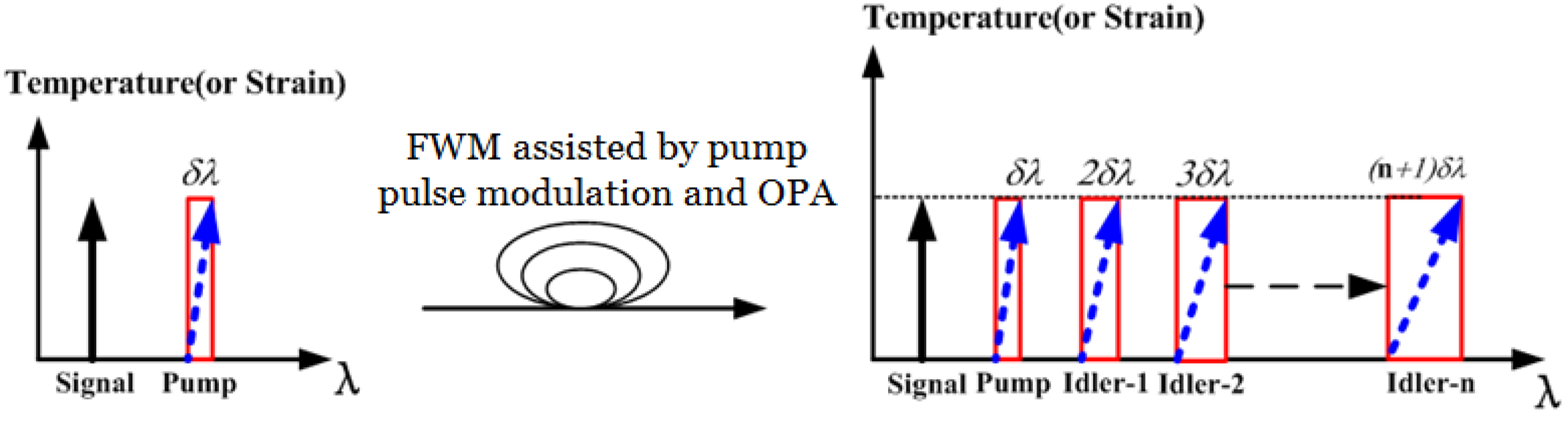
In a high order FWM process, the wavelength drift at idler-n is
(n + 1)δλ. By taking the wavelength drift of the FBG sensor as the frequency chirp for the pump in a degenerated FWM process, the sensitivity of the FBG sensor can thus be magnified due to the frequency chirp magnification as depicted in
Figure 1a. The enhancement by a factor of
(n + 1) can be obtained for idler-n in a single-stage high-order degenerated FWM process.
Figure 1.
Schematic illustration of the principle. (a) Wavelength drift magnification; (b) temperature/strain sensitivity enhancement.
Figure 1.
Schematic illustration of the principle. (a) Wavelength drift magnification; (b) temperature/strain sensitivity enhancement.
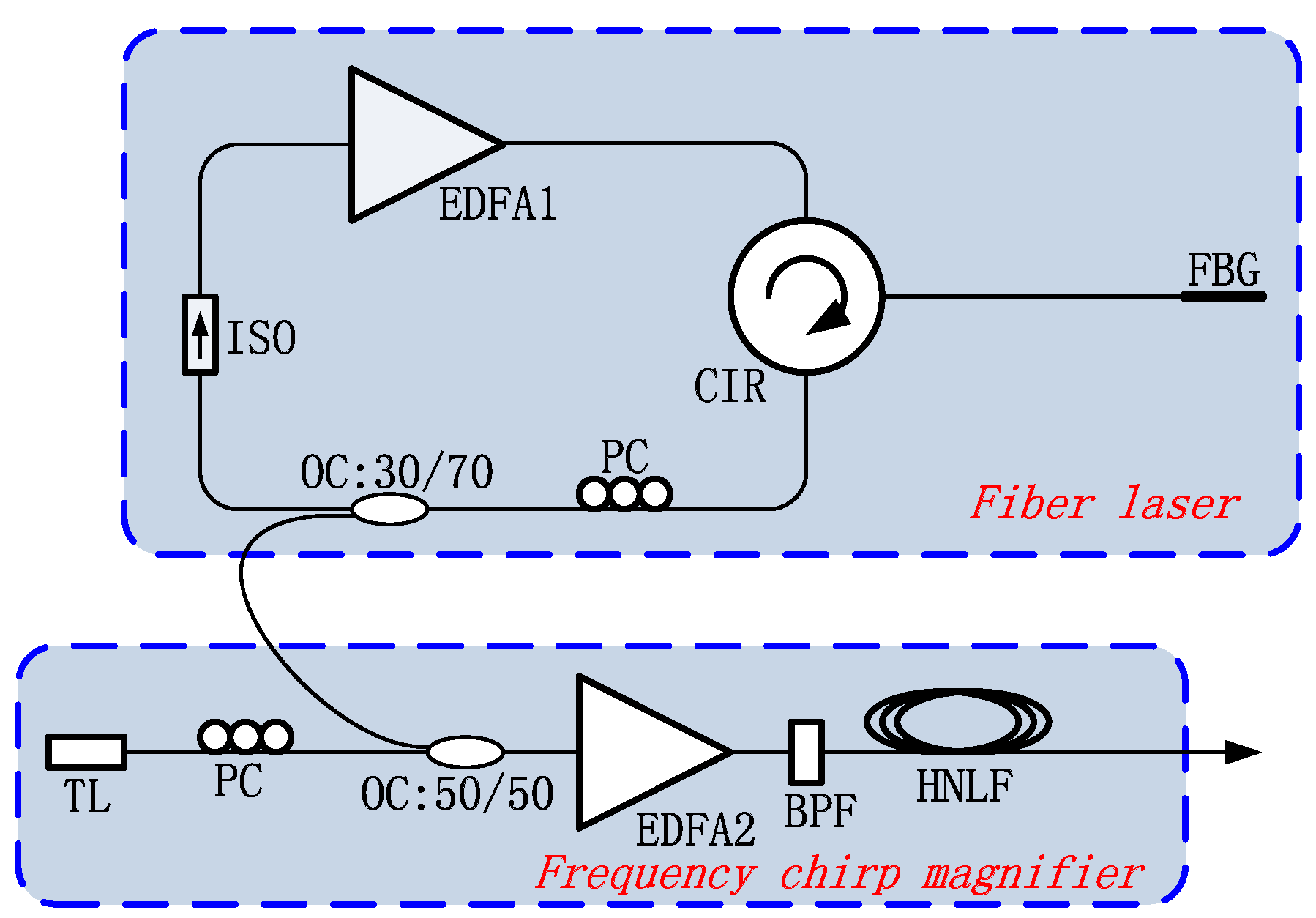
Shown in
Figure 2 is the experimental setup, which consists of the fiber laser system based on FBG and the FCM system based on degenerated FWM. In the fiber laser system, we can construct a fiber laser with the output lasing wavelength located at the FBG resonant wavelength. In the frequency chirp magnifier system, we can realize an enhanced wavelength shift due to the FCM at high order idlers of the degenerated FWM. The degenerated FWM is realized in the 500-m HNLF, which has a nonlinear coefficient of about 11 W
−1 km
−1 and a zero-dispersion wavelength of 1550 nm. At 1550 nm, the dispersion slope is +0.019 ps/nm
2/km.
Figure 2.
Experimental setup. EDFA, erbium-doped fiber amplifier; CIR, circulator; PC, polarization controller; ISO, isolator; OC, optical coupler; TL, tunable laser; BPF, band pass filter; HNLF, highly nonlinear fiber.
Figure 2.
Experimental setup. EDFA, erbium-doped fiber amplifier; CIR, circulator; PC, polarization controller; ISO, isolator; OC, optical coupler; TL, tunable laser; BPF, band pass filter; HNLF, highly nonlinear fiber.
The lasing wavelength of the FBG fiber laser is located at 1550.32 nm, which corresponds to the FBG’s initial resonant wavelength at room temperature. By stretching the FBG, a certain amount of strain is loaded onto the FBG. Shown in
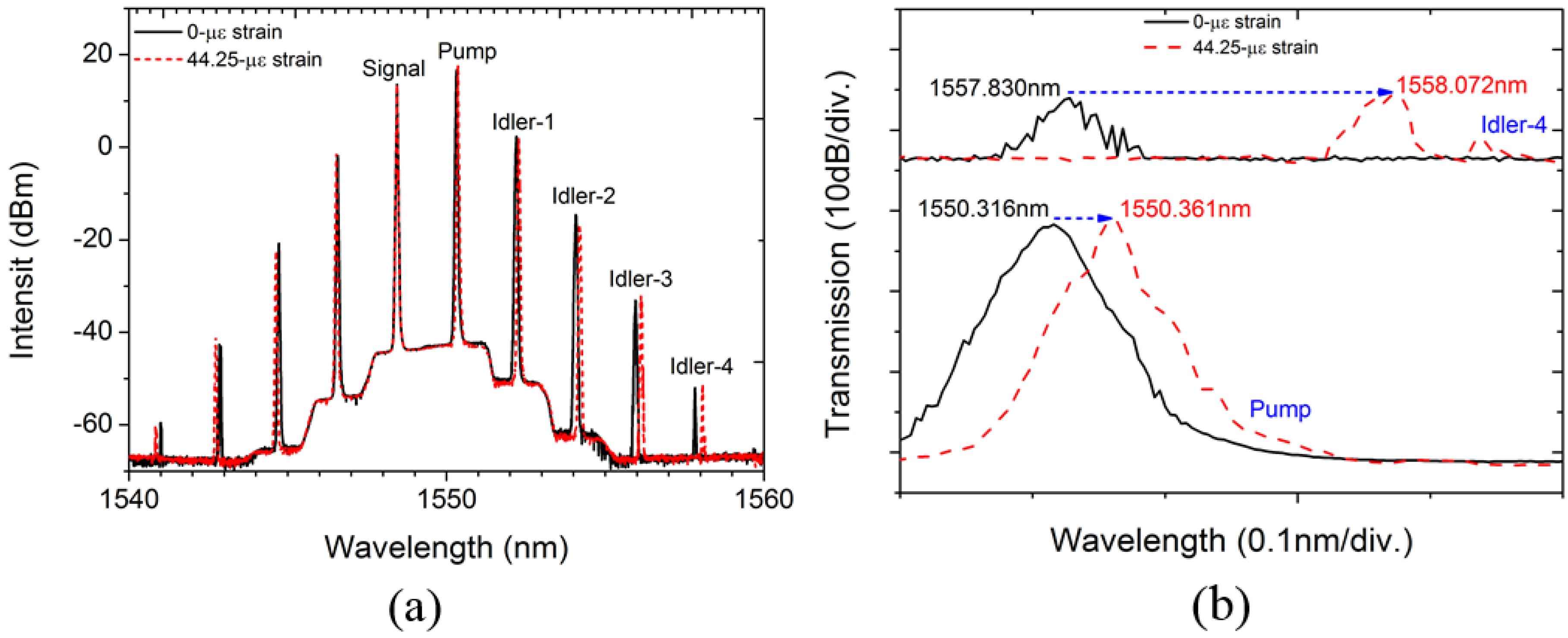
Figure 3a are the optical spectra after the FCM with the loading of 50-μm stretching. Four idlers have been generated after the degenerated FWM in the HNLF, considering the fiber laser at 1550.32 nm as the pump. At the output of the FCM system, the wavelength drift induced by the 50-μm stretching over a 1130-mm length has been significantly magnified. As shown in the zoom-in spectra in
Figure 3b, the wavelength drift of 0.045 nm for the pump has been magnified to 0.242 nm for Idler-4.
The strain of 44.25 με is obtained by stretching the 1130-mm fiber with a 50-μm length increment. With such a strain, wavelength drifts are measured to be 0.045, 0.076, 0.114, 0.174 and 0.238 nm, respectively, for the pump, Idler-1, Idler-2, Ider-3 and Idler-4. Thus, the corresponding strain sensitivities are 1.02, 1.72, 2.58, 3.93 and 5.38 pm/με, respectively. About a five-times magnified strain sensitivity of 5.38 pm/με is obtained with respect to an initial intrinsic strain sensitivity of 1.02 pm/με for the FBG.
Figure 3.
Measured optical spectra after degenerated FWM (a) and the zoom-in spectra for the pump and Idler-4 (b). The spectra indicate significantly magnified wavelength drift after 50-μm stretching over a 1,130-mm total fiber length.
Figure 3.
Measured optical spectra after degenerated FWM (a) and the zoom-in spectra for the pump and Idler-4 (b). The spectra indicate significantly magnified wavelength drift after 50-μm stretching over a 1,130-mm total fiber length.
3. Cascaded and Two-Stage FWM for Sensitivity Enhancement
The single-stage FWM for the sensitivity enhancement in
Section 2 is limited in the FWM efficiency. To further improve the sensitivity of the FBG sensor, we can utilize cascaded multi-stage FWM, e.g., two-stage FWM.
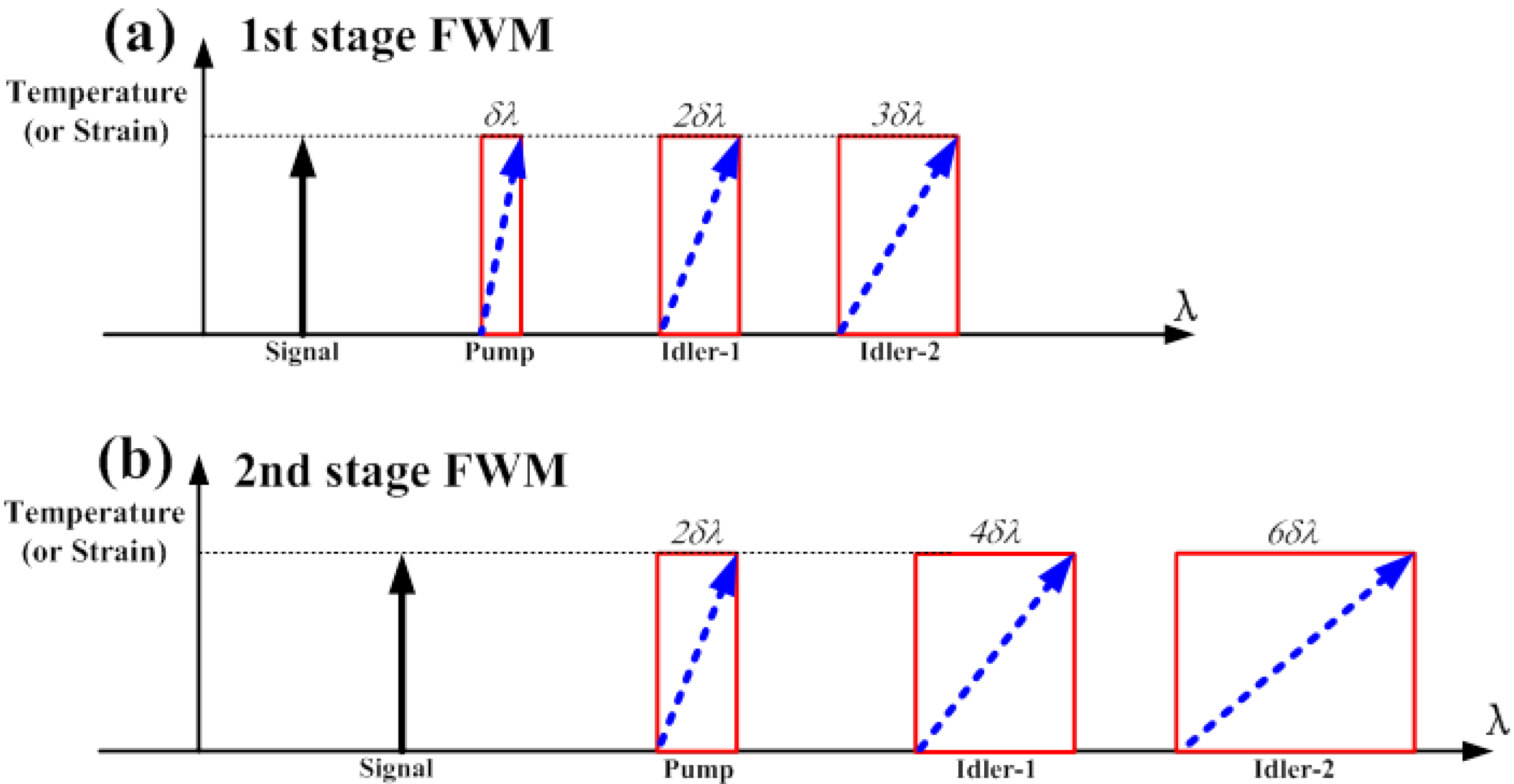
In a two-stage FWM process, the frequency chirp can be further magnified, and the enhancement of the sensitivity is more efficient, as shown in
Figure 4. The total FCM amount is the multiplication of the first-stage and second-stage FCM factors. For instance, by using Idler-1 generated from the first-stage FWM as the pump light in the second stage FWM, a six-times magnification of the sensitivity can be obtained at Idler-2 generated from the second-stage FWM.
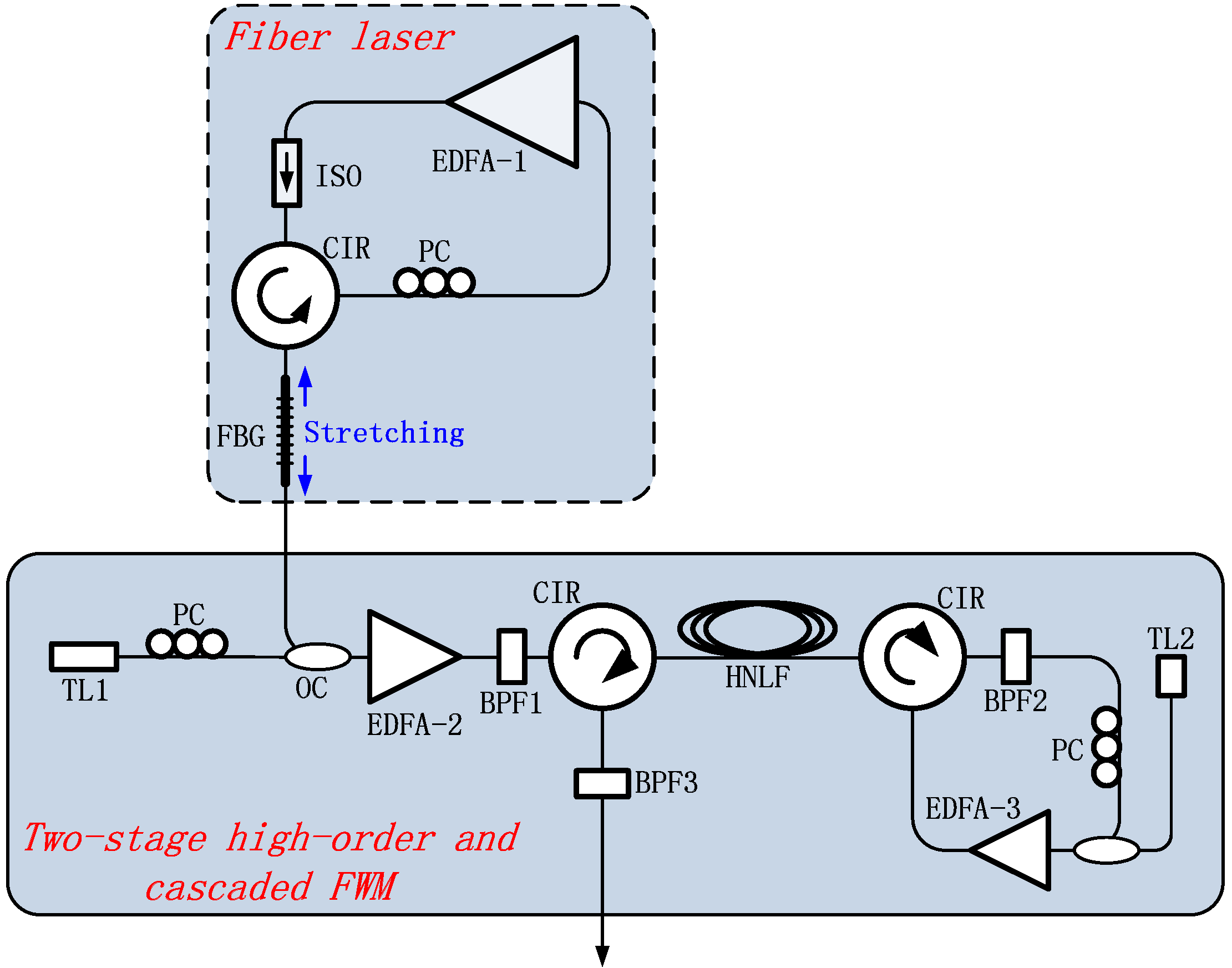
Figure 5 shows the experimental setup, which also consists of two systems, the fiber laser system based on FBG and the FWM system based on HNLF. In the fiber laser system, the output port of Erbium-Doped Fiber Amplifier 1 (EDFA-1) is connected to a circulator (Port 1) through an isolator, and thus, the light from EDFA-1 is directed to the FBG through Port 2 of the circulator. The FBG adopted in this work has a reflectivity of 3 dB, and its FWHM bandwidth is about 0.08 nm. The reflected light from the FBG is redirected to the input of EDFA-1 through a polarization controller. Thus, a fiber laser is constructed with the output lasing wavelength located at the FBG resonant wavelength. In the FWM system, the fiber laser with output power of 1 mW and the tunable laser (TL1) with output power of 10 mW are combined and launched into EDFA-2. The amplified pump from the FBG laser and the signal from TL are then directed into the 500-m HNLF through a circulator after filtering the amplified spontaneous emission (ASE) noise (Band Pass Filter 1 (BPF1)). The first order idler (Idler-1) is filtered (BPF2) after the first stage FWM and then combines with another laser source (TL2) for the second-stage FWM by using the same HNLF, but in an opposite direction. Therefore, by using a single-segment HNLF (the same 500-m HNLF in
Figure 2), high-order and cascaded FWM can be realized for obtaining an efficient frequency chirp magnification. The fiber laser in
Figure 5 has a lasing wavelength located at 1550.73 nm.
Figure 4.
Schematic illustration of the principle. (a) First-stage FWM; (b) second-stage FWM.
Figure 4.
Schematic illustration of the principle. (a) First-stage FWM; (b) second-stage FWM.
Figure 5.
Experimental setup. EDFA, erbium-doped fiber amplifier; CIR, circulator; PC, polarization controller; ISO, isolator; OC, optical coupler; TL, tunable laser; BPF, band pass filter; HNLF, highly nonlinear fiber.
Figure 5.
Experimental setup. EDFA, erbium-doped fiber amplifier; CIR, circulator; PC, polarization controller; ISO, isolator; OC, optical coupler; TL, tunable laser; BPF, band pass filter; HNLF, highly nonlinear fiber.
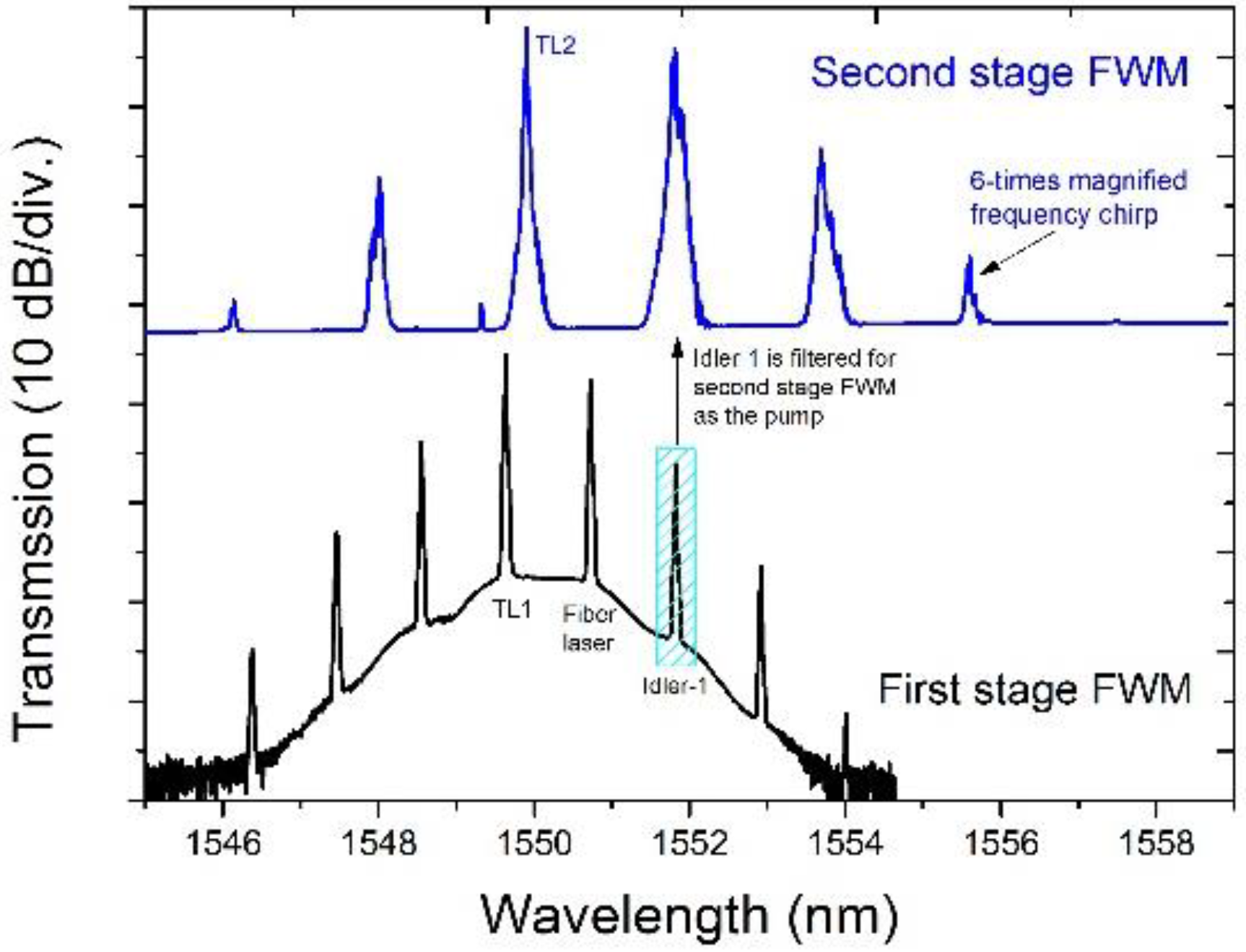
Shown in
Figure 6 are the optical spectra of the high-order and cascaded FWM. In the first-stage FWM, the pump wavelength is 1550.73 nm, and the signal wavelength (TL1) is 1549.64 nm. The output power of EDFA-2 is 300 mW, which leads to a power of about −12.3 dBm for Idler-1, as shown in
Figure 3 (the lower curve). Ilder-2 is then filtered for the second-stage FWM as the pump. The signal is generated by another laser (TL2) at 1550.50 nm. In the second-stage FWM, we obtain a second order idler at 1556.2 nm, which has a six-times magnified frequency chirp compared with the FBG-based laser signal. The output power of EDFA-3 is 240 mW.
Figure 6.
Measured optical spectra for the cascaded two-stage FWM.
Figure 6.
Measured optical spectra for the cascaded two-stage FWM.
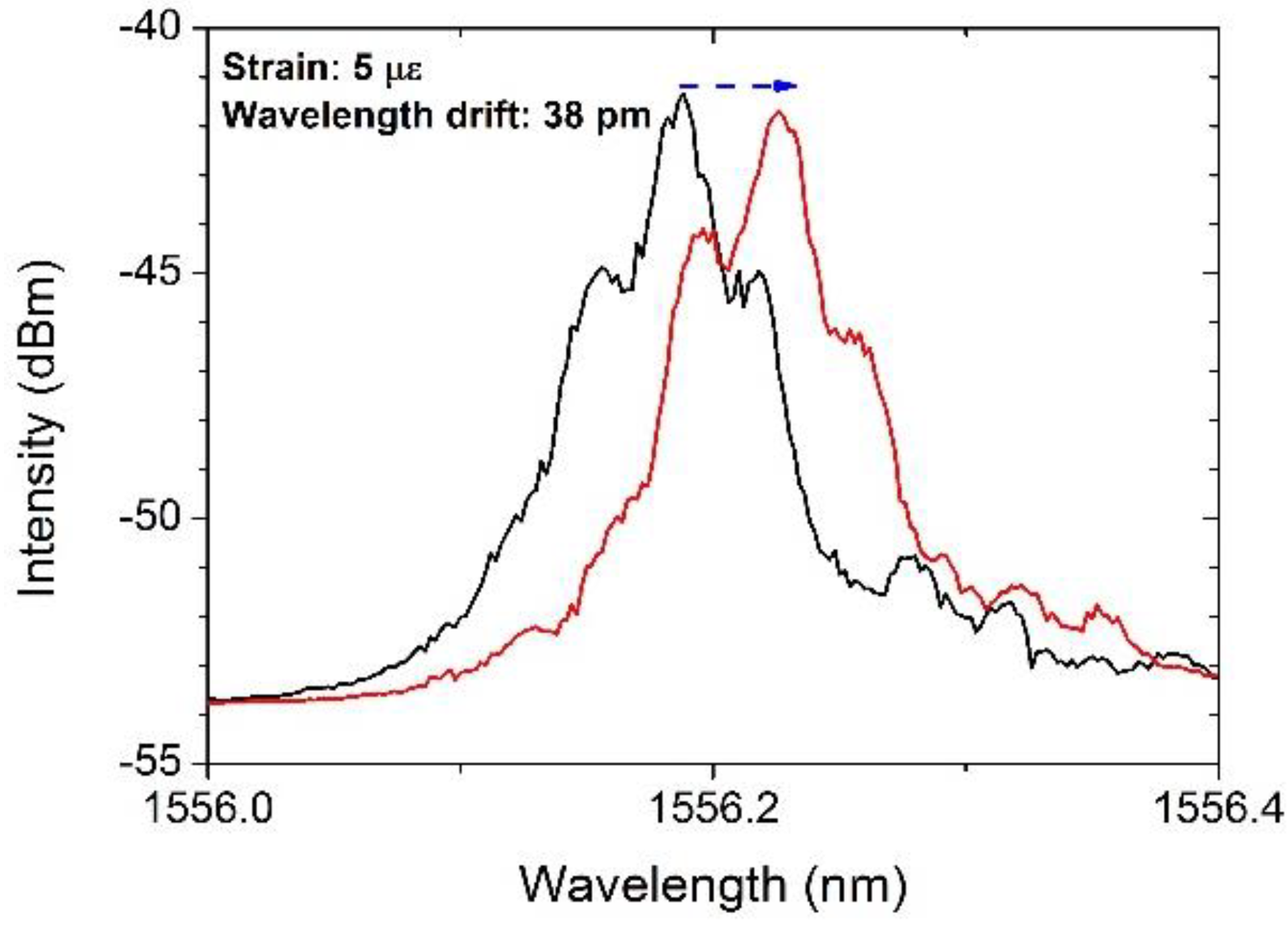
In the strain sensing experiment, a 5-με strain is applied to the FBG, and the fiber laser wavelength will consequently drift. However, such a small amount of strain can only shift the resonant wavelength of the FBG by several pm. After the frequency chirp magnification by high-order and cascaded FWM, as depicted in
Figure 6, the resonant wavelength drift of the FBG can be magnified by a factor of six at the second order idler in the second-stage FWM. The magnified wavelength drift is shown in
Figure 7, in which, a 38-pm wavelength drift is obtained with a strain of 5 με. Thus, the corresponding strain sensitivity is 7.6 pm/με. Such high strain sensitivity is obtained with a conventional FBG without sensor head processing. Therefore, it can be applied to a wide range of fiber sensing applications.
Figure 7.
Six-times magnified wavelength drift of 38 pm at the second order idler in the second-stage FWM.
Figure 7.
Six-times magnified wavelength drift of 38 pm at the second order idler in the second-stage FWM.
4. High-Order FWM and OPA for Sensitivity Enhancement
In
Section 2 and
Section 3, the sensitivity enhancements are based on FWM with continuous wave operation, which limits the FWM efficiency, and thus, it is quite difficult to further improve the sensitivity. There are several methods to improve the FWM efficiency and, thus, generate more idlers. One of them is using pump pulse modulation to increase the peak power. Another is using dispersion-optimized highly nonlinear fiber (HNLF) with larger nonlinear coefficient and smaller dispersion/dispersion slope, so that phase matching can be easily achieved and OPA can be induced [
23,
24,
25].
As depicted in
Figure 8, in a high-order FWM process assisted by pump pulse modulation and OPA, a large number of idlers can be generated, and the frequency chirp for the
n-th order idler is magnified by a factor of
(n + 1) compared with that of the pump. The increased nonlinear efficiency due to higher peak power and OPA will generate more high-order idlers, even with only single-stage FWM.
Figure 8.
Temperature/strain sensitivity enhancement by high-order FWM and optical parametric amplification (OPA). The pump is pulse modulated.
Figure 8.
Temperature/strain sensitivity enhancement by high-order FWM and optical parametric amplification (OPA). The pump is pulse modulated.
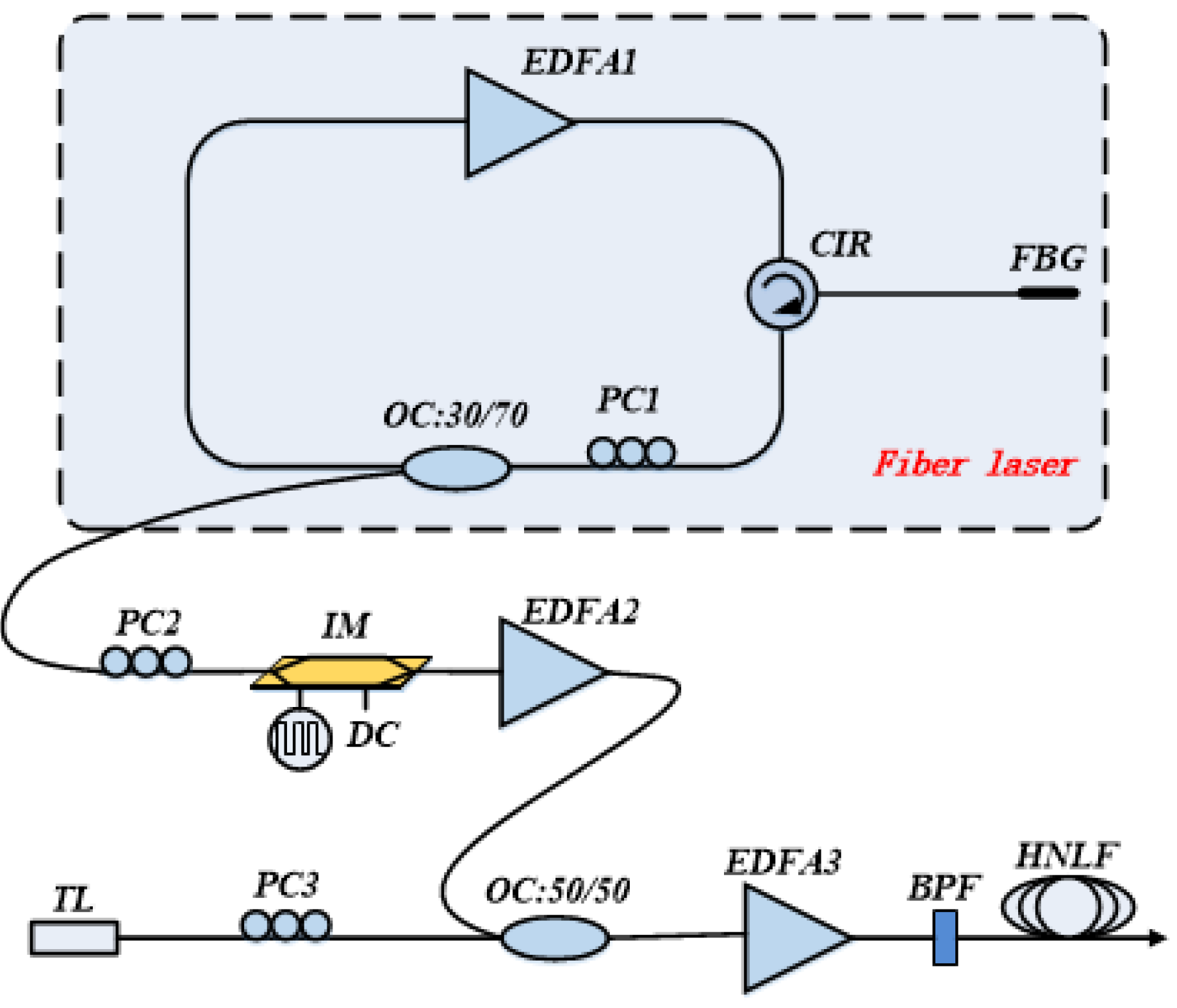
Figure 9.
Experimental setup. EDFA, erbium-doped fiber amplifier; CIR, circulator; PC, polarization controller; IM, intensity modulator; DC, direct current; OC, optical coupler; TL, tunable laser; BPF, band pass filter; HNLF, highly nonlinear fiber.
Figure 9.
Experimental setup. EDFA, erbium-doped fiber amplifier; CIR, circulator; PC, polarization controller; IM, intensity modulator; DC, direct current; OC, optical coupler; TL, tunable laser; BPF, band pass filter; HNLF, highly nonlinear fiber.
Figure 9 shows the experiment setup. In the fiber laser system, the FBG adopted in this work has a reflectivity of 99%, and the FWHM bandwidth is about 0.18 nm. The FBG laser has the same structure as that in
Figure 2. The FBG laser with an output power of 13.41 mW is modulated through an intensity modulation to generate a pulse train. The pulse train has a frequency of 100 kHz and a duty cycle of 9.775%. At the end of EDFA-2, the amplified FBG laser with an output power of 15.47 mW and the TL with an output power of 7.28 mW are combined and launched into EDFA-3. The amplified pump from the FBG laser and the signal from TL are then directed into 1-km HNLF after a BPF. The HNLF in this work has a nonlinear coefficient of about 30 (W
−1 km
−1). At 1550 nm, the dispersion is +0.2 ps/nm/km, and the dispersion slope is +0.020 ps/nm
2/km.
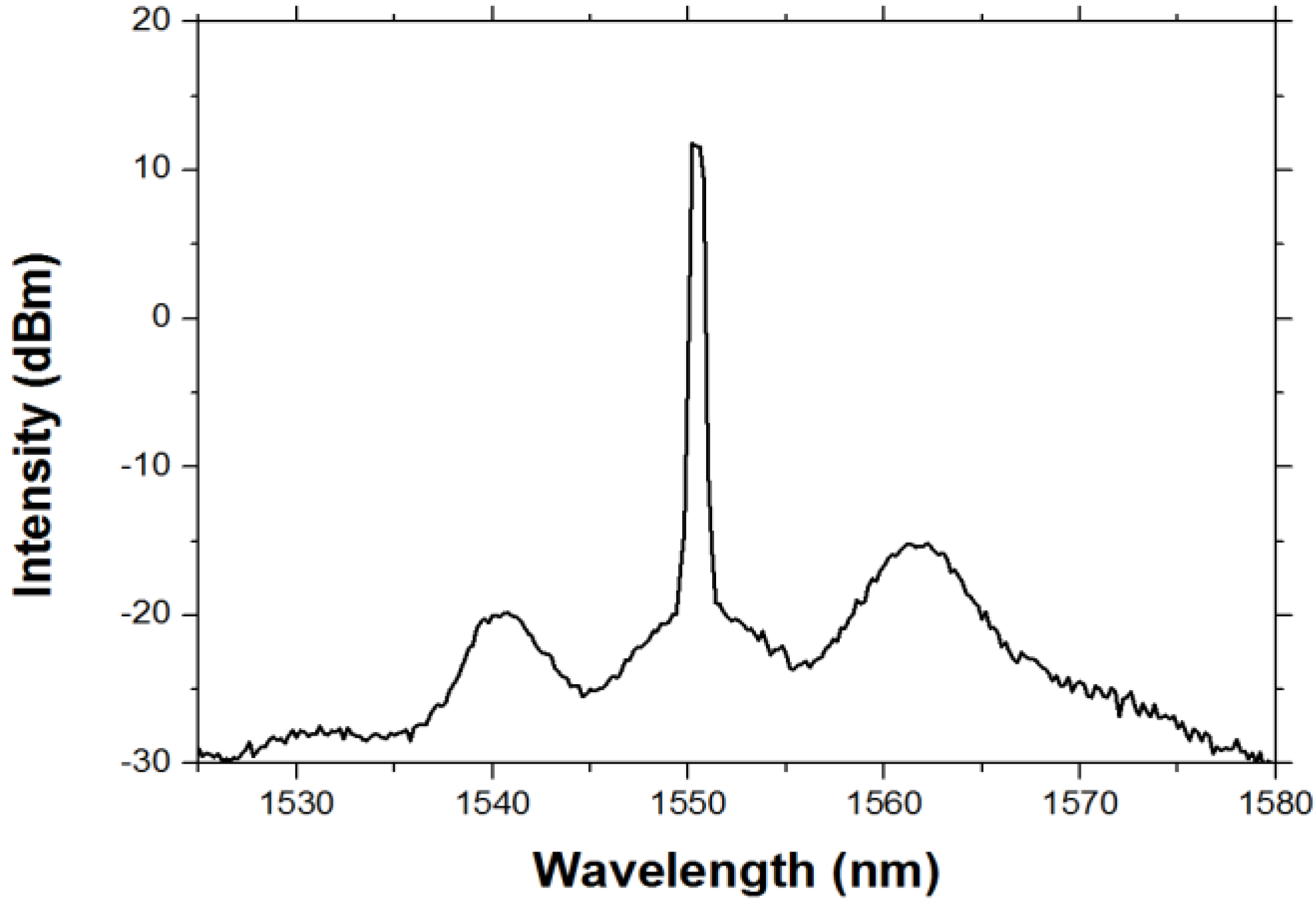
Figure 10 shows the ASE spectrum of the OPA. It is measured by using the pulse-modulated pump with an average power of about 15.47 mW. The ASE profile indicates significant OPA gain, which benefits the FWM efficiency and, thus, generates more idlers.
Figure 10.
The ASE gain spectrum due to parametric amplification.
Figure 10.
The ASE gain spectrum due to parametric amplification.
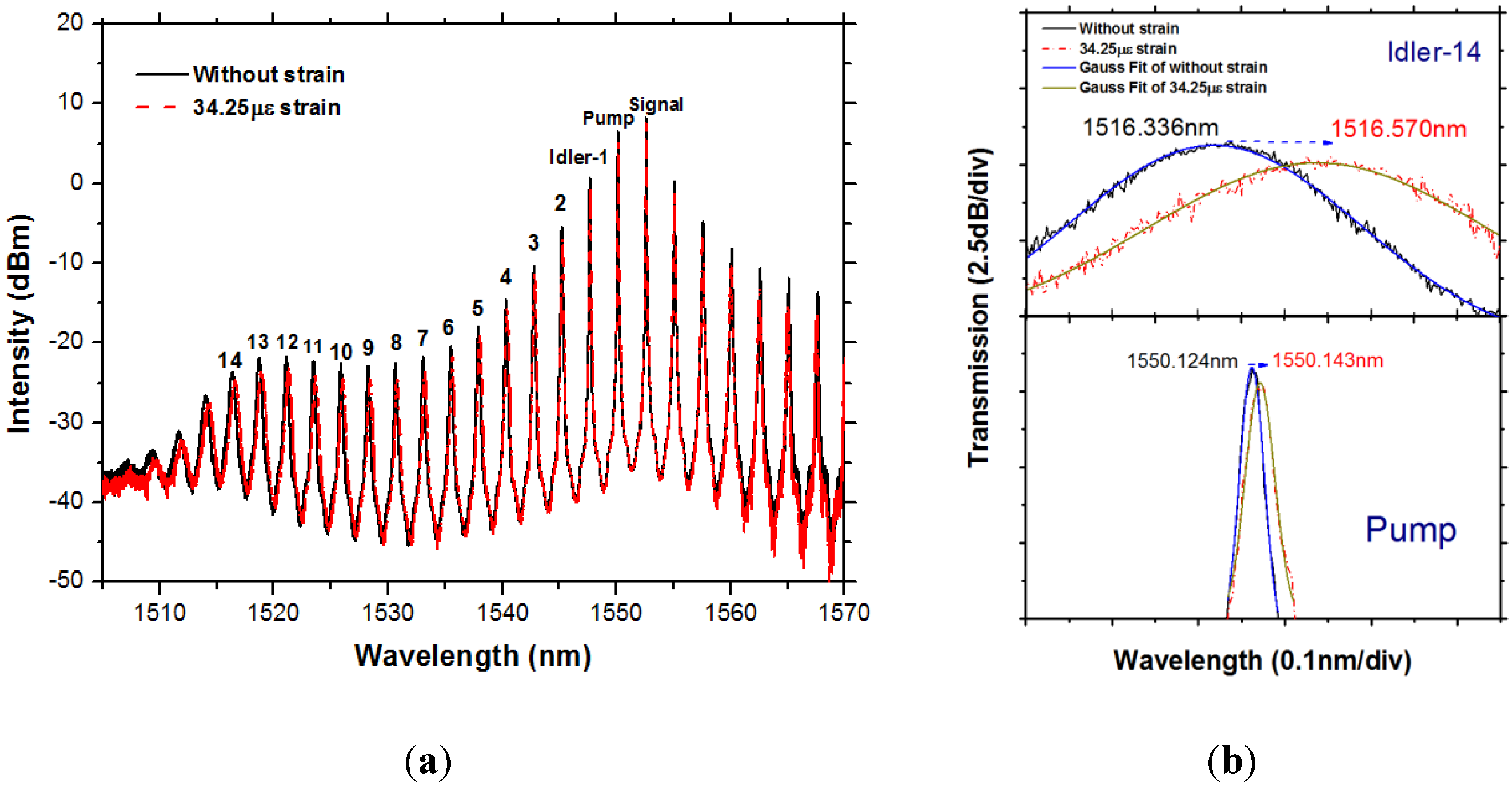
Figure 11.
Measured optical spectra after degenerated FWM (a) and the zoom-in spectra for the pump and Idler-14 (b). The spectra indicate significantly magnified wavelength drift after a 50-μm stretching over a 1460-mm total fiber length.
Figure 11.
Measured optical spectra after degenerated FWM (a) and the zoom-in spectra for the pump and Idler-14 (b). The spectra indicate significantly magnified wavelength drift after a 50-μm stretching over a 1460-mm total fiber length.
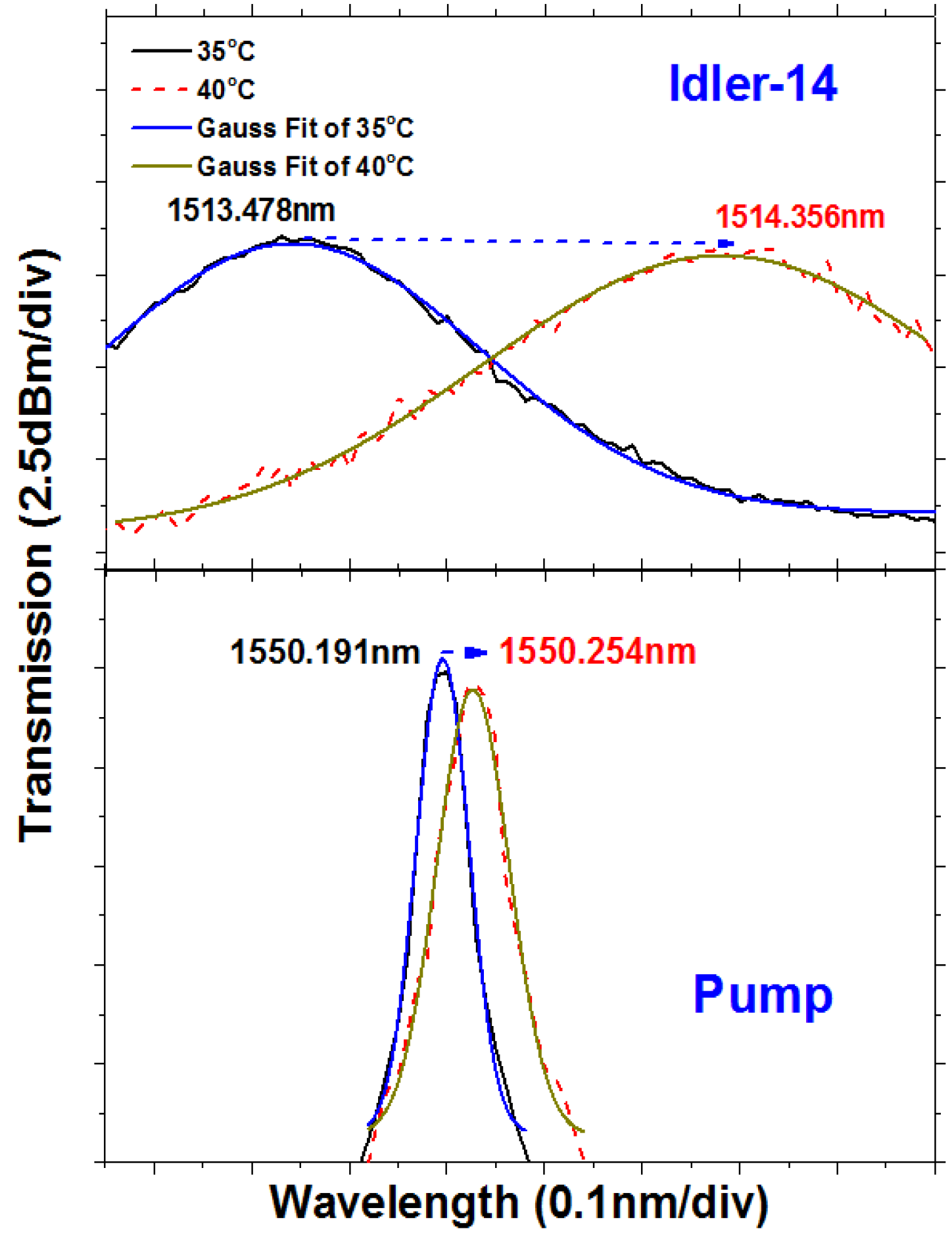
The FBG laser has a wavelength located at 1550.124 nm, and the signal wavelength (TL) is 1552.891 nm. There are more than 14 idlers at the short-wavelength side, as shown in
Figure 11a. Different strains of 34.25, 68.49, 102.74 and 136.99 με are loaded, and the magnified wavelength drift can be observed along with the increase of the idler number. Shown in the zoom-in spectra for a 34.25-με strain in
Figure 11b, the wavelength drift of 0.019 nm for the pump (from 1550.124 nm–1550.143 nm) has been magnified to 0.234 nm for Idler-14 (from 1516.336 nm–1516.570 nm). The results indicate a strain sensitivity of 13.3 pm/με, which is ~14-times magnified with respect to an initial intrinsic strain sensitivity of 0.96 pm/με for the FBG.
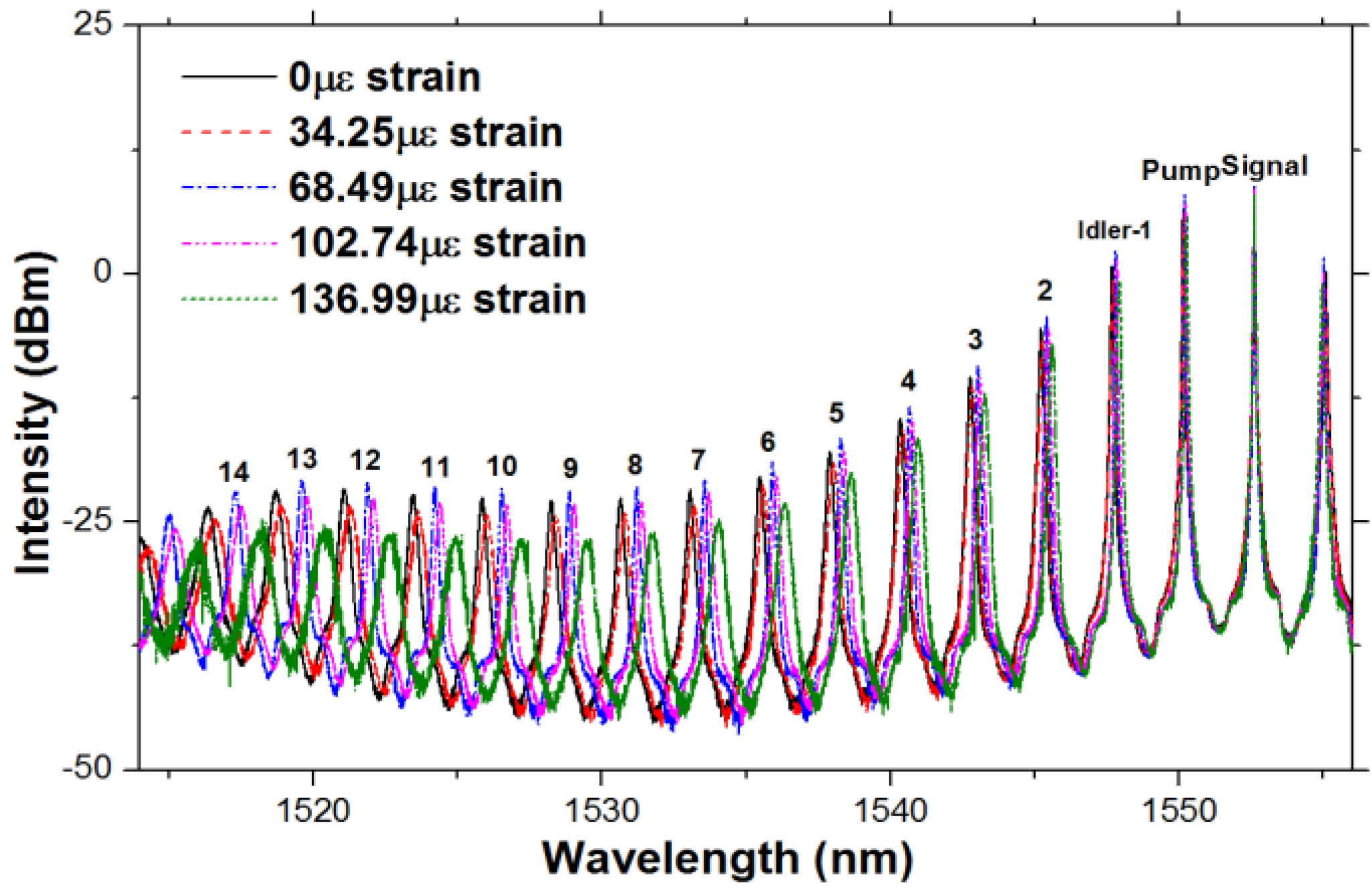
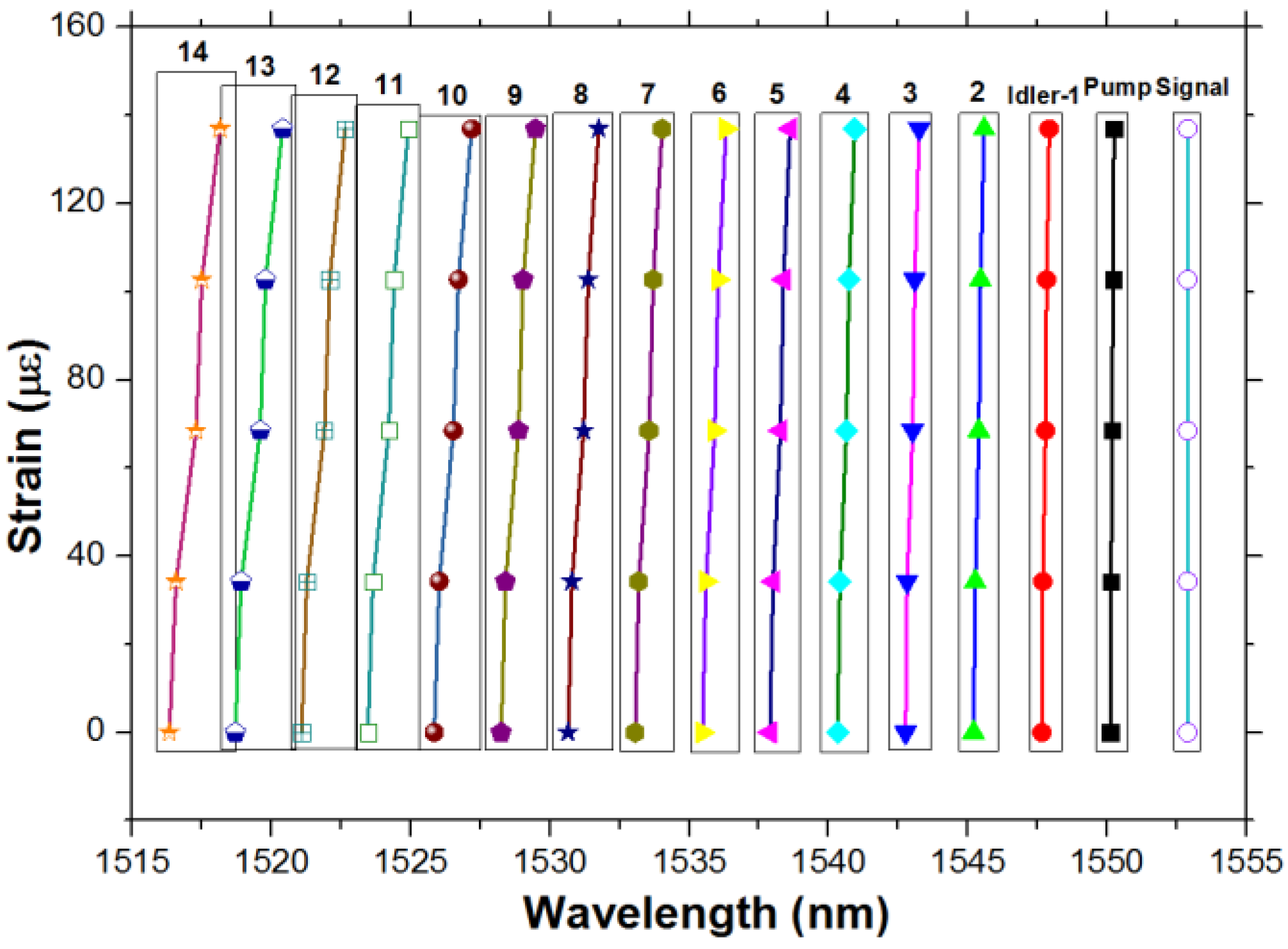
The optical spectra in
Figure 12 show the wavelength drift magnification with different stretching length to load different strains to the FBG. The magnification of the strain sensitivity is shown in
Figure 13, in which the curves have different slopes indicating magnified sensitivity. The slope of Idler-14 in
Figure 13 indicates a strain sensitivity of 13.3 pm /με (corresponding to an initial intrinsic strain sensitivity of 0.96 pm/με for the FBG).
Figure 12.
Optical spectra for FCM assisted by pump pulse modulation and OPA with different amount of strain (0, 34.25, 68.49, 102.74, 136.99 με).
Figure 12.
Optical spectra for FCM assisted by pump pulse modulation and OPA with different amount of strain (0, 34.25, 68.49, 102.74, 136.99 με).
Figure 13.
Strain sensitivity enhancement due to FCM assisted by pump pulse modulation and OPA with different amounts of strain.
Figure 13.
Strain sensitivity enhancement due to FCM assisted by pump pulse modulation and OPA with different amounts of strain.
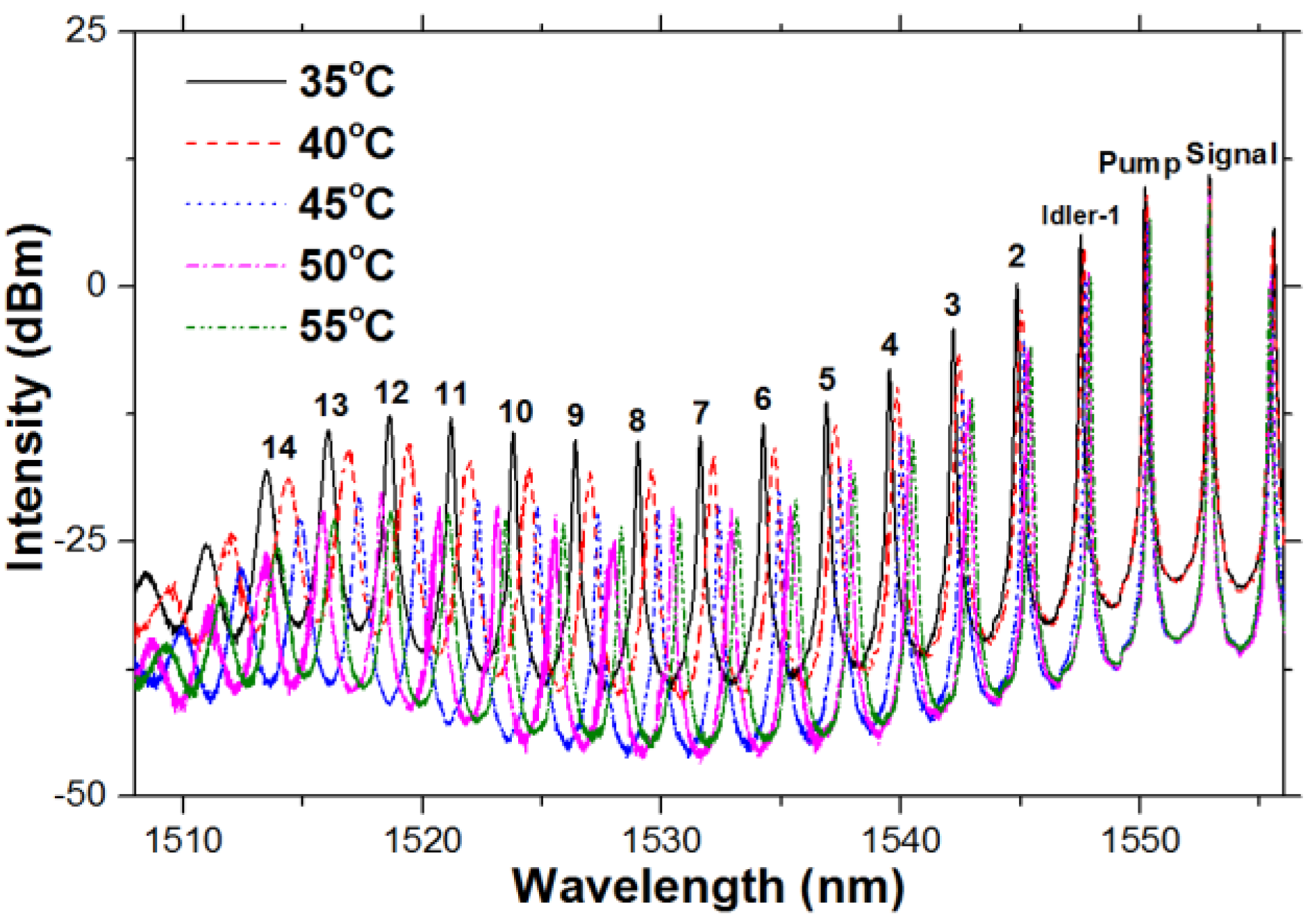
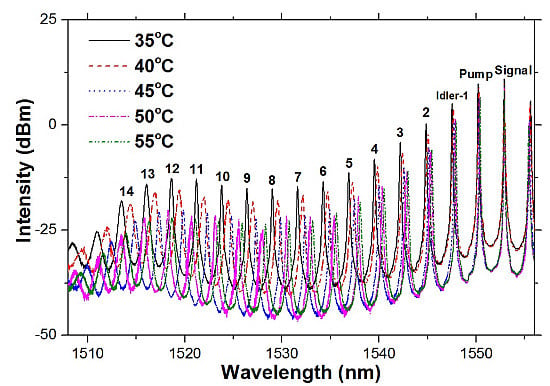
The temperature sensitivity of FBG can also be magnified based on the proposed method. The temperature of the FBG is adjusted by using a water bath. Shown in
Figure 14 are the wavelength drifts for the pump and Idler-14 with the temperature increasing from 35 °C–40 °C. We also measured the wavelength drift spectra at several temperatures (45, 50 and 55°C), as shown in
Figure 15.
Figure 14.
Optical spectra for the pump and idler-14 at temperatures of 35 °C and 40 °C.
Figure 14.
Optical spectra for the pump and idler-14 at temperatures of 35 °C and 40 °C.
Figure 15.
Optical spectra for wavelength drift magnification at different temperatures (35, 40, 45, 50 and 55 °C).
Figure 15.
Optical spectra for wavelength drift magnification at different temperatures (35, 40, 45, 50 and 55 °C).
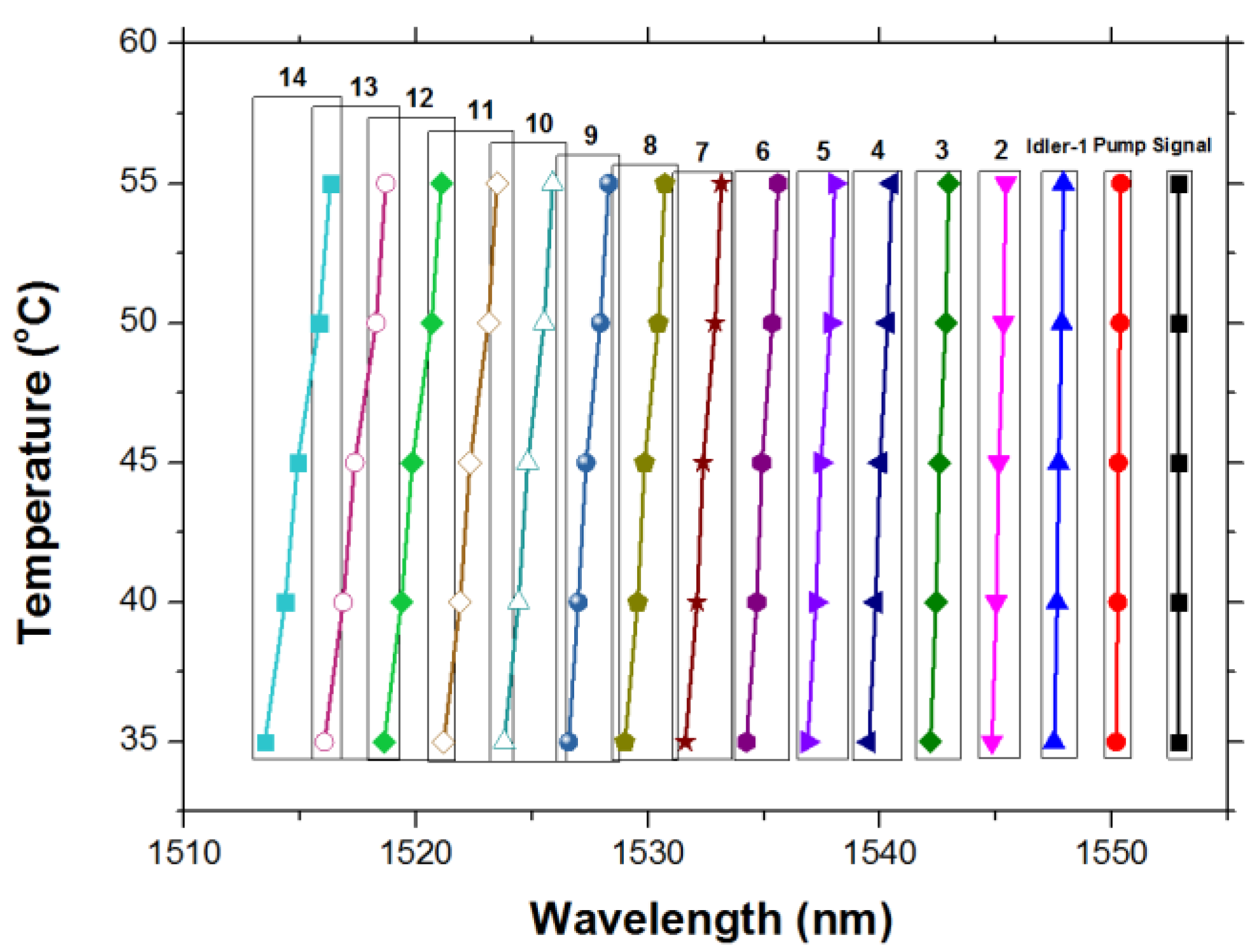
The wavelength drift from 35 °C–55 °C is measured to be 0.204, 0.4, 0.597 and 2.824 nm, respectively for the pump, Idler-1, Idler-2 and Idler-14. Therefore, the corresponding temperature sensitivities are 10.2, 20, 29.85 and 141.2pm/°C. Shown in
Figure 16 are temperature sensing curves for pump and idlers. The temperature sensitivity has been magnified by a factor of 14 at Ilder-14, which is a little less than our expected magnification factor of 15 times.
The measured sensitivity enhancements for the strain and temperature are both about 14 times at Idler-14, which is a little bit smaller compared with the expected value of 15 times. This is due to the limited resolution of OSA for precisely measuring the center wavelength of the pump and the idlers. The spectrum broadening by the pulse modulation is insignificant, since the modulation frequency is small. However, obvious spectrum broadening is observed at high-order idlers, as shown in
Figure 11 and
Figure 14. This is due to the multi-mode lasing of the FBG fiber laser, which makes the linewidth of the FBG laser quite large. One can use phase-shifted FBG with a much narrower bandwidth to realize single longitudinal mode operation, so that a much narrower linewidth of the FBG laser can be obtained, and the spectrum broadening at high-order idlers can be significantly reduced. On the other hand, one can also use low frequency modulation with a small duty cycle for reducing the modulation spectrum broadening. By doing so, the limitation can be effectively eased.
Figure 16.
Strain sensitivity enhancement due to frequency chirp magnification.
Figure 16.
Strain sensitivity enhancement due to frequency chirp magnification.
FWM has been utilized for many signal processing functions, including wavelength conversion, time-frequency conversion, phase-sensitive amplification, and so on. All of those applications of FWM are post-processing of the signal, which is of limited significance for optical communications, since it is a standard procedure. However, as for optical sensing, the post-processing of the sensing signal by FWM to enhance the sensitivity of a fiber sensor gives us the capability of improving the sensing performance without changing the sensor itself. Additionally, that is of great significance in field applications.