Study on the Effect of Clamping Structure on Wavefront Aberration of Large-Aperture Nd:Glass Laser Amplifier
Abstract
1. Introduction
2. Configuration
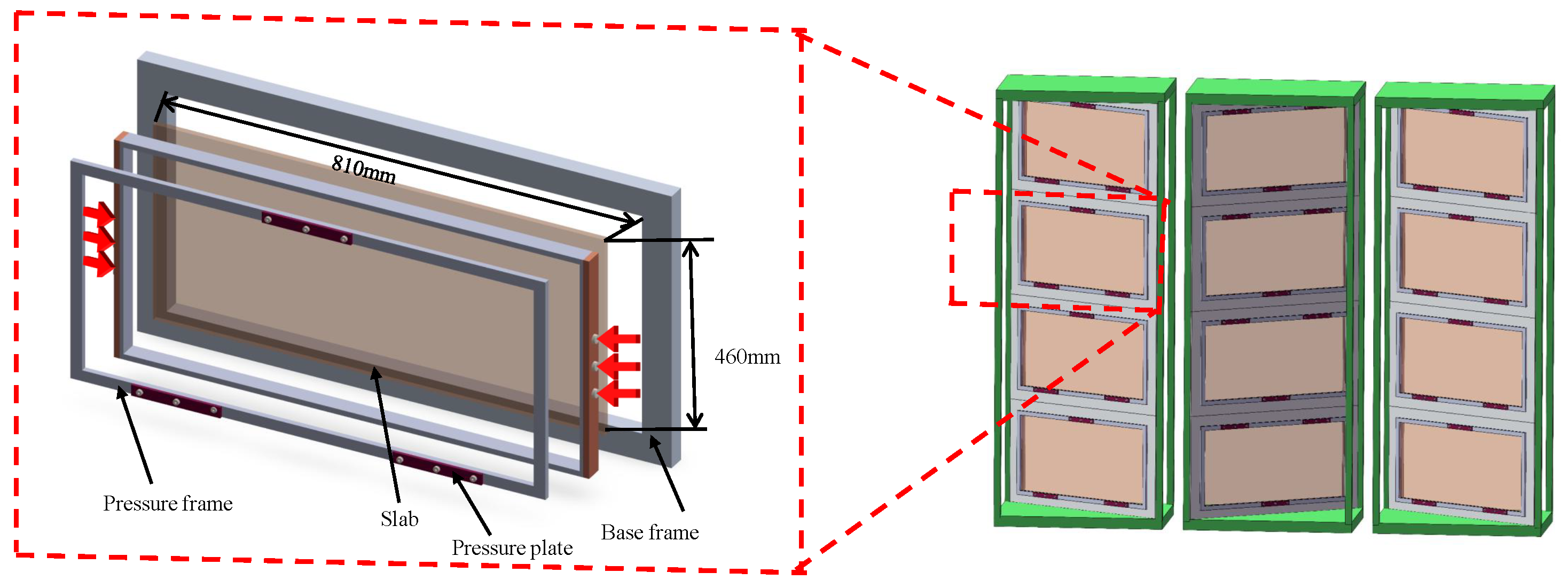
2.1. Large-Diameter Nd:Glass Clamping Structure
2.2. Experimental Setup and Measurement Methods
3. Theory
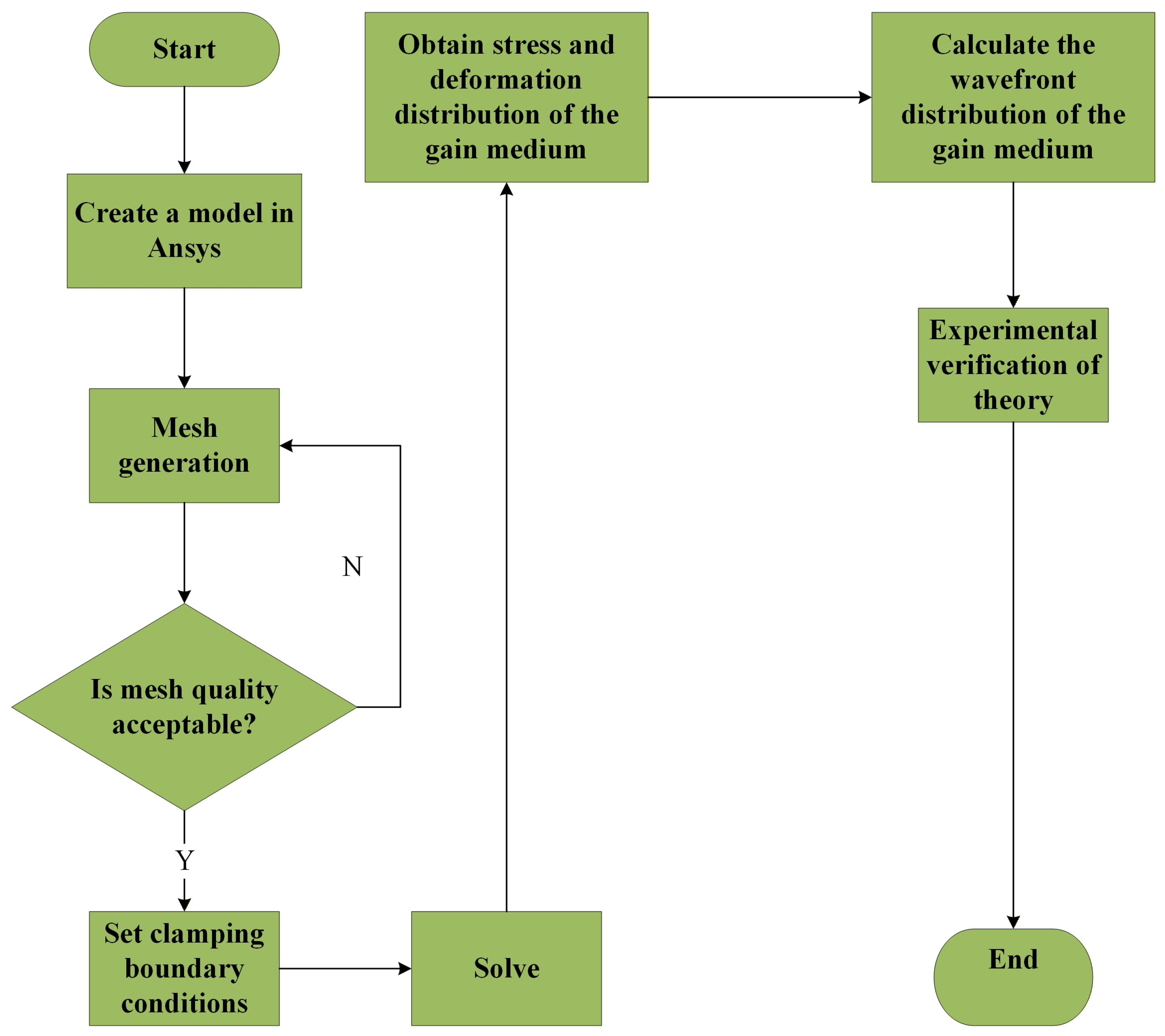
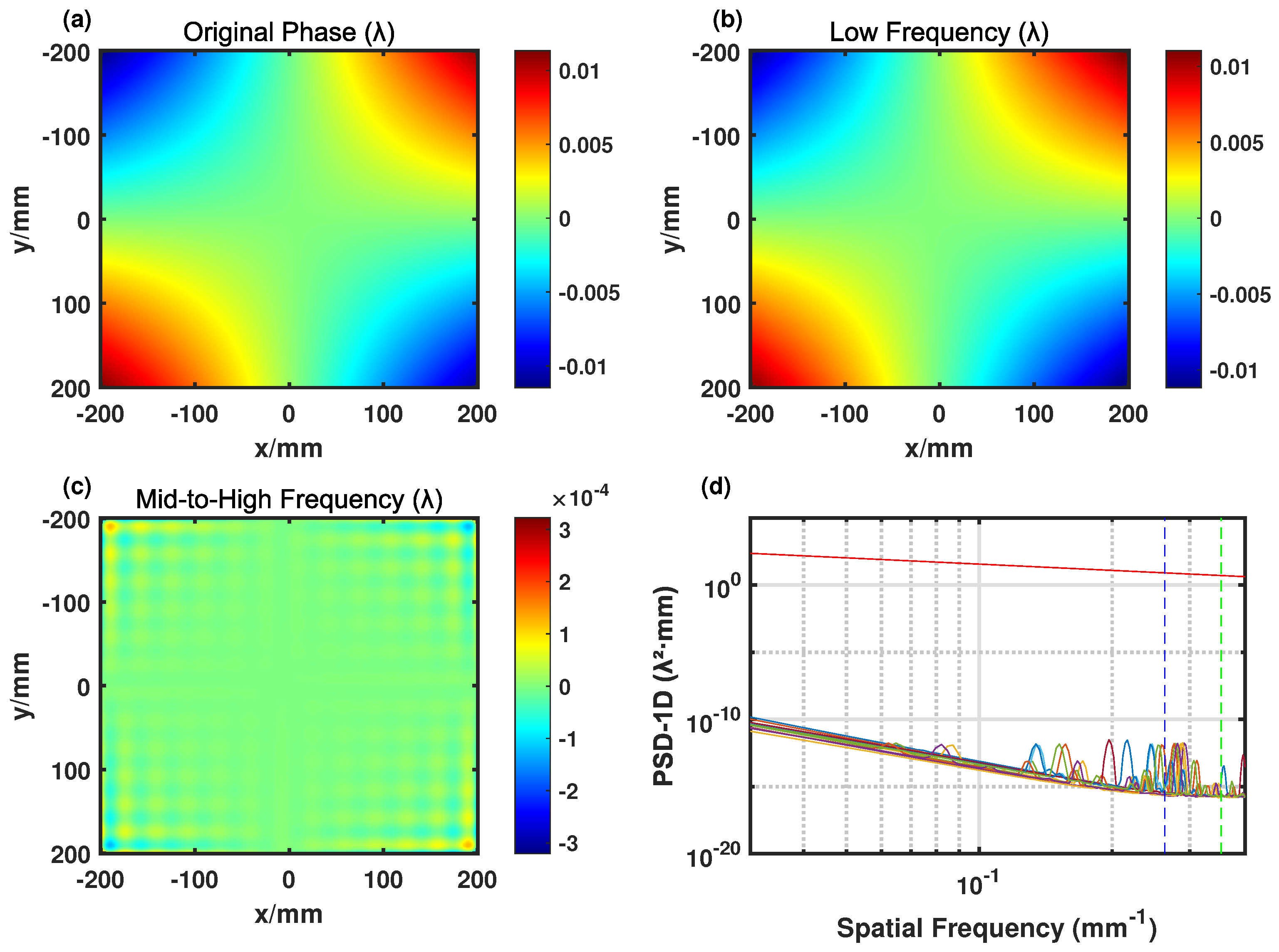
3.1. Simulation Processes and Modeling
3.2. Mechanical Model
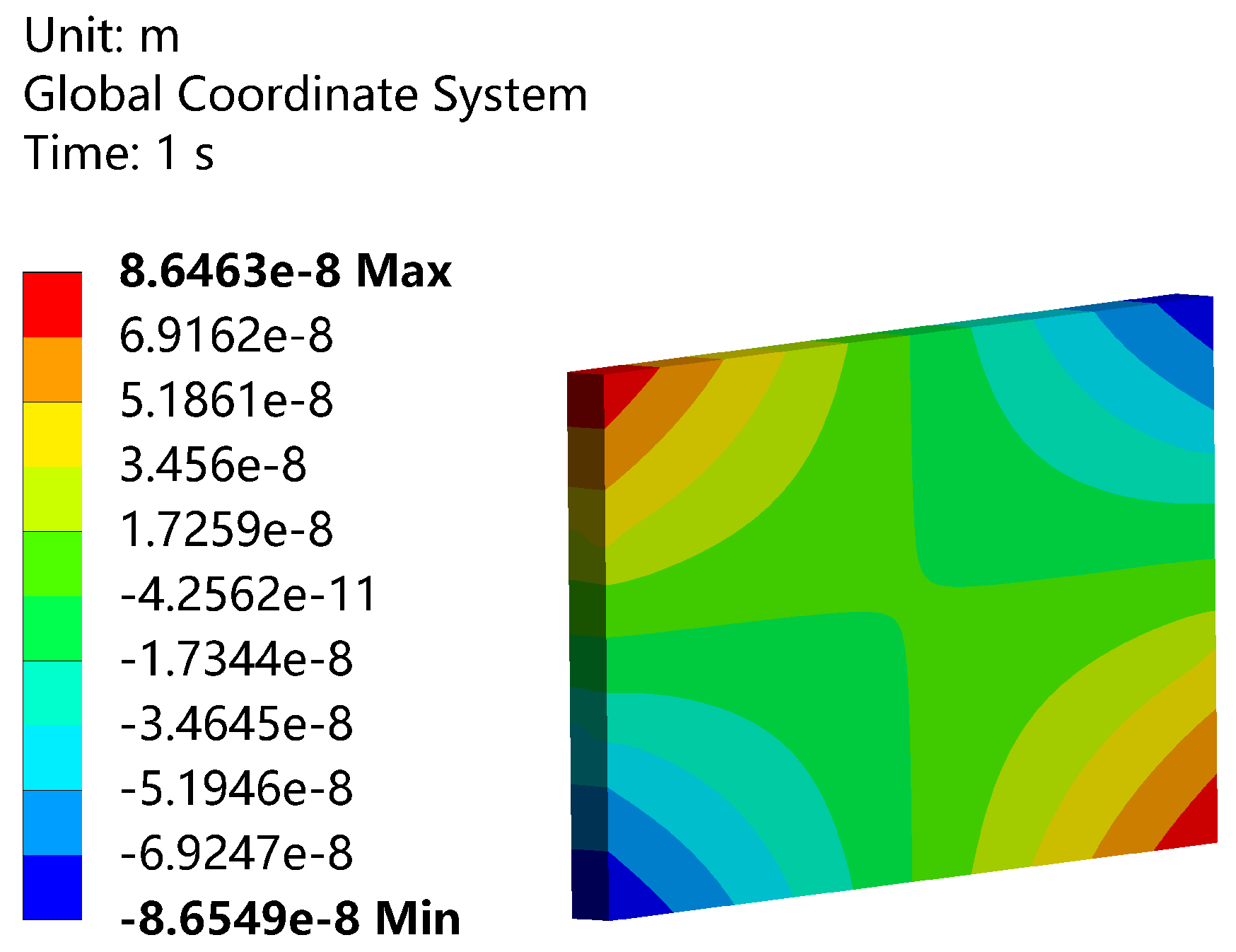
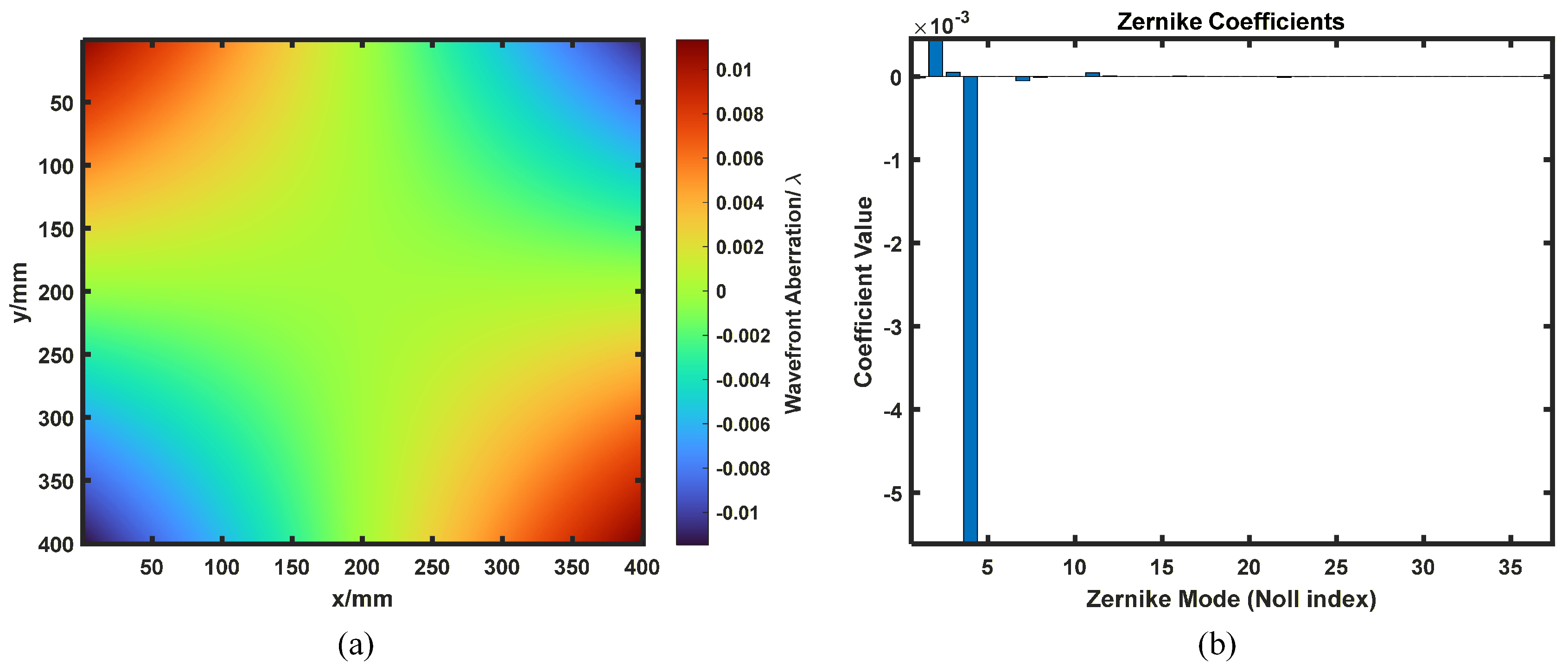
4. Result and Discussion
4.1. Wavefront Analysis Under Lateral Symmetric Clamping
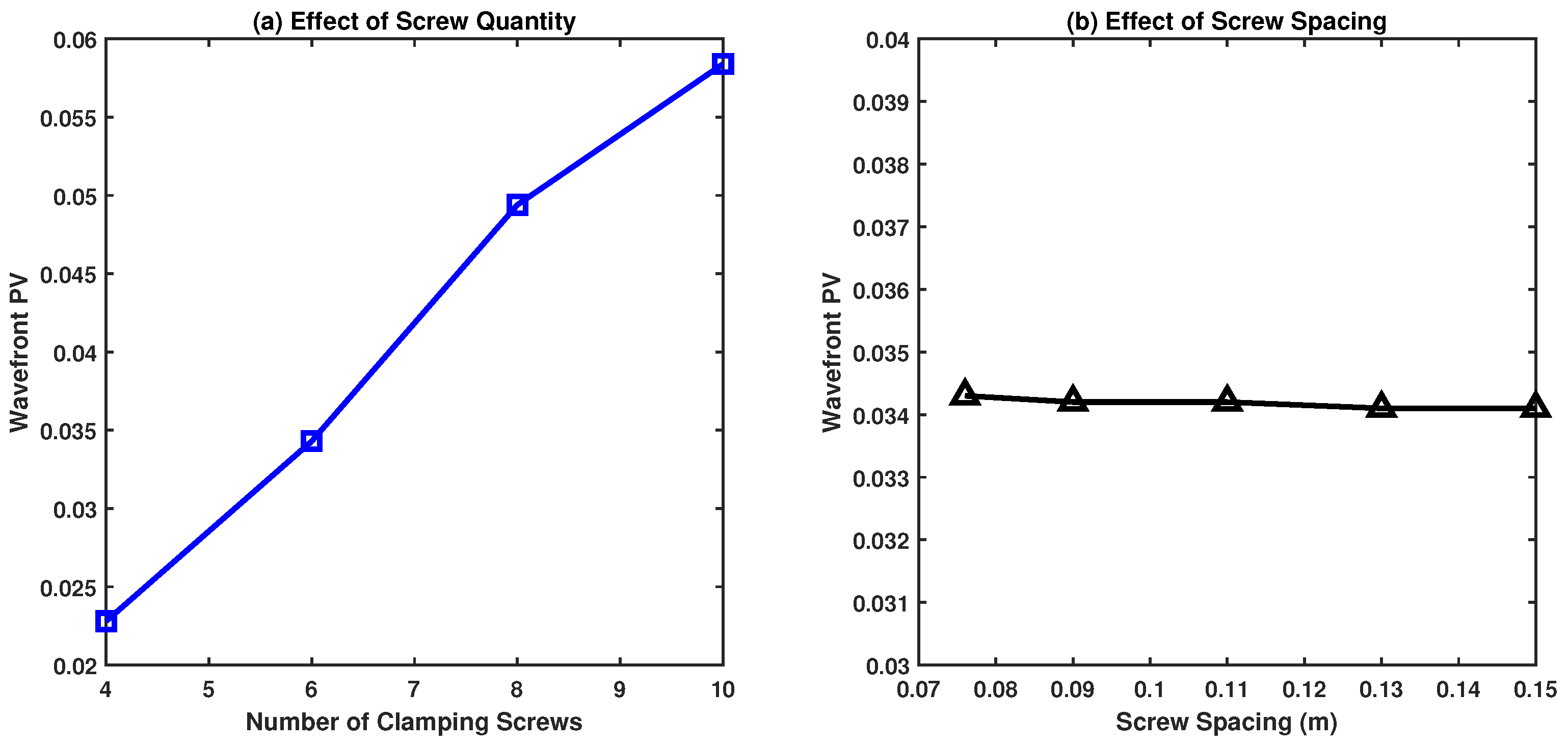
4.2. Effect of Set Screw Configuration on the Wavefront in Symmetrically Clamped Optics
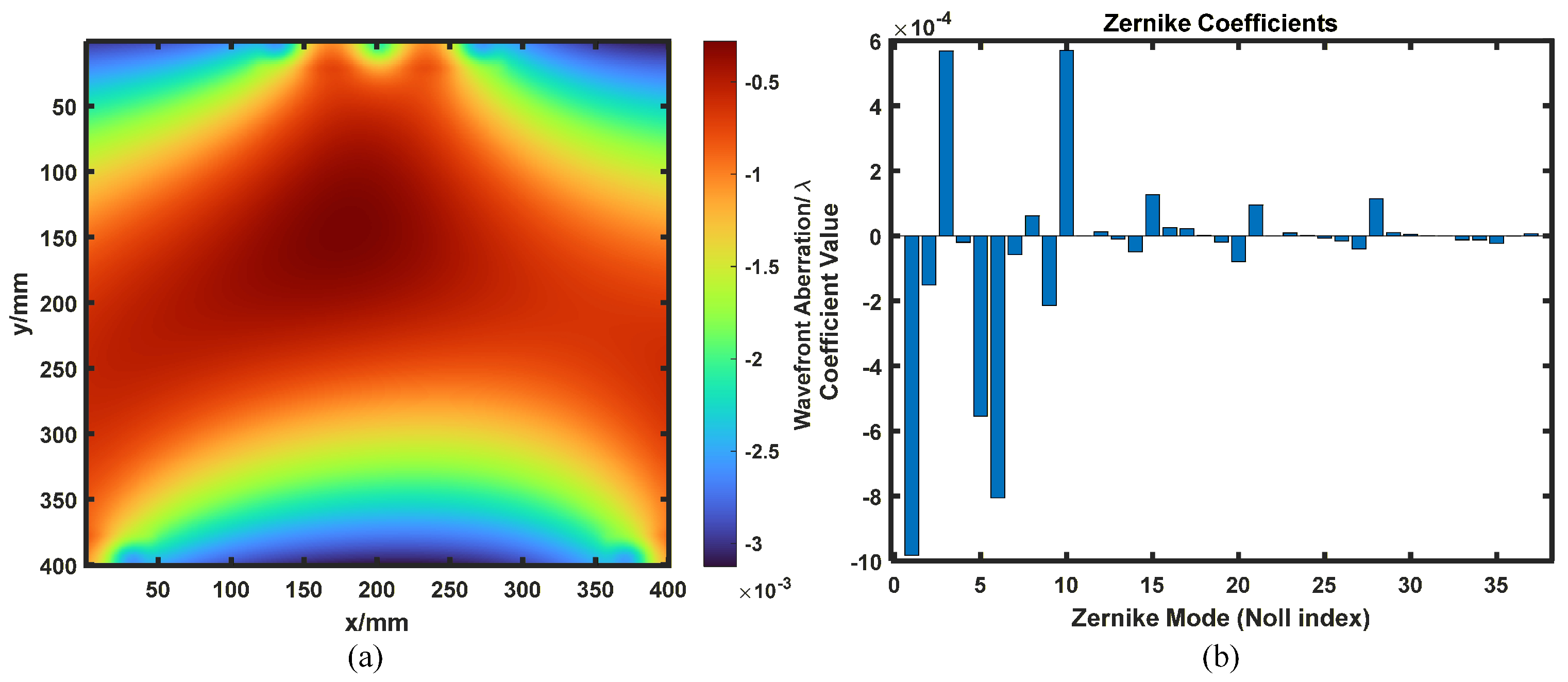
4.3. Wavefront Analysis Under Frontal Clamping
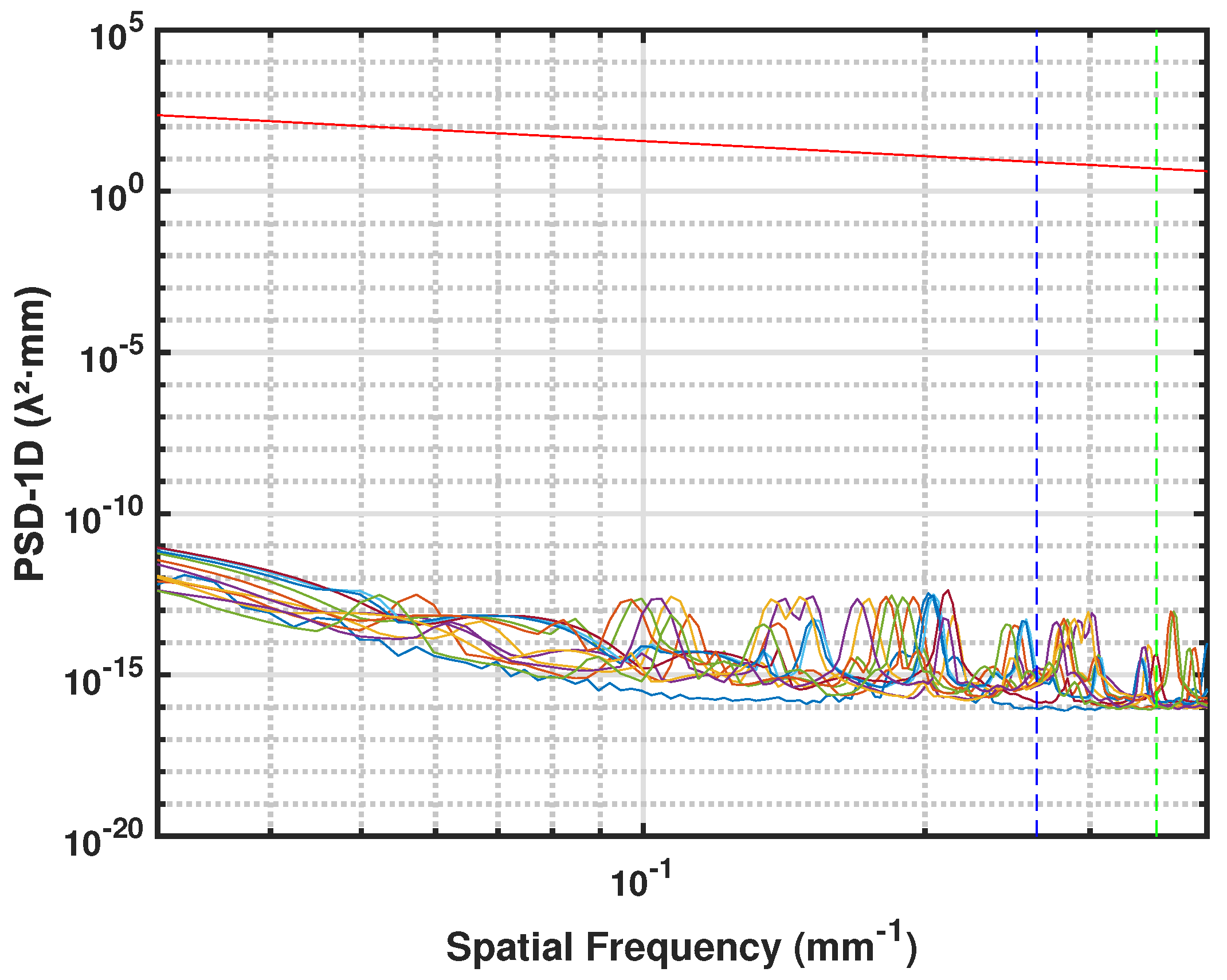
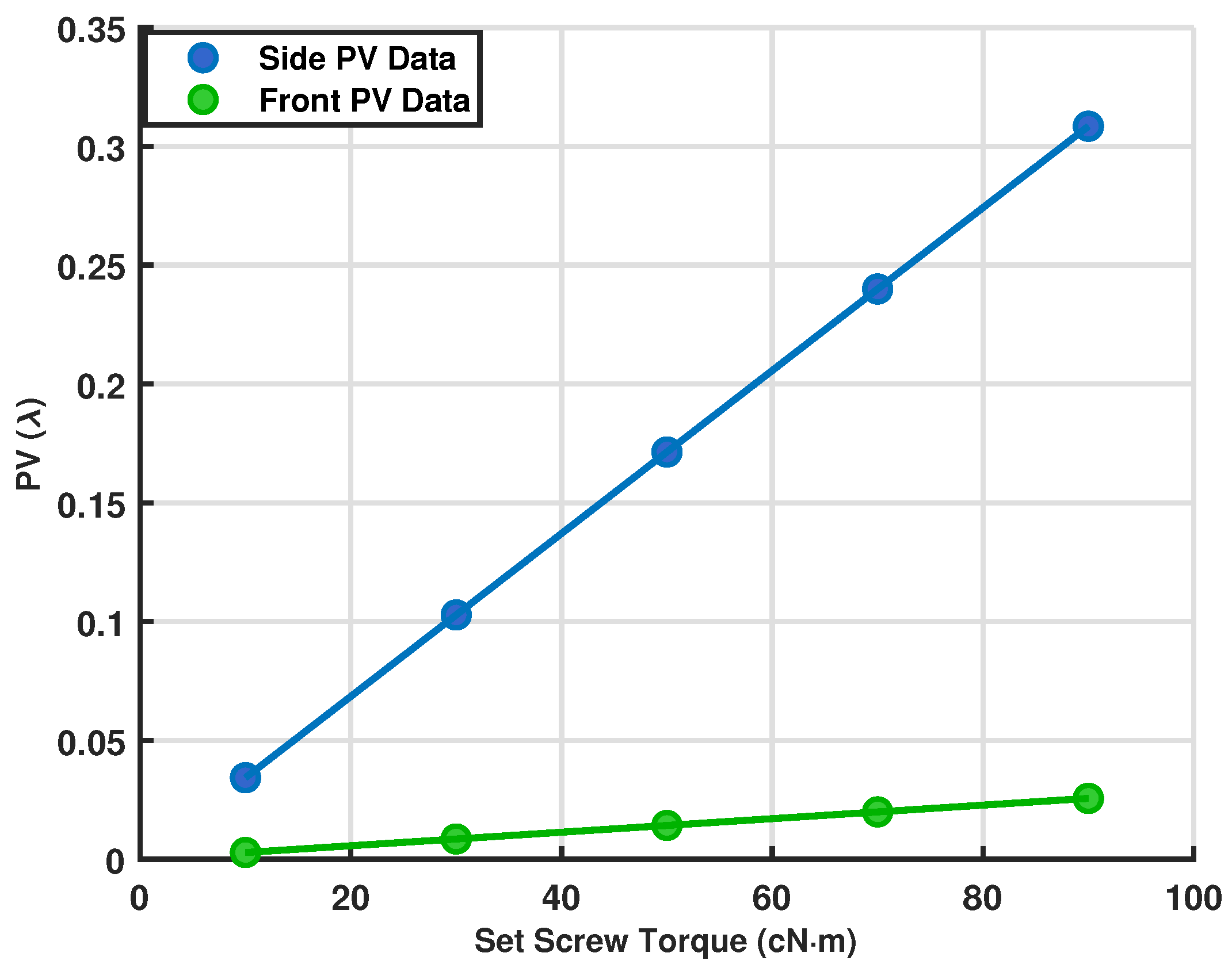
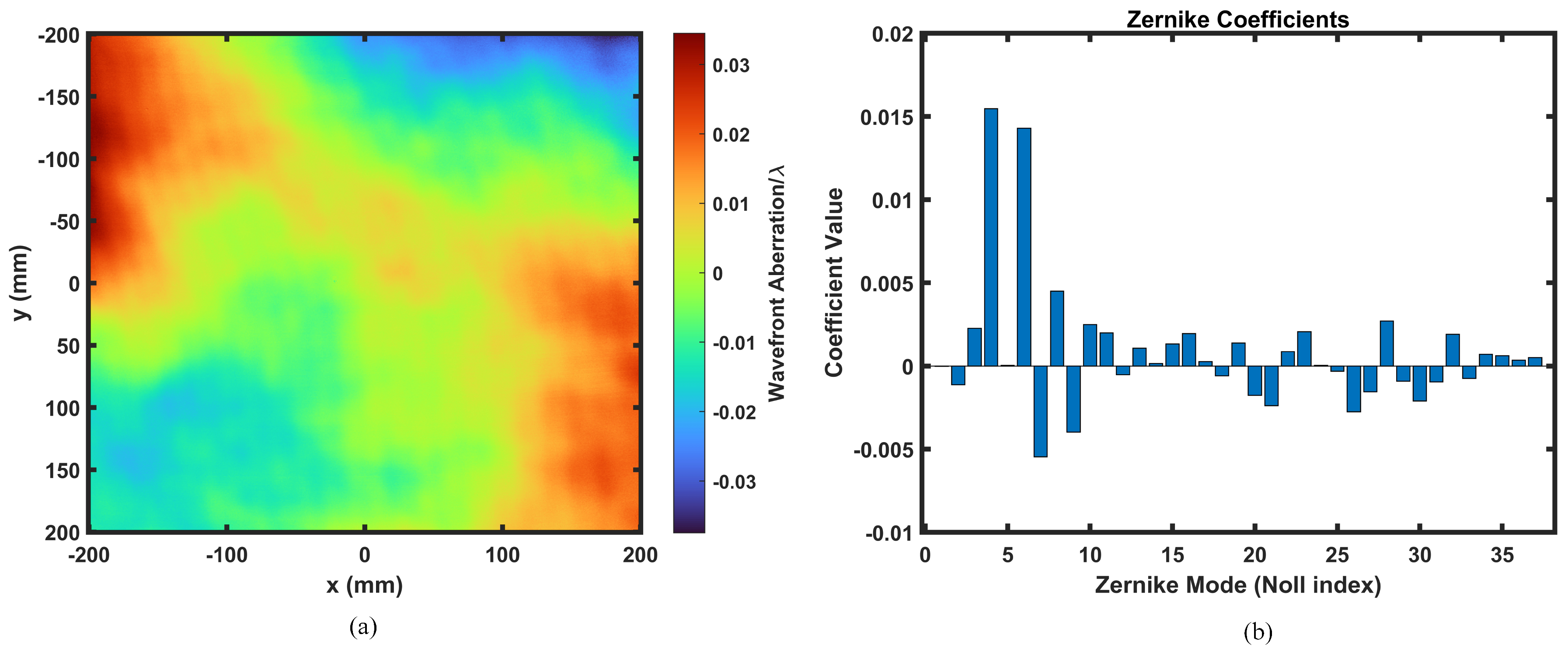
4.4. Experimental Results and Analysis
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Moses, E.I. Advances in inertial confinement fusion at the National Ignition Facility (NIF). Fusion Eng. Des. 2010, 85, 983–986. [Google Scholar] [CrossRef]
- Spaeth, M.L.; Manes, K.R.; Kalantar, D.H.; Miller, P.E.; Heebner, J.E.; Bliss, E.S.; Spec, D.R.; Parham, T.G.; Whitman, P.K.; Wegner, P.J.; et al. Description of the NIF Laser. Fusion Sci. Technol. 2016, 69, 25–145. [Google Scholar] [CrossRef]
- Beullier, J.; Erlandson, A.; Grebot, E.; Guenet, J.; Guenet, M.; Horvath, J.; Jancaitis, K.; Larson, D.; Lawson, J.; Letouze, G. Design and Performance of the Main Amplifier System for the National Ignition Facility; Office of Scientific Technical Information Technical Reports: Oak Ridge, TN, USA, 1999. [Google Scholar]
- Besnard, D. The Megajoule laser program—Ignition at hand. Eur. Phys. J. D 2006, 44, 207–213. [Google Scholar] [CrossRef]
- André, M.L. The French Megajoule Laser Project (LMJ). Fusion Eng. Des. 1999, 44, 43–49. [Google Scholar] [CrossRef]
- Fleurot, N.; Cavailler, C.; Bourgade, J. The Laser Mégajoule (LMJ) Project dedicated to inertial confinement fusion: Development and construction status. Fusion Eng. Des. 2005, 74, 147–154. [Google Scholar] [CrossRef]
- Li, S.; Lu, Z.; Fan, X.; Ding, L. Numerical investigation of the influence of wavefront distortion on the laser near-field characteristics. Laser Part. Beams 2017, 35, 1–8. [Google Scholar] [CrossRef]
- Yang, S.; Xing, T.; Ke, C.; Liang, J.; Ke, X. Effect of Wavefront Distortion on the Performance of Coherent Detection Systems: Theoretical Analysis and Experimental Research. Photonics 2023, 10, 493. [Google Scholar] [CrossRef]
- Ke, X.; Li, M. Laser beam distorted wavefront correction based on deformable mirror eigenmodes. Opt. Eng. 2019, 58, 1. [Google Scholar] [CrossRef]
- Wang, X.; Wang, J.; Guo, J.; Lu, X.; Wang, Y.; Xiao, Q.; Fan, W.; Li, X. Numerical Simulation of Thermo-Optic Effects in an Nd:glass Slab with Low Thermally Induced Wavefront Distortion. Photonics 2021, 8, 91. [Google Scholar] [CrossRef]
- Spaeth, M.; Manes, K.; Widmayer, C.; Williams, W.; Whitman, P.; Henesian, M.; Stowers, I.; Honig, J. The National Ignition Facility Wavefront Requirements and Optical Architecture. Opt. Eng. 2004, 43, 2854–2865. [Google Scholar] [CrossRef]
- Fu, X.; Liu, Q.; Gong, M. Wavefront aberration induced by beam passage through a water-convection-cooled Nd:YAG thin disk. J. Opt. 2013, 15, 055704. [Google Scholar] [CrossRef]
- Lupi, J.F.; Dalbies, P.M.; Cavaro, S.; Manac’h, P.; Bordenave, E.; Sajer, J.M.; Moreau, J.G.; Blanchot, N.; Neauport, J. Liquid-cooled Nd:phosphate split-slab large aperture amplifier pumped by flash-lamps. Opt. Laser Technol. 2022, 152, 108101. [Google Scholar] [CrossRef]
- Chonion, R.; Sajer, J.M.; Bordenave, E.; Le Palud, F.; Dalbies, P.M.; Neauport, J. Multiphysics model of liquid-cooled Nd:phosphate split-slabs in large aperture optical amplifiers. Opt. Express 2020, 28, 20162–20176. [Google Scholar] [CrossRef] [PubMed]
- Xiang, Y.; Li, K.; Wang, W.; Feng, B.; Han, W.; Wang, F. Surface Aberration Analysis for Large-Aperture and Ultra-Thin Crystal and New Type of Clamping Method with Low-Stress. Chin. J. Lasers 2017, 44, 0208001. (In Chinese) [Google Scholar] [CrossRef]
- Khorin, P.; Dzyuba, A.; Khonina, S. Optical wavefront aberration: Detection, recognition, and compensation techniques—A comprehensive review. Opt. Laser Technol. 2025, 191, 113342. [Google Scholar] [CrossRef]
- Timoshenko, S.; Goodier, J. Theory of Elasticity, 2nd ed.; McGraw-Hill: Columbus, OH, USA, 1951. [Google Scholar]
- Liu, B.; Sun, X.; Wang, H.; Yuan, Q.; Tian, M.; Chu, D.; Geng, Y. Polarization smoothing based on full Poincaré beams modulated by stress-engineered optics. Opt. Express 2024, 32, 11491–11508. [Google Scholar] [CrossRef]
- Huang, W.; Li, X.; Wang, J.; Lu, X.; Zhang, Y.; Fan, W.; Lin, Z. Theoretical and experimental investigations on wavefront distortion and thermal-stress induced birefringence in a laser diode pumped helium gas-cooled multislab Nd:glass laser amplifier. Acta Phys. Sin. 2015, 64, 087801. (In Chinese) [Google Scholar] [CrossRef]
- Noll, R.J. Zernike polynomials and atmospheric turbulence. J. Opt. Soc. Am. 1976, 66, 207–211. [Google Scholar] [CrossRef]
- Su, J.; Wei, X.; Ma, C.; Yuan, J. Study on the Wavefront PSD Retrieved Algorithm and Focal Properties of High Power Laser Beam. Chin. J. Lasers 2002, A29, 285–288. (In Chinese) [Google Scholar]


| Parameter | Value |
|---|---|
| Material Parameters | |
| Density/ | 2870 kg/m3 |
| Elastic modulus/E | 58.3 GPa |
| Poisson’s ratio/ | 0.26 |
| Index of refraction/ (1053 nm) | 1.535 |
| Specific heat/c | 0.72 kJ/(kg·K) |
| Thermal conductivity/k | 0.59 W/(m·K) |
| Thermal expansion coefficient/ | 116 × 10−7 K−1 |
| Parameter | Change Direction | Normalized Sensitivity S | Influence Level |
|---|---|---|---|
| Young’s modulus E | High | ||
| Young’s modulus E | High | ||
| Poisson’s ratio | Low | ||
| Poisson’s ratio | Low |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license.
Share and Cite
Chen, Y.; Chen, L.; Shao, T.; Xie, Y.; Sun, X.; Pang, H.; An, Q.; Wu, H.; Liu, L. Study on the Effect of Clamping Structure on Wavefront Aberration of Large-Aperture Nd:Glass Laser Amplifier. Photonics 2026, 13, 18. https://doi.org/10.3390/photonics13010018
Chen Y, Chen L, Shao T, Xie Y, Sun X, Pang H, An Q, Wu H, Liu L. Study on the Effect of Clamping Structure on Wavefront Aberration of Large-Aperture Nd:Glass Laser Amplifier. Photonics. 2026; 13(1):18. https://doi.org/10.3390/photonics13010018
Chicago/Turabian StyleChen, Yangyang, Lin Chen, Ting Shao, Yu Xie, Xibo Sun, Huan Pang, Qier An, Honghong Wu, and Lanqin Liu. 2026. "Study on the Effect of Clamping Structure on Wavefront Aberration of Large-Aperture Nd:Glass Laser Amplifier" Photonics 13, no. 1: 18. https://doi.org/10.3390/photonics13010018
APA StyleChen, Y., Chen, L., Shao, T., Xie, Y., Sun, X., Pang, H., An, Q., Wu, H., & Liu, L. (2026). Study on the Effect of Clamping Structure on Wavefront Aberration of Large-Aperture Nd:Glass Laser Amplifier. Photonics, 13(1), 18. https://doi.org/10.3390/photonics13010018




