Advances in Optical Metrology: High-Bandwidth Digital Holography for Transparent Objects Analysis
Abstract
1. Introduction
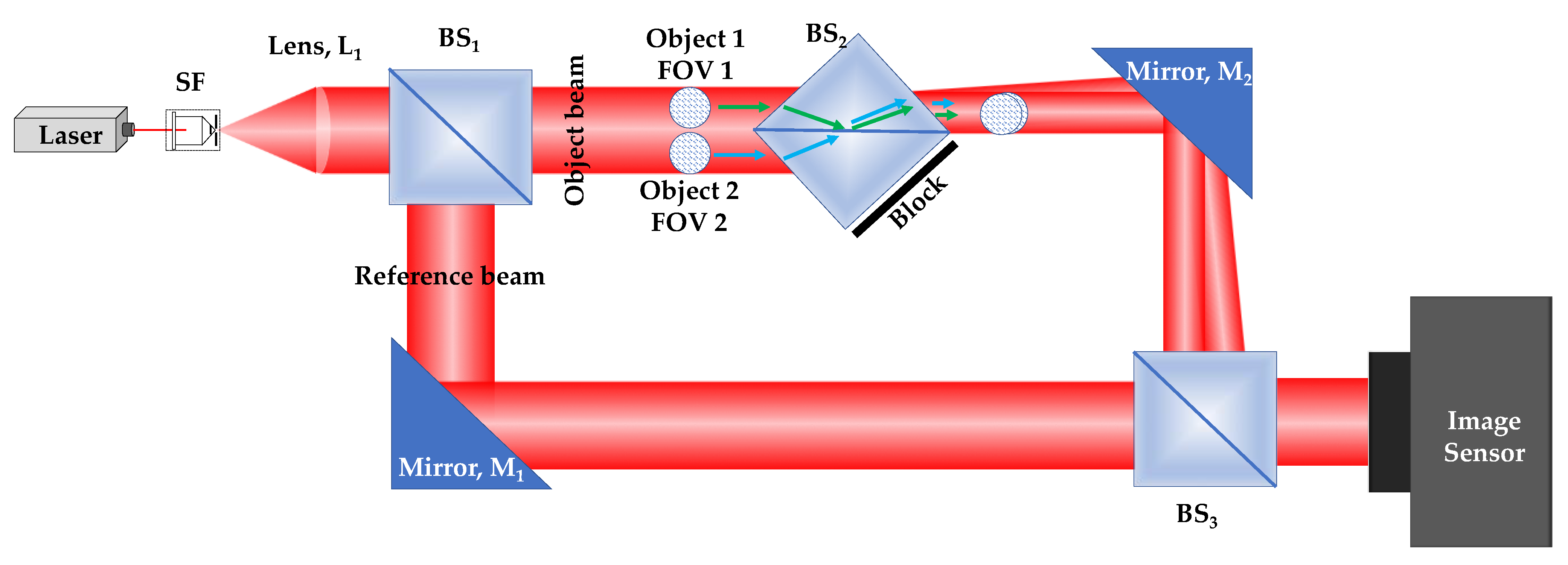
2. Materials and Methods
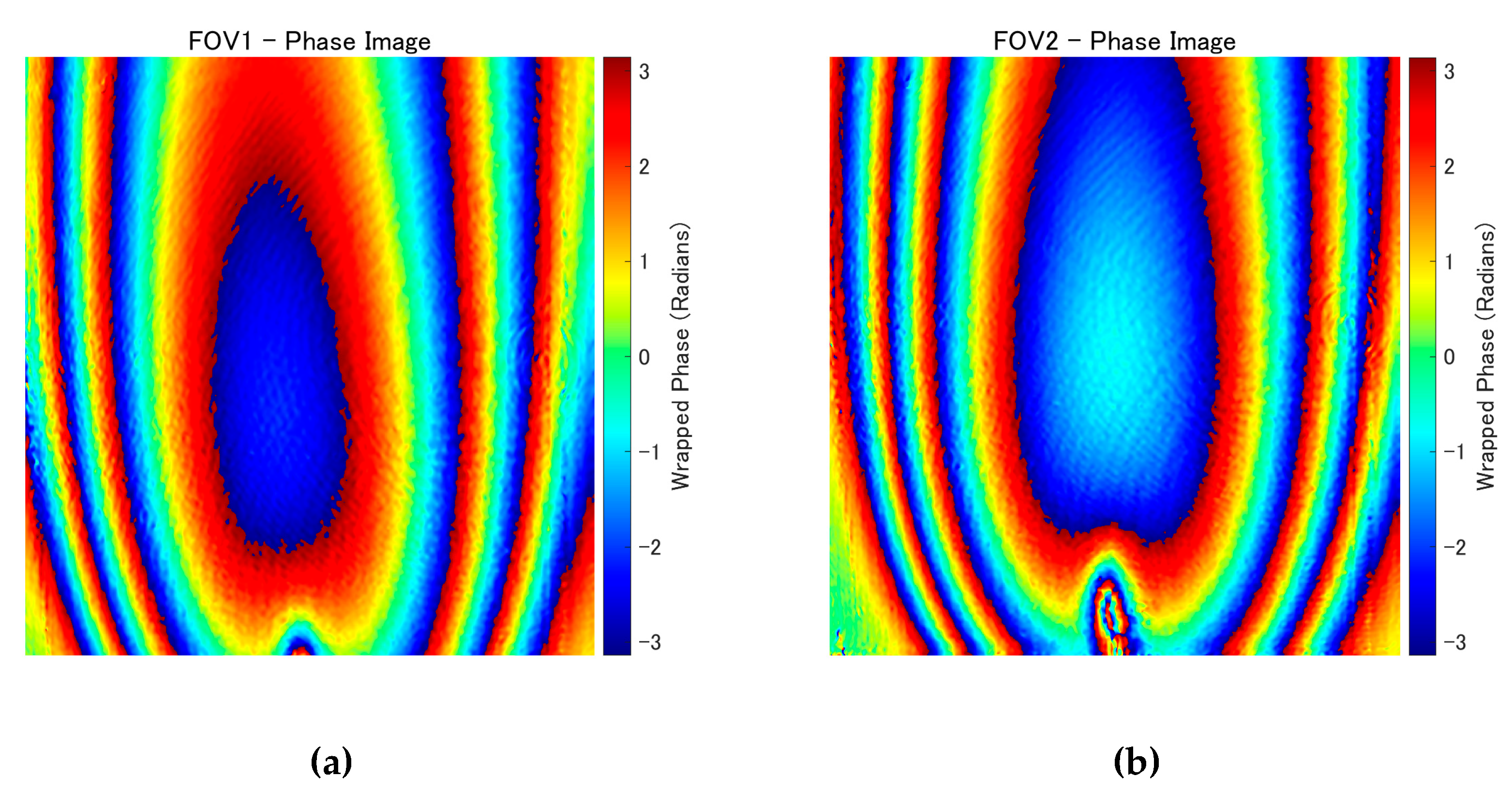
3. Results
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Santiago, J.G.; Wereley, S.T.; Meinhart, C.D.; Beebe, D.J.; Adrian, R.J. A Particle Image Velocimetry System for Microfluidics. Exp. Fluids 1998, 25, 316–319. [Google Scholar] [CrossRef]
- Docquier, N.; Candel, S. Combustion Control and Sensors: A Review. Prog. Energy Combust. Sci. 2002, 28, 107–150. [Google Scholar] [CrossRef]
- Wang, L.V.; Hu, S. Photoacoustic Tomography: In Vivo Imaging from Organelles to Organs. Science 2012, 335, 1458–1462. [Google Scholar] [CrossRef] [PubMed]
- Song, G.; Wang, Y.; Tan, D.Q. A Review of Surface Roughness Impact on Dielectric Film Properties. IET Nanodielectrics 2022, 5, 1–23. [Google Scholar] [CrossRef]
- Zhang, K.; Choi, S.; Sasaki, O.; Luo, S.; Suzuki, T.; Liu, Y.; Pu, J. Large Thickness Measurement of Glass Plates with a Spectrally Resolved Interferometer Using Variable Signal Positions. OSA Contin. 2021, 4, 1792. [Google Scholar] [CrossRef]
- Kumar, Y.P.; Chatterjee, S. Thickness Measurement of Transparent Glass Plates Using a Lateral Shearing Cyclic Path Optical Configuration Setup and Polarization Phase Shifting Interferometry. Appl. Opt. 2010, 49, 6552. [Google Scholar] [CrossRef]
- Kim, S.; Kim, Y.; Shin, S.-C.; Hibino, K.; Sugita, N. Interferometric Thickness Measurement of Glass Plate by Phase-Shifting Analysis Using Wavelength Scanning with Elimination of Bias Phase Error. Opt. Rev. 2021, 28, 48–57. [Google Scholar] [CrossRef]
- Omega Engineering. Temperature Measurement Handbook; Omega Press: New Lebanon, NY, USA, 1995. [Google Scholar]
- Maldague, X.P. Theory and Practice of Infrared Technology for Nondestructive Testing; Wiley Series in Microwave and Optical Engineering; Wiley: New York, NY, USA, 2001; ISBN 978-0-471-18190-3. [Google Scholar]
- Hariharan, P. Optical Interferometry; Elsevier: Amsterdam, The Netherlands, 2003; ISBN 978-0-12-311630-7. [Google Scholar]
- Schnars, U.; Jüptner, W. Direct Recording of Holograms by a CCD Target and Numerical Reconstruction. Appl. Opt. 1994, 33, 179. [Google Scholar] [CrossRef]
- Sheridan, J.T.; Kostuk, R.K.; Gil, A.F.; Wang, Y.; Lu, W.; Zhong, H.; Tomita, Y.; Neipp, C.; Francés, J.; Gallego, S.; et al. Roadmap on Holography. J. Opt. 2020, 22, 123002. [Google Scholar] [CrossRef]
- Kreis, T.M. Frequency Analysis of Digital Holography. Opt. Eng. 2002, 41, 771. [Google Scholar] [CrossRef]
- Shaked, N.T.; Katz, B.; Rosen, J. Review of Three-Dimensional Holographic Imaging by Multiple-Viewpoint-Projection Based Methods. Appl. Opt. 2009, 48, H120. [Google Scholar] [CrossRef] [PubMed]
- Stępień, P.; Korbuszewski, D.; Kujawińska, M. Digital Holographic Microscopy with Extended Field of View Using Tool for Generic Image Stitching. ETRI J. 2019, 41, 73–83. [Google Scholar] [CrossRef]
- Di, J.; Zhao, J.; Jiang, H.; Zhang, P.; Fan, Q.; Sun, W. High Resolution Digital Holographic Microscopy with a Wide Field of View Based on a Synthetic Aperture Technique and Use of Linear CCD Scanning. Appl. Opt. 2008, 47, 5654. [Google Scholar] [CrossRef] [PubMed]
- Sha, B.; Liu, X.; Ge, X.-L.; Guo, C.-S. Fast Reconstruction of Off-Axis Digital Holograms Based on Digital Spatial Multiplexing. Opt. Express 2014, 22, 23066. [Google Scholar] [CrossRef]
- Girshovitz, P.; Shaked, N.T. Doubling the Field of View in Off-Axis Low-Coherence Interferometric Imaging. Light Sci. Appl. 2014, 3, e151. [Google Scholar] [CrossRef]
- Shaked, N.T.; Micó, V.; Trusiak, M.; Kuś, A.; Mirsky, S.K. Off-Axis Digital Holographic Multiplexing for Rapid Wavefront Acquisition and Processing. Adv. Opt. Photon. 2020, 12, 556. [Google Scholar] [CrossRef]
- Rubin, M.; Dardikman, G.; Mirsky, S.K.; Turko, N.A.; Shaked, N.T. Six-Pack off-Axis Holography. Opt. Lett. 2017, 42, 4611. [Google Scholar] [CrossRef]
- Tayebi, B.; Sharif, F.; Jafarfard, M.R.; Kim, D.Y. Double-Field-of-View, Quasi-Common-Path Interferometer Using Fourier Domain Multiplexing. Opt. Express 2015, 23, 26825. [Google Scholar] [CrossRef]
- Tayebi, B.; Kim, W.; Yoon, B.-J.; Han, J.-H. Real-Time Triple Field of View Interferometry for Scan-Free Monitoring of Multiple Objects. IEEE/ASME Trans. Mechatron. 2018, 23, 160–166. [Google Scholar] [CrossRef]
- Zhang, W.; Cao, L.; Jin, G.; Brady, D. Full Field-of-View Digital Lens-Free Holography for Weak-Scattering Objects Based on Grating Modulation. Appl. Opt. 2018, 57, A164. [Google Scholar] [CrossRef]
- Lee, B.; Jang, C.; Kim, D.; Lee, B. Single Grating Reflective Digital Holography With Double Field of View. IEEE Trans. Ind. Inf. 2019, 15, 6155–6161. [Google Scholar] [CrossRef]
- Kumar, M.; Pensia, L.; Kumar, R. Single-Shot off-Axis Digital Holographic System with Extended Field-of-View by Using Multiplexing Method. Sci. Rep. 2022, 12, 16462. [Google Scholar] [CrossRef] [PubMed]
- Pensia, L.; Kumar, M.; Kumar, R. Dual Field-of-View Off-Axis Spatially Multiplexed Digital Holography Using Fresnel’s Bi-Mirror. Sensors 2024, 24, 731. [Google Scholar] [CrossRef] [PubMed]
- Kumar, M.; Yoneda, N.; Pensia, L.; Muniraj, I.; Anand, V.; Kumar, R.; Murata, T.; Awatsuji, Y.; Matoba, O. Light Origami Multi-Beam Interference Digital Holographic Microscope for Live Cell Imaging. Opt. Laser Technol. 2024, 176, 110961. [Google Scholar] [CrossRef]
- Kumar, M.; Murata, T.; Matoba, O. Double Field-of-View Single-Shot Common-Path off-Axis Reflective Digital Holographic Microscope. Appl. Phys. Lett. 2023, 123, 223702. [Google Scholar] [CrossRef]
- Pensia, L.; Kumar, M.; Kumar, R. A Compact Digital Holographic System Based on a Multifunctional Holographic Optical Element with Improved Resolution and Field of View. Opt. Lasers Eng. 2023, 169, 107744. [Google Scholar] [CrossRef]
- Kumar, M.; Matoba, O. 2D Full-Field Displacement and Vibration Measurements of Specularly Reflecting Surfaces by Two-Beam Common-Path Digital Holography. Opt. Lett. 2021, 46, 5966. [Google Scholar] [CrossRef]
- Kumar, M.; Pensia, L.; Kumar, R.; Matoba, O. Lensless Fourier Transform Multiplexed Digital Holography. Opt. Lett. 2025, 50, 1909. [Google Scholar] [CrossRef]
- Kumar, M.; Pensia, L.; Kumar, R.; Matoba, O. Vibration Measurement of 3-D Objects With Single-Shot Double Field-of-View High-Speed Digital Holography. IEEE Trans. Instrum. Meas. 2025, 74, 4507408. [Google Scholar] [CrossRef]
- Pensia, L.; Kumar, M.; Matoba, O.; Kumar, R. Enhancing Field of View of Digital Holography Using an Angular Multiplexed Holographic Optical Element. Opt. Lett. 2025, 50, 3970. [Google Scholar] [CrossRef]
- Ji, J.; Xie, H.; Yang, L. Learned Large Field-of-View Imager with a Simple Spherical Optical Module. Opt. Commun. 2023, 526, 128918. [Google Scholar] [CrossRef]
- Huang, Z.; Cao, L. High Bandwidth-Utilization Digital Holographic Multiplexing: An Approach Using Kramers–Kronig Relations. Adv. Photonics Res. 2022, 3, 2100273. [Google Scholar] [CrossRef]
- Mundt, J.; Kreis, T.M. Digital Holographic Recording and Reconstruction of Large Scale Objects for Metrology and Display. Opt. Eng. 2010, 49, 125801. [Google Scholar] [CrossRef]
- Kumar, R.; Dwivedi, G.; Singh, O. Portable Digital Holographic Camera Featuring Enhanced Field of View and Reduced Exposure Time. Opt. Lasers Eng. 2021, 137, 106359. [Google Scholar] [CrossRef]
- Kim, K.; Jung, J.; Kim, C.; Ahn, G.; Kim, Y.-J. AI-Driven Pseudo-Light Source for Achieving High Coherence and Low Speckle Noise Simultaneously in Dual-Wavelength Digital Holographic Microscopy. Opt. Laser Technol. 2025, 181, 111572. [Google Scholar] [CrossRef]
- Settles, G.S.; Hargather, M.J. A Review of Recent Developments in Schlieren and Shadowgraph Techniques. Meas. Sci. Technol. 2017, 28, 042001. [Google Scholar] [CrossRef]
- Sweeney, D.W.; Vest, C.M. Measurement of Three-Dimensional Temperature Fields above Heated Surfaces by Holographic Interferometry. Int. J. Heat Mass Transf. 1974, 17, 1443–1454. [Google Scholar] [CrossRef]
- Farrell, P.V.; Springer, G.S.; Vest, C.M. Heterodyne Holographic Interferometry: Concentration and Temperature Measurements in Gas Mixtures. Appl. Opt. 1982, 21, 1624. [Google Scholar] [CrossRef]
- Reuss, D.L. Temperature Measurements in a Radially Symmetric Flame Using Holographic Interferometry. Combust. Flame 1983, 49, 207–219. [Google Scholar] [CrossRef]
- Keren, E.; Bar-Ziv, E.; Glatt, I.; Kafri, O. Measurements of Temperature Distribution of Flames by Moire Deflectometry. Appl. Opt. 1981, 20, 4263. [Google Scholar] [CrossRef]
- Farrell, P.V.; Hofeldt, D.L. Temperature Measurement in Gases Using Speckle Photography. Appl. Opt. 1984, 23, 1055. [Google Scholar] [CrossRef] [PubMed]
- Stella, A.; Guj, G.; Giammartini, S. Measurement of Axisymmetric Temperature Fields Using Reference Beam and Shearing Interferometry for Application to Flames. Exp. Fluids 2000, 29, 1–12. [Google Scholar] [CrossRef]
- Kumar, M.; Shakher, C. Measurement of Temperature and Temperature Distribution in Gaseous Flames by Digital Speckle Pattern Shearing Interferometry Using Holographic Optical Element. Opt. Lasers Eng. 2015, 73, 33–39. [Google Scholar] [CrossRef]
- Kumar, M.; Agarwal, S.; Kumar, V.; Khan, G.S.; Shakher, C. Experimental Investigation on Butane Diffusion Flames under the Influence of Magnetic Field by Using Digital Speckle Pattern Interferometry. Appl. Opt. 2015, 54, 2450. [Google Scholar] [CrossRef]
- Doleček, R.; Psota, P.; Lédl, V.; Vít, T.; Václavík, J.; Kopecký, V. General Temperature Field Measurement by Digital Holography. Appl. Opt. 2013, 52, A319. [Google Scholar] [CrossRef]
- Guerrero-Mendez, C.; Anaya, T.S.; Araiza-Esquivel, M.; Balderas-Navarro, R.E.; Aranda-Espinoza, S.; López-Martínez, A.; Olvera-Olvera, C. Real-Time Measurement of the Average Temperature Profiles in Liquid Cooling Using Digital Holographic Interferometry. Opt. Eng. 2016, 55, 121730. [Google Scholar] [CrossRef]
- Kumar, M.; Matoba, O.; Quan, X.; Rajput, S.K.; Awatsuji, Y.; Tamada, Y. Single-Shot Common-Path off-Axis Digital Holography: Applications in Bioimaging and Optical Metrology [Invited]. Appl. Opt. 2021, 60, A195. [Google Scholar] [CrossRef]
- Kumon, Y.; Hashimoto, S.; Inoue, T.; Nishio, K.; Kumar, M.; Matoba, O.; Xia, P.; Rajput, S.K.; Awatsuji, Y. Three-Dimensional Video Imaging of Dynamic Temperature Field of Transparent Objects Recorded by a Single-View Parallel Phase-Shifting Digital Holography. Opt. Laser Technol. 2023, 167, 109808. [Google Scholar] [CrossRef]
- Xia, P.; Ri, S.; Inoue, T.; Awatsuji, Y.; Matoba, O. Three-Dimensional Dynamic Measurement of Unstable Temperature Fields by Multi-View Single-Shot Phase-Shifting Digital Holography. Opt. Express 2022, 30, 37760. [Google Scholar] [CrossRef]
- Dardikman, G.; Shaked, N.T. Is Multiplexed Off-Axis Holography for Quantitative Phase Imaging More Spatial Bandwidth-Efficient than on-Axis Holography? [Invited]. J. Opt. Soc. Am. A 2019, 36, A1. [Google Scholar] [CrossRef]
- Bioucas-Dias, J.M.; Valadao, G. Phase Unwrapping via Graph Cuts. IEEE Trans. Image Process. 2007, 16, 698–709. [Google Scholar] [CrossRef]


Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kumar, M.; Pensia, L.; Kaur, K.; Kumar, R.; Awatsuji, Y.; Matoba, O. Advances in Optical Metrology: High-Bandwidth Digital Holography for Transparent Objects Analysis. Photonics 2025, 12, 617. https://doi.org/10.3390/photonics12060617
Kumar M, Pensia L, Kaur K, Kumar R, Awatsuji Y, Matoba O. Advances in Optical Metrology: High-Bandwidth Digital Holography for Transparent Objects Analysis. Photonics. 2025; 12(6):617. https://doi.org/10.3390/photonics12060617
Chicago/Turabian StyleKumar, Manoj, Lavlesh Pensia, Karmjit Kaur, Raj Kumar, Yasuhiro Awatsuji, and Osamu Matoba. 2025. "Advances in Optical Metrology: High-Bandwidth Digital Holography for Transparent Objects Analysis" Photonics 12, no. 6: 617. https://doi.org/10.3390/photonics12060617
APA StyleKumar, M., Pensia, L., Kaur, K., Kumar, R., Awatsuji, Y., & Matoba, O. (2025). Advances in Optical Metrology: High-Bandwidth Digital Holography for Transparent Objects Analysis. Photonics, 12(6), 617. https://doi.org/10.3390/photonics12060617




