A Transformer-Based Approach to Facilitate Inverse Design of Achromatic Metasurfaces
Abstract
1. Introduction
2. Theory and Methodology
2.1. Forward Prediction
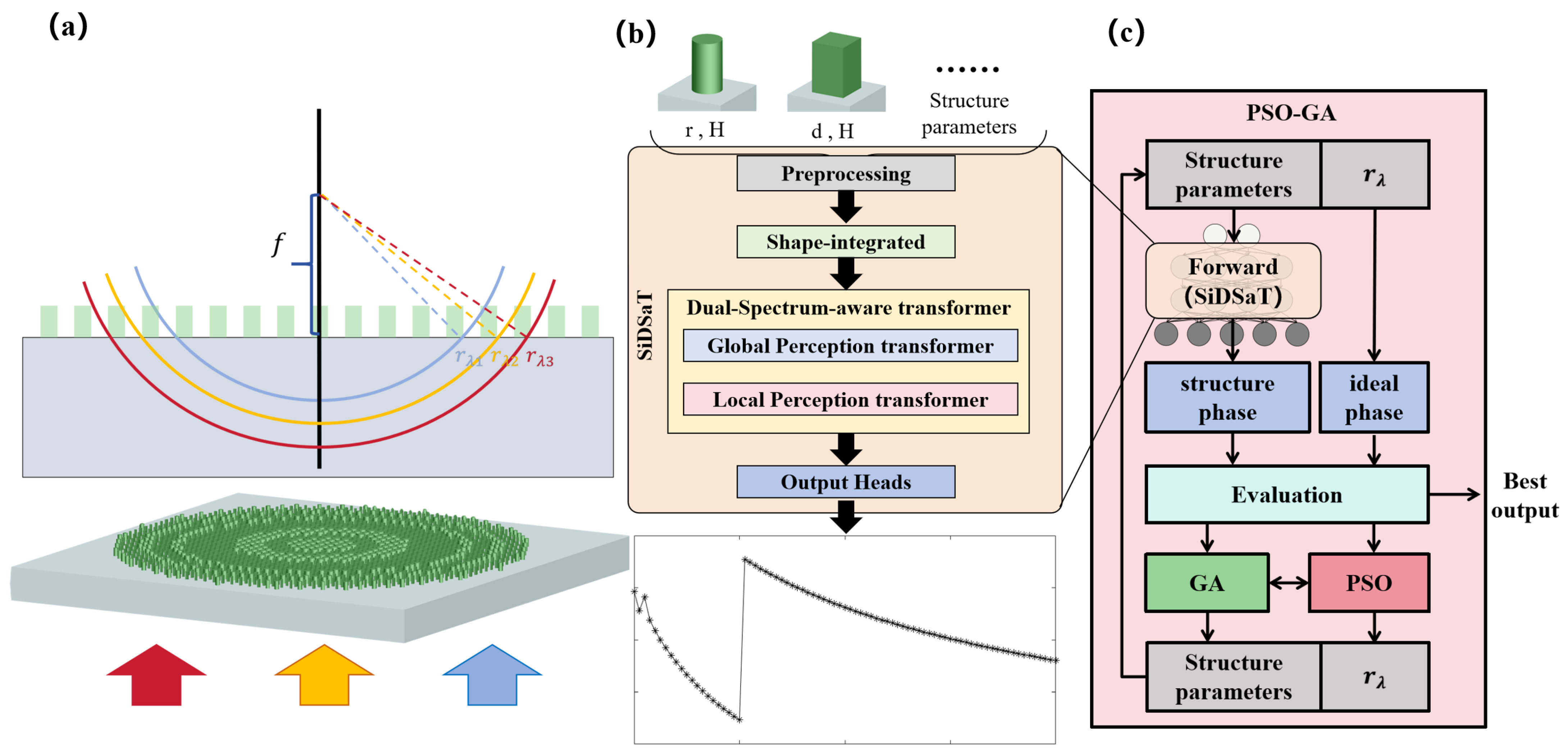
2.1.1. Architecture of SiDSaT
2.1.2. Dataset Generation
2.2. Inverse Design
2.2.1. The Principle of Achromatic Metalens
2.2.2. Constraint Analysis for Metalens Design
2.2.3. PSO-GA-Based Inverse Design Strategy
3. Results and Discussion
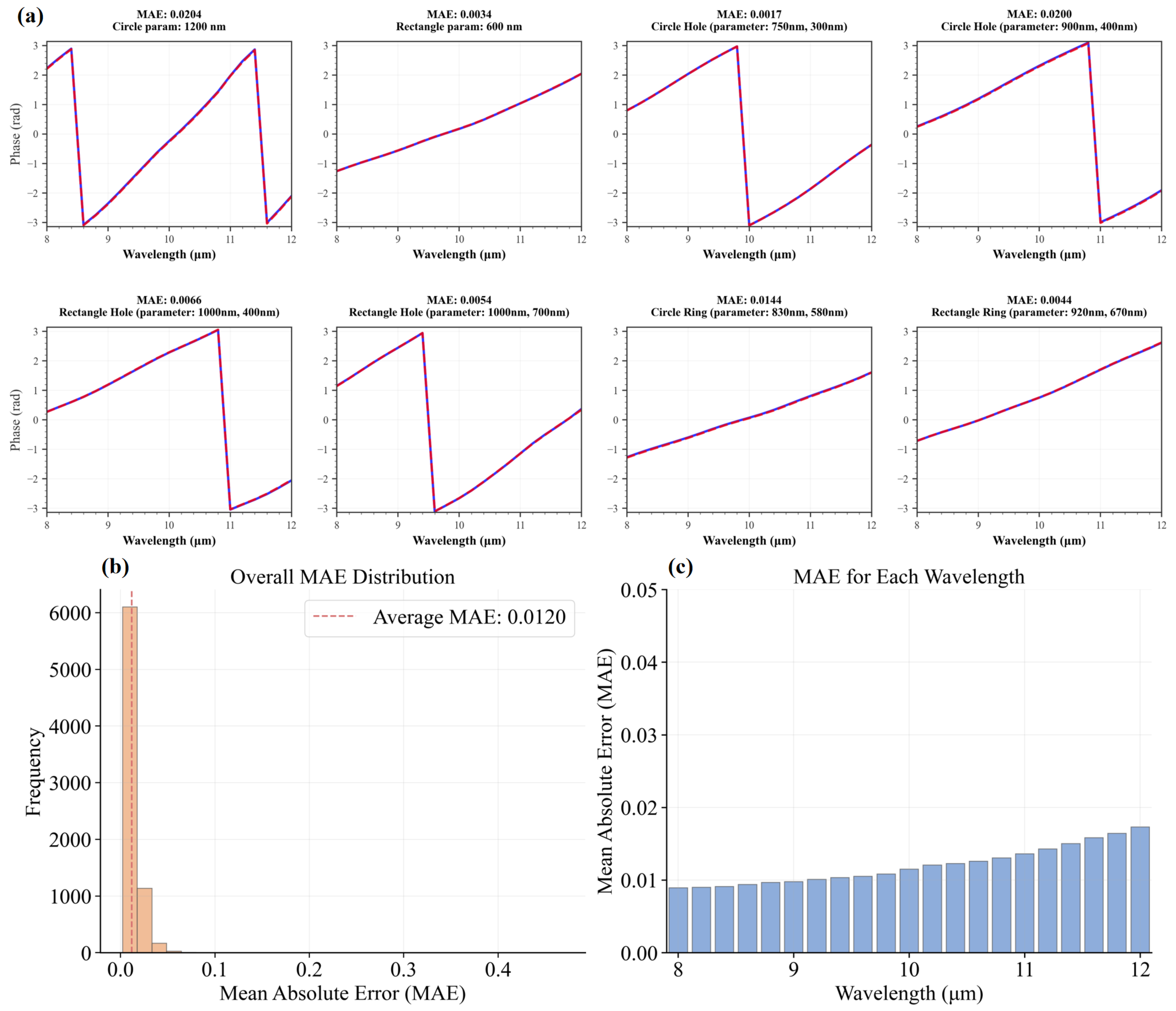
3.1. Evaluation of SiDSaT
3.1.1. Predicted Results of Our Dataset
3.1.2. Ablation Study
3.2. Evaluation of PSO-GA
3.2.1. Application in Single-Wavelength Metalenses
3.2.2. Application in Broadband Metalenses
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| BNNs | Bidirectional Neural Networks |
| BAMLs | Comparison of Broadband Achromatic Metalenses |
| DNNs | Deep Neural Networks |
| DOF | Depth of Focus |
| EM | Electromagnetic |
| FCNs | Fully Connected Networks |
| FCL | Fully Connected Layer |
| FDTD | Finite-Difference Time-Domain |
| FWHM | Full Width at Half Maximum |
| GPT | Global Perception Transformer |
| LPT | Local Perception Transformer |
| MAE | Mean Absolute Error |
| NA | Numerical Aperture |
| NFF | Norm and Feed Forward |
| NTNs | Neural Tensor Networks |
| PSO | Particle Swarm Optimization |
| GA | Genetic Algorithm |
| SiDSaT | Shape-integrated Dual-Spectrum-aware Transformer |
Appendix A
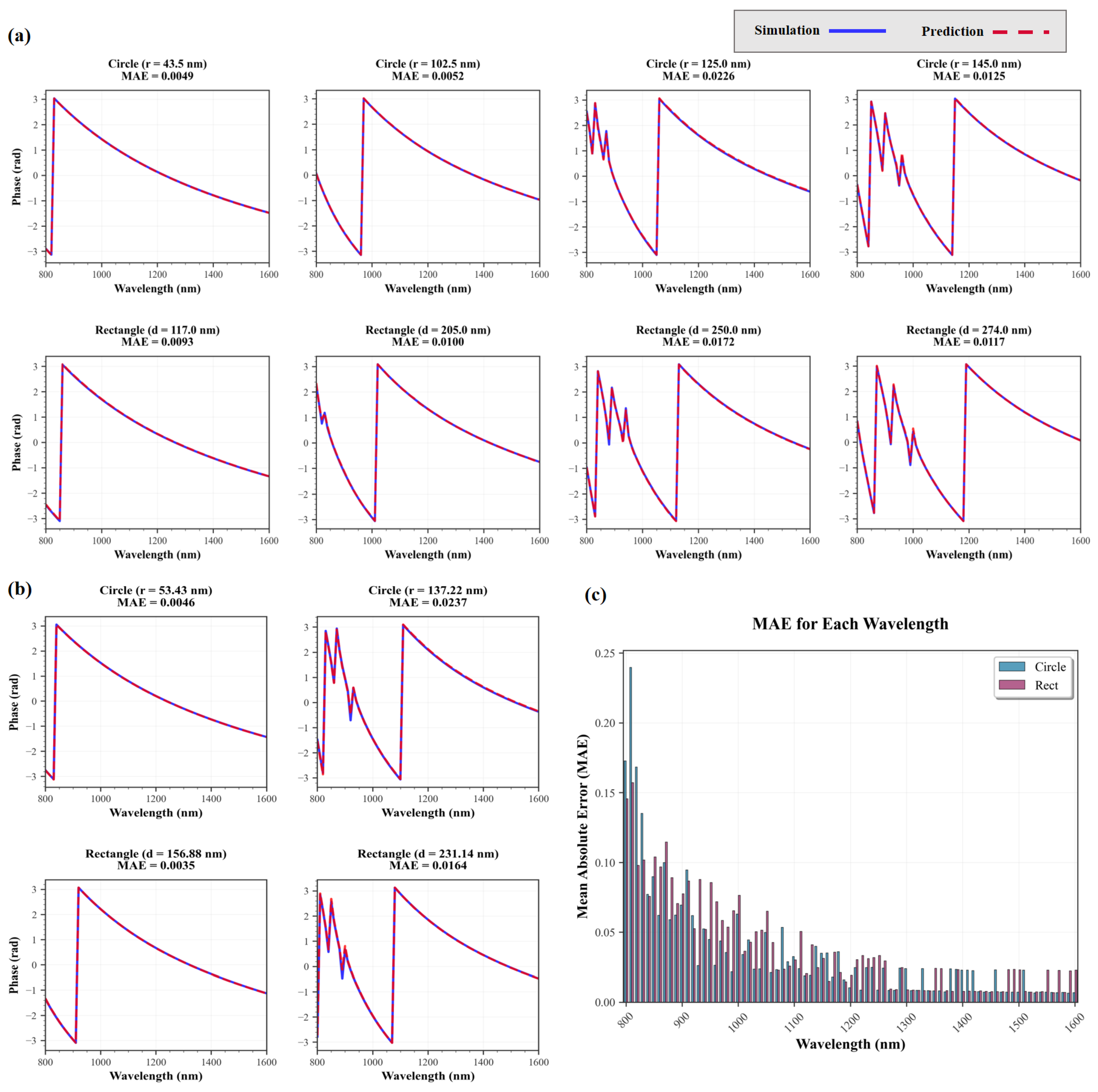
Appendix A.1. Additional Validation on an All-Silicon Multi-Geometry Dataset
Appendix A.2. Additional Validation on a Tandem Solar Cell (TSC) Transmittance Dataset

Appendix B
| Reference | Operating Band (nm) | Focal Length | Max Focal Shift | NA | Materials | Achromatization Strategy | Operation Mode and Polarization |
|---|---|---|---|---|---|---|---|
| Our work | 1000–1400 | 400 μm | ≈90 μm (22.5%) | 0.080 | TiO2 nanopillars on SiO2 substrate | Asymptotic phase compensation; Primitive meta-atom; SiDSaT-embedded PSO-GA strategy | Transmission; Polarization insensitive |
| 1000–1300 | ≈40 μm (10%) | ||||||
| Wang et al. [45] (2017) | 1200–1680 | 100 μm | ≈20 μm (20%) | 0.268 | Au multi-nanorods/SiO2 spacer/Au back reflector (on Si substrate) | Integrated Resonant Unit | Reflection; Polarization selective |
| Hsiao et al. [46] (2018) | 420–650 | 150 μm | ≈30 μm (20%) | 0.124 | Al multi-nanorods/SiO2 spacer/Al back reflector (on Si substrate) | Integrated Resonant Unit | Reflection; Polarization selective |
| Shrestha et al. [16] (2018) | 1200–1650 | 200 μm | ≈30 μm (15%) | 0.24 | a-Si nanopillars on fused silica | Complex meta-atom | Transmission; Polarization insensitive |
| Sun et al. [47] (2022) | 450–1400 | 214 μm | ≈25 μm (12%) | 0.107 | Si3N4 nanopillars on fused silica | Aperture Partition and Phase Coordination Method (APPCM, dual-lens-zone design) | Transmission; Polarization selective |
| Hu et al. [18] (2023) | 400–1000 | 150 μm | ≈32 μm (21%) | 0.164 | TiO2 nanopillars on SiO2 substrate | Asymptotic phase compensation; Complex meta-atom | Transmission; Polarization insensitive |
| Li & Lv [48] (2024) | 1000–1250 | 6.5 μm | ≈0 μm | 0.5 | Si nanopillars on SiO2 substrate | PSO-GA hybrid optimization | Transmission; Polarization selective |
| Song et al. [49] (2024) | 430–750 | 50 μm | ≈6 μm (12%) | 0.255 | LNOI thin film on LNOI substrate | Multi-Zone Taylor Expansion Method (MZTEM) | Transmission; Polarization insensitive |
| Hou et al. [42] (2025) | 450–650 | 60 μm | ≈3 μm (5%) | 0.164 | TiO2 anisotropic nanopillars on SiO2 substrate | Anisotropic nanofin phase control with PSO | Transmission; Polarization selective |
References
- Chen, W.T.; Zhu, A.Y.; Capasso, F. Flat Optics with Dispersion-Engineered Metasurfaces. Nat. Rev. Mater. 2020, 5, 604–620. [Google Scholar] [CrossRef]
- Liu, Y.; Zhang, X. Metamaterials: A New Frontier of Science and Technology. Chem. Soc. Rev. 2011, 40, 2494–2507. [Google Scholar] [CrossRef] [PubMed]
- Yuan, Q.; Ge, Q.; Chen, L.; Zhang, Y.; Yang, Y.; Cao, X.; Wang, S.; Zhu, S.; Wang, Z. Recent Advanced Applications of Metasurfaces in Multi-Dimensions. Nanophotonics 2023, 12, 2295–2315. [Google Scholar] [CrossRef] [PubMed]
- Zhang, L.; Zhou, C.; Liu, B.; Ding, Y.; Ahn, H.-J.; Chang, S.; Duan, Y.; Rahman, M.T.; Xia, T.; Chen, X.; et al. Real-Time Machine Learning–Enhanced Hyperspectro-Polarimetric Imaging via an Encoding Metasurface. Sci. Adv. 2024, 10, eadp5192. [Google Scholar] [CrossRef]
- Faraon, A.; Arbabi, A.; Kamali, S.M.; Arbabi, E.; Majumdar, A. Applications of Wavefront Control Using Nano-Post-Based Dielectric Metasurfaces. In Dielectric Metamaterials; Woodhead Publishing: Duxford, UK, 2020; pp. 175–194. [Google Scholar] [CrossRef]
- Mo, H.; Ji, Z.; Zheng, Y.; Liang, W.; Yu, H.; Li, Z. Broadband Achromatic Imaging of Metasurface Lenses (Invited). Infrared Laser Eng. 2021, 50, 40–49. [Google Scholar]
- Zhou, Y.; Liang, G.; Wen, Z.; Zhang, Z.; Shang, Z.; Chen, G. Research Progress on Optical Super-Resolution Planar Metasurface Lenses. Opto-Electron. Eng. 2021, 48, 13–31. [Google Scholar]
- Zheng, Y.; Qin, F.; Li, X. Research Progress on Super-Diffraction-Limit Light Field Manipulation of Supercritical Lenses (Invited). Acta Photonica Sin. 2022, 51, 174–186. [Google Scholar]
- Tang, J.; Gong, Y.; Pang, K. Two-Dimensional Metasurfaces: Applications and Research Progress in Metalenses. Laser Optoelectron. Prog. 2023, 60, 43–57. [Google Scholar]
- Khorasaninejad, M.; Chen, W.T.; Devlin, R.C.; Oh, J.; Zhu, A.Y.; Capasso, F. Metalenses at Visible Wavelengths: Diffraction-Limited Focusing and Subwavelength Resolution Imaging. Science 2016, 352, 1190–1194. [Google Scholar] [CrossRef]
- Hu, Y.; Ou, X.; Zeng, T.; Lai, J.; Zhang, J.; Li, X.; Luo, X.; Li, L.; Fan, F.; Duan, H. Electrically Tunable Multifunctional Polarization-Dependent Metasurfaces Integrated with Liquid Crystals in the Visible Region. Nano Lett. 2021, 21, 4554–4562. [Google Scholar] [CrossRef]
- Li, L.; Zhang, J.; Hu, Y.; Lai, J.; Wang, S.; Yang, P.; Li, X.; Duan, H. Broadband Polarization-switchable Multi-focal Noninterleaved Metalenses in the Visible. Laser Photonics Rev. 2021, 15, 2100198. [Google Scholar] [CrossRef]
- Khorasaninejad, M.; Zhu, A.Y.; Roques-Carmes, C.; Chen, W.T.; Oh, J.; Mishra, I.; Devlin, R.C.; Capasso, F. Polarization-Insensitive Metalenses at Visible Wavelengths. Nano Lett. 2016, 16, 7229–7234. [Google Scholar] [CrossRef] [PubMed]
- Xing, Z.; Liao, J.; Xu, Z.; Cheng, X.; Zhang, J. The Design of Highly Reflective All-Dielectric Metasurfaces Based on Diamond Resonators. Photonics 2024, 11, 1015. [Google Scholar] [CrossRef]
- Khorasaninejad, M.; Shi, Z.; Zhu, A.Y.; Chen, W.T.; Sanjeev, V.; Zaidi, A.; Capasso, F. Achromatic Metalens over 60 Nm Bandwidth in the Visible and Metalens with Reverse Chromatic Dispersion. Nano Lett. 2017, 17, 1819–1824. [Google Scholar] [CrossRef]
- Shrestha, S.; Overvig, A.C.; Lu, M.; Stein, A.; Yu, N. Broadband Achromatic Dielectric Metalenses. Light Sci. Appl. 2018, 7, 85. [Google Scholar] [CrossRef]
- Chen, W.T.; Zhu, A.Y.; Sanjeev, V.; Khorasaninejad, M.; Shi, Z.; Lee, E.; Capasso, F. A Broadband Achromatic Metalens for Focusing and Imaging in the Visible. Nat. Nanotechnol. 2018, 13, 220–226. [Google Scholar] [CrossRef]
- Hu, Y.; Jiang, Y.; Zhang, Y.; Yang, X.; Ou, X.; Li, L.; Kong, X.; Liu, X.; Qiu, C.-W.; Duan, H. Asymptotic Dispersion Engineering for Ultra-Broadband Meta-Optics. Nat. Commun. 2023, 14, 6649. [Google Scholar] [CrossRef]
- Cano-Renteria, F.; Tegmark, M.; Soljacic, M.; Joannopoulos, J.D.; Peurifoy, J.; Shen, Y.; Jing, L.; Yang, Y.; DeLacy, B.G. Nanophotonic Particle Simulation and Inverse Design Using Artificial Neural Networks. In Proceedings of the Physics and Simulation of Optoelectronic Devices XXVI, San Francisco, CA, USA, 29 January–1 February 2018; Osiński, M., Arakawa, Y., Witzigmann, B., Eds.; SPIE: San Francisco, CA, USA, 2018; p. 6. [Google Scholar]
- Yu, N.; Genevet, P.; Kats, M.A.; Aieta, F.; Tetienne, J.-P.; Capasso, F.; Gaburro, Z. Light Propagation with Phase Discontinuities: Generalized Laws of Reflection and Refraction. Science 2011, 334, 333–337. [Google Scholar] [CrossRef]
- Huang, H.; Overvig, A.C.; Xu, Y.; Malek, S.C.; Tsai, C.-C.; Alù, A.; Yu, N. Leaky-Wave Metasurfaces for Integrated Photonics. Nat. Nanotechnol. 2023, 18, 580–588. [Google Scholar] [CrossRef]
- Jiang, X.; Yuan, H.; Chen, D.; Zhang, Z.; Du, T.; Ma, H.; Yang, J. Metasurface Based on Inverse Design for Maximizing Solar Spectral Absorption. Adv. Opt. Mater. 2021, 9, 2100575. [Google Scholar] [CrossRef]
- An, S.; Fowler, C.; Zheng, B.; Shalaginov, M.Y.; Tang, H.; Li, H.; Zhou, L.; Ding, J.; Agarwal, A.M.; Rivero-Baleine, C.; et al. A Deep Learning Approach for Objective-Driven All-Dielectric Metasurface Design. ACS Photonics 2019, 6, 3196–3207. [Google Scholar] [CrossRef]
- Gao, Y.; Chen, W.; Li, F.; Zhuang, M.; Yan, Y.; Wang, J.; Wang, X.; Dong, Z.; Ma, W.; Zhu, J. Meta-attention Deep Learning for Smart Development of Metasurface Sensors. Adv. Sci. 2024, 11, 2405750. [Google Scholar] [CrossRef]
- Lv, J.; Zhang, R.; Liu, C.; Ge, Z.; Gu, Q.; Feng, F.; Si, G. Polarization-Controlled Metasurface Design Based on Deep ResNet. Opt. Laser Technol. 2024, 179, 111396. [Google Scholar] [CrossRef]
- Ji, W.; Chang, J.; Xu, H.-X.; Gao, J.R.; Gröblacher, S.; Urbach, H.P.; Adam, A.J.L. Recent Advances in Metasurface Design and Quantum Optics Applications with Machine Learning, Physics-Informed Neural Networks, and Topology Optimization Methods. Light Sci. Appl. 2023, 12, 169. [Google Scholar] [CrossRef]
- Ma, W.; Liu, Z.; Kudyshev, Z.A.; Boltasseva, A.; Cai, W.; Liu, Y. Deep Learning for the Design of Photonic Structures. Nat. Photonics 2021, 15, 77–90. [Google Scholar] [CrossRef]
- Kanmaz, T.B.; Ozturk, E.; Demir, H.V.; Gunduz-Demir, C. Deep-Learning-Enabled Electromagnetic near-Field Prediction and Inverse Design of Metasurfaces. Optica 2023, 10, 1373. [Google Scholar] [CrossRef]
- Ma, T.; Wang, H.; Guo, L.J. OptoGPT: A Foundation Model for Inverse Design in Optical Multilayer Thin Film Structures. Opto-Electron. Adv. 2024, 7, 240062. [Google Scholar] [CrossRef]
- An, S.; Zheng, B.; Shalaginov, M.Y.; Tang, H.; Li, H.; Zhou, L.; Ding, J.; Agarwal, A.M.; Rivero-Baleine, C.; Kang, M.; et al. Deep Learning Modeling Approach for Metasurfaces with High Degrees of Freedom. Opt. Express 2020, 28, 31932. [Google Scholar] [CrossRef] [PubMed]
- Hong, P.; Hu, L.; Zhou, Z.; Qin, H.; Chen, J.; Fan, Y.; Yin, T.; Kou, J.; Lu, Y. Recent Advances in Inverse Design for Photonics (Invited). Acta Photonica Sin. 2023, 52, 9–32. [Google Scholar]
- Madina; Cheng, H.; Tian, J.; Chen, S. Inverse Design Methods and Applications for Artificial Photonic Devices (Invited). Acta Photonica Sin. 2022, 51, 174–195. [Google Scholar]
- An, X. Design of Broadband Achromatic Metalens Based on Deep Learning. Master’s Thesis, Huazhong University of Science and Technology, Wuhan, China, 2021. [Google Scholar]
- Malkiel, I.; Mrejen, M.; Nagler, A.; Arieli, U.; Wolf, L.; Suchowski, H. Plasmonic Nanostructure Design and Characterization via Deep Learning. Light Sci. Appl. 2018, 7, 60. [Google Scholar] [CrossRef]
- Gao, L.; Li, X.; Liu, D.; Wang, L.; Yu, Z. A Bidirectional Deep Neural Network for Accurate Silicon Color Design. Adv. Mater. 2019, 31, 1905467. [Google Scholar] [CrossRef] [PubMed]
- Nadell, C.C.; Huang, B.; Malof, J.M.; Padilla, W.J. Deep Learning for Accelerated All-Dielectric Metasurface Design. Opt. Express 2019, 27, 27523. [Google Scholar] [CrossRef] [PubMed]
- Liu, Z.; Zhu, D.; Rodrigues, S.P.; Lee, K.-T.; Cai, W. Generative Model for the Inverse Design of Metasurfaces. Nano Lett. 2018, 18, 6570–6576. [Google Scholar] [CrossRef]
- Gu, Y.; Harlim, J.; Liang, S.; Yang, H. Stationary Density Estimation of Itô Diffusions Using Deep Learning. SIAM J. Numer. Anal. 2023, 61, 45–82. [Google Scholar] [CrossRef]
- An, S.; Zheng, B.; Julian, M.; Williams, C.; Tang, H.; Gu, T.; Zhang, H.; Kim, H.J.; Hu, J. Deep Neural Network Enabled Active Metasurface Embedded Design. Nanophotonics 2022, 11, 4149–4158. [Google Scholar] [CrossRef]
- Chen, W.; Gao, Y.; Li, Y.; Yan, Y.; Ou, J.-Y.; Ma, W.; Zhu, J. Broadband Solar Metamaterial Absorbers Empowered by Transformer-Based Deep Learning. Adv. Sci. Weinh. Baden-Wurtt. Ger. 2023, 10, e2206718. [Google Scholar] [CrossRef]
- Yu, Q.; Shen, X.; Yi, L.; Liang, M.; Li, G.; Guan, Z.; Wu, X.; Castel, H.; Hu, B.; Yin, P.; et al. Fragment-Fusion Transformer: Deep Learning-Based Discretization Method for Continuous Single-Cell Raman Spectral Analysis. ACS Sens. 2024, 9, 3907–3920. [Google Scholar] [CrossRef]
- Hou, L.; Zhou, H.; Zhang, D.; Lu, G.; Zhang, D.; Liu, T.; Xiao, S.; Yu, T. High-Efficiency Broadband Achromatic Metalens in the Visible. Appl. Phys. Lett. 2025, 126, 101704. [Google Scholar] [CrossRef]
- Wu, H. Research on Long-Wave Infrared Broadband Achromatic Metalens. Master’s Thesis, Huazhong University of Science and Technology, Wuhan, China, 2021. [Google Scholar]
- Razi, A.; Safdar, A.; Irfan, R. Enhancing Tandem Solar Cell’s Efficiency through Convolutional Neural Network-Based Optimization of Metasurfaces. Mater. Des. 2023, 236, 112475. [Google Scholar] [CrossRef]
- Wang, S.; Wu, P.C.; Su, V.-C.; Lai, Y.-C.; Hung Chu, C.; Chen, J.-W.; Lu, S.-H.; Chen, J.; Xu, B.; Kuan, C.-H.; et al. Broadband Achromatic Optical Metasurface Devices. Nat. Commun. 2017, 8, 187. [Google Scholar] [CrossRef]
- Hsiao, H.; Chen, Y.H.; Lin, R.J.; Wu, P.C.; Wang, S.; Chen, B.H.; Tsai, D.P. Integrated Resonant Unit of Metasurfaces for Broadband Efficiency and Phase Manipulation. Adv. Opt. Mater. 2018, 6, 1800031. [Google Scholar] [CrossRef]
- Sun, P.; Zhang, M.; Dong, F.; Feng, L.; Chu, W. Broadband Achromatic Polarization Insensitive Metalens over 950 Nm Bandwidth in the Visible and Near-Infrared. Chin. Opt. Lett. 2022, 20, 13601. [Google Scholar] [CrossRef]
- Li, Z.; Lv, Y. Optimization for Si Nano-Pillar-Based Broadband Achromatic Metalens. IEEE Photonics J. 2024, 16, 5000307. [Google Scholar] [CrossRef]
- Song, R.; Lu, X.; Wang, F.; Song, X.; Chen, Z.; Li, Y. Multi-Zone Taylor Expansion Method for Broadband Achromatic Polarization-Insensitive Metalens Design. Phys. Scr. 2024, 99, 25530. [Google Scholar] [CrossRef]





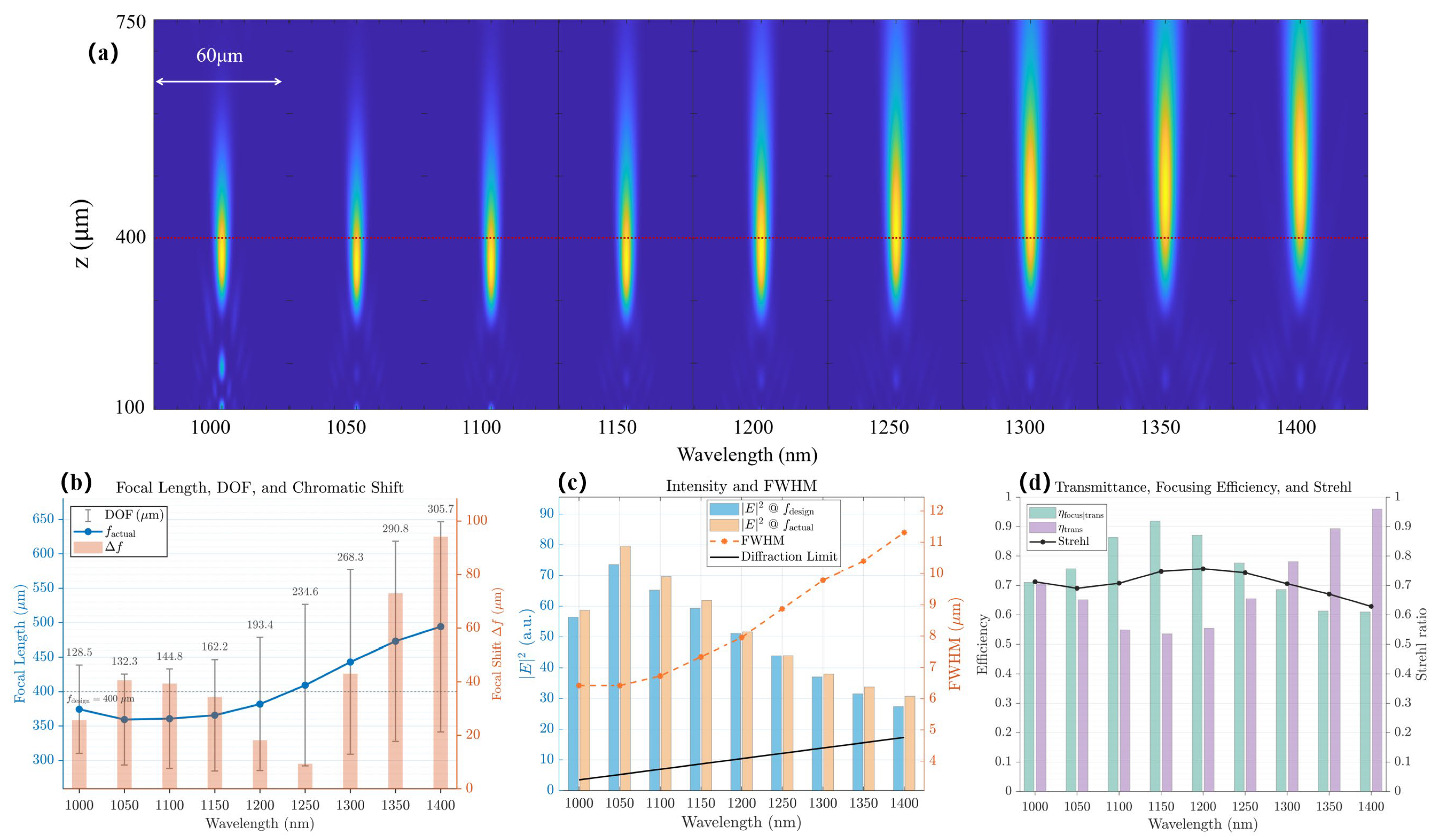
| Metalens 1 | Metalens 2 | Metalens 3 | Metalens 4 | |
|---|---|---|---|---|
| Wavelength | 850 nm | 850 nm | 1064 nm | 1310 nm |
| Diameter | 60 μm | 60 μm | 40 μm | 40 μm |
| Target Focal Length | 200 μm | 100 μm | 50 μm | 50 μm |
| Actual Focal Length | 199.2 μm | 101.0 μm | 48.7 μm | 50.0 μm |
| NA | 0.1483 | 0.2873 | 0.3714 | 0.3714 |
| FWHM | 3.058 μm | 1.834 μm | 1.644 μm | 2.060 μm |
| Focus Ratio | 1.04 | 1.21 | 1.12 | 1.14 |
| DOF | 35.760 μm | 10.835 μm | 7.504 μm | 8.109 μm |
| 0.6041 | 0.8798 | 0.8116 | 0.8428 | |
| 0.7644 | 0.7409 | 0.6921 | 0.6289 | |
| Strehl Ratio | 0.9108 | 0.7194 | 0.7498 | 0.6314 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bian, X.; Cheng, X.; Liao, J.; Hua, Z.; Xu, Z.; Zhang, J.; Xing, Z. A Transformer-Based Approach to Facilitate Inverse Design of Achromatic Metasurfaces. Photonics 2025, 12, 913. https://doi.org/10.3390/photonics12090913
Bian X, Cheng X, Liao J, Hua Z, Xu Z, Zhang J, Xing Z. A Transformer-Based Approach to Facilitate Inverse Design of Achromatic Metasurfaces. Photonics. 2025; 12(9):913. https://doi.org/10.3390/photonics12090913
Chicago/Turabian StyleBian, Xucong, Xiang’ai Cheng, Jiahui Liao, Zixiao Hua, Zhongjie Xu, Jiangbin Zhang, and Zhongyang Xing. 2025. "A Transformer-Based Approach to Facilitate Inverse Design of Achromatic Metasurfaces" Photonics 12, no. 9: 913. https://doi.org/10.3390/photonics12090913
APA StyleBian, X., Cheng, X., Liao, J., Hua, Z., Xu, Z., Zhang, J., & Xing, Z. (2025). A Transformer-Based Approach to Facilitate Inverse Design of Achromatic Metasurfaces. Photonics, 12(9), 913. https://doi.org/10.3390/photonics12090913





