Inverse Design of Tunable Graphene-Based Terahertz Metasurfaces via Deep Neural Network and SHADE Algorithm
Abstract
1. Introduction
2. Materials and Methods
2.1. Structure Design
2.1.1. Metasurface Architecture Overview
2.1.2. Parametric Encoding Methodology
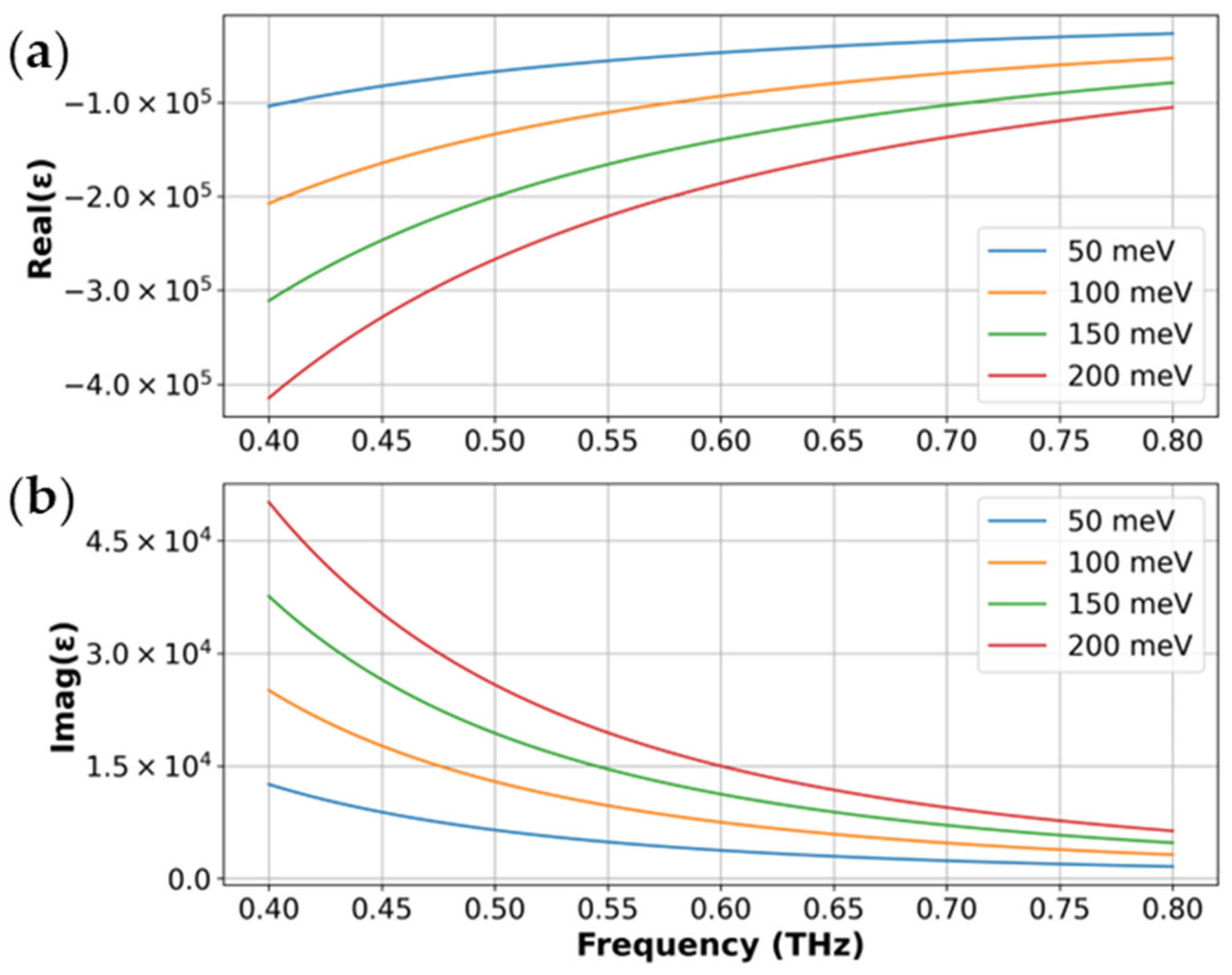
2.2. Graphene Modeling
2.3. Surrogate Model Construction
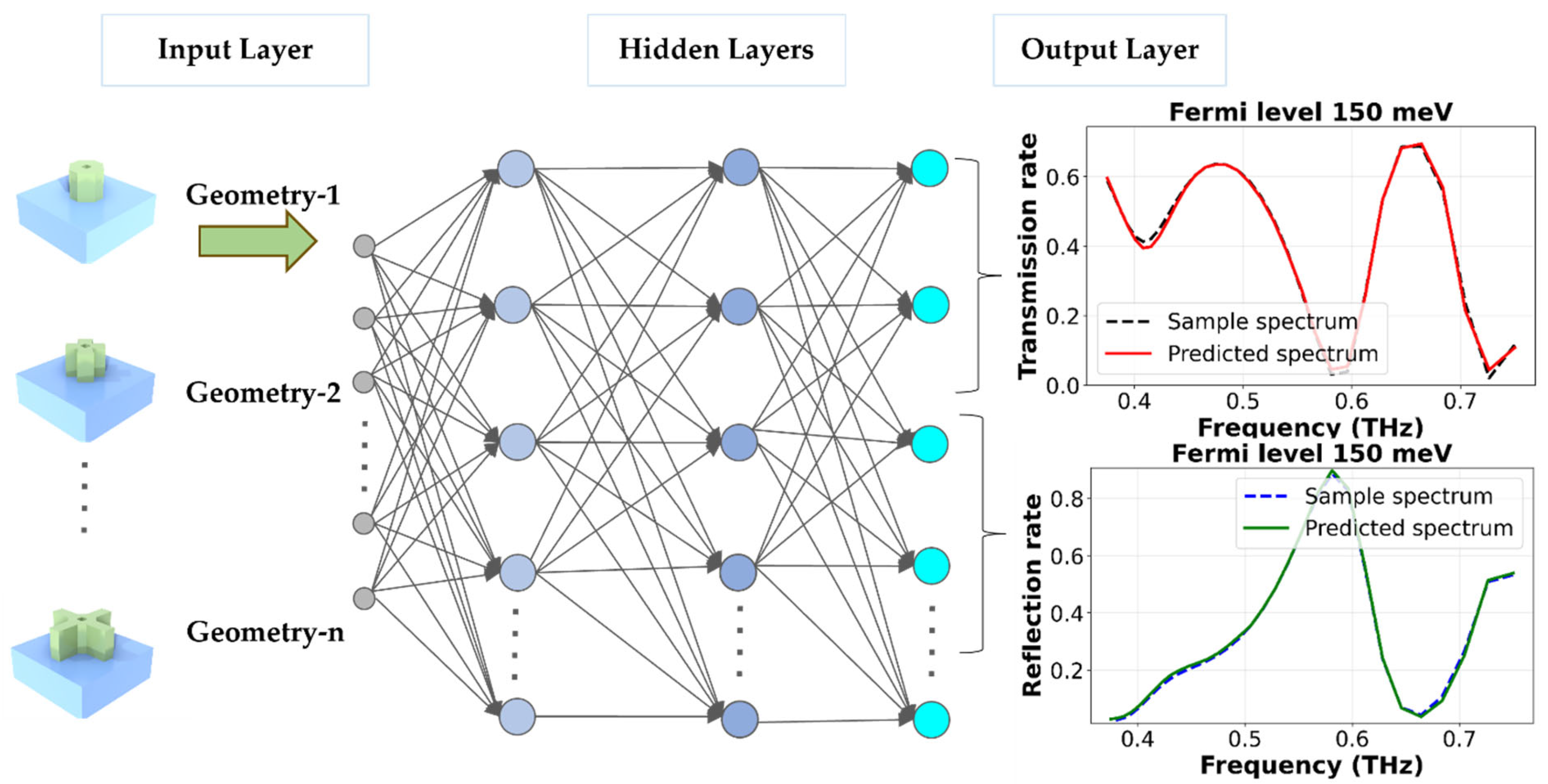
2.3.1. Deep Neural Network Framework for Electromagnetic Response Prediction
2.3.2. Network Architecture
2.4. Optimization Strategy
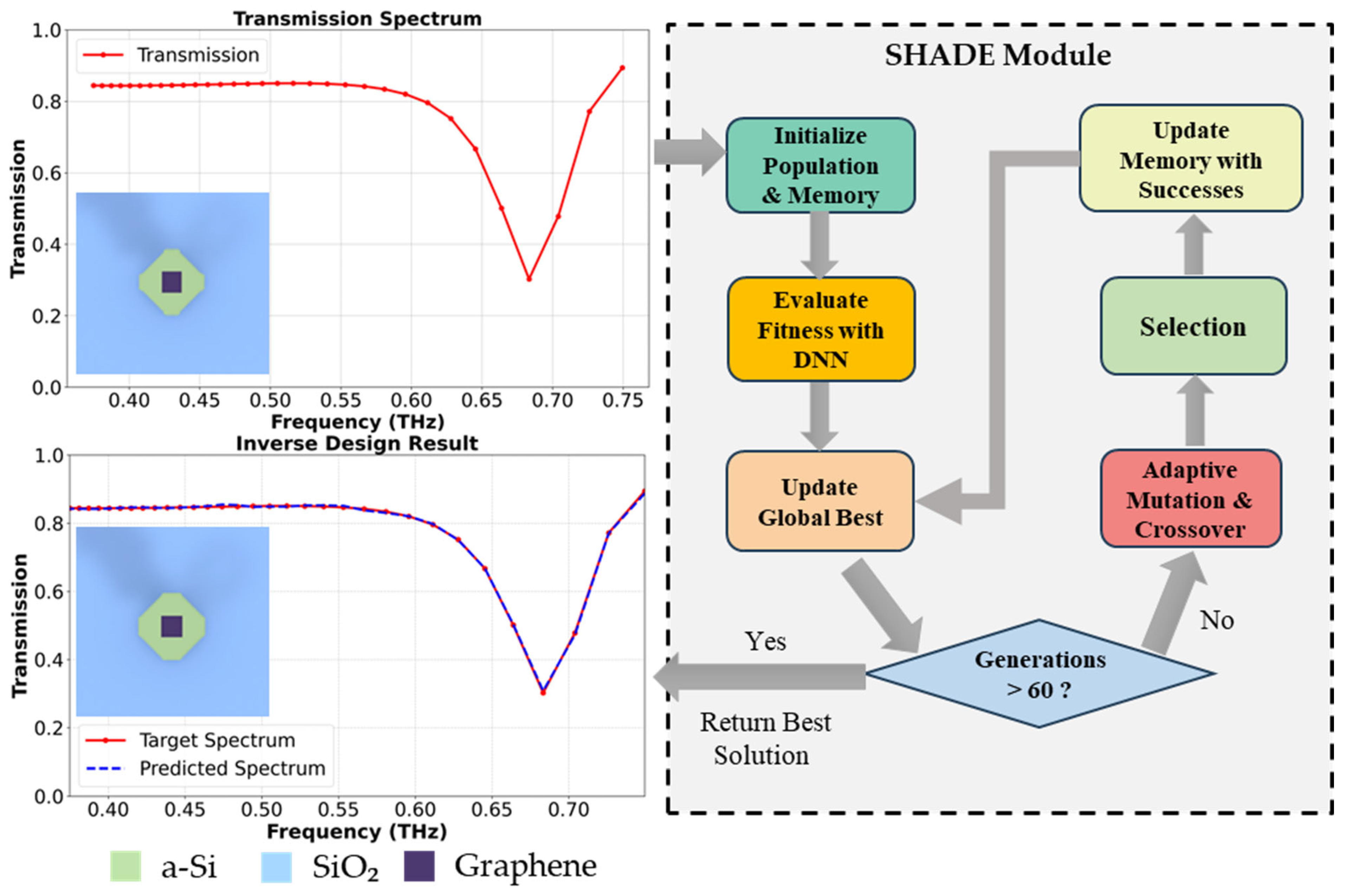
2.4.1. SHADE Algorithm
2.4.2. SHADE Implementation for Metasurface Inverse Design
2.4.3. Surrogate-Assisted Evolutionary Optimization Framework
3. Results and Discussion
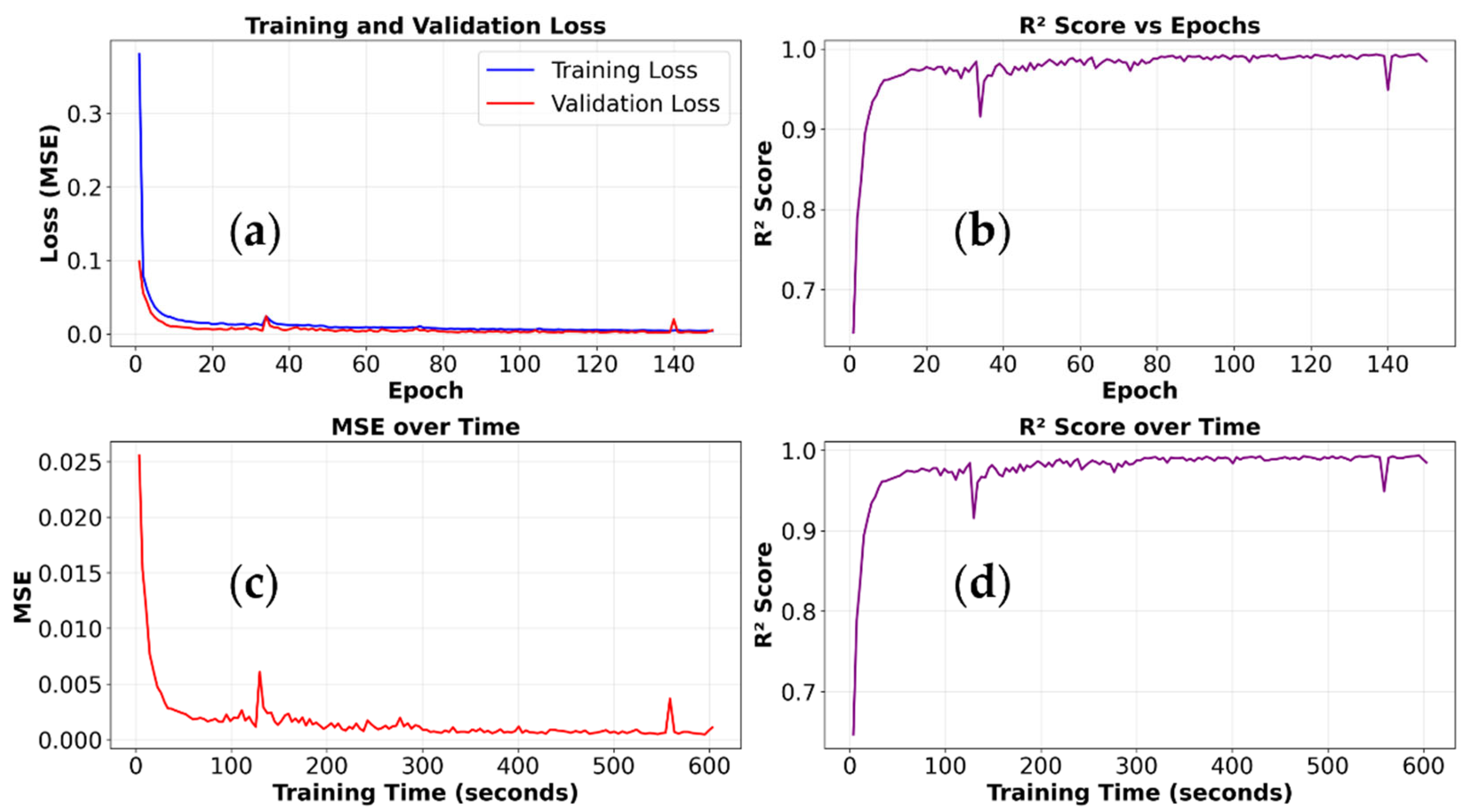
3.1. Deep Neural Network Surrogate Model Performance Evaluation
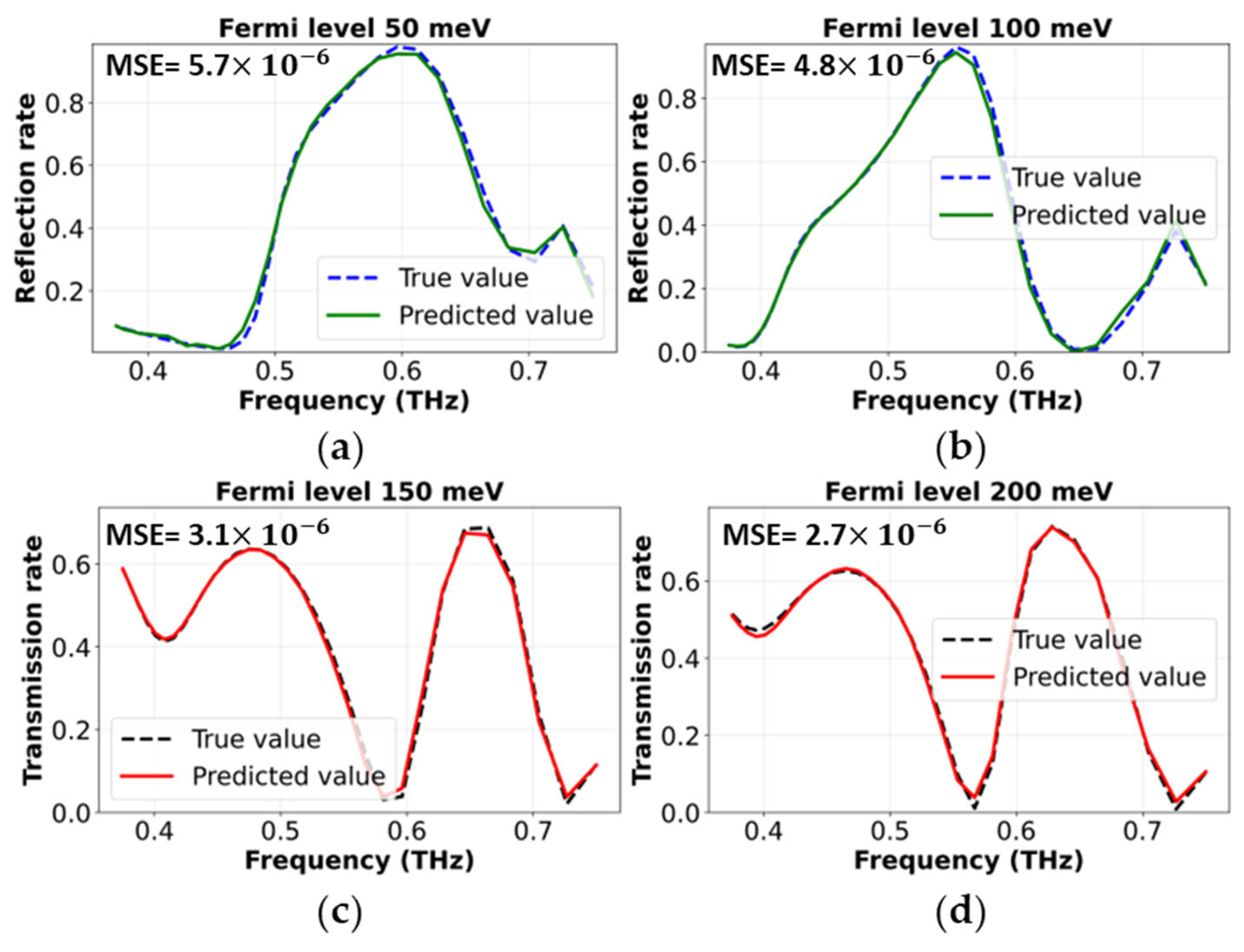
3.2. Spectral Prediction Accuracy Validation
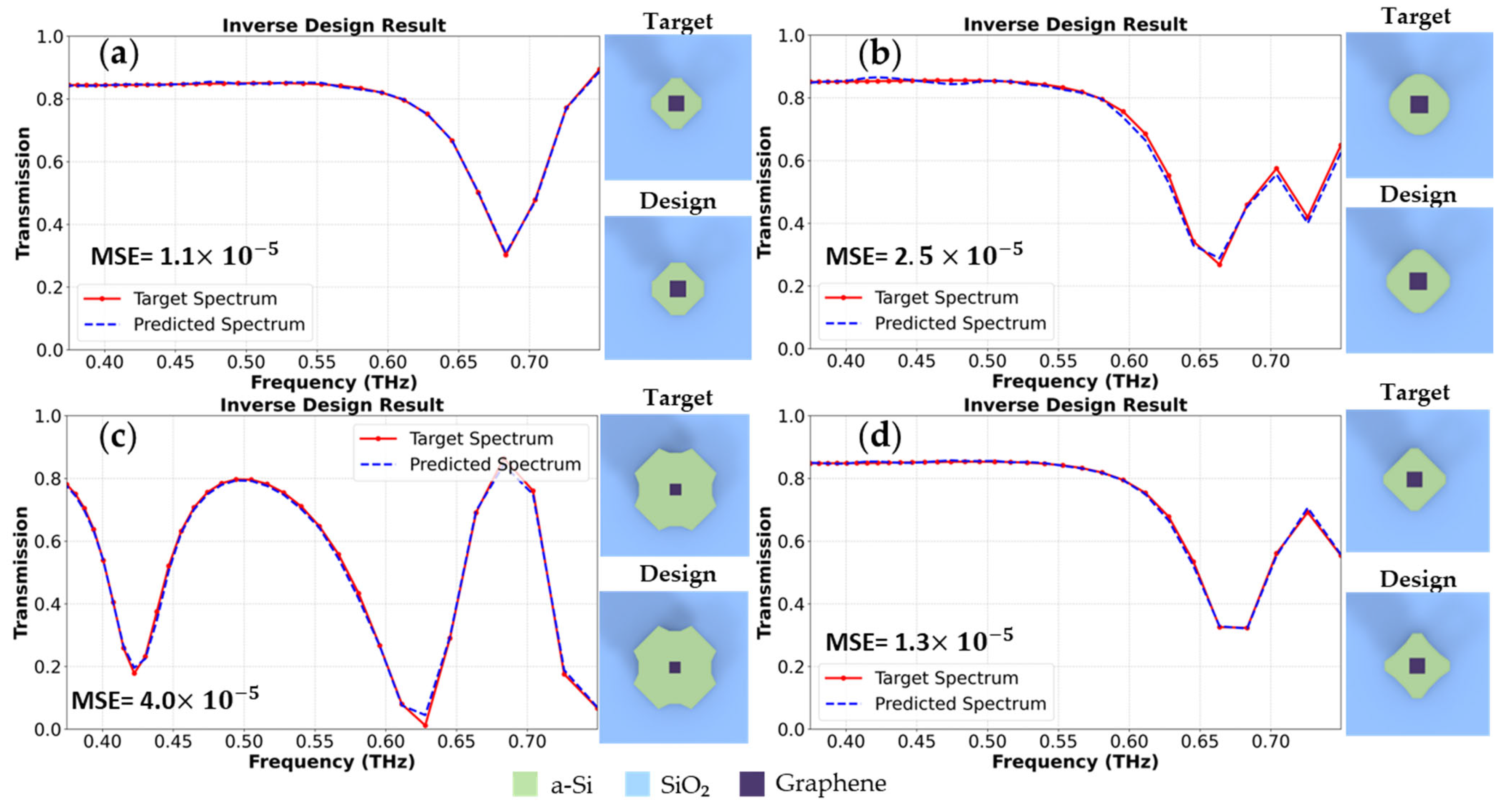
3.3. Comprehensive Inverse Design Results
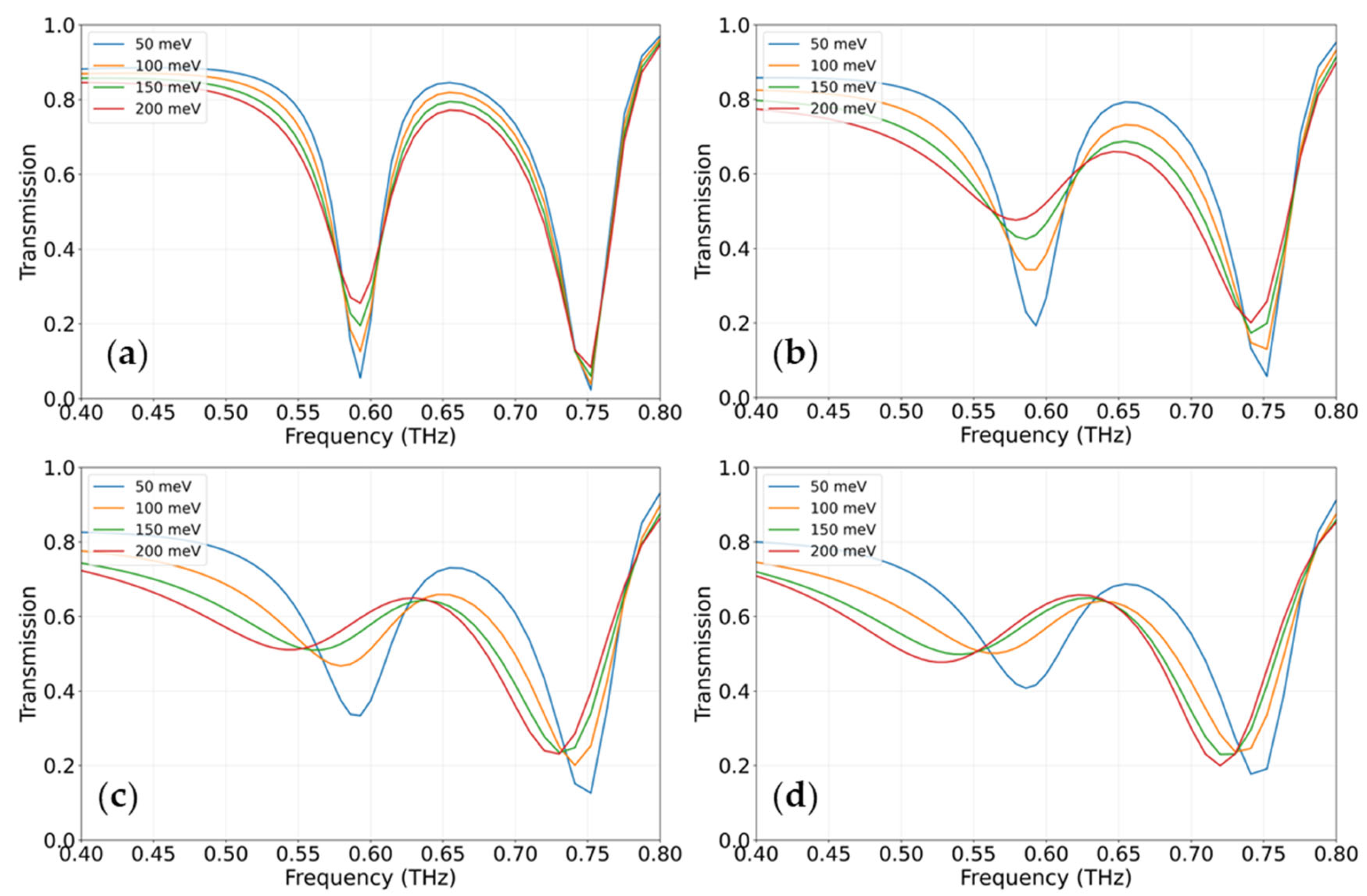
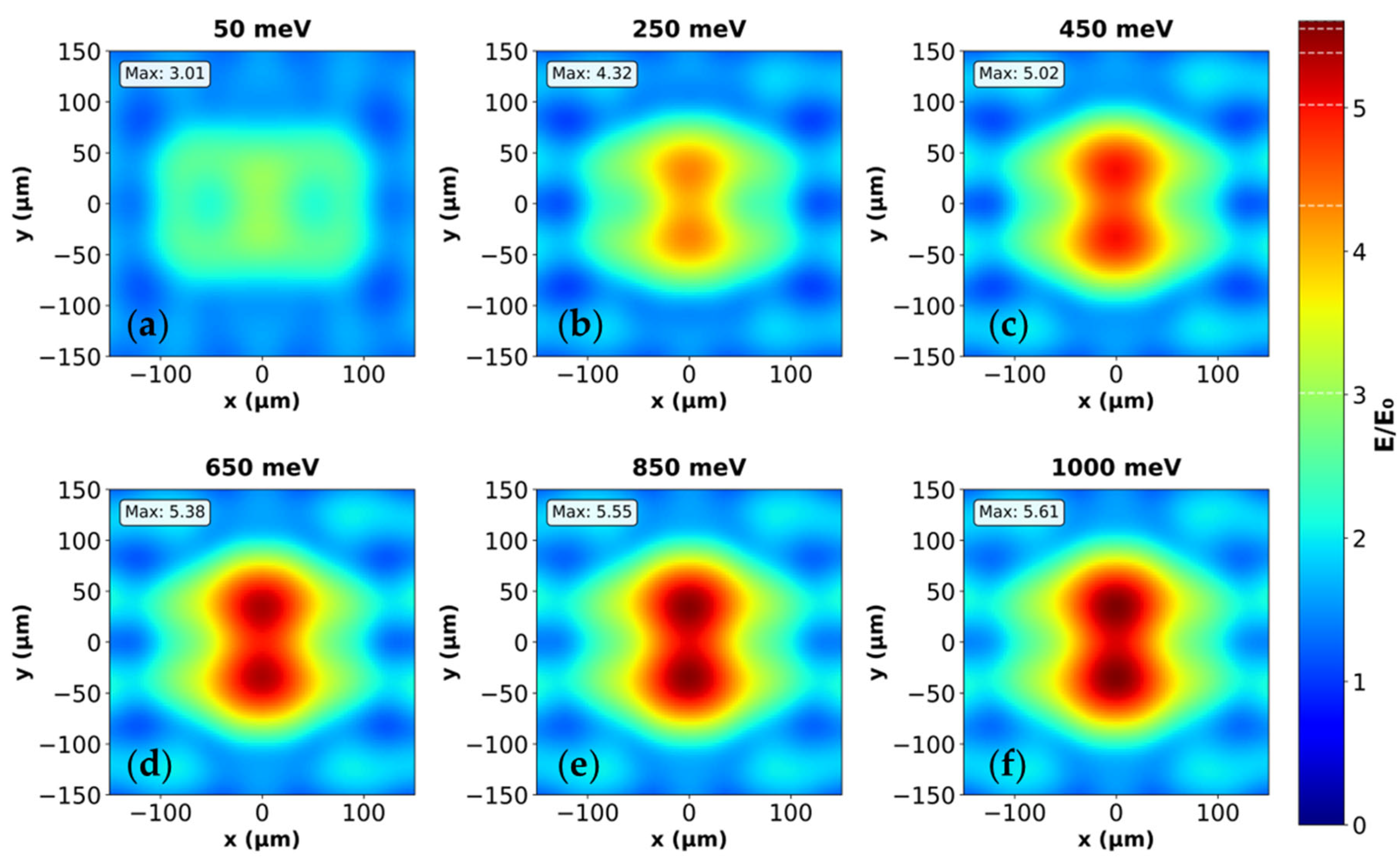
3.4. Electromagnetic Field Distribution Analysis and Structural Validation
3.5. Surrogate-Assisted Optimization Framework Performance Analysis
3.6. Fabrication Feasibility and Process Integration
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Markelz, A.G.; Mittleman, D.M. Perspective on Terahertz Applications in Bioscience and Biotechnology. ACS Photonics 2022, 9, 1117–1126. [Google Scholar] [CrossRef]
- Jiang, W.; Zhou, Q.; He, J.; Habibi, M.A.; Melnyk, S.; El-Absi, M.; Han, B.; Renzo, M.D.; Schotten, H.D.; Luo, F.-L.; et al. Terahertz Communications and Sensing for 6G and Beyond: A Comprehensive Review. IEEE Commun. Surv. Tutor. 2024, 26, 2326–2381. [Google Scholar] [CrossRef]
- Zhu, Z.; Bian, Y.; Zhang, X.; Zeng, R.; Yang, B. Study of Crystallinity and Conformation of Poly(Lactic Acid) by Terahertz Spectroscopy. Anal. Chem. 2022, 94, 11104–11111. [Google Scholar] [CrossRef] [PubMed]
- You, X.; Ako, R.T.; Sriram, S.; Withayachumnankul, W. 3D Terahertz Confocal Imaging with Chromatic Metasurface. Laser Photonics Rev. 2025, 19, 2401011. [Google Scholar] [CrossRef]
- Wu, L.; Yang, L.; Cai, B.; Cheng, Y.; Cheng, Z. Ultra-Broadband Plasmonic Perfect Metamaterial Absorber Based on All-Dielectric Triple-Vertical-Ring Nanostructure MXene for Full-Spectrum Solar Energy. Physica B 2025, 708, 417205. [Google Scholar] [CrossRef]
- Liu, H.; Li, J.; Yang, H.; Wang, J.; Li, B.; Zhang, H.; Yi, Y. TiN-Only Metasurface Absorber for Solar Energy Harvesting. Photonics 2025, 12, 443. [Google Scholar] [CrossRef]
- Li, W.; Cheng, S.; Yi, Z.; Zhang, H.; Song, Q.; Hao, Z.; Sun, T.; Wu, P.; Zeng, Q.; Raza, R. Advanced Optical Reinforcement Materials Based on Three-Dimensional Four-Way Weaving Structure and Metasurface Technology. Appl. Phys. Lett. 2025, 126, 033503. [Google Scholar] [CrossRef]
- Li, Z.; Cheng, S.; Zhang, H.; Yang, W.; Yi, Z.; Yi, Y.; Wang, J.; Ahmad, S.; Raza, R. Ultrathin Broadband Terahertz Metamaterial Based on Single-Layer Nested Patterned Graphene. Phys. Lett. A 2025, 534, 130262. [Google Scholar] [CrossRef]
- Huang, Z.; Wang, Z.; Cheng, Y.; Li, X.; Wang, J.; Zhou, L.; Xu, H.; Luo, X.; Chen, L. Metasurfaces Empower Optical Multiparameter Imaging: A Review. Sci. China Phys. Mech. Astron. 2025, 68, 274201. [Google Scholar] [CrossRef]
- Rong, C.; Wu, L.; Tao, J.; Cheng, Y.; Wang, K.; Chen, L.; Luo, H.; Chen, F.; Li, X. Metasurface-Based Optical Neural Network and Its Application in Next-Generation Optical Communications and Networks. J. Light. Technol. 2025, 43, 8538–8562. [Google Scholar] [CrossRef]
- Ji, W.; Chang, J.; Xu, H.-X.; Gao, J.R.; Gröblacher, S.; Urbach, P.; Adam, A.J.L. Recent Advances in Metasurface Design and Quantum Optics Applications with Machine Learning, Physics-Informed Neural Networks, and Topology Optimization Methods. Light Sci. Appl. 2023, 12, 169. [Google Scholar] [CrossRef]
- She, Y.; Ji, C.; Huang, C.; Peng, J.; Yuan, L.; Liao, J.; Huang, J.; Luo, X. An Intelligent Metasurface for Self-Adaptive Electromagnetic Manipulation of Transmission/Absorption Frequency and Amplitude. Adv. Opt. Mater. 2023, 11, 2301378. [Google Scholar] [CrossRef]
- Mishra, R.; Panwar, R.; Singh, D. Equivalent Circuit Model for the Design of Frequency-Selective, Terahertz-Band, Graphene-Based Metamaterial Absorbers. IEEE Magn. Lett. 2018, 9, 3707205. [Google Scholar] [CrossRef]
- Gao, M.; Jiang, D.; Zhu, G.; Wang, B. Deep Learning-Enhanced Inverse Modeling of Terahertz Metasurface Based on a Convolutional Neural Network Technique. Photonics 2024, 11, 424. [Google Scholar] [CrossRef]
- Zaitsev, A.; Grebenchukov, A.; Khodzitsky, M. Tunable THz Graphene Filter Based on Cross-In-Square-Shaped Resonators Metasurface. Photonics 2019, 6, 119. [Google Scholar] [CrossRef]
- Wang, Y.; Sun, G.; Zhang, X.; Zhang, X.; Cui, Z. Advancement in Carbon Nanotubes Optoelectronic Devices for Terahertz and Infrared Applications. Adv. Electron. Mater. 2024, 10, 2400124. [Google Scholar] [CrossRef]
- Kim, J.; Kim, J.-Y.; Kim, J.; Hyeong, Y.; Neseli, B.; You, J.-B.; Shim, J.; Shin, J.; Park, H.-H.; Kurt, H. Inverse Design of Nanophotonic Devices Enabled by Optimization Algorithms and Deep Learning: Recent Achievements and Future Prospects. Nanophotonics 2025, 14, 121–151. [Google Scholar] [CrossRef] [PubMed]
- Yeung, C.; Tsai, R.; Pham, B.; King, B.; Kawagoe, Y.; Ho, D.; Liang, J.; Knight, M.W.; Raman, A.P. Global Inverse Design across Multiple Photonic Structure Classes Using Generative Deep Learning. Adv. Opt. Mater. 2021, 9, 2100548. [Google Scholar] [CrossRef]
- Ding, Z.; Su, W.; Luo, Y.; Ye, L.; Li, W.; Zhou, Y.; Tang, B.; Yao, H. Artificial Neural Network-Based Inverse Design of Metasurface Absorber with Tunable Absorption Window. Mater. Des. 2023, 234, 112331. [Google Scholar] [CrossRef]
- Kanmaz, T.B.; Ozturk, E.; Demir, H.V.; Gunduz-Demir, C. Deep-Learning-Enabled Electromagnetic near-Field Prediction and Inverse Design of Metasurfaces. Optica 2023, 10, 1373–1382. [Google Scholar] [CrossRef]
- Elsawy, M.M.R.; Lanteri, S.; Duvigneau, R.; Brière, G.; Mohamed, M.S.; Genevet, P. Global Optimization of Metasurface Designs Using Statistical Learning Methods. Sci. Rep. 2019, 9, 17918. [Google Scholar] [CrossRef]
- Ghorbani, F.; Beyraghi, S.; Shabanpour, J.; Oraizi, H.; Soleimani, H.; Soleimani, M. Deep Neural Network-Based Automatic Metasurface Design with a Wide Frequency Range. Sci. Rep. 2021, 11, 7102. [Google Scholar] [CrossRef]
- Zhu, R.; Zhang, Z.; Wang, J.; Xu, C.; Sui, S.; Wang, X.; Liu, T.; Zhu, Y.; Zhang, L.; Wang, J.; et al. Genetic-Algorithm-Empowered Metasurface Design: Simultaneous Realization of High Microwave Frequency-Selection and Low Infrared Surface-Emissivity. Opt. Express 2021, 29, 20150–20159. [Google Scholar] [CrossRef]
- Huang, Z.; Zhang, B.; Wang, Y.; Li, H.; Xu, J.; Ding, J. Realizing Multi-Function Absorptions through Arbitrary Octagonal Meta-Atoms. Opt. Express 2024, 32, 4473–4484. [Google Scholar] [CrossRef] [PubMed]
- Zhang, J.; Qian, C.; Fan, Z.; Chen, J.; Li, E.; Jin, J.; Chen, H. Heterogeneous Transfer-Learning-Enabled Diverse Metasurface Design. Adv. Opt. Mater. 2022, 10, 2200748. [Google Scholar] [CrossRef]
- Tanabe, R.; Fukunaga, A. Success-History Based Parameter Adaptation for Differential Evolution. In Proceedings of the 2013 IEEE Congress on Evolutionary Computation, Cancun, Mexico, 20–23 June 2013; pp. 71–78. [Google Scholar]
- Piotrowski, A.P. L-SHADE Optimization Algorithms with Population-Wide Inertia. Inf. Sci. 2018, 468, 117–141. [Google Scholar] [CrossRef]
- Chen, J.; Li, X.; Chen, Y.; Zhang, Z.; Yu, Y.; He, X.; Chen, H.; Yang, J.; Zhang, Z.; Yao, X. Temperature Self-Adaptive Ultra-Thin Solar Absorber Based on Optimization Algorithm. Photonics 2023, 10, 546. [Google Scholar] [CrossRef]
- Ren, Z.; Sun, Y.; Lin, Z.; Wang, C. Ultra-Narrow Band Perfect Metamaterial Absorber Based on Dielectric-Metal Periodic Configuration. Opt. Mater. 2019, 89, 308–315. [Google Scholar] [CrossRef]
- Yu, H.; Zhao, Z.; Qian, Q.; Xu, J.; Gou, P.; Zou, Y.; Cao, J.; Yang, L.; Qian, J.; An, Z. Metamaterial Perfect Absorbers with Solid and Inverse Periodic Cross Structures for Optoelectronic Applications. Opt. Express 2017, 25, 8288–8295. [Google Scholar] [CrossRef] [PubMed]
- Gallagher, C.P.; Hamilton, J.K.; Hooper, I.R.; Sambles, J.R.; Hibbins, A.P.; Lawrence, C.R.; Bows, J. Multi-Resonant Tessellated Anchor-Based Metasurfaces. Sci. Rep. 2023, 13, 3641. [Google Scholar] [CrossRef]
- Shailesh; Srivastava, G.; Kumar, S.; Sharma, D.; Goyal, B.; Soliman, N.F. A Common Grounded Ultra-Wideband Diversity/MIMO Antenna with High Inter-Element Isolation. Sci. Rep. 2025, 15, 27334. [Google Scholar] [CrossRef]
- Low, T.; Avouris, P. Graphene Plasmonics for Terahertz to Mid-Infrared Applications. ACS Nano 2014, 8, 1086–1101. [Google Scholar] [CrossRef]
- Sensale-Rodriguez, B.; Yan, R.; Kelly, M.M.; Fang, T.; Tahy, K.; Hwang, W.S.; Jena, D.; Liu, L.; Xing, H.G. Broadband Graphene Terahertz Modulators Enabled by Intraband Transitions. Nat. Commun. 2012, 3, 780. [Google Scholar] [CrossRef] [PubMed]
- Hanson, G.W. Dyadic Green’s Functions and Guided Surface Waves for a Surface Conductivity Model of Graphene. J. Appl. Phys. 2008, 103, 064302. [Google Scholar] [CrossRef]
- Pond, J.; Duque-Gomez, F.; Alam, A.; Armenta, R.; Niegemann, J.; McGuire, D.; Reid, A. Modeling Graphene Based Surface Plasmon Waveguides and Devices. In Proceedings of the Integrated Optics: Devices, Materials, and Technologies XX, SPIE, San Francisco, CA, USA, 25–30 January 2016; Volume 9750, pp. 235–248. [Google Scholar]
- Zhang, W.; Weng, Q.; Xu, Y.; Liu, H.; Li, X.-S. Ultra-Highly Sensitive Fano Resonator with Dynamic Tunability Based on Plasmonics. Opt. Commun. 2025, 578, 131477. [Google Scholar] [CrossRef]
- Zhang, W.; Zhong, L.; Cheng, J.; Xu, Y.; Ye, L.-H.; Li, X.-S. Dynamically Tunable Fano Resonator with High Sensitivity in the Terahertz Band. Appl. Opt. 2024, 63, 6285–6291. [Google Scholar] [CrossRef]
- Zhang, D.; Li, Z.; Fan, K.; Chen, T.; Jia, B.; Pan, S.; Tang, Y. Dynamically Tunable Terahertz Metamaterial Sensor Based on Metal–Graphene Hybrid Structural Unit. AIP Adv. 2022, 12, 025206. [Google Scholar] [CrossRef]
- Biabanifard, M.; Arsanjani, A.; Abrishamian, M.S.; Abbott, D. Tunable Terahertz Graphene-Based Absorber Design Method Based on a Circuit Model Approach. IEEE Access 2020, 8, 70343–70354. [Google Scholar] [CrossRef]
- Andryieuski, A.; Lavrinenko, A.V. Graphene Metamaterials Based Tunable Terahertz Absorber: Effective Surface Conductivity Approach. Opt. Express 2013, 21, 9144–9155. [Google Scholar] [CrossRef]
- Zhu, A.; Zhang, M.; Hou, W.; Cheng, L.; Hu, C.; Xu, C. A High-Sensitivity Graphene Metasurface and Four-Frequency Switch Application Based on Plasmon-Induced Transparency Effects. Photonics 2025, 12, 218. [Google Scholar] [CrossRef]
- Ge, J.; You, C.; Feng, H.; Li, X.; Wang, M.; Dong, L.; Veronis, G.; Yun, M. Tunable Dual Plasmon-Induced Transparency Based on a Monolayer Graphene Metamaterial and Its Terahertz Sensing Performance. Opt. Express 2020, 28, 31781–31795. [Google Scholar] [CrossRef]
- Shang, J.; Yu, T.; Lin, J.; Gurzadyan, G.G. Ultrafast Electron−Optical Phonon Scattering and Quasiparticle Lifetime in CVD-Grown Graphene. ACS Nano 2011, 5, 3278–3283. [Google Scholar] [CrossRef] [PubMed]
- Chen, J.; Badioli, M.; Alonso-González, P.; Thongrattanasiri, S.; Huth, F.; Osmond, J.; Spasenović, M.; Centeno, A.; Pesquera, A.; Godignon, P.; et al. Optical Nano-Imaging of Gate-Tunable Graphene Plasmons. Nature 2012, 487, 77–81. [Google Scholar] [CrossRef] [PubMed]
- Fei, Z.; Rodin, A.S.; Andreev, G.O.; Bao, W.; McLeod, A.S.; Wagner, M.; Zhang, L.M.; Zhao, Z.; Thiemens, M.; Dominguez, G.; et al. Gate-Tuning of Graphene Plasmons Revealed by Infrared Nano-Imaging. Nature 2012, 487, 82–85. [Google Scholar] [CrossRef] [PubMed]
- Yu, Y.-J.; Zhao, Y.; Ryu, S.; Brus, L.E.; Kim, K.S.; Kim, P. Tuning the Graphene Work Function by Electric Field Effect. Nano Lett. 2009, 9, 3430–3434. [Google Scholar] [CrossRef]
- Kühne, J.; Wang, J.; Weber, T.; Kühner, L.; Maier, S.A.; Tittl, A. Fabrication Robustness in BIC Metasurfaces. Nanophotonics 2021, 10, 4305–4312. [Google Scholar] [CrossRef]
- Liu, V.; Fan, S. S4: A Free Electromagnetic Solver for Layered Periodic Structures. Comput. Phys. Commun. 2012, 183, 2233–2244. [Google Scholar] [CrossRef]
- Wan, M.; Yashchyshyn, Y.; Li, X.; Godziszewski, K.; Sun, D.-W.; Sheridan, J.T. Characterization of Silicon in the Terahertz. In Proceedings of the SPIE OPTO, Terahertz, RF, Millimeter, and Submillimeter-Wave Technology and Applications XIII, San Francisco, CA, USA, 1–6 February 2020; Volume 11279, pp. 278–284. [Google Scholar]
- Fan, B.W.; Peng, Z.H.; Miao, W.; Shi, S.C. Measurement of Dielectric Constant and Loss Tangent of Several Common Dielectrics by Terahertz Time Domain Spectroscopy. In Proceedings of the SPIE/COS Photonics Asia, Infrared, Millimeter-Wave, and Terahertz Technologies VIII, Nantong, China, 10–12 October 2021; Volume 11906, pp. 49–55. [Google Scholar]
- Glorot, X.; Bengio, Y. Understanding the Difficulty of Training Deep Feedforward Neural Networks. In Proceedings of the Thirteenth International Conference on Artificial Intelligence and Statistics, Chia Laguna Resort, Sardinia, Italy, 31 March 2010; Volume 9, pp. 249–256. [Google Scholar]
- Ji, J.; Xiang, C.; Gammelgaard, L.; Shivayogimath, A.; Zhou, B.; Jepsen, P.U.; Bøggild, P. Ultrabroadband THz Probing of Anisotropic Optical Conductivity and Plasmonic Damping in Graphene Nanostructures. 2D Mater. 2025, 12, 025005. [Google Scholar] [CrossRef]
- Feng, M.; Zhang, B.; Ling, H.; Zhang, Z.; Wang, Y.; Wang, Y.; Zhang, X.; Hua, P.; Wang, Q.; Song, A.; et al. Active Metal–Graphene Hybrid Terahertz Surface Plasmon Polaritons. Nanophotonics 2022, 11, 3331–3338. [Google Scholar] [CrossRef]
- Deinert, J.-C.; Alcaraz Iranzo, D.; Pérez, R.; Jia, X.; Hafez, H.A.; Ilyakov, I.; Awari, N.; Chen, M.; Bawatna, M.; Ponomaryov, A.N.; et al. Grating-Graphene Metamaterial as a Platform for Terahertz Nonlinear Photonics. ACS Nano 2021, 15, 1145–1154. [Google Scholar] [CrossRef]
- Qiu, T.; Shi, X.; Wang, J.; Li, Y.; Qu, S.; Cheng, Q.; Cui, T.; Sui, S. Deep Learning: A Rapid and Efficient Route to Automatic Metasurface Design. Adv. Sci. 2019, 6, 1900128. [Google Scholar] [CrossRef]
- Zhang, Q.; Liu, C.; Wan, X.; Zhang, L.; Liu, S.; Yang, Y.; Cui, T.J. Machine-Learning Designs of Anisotropic Digital Coding Metasurfaces. Adv. Theory Simul. 2019, 2, 1800132. [Google Scholar] [CrossRef]
- Li, N.; Xu, Z.; Dong, Y.; Hu, T.; Zhong, Q.; Fu, Y.H.; Zhu, S.; Singh, N. Large-Area Metasurface on CMOS-Compatible Fabrication Platform: Driving Flat Optics from Lab to Fab. Nanophotonics 2020, 9, 3071–3087. [Google Scholar] [CrossRef]
- Terekhov, P.; Chang, S.; Rahman, M.T.; Shafi, S.; Ahn, H.-J.; Zhao, L.; Ni, X. Enhancing Metasurface Fabricability through Minimum Feature Size Enforcement. Nanophotonics 2024, 13, 3147–3154. [Google Scholar] [CrossRef]
- Gao, W.; Xiao, P.; Henkelman, G.; Liechti, K.M.; Huang, R. Interfacial Adhesion between Graphene and Silicon Dioxide by Density Functional Theory with van Der Waals Corrections. J. Phys. D Appl. Phys. 2014, 47, 255301. [Google Scholar] [CrossRef]
- Müller, M.; Bouša, M.; Hájková, Z.; Ledinský, M.; Fejfar, A.; Drogowska-Horná, K.; Kalbáč, M.; Frank, O. Transferless Inverted Graphene/Silicon Heterostructures Prepared by Plasma-Enhanced Chemical Vapor Deposition of Amorphous Silicon on CVD Graphene. Nanomaterials 2020, 10, 589. [Google Scholar] [CrossRef] [PubMed]
- Pham, T.T.; Huynh, T.H.; Colomer, J.-F.; Reckinger, N.; Hackens, B.; Sporken, R. Semi-Dry Transfer of CVD Graphene on Si: Surface Morphology and Electronic Properties. Nanoscale 2025, 17, 11060–11070. [Google Scholar] [CrossRef] [PubMed]




| Method | Accuracy (%) | Frequency Range | Design Time | Application Domain |
|---|---|---|---|---|
| REACTIVE [56] | 76.51 | THz range | 200× faster than conventional | General metasurface |
| DNN (Wide-frequency) [22] | 92.0 | 4–45 GHz | Not mentioned | Wideband metasurface |
| cDCGAN Global Design [18] | >90 | 4–12 μm | Not mentioned | Multi-class metasurface |
| CNN + GA Inverse Design [57] | 90.05 | 0.2–2 THz | 10 min | Random metasurface patterns |
| SHADE + DNN (This work) | 96.7 | 0.4–0.8 THz | 10.2 s | Tunable graphene metasurface |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, S.; Lin, J.; Sun, J.; Li, X.-S. Inverse Design of Tunable Graphene-Based Terahertz Metasurfaces via Deep Neural Network and SHADE Algorithm. Photonics 2025, 12, 910. https://doi.org/10.3390/photonics12090910
Chen S, Lin J, Sun J, Li X-S. Inverse Design of Tunable Graphene-Based Terahertz Metasurfaces via Deep Neural Network and SHADE Algorithm. Photonics. 2025; 12(9):910. https://doi.org/10.3390/photonics12090910
Chicago/Turabian StyleChen, Siyu, Junyi Lin, Jingchun Sun, and Xue-Shi Li. 2025. "Inverse Design of Tunable Graphene-Based Terahertz Metasurfaces via Deep Neural Network and SHADE Algorithm" Photonics 12, no. 9: 910. https://doi.org/10.3390/photonics12090910
APA StyleChen, S., Lin, J., Sun, J., & Li, X.-S. (2025). Inverse Design of Tunable Graphene-Based Terahertz Metasurfaces via Deep Neural Network and SHADE Algorithm. Photonics, 12(9), 910. https://doi.org/10.3390/photonics12090910





