Self-Learning-Based Fringe Domain Conversion for 3D Surface Measurement of Translucent Objects at the Mesoscopic Scale

Abstract

Three-dimensional measurement of translucent objects using structured light techniques remained fundamentally challenging due to severe degradation of fringe patterns caused by subsurface scattering, which inevitably introduced phase errors and compromised measurement accuracy. Although deep learning had emerged as a powerful tool for fringe analysis, its practical implementation was hindered by the impractical requirement for large-scale labeled datasets, particularly in scattering-dominant measurement scenarios. To overcome these limitations, we developed a self-learning-based fringe domain conversion method inspired by image style transfer principles, where degraded and ideal fringe patterns were treated as distinct domains for cyclic translation. The proposed framework employed dual generators and discriminators to establish cycle-consistency constraints while incorporating both numerical intensity-based and physical phase-derived optimization targets, effectively suppressing phase errors and improving fringe modulation without requiring paired training data. Experimental validation demonstrated superior performance in reconstructing high-fidelity 3D morphology of translucent objects, establishing this approach as a robust solution for precision metrology of complex scattering media.

1. Introduction

Structured light techniques, with their non-contact nature, high accuracy, and high sensitivity, have emerged as one of the most popular 3D measurement technologies [1,2,3]. They are widely applied in industrial manufacturing, including workpiece defect inspection, reverse engineering, and industrial material analysis. These techniques are based on the point-to-point triangulation principle, which ensures superior performance for diffuse-reflective surfaces. Even in the presence of highly reflective surfaces, numerous high dynamic range approaches have developed to enhance measurement accuracy [4,5,6].

However, as measurement scenarios grow increasingly complex, the capability to measure only diffuse objects is no longer sufficient to meet modern application demands. When confronted with translucent or even transparent objects, conventional structured light techniques often fail. This is primarily due to the subsurface scattering effect in translucent media, which violates the fundamental point-to-point triangulation rule underlying structured light measurements. As a result, the acquired fringe patterns suffer from low modulation, low contrast, and low signal-to-noise ratio (SNR). The degraded structured light fringes introduce severe phase noise and geometric errors, making it extremely challenging to recover high-precision 3D morphology of translucent materials. High-precision measurement of translucent scattering media is critically important in industrial and medical applications, such as resin composite deformation analysis, jade artifact inspection, and 3D reconstruction of biological tissues [7,8,9]. Therefore, there is an urgent need to develop reliable methods for translucent objects.

To address these challenges, researchers have developed a series of innovative methods. Nayar et al. pioneered the analysis of illumination components in complex scenes, distinguishing between the direct illumination (the desired signal) and indirect illumination (considered interference) [10]. The indirect contributions, including interreflections, subsurface scattering, ambient light, and their coupling are collectively termed global illumination. Notably, subsurface scattering from translucent objects constitutes a major global illumination component. Building on this insight, Nayar proposed high-frequency illumination to separate direct and global illumination, effectively suppressing global components and demonstrating promise for translucent object measurement. Inspired by Nayar’s work, Chen et al. introduced the modulated phase-shifting method, which employs high-frequency modulation of low-frequency patterns to isolate indirect light [11]. However, such high-frequency fringe projection strategies often result in low-contrast images, limiting their practical utility. Subsequently, Gupta et al. developed the micro-phase-shifting method and XOR Gray-code method, enabling high-quality phase recovery without requiring indirect light separation [12,13]. By projecting two sets of high-frequency fringes and constructing an all-high-frequency Gray-code pattern, this approach achieves measurements under global illumination. However, it assumes the presence of only low-frequency indirect components, thus offering only partial mitigation of indirect reflection effects.

Further advancements leveraged polarization properties to suppress scattering. Chen et al. combined polarization techniques with optical fibers to separate light intensities, achieving high fringe contrast and high-quality measurements of translucent objects [14,15]. Nevertheless, this method increases system complexity, involves cumbersome operations, and suffers from low measurement efficiency. Lutzke et al. employed Monte Carlo (MC) simulations to model translucent imaging, facilitating the study of error compensation algorithms [16,17]. Rao et al. proposed a local blur-based error compensation method, analyzing phase errors induced by defocus effects of cameras/projectors and approximating subsurface scattering as localized blur [18]. While effective, this method has two limitations: (1) applicability only to short-range scattering, (2) low computational efficiency. Xu et al. established a relationship between phase error and fringe frequency, employing temporal denoising and improved phase unwrapping to significantly enhance measurement quality [19]. This method proves that fringe noise can be effectively reduced by time domain averaging to improve the fringe modulation. However, this method requires multiple temporal samples per fringe image, leading to high time costs.

Jiang et al. integrated single-pixel imaging (SPI) with structured light, achieving promising results for translucent measurements [20,21]. This technique calculates the optical transmission coefficient for each pixel, restoring high modulation fringes that are not disturbed by scattered light. For instance, Lyu et al. applied SPI to underwater environments, which effectively enhanced the fringe contrast to overcome the scattering effect of turbid liquid [22]. However, SPI’s need for massive image acquisitions severely restricts measurement speed, limiting it to static scenarios. Wu et al. later introduced multi-scale parallel SPI, drastically reducing the required fringe count and enabling dynamic measurements in complex scenes, including high-quality 3D reconstruction of translucent objects [23]. Despite this, SPI-assisted methods still cannot match the efficiency of conventional structured light techniques (e.g., nine frames for three-frequency phase unwrapping or seven for Gray codes). Moreover, parallel SPI demands substantial computational resources due to per-pixel calculations of light transport coefficients and direct illumination peak localization.

Recently, learning-based methods have gained traction in structured light measurement, particularly for fringe analysis, error compensation, and phase recovery [24,25,26,27]. Feng et al. proposed the first deep learning-based fringe analysis framework [28], where a neural network directly maps single-frame fringes to numerator/denominator images of the arctangent function, enabling single-frame phase extraction. Capitalizing on deep neural networks’ powerful nonlinear fitting capability, this approach excels in fringe restoration and enhancement. In our latest work [29], we combined deep learning with Bayesian inference for scattering media measurement, enhancing degraded fringes into high modulation patterns and significantly improving measurement quality. However, as a supervised learning method, it faces challenges in dataset preparation: ground-truth labels require spray-based coating, which may damage specimens and involves tedious operations.

In this work, we developed a self-learning fringe domain transformation framework to achieve fringe modulation enhancement and denoising for translucent objects measurement. The proposed method established a cyclic generative architecture that systematically transformed degraded fringe patterns into high-modulation counterparts through a cycle-consistency mechanism. By integrating both numerical constraints on fringe intensity distributions and physical constraints governing phase relationships, the framework successfully suppressed phase-shift errors and improved phase quality. The elimination of labeled data requirements represented a significant advancement, reducing dependence on curated datasets while maintaining measurement accuracy. Experimental validation across multiple scattering media demonstrated the method’s robustness in recovering fine surface features under challenging optical conditions.

2. Methods

2.1. Subsurface Scattering in Structured Light Projection

In conventional structured light measurement systems operating under ideal conditions, the point-to-point triangulation principle governs the optical behavior, where each camera pixel receives light exclusively from a corresponding projector pixel. This paradigm holds true for Lambertian surfaces, where captured fringe patterns can be mathematically described as

$$I_n(x,y)=a(x,y)+b(x,y)\cos \left[\mathit{\Phi }(x,y)+\frac{2\pi n}{N}\right],$$

(1)

where a(x, y) represents background intensity, b(x, y) denotes fringe modulation, Φ(x, y) is the phase distribution, and N is the phase shifted step, n = 1, 2, …, N. When measuring translucent objects, the incident structured light partially penetrates the surface and undergoes multiple subsurface scattering events within the superficial layers before re-emerging. This subsurface scattering effect introduces significant deviations from ideal measurement conditions. As illustrated in Figure 1, for any measured pixel A, the received intensity incorporates not only its direct reflection component but also scattering contributions from neighboring surface points (A₁–A_n), which violated the fundamental point-to-point measurement principle. As a result, the camera detects a composite signal comprising both direct surface reflection (desired fringe) and subsurface scattering components (noise). For a fringe image, the intensity of each pixel is destroyed by the scattering noise, so the signal-to-noise ratio (SNR) and the contrast of the fringe is significantly reduced. Physically, this phenomenon can be modeled as the convolution of ideal fringe patterns with a point spread function (PSF), yielding the degraded pattern expression:

$$I_n^S(x,y)=E(x,y)+\left[R(x,y)I_n(x,y)+S_n(x,y)\right]\cdot G(x,y),$$

(2)

where E(x, y) and R(x, y) denote the environmental intensity and the media reflectance, respectively; G(x, y) is the white random noise; and S_n(x, y) represents the scattering component,

$$\begin{array}{ccc}\hfill S_n(x,y)& =& I_n(i,j)\otimes P(x,y)\hfill \\ & =& {\displaystyle \sum _{i=0}^{H-1}{\displaystyle \sum _{j=0}^{W-1}\left[I_n(i,j)P(x-i,y-j)\right]}},\hfill \end{array}$$

(3)

where P(x, y) represents the PSF and H and W represent the height and width of the fringe patterns. Consequently, translucent object measurement transforms the conventional point-to-point model into an area-to-point paradigm, manifesting as low fringe modulation and poor SNR. The coupled scattering components introduce systematic phase errors, fundamentally limiting measurement accuracy in such scenarios.

2.2. Self-Learning-Based Fringe Domain Conversion

The developed self-learning-based fringe domain conversion framework aims to enhance the contrast and eliminate the noise of the fringes. It treats fringe patterns from translucent surfaces and ideal fringe patterns from diffuse surfaces as distinct image domains for cross-domain mapping. These two kinds of fringe patterns belong to degraded domain and enhanced domain. As shown in Figure 2, our approach implemented a cyclic generative architecture to transform low-modulation, low-SNR fringe patterns into high-quality sinusoidal fringes, which employed two generators G and F and two discriminators D_X and D_Y to establish bidirectional fringe domain mapping.

First, generator G converted degraded-domain images to the enhanced domain, while F performed the inverse transformation. The discriminators maintain domain-specific characteristics by evaluating image authenticity. Cycle-consistency constraints [30] preserved structural integrity by minimizing differences between original and reconstructed images. The system processed three key components simultaneously: fringe terms M(x, y) and D(x, y), along with wrapped phase φ(x, y), ensuring comprehensive fringe enhancement while maintaining phase accuracy. The wrapped phase is calculated as follows:

$$\phi (x,y)=\arctan \left\{{\displaystyle \frac{{\displaystyle {\sum }_{n=1}^N{I}_n(x,y)\sin (\frac{2\pi n}{N})}}{{\displaystyle {\sum }_{n=1}^N{I}_n(x,y)\cos (\frac{2\pi n}{N})}}}\right\}.$$

(4)

The normalized numerator M(x, y) and denominator D(x, y) of the arctangent function can be calculated by the following equation [31]:

$$\left\{\begin{array}{l}M(x,y)=\sin \left[\phi (x,y)\right]\\ D(x,y)=\cos \left[\phi (x,y)\right]\end{array}\right..$$

(5)

The proposed network architecture specifically addressed the challenges of processing low-SNR fringe patterns through specialized modules in both generator and discriminator as shown in Figure 3a and Figure 3b, respectively. The generator utilized the first stage of HINet structure [32], which employed a 3 × 3 convolutional layer to preserve high-frequency fringe details while filtering random noise. Its encoder progressively extracted multi-scale features through four cascaded half-instance normalization blocks as shown in Figure 4a, which uniquely combined instance and batch normalization to maintain fringe periodicity while suppressing scattering-induced artifacts. The integrated attention mechanism dynamically weighted feature importance, effectively enhancing valid fringe signals over noise components. During decoding, four residual blocks with skip connections recovered lost modulation details from degraded patterns as shown in Figure 4b, while the 2 × 2 deconvolution layers precisely reconstructed fringe spacing. Meanwhile, the supervised attention (SA) block actively suppressed invalid features caused by strong scattering as shown in Figure 4c. The discriminator’s 4 × 4 convolutional layers with LeakyReLU progressively learned hierarchical features from both spatial and frequency domains, enabling robust identification of authentic fringe characteristics against scattering noise. Its final binary classifier focused particularly on fringe continuity and modulation depth (>0.6 for enhanced patterns), ensuring physically plausible transformations. This comprehensive architecture demonstrated superior performance in preserving phase information while enhancing low-contrast fringes to near-ideal quality.

2.3. Design of the Loss Function

To achieve optimal generation performance while strictly maintaining cycle consistency, we designed a composite loss function comprising three critical components: cycle consistency loss (L_cyc), adversarial loss (L_adv), and identity loss (L_ide), with weighting coefficients (α = 10, β = 1, γ = 5) carefully balanced to prevent any single objective from dominating the training process. The total loss function can be expressed as

$$L_{total}=\alpha L_{cyc}+\beta L_{adv}+\gamma L_{ide}.$$

(6)

The empirically determined weightings (α > γ > β) reflected the hierarchical importance of these objectives, with the dominant cycle consistency term (α = 10) guaranteeing structural similarity index (SSIM) in round-trip transformations, while the identity loss (γ = 5) preserved original fringe modulation in target-domain images. This balanced loss formulation demonstrated effectiveness in handling challenging scattering conditions.

Specifically, the cycle consistency loss is designed as

$$L_{cyc}(G,F)=E_{X~P_{data}(X)}{‖F(G(X))-X‖}_1+E_{Y~P_{data}(Y)}{‖G(F(Y))-Y‖}_1,$$

(7)

where F(X) and F(Y) are the images that are generated after the image is entered into the generator F. This cyclic consistency mechanism enforced bidirectional domain preservation through L1-norm constraints. When a degraded-domain fringe pattern X underwent sequential transformations through both generators (X → G(X) → F(G(X))), the reconstructed pattern maintained essential structural similarity with the original input. Similarly, enhanced-domain patterns Y preserved their core features when processed through the inverse transformation path (Y → F(Y) → G(F(Y))).

The adversarial loss is defined as

$$L_{adv}(G,D_Y,X,Y)=E_{X~P_{data}(X)}\left[\log D_Y(Y)\right]+E_{Y~P_{data}(Y)}[\log (1-D_Y(G(X)))]+\lambda L_{TV}(Y),$$

(8)

where X and Y are degraded domain image and enhanced domain image, respectively, and G(X) is the image generated after the image input generator G. This adversarial loss followed conventional GAN formulation, where the generator G learned to produce enhanced-domain patterns indistinguishable from real samples (Y ≈ G(X)) while the discriminator D_Y progressively improved its ability to differentiate between generated and authentic enhanced-domain fringes. Additionally, our adversarial training was augmented with total variation (TV) regularization (λ = 0.1) to suppress noise artifacts by minimizing pixel-wise intensity variations (TV loss = Σ|∇G(X)|), resulting in smoother output patterns compared to baseline implementations.

The identity loss is expressed as

$$L_{ide}(G,F,X,Y)=E_{Y~P_{data}(Y)}{‖G(Y)-Y‖}_1+E_{X~P_{data}(X)}{‖F(X)-X‖}_1.$$

(9)

It served as a regularizer to prevent unnecessary modifications to already domain-appropriate images, particularly crucial for maintaining fringe periodicity in enhanced-domain inputs where excessive processing could alter valid sinusoidal patterns.

It is noted that the network training simultaneously optimized losses for both M, D and the calculated wrapped phase φ as follows:

$$L={\omega }_1{L}_{total\_M}(M_{pre},M)+{\omega }_2{L}_{total\_D}(D_{pre},D)+{\omega }_3{L}_{total\_\phi }[\arctan ({\displaystyle \frac{M_{pre}}{D_{pre}}}),\arctan ({\displaystyle \frac{M}{D}})],$$

(10)

where L_{total_M} and L_{total_D} provided numerical constraints on intensity transformation fidelity, L_{total_φ} enforced physical constraints to mitigate phase shifted errors, ω₁–ω₃ are the weights of each constraint. During the training process, L_{total_M} and L_{total_D} decrease faster than L_{total_φ}, and L_{total_φ} is only used as an auxiliary term to constrain the suppression of phase shift error. Based on the above considerations, the weight ω₃ is set to a smaller value to prevent the initial training from focusing on the reduction of L_{total_φ}.

2.4. Training Dataset and Implementation

In conventional supervised deep learning approaches for structured light measurement, each input fringe pattern requires precisely matched ground truth data. For translucent object measurement, obtaining ideal reference fringes typically involves coating specimens with diffusible sprays to convert their surface properties from translucent to Lambertian, thereby eliminating subsurface scattering effects. This process proves particularly cumbersome, often requiring several hours of drying time per specimen, which significantly impedes practical dataset preparation.

The proposed self-supervised framework fundamentally overcomes this limitation by eliminating the need for paired training data. Our method simply requires two distinct sets of unpaired fringe patterns: one collected from various translucent samples and another from diffuse reference targets, with no spatial or temporal correspondence needed between them. Specifically, we acquired fringe data from 10 different translucent specimens (including dental composites and silicone phantoms) and 10 diffuse reference samples, capturing multiple surface positions per sample. Through systematic data augmentation involving rotation (±30°), scaling (0.8–1.2×), and translation (±10% FOV), we generated 1000 real unpaired fringe patterns.

To substantially expand the diversity of training patterns, we leveraged our established physical simulation framework to generate 3000 simulation fringe pairs per domain, meticulously modeling the degraded domain through convolution of ideal fringes, while the enhanced domain comprised purely synthetic sinusoidal patterns with high modulation. These simulation datasets were deliberately generated through independent processes for each domain to preserve the essential unpaired characteristic of the training set. By integrating experimentally measured fringe patterns from physical specimens with carefully simulated data generated through our physics-based modeling framework, we established a comprehensive training dataset comprising 4000 samples each for both the degraded and enhanced domains, which served as the foundation for our self-supervised learning network. The strategic combination of empirical and simulated data enabled robust network training while maintaining the critical unpaired relationship between domains, with the physical measurements capturing authentic scattering phenomena and the synthetic data ensuring sufficient variation in fringe frequencies and modulation depths. This balanced dataset composition proved particularly effective for the cycle-consistent domain transformation task, as evidenced by the network’s ability to generalize across different material types.

The network training was implemented in PyTorch 2.7.1 with 512 × 512 pixels inputs to optimize GPU memory utilization on an NVIDIA RTX 4060 (8 GB VRAM) platform. The learning rate strategy of the generator adopts cosine annealing that varied from an initial 2 × 10⁻⁶ to a minimum of 1 × 10⁻⁶. The discriminator adopts an attenuation strategy based on the training period and linearly reduces the learning rate. The initial learning rate is set to 2 × 10⁻⁴. The training period is 50 epochs, which is completed in approximately 9 h.

3. Experiments

We conducted multiple sets of 3D measurements on translucent media using a self-built mesoscale FPP measurement system, where the projector is TI DLP2010EVM-LC with a resolution of 854 × 480 and the camera is Basler daA720-520uc with a resolution of 720 × 540. The measurement volume is approximately 17 mm (length) × 10 mm (width) × 10 mm (depth). The test objects comprised various subsurface scattering materials, including optical glue, frosted glass, jade, and silicone. To validate the performance of the proposed self-learning method, the experimental results were compared with those obtained from traditional phase-shifting profilometry (PSP), supervised learning-based method [29], and the spray-coating method. The spray-coating results were regarded as ground truth. In all experiments, multi-frequency heterodyne phase unwrapping was employed, followed by 3D reconstruction using a stereo calibration model.

The first experiment involved the measurement of optical glue. Figure 5a shows the region of interest on the test object. Figure 5b–e present the fringe M computed using traditional PSP, the supervised learning-based method, the proposed method, and the spray-coating method, respectively. The traditional PSP exhibited significantly low modulation, whereas both deep learning-based methods enhanced the fringes to high quality. Due to non-uniform reflectivity, the spray-coated sample also displayed uneven fringe modulation. Figure 5f–i show the wrapped phase maps obtained by the four methods. Except for the noisy phase from traditional PSP, the other methods yielded satisfactory results, demonstrating the superiority of the proposed approach in fringe enhancement. Figure 6 compares the 3D reconstructions obtained by the four methods. Severe phase noise in traditional PSP led to substantial geometric errors and depth information loss, resulting in a rough surface that poorly represented the true 3D profile. In contrast, both deep learning-based methods achieved complete and smooth 3D reconstructions. Notably, the proposed method produced a smoother surface than the supervised learning-based approach, though this may slightly compromise fine details in complex surface measurements. While the spray-coating method inherently avoids subsurface scattering effects, coating non-uniformity may introduce measurement inaccuracies.

The second experiment involved high-resolution measurement of a localized region on a frosted glass cup surface. Figure 7a delineates the region of interest (ROI). Figure 7b–e present the fringe patterns obtained from four distinct methodologies, with localized insets revealing critical details. The conventional phase-shifting profilometry (PSP) yielded severely degraded fringe quality, with near-complete fringe disappearance in specific regions (Figure 7b). The supervised learning approach demonstrated notable enhancement in low-modulation regions; however, its performance deteriorated in areas with abrupt surface gradients, manifesting as residual noise artifacts (Figure 7c). In contrast, our proposed method successfully reconstructed high-fidelity fringe patterns across all challenging regions (Figure 7d). This superior performance stems from our fringe-domain transformation model, which leverages advanced image generation capabilities to optimize local fringe quality through global feature integration. The close agreement between our results and the spray-coating reference (Figure 7e) further validates the method’s reliability. Corresponding wrapped phase maps are shown in Figure 7f–i. The phase quality directly correlates with fringe modulation characteristics, as expected from fundamental phase retrieval principles.

Three-dimensional reconstructions derived from these phase maps are presented in Figure 8. The conventional method exhibited significant data loss in high-gradient regions due to fringe extinction. While both deep learning approaches improved reconstruction completeness, residual artifacts persisted. Our method achieved superior topological continuity compared to the supervised alternative. 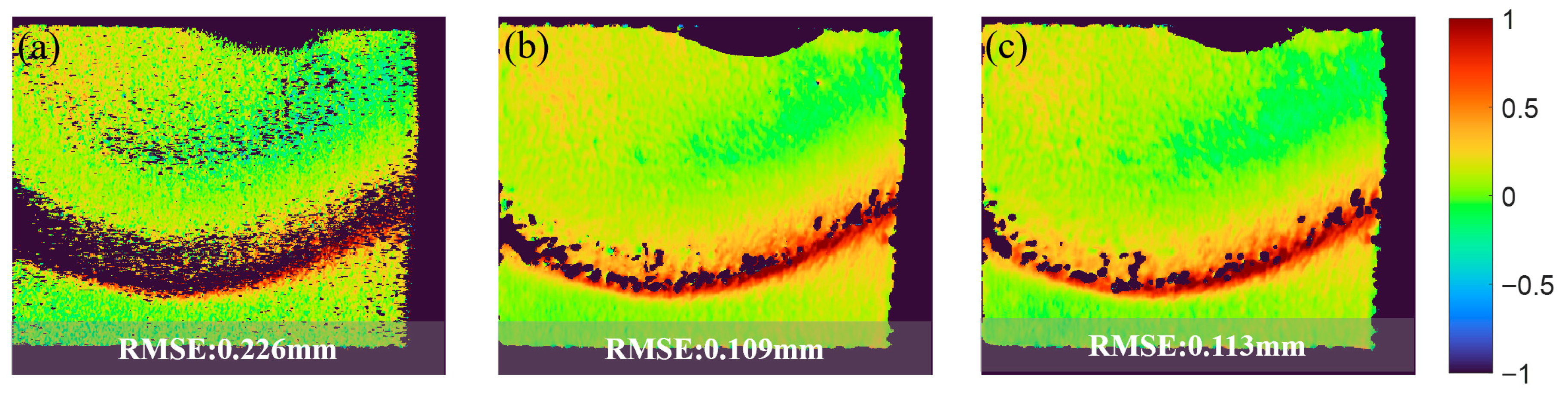Cross-sectional profiles (Figure 8e,f) provide quantitative comparison. The conventional method’s profile contained substantial noise, whereas the other three methods produced smooth contours. Notably, our results showed a near-perfect overlap with the supervised learning output, demonstrating that our self-supervised approach achieves comparable performance to supervised methods in 3D metrology. Quantitative error analysis relative to the spray-coating reference is shown in Figure 9. Our method reduced the RMSE by 50% compared to conventional PSP. More significantly, it achieved equivalent RMSE to the supervised method, confirming measurement accuracy parity while eliminating the need for labeled training data.

The third experiment evaluated the proposed method’s performance on complex surfaces using a semi-transparent jade sample with intricate facial features (Figure 10). Both deep learning approaches successfully enhanced degraded fringe patterns to high-modulation states (Figure 10c,d). While the spray-coating method exhibited non-uniform modulation distribution, it preserved the finest details (Figure 10e), establishing an optimal reference for 3D reconstruction. Phase analysis revealed significant noise contamination in conventional PSP results, leading to rough surface reconstructions. Although the learning-based methods produced cleaner phase maps, excessive smoothing caused subtle height information loss—a common trade-off in data-driven approaches. Three-dimensional reconstruction results are presented in Figure 11. The conventional method failed to capture complex geometrical variations (Figure 11a), while both learning-based approaches achieved comparable detail reconstruction (Figure 11b,c). The spray-coating reference (Figure 11d) demonstrated superior edge definition and natural transitions, highlighting remaining challenges for computational methods. Quantitative error analysis (Figure 12) confirmed our method’s parity with supervised learning in RMSE performance.

The last experiment is measuring the dynamic process of extrusion deformation of a translucent silica gel. Because the dynamic process is not repeatable, it is impossible to compare the results of the spraying method. We compare the 3D shape reconstruction results of the three methods under five frames. Figure 13a1,a2 show the sketch map before and after the deformation of the measured object, and Figure 13a3 is the captured image of the measured object. Figure 13b–d are the results of traditional PSP, supervised learning method and the proposed method, respectively. The experimental results show that the proposed approach not only significantly outperformed conventional PSP in dynamic measurement conditions but also achieved reconstruction quality equivalent to supervised learning while maintaining robust resistance to motion-induced artifacts. These results collectively validate our method’s effective applicability to time-varying measurements of scattering media, demonstrating performance parity with supervised approaches and representing a notable advancement in dynamic 3D metrology capabilities. It should be noted the since the image acquisition and network processing programs have not been integrated, the experimental results are not inferenced in real time. The off-line inference speed of the proposed method for each pair of M and D is about 6 ms. The successful implementation under dynamic conditions highlights the method’s practical utility for real-world applications involving deformable translucent materials.

4. Discussion

Multiple experiments on translucent materials have demonstrated that the proposed method exhibits superior performance in both measurement accuracy and efficiency. Compared to existing methods, its main breakthroughs are discussed as follows:

First, there is no sacrifice in measurement efficiency. Although existing methods such as temporal denoising [19], single-pixel imaging [20], and error compensation [18] can improve the measurement accuracy of translucent materials, they reduce measurement efficiency to varying degrees, making dynamic measurement difficult. For example, temporal denoising requires repeated sampling of the same scene for n times, resulting in the need to project and capture n times more fringe patterns. Single-pixel imaging also relies on a larger number of Fourier basis patterns to recover the light transport coefficients (LTC). Furthermore, it requires independent computation of the LTC for each pixel, leading to significant computational overhead and time consumption. Error compensation methods, based on phase error models, require recovering the PSF for each pixel, which significantly reduces computational efficiency. In contrast, our method does not require additional fringe images or pixel-wise physical model calculations. The global image enhancement of the deep network enables the proposed method to achieve fast 3D measurement.

Second, there is no need for additional hardware. Some existing methods suppress subsurface scattering effects by leveraging the polarization properties of light [14,15]. This approach requires adding extra polarizing components to the system, which increases cost and system complexity to some extent. In comparison, our method does not rely on any additional hardware; it enhances the modulation and reduces noise in the original degraded images, ultimately enabling flexible 3D measurement under scattering conditions.

Third, no paired labeled data are required for training. Existing deep learning-based image processing often depends on paired datasets [33,34]. While these supervised learning approaches perform excellently in image enhancement, they are often limited in applications where labeled data is difficult to obtain. Therefore, compared to traditional supervised learning methods, our method effectively eliminates the dependency on labeled data through a self-learning strategy using unpaired data. At the same time, our method achieves accuracy and speed comparable to supervised learning approaches.

However, there are still several aspects that require improvement: (1) The training of the generative adversarial model is relatively complex and time-consuming. We hope to optimize the network learning mechanism and incorporate more potential physical constraints to enhance its self-learning effectiveness. (2) Our current self-supervised learning implementation uses four network models (two generators and two discriminators). In the future, we aim to explore lightweight self-learning strategies to reduce computational resource requirements. (3) The multi-frequency heterodyne method requires nine fringe images. We hope to further reduce the number of fringe patterns in the future to increase measurement speed.

5. Conclusions

We presented a novel self-learning-based fringe domain transformation framework for high-precision 3D measurement of translucent objects. The proposed method employs a cyclic generative architecture to effectively convert low-modulation fringe patterns into high-quality sinusoidal patterns, substantially improving phase retrieval accuracy. Experimental validation on various translucent media including optical glue, frosted glass, jade, and silicone materials demonstrates significant enhancement in both fringe modulation and signal-to-noise ratio under challenging subsurface scattering conditions. These advancements enable robust preservation of fine geometric features during 3D reconstruction, yielding superior measurement fidelity compared to conventional PSP. The proposed technique shows particular promise for industrial and medical metrology applications requiring non-contact characterization of complex translucent materials.