Reconfigurable All-Optical Synapse Based on Photonic Crystal Nanobeam Cavities with Ferroelectric Carrier Injection Valve
Abstract
1. Introduction
2. Device Design and Prediction Methodology
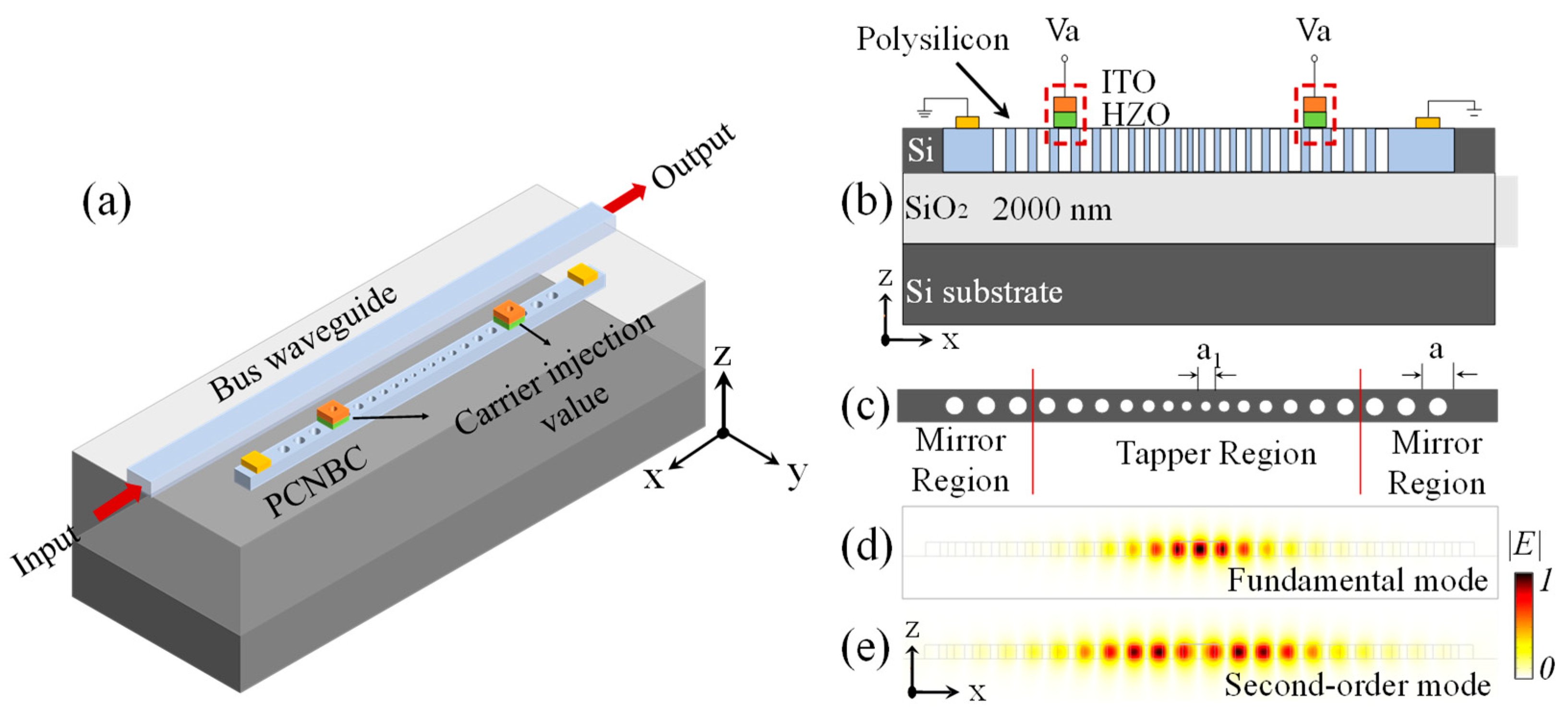
2.1. Device Design
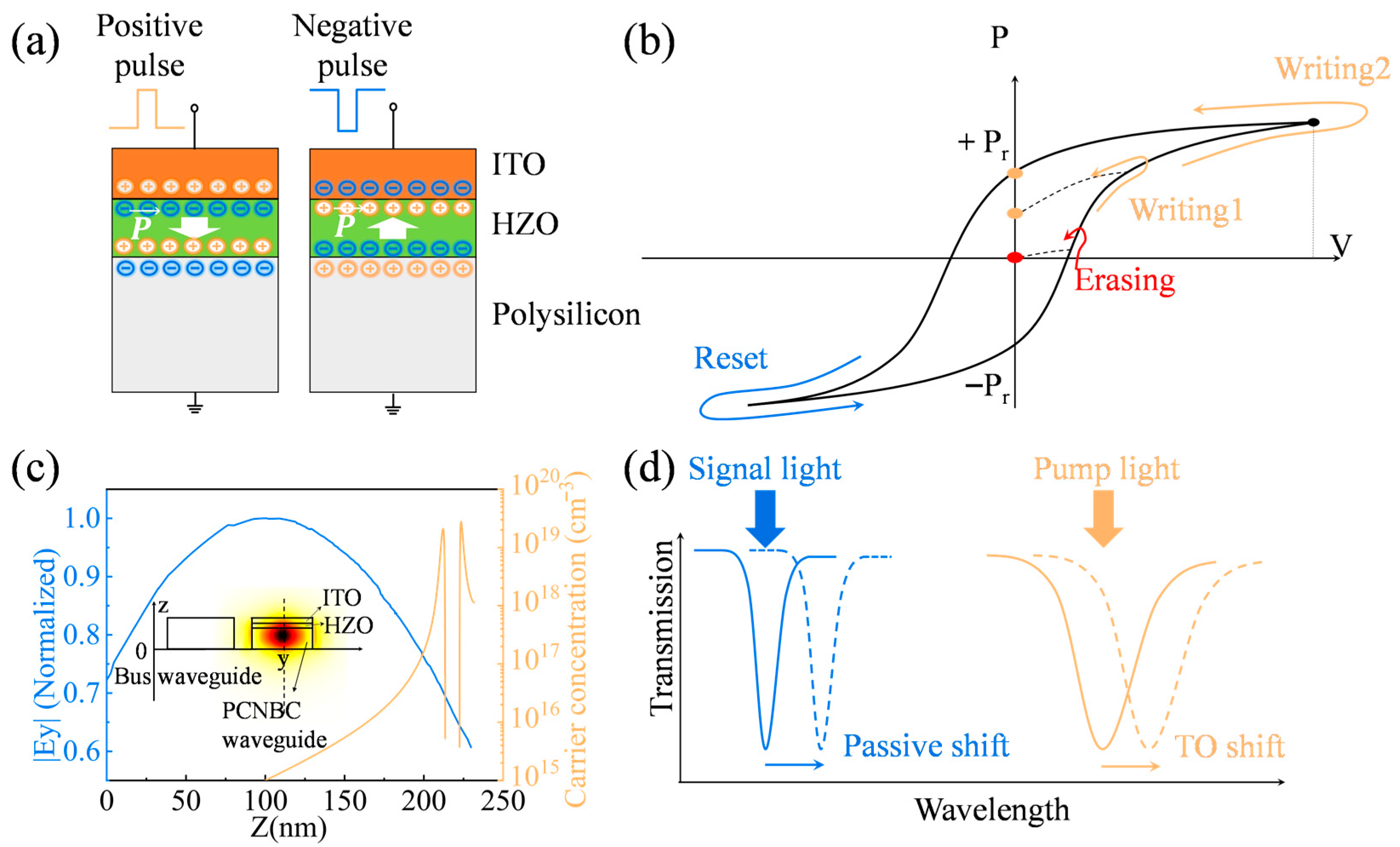
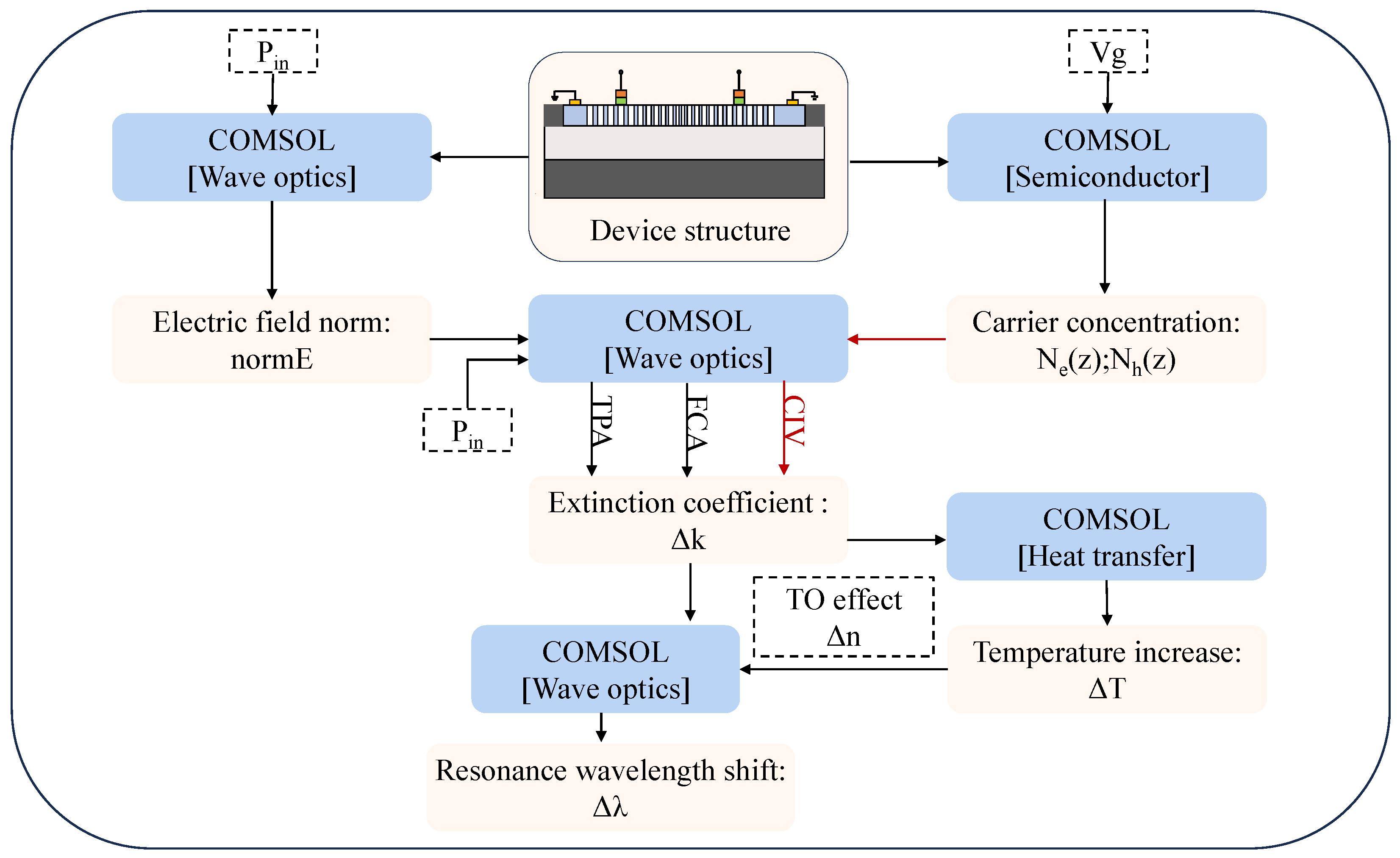
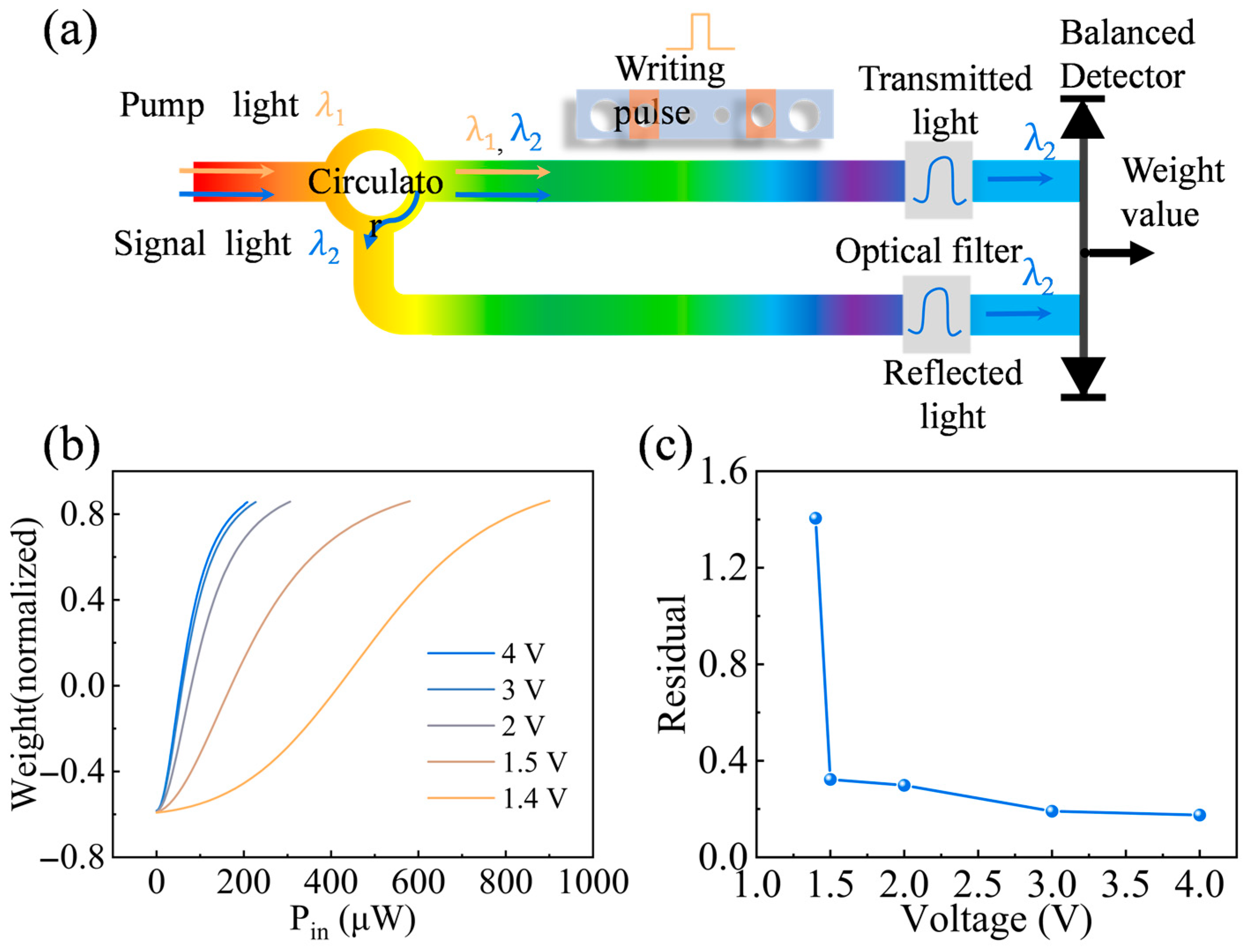
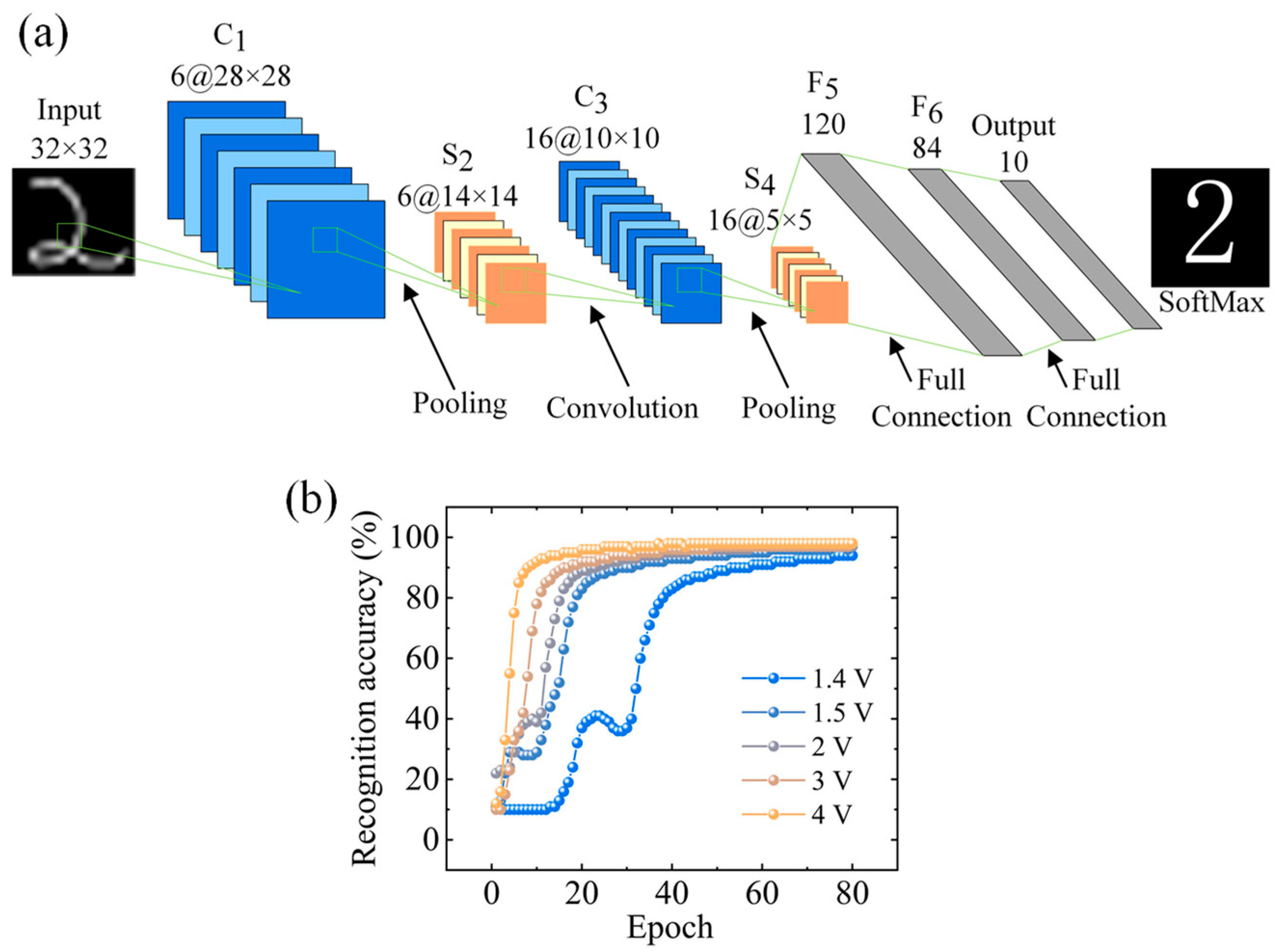
2.2. Establishing a Prediction Methodology
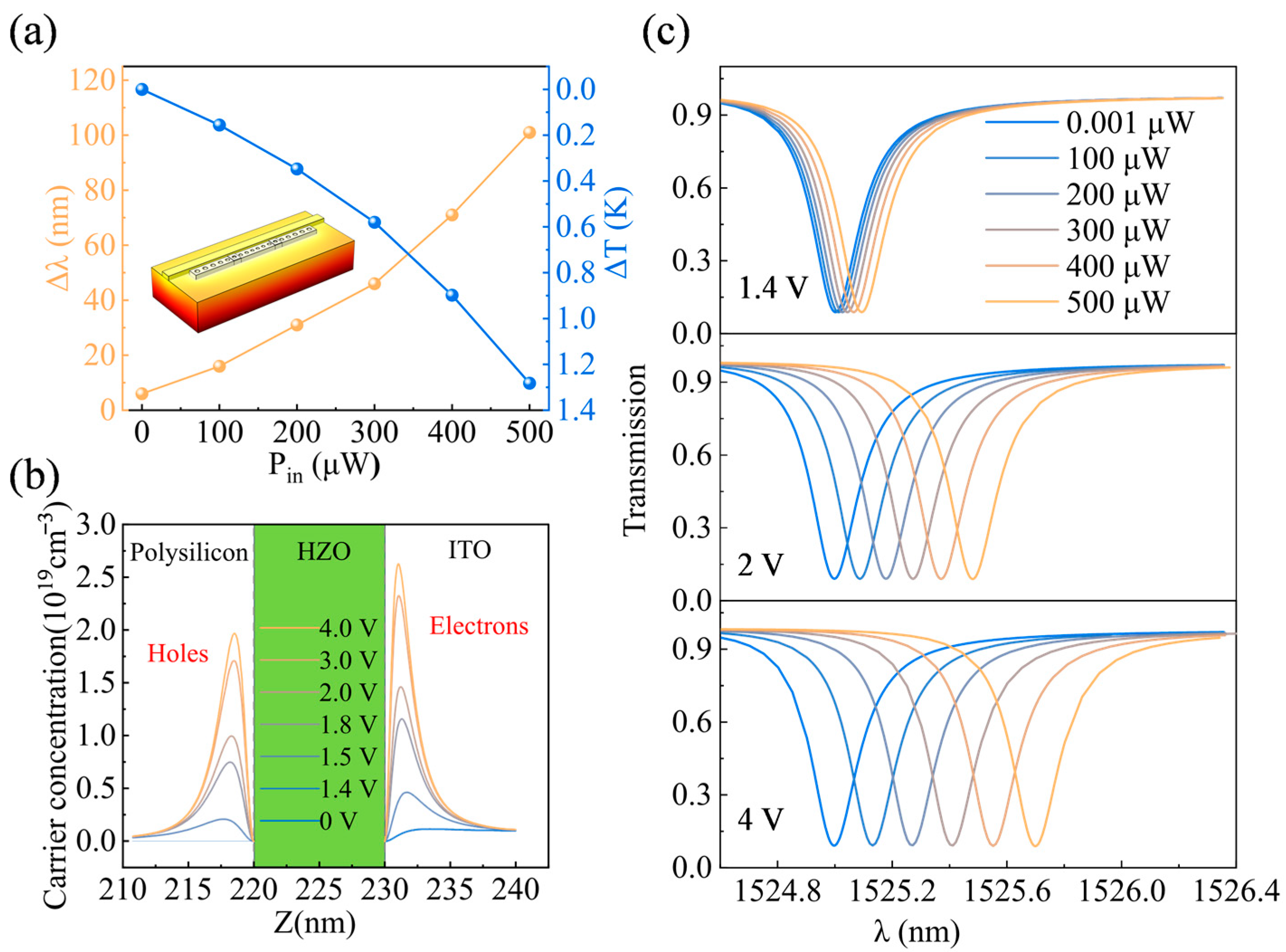
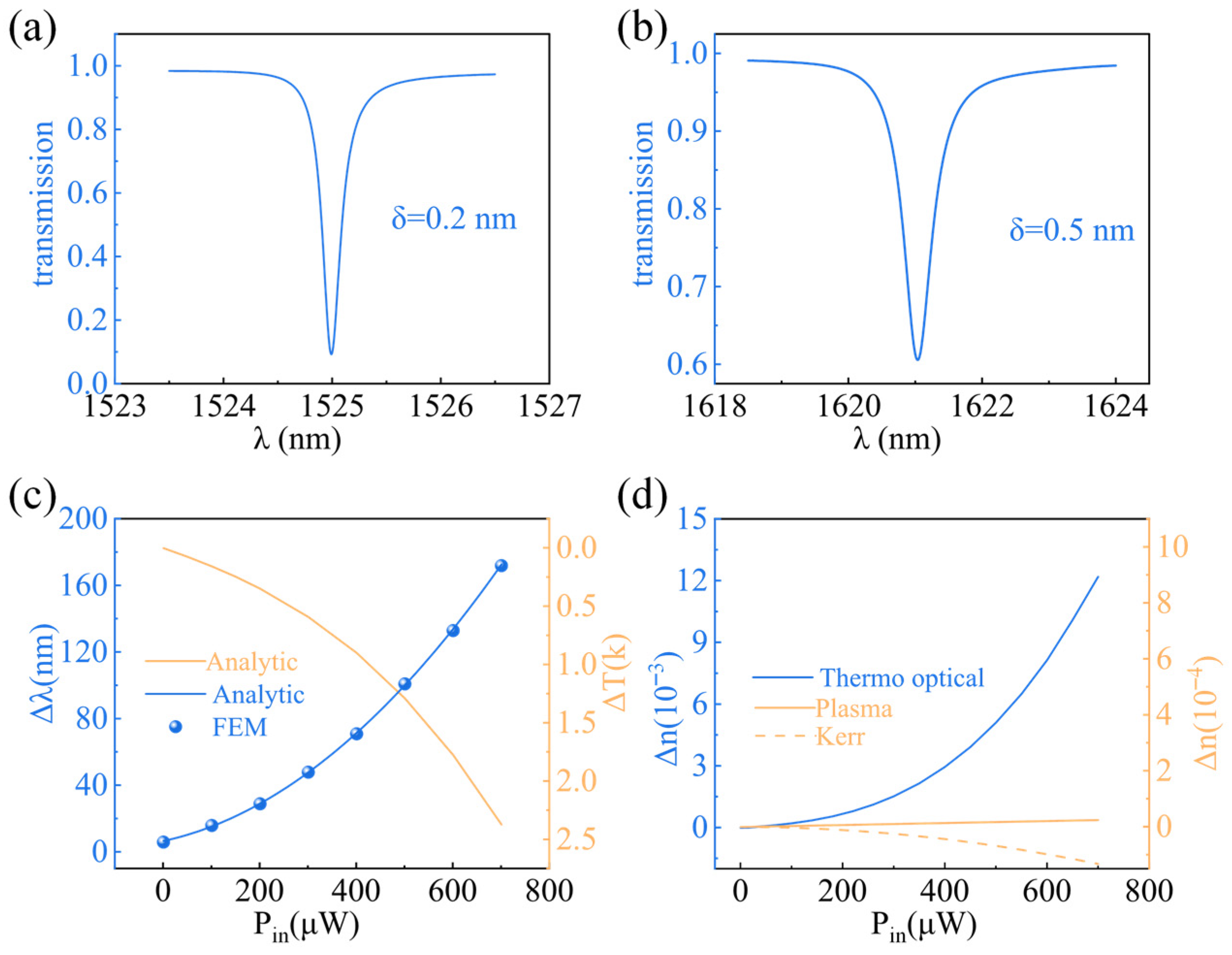
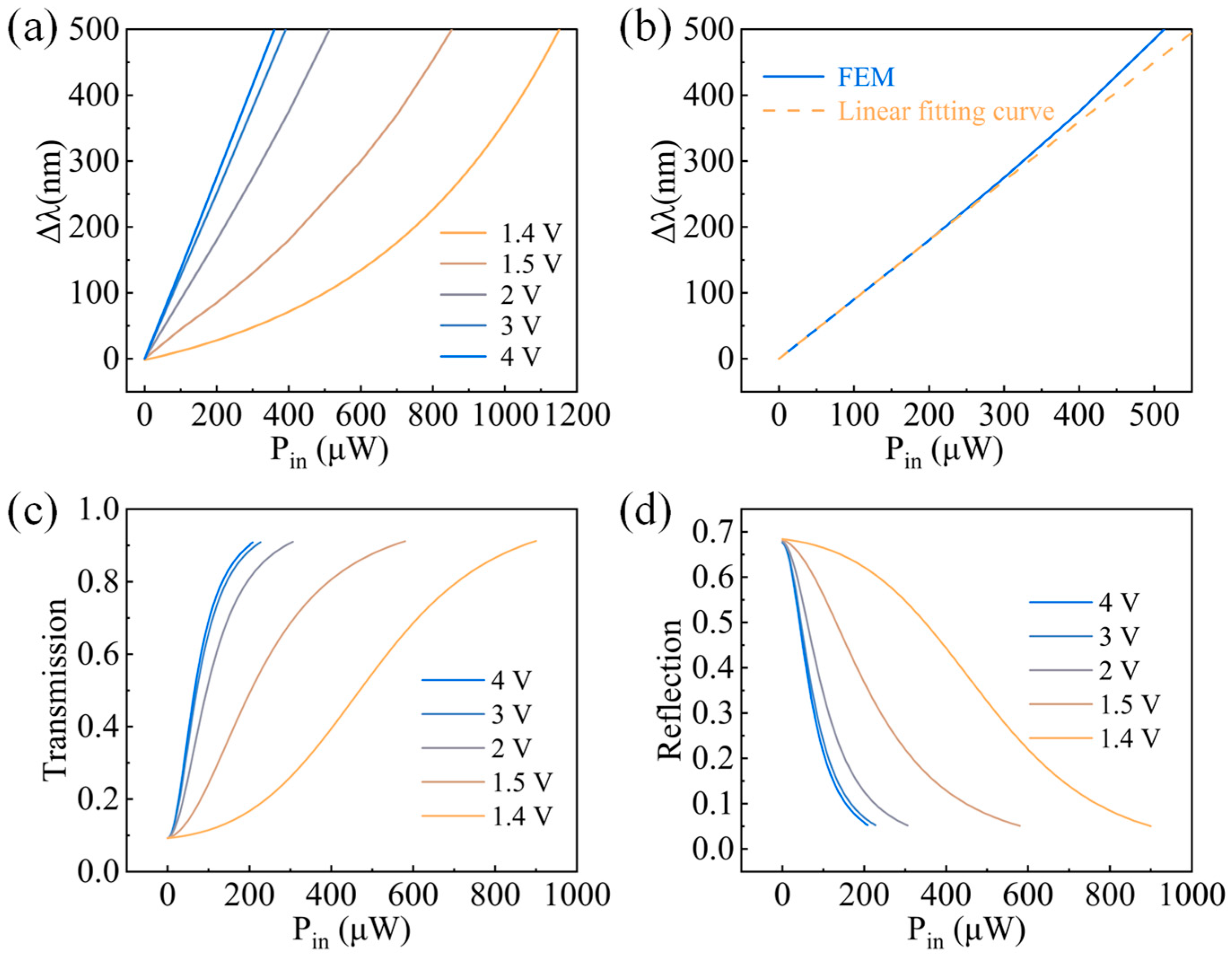
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Kim, S.Y.; Yu, J.M.; Lee, G.S.; Yun, D.H.; Kim, M.S.; Kim, J.K.; Kim, D.J.; Lee, G.B.; Kim, M.S.; Han, J.K.; et al. Synaptic Segmented Transistor with Improved Linearity by Schottky Junctions and Accelerated Speed by Double-Layered Nitride. ACS Appl. Mater. Interfaces 2022, 14, 32261–32269. [Google Scholar] [CrossRef]
- Lisman, J. A mechanism for the Hebb and the anti-Hebb processes underlying learning and memory. Proc. Natl. Acad. Sci. USA 1989, 86, 9574–9578. [Google Scholar] [CrossRef] [PubMed]
- Churchland, M.M.; Cunningham, J.P.; Kaufman, M.T.; Foster, J.D.; Nuyujukian, P.; Ryu, S.I.; Shenoy, K.V. Neural population dynamics during reaching. Nature 2012, 487, 51–56. [Google Scholar] [CrossRef] [PubMed]
- Wen, Z.; Nguyen, H.N.; Guo, Z.; Lalli, M.A.; Wang, X.; Su, Y.; Kim, N.S.; Yoon, K.J.; Shin, J.; Zhang, C.; et al. Synaptic dysregulation in a human iPS cell model of mental disorders. Nature 2014, 515, 414–418. [Google Scholar] [CrossRef] [PubMed]
- Zhou, T.; Lin, X.; Wu, J.; Chen, Y.; Xie, H.; Li, Y.; Fan, J.; Wu, H.; Fang, L.; Dai, Q. Large-scale neuromorphic optoelectronic computing with a reconfigurable diffractive processing unit. Nat. Photonics 2021, 15, 367–373. [Google Scholar] [CrossRef]
- Prucnal, P.R.; Shastri, B.J. Neuromorphic Photonics, 1st ed.; CRC Press: Boca Raton, FL, USA, 2017. [Google Scholar]
- Zhang, J.; Dai, S.; Zhao, Y.; Zhang, J.; Huang, J. Recent progress in photonic synapses for neuromorphic systems. Adv. Intell. Syst. 2020, 2, 1900136. [Google Scholar] [CrossRef]
- Jha, A.; Huang, C.; Delima, T.F.; Peng, H.-T.; Shastri, B.; Prucnal, P.R. Nanophotonic cavity based synapse for scalable photonic neural networks. IEEE J. Sel. Top. Quantum Electron. 2022, 28, 6100908. [Google Scholar] [CrossRef]
- Zhang, Y.; Zeng, C.; Li, D.; Gao, G.; Huang, Z.; Yu, J.; Xia, J. High-quality-factor photonic crystal ring resonator. Opt. Lett. 2014, 39, 1282–1285. [Google Scholar] [CrossRef]
- Kim, M.K.; Kim, J.Y.; Kang, J.H.; Ahn, B.H.; Lee, Y.H. On-demand photonic crystal resonators. Laser Photonics Rev. 2011, 5, 479–495. [Google Scholar] [CrossRef]
- Maleki, M.J.; Soroosh, M.; Akbarizadeh, G.; Parandin, F.; Haddadan, F. Photonic crystal resonators in designing optical decoders. J. Optoelectron. Nanostructures 2023, 8, 1–24. [Google Scholar]
- Qiang, Z.; Soref, R.A.; Zhou, W. Photonic crystal ring resonators: Characteristics and applications. J. Nanosci. Nanotechnol. 2010, 10, 1495–1507. [Google Scholar] [CrossRef]
- Deotare, P.B.; McCutcheon, M.W.; Frank, I.W.; Khan, M.; Lončar, M. High quality factor photonic crystal nanobeam cavities. Appl. Phys. Lett. 2009, 94, 121106. [Google Scholar] [CrossRef]
- Quan, Q.; Deotare, P.B.; Loncar, M. Photonic crystal nanobeam cavity strongly coupled to the feeding waveguide. Appl. Phys. Lett. 2010, 96, 203102. [Google Scholar] [CrossRef]
- Shakoor, A.; Nozaki, K.; Kuramochi, E.; Nishiguchi, K.; Shinya, A.; Notomi, M. Compact 1D-silicon photonic crystal electro-optic modulator operating with ultra-low switching voltage and energy. Opt. Express 2014, 22, 28623–28634. [Google Scholar] [CrossRef]
- Zhou, H.; Qiu, C.; Jiang, X.; Zhu, Q.; He, Y.; Zhang, Y.; Su, Y.; Soref, R. Compact, submilliwatt, 2× 2 silicon thermo-optic switch based on photonic crystal nanobeam cavities. Photonics Res. 2017, 5, 108–112. [Google Scholar] [CrossRef]
- Nahmias, M.A.; De Lima, T.F.; Tait, A.N.; Peng, H.-T.; Shastri, B.J.; Prucnal, P.R. Photonic multiply-accumulate operations for neural networks. IEEE J. Sel. Top. Quant. Electron. 2019, 26, 7701518. [Google Scholar] [CrossRef]
- Uesugi, T.; Song, B.-S.; Asano, T.; Noda, S. Investigation of optical nonlinearities in an ultra-high-Q Si nanocavity in a two-dimensional photonic crystal slab. Opt. Express 2006, 14, 377–386. [Google Scholar] [CrossRef]
- Yao, D.; Jiang, Z.; Zhang, Y.; Xie, H.; Wang, T.; Wang, J.; Gan, X.; Han, G.; Liu, Y.; Hao, Y. Ultrahigh thermal-efficient all-optical silicon photonic crystal nanobeam cavity modulator with TPA-induced thermo-optic effect. Opt. Lett. 2023, 48, 2325–2328. [Google Scholar] [CrossRef]
- Chanthbouala, A.; Garcia, V.; Cherifi, R.O.; Bouzehouane, K.; Fusil, S.; Moya, X.; Xavier, S.; Yamada, H.; Deranlot, C.; Mathur, N.D. A ferroelectric memristor. Nat. Mater. 2012, 11, 860–864. [Google Scholar] [CrossRef]
- Tian, B.-B.; Zhong, N.; Duan, C.-G. Recent advances, perspectives, and challenges in ferroelectric synapses. Chin. Phys. B. 2020, 29, 097701. [Google Scholar] [CrossRef]
- Yao, D.; Li, L.; Zhang, Y.; Peng, Y.; Zhou, J.; Han, G.; Liu, Y.; Hao, Y. Energy-efficient non-volatile ferroelectric based electrostatic doping multilevel optical readout memory. Opt. Express 2022, 30, 13572–13582. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Y.; McCutcheon, M.W.; Burgess, I.B.; Loncar, M. Ultra-high-Q TE/TM dual-polarized photonic crystal nanocavities. Opt. Lett. 2009, 34, 2694–2696. [Google Scholar] [CrossRef]
- Ancona, M. Density-gradient theory: A macroscopic approach to quantum confinement and tunneling in semiconductor devices. J. Comput. Electron. 2011, 10, 65–97. [Google Scholar] [CrossRef]
- Smith, R.C.; Ounaies, Z. A domain wall model for hysteresis in piezoelectric materials. J. Intell. Mater. Syst. Struct. 2000, 11, 62–79. [Google Scholar] [CrossRef]
- Kim, S.J.; Mohan, J.; Summerfelt, S.R.; Kim, J. Ferroelectric Hf0.5Zr0.5O2 thin films: A review of recent advances. JOM 2019, 71, 246–255. [Google Scholar] [CrossRef]
- Barclay, P.E.; Srinivasan, K.; Painter, O. Nonlinear response of silicon photonic crystal microresonators excited via an integrated waveguide and fiber taper. Opt. Express 2005, 13, 801–820. [Google Scholar] [CrossRef]
- Reggiani, S.; Valdinoci, M.; Colalongo, L.; Rudan, M.; Baccarani, G.; Stricker, A.D.; Illien, F.; Felber, N.; Fichtner, W.; Zullino, L. Electron and hole mobility in silicon at large operating temperatures. I. Bulk mobility. IEEE Trans. Electron. Devices 2002, 49, 490–499. [Google Scholar] [CrossRef]
- Hook, J.R.; Hall, H.E. Solid State Physics, 2nd ed.; John Wiley & Sons: Hoboken, NJ, USA, 2013. [Google Scholar]
- Zhang, Y.; Li, L.; Xie, H.; Jiang, Z.; Li, Y.; Wang, T.; Yao, D.; Liu, Y.; Han, G.; Hao, Y. Compact non-volatile ferroelectric electrostatic doping optical memory based on the epsilon-near-zero effect. Appl. Opt. 2023, 62, 950–955. [Google Scholar] [CrossRef] [PubMed]
- Dinu, M.; Quochi, F.; Garcia, H. Third-order nonlinearities in silicon at telecom wavelengths. Appl. Phys. Lett. 2003, 82, 2954–2956. [Google Scholar] [CrossRef]
- Yang, R.; Wang, Y.; Li, S.; Hu, D.; Chen, Q.; Zhuge, F.; Ye, Z.; Pi, X.; Lu, J. All-optically controlled artificial synapse based on full oxides for low-power visible neural network computing. Adv. Funct. Mater. 2024, 34, 2312444. [Google Scholar] [CrossRef]
- Li, Y.T.; Li, J.Z.; Ren, L.; Xu, K.; Chen, S.; Han, L.; Liu, H.; Guo, X.L.; Yu, D.L.; Li, D.H.; et al. Light-controlled reconfigurable optical synapse based on carbon nanotubes/2D perovskite heterostructure for image recognition. ACS Appl. Mater. Interfaces 2022, 14, 28221–28229. [Google Scholar] [CrossRef] [PubMed]
- Chen, K.; Hu, H.; Song, I.; Gobeze, H.B.; Lee, W.J.; Abtahi, A.; Schanze, K.S.; Mei, J. Organic optoelectronic synapse based on photon-modulated electrochemical doping. Nat. Photonics 2023, 17, 629–637. [Google Scholar] [CrossRef]
- Shrivastava, S.; Keong, L.B.; Pratik, S.; Lin, A.S.; Tseng, T.Y. Fully photon controlled synaptic memristor for neuro-inspired computing. Adv. Electron. Mater. 2023, 9, 2201093. [Google Scholar] [CrossRef]
| Parameter | Description | Value | Source |
|---|---|---|---|
| β | TPA coefficient | 0.83 cm·GW−1 | [26] |
| nsi | The refractive index of silicon | 3.48 | |
| VTPA | Cavity volume for TPA | 2.325 V0 (mode 1) | FEM |
| VFCA | Cavity volume for free carriers | 1.686 V0 ( mode 1) | FEM |
| V0 | Mode volume | (λ/nsi)3 | |
| τrecon | Carrier recombination time | 0.5 ns | [27] |
| R | Thermal resistance | 3880 K·mW−1 | FEM |
| μe | Electron mobility | 80 cm·(V·s)−1 | [28] |
| μh | Hole mobility | 40 cm/V·s | [28] |
| me * | Electron effective mass | 0.3 m0 | [29] |
| mh * | Hole effective mass | 0.45 m0 | [29] |
| m0 | Effective mass | 9.109 × 10−31 kg | [29] |
| TOC | Thermal optic coefficient | 1.85 × 10−4 K−1 | [30] |
| n2 | Kerr coefficient | 0.45 × 10−13 cm2·W | [31] |
| τCIV | Energy decay rate corresponding to ferroelectric doping | 0 V = 3.85 ns 2 V = 0.95 ns 4 V = 0.27 ns | FEM |
| Type | Dimension | Modulation Scheme | Recognition Accuracy | Reconfigurable |
|---|---|---|---|---|
| Heterojunction [32] | ≥200 µm2 | All-optical | ≥93% | No |
| Heterostructure [33] | ≥10 µm2 | Optoelectronic | ≥77% | Yes |
| Electrochemical transistors [34] | ≥20 µm2 | Optoelectronic | - | No |
| Memristor [35] | - | Optoelectronic | ≥93% | No |
| Ferroelectric injection valve [This work] | 7 µm2 | All-optical | ≥94% | Yes |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, D.; Xie, H.; Yao, D.; Zhang, E.; Song, J.; Wang, Y.; Zhang, Y.; Ran, X.; Fang, D.; Lu, X.; et al. Reconfigurable All-Optical Synapse Based on Photonic Crystal Nanobeam Cavities with Ferroelectric Carrier Injection Valve. Photonics 2025, 12, 871. https://doi.org/10.3390/photonics12090871
Li D, Xie H, Yao D, Zhang E, Song J, Wang Y, Zhang Y, Ran X, Fang D, Lu X, et al. Reconfigurable All-Optical Synapse Based on Photonic Crystal Nanobeam Cavities with Ferroelectric Carrier Injection Valve. Photonics. 2025; 12(9):871. https://doi.org/10.3390/photonics12090871
Chicago/Turabian StyleLi, Duomao, Han Xie, Danyang Yao, Erqi Zhang, Jiaren Song, Youbin Wang, Yiwei Zhang, Xu Ran, Dongming Fang, Xiaoli Lu, and et al. 2025. "Reconfigurable All-Optical Synapse Based on Photonic Crystal Nanobeam Cavities with Ferroelectric Carrier Injection Valve" Photonics 12, no. 9: 871. https://doi.org/10.3390/photonics12090871
APA StyleLi, D., Xie, H., Yao, D., Zhang, E., Song, J., Wang, Y., Zhang, Y., Ran, X., Fang, D., Lu, X., Ma, X., & Hao, Y. (2025). Reconfigurable All-Optical Synapse Based on Photonic Crystal Nanobeam Cavities with Ferroelectric Carrier Injection Valve. Photonics, 12(9), 871. https://doi.org/10.3390/photonics12090871





