Numerical Investigation on the Effect of Smoothing by Spectral Dispersion on Transverse Stimulated Raman Scattering Gain in KDP Crystals
Abstract
1. Introduction
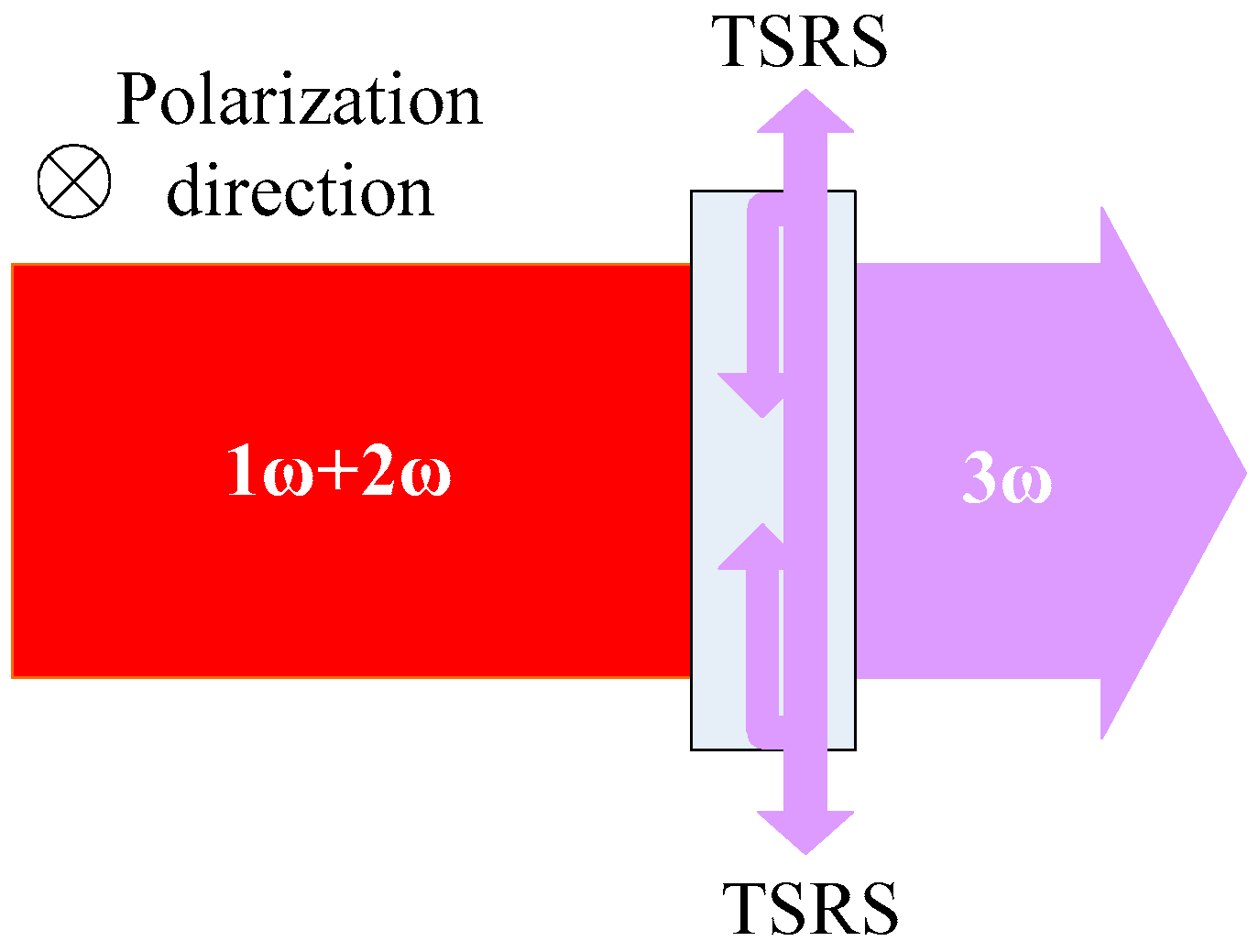
2. Fundamental Theory of TSRS
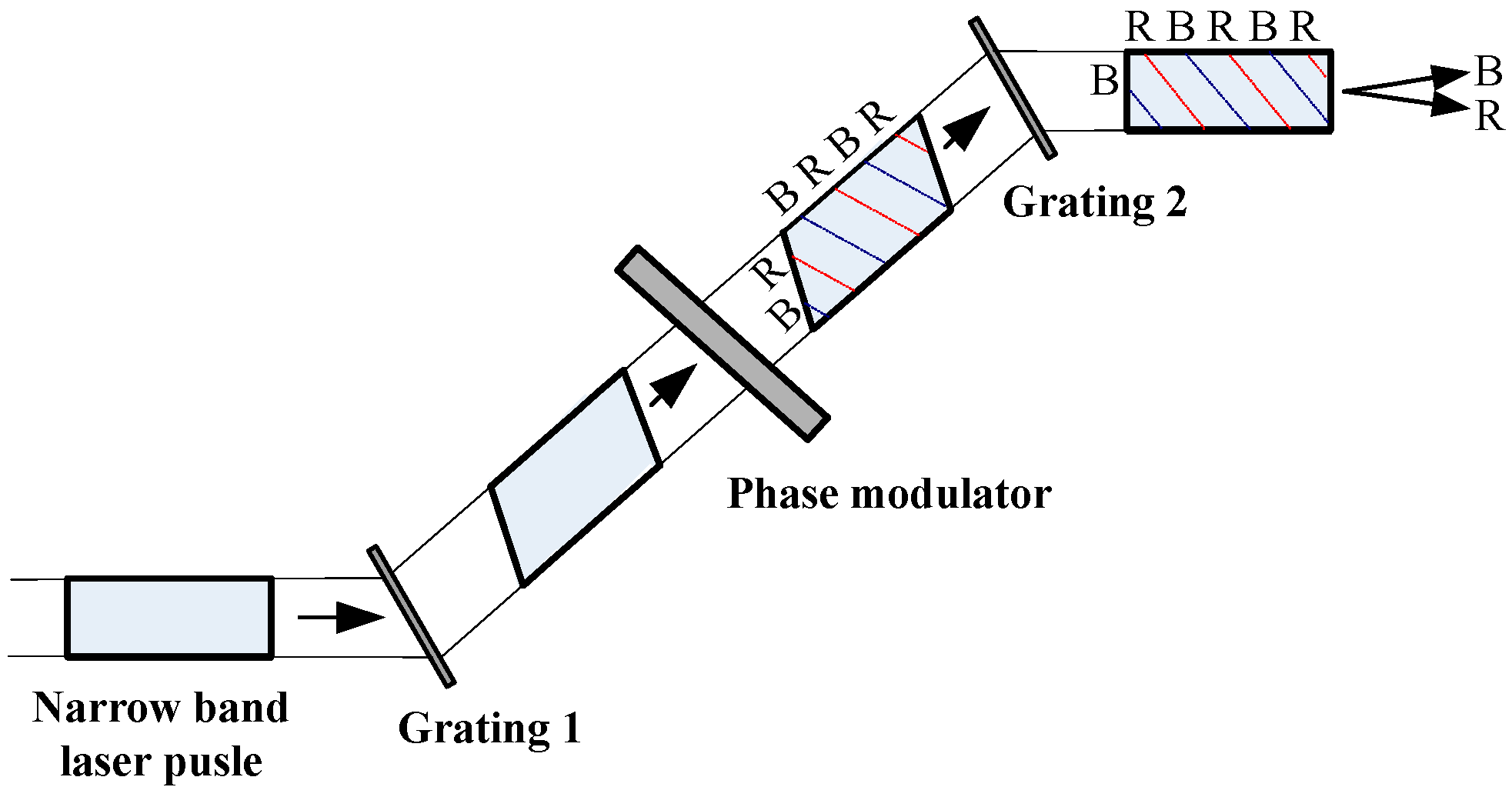
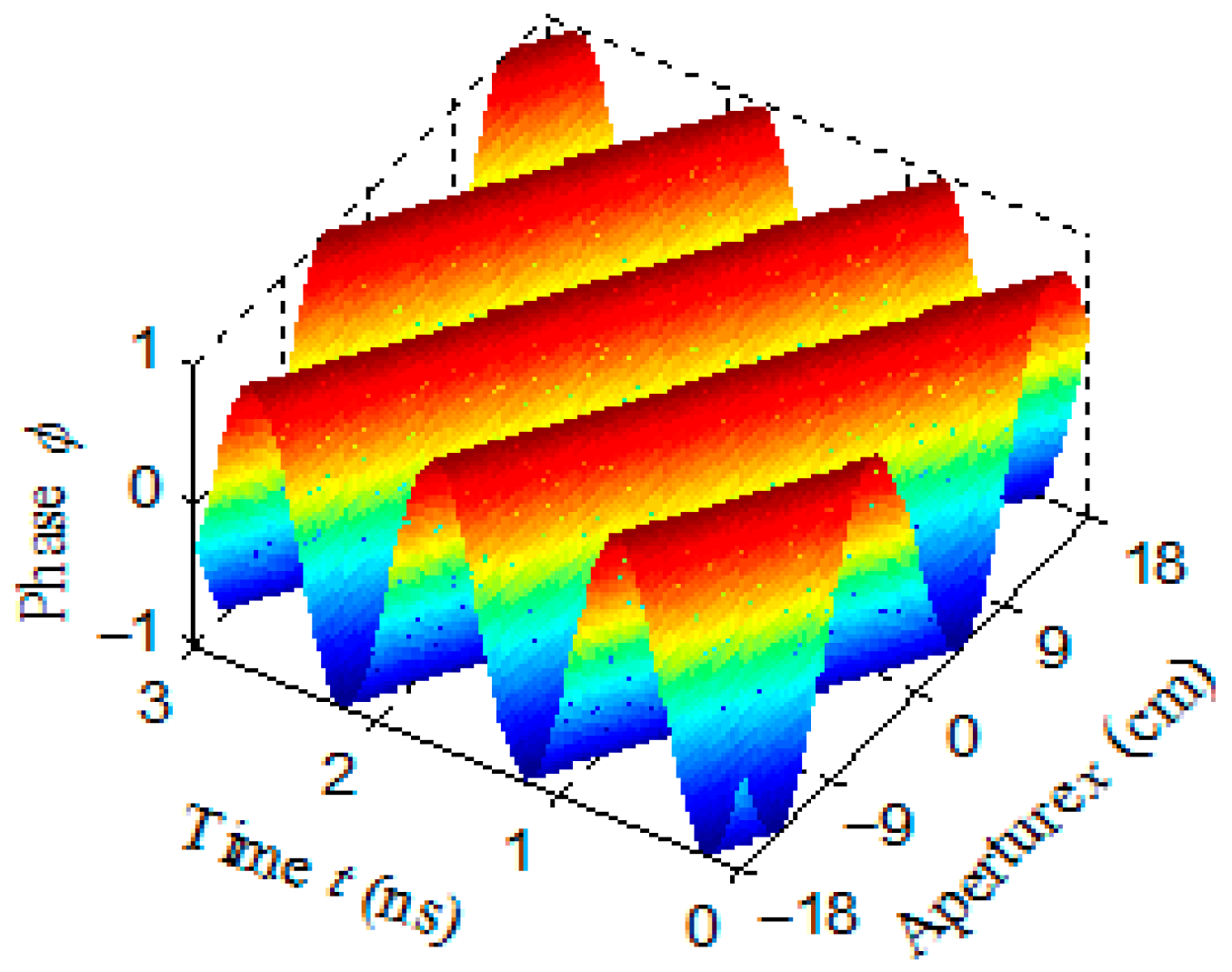
3. Results Fundamental Theory of SSD
4. Effect of SSD on TSRS Gain and Suppression Effectiveness
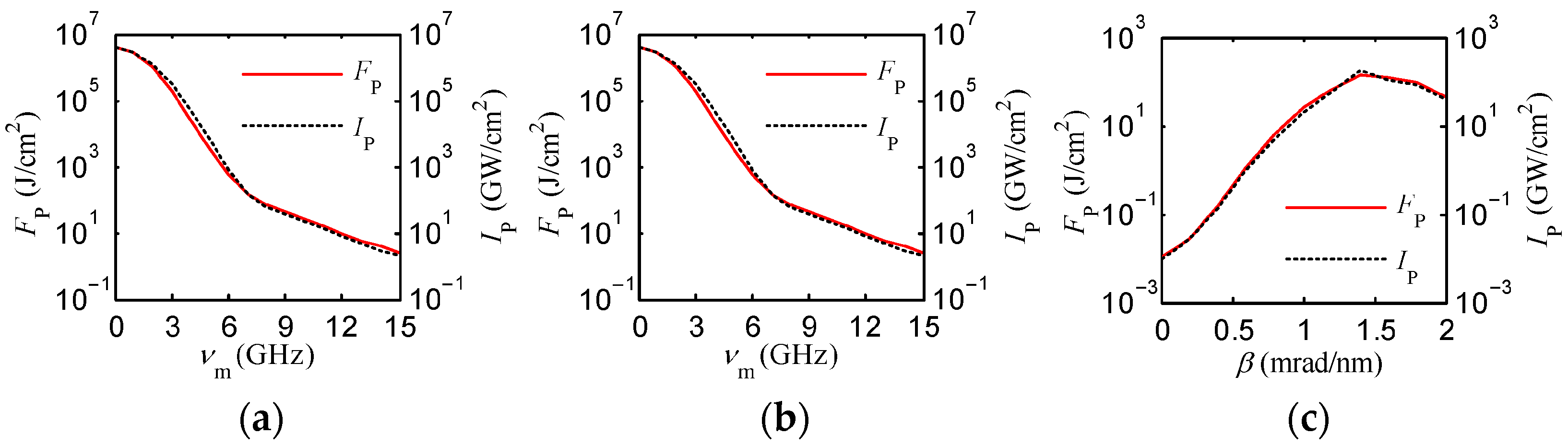
4.1. Effect of SSD on TSRS Gain
4.2. TSRS Suppression Performance
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Barker, C.E.; Sacks, R.A.; Wonterghem, B.M.V.; Caird, J.A.; Nielsen, N.D. Transverse stimulated Raman scattering in KDP. SPIE 1995, 2633, 501–505. [Google Scholar] [CrossRef]
- Han, W.; Zhou, L.D.; Li, F.Q.; Wang, J.; Wang, F.; Feng, B. Laser-induced damage of a large-aperture potassium dihydrogen phosphate crystal due to transverse stimulated Raman scattering. Laser Phys. 2013, 23, 116001. [Google Scholar] [CrossRef]
- Wang, J.; Zhang, X.M.; Li, F.Q.; Han, W.; Li, K.Y.; Feng, B. Risk Evaluation of Transverse Stimulated Raman Scattering in Large-Aperture, High Fluence KDP crystal. Chin. J. Lasers 2011, 38, 0502011. [Google Scholar] [CrossRef]
- Han, W.; Wang, F.; Zhou, L.D.; Li, F.; Feng, B.; Cao, H.; Zhao, J.; Li, S.; Zheng, K.; Wei, X. Suppression of transverse stimulated Raman scattering with laser-induced damage array in a large-aperture potassium dihydrogen phosphate crystal. Opt. Express 2013, 21, 30481–30491. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Y.L.; Ye, H.X.; Yan, X.W.; Wang, M.Z.; Jiang, X.Y.; Wang, Z.G.; Zheng, J.G.; Li, M.Z.; Jing, F.; Wei, X.F. Suppression of transverse stimulated Raman scattering or transverse stimulated Brillouin scattering. Proc. SPIE 2010, 7843, 78432A. [Google Scholar] [CrossRef]
- Fan, X.M.; Li, S.S.; Huang, X.D.; Zhang, J.X.; Wang, C.Y.; Li, H.R.; Sun, Y.Z.; Sun, H.Z. Using polarization control plate to suppress transverse stimulated Raman scattering in large-aperture KDP crystal. Laser Part. Beams 2018, 36, 454–457. [Google Scholar] [CrossRef]
- Huang, H.; Kosc, T.Z.; Kessler, T.J.; Demos, S.G. Modeling of transverse stimulated Raman scattering in KDP/DKDP in large-aperture plates suitable for polarization control. High Power Laser Sci. Eng. 2023, 11, e9. [Google Scholar] [CrossRef]
- Chai, X.X.; Li, F.Q.; Wang, S.L.; Feng, B.; Zhu, Q.H.; Liu, B.A.; Sun, X.; Xu, X.G. Influence of deuteration degree on the transverse stimulated Raman scattering gain coefficient of DKDP crystal. Acta Phys. Sin. 2015, 64, 034213. [Google Scholar] [CrossRef]
- Skeldon, M.D.; Bahr, R. Stimulated rotational Raman scattering in air with a high-power broadband laser. Opt. Lett. 1991, 16, 366–368. [Google Scholar] [CrossRef] [PubMed]
- Lin, Y.; Kessler, T.J.; Lawrence, G.N. Raman scattering in air: Four-dimensional analysis. Appl. Opt. 1994, 33, 4781–4791. [Google Scholar] [CrossRef] [PubMed]
- Wang, C.S. Theory of stimulated Raman scattering. Phys. Rev. 1969, 182, 482–494. [Google Scholar] [CrossRef]
- Carman, R.L.; Shimizu, F.; Wang, C.S.; Bloembergen, N. Theory of Stokes pulse shapes in transient stimulated Raman scattering. Phys. Rev. A 1970, 2, 60–72. [Google Scholar] [CrossRef]
- Skupsky, S.; Short, R.W.; Kessler, T.; Craxton, R.S.; Letzring, S.; Soures, J.M. Improved laser-beam uniformity using the angular dispersion of frequency-modulated light. J. Appl. Phys. 1989, 66, 3456–3462. [Google Scholar] [CrossRef]
- Volosov, V.D.; Goryachkina, E.V. Compensation of phase matching dispersion in generation of nonmonochromatic radiation harmonics. I. Doubling of neodymium-glass radiation frequency under free-oscillation conditions. Sov. J. Quantum Electron. 1976, 6, 854–857. [Google Scholar] [CrossRef]
- Dorrer, C.; Spilatro, M.; Herman, S.; Borger, T.; Hill, E.M. Broadband sumfrequency generation of spectrally incoherent pulses. Opt. Express 2021, 29, 16135–16152. [Google Scholar] [CrossRef] [PubMed]
- Boscheron, A.C.L.; Sauteret, C.J.; Migus, A. Efficient broadband sum frequency based on controlled phase modulated input fields: Theory for 351-nm ultrabroadband or ultrashort-pulse generation. J. Opt. Soc. Am. B 1996, 13, 818–826. [Google Scholar] [CrossRef]
- Zhang, X.; Ji, L.L.; Liu, D.; Gao, Y.Q.; Sui, Z.; Zhao, X.H.; Xiang, X. Numerical simulation on third-harmonic generation of super-luminescent light by mixing roadband and narrowband lasers. Chin. J. Lasers 2021, 48, 2108001. [Google Scholar] [CrossRef]
- Yang, L.; Ji, L.L.; Liu, D.; Rao, D.X.; Zhang, T.; Shan, C.; Shi, H.; Zhao, X.; Cui, Y.; Gao, Y.; et al. Optimization of 1.03 μm femtosecond pulse laser tripling efficiency based on temporal walk-off compensation. Opt. Commun. 2023, 537, 129413. [Google Scholar] [CrossRef]
- Webb, M.S.; Eimerl, D.; Velsko, S.P. Wavelength insensitive phase-matched second-harmonic generation in partially deuterated KDP. J. Opt. Soc. Am. B 1992, 9, 1118–1127. [Google Scholar] [CrossRef]
- Hao, G.K.; Xu, M.X.; Sun, X.; Liu, B.A.; Zhang, L.S.; Ren, H.K.; Bai, J.Y.; Gao, J.Y. Rapid growth of the gradient deuterium deuterated potassium dihydrogen phosphate crystal. Cryst. Growth Des. 2024, 24, 567–572. [Google Scholar] [CrossRef]
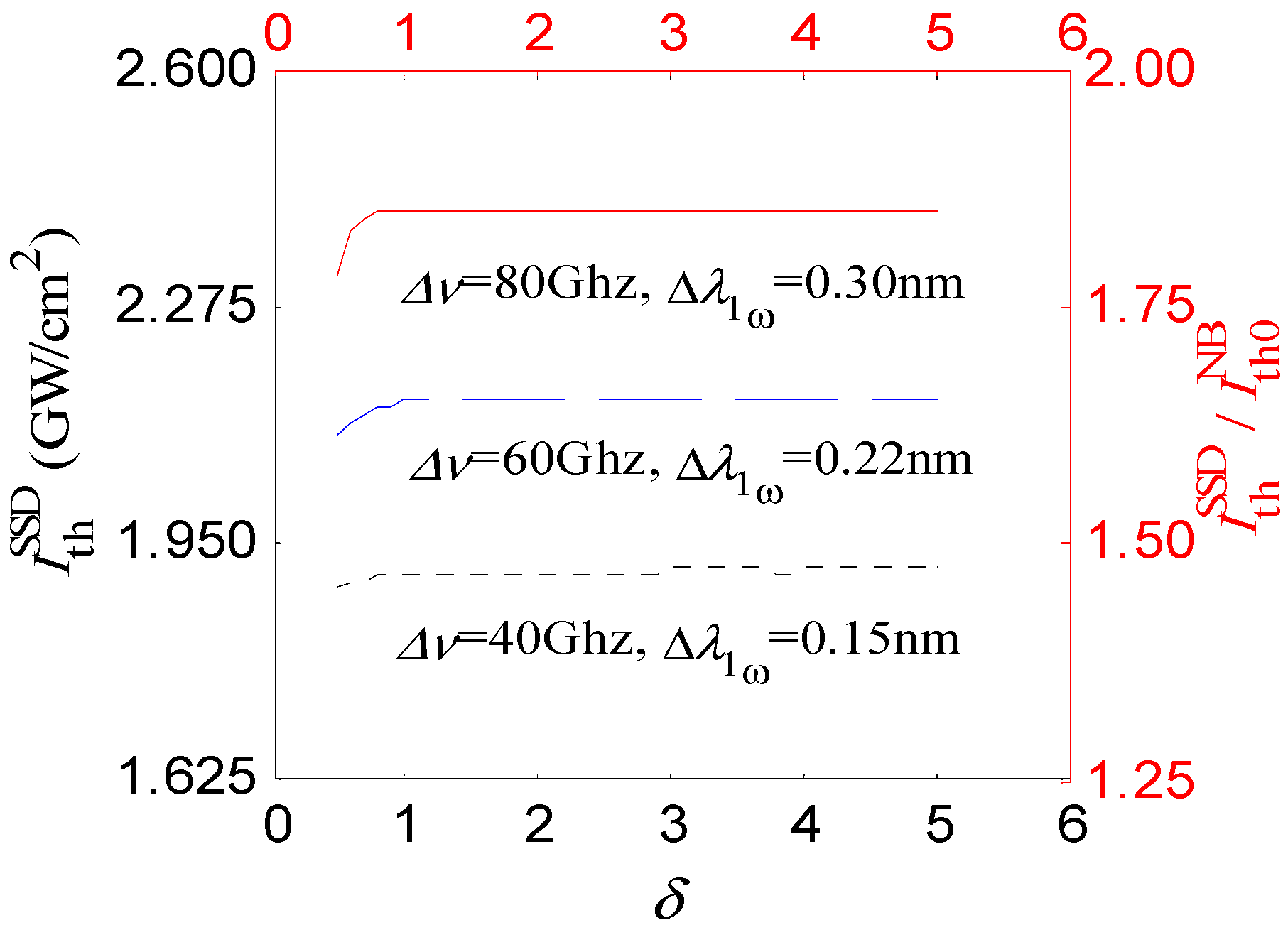
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fan, X.; Wang, C.; Wang, Y.; Zhang, J.; Shang, Y.; Li, S.; Qin, F.; Du, Z.; Wang, C. Numerical Investigation on the Effect of Smoothing by Spectral Dispersion on Transverse Stimulated Raman Scattering Gain in KDP Crystals. Photonics 2025, 12, 843. https://doi.org/10.3390/photonics12090843
Fan X, Wang C, Wang Y, Zhang J, Shang Y, Li S, Qin F, Du Z, Wang C. Numerical Investigation on the Effect of Smoothing by Spectral Dispersion on Transverse Stimulated Raman Scattering Gain in KDP Crystals. Photonics. 2025; 12(9):843. https://doi.org/10.3390/photonics12090843
Chicago/Turabian StyleFan, Xinmin, Chunhong Wang, Yan Wang, Jianxin Zhang, Yong Shang, Shun Li, Fuyong Qin, Zaifa Du, and Chunyan Wang. 2025. "Numerical Investigation on the Effect of Smoothing by Spectral Dispersion on Transverse Stimulated Raman Scattering Gain in KDP Crystals" Photonics 12, no. 9: 843. https://doi.org/10.3390/photonics12090843
APA StyleFan, X., Wang, C., Wang, Y., Zhang, J., Shang, Y., Li, S., Qin, F., Du, Z., & Wang, C. (2025). Numerical Investigation on the Effect of Smoothing by Spectral Dispersion on Transverse Stimulated Raman Scattering Gain in KDP Crystals. Photonics, 12(9), 843. https://doi.org/10.3390/photonics12090843





