Impact of LD Spectra on Efficiency of Yb-Doped Fiber Laser
Abstract
1. Introduction
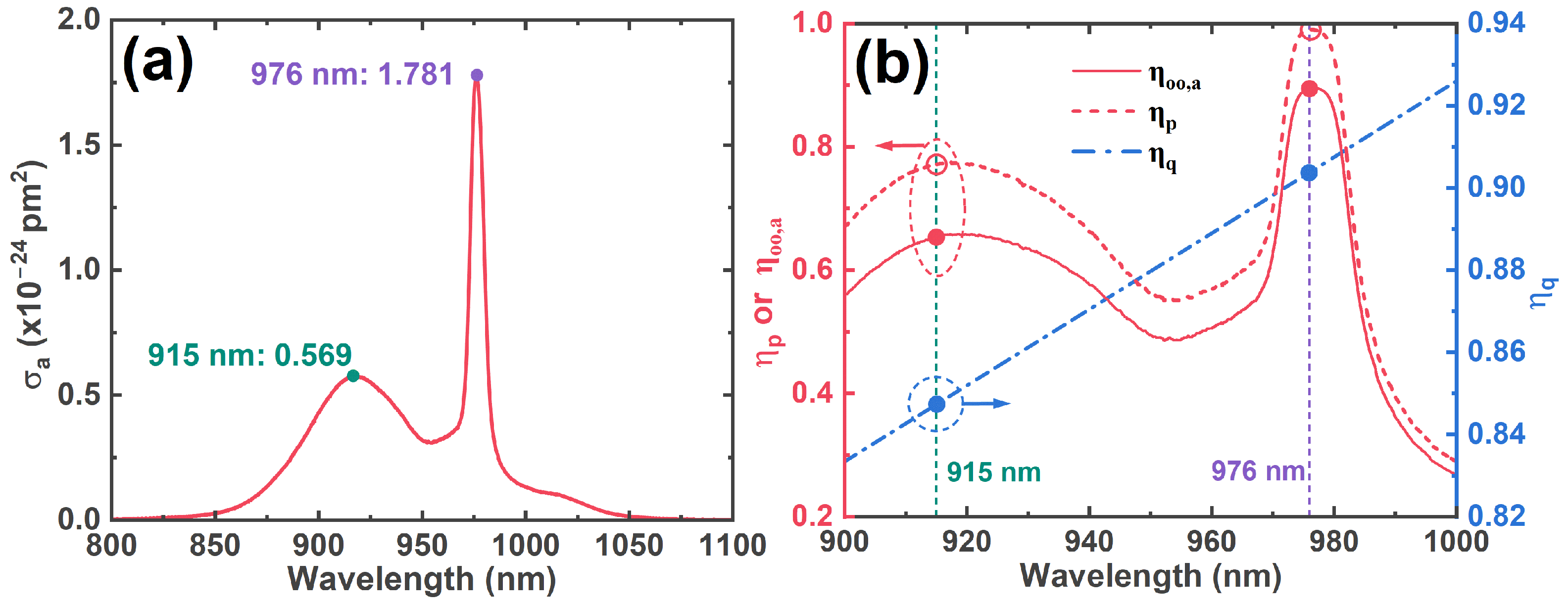
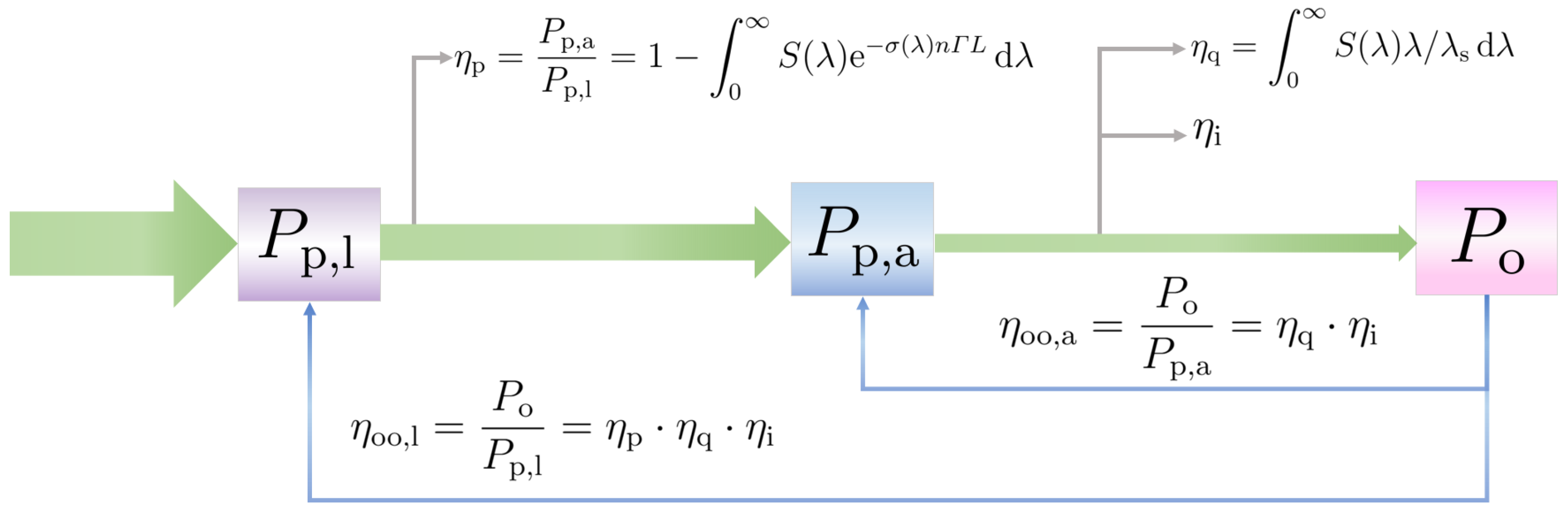
2. Theoretical Analysis
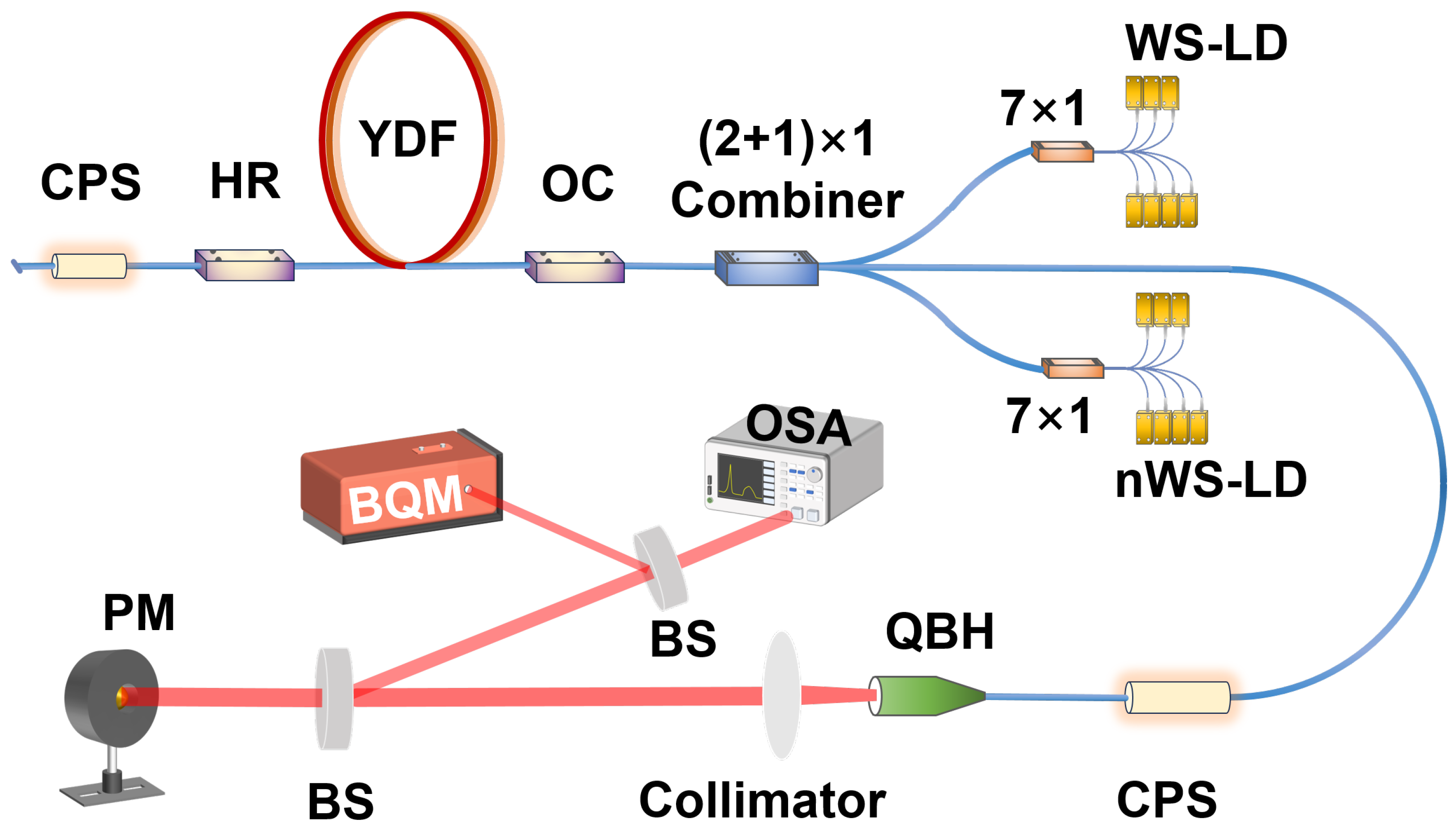
3. Experimental Setup
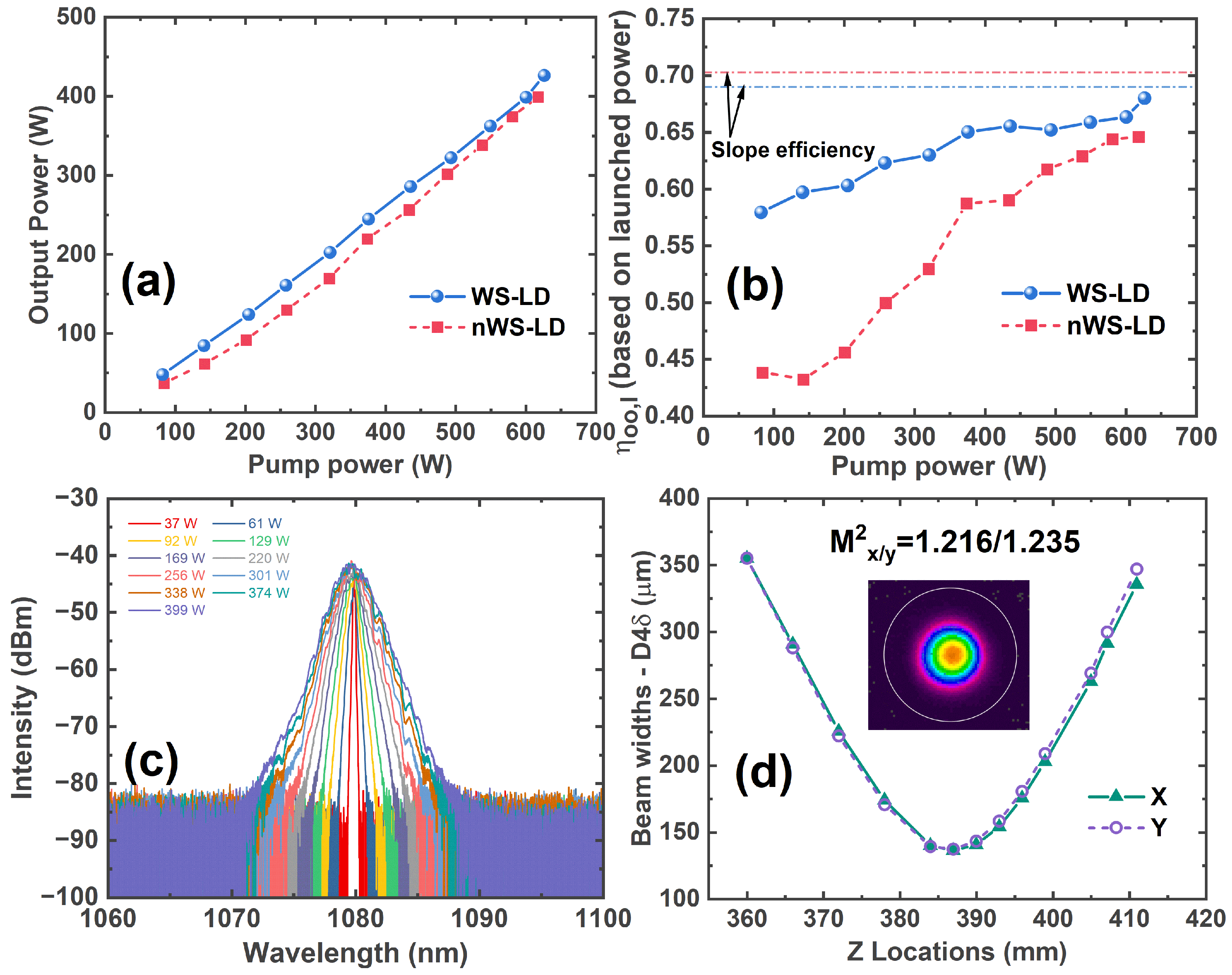
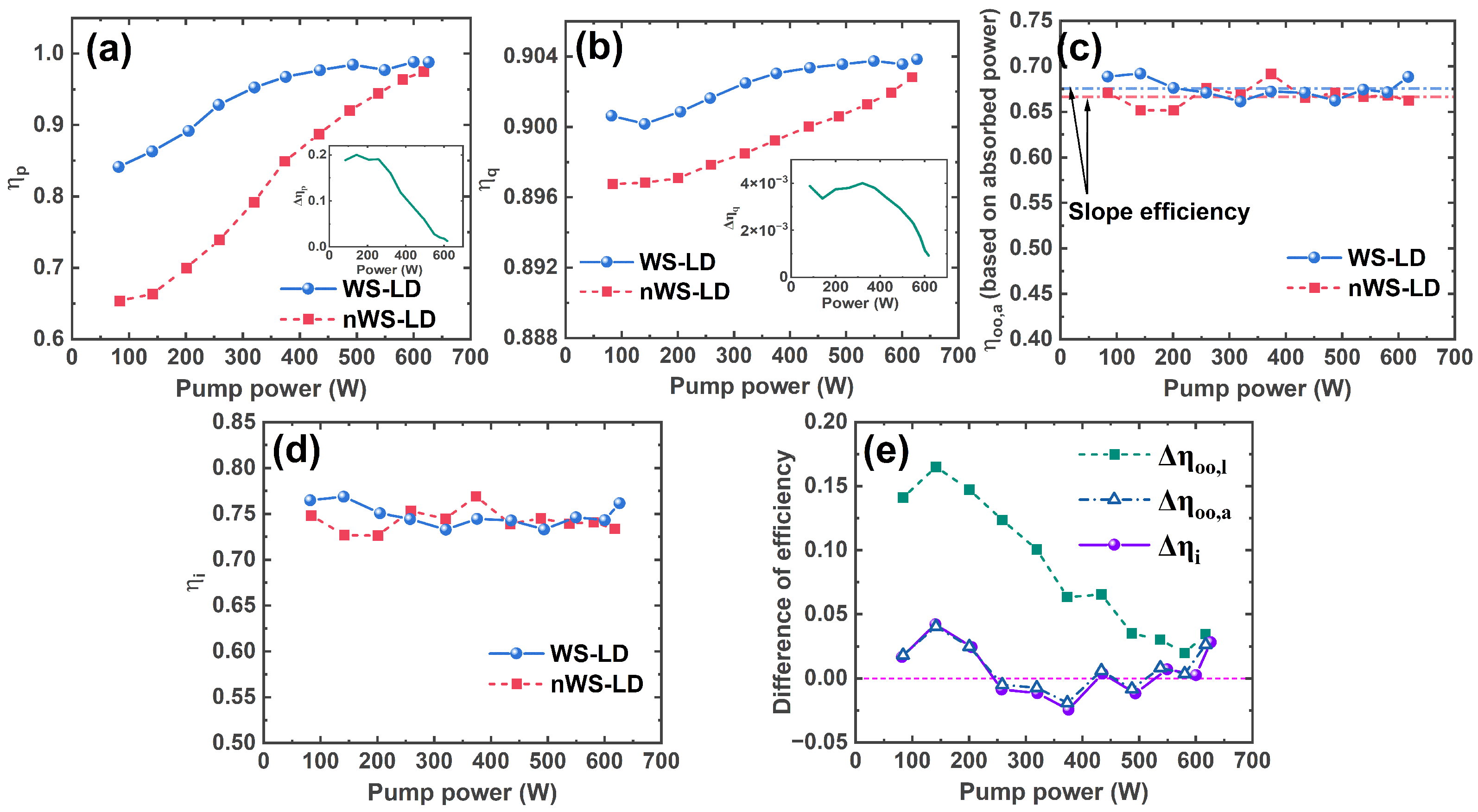
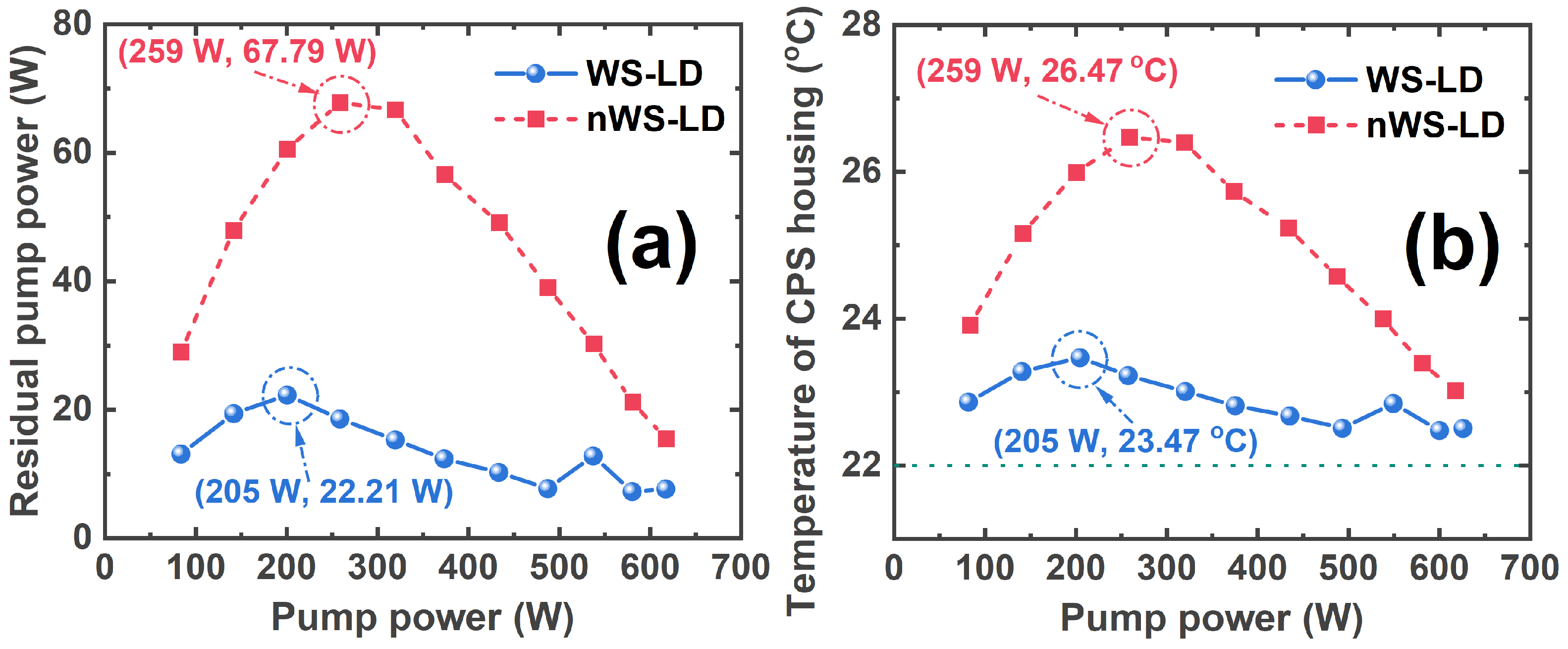
4. Results and Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Horley, R.; Norman, S.; Zervas, M.N. Progress and development in fibre laser technology. Proc. SPIE 2007, 6738, 67380K. [Google Scholar] [CrossRef]
- Nilsson, J.; Payne, D.N. High-power fiber lasers. Science 2011, 332, 921–922. [Google Scholar] [CrossRef]
- Jauregui, C.; Limpert, J.; Tünnermann, A. High-power fiber lasers. Nat. Photon. 2013, 7, 861–867. [Google Scholar] [CrossRef]
- Zervas, M.N.; Codemard, C.A. High power fiber lasers: A Review. IEEE J. Sel. Top. Quantum Electron. 2014, 20, 219–241. [Google Scholar] [CrossRef]
- Li, X.; Yu, H.; Zou, S.; He, C.; Ning, C.; Wu, W.; Chen, X.; Lin, X. A 606 W burst-mode picosecond Yb-doped all-fiber laser with an intra-burst repetition rate of 469 MHz. High Power Laser Sci. Eng. 2024, 12, e87. [Google Scholar] [CrossRef]
- Yang, S.; Smith, C.R.; Petersen, C.R.; Bang, O. All-Fiber 2 μm Mamyshev Oscillator: Mapping of Different Operating Regimes. Laser Photon. Rev. 2025, 19, 2500074. [Google Scholar] [CrossRef]
- Li, Y.; Zhong, Z.; Zhang, L.; Wei, Z.; Khalil, D.; Kotb, H.; Wei, H.; Zhu, M.; Wen, J.; Pang, F.; et al. Replica symmetry breaking dynamics in high-order optical mode multi-Stokes coherent random fiber laser. APL Photon. 2025, 10, 070804. [Google Scholar] [CrossRef]
- Ermolaev, M.; Moshegov, N.; Berezin, I.; Trubenko, P.; Shifrovich, I.; Berishev, I.; Mukhametzhanov, I.; Chuyanov, V.; Kompan, F.; Miftakhutdinov, D.; et al. Next-generation high-power laser diode pump modules. Proc. SPIE 2025, 13345, 133450D. [Google Scholar] [CrossRef]
- Ding, L.; Liu, P.; Chen, H.; Huang, L. Advance on the high-power and high-brightness diode laser modules for pumping and direct use applications. Proc. SPIE 2024, 12867, 128670V. [Google Scholar] [CrossRef]
- Wu, J.; Wan, Y.; Wang, P.; Zhang, H.; Wang, X.; Zhou, P.; Du, S.; Xu, X. Wide temperature operation of kilowatt fiber oscillators. Appl. Opt. 2022, 61, 417–421. [Google Scholar] [CrossRef]
- Paschotta, R.; Nilsson, J.; Tropper, A.; Hanna, D. Ytterbium-doped fiber amplifiers. IEEE J. Quantum Electron. 1997, 33, 1049–1056. [Google Scholar] [CrossRef]
- Liu, X.; Hu, M.; Caneau, C.; Bhat, R.; Zah, C. Thermal management strategies for high power semiconductor pump lasers. IEEE Trans. Compon. Packag. Technol. 2006, 29, 268–276. [Google Scholar] [CrossRef]
- Hejaz, K.; Norouzey, A.; Poozesh, R.; Heidariazar, A.; Roohforouz, A.; Nasirabad, R.R.; Jafari, N.T.; Golshan, A.H.; Babazadeh, A.; Lafouti, M. Controlling mode instability in a 500 W ytterbium-doped fiber laser. Laser Phys. 2014, 24, 025102. [Google Scholar] [CrossRef]
- Yang, M.; Wang, P.; Xu, X.; Wu, H.; Pan, Z.; Ye, Y.; Yan, Z.; Xi, X.; Zhang, H.; Wang, X. 1010 nm directly LD-pumped 6kW monolithic fiber laser employing long-tapered Yb3+-doped fiber. Photonics 2024, 11, 1033. [Google Scholar] [CrossRef]
- Chen, J.; Wu, J.; Li, F.; Peng, W.; Wu, H.; Zhang, H.; Wang, X. Kilowatt high power ytterbium-doped fiber laser operation in a record wide temperature range from −50 °C to 50 °C. Opt. Express 2024, 32, 47098–47110. [Google Scholar] [CrossRef]
- Li, Q.; Zhang, H.; Shen, X.; Yan, P.; Hao, H.; Gong, M. Stimulated Raman scattering threshold for partially coherent light in silica fibers. Opt. Express 2024, 23, 28438–28448. [Google Scholar] [CrossRef]
- Zeng, L.; Wang, X.; Wang, L.; Ye, Y.; Wang, P.; Yang, B.; Xi, X.; Pan, Z.; Zhang, H.; Shi, C.; et al. Optimization and demonstration of direct LD pumped High-Power fiber lasers to balance SRS and TMI effects. Photonics 2023, 10, 539. [Google Scholar] [CrossRef]
- Tian, X.; Rao, B.; Wang, M.; Xi, X.; Yang, B.; Chen, Z.; Xiao, H.; Wang, X.; Ma, P.; Wang, Z.; et al. 6 kW single stage narrow linewidth fiber amplifier based on the balance between mode instability and nonlinear effects. IEEE Photon. J. 2023, 15, 1502105. [Google Scholar] [CrossRef]
- Dawson, J.W.; Messerly, M.J.; Beach, R.J.; Shverdin, M.Y.; Stappaerts, E.A.; Sridharan, A.K.; Pax, P.H.; Heebner, J.E.; Siders, C.W.; Barty, C. Analysis of the scalability of diffraction-limited fiber lasers and amplifiers to high average power. Opt. Express 2008, 16, 13240. [Google Scholar] [CrossRef]
- Tao, R.; Ma, P.; Wang, X.; Zhou, P.; Liu, Z. Mitigating of modal instabilities in linearly-polarized fiber amplifiers by shifting pump wavelength. J. Optics. 2015, 17, 4–7. [Google Scholar] [CrossRef]
- Tao, R.; Ma, P.; Wang, X.; Zhou, P.; Liu, Z. Study of wavelength dependence of mode instability based on a semi-analytical model. IEEE J. Quantum Electron. 2015, 51, 1600106. [Google Scholar] [CrossRef]
- Wan, Y.; Yang, B.; Wang, P.; Xi, X.; Zhang, H.; Wang, X. Optimizing the pump wavelength to improve the transverse mode instability threshold of fiber laser by 3.45 times. J. Modern Opt. 2021, 68, 967–974. [Google Scholar] [CrossRef]
- Wan, Y.; Yang, B.; Xi, X.; Zhang, H.; Wang, P.; Wang, X.; Xu, X. Comparison and optimization on transverse mode instability of fiber laser amplifier pumped by wavelength-stabilized and non-wavelength-stabilized 976 nm laser diode. IEEE Photon. J. 2022, 14, 1503905. [Google Scholar] [CrossRef]
- Rezaei-Nasirabad, R.; Azizi, S.; Paygan, D.; Tavassoli, M.; Abedinajafi, A.; Roohforouz, A.; Chenar, R.E.; Golshan, A.H.; Hejaz, K.; Vatani, V. 2.5 kW TMI-free co-pump Yb-doped fiber oscillator by 971.5 nm pumping wavelength. Opt. Laser Technol. 2023, 157, 108652. [Google Scholar] [CrossRef]
- Wan, Y.; Xi, X.; Shen, Y.; Wang, X. Influence of central wavelength of pump source and pump direction on transverse mode instability threshold of fiber laser. Opt. Laser Technol. 2023, 162, 109270. [Google Scholar] [CrossRef]
- Huang, Z.; Tang, X.; Zhao, P.; Li, Z.; Li, C.; Li, Q.; Guo, C.; Lin, H.; Wang, J.; Jing, F. Influence of spectral properties of wavelength-locked and wavelength-unlocked diode laser on fiber laser performances. Laser Phys. 2016, 26, 075104. [Google Scholar] [CrossRef]
- Meng, X.; Li, F.; Yang, B.; Wang, P.; Yan, Z.; Yan, Z.; Ye, Y.; Xi, X.; Zhang, H.; Pan, Z.; et al. A 5 kW nearly-single-mode monolithic fiber laser emitting at ~1050 nm employing asymmetric bi-tapered ytterbium-doped fiber. Photonics 2023, 10, 1158. [Google Scholar] [CrossRef]
- Meng, X.; Li, F.; Yang, B.; Ye, Y.; Chai, J.; Xi, X.; Wang, P.; Wu, H.; Shi, C.; Zhang, H.; et al. A 4.8-kW high-efficiency 1050-nm monolithic fiber laser amplifier employing a pump-sharing structure. Front. Phys. 2023, 11, 1255125. [Google Scholar] [CrossRef]
- Meng, X.; Li, F.; Chen, J.; Xi, X.; Yang, B.; Wang, P.; Pan, Z.; Yan, Z.; Zhang, H.; Wang, X.; et al. 20 kW monolithic fiber amplifier with directly dual-wavelength laser diodes counter pumping. IEEE Photon. J. 2024, 16, 1503006. [Google Scholar] [CrossRef]
- Zeng, L.; Wen, Y.; Wang, X.; Wang, P.; Xi, X.; Yang, B.; Zhang, H.; Xi, F.; Han, K.; Wang, Z.; et al. Experimental research on abnormal transverse mode instability in high-power fiber lasers. Chin. J. Lasers 2024, 51, 0601001. [Google Scholar] [CrossRef]
- Tao, R.; Wang, X.; Zhou, P. Comprehensive Theoretical Study of mode instability in High-Power Fiber Lasers by employing a universal Model and its implications. IEEE J. Sel. Top. Quantum Electron. 2018, 24, 0903319. [Google Scholar] [CrossRef]
- Jauregui, C.; Stihler, C.; Limpert, J. Transverse mode instability. Adv. Opt. Photon. 2020, 12, 429. [Google Scholar] [CrossRef]
- Dong, L.; Ballato, J.; Kolis, J. Power scaling limits of diffraction-limited fiber amplifiers considering transverse mode instability. Opt. Express 2023, 31, 6690. [Google Scholar] [CrossRef]
- Abakumov, G.; Vorob’ev, S.; Simonov, A. Induced pump absorption, lasing threshold, and efficiency of organic compound lasers. Sov. J. Quantum Electron. 1977, 7, 1094. [Google Scholar] [CrossRef]
- Petričević, V.; Seas, A.; Alfano, R. Slope efficiency measurements of a chromium-doped forsterite laser. Opt. Lett. 1991, 16, 811. [Google Scholar] [CrossRef]
- Laporta, P.; Brussard, M. Design criteria for mode size optimization in diode-pumped solid-state lasers. IEEE J. Quantum Electron. 1991, 27, 2319. [Google Scholar] [CrossRef]
- Wagener, J.; Wysocki, P.; Digonnet, M.F.; Shaw, H. Effect of concentration on the efficiency of erbium-doped silica fiber lasers. Proc. SPIE 1993, 1789, 80. [Google Scholar] [CrossRef]
- Dimov, S. Dynamical behaviour and harmonic generation of a 946-nm pulsed, flashlamp-pumped Nd:YAG laser. Opt. Quantum Electron. 1993, 25, 545. [Google Scholar] [CrossRef]
- Sun, J.; Liu, L.; Han, L.; Zhu, Q.; Shen, X.; Yang, K. 100 kW ultra high power fiber laser. Opt. Contin. 2022, 1, 1932. [Google Scholar] [CrossRef]
- Zervas, M.N.; Marshall, A.; Kim, J. Effective absorption in cladding-pumped fibers. Proc. SPIE 2011, 7914, 79141T. [Google Scholar] [CrossRef]
- Jacquier, B. Rare Earth-Doped Fiber Lasers and Amplifiers; Springer: Boston, MA, USA, 1997. [Google Scholar] [CrossRef]
- Becker, P.C.; Olsson, N.A.; Simpson, J.R. Erbium-Doped Fiber Amplifiers: Fundamentals and Technology; Academic Press: Cambridge, MA, USA, 1999. [Google Scholar] [CrossRef]
- Koester, C.J.; Snitzer, E. Amplification in a fiber laser. Appl. Opt. 1964, 3, 1182–1186. [Google Scholar] [CrossRef]
- Li, D.; Wang, T.; Zhao, J.; Rao, L. Influence of ambient temperature on the performance of the semiconductor laser. In Proceedings of the 15th International Conference on Optical Communications and Networks (ICOCN), Hangzhou, China, 24–27 September 2016. [Google Scholar] [CrossRef]
- Redlich, C.; Lingnau, B.; Huang, H.; Raghunathan, R.; Schires, K.; Poole, P.; Grillot, F.; Ludge, K. Linewidth rebroadening in quantum dot semiconductor lasers. IEEE J. Sel. Top. Quantum Electron. 2017, 23, 1901110. [Google Scholar] [CrossRef]
- Andreou, S.; Williams, K.A.; Bente, E.A.J.M. Monolithically integrated InP-based DBR lasers with an intra-cavity ring resonator. Opt. Express 2019, 27, 26281. [Google Scholar] [CrossRef]
- Agrawa, G.P. Nonlinear Fiber Optics, 5th ed.; Academic Press: Cambridge, MA, USA, 2013. [Google Scholar] [CrossRef]
- Ye, Y.; Meng, X.; Xi, X.; Yan, Z.; Yang, B.; Pan, Z.; Wu, H.; Zhang, H.; Shi, C.; Wang, X.; et al. Towards a tapered Yb-doped fiber-based narrow linewidth single-mode fiber laser with a high signal to Raman ratio. Opt. Express 2023, 31, 26831. [Google Scholar] [CrossRef] [PubMed]
- Fu, C.; Li, Y.; Liu, W.; Lu, F.; Lu, K. Conversion efficiency of double-clad fiber laser. SPIE 2000, 4225, 160–163. [Google Scholar] [CrossRef]
- Caird, J.; Payne, S.; Staber, P.; Ramponi, A.; Chase, L.; Krupke, W. Quantum electronic properties of the Na3Ga2Li3F12:Cr3+ laser. IEEE J. Quantum Electron. 1988, 24, 1077. [Google Scholar] [CrossRef]
- Ramírez, M.; Jaque, D.; García, J.S.; Bausá, L.; Santiuste, J.M. 74% Slope efficiency from a diode-pumped Yb3+:LiNbO3:MgO laser crystal. Appl. Phys. B 2003, 77, 621–623. [Google Scholar] [CrossRef]
- Liu, Y.; Li, M.; Huang, S.; Wu, W.; Feng, X.; Shen, B.; Song, H.; Tao, R.; Wang, J.; Jing, F. >500 W passively-cooled fiber cladding light stripper. High Power Laser Part Beams 2021, 33, 021005. [Google Scholar] [CrossRef]
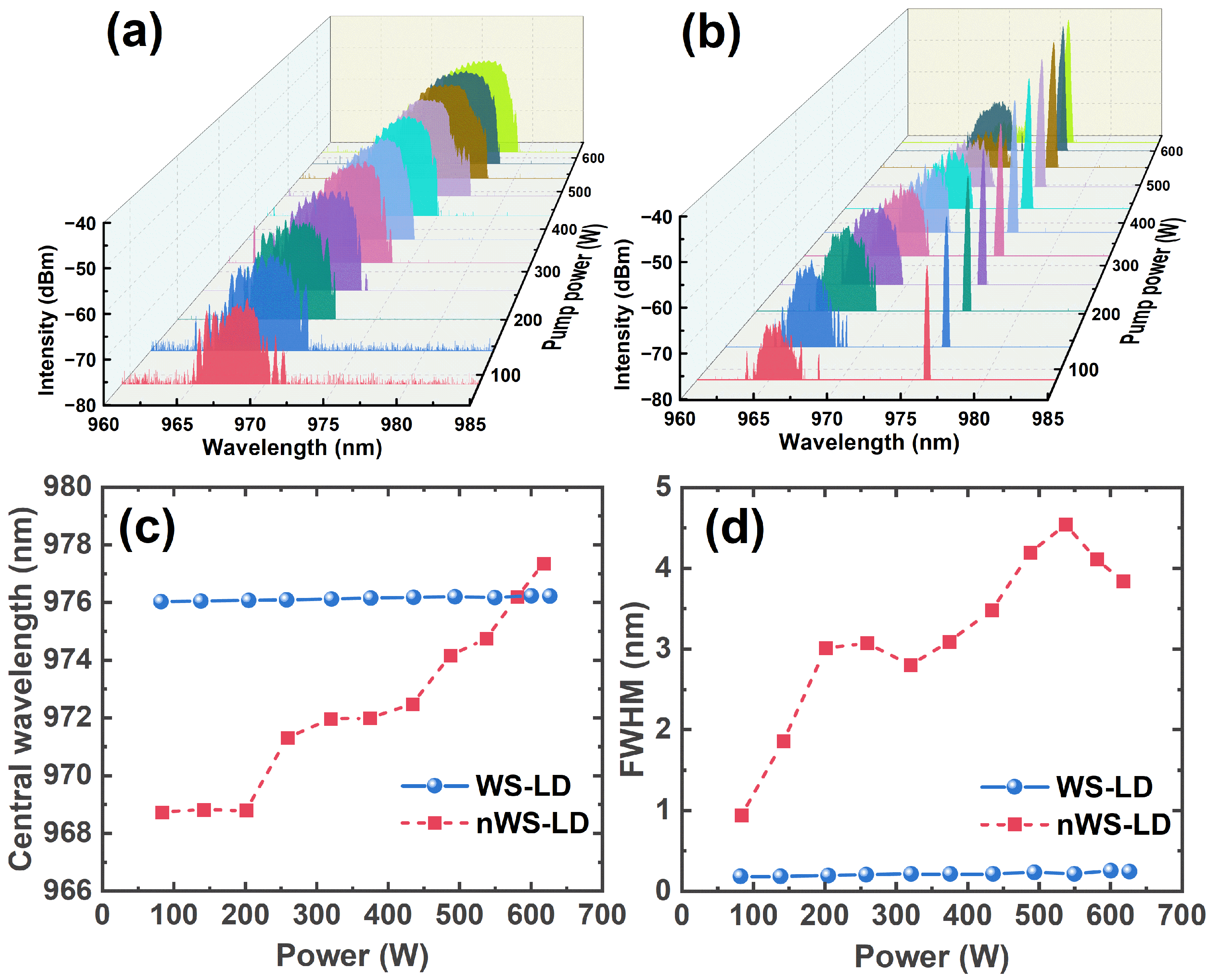

| Current/A | nWS-LD | WS-LD | ||||
|---|---|---|---|---|---|---|
| Power/W | /nm | FWHM/nm | Power/W | /nm | FWHM/nm | |
| 1 | 84 | 968.73 | 0.94 | 82 | 976.03 | 0.18 |
| 2 | 142 | 968.81 | 1.86 | 138 | 976.05 | 0.18 |
| 3 | 201 | 968.79 | 3.01 | 205 | 976.07 | 0.19 |
| 4 | 259 | 971.31 | 3.07 | 258 | 976.09 | 0.20 |
| 5 | 320 | 971.96 | 2.80 | 321 | 976.12 | 0.21 |
| 6 | 374 | 971.99 | 3.09 | 376 | 976.15 | 0.21 |
| 7 | 434 | 972.47 | 3.48 | 436 | 976.18 | 0.21 |
| 8 | 488 | 974.16 | 4.19 | 494 | 976.20 | 0.23 |
| 9 | 538 | 974.74 | 4.54 | 550 | 976.17 | 0.21 |
| 10 | 581 | 976.19 | 4.11 | 601 | 976.23 | 0.25 |
| 11 | 618 | 977.35 | 3.84 | 627 | 976.22 | 0.24 |
| Mean | – | 972.41 | 3.18 | – | 976.14 | 0.21 |
| Std. | – | 2.97 | 1.06 | – | 0.07 | 0.02 |
| Figure No. | Slope | Intercept | R2 | LD Type | Pump Power |
|---|---|---|---|---|---|
| (a) | 0.7026 ± 0.0176 | −41.8948 ± 7.1402 | 0.9938 | nWS-LD | launched |
| (b) | 0.6899 ± 0.0073 | −14.9402 ± 3.0102 | 0.9988 | WS-LD | launched |
| (c) | 0.6756 ± 0.0065 | −0.6763 ± 2.6029 | 0.9991 | nWS-LD | absorbed |
| (d) | 0.6665 ± 0.0049 | 0.6175 ± 1.8293 | 0.9995 | WS-LD | absorbed |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, F.; Shi, Y.; Zhang, C.; Chu, Q.; Huang, L.; Zhang, H.; Shu, Q.; Wen, Y.; Jiang, X.; Gao, Z.; et al. Impact of LD Spectra on Efficiency of Yb-Doped Fiber Laser. Photonics 2025, 12, 806. https://doi.org/10.3390/photonics12080806
Li F, Shi Y, Zhang C, Chu Q, Huang L, Zhang H, Shu Q, Wen Y, Jiang X, Gao Z, et al. Impact of LD Spectra on Efficiency of Yb-Doped Fiber Laser. Photonics. 2025; 12(8):806. https://doi.org/10.3390/photonics12080806
Chicago/Turabian StyleLi, Fengyun, Yi Shi, Chun Zhang, Qiuhui Chu, Lingli Huang, Haoyu Zhang, Qiang Shu, Yu Wen, Xingchen Jiang, Zixiang Gao, and et al. 2025. "Impact of LD Spectra on Efficiency of Yb-Doped Fiber Laser" Photonics 12, no. 8: 806. https://doi.org/10.3390/photonics12080806
APA StyleLi, F., Shi, Y., Zhang, C., Chu, Q., Huang, L., Zhang, H., Shu, Q., Wen, Y., Jiang, X., Gao, Z., Lin, H., & Tao, R. (2025). Impact of LD Spectra on Efficiency of Yb-Doped Fiber Laser. Photonics, 12(8), 806. https://doi.org/10.3390/photonics12080806






