Customized Chirality of an Optical Vortex Pair: Helical Dichroism and Enantioselective Force
Abstract
1. Introduction
2. Theoretical Model and Formulae
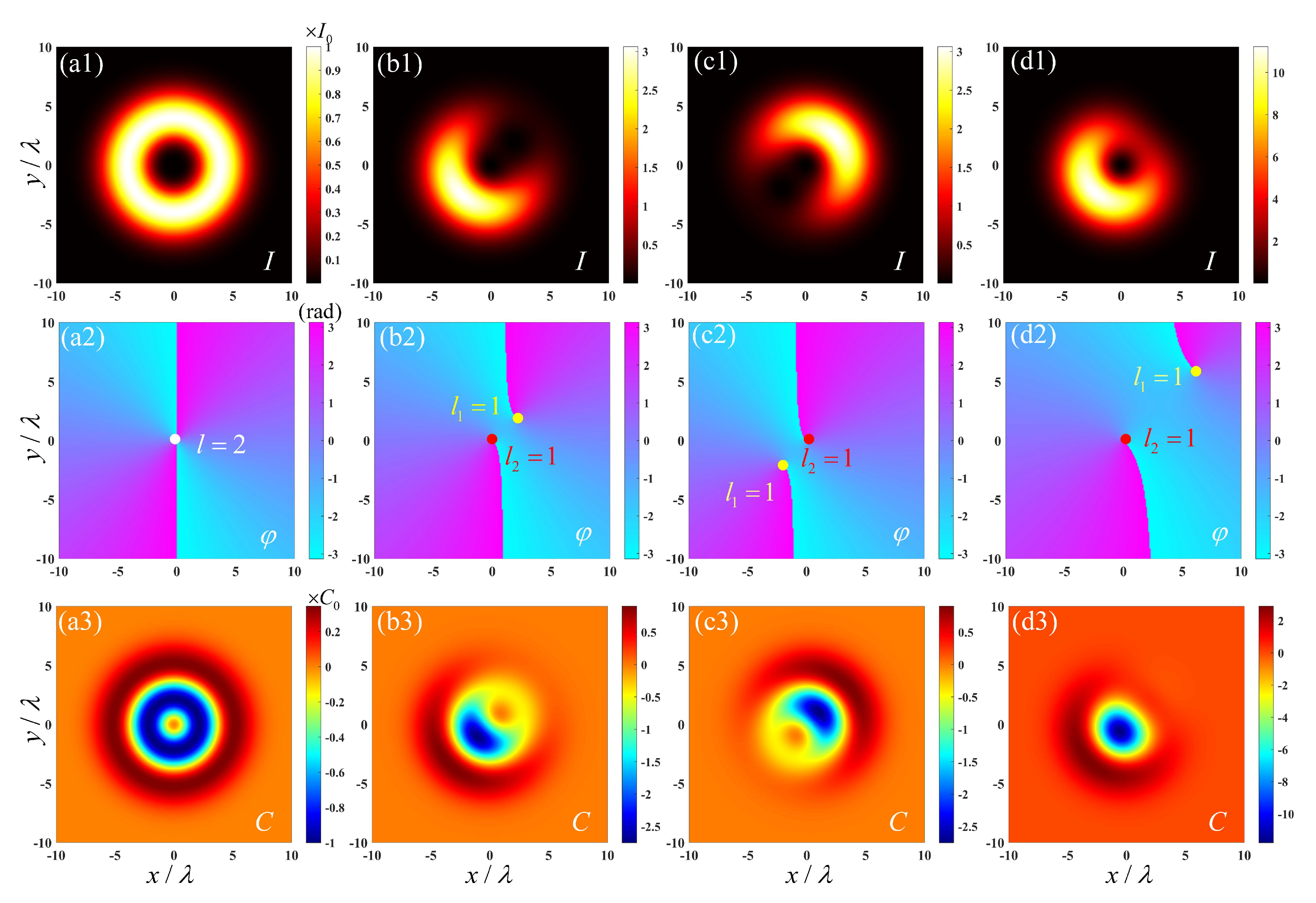
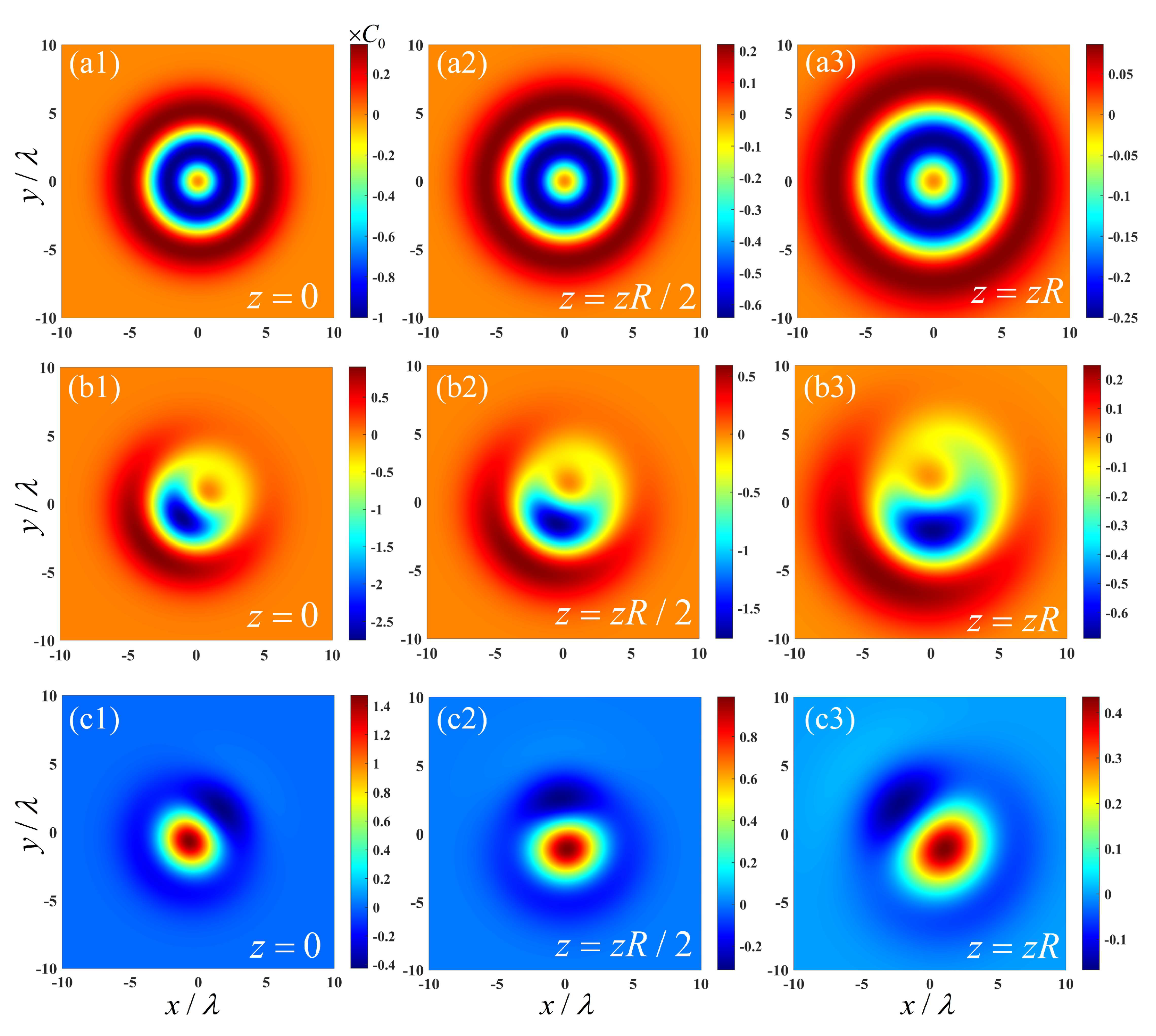
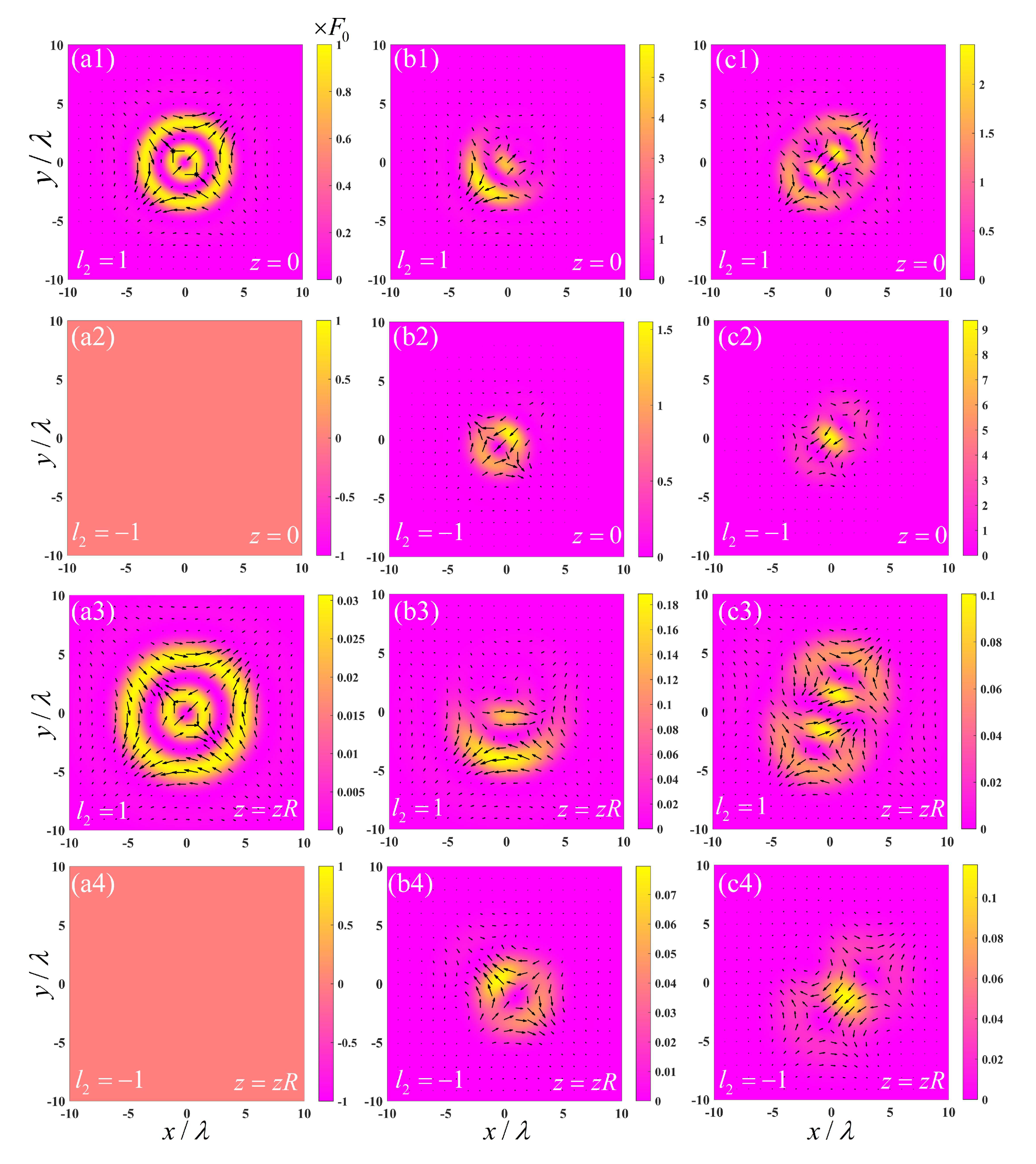
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Jaggard, D.L.; Mickelson, A.R.; Papas, C.H. On electromagnetic waves in chiral media. Appl. Phys. 1979, 18, 211–216. [Google Scholar] [CrossRef]
- Chern, R.L. Wave propagation in chiral media: Composite Fresnel equations. J. Opt. 2013, 15, 075702. [Google Scholar] [CrossRef]
- Hentschel, M.; Schäferling, M.; Duan, X.; Giessen, H.; Liu, N. Chiral plasmonics. Sci. Adv. 2017, 3, e1602735. [Google Scholar] [CrossRef] [PubMed]
- Zhao, Y.; Askarpour, A.N.; Sun, L.; Shi, J.; Li, X.; Alù, A. Chirality detection of enantiomers using twisted optical meta- materials. Nat. Commun. 2017, 8, 14180. [Google Scholar] [CrossRef]
- Mun, J.; Kim, M.; Yang, Y.; Badloe, T.; Ni, J.C.; Chen, Y.; Qiu, C.W.; Rho, J. Electromagnetic chirality: From fundamentals to nontraditional chiroptical phenomena. Light Sci. Appl. 2020, 9, 139. [Google Scholar] [CrossRef]
- Bliokh, K.Y.; Nori, F. Characterizing optical chirality. Phys. Rev. A 2011, 83, 021803(R). [Google Scholar] [CrossRef]
- Micsonai, A.; Wien, F.; Kernya, L.; Lee, Y.-H.; Goto, Y.; Réfrégiers, M.; Kardos, J. Accurate secondary structure prediction and fold recognition for circular dichroism spectroscopy. Proc. Natl. Acad. Sci. USA 2015, 112, E3095–E3103. [Google Scholar] [CrossRef]
- Miles, A.J.; Wallace, B.A. Circular dichroism spectroscopy of membrane proteins. Chem. Soc. Rev. 2016, 45, 4859–4872. [Google Scholar] [CrossRef]
- Vinegrad, E.; Vestler, D.; Ben-Moshe, A.; Barnea, A.R.; Markovich, G.; Cheshnovsky, O. Circular dichroism of single particles. ACS Photonics 2018, 5, 2151–2159. [Google Scholar] [CrossRef]
- Daly, S.; Rosu, F.; Gabelica, V. Mass-resolved electronic circular dichroism ion spectroscopy. Science 2020, 368, 1465–1468. [Google Scholar] [CrossRef]
- Karabchevsky, A. Single-shot circular dichroism spectroscopy. Light Sci. Appl. 2022, 11, 133. [Google Scholar] [CrossRef]
- Adhikari, S.; Efremova, M.V.; Spaeth, P.; Koopmans, B.; Lavrijsen, R.; Orrit, M. Single-particle photothermal circular dichroism and photothermal magnetic circular dichroism microscopy. Nano Lett. 2024, 24, 5093–5103. [Google Scholar] [CrossRef] [PubMed]
- Lu, W.L.; Chen, H.J.; Guo, S.D.; Liu, S.Y.; Lin, Z.F. Selectively transporting small chiral particles with circularly polarized Airy beams. Opt. Lett. 2018, 43, 2086–2089. [Google Scholar] [CrossRef] [PubMed]
- Zheng, H.X.; Li, X.; Ng, J.; Chen, H.J.; Lin, Z.F. Tailoring the gradient and scattering forces for longitudinal sorting of generic-size chiral particles. Opt. Lett. 2020, 45, 4515–4518. [Google Scholar] [CrossRef] [PubMed]
- Yamanishi, J.; Ahn, H.Y.; Yamane, H.; Hashiyada, S.; Ishihara, H.; Nam, K.T.; Okamoto, H. Optical gradient force on chiral particles. Sci. Adv. 2022, 8, eabq2604. [Google Scholar] [CrossRef]
- Jin, R.; Zhang, X.; Huo, P.; Cai, Z.; Lu, L.; Yiu, Y. Harnessing Enantioselective Optical Forces by Quasibound States in the Continuum. Phys. Rev. Lett. 2024, 133, 086901. [Google Scholar] [CrossRef]
- Shen, Y.; Wang, X.; Xie, Z.; Min, C.; Fu, X.; Liu, Q.; Gong, M.; Yuan, X. Optical vortices 30 years on: OAM manipulation from topological charge to multiple singularities. Light Sci. Appl. 2019, 8, 90. [Google Scholar] [CrossRef]
- Berry, M.V. The singularities of light: Intensity, phase, polarisation. Light Sci. Appl. 2023, 12, 238. [Google Scholar] [CrossRef]
- Zeng, X.L.; Russell, P.S.J.; Chen, Y.; Wang, Z.Q.; Wong, G.K.L.; Roth, P.; Frosz, M.H.; Stiller, B. Optical vortex Brillouin Lase. Laser Photonics Rev. 2023, 17, 2200277. [Google Scholar] [CrossRef]
- Chen, B.; Zhou, Y.G.; Liu, Y.; Ye, C.C.; Cao, Q.; Huang, P.N.; Kim, C.; Zheng, Y.; Oxenløwe, L.K.; Yvind, K.; et al. Integrated optical vortex microcomb. Nat. Photonics 2024, 18, 625–631. [Google Scholar] [CrossRef]
- Forbes, K.A. Nonlinear chiral molecular photonics using twisted light: Hyper-Rayleigh and hyper-Raman optical activity. J. Opt. 2020, 22, 095401. [Google Scholar] [CrossRef]
- Forbes, K.A. Raman optical activity using twisted photons. Phys. Rev. Lett. 2019, 122, 103201. [Google Scholar] [CrossRef] [PubMed]
- Forbes, K.A.; Jones, G.A. Optical vortex dichroism in chiral particles. Phys. Rev. A 2021, 103, 053515. [Google Scholar] [CrossRef]
- Ni, J.; Liu, S.; Hu, G.; Hu, Y.; Lao, Z.; Li, J.; Zhang, Q.; Wu, D.; Dong, S.; Chu, J.; et al. Giant helical dichroism of single chiral nanostructures with photonic orbital angular momentum. ACS Nano 2021, 15, 2893–2900. [Google Scholar] [CrossRef] [PubMed]
- Dai, N.; Liu, S.; Ren, Z.; Cao, Y.; Ni, J.; Wang, D.; Yang, L.; Hu, Y.; Li, J.; Chu, J.; et al. Robust helical dichroism on microadditively manufactured copper helices via photonic orbital angular momentum. ACS Nano 2023, 17, 1541–1549. [Google Scholar] [CrossRef] [PubMed]
- Forbes, K.A.; Green, D. Topological-charge-dependent dichroism and birefringence of optical vortices. Laser Photonics Rev. 2024, 18, 2400109. [Google Scholar] [CrossRef]
- Cheeseman, L.; Forbes, K.A. Nonlinear vortex dichroism in chiral molecules. Adv. Opt. Mater. 2025, 13, 2402151. [Google Scholar] [CrossRef]
- Forbes, K.A.; Green, D. Enantioselective optical gradient forces using 3D structured vortex light. Opt. Commun. 2022, 515, 128197. [Google Scholar] [CrossRef]
- Woźniak, P.; Leon, I.D.; Höflich, K.; Leuchs, G.; Banzer, P. Interaction of light carrying orbital angular momentum with a chiral dipolar scatterer. Optica 2019, 6, 961. [Google Scholar] [CrossRef]
- Ni, J.; Liu, S.; Wu, D.; Lao, Z.; Wang, Z.; Huang, K.; Ji, S.; Li, J.; Huang, Z.; Xiong, Q.; et al. Gigantic vortical differential scattering as a monochromatic probe for multiscale chiral structures. Proc. Natl. Acad. Sci. USA 2021, 118, 2020055118. [Google Scholar] [CrossRef]
- Müllner, S.; Büscher, F.; Möller, A.; Lemmens, P. Discrimination of chiral and helical contributions to Raman scattering of liquid crystals using vortex beams. Phys. Rev. Lett. 2022, 129, 207801. [Google Scholar] [CrossRef]
- Porfirev, A.; Khonina, S.; Kuchmizhak, A. Light-matter interaction empowered by orbital angular momentum: Control of matter at the micro- and nanoscale. Prog. Quantum Electron. 2023, 88, 100459. [Google Scholar] [CrossRef]
- Green, D.; Forbes, K.A. Optical chirality of vortex beams at the nanoscale. Nanoscale 2022, 15, 540–552. [Google Scholar] [CrossRef]
- Forbes, K.A.; Green, D. Customized optical chirality of vortex structured light through state and degree-of-polarization control. Phys. Rev. A 2023, 127, 063504. [Google Scholar] [CrossRef]
- Forbes, K.A. Spin angular momentum and optical chirality of Poincaré vector vortex beams. J. Opt. 2024, 26, 125401. [Google Scholar] [CrossRef]
- Rozas, D.; Law, C.T.; Swartzlander, G.A. Propagation dynamics of optical vortice. J. Opt. Soc. Am. B 1997, 14, 3054–3065. [Google Scholar] [CrossRef]
- Rozas, D.; Sacks, Z.S.; Swartzlander, G.A. Experimental Observation of Fluidlike Motion of Optical Vortices. Phys. Rev. Lett. 1997, 79, 3399. [Google Scholar] [CrossRef]
- Chen, M.; Roux, F.S. Accelerating the annihilation of an optical vortex dipole in a Gaussian beam. J. Opt. Soc. Am. A 2008, 25, 1279–1286. [Google Scholar] [CrossRef]
- Roux, F.S. Canonical vortex dipole dynamics. J. Opt. Soc. Am. B 2004, 21, 655–663. [Google Scholar] [CrossRef]
- Dan, W.-S.; He, J.; Zang, X.; Wang, F.; Zhou, Y.-M.; Chu, X.-X.; Zhou, G.-Q. Abrupt autofocusing performance of a circular Airyprime beam with vortex pairs. Result Phys. 2023, 47, 106377. [Google Scholar] [CrossRef]
- Zhen, W.; Wang, X.-L.; Ding, J.; Wang, H.-T. Controlling the symmetry of the photonic spin Hall effect by an optical vortex pair. Phys. Rev. A 2023, 108, 023514. [Google Scholar] [CrossRef]
- Sun, C.; Chen, X.; Xu, H.; Liang, G. Fusion of fractional vortex pairs and their transition to integer vortex controlled by optical power. Chin. Phys. B 2025, 34, 054202. [Google Scholar] [CrossRef]



Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Han, X.; Niu, H.; Shi, J.; Dong, W.; Wang, J. Customized Chirality of an Optical Vortex Pair: Helical Dichroism and Enantioselective Force. Photonics 2025, 12, 781. https://doi.org/10.3390/photonics12080781
Han X, Niu H, Shi J, Dong W, Wang J. Customized Chirality of an Optical Vortex Pair: Helical Dichroism and Enantioselective Force. Photonics. 2025; 12(8):781. https://doi.org/10.3390/photonics12080781
Chicago/Turabian StyleHan, Xingxing, Haibo Niu, Jing Shi, Weili Dong, and Jiajie Wang. 2025. "Customized Chirality of an Optical Vortex Pair: Helical Dichroism and Enantioselective Force" Photonics 12, no. 8: 781. https://doi.org/10.3390/photonics12080781
APA StyleHan, X., Niu, H., Shi, J., Dong, W., & Wang, J. (2025). Customized Chirality of an Optical Vortex Pair: Helical Dichroism and Enantioselective Force. Photonics, 12(8), 781. https://doi.org/10.3390/photonics12080781




