Wavefront-Corrected Algorithm for Vortex Optical Transmedia Wavefront-Sensorless Sensing Based on U-Net Network
Abstract
1. Introduction
2. Theoretical Model
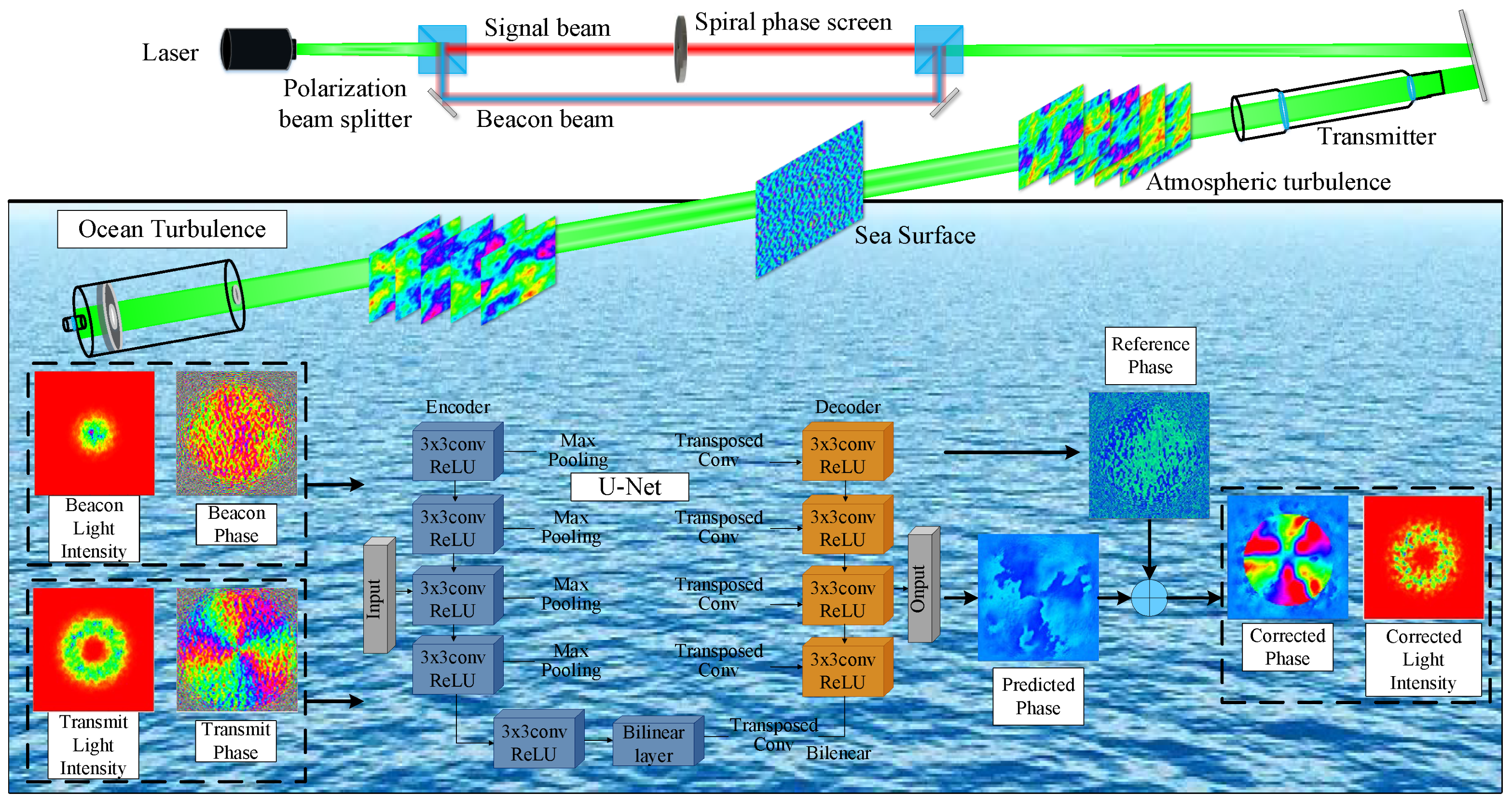
2.1. Modeling of Vortex Optical Transmedium Transport
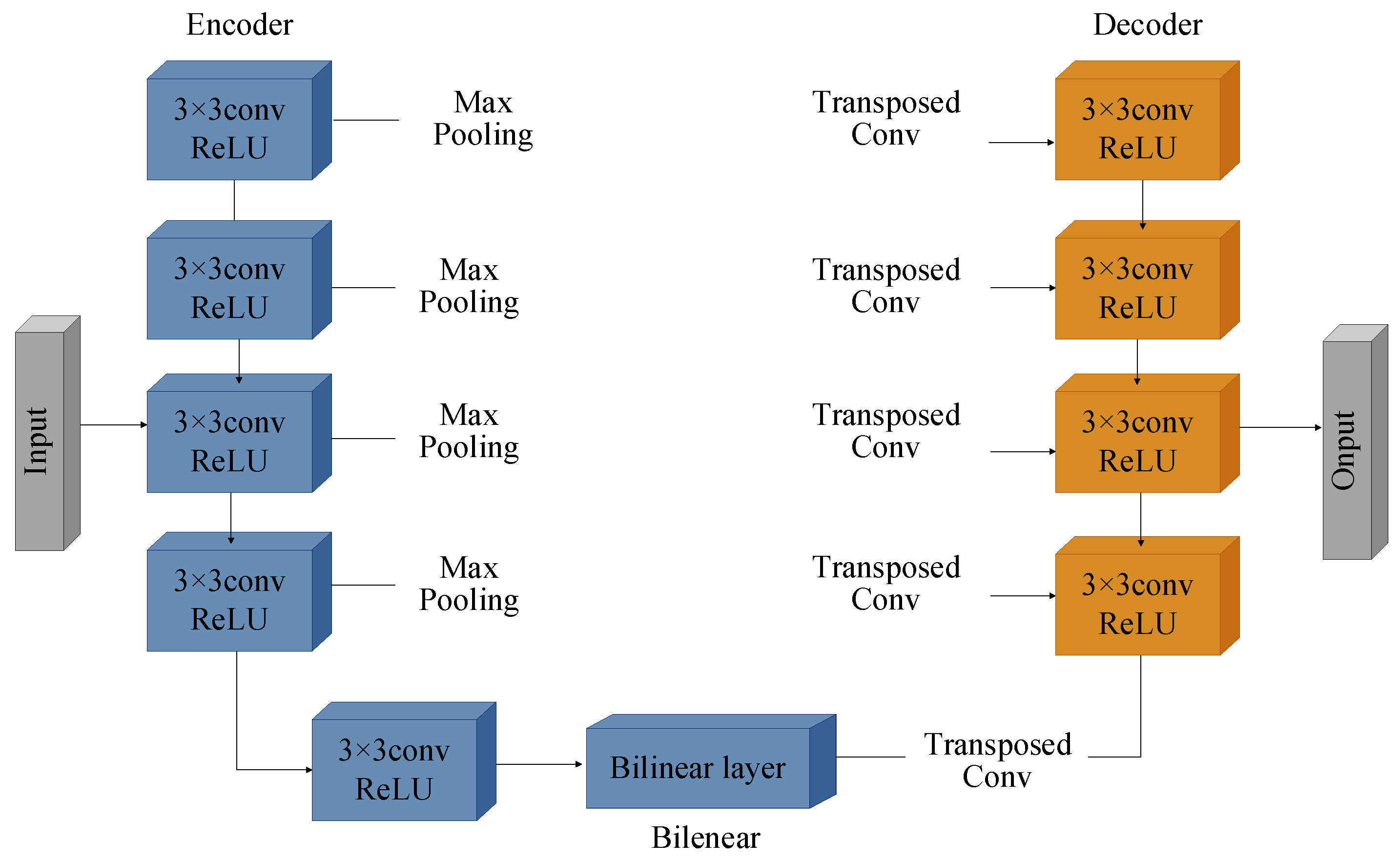
2.2. Phase Prediction Method Based on Improved U-Net
3. Results and Discussion
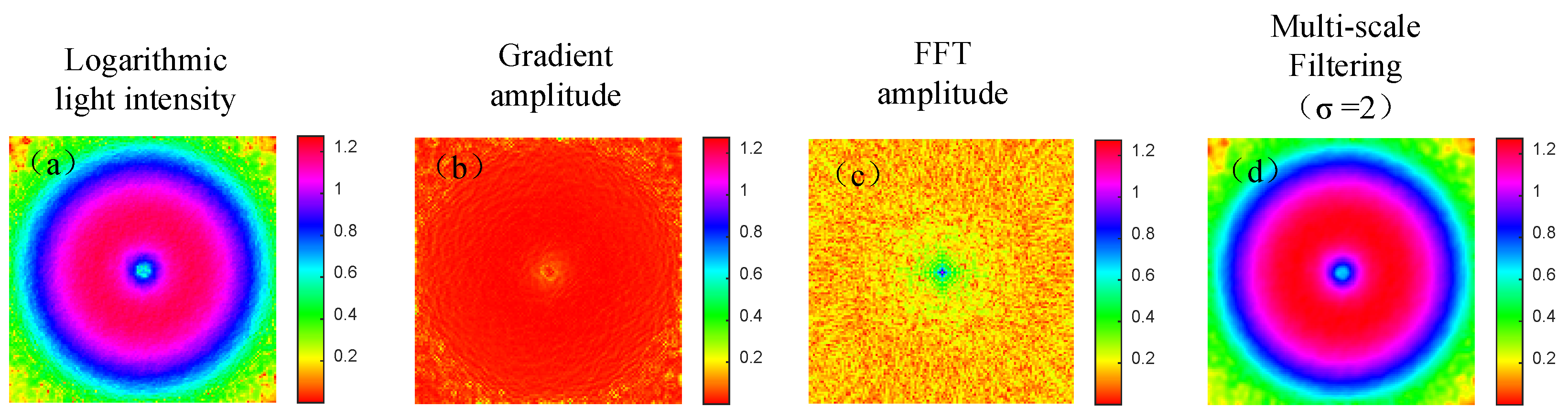
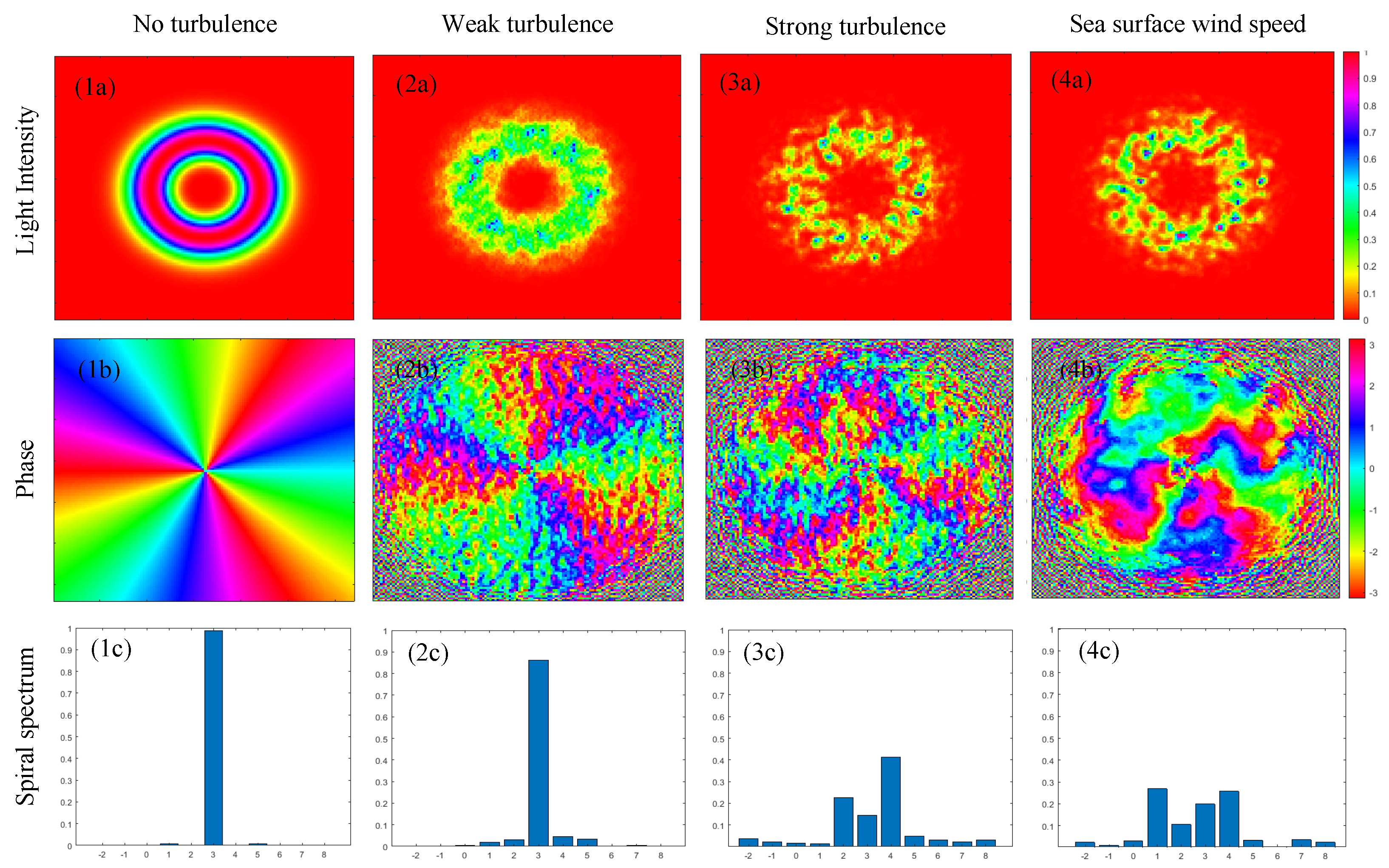
3.1. Transmission Characterization
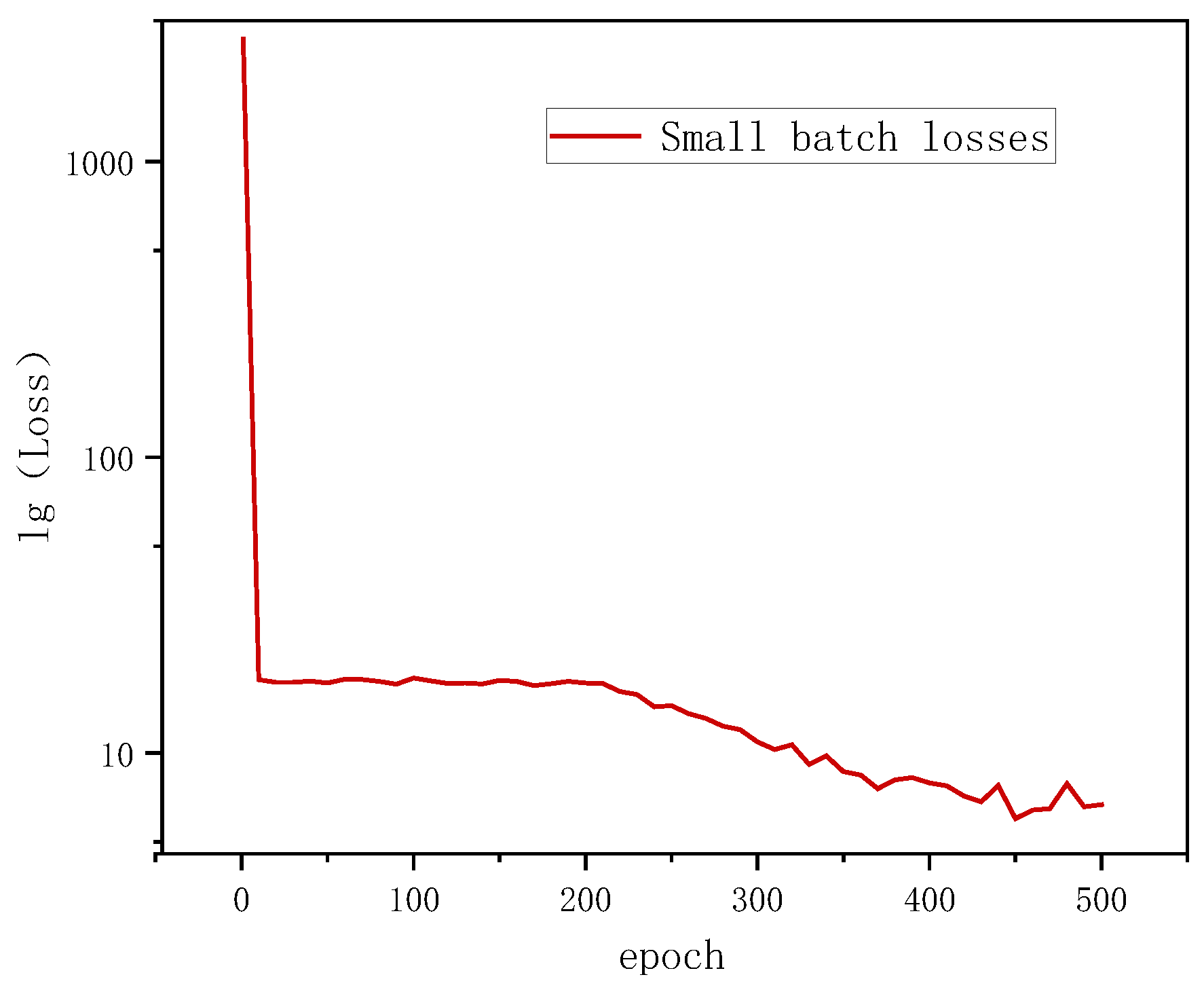
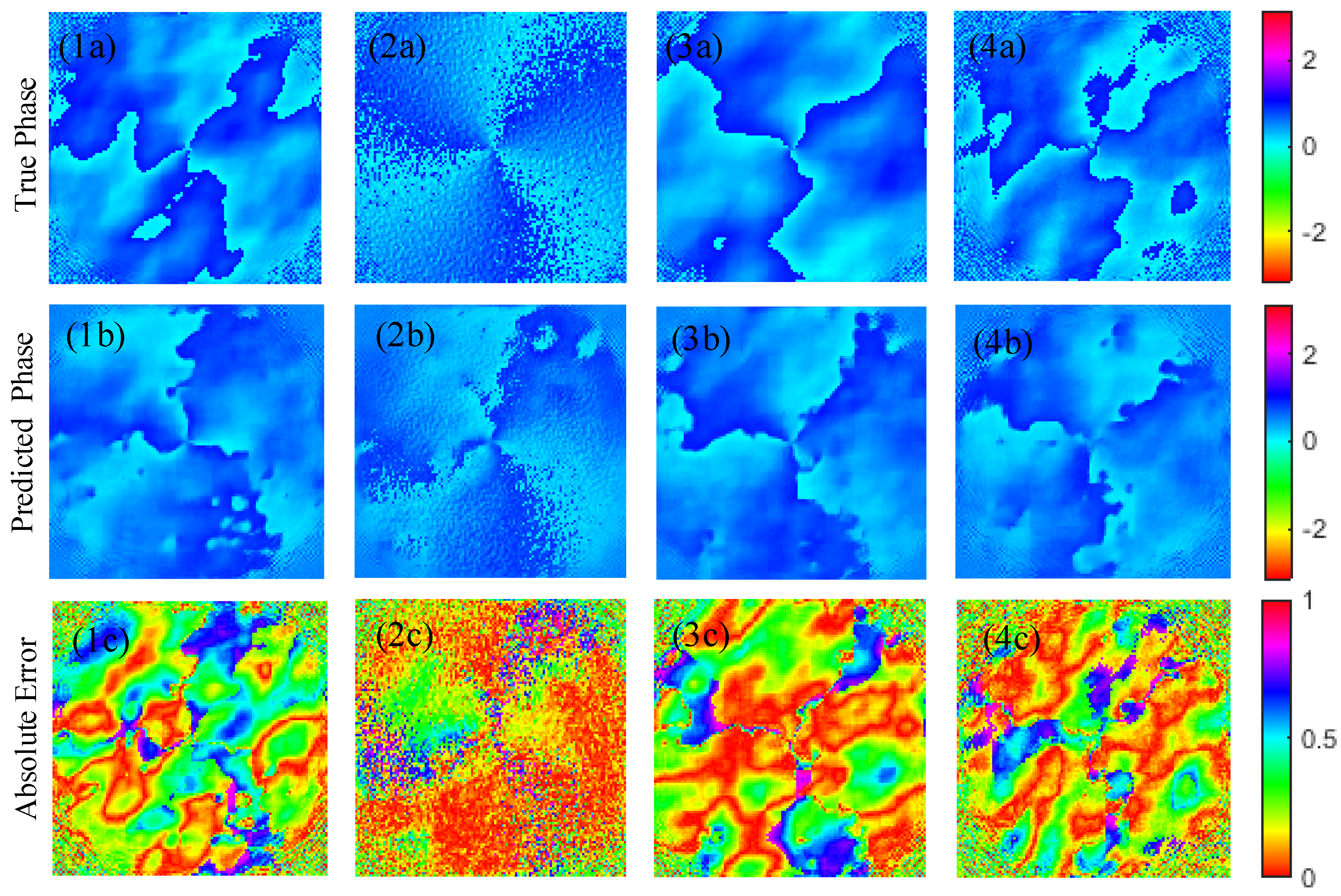
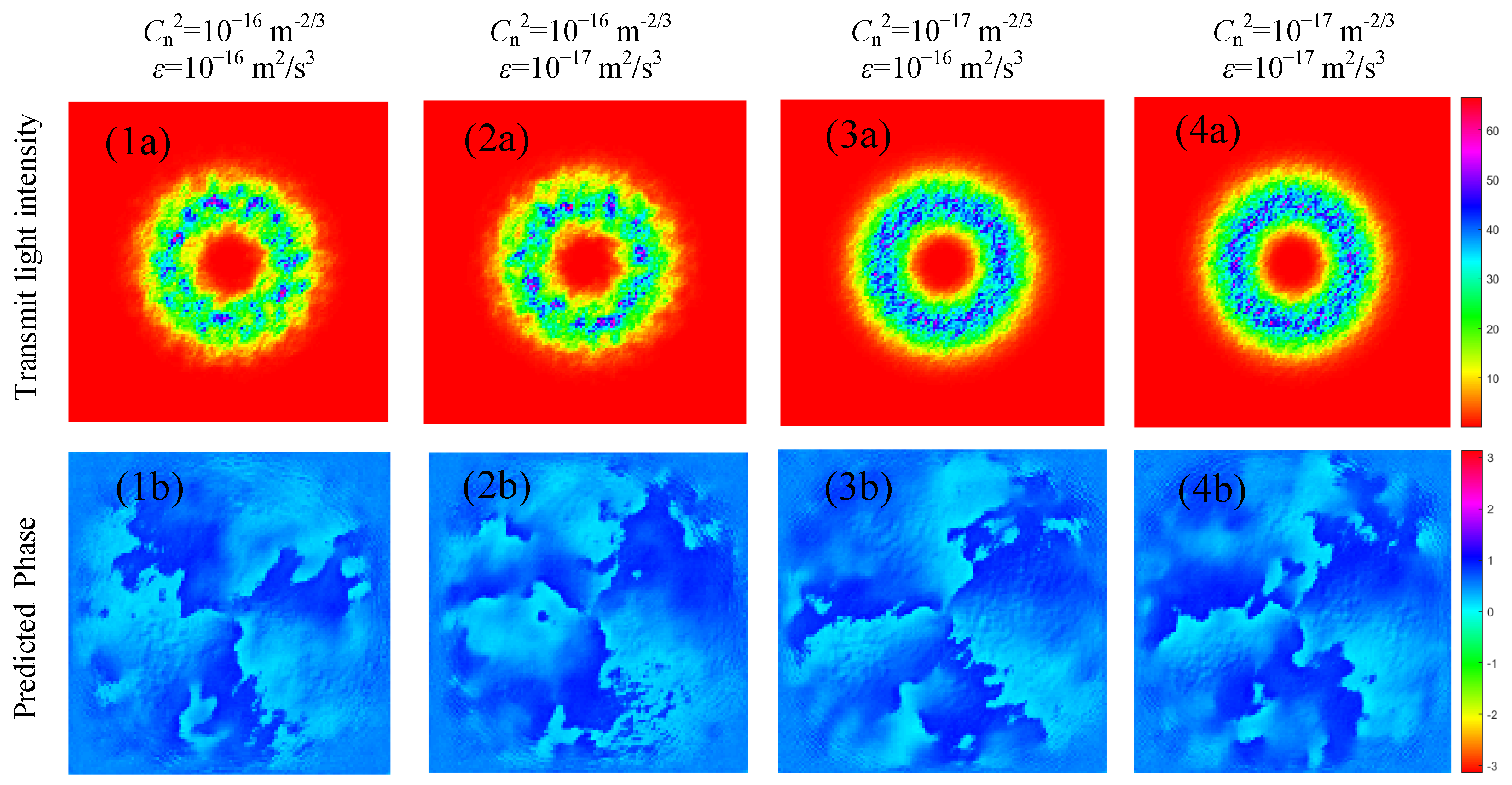
3.2. U-Net Phase Prediction Model
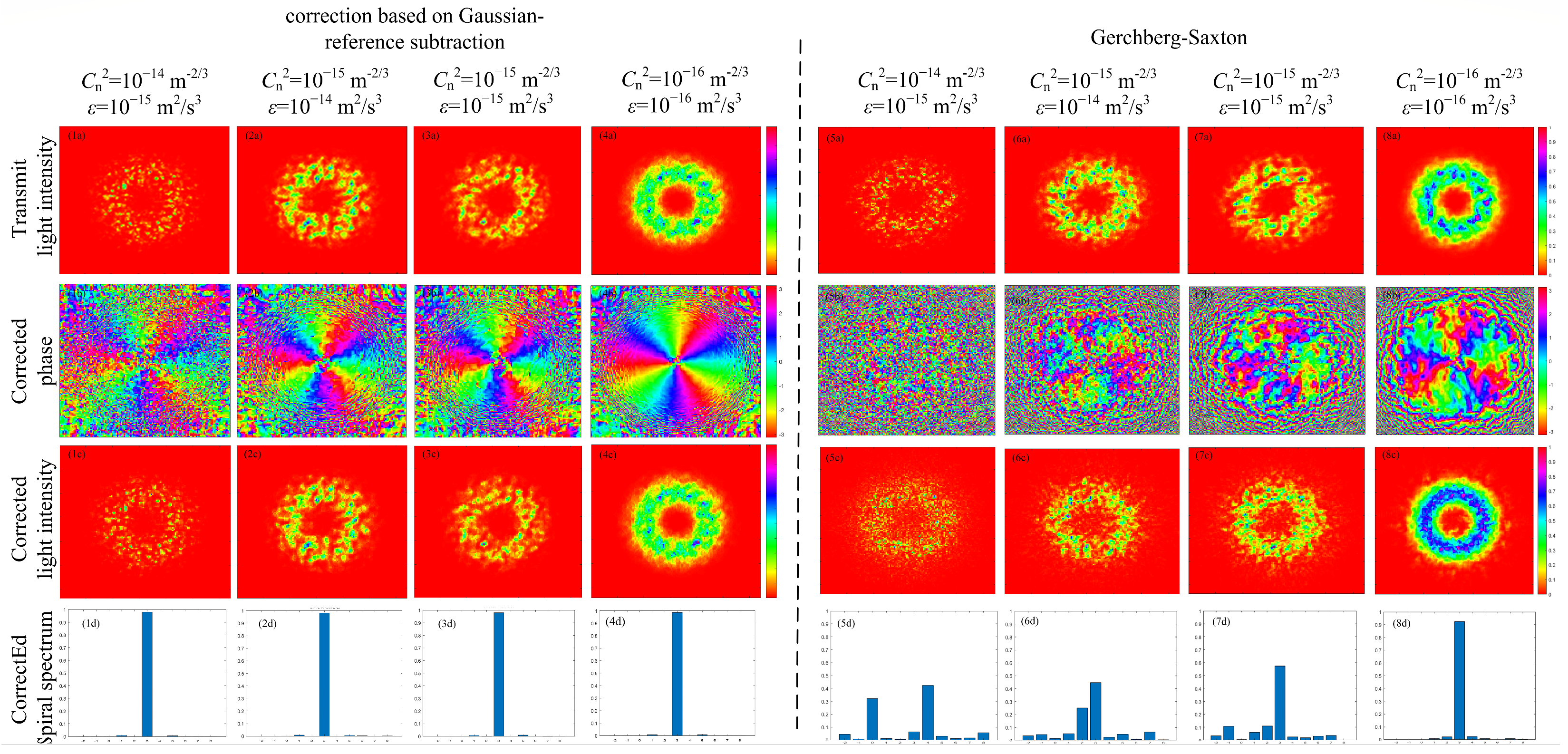
3.3. Closed-Loop
4. Conclusions and Outlook
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| OAM | Orbital angular momentum |
References
- Allen, L.; Beijersbergen, M.W.; Spreeuw, R.J.C.; Woerdman, J.P. Orbital angular momentum of light and the transformation of Laguerre-Gaussian laser modes. Phys. Rev. A 1992, 45, 8185. [Google Scholar] [CrossRef]
- Cheng, M.; Jiang, W.; Guo, L.; Li, J.; Forbes, A. Metrology with a twist: Probing and sensing with vortex light. Light Sci. Appl. 2025, 14, 4. [Google Scholar] [CrossRef]
- Li, S.; Chen, S.; Gao, C.; Willner, A.E.; Wang, J. Atmospheric turbulence compensation in orbital angular momentum communications: Advances and perspectives. Opt. Commun. 2018, 408, 68–81. [Google Scholar] [CrossRef]
- Hasselmann, D.E.; Dunckel, M.; Ewing, J.A. Directional wave spectra observed during JONSWAP 1973. J. Phys. Oceanogr. 1980, 10, 1264–1280. [Google Scholar] [CrossRef]
- Wang, X.; Ma, Y.; Yuan, Q.; Chen, W.; Wang, L.; Zhao, S. Properties of focused Laguerre-Gaussian beam propagating in anisotropic ocean turbulence. Chin. Phys. B 2024, 33, 024208. [Google Scholar] [CrossRef]
- Zhan, H.; Wang, L.; Peng, Q.; Wang, W.; Zhao, S. Progress in adaptive optics wavefront correction technology of vortex beam (Invited). Infrared Laser Eng. 2021, 50, 20210428. [Google Scholar]
- Brüning, C.; Alpers, W.; Hasselmann, K. Monte-Carlo simulation studies of the nonlinear imaging of a two dimensional surface wave field by a synthetic aperture radar. Int. J. Remote. Sens. 1990, 11, 1695–1727. [Google Scholar] [CrossRef]
- Xu, Y.; Shi, H.; Zhang, Y. Effects of anisotropic oceanic turbulence on the power of the bandwidth-limited OAM mode of partially coherent modified Bessel correlated vortex beams. J. Opt. Soc. Am. A 2018, 35, 1839–1845. [Google Scholar] [CrossRef]
- Aghajani, A.; Kashani, F.D.; Yousefi, M. Laboratory study of aberration calculation in underwater turbulence using Shack-Hartmann wavefront sensor and Zernike polynomials. Opt. Express 2024, 32, 15978–15992. [Google Scholar] [CrossRef]
- Yang, H.; Zang, X.; Zhang, Z.; Liu, J. Wavefront correction system based on RUN optimization algorithm. Acta Photon. Sin. 2023, 52, 1111004. [Google Scholar]
- Zhao, S.M.; Leach, J.; Gong, L.Y.; Ding, J.; Zheng, B.Y. Aberration corrections for free-space optical communications in atmosphere turbulence using orbital angular momentum states. Opt. Express 2011, 20, 452–461. [Google Scholar] [CrossRef] [PubMed]
- Yang, H.; Su, H.; Zhang, Z. Wavefront correction based on KL modes by SPGD control algorithm. Chin. J. Lasers 2023, 50, 1405001. [Google Scholar]
- Basu, D.; Chejarla, S.; Maji, S.; Bhattacharya, S.; Srinivasan, B. An adaptive optical technique for structured beam generation based on phase retrieval using modified Gerchberg–Saxton algorithm. Opt. Laser Technol. 2024, 170, 110244. [Google Scholar] [CrossRef]
- Nishizaki, Y.; Valdivia, M.; Horisaki, R.; Kitaguchi, K.; Saito, M.; Tanida, J.; Vera, E. Deep learning wavefront sensing. Opt. Express 2019, 27, 240–251. [Google Scholar] [CrossRef]
- Lu, C.; Tian, Q.; Zhu, L.; Gao, R.; Yao, H.; Tian, F.; Zhang, Q.; Xin, X. Mitigating the ambiguity problem in the CNN-based wavefront correction. Opt. Lett. 2022, 47, 3251–3254. [Google Scholar] [CrossRef]
- Wu, Y.; Guo, Y.; Bao, H.; Rao, C. Sub-Millisecond Phase Retrieval for Phase-Diversity Wavefront Sensor. Sensors 2020, 20, 4877. [Google Scholar] [CrossRef]
- Liu, W.; Luo, J.; Yang, Y.; Wang, W.; Deng, J.; Yu, L. Automatic lung segmentation in chest X-ray images using improved U-Net. Sci. Rep. 2022, 12, 8649. [Google Scholar] [CrossRef]
- Fan, C.; Chen, Z.; Lin, H.; Wang, X. TCGFusion: A network for PET-MRI fusion based on GAN and transformer. Multimed. Tools Appl. 2024, 83, 37505–37522. [Google Scholar] [CrossRef]
- Zhao, Z.Q.; Zheng, P.; Xu, S.; Wu, X. Object detection with deep learning: A review. IEEE Trans. Neural Netw. Learn. Syst. 2019, 30, 3212–3232. [Google Scholar] [CrossRef]
- Guo, H.; Tang, W.; Wang, Z.; Yuan, L.; Li, Y.; He, D.; Wang, Q.; Huang, Y. Liquid crystal wavefront correction based on improved machine learning for free-space optical communication. Appl. Opt. 2023, 62, 9470–9475. [Google Scholar] [CrossRef]
- Tian, Q.; Lu, C.; Liu, B.; Zhu, L.; Pan, X.; Zhang, Q.; Yang, L.; Tian, F.; Xin, X. DNN-based aberration correction in a wavefront sensorless adaptive optics system. Opt. Express 2019, 27, 10765–10776. [Google Scholar] [CrossRef]
- Ma, H.; Liu, H.; Qiao, Y.; Li, X.; Zhang, W. Numerical study of adaptive optics compensation based on Convolutional Neural Networks. Opt. Commun. 2019, 433, 283–289. [Google Scholar] [CrossRef]
- Fan, W.-Q.; Gao, F.-L.; Xue, F.-C.; Guo, J.-J.; Xiao, Y.; Gu, Y.-J. Experimental recognition of vortex beams in oceanic turbulence combining the Gerchberg–Saxton algorithm and convolutional neural network. Appl. Opt. 2024, 63, 982–989. [Google Scholar] [CrossRef] [PubMed]
- Zhan, H.; Wang, L.; Wang, W. Generative adversarial network based adaptive optics scheme for vortex beam in oceanic turbulence. J. Light. Technol. 2022, 40, 4129–4135. [Google Scholar] [CrossRef]
- Liu, J.; Du, Q.; Liu, F.; Wang, K.; Yu, J.; Wei, D. Vortex beam phase correction based on deep phase estimation network. Acta Opt. Sin. 2023, 43, 0601013. [Google Scholar]
- Andrews, L.C.; Phillips, R.L. Laser Beam Propagation Through Random Media; SPIE Press: Bellingham, WA, USA, 2003. [Google Scholar]
- Yang, S.; Li, M.; Ke, C.; Ding, D.; Ke, X. Coherent demultiplexing of vortex beam multiplexing transmission. Acta Opt. Sin. 2023, 43, 2006003. [Google Scholar]
- Liu, T.; Zhu, C.; Sun, C.; Zhang, J.; Lei, Y.; Zhang, R. Improved subharmonic method for simulation of atmospheric turbulence phase screen. Acta Photon. Sin. 2019, 48, 0201002. [Google Scholar]
- Su, D.; Wu, S.; Liu, L.; Liu, L. Ocean wave spectrum modeling-based sea surface polarization simulation. Laser Optoelectron. Prog. 2021, 58, 1411001. [Google Scholar]
- Nikishov, V.I. Spectrum of turbulent fluctuations of the sea-water refraction index. Int. J. Fluid Mech. Res. 2000, 27, 82–98. [Google Scholar] [CrossRef]
- Yin, K.; Huang, Z.; Lin, W.; Xing, T. Digital simulation of diffraction optical elements based on diffraction angular spectrum theory. Opto-Electron. Eng. 2012, 39, 125–128. [Google Scholar]
- Fan, Z.; Song, Q.; Li, J.; Tankam, P. The study of color digital holography free from the zero-order diffraction interruption. Acta Phys. Sin. 2011, 60, 034204. [Google Scholar] [CrossRef]
- Fan, R.; Hao, J.; Chen, R.; Wang, J.; Lin, Y.; Jin, J.; Yang, R.; Zheng, X.; Wang, K.; Lin, D.; et al. Phase retrieval based on deep learning with bandpass filtering in holographic data storage. Opt. Express 2024, 32, 4498–4510. [Google Scholar] [CrossRef]
- Li, R.; Pedrini, G.; Huang, Z.; Reichelt, S.; Cao, L. Physics-enhanced neural network for phase retrieval from two diffraction patterns. Opt. Express 2022, 30, 32680–32692. [Google Scholar] [CrossRef]
- Cao, Y.; Zhang, Z.; Peng, X. Wavefront distortion restoration method based on residual attention network. Acta Photon. Sin. 2022, 51, 1206002. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, S.; Zhao, Y.; Liu, B.; Zou, S.; Ke, C. Wavefront-Corrected Algorithm for Vortex Optical Transmedia Wavefront-Sensorless Sensing Based on U-Net Network. Photonics 2025, 12, 780. https://doi.org/10.3390/photonics12080780
Yang S, Zhao Y, Liu B, Zou S, Ke C. Wavefront-Corrected Algorithm for Vortex Optical Transmedia Wavefront-Sensorless Sensing Based on U-Net Network. Photonics. 2025; 12(8):780. https://doi.org/10.3390/photonics12080780
Chicago/Turabian StyleYang, Shangjun, Yanmin Zhao, Binkun Liu, Shuguang Zou, and Chenghu Ke. 2025. "Wavefront-Corrected Algorithm for Vortex Optical Transmedia Wavefront-Sensorless Sensing Based on U-Net Network" Photonics 12, no. 8: 780. https://doi.org/10.3390/photonics12080780
APA StyleYang, S., Zhao, Y., Liu, B., Zou, S., & Ke, C. (2025). Wavefront-Corrected Algorithm for Vortex Optical Transmedia Wavefront-Sensorless Sensing Based on U-Net Network. Photonics, 12(8), 780. https://doi.org/10.3390/photonics12080780




