1. Introduction
Uncorrected refractive error is the main cause of visual disability worldwide both in adults and children, which represents a public health problem [
1,
2]. Studies show that the prevalence of uncorrected refractive error can mainly be attributed to the small number of eye-care professionals and a lack of availability of their services in many remote areas [
2,
3,
4].
Myopia has become a worldwide pandemic [
5]. It is forecast that by the year 2050, more than half of the world’s population will be myopic and that 10% of myopes will suffer from high myopia (<−6.00 D) [
6]. This is concerning because high myopia is associated with an increased risk of ocular pathologies [
7,
8,
9,
10] in addition to posing a risk of permanent vision loss [
11]. The main factors limiting access to myopia control measures are limited ophthalmological or optometric care facilities, especially where health centers are overcrowded, and in poor urban populations [
3,
12].
Despite poverty and a lack of vision professionals, approximately 70% of the world’s population were smartphone users in 2023 [
13]. One strategy to address the problem of a lack of availability of facilities to measure refractive errors could potentially be to take advantage of the latest mobile technologies, including advances in display technology, which have allowed smartphone screens to achieve pixel densities suitable for tele-optometry applications [
14,
15,
16], such as presenting high-resolution on-screen visual stimuli. Most smartphones can generate screen resolutions of up to FullHD with luminance values greater than 1000 cd/m
2 [
17] to present adequate stimuli for tele-optometry applications [
18]. The widespread availability of these devices in practically the entire world population holds an important opportunity to address the aforementioned access to facilities problem [
19,
20].
Several remote refraction solutions have recently emerged on the market. Some require additional hardware, such as the Netra autorefractor (EyeNetra, Cambridge, MA, USA) [
21], Eye XM Virtual Visit (EyeNexo LLC, Boston, MA, USA) [
22], or EyeQue, which use optical attachments or specialized displays. Others rely solely on electronic devices, including myRx Refraction Exam (Luna Solutions, LLC, Draper, UT, USA) [
23], Opternative (Visibly, Inc., Chicago, IL, USA), Virtual Vision Test (Warby Parker, Inc., New York City, NY, USA) [
24], OKKO Health, and the Easee Web-based tool [
25]. While these tools aim to improve accessibility, most rely on simplified visual acuity assessments or questionnaires, and several lack independent clinical validation. A common limitation among these systems is their reduced sensitivity to hyperopic and presbyopic refractive errors, which may compromise their utility in pediatric screening or comprehensive vision assessments. Moreover, some applications impose strict refractive range limits or require professional oversight, which can limit their scalability.
One practical limitation of the technologies that need extra hardware is that an initial purchase of the accessory is needed. Accessories usually include a system to change the optical vergence of the target, allowing the eye to relax and facilitating measurements in hyperopic subjects. On the other hand, technologies that do not require extra hardware achieve changes in target vergence by adjusting the user’s face–device distance. This poses two main challenges: (1) the spatial frequency content of the on-screen stimuli changes with the distance; (2) it is not possible to place the stimulus at a distance greater than infinity (0 D) and measure hyperopia.
Refractive errors, particularly myopia, represent a growing global public health concern, especially in regions with limited access to eye-care professionals [
26,
27,
28]. In response to this challenge, the present study evaluates the potential of a smartphone-based application to accurately measure refractive error and monitor myopia progression, achieving a level of precision comparable to traditional clinical methods. By offering an accessible and cost-effective solution, this approach may significantly enhance the delivery of eye-care services in underserved areas. Moreover, its integration into clinical practice could transform tele-optometry by enabling large-scale remote eye examinations, thereby facilitating the early detection and management of refractive conditions. Specifically, this study proposes a novel methodology for estimating spherical refraction by determining the remote point using a smartphone-based system.
The objective of the present work was to compare the preliminary results of the measurements of the refractive error obtained with a novel app with the results of a standard clinical subjective refraction to ascertain whether or not it is possible to monitor the progression of myopia remotely using a smartphone.
2. Materials and Methods
This study involved the evaluation of over-spherical refraction obtained through far point (FP) measurements using smartphones in a cohort of young individuals who were artificially myopized to varying degrees. After the participants’ refractive errors were corrected, myopization was induced using positive trial lenses. The experiment was conducted with the approval of the Ethics Committee of the University of Murcia and in accordance with the principles of the Declaration of Helsinki.
2.1. Participants
Thirty university participants aged between 18 and 38 years (mean 22 ± 5 years) were recruited for this study. Monocular clinical measurements of standard subjective sphero-cylindrical refraction and best corrected visual acuity of the right eye (OD) were performed by an experienced optometrist to establish a clinical baseline for comparison with the spherical refraction measured by the smartphone application (AppRx). Participant recruitment was subject to specific inclusion and exclusion criteria: individuals aged 18 to 38 years with no known ocular or systemic conditions affecting visual acuity or contrast sensitivity were included. Exclusion criteria encompassed the presence of ocular pathologies such as amblyopia, glaucoma, diabetic retinopathy, age-related macular degeneration, Kjer’s optic neuropathy, or any other ocular disease that could impair visual acuity or chromatic discrimination thresholds. For participants who were contact lens users, they were instructed to discontinue lens wear for a specified period (24–48 h) prior to the study visit to ensure accurate baseline refraction.
2.2. Clinical Measurements
To determine the clinical refraction, the standard subjective method was used [
29,
30], guided by objective refraction findings obtained through retinoscopy, with the aim of achieving maximum plus for maximum visual acuity [
30,
31], using an Early Treatment Diabetic Retinopathy Study chart at a distance of 6 m. Myopization was induced in increments of 0.25 D, ranging from 0.00 D to +1.50 D, resulting in seven different myopic conditions tested per participant. The values induced were considered the clinical refraction (CliRx), against which the application-based measurements (AppRx) were compared. Ambient illumination was maintained at a consistent level of approximately 250 lux for both clinical and app-based measurements. The mean spherical equivalent refraction obtained from the subjective clinical measurements was −0.93 ± 1.87 D, with a minimum value of −6.25 D and a maximum of +1.50 D.
2.3. Mobile Application Measurements
AppRxs were obtained using a customized application developed by Visionapp Solutions S.L. (Murcia, Spain). This non-commercialized app monitored and recorded at a rate of 20 Hz the distance between the subject’s face and the device using images captured by the device’s front-facing camera.
A Xiaomi Redmi
TM Note 11 (Xiaomi, Beijing, China) device with a 6.43-inch screen and 409 DPI pixel was employed for measuring FP. For this device, the blue stimulus exhibited a luminance of 32 cd/m
2, and the black background exhibited a luminance of 2.5 cd/m
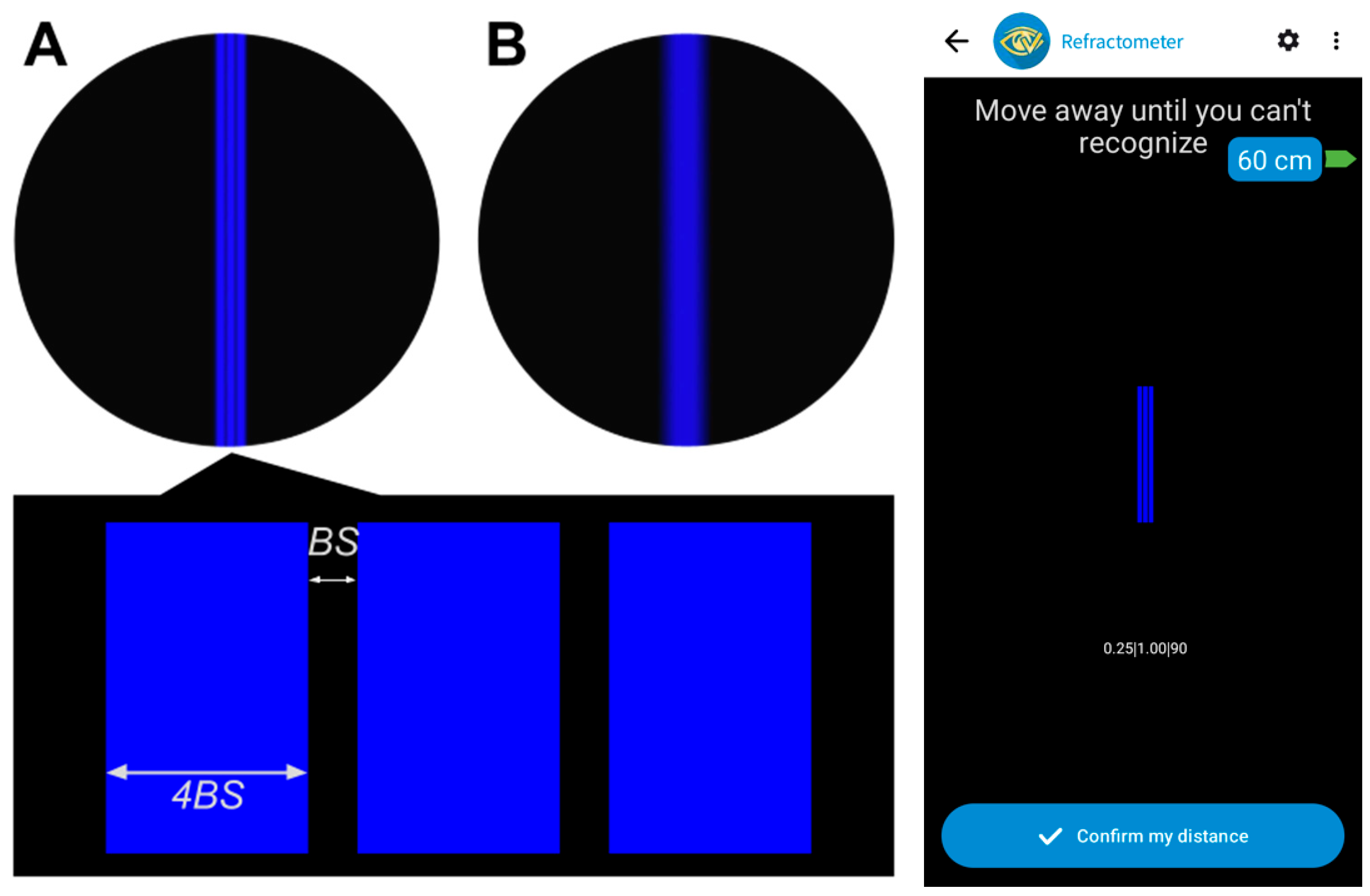
2, resulting in a Michelson contrast of 0.855. The visual stimulus used in these measurements consisted of three parallel vertical blue lines against a black background, with a narrow black space (BS in
Figure 1) between the lines, which was four times narrower than the width of the blue lines. This specific pattern was chosen for its high contrast, which significantly enhances the visibility of light dispersion on the black background. Furthermore, the use of lines oriented in a single direction provides versatility for future studies aimed at measuring refractive powers in different meridians, which will be useful for characterizing astigmatism. The B-channel of the organic light-emitting diode display [
32] was chosen to generate extra myopia of about 0.7 D due to the ocular longitudinal chromatic aberration (LCA) [
33,
34]. Consequently, digital displays with a blue stimulus on a dark background move the whole interval of clear vision a vergence of about 2/3D closer to the subject. This, avoids the use of mobile devices at long distances, allowing greater precision for determining face–device distances by capturing larger face images with the front camera, while also allowing a more comfortable working distance for the subject [
35]. Further details of the methodology used by the app to measure the face–device distance, its accuracy, and its dependency on the type of camera used by the smartphone can be found in Salmerón-Campillo et al. [
35].
The stimulus’s fundamental spatial frequency determined the width and separation of the three lines, kept constant during the test by dynamically adapting the BS value based on the face–device distance. The spatial frequency utilized corresponded to 80% of the subject’s clinical decimal VA.
2.4. Experimental Procedure
As a preliminary step, the app was configured so that the displayed stimulus followed the required characteristics, defined in detail in the mobile application measurements subsection. Then, the subject’s refraction was corrected using trial lenses. This initial correction served as the baseline for all subsequent measurements. To calibrate face–device distance measurement, subjects were asked to hold the device at a calibration distance of 30 cm from their face and tap an on-screen confirm button. Further details of the calibration distance process were described in previous studies [
36,
37].
The experimental setup consisted of a mobile device held in a tripod. Subjects covered their left eye and were seated on an office chair positioned at a distance of 1.43 m away from the device. This distance approximately corresponds to the FP of an emmetropic eye using blue light and taking into account its LCA. Initially, we ensured that the subject’s refraction was corrected. At this distance, the
Figure 1A stimulus was shown on screen. Their spatial frequency was set to 80% of the subject’s clinical decimal VA, and we confirmed that, with their baseline correction, the three blue lines could be clearly distinguished by the subject. This step ensured that the subject’s baseline refractive state was accurately compensated before inducing experimental conditions.
Subjects were guided through the process by the app’s interface, which instructed them to adjust their face–device distance by moving closer or away. When moving closer, the task was to perceive the lines distinctly (
Figure 1A), and when moving away, the task was to perceive the three lines as indistinguishable (
Figure 1B). When this was confirmed by the subject, their distance representing the FP in blue light was recorded by the app. A maximum distance of 3 m (−0.33 D) was set as the upper limit for moving away. This is a distance beyond the FP of an emmetropic eye using blue light (−0.33 D + 0.70 D = +0.37 D), so even emmetropic refractions could be measured.
To validate the app’s performance across various refractive errors, the researcher induced seven different levels of spherical myopia using positive trial lenses added on top of the subject’s baseline full correction, including a plano lens. These lenses ranged from 0.00 D to 1.50 D and were presented in a randomized order. For each induced myopic condition (e.g., adding a +1.00 D lens on top of the correction effectively created a −1.00 D myopic state to be measured by the app), the FP was determined, obtaining three repeated measurements per lens. Each of the distances collected by the app were then transformed into vergences to obtain AppRx, taking into account the LCA and the depth of focus (DoF) of the human eye, as is shown in the following subsection. The primary aim of this experimental design was to validate the app’s ability to accurately measure changes in spherical refractive error under controlled conditions, serving as a critical step in the development of a final application intended for detecting shifts in spherical refractive errors.
2.5. Computing Refraction Measured by the App
The associated FP vergence was calculated (Equation (1)), considering the measured far point distances and the vergence shift originated by the LCA, which equals to −0.70 D in the case of blue light:
Subsequently, the average and standard deviation of the three
for each CliRx and subject were computed, yielding
and
, respectively. Then, the relationship between AppRx and
was determined (Equation (2)). Apparently, these two quantities should match, having an equal value. However, they actually differ due to the effect of the depth of focus (
DoF):
The
DoF refers to the range of vergences around the best focus where the retinal image remains perceptually sharp. It acts as a buffer zone, within which small changes in vergence do not lead to a noticeable blur. This
DoF is associated with several factors [
38,
39]. Some of these factors are subjective and variable, as is the case with individual perception and tolerance of the blur [
40], or pupil size, which may introduce a random error in the estimation of AppRx. But others can represent a constant bias (systematic error) that may be minimized after an empirical calibration. In our calibration analysis,
DoF was modeled as a linear function depending on the measured FP vergence (Equation (3)):
where
DoF and
a are expressed in units of
(diopters), and
b is dimensionless. This approach accounts for the maximum set distance of 3 m allowed in the ‘move away’ task. Consequently, there is a limit to the positive vergence results for less myopic conditions. For instance, an emmetropic eye with
DoF = 0.50 D would move away until 0.50 D, but the limit was 0.37 D. Therefore, such a subject would not complete the task within the allowed distance range. Hence, the effective DoF was assumed to be lower in less myopic conditions and higher in more myopic conditions. Thus, the
DoF was allowed to linearly change with
rather than assuming it to be constant.
With this theoretical background, Equations (2) and (3) yield a linear relationship between AppRx and
(Equation (4)):
where
, and
Since the values of α and β were initially unknown, they were calibrated by performing a reverse linear regression versus CliRx. The accuracy of the AppRx results from this procedure compared to CliRx was estimated using a Leave-One-Out Cross-Validation (LOOCV) technique [
41]. This approach prevents using the same dataset for calibration and accuracy estimation, which would otherwise lead to overly optimistic results.
2.6. Statistical Analysis
Coefficients
and
were estimated by performing a reverse linear regression [
42,
43] to establish a direct relationship between
and AppRx (Equation (2)). In this procedure, the independent variable was set to be CliRx, while the dependent variable was
. The intercept and slope of this linear fit yielded the
and
values. Key parameters such as the standard deviation of the coefficients were computed, as well as the determination coefficient (
) and
p-value of the linear correlation.
On the other hand, a comparative analysis between AppRx and CliRx was performed. As using these
and
coefficients would result in overly optimistic and potentially unrealistic accuracy estimates (because we trained these coefficients with the same dataset where we are evaluating the AppRx results), a Leave-One-Out Cross-Validation (LOOCV) technique implementing reverse linear regression was employed [
41]. With this procedure, in a dataset of N measures, N different reverse linear regressions
vs. CliRx were trained, with N-1 samples in each of them. In each linear fit, one sample is left out. These regressions lead to a set of
and
. For each
sample,
was calculated using the
and
coefficients, which were obtained by using all the samples except for this left-out sample. Therefore, this technique provides an unbiased estimate of the accuracy of AppRx compared to CliRx.
For these LOOCV results, a Bland–Altman analysis was performed. Differences between AppRx and CliRx were evaluated, showing the average difference and its limits of agreement (LoA). Student’s t-test was performed, with its null hypothesis being that the average of the differences between AppRx and CliRx is zero. Its p-value was obtained to evaluate the significance of the differences between LOOCV AppRx and CliRx. A scatter plot and Bland–Altman plot were included. Additionally, the cumulative relative distribution of absolute errors between AppRx and CliRx was evaluated.
Finally, intra-subject dispersion was addressed by evaluating the average and the cumulative relative distribution of the standard deviation of the three measurements of the vergence of the FP, , which is the intra-subject standard deviation (SD).
3. Results
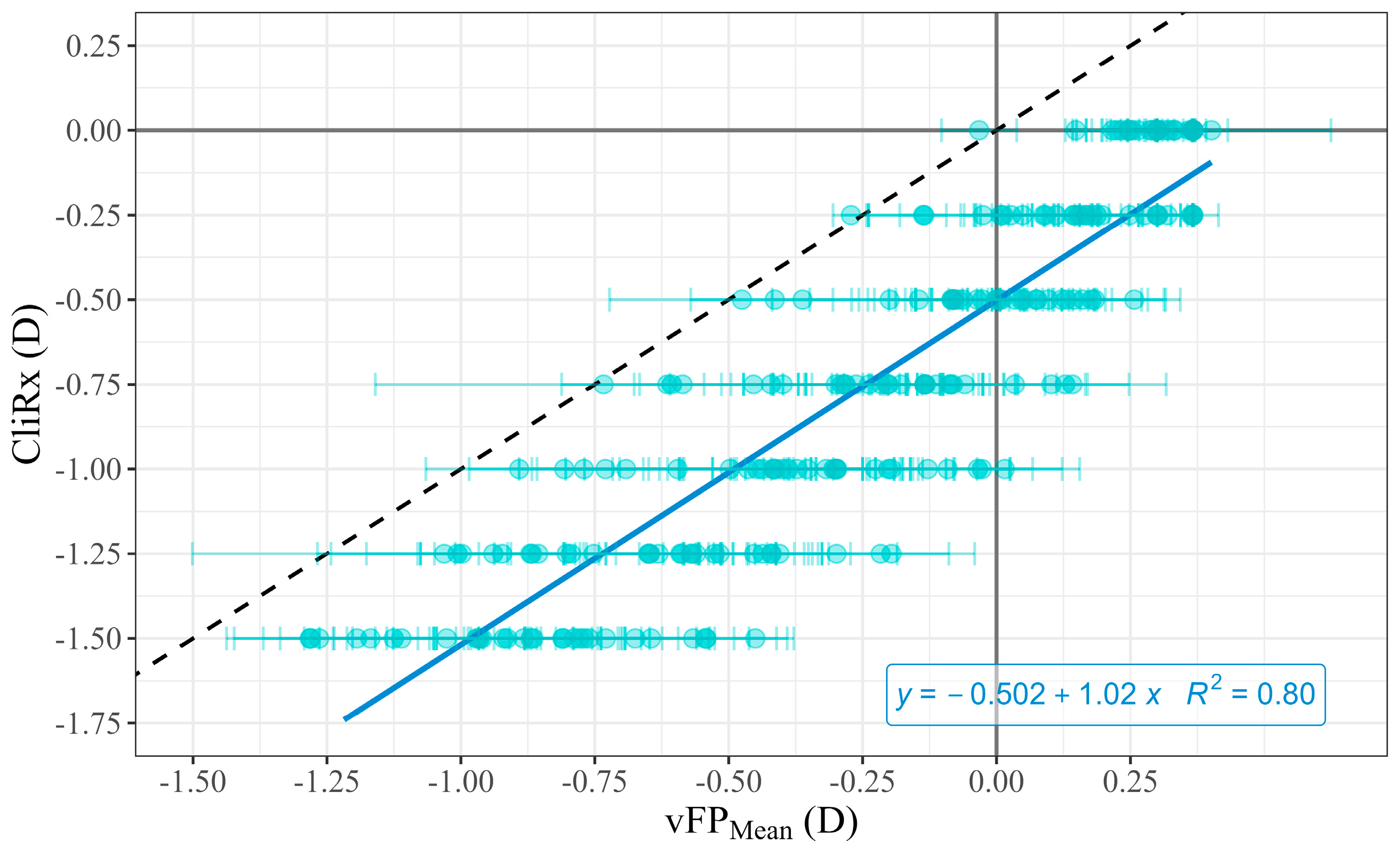
Figure 2 shows the reverse linear regression analysis between CliRx and
across subjects. The reverse linear fit between
and CliRx (Equation (2),
Figure 2) yielded the following coefficients, with their corresponding standard deviation:
Therefore, using these values in Equation (2), can be expressed in terms of .
The determination coefficient R2 of the correlation was 0.80 with a . This indicates a significant and strong correlation between and CliRx. According to (Equation (2)), the deduced DoF shows a nearly constant DoF of around 0.50 D.
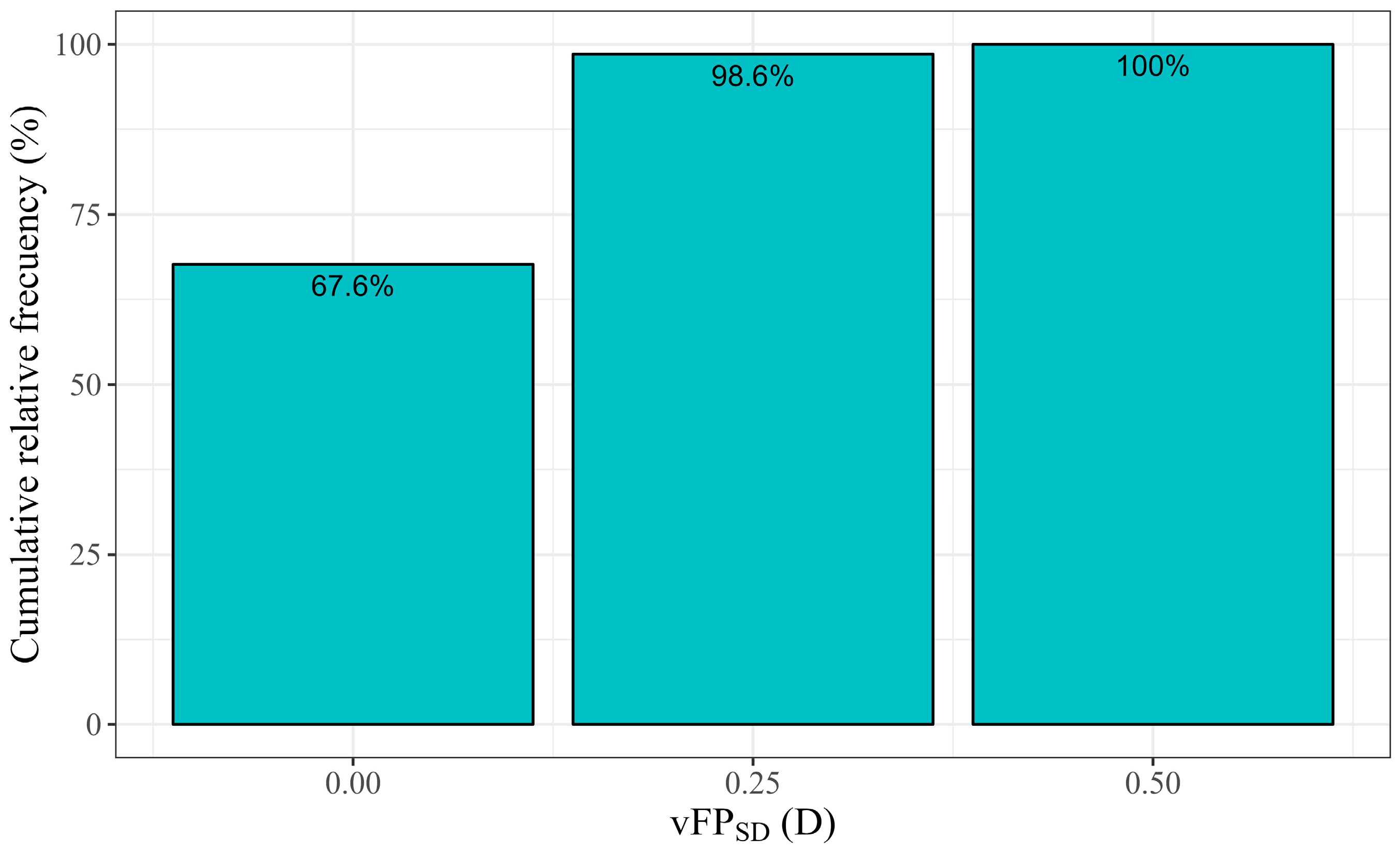
The mean intra-subject standard deviation (
) was 0.10 D. Its distribution is illustrated in
Figure 3 and was ≤0.25 D in 98.6% of the cases.
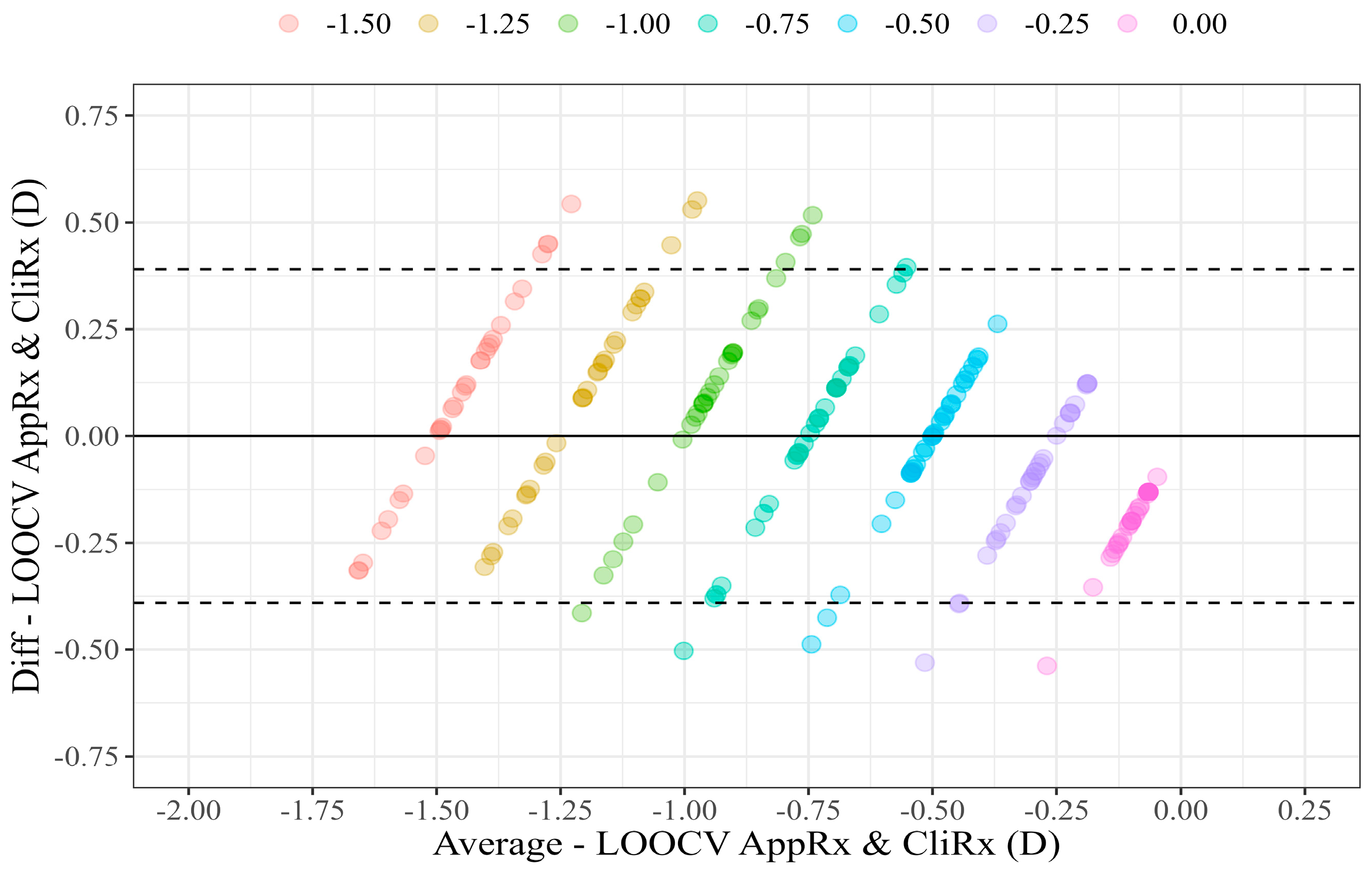
The LOOCV results are illustrated in the scatter plot (
Figure 4) and Bland–Altman plot (
Figure 5), comparing LOOCV AppRx estimates and CliRx.
The Bland–Altman analysis yielded an average AppRx and CliRx difference of 0.00 D, with an LoA of (−0.44 D, 0.44 D). The p-value of Student’s t-test for the null hypothesis where the mean difference is zero was 0.981, indicating no significant bias between LOOCV AppRx and CliRx.
The relative cumulative distribution of the absolute errors of LOOCV AppRx compared to CliRx is shown in
Figure 6. It indicates that 89.5% of the measures had an error ≤ 0.25 D, and all errors were ≤0.50 D.
4. Discussion
Subjective spherical refraction (AppRx) was measured using a novel method based on a mobile app. This method uses blue on-screen stimuli, which maintain their spatial frequency due to face–device real-time distance measurement and stimuli rescaling.
A high correlation was found between clinical values (CliRx) and AppRx (
p < 0.0001), with a determination coefficient of R
2 = 0.80 (
Figure 2). Additionally, repeatability was found to be high: the average
was 0.104 D, and the standard deviation of the FP measured ≤0.25 D in 98.6% of the cases (
Figure 3).
The calibration process revealed that the app’s raw FP measurements underestimated myopia by approximately half a diopter ( = −0.502), with this gap being fairly constant ( = 1.017). This underestimation can be interpreted as a systematic DoF effect, although we may note that this is a reasonable hypothesis which should be confirmed. In this case, two factors could influence the DoF.
The first is the use of a stimulus set at 80% of the subject’s maximum resolvable spatial frequency (i.e., visual acuity). The remaining 20% margin may allow for some degree of defocus before the three lines become indistinguishable. As an approximation, for a subject with a clinical visual acuity of 0.0 LogMAR, 80% of their decimal acuity corresponds to about 0.1 LogMAR. According to a widely accepted rule of thumb in optometry, a defocus of 0.25 D is typically associated with a loss of 0.1 LogMAR of visual acuity [
30]. Therefore, using this reduced spatial frequency in the stimulus design could be associated with approximately 0.25 D of
DoF.
The second factor relates to the nature of the task performed by the subject—moving away from the device until the stimulus can no longer be resolved—which, as mentioned before, differs from the standard clinical procedure of reducing lens power until the smallest resolvable optotype (highest spatial frequency) can be identified [
29]. This “moving-away” task may introduce a bias, as subjects might continue to increase the distance beyond the exact FP, potentially resulting in a consistent underestimation of myopia.
After applying the LOOCV technique, Bland–Altman analysis showed that the mean difference between LOOCV AppRx and CliRx was 0.00 D (
p = 0.981), with an LoA of ±0.44 D (
Figure 5). In comparison, the previously reported LoA for clinical subjective refraction of spherical error typically ranges from ±0.70 D to ±0.77 D [
44,
45,
46], which is wider than those obtained in the present study. This suggests that, within our controlled experiment conditions, the method evaluated here demonstrates potentially higher precision than traditional clinical subjective refraction. However, several considerations must be made when interpreting this comparison. First, clinical refraction typically includes the assessment of sphere, cylinder, and axis, whereas the current method focuses solely on the spherical component. Second, the evaluation range in this study was limited to a narrow span of refractive error (0.00 D to −1.50 D). This may contribute to higher precision within this specific range but limits the generalizability of the results to broader refractive errors. In contrast, the cited studies assessed the repeatability of clinical subjective refraction across a wider spectrum of refractive errors, which affects the direct comparability and replicability of the conclusion that the studied method is more precise.
Regarding other mobile apps related to refraction, we can compare our results with those reported in previous studies. Luo et al. [
22] examined a subjective spherical refraction mobile app. They used the Eye XM Virtual Visit app to measure the spherical refractive error in 113 myopic subjects, although their LoA was higher, at ±1.63 D. In a later study with 34 subjects, the LoA for the spherical component was similar, at ±1.69 D. On the other hand, Tousignant et al. used the Netra auto-refractor to measure refractions in 36 subjects. They obtained a larger mean difference between the clinical refraction and the refraction with the accessory, of 0.53 D and an even larger LoA (±1.40 D) [
21]. Wisse et al. [
25] validated a web-based refraction tool in 200 eyes. In mild myopia cases (0.00 D, −3.00 D) the LoA values were (−0.94 D, 0.98 D), wider than those of the app evaluated in this study and wider than typical clinical standards. Remarkably, this same tool was evaluated in real-world data with thousands of eyes. However, in this case, the LoA values were found too wide to meet clinical standards, with LoA values of (−1.35 D, 1.37 D) in myopic subjects. In conclusion, none of the cited works achieved the LoA of the studied app or those of standard clinical refraction. Nonetheless, we may note that refraction-measuring ranges varied between studies, which could limit the generalizability of the comparisons.
Overall, this study may present some limitations. Only one device was used to perform the measurements. However, at least in terms of face-to-device distance measurement accuracy, this does not appear to be a significant issue. Previous studies using various smartphones, including iOS devices, have reported similar accuracy in measuring subject–device distance, typically with errors below 0.1 D [
36]. This may be expected since the calibration procedure is independent of the optics of the front camera of the device [
36]. Therefore, similar performance can be expected if other devices were used.
With regard to the stimulus used for FP measurements, the use of parallel lines oriented in a single direction restricts the method’s sensitivity to astigmatic changes, as the FP would change depending on the line orientation and refraction axis. Additionally, user discomfort at extended working distances (approximately 1.40 m) must be considered, particularly in the context of manual or voice-based control mechanisms. From an optical standpoint, neglecting DoF, a viewing distance of 3.00 m under blue-light conditions corresponds to a vergence of +0.37 D. Consequently, the current FP-based measurement method is not suitable for reliably detecting hyperopic refractive errors exceeding +0.37 D.
With regard to the sample size, it is relatively limited, and further investigations involving larger cohorts are warranted to clinically validate the proposed methodology. Follow-up studies are currently underway with expanded participant pools. It is also essential to emphasize that these results are applicable solely to healthy individuals with no known ocular or systemic conditions. Pathologies such as diabetic retinopathy or Kjer’s optic neuropathy have been documented to impair contrast sensitivity and chromatic discrimination thresholds, particularly under blue-light stimulation, potentially confounding the measurement outcomes [
47,
48]. A longitudinal study is needed to evaluate the app’s applicability in monitoring myopia progression, as well as its actual usability by children.
In conclusion, the proposed over-refraction methodology demonstrates high accuracy and precision, with limits of agreement below half a diopter. These results highlight its potential as a valuable tool for accurately monitoring refractive changes over time. Further research is required to validate these results across broader refractive ranges and clinical populations.