1. Introduction
The efforts to understand the workings of the Universe have led us to reconsider the concept of physical reality and the possibility of fully comprehending it [
1,
2]. So far, rather than intuition, mathematics has been the primary tool enabling us to approach this reality. Using this same tool, we have recently begun to harness the potential of quantum applications across various technologies, from computing to quantum communication. Paradoxically, we can exploit what “nobody understands” (quantum mechanics) [
3]. This uncertainty is exemplified in the quantum double-slit experiment [
4], where individual photons pass through the slits, maintaining an anti-correlation between the two possible paths for each slit, yet still producing interference. How, then, is it possible for photons to traverse the double slit without splitting and still create interference? Furthermore, experimentally, our choice to determine through which slit the photon passes affects the visibility of the interference pattern. The photon “knows” how to behave when it is observed.
This paradox suggests that observation influences the photon’s behavior, raising profound questions about the nature of reality, measurement, and the role of the observer in quantum mechanics. In this sense, by demonstrating interference, the double-slit experiment offers a glimpse into the bewildering world of quantum mechanics, where the distinction between wave and particle properties becomes increasingly blurred. The experiment challenges our classical understanding of particles as distinct entities. It compels us to reconsider the limits of what can be known, as well as how the act of measurement itself influences the fabric of reality.
A striking example of this perplexing phenomenon is Wheeler’s “delayed-choice gedanken experiment” (WDCGE), or “law without law” [
5], which further blurs the line between wave and particle behavior. In this experiment, individual photons directed into a Mach–Zehnder interferometer can behave as waves or particles, depending on the detection outcome at the interferometer’s output, particularly when the second beam splitter is unexpectedly removed. In such cases, the registered photons seem to “choose” to act as particles before exiting the interferometer or as waves when the second beam splitter remains in place. This experiment, performed in 2007 [
6] and 2015 [
7], provides experimental demonstrations of the delayed-choice gedanken experiment. However, the notion that quantum-state photons might possess privileged information or a mechanism enabling them to determine their behavior before the experiment concludes remains an unresolved mystery.
Perhaps part of this enigma stems from the way we perceive reality. Specifically, we may need to reconsider our concepts of wave and particle, which, at the quantum level, likely remain influenced by our classical interpretations.
In this article, we revisit Wheeler’s delayed-action “gedanken experiment” to show that, beyond complementarity and the choice to observe the complete information of a system, the two fundamental phenomena that transcend independently of the observer and the measurement process are the preparation of the system and the collapse of the state. We will note that in this class of experiments, the complementarity wave or particle behavior emerges depending on the conditions of the experiment, and that [
8] “it is a general feature of delayed-choice experiments that quantum effects can mimic an influence of future actions on past events. However, there is no paradox if the quantum state is viewed only as a
catalog of our knowledge”. However, the present article shows that the state conceived in the WDCGE after
must always be considered a wave state, with no possibility of being traced back to the past, like a particle.
4. Wheeler’s Delayed-Choice Gedanken Experiment with Two Polarization-Entangled Photons
Entangled states have been considered on the WDCGE to study delayed decoherence [
12] and the delayed-choice entanglement swapping in the context of quantum steering [
13].
Theoretically, we can use an entangled polarized pair of photons in ports 0 and 1 of the
, which could be generated through Spontaneous Parametric Down Conversion (SPDC).
The state at the output of
(beam splitter 1) will be
We can choose the output state as a function of the phase
. If
,
, while for
,
, where
and
Equation (
4) is a state of two photons entangled with the vacuum. Its behavior is not very different from that in Equation (
1) since if we placed a detector that identifies the number of photons, we would find that, with equal probability, two photons would be registered in detector
A or two photons in detector
B, with perfect anti-correlation. In such a case, the WDCGE experiment is valid in all its reasoning, with the only difference being that we will have two photons behave like two particles or one wave from two particles, depending on the presence of
, respectively. On the other hand, Equation (
5) is one of the Bell states.
can also be considered as two photons entangled with the vacuum, like Equation (
1), but the entangled orthogonal photon contributions mutually fill the vacuum states.
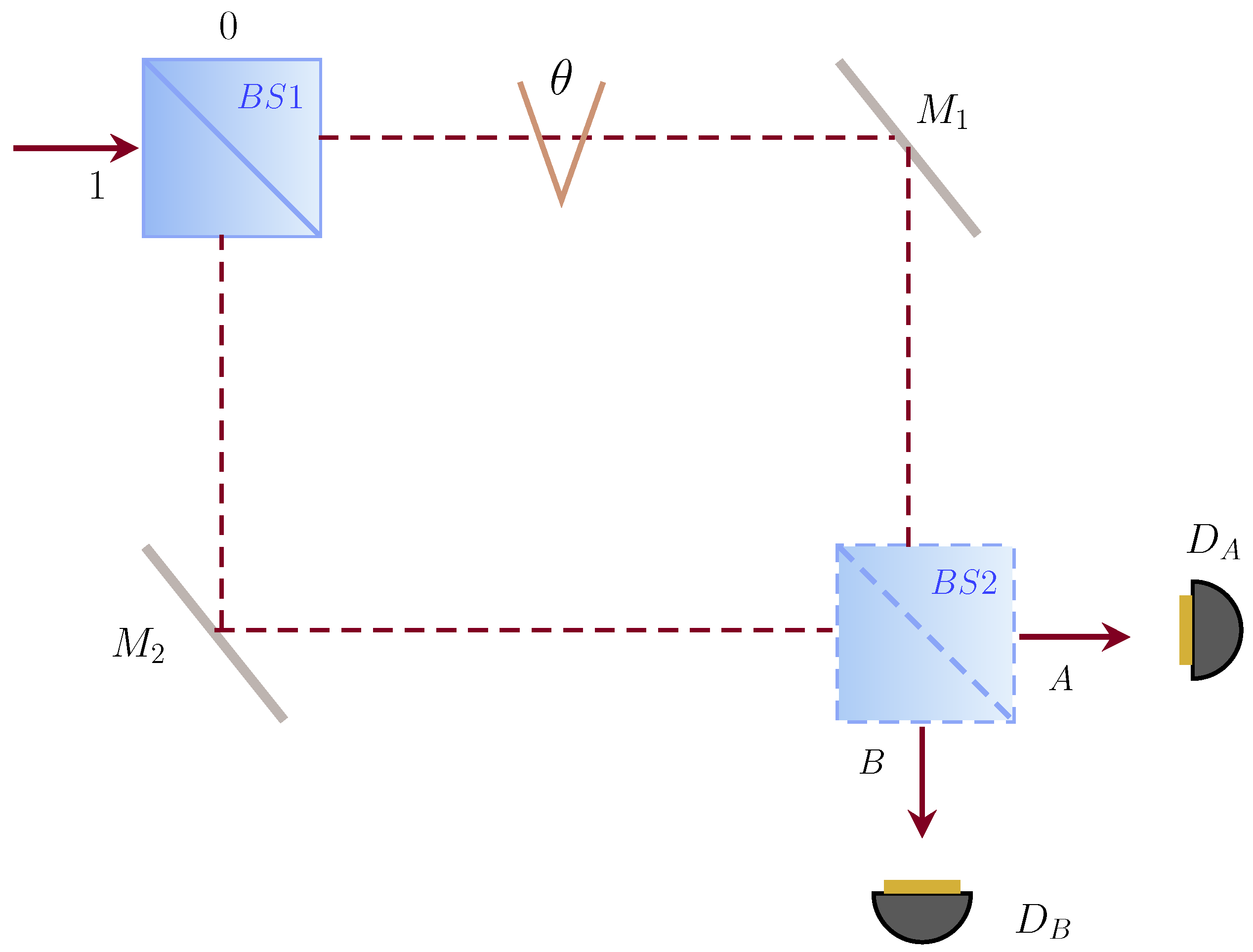
If we work, in this gedanken experiment, with the phase
, we can frame the WDCGE with two polarization-entangled photons. This completes the setup of the Mach–Zehnder interferometer as shown in
Figure 3, where we have placed a phase-shifting element
in one of the two arms of the interferometer, and where it is possible to omit the second beam splitter randomly. Assuming initially that
is in its position, the output state of the
can be written as
which we can rewrite as
with clear correspondence. Again, a few simple cases can be analyzed for
,
, while for
, then
. It is also interesting that, for
,
, and the case
with
.
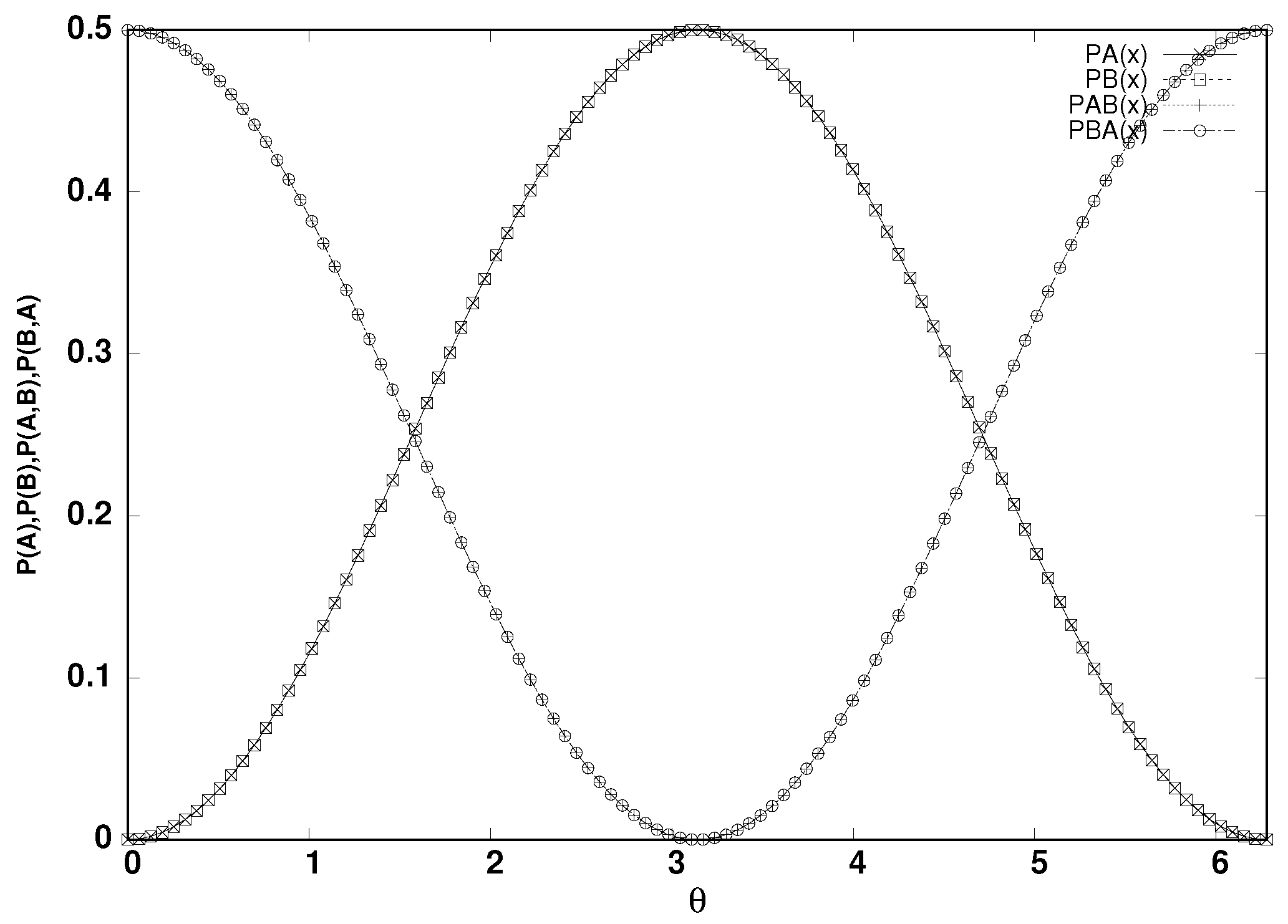
The four interference patterns are defined as follows:
The probabilities
and
refer to the probability that the two photons exit through port
A or port
B. The probabilities
and
refer to the photon states
and
, respectively. These joint probabilities produce signal coincidences in the
and
detectors. We can see four curves in the interference graph shown in
Figure 4. The interference pattern oscillates between the two entangled possibilities
and
. When photon coincidences can be detected, the probabilities are maximized at
.
On the other hand, if the second beam splitter is absent, then the interference specified by Equations (
8)–(
11) could not take place, and according to the WDCGE, we could say that the photons would be detected as individual particles in the detectors. However, when coincidences occur (
) in the
and
detectors, we then have two options:
In the case specified in Equation (
12), we can assert that the horizontally polarized photon reached the detector
traveling through the path
. In contrast, the vertically polarized photon reached the detector
and traveled through the path
.
The same can be stated for Equation (
13), in which the vertical photon was detected at
after traversing the path
. In contrast, the horizontally polarized photon detected at
traveled along the path
.
However, we can demonstrate that the two photons exhibit wave-like behavior in these implications of particle-like behavior, even in the absence of the second beam splitter. To illustrate this, we propose the placement of the polarizers
and
along the photon paths before they reach the detectors [
14]. The probability
indicates the probability of locating both photons at their respective detectors when the polarizers are oriented at the angles
and
. We can define the quantity
, which specifies the coincidence detection rate after the photons pass through the polarizers, oriented at diagonal angles relative to the orthogonal orientations. This quantity,
, will indicate the presence of wave-like states, because this value is sensitive to the presence of the quantum components of the photon that are in phase.
For these calculations, we define vertical and horizontal orientations on polarizers in agreement with the orientation of the SPDC polarization states, and let in order to have .
Calculating each of these probabilities, we found that
Thus,
Then, in the hypothetical case where the photon pairs from the state
travel independently through the
, that is,
ó
, the coincidences in the detectors have the following probability rules:
The difference between the two values—the wave behavior in Equation (
15) and particle behavior in Equation (
17)—arises from the absence of cross terms that generate quantum coherence and, ultimately, interference when we treat each component of the state
separately, as a classical mixture. Measurement
(Equation (
15)) without the second beam splitter
indicates that each of the two photons behaves as a wave, whereas the result
corresponds to the case of phase-shifted waves that make up the state
. This represents an important situation for discussion. The probabilities, Equation (
16), represent the two state options that can travel through the beam splitter, acting as individual particles, which means that, randomly and with probability
, the two particles travel through the trajectory
or through the trajectory
.
However, it is possible to project
onto two anti-correlated states. If we select the two angle combinations in the polarizers, (
,
) and (
,
), we obtain photon statistics without coincidences that can be reproduced by the two states:
which would imply that the state
can be understood as the coherent coupling of two waves.
The effect of incoherence will occur naturally when each pair, phase-shifted by the factor (), do not simultaneously pass through the polarizers with an orientation equivalent to D or A, as the vertical polarization wave could not coherently combine with the horizontal polarization wave, thus altering the probability of passing through the polarizers, as mentioned above.
However, it is possible to perform a hypothetical calculation of the EB quantity for a strict 2-photon state behaving like particles. Imagine that we send a two-photon state
(through the same input port 1) to a PBS. The output state will be
, where we have matched, in the case of the open IMZ,
and
. The coincidence probabilities of the photon pairs after crossing the polarizers in the mentioned orientations are
Hence, for a two-photon state behaving like particles, it has a value of
, as well as for a statistical mixture of incoherent waves. This is important to mention here, because if in the WDCGE experiment both phases are not well adjusted, i.e.,
and
, the wave-like behavior of the photons could be confused with particle behavior.
On the other hand, we can also calculate the
coefficient, including the second beam splitter.
In this way,
implies the evident wave behavior independent of the interferometer phase.
In conclusion, each photon behaves like a wave independently of the presence of BS2.
5. Entropy and Wave–Particle Duality
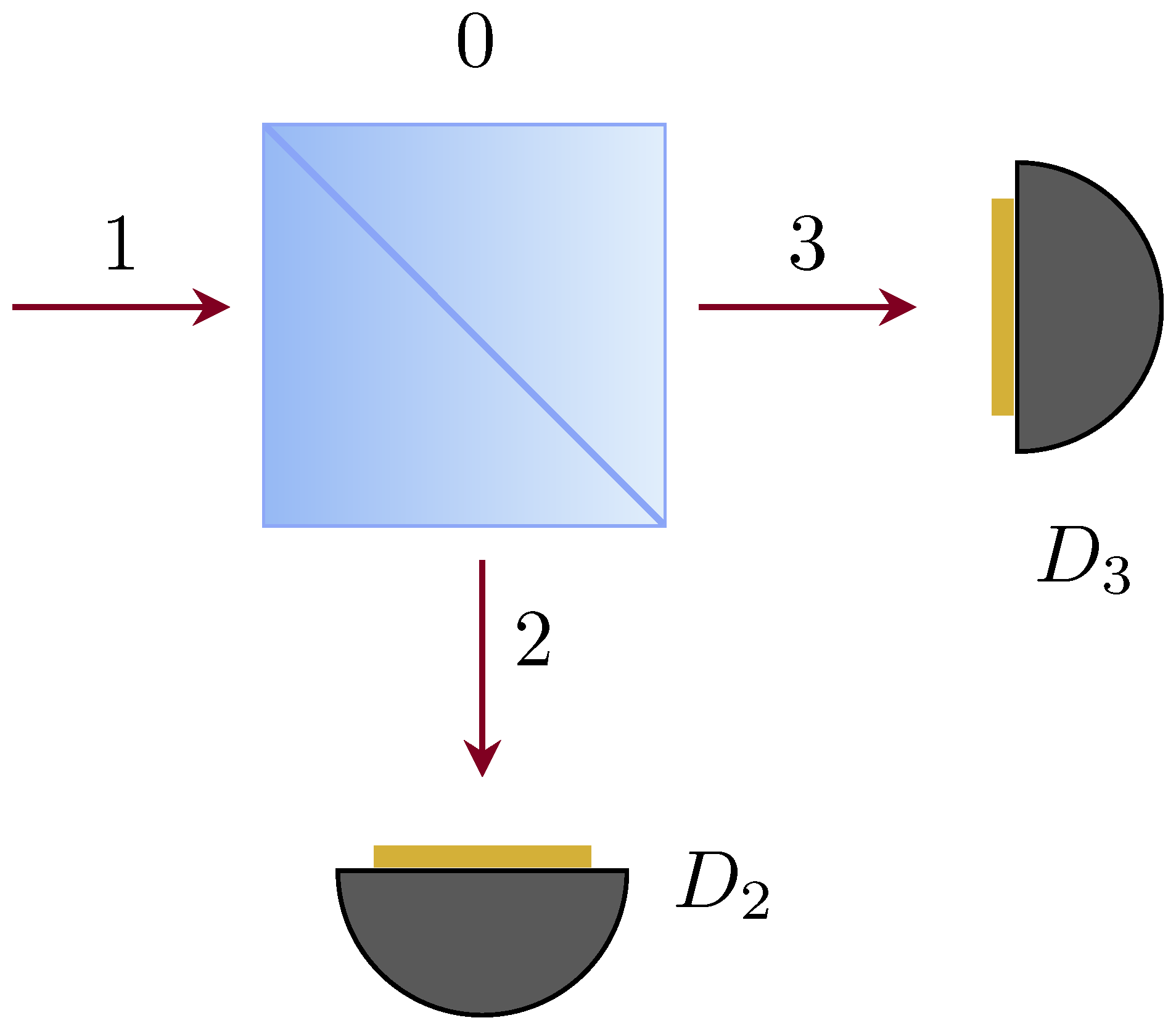
Counting the photons crossing a 50:50 beam splitter (see
Figure 1) allows us to calculate the probability of detecting a photon in the detector
depending on its state (
1), so
(
). With such probabilities, we can obtain the Shannon entropy:
The entropy associated with the wave (
1) has entropy
. This is clear because in the photon-counting experiment, the statistics are random in both detectors with anti-correlation. On the other hand, for the case in which it is possible to know precisely if each photon crosses the BS1 as transmitted or reflected, the trajectory is fixed and defined, so it is clear that
or
. In this case,
. Then, zero entropy is associated with particle behavior in this context [
15,
16]. By completing the MZI and measuring the photon count with the MZI open, obtaining the value
implies that the photons behave like a wave. With the MZI closed, there is no doubt about the wave behavior. In cases
, we have the superposition of wave states with particle states in different proportions depending on the transmission and reflection properties at the beam splitter. Now, in the case of the previous section, we can analyze the entropy of the entangled state in the two WDCGE cases.
With the state arriving at detectors, the photon-counting statistic in each detector, regardless of polarization, ensures in the context of the WDCGE that there is always a photon traveling through one of the arms of the interferometer. The probability of finding a photon in each detector is and , so the entropy associated with both counts will be and . However, let us consider polarization by placing the polarizers before the detectors, in the horizontal combination (), the probability of recording photons with horizontal polarization is and , so and . Similarly, with the polarizer orientation (), and , which implies that there are two in-phase waves with orthogonal polarization propagating towards the detectors.
For this case, the entropy at can be changed on demand and , precisely because each wave of defined polarization, H or V, can only interfere with each other.
In both cases, open or closed MZI, the photons behave as waves, in agreement with the previous section.