Advances in and Applications of Microwave Photonics in Radar Systems: A Review
Abstract
1. Introduction
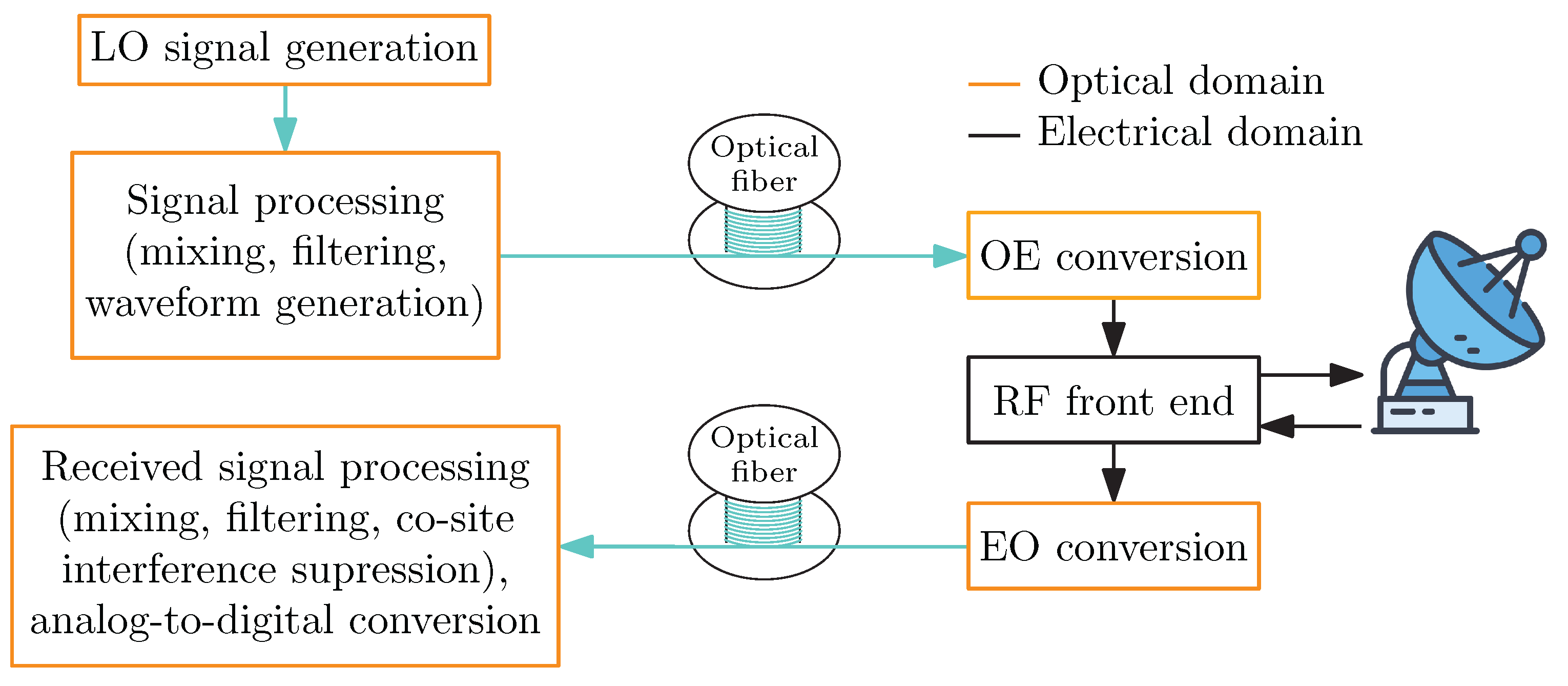
2. Microwave Photonics in Radar Systems
2.1. Signal Transmission
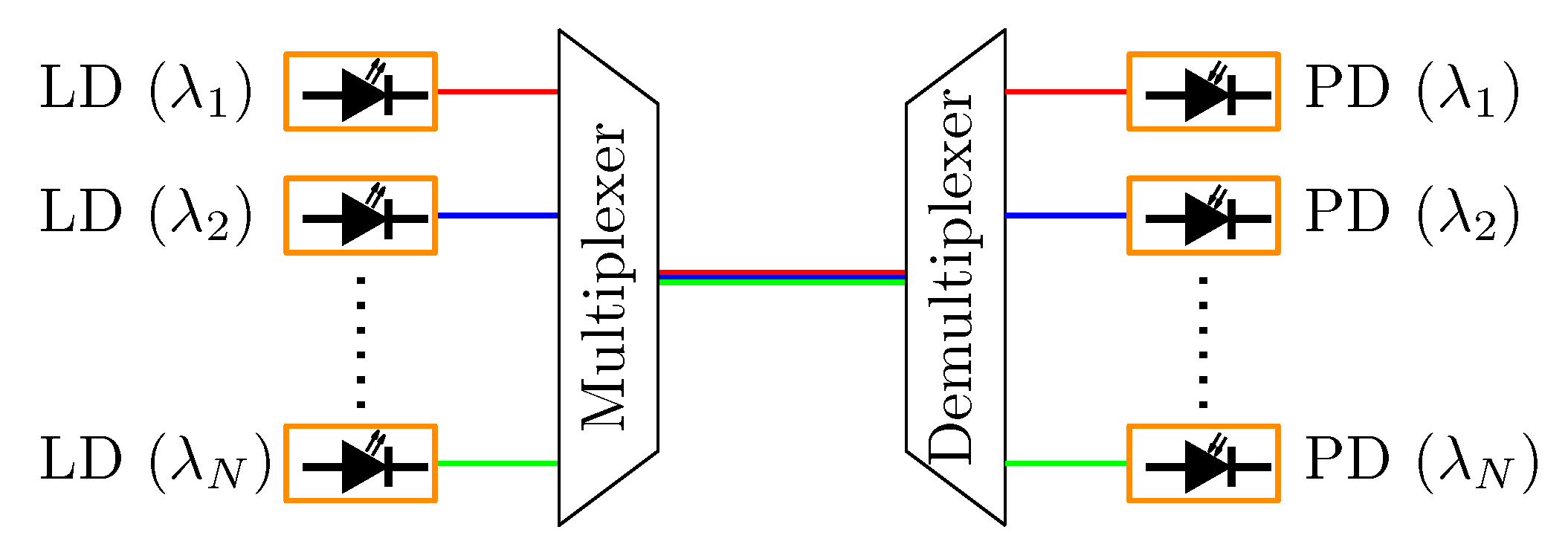
- WDM enables the simultaneous transmission of multiple optical signals by assigning each signal a unique wavelength, allowing them to travel through a single optical fiber without interference [29]. This technique takes advantage of the large bandwidth available in optical fibers to significantly increase data capacity. Figure 2 illustrates a typical WDM system, which employs a multiplexer on the transmitter side to combine the input signals and a demultiplexer on the receiver side to separate them. Widely adopted in telecommunications, WDM improves fiber data throughput without requiring any additional physical infrastructure.
- PDM is a technique that transmits two independent data channels on a single wavelength using orthogonal polarization states [30,31,32]. Although multiplexing two optical beams with orthogonal polarizations in an optical fiber is relatively straightforward, demultiplexing them can be challenging. This is due to the constant variation in the polarization states within single-mode fibers (SMFs), even though the polarizations remain orthogonal. Furthermore, polarization-maintaining fibers (PMFs) are limited to supporting a single polarization state, making them less suitable for PDM [33].
- SDM employs multiple, spatially separate channels within a single optical fiber to enhance data transmission [34]. In the literature, different configurations that use multicore fiber (MCF) or multimode fiber (MMF) have been proposed as promising candidates for next-generation multiplexing technologies in optical fiber communications [35].
2.2. Local Oscillator Generation
2.3. Radar Waveforming
2.4. Mixing
2.5. Filtering
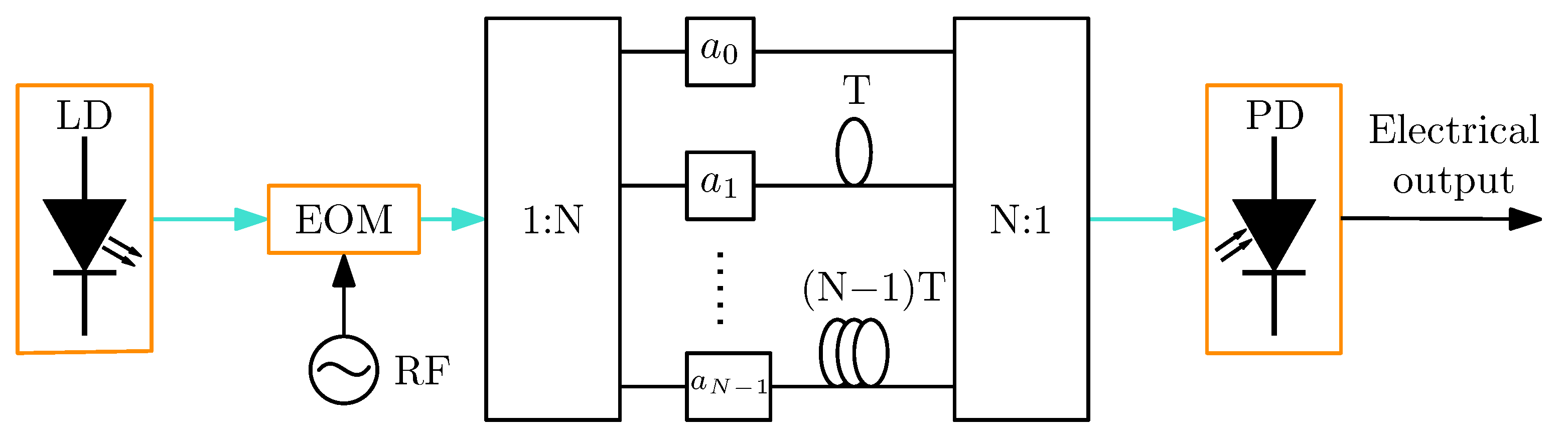
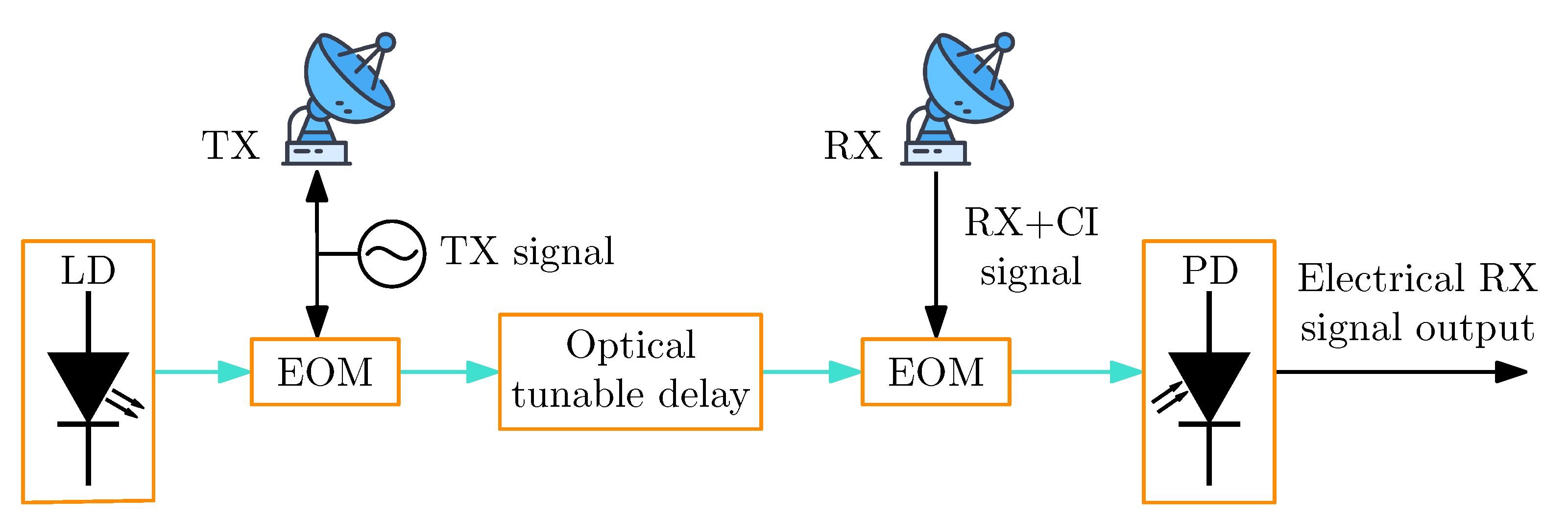
2.6. Co-Site Interference Suppression
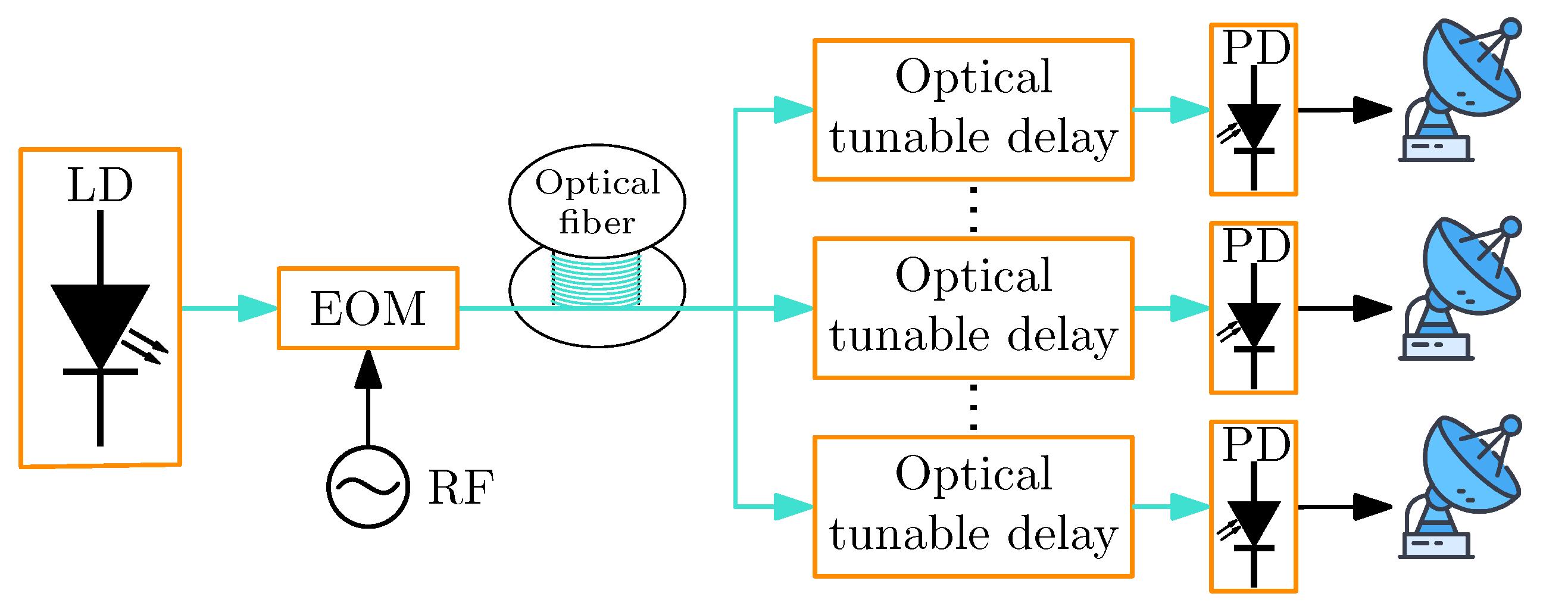
2.7. Optical Beamforming Networks
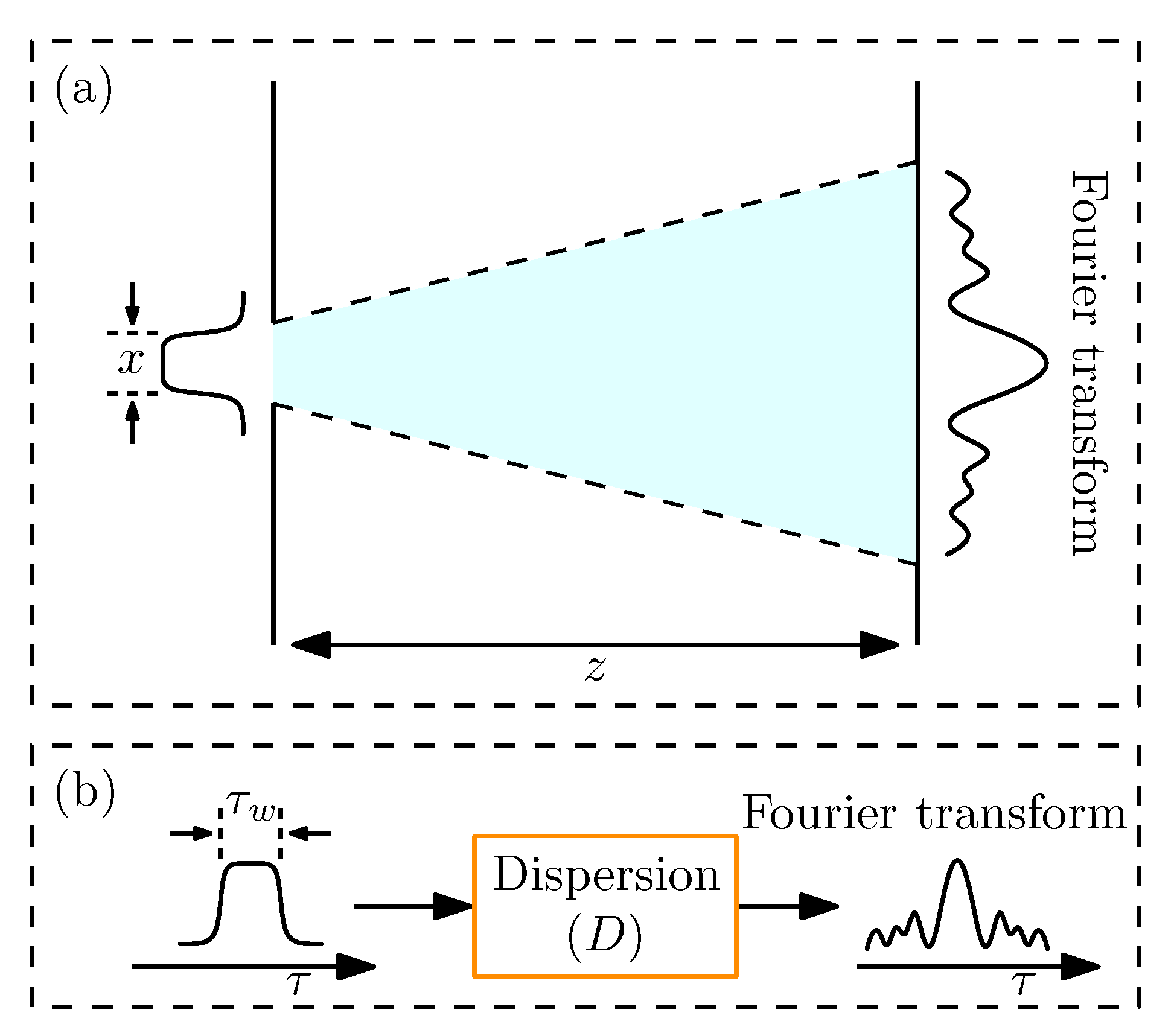
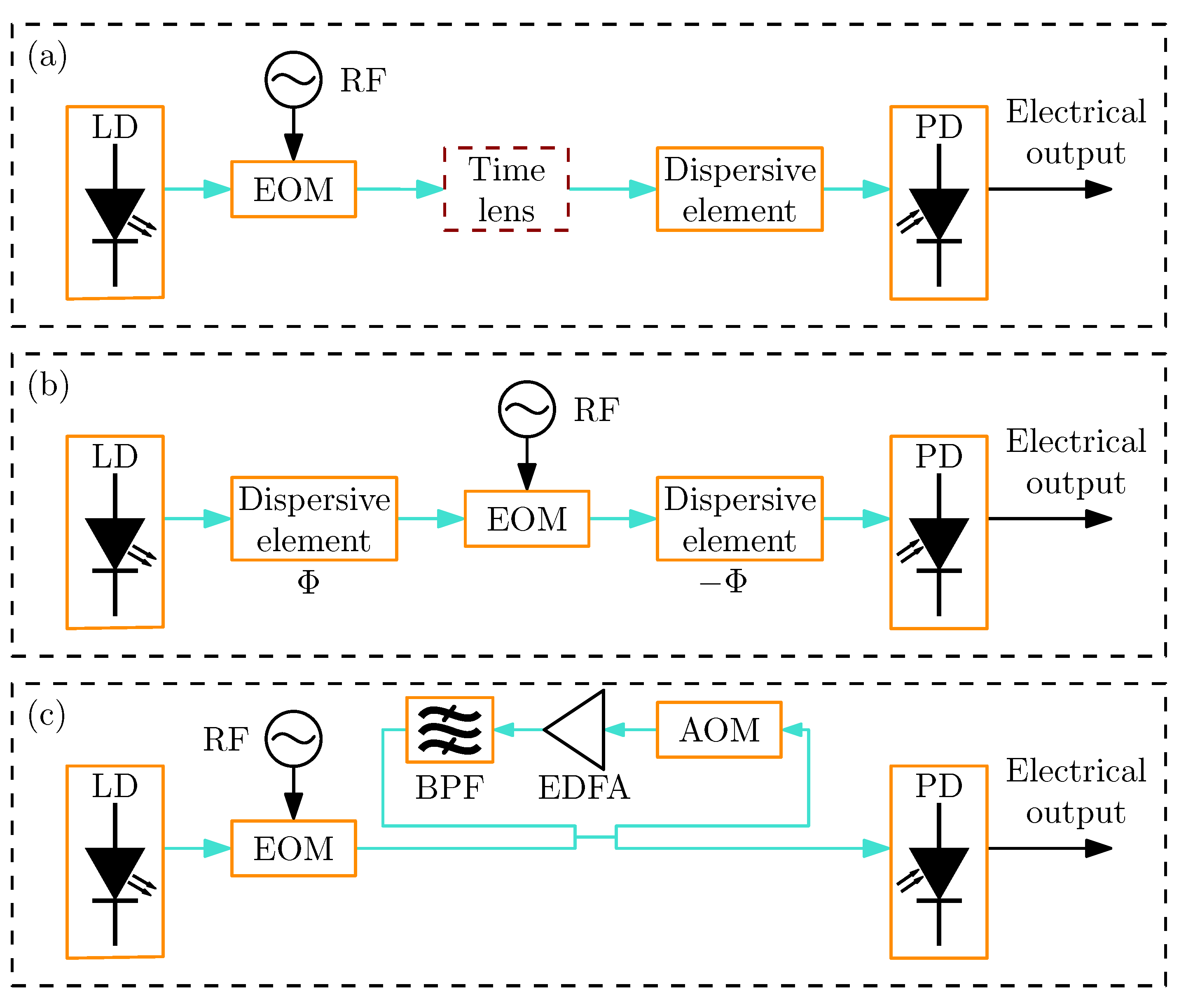
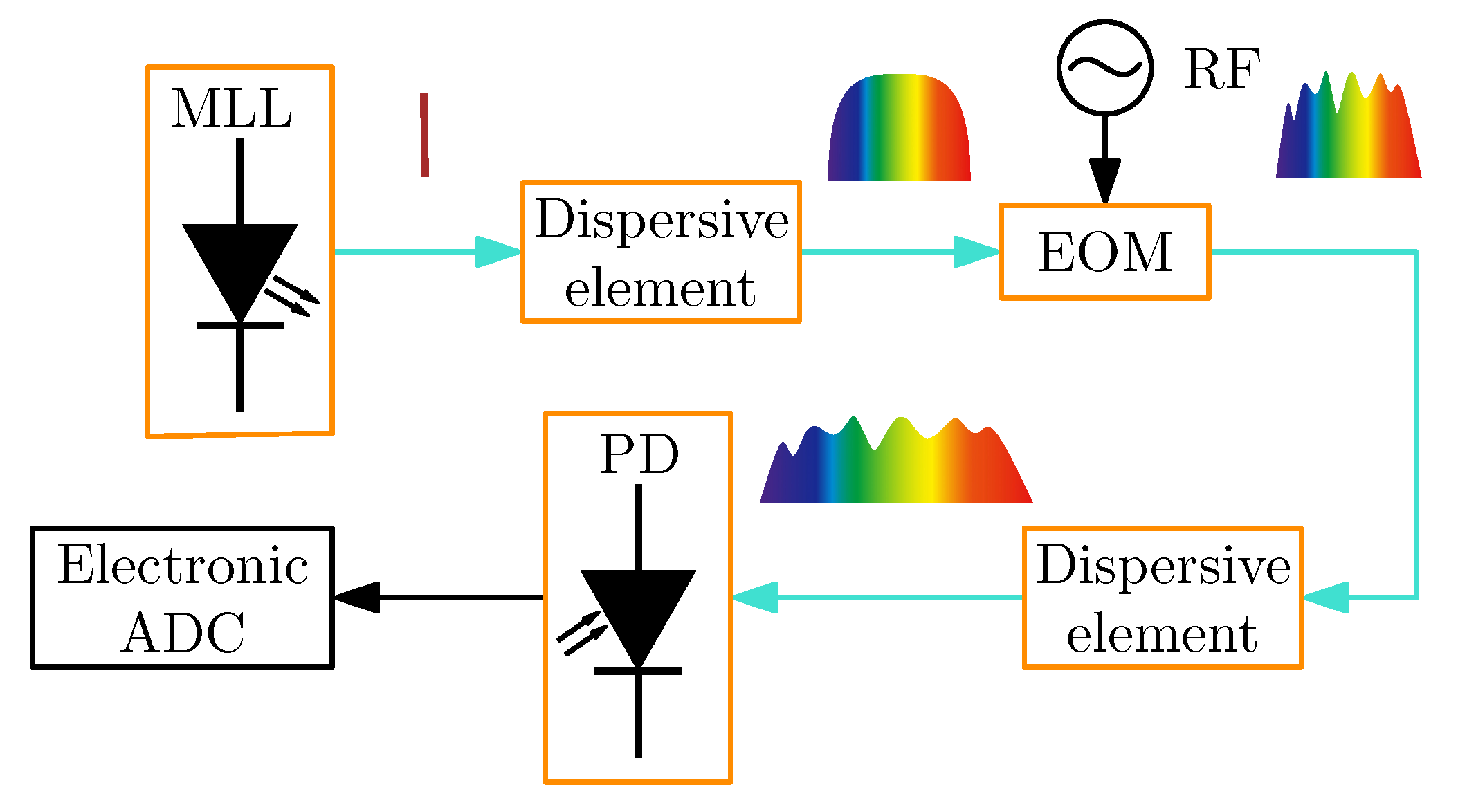
2.8. Optical Real-Time Fourier Transformation
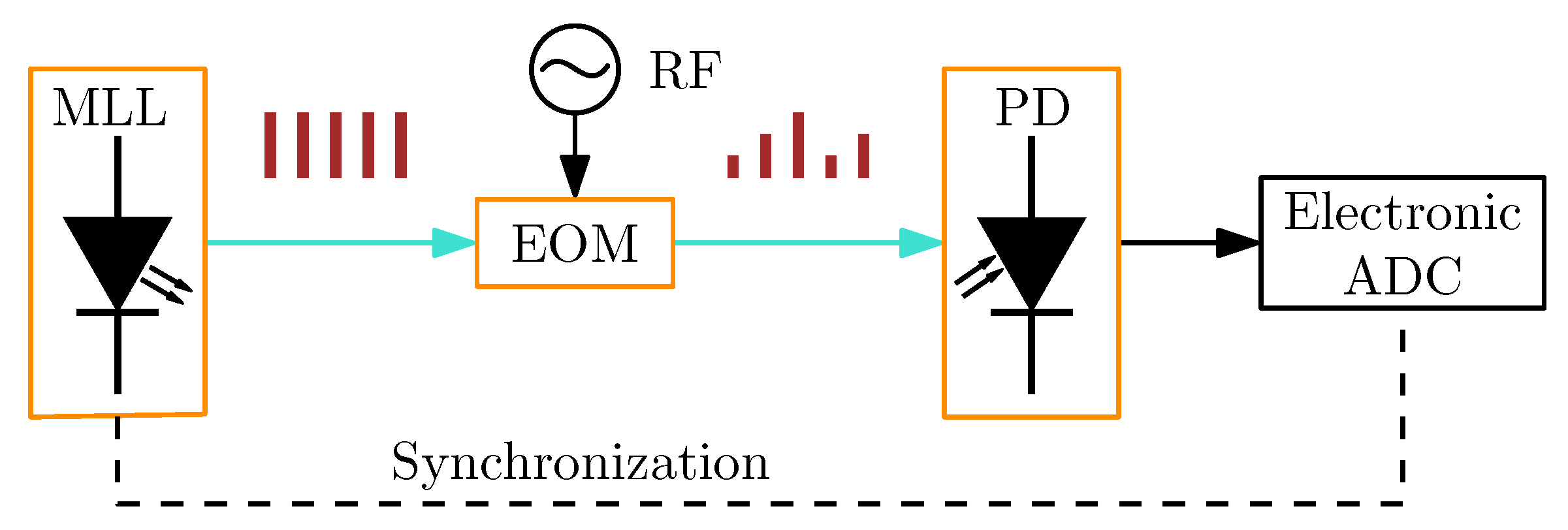
2.9. Analog-to-Digital Converters
3. In-Field Demonstrations of Microwave Photonic Radar
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Seeds, A.J.; Williams, K.J. Microwave Photonics. J. Light. Technol. 2006, 24, 4628–4641. [Google Scholar] [CrossRef]
- Zhang, F.; Sun, G.; Zhou, Y.; Gao, B.; Pan, S. Towards High-Resolution Imaging With Photonics-Based Time Division Multiplexing MIMO Radar. IEEE J. Sel. Top. Quantum Electron. 2022, 28, 6000310. [Google Scholar] [CrossRef]
- De, S.; Raj, A.A.B. A survey on photonics technologies for radar applications. J. Opt. 2023, 52, 90–119. [Google Scholar] [CrossRef]
- Blatnik, A.; Zmrzlak, L.; Batagelj, B. Radio Front-End for Frequency Agile Microwave Photonic Radars. Electronics 2024, 13. [Google Scholar] [CrossRef]
- Nagatsuma, T.; Horiguchi, S.; Minamikata, Y.; Yoshimizu, Y.; Hisatake, S.; Kuwano, S.; Yoshimoto, N.; Terada, J.; Takahashi, H. Terahertz wireless communications based on photonics technologies. Opt. Express 2013, 21, 23736–23747. [Google Scholar] [CrossRef]
- Pinna, S.; Melo, S.; Laghezza, F.; Scotti, F.; Lazzeri, E.; Scaffardi, M.; Ghelfi, P.; Bogoni, A. Photonics-Based Radar for Sub-mm Displacement Sensing. IEEE J. Sel. Top. Quantum Electron. 2017, 23, 168–175. [Google Scholar] [CrossRef]
- Serafino, G.; Scotti, F.; Lembo, L.; Hussain, B.; Porzi, C.; Malacarne, A.; Maresca, S.; Onori, D.; Ghelfi, P.; Bogoni, A. Toward a New Generation of Radar Systems Based on Microwave Photonic Technologies. J. Light. Technol. 2019, 37, 643–650. [Google Scholar] [CrossRef]
- Pan, S.; Zhang, Y. Microwave Photonic Radars. J. Light. Technol. 2020, 38, 5450–5484. [Google Scholar] [CrossRef]
- Zhang, F.; Guo, Q.; Pan, S. Photonics-based real-time ultra-high-range-resolution radar with broadband signal generation and processing. Sci. Rep. 2017, 7, 13848. [Google Scholar] [CrossRef]
- Harmuth, H.F. Frequency-Sharing and Spread-Spectrum Transmission with Large Relative Bandwidth. IEEE Trans. Electromagn. Compat. 1978, EMC-20, 232–239. [Google Scholar] [CrossRef]
- Waldschmidt, C.; Hasch, J.; Menzel, W. Automotive Radar — From First Efforts to Future Systems. IEEE J. Microwaves 2021, 1, 135–148. [Google Scholar] [CrossRef]
- Yi, L.; Li, Y.; Nagatsuma, T. Photonic Radar for 3D Imaging: From Millimeter to Terahertz Waves. IEEE J. Sel. Top. Quantum Electron. 2023, 29, 8500714. [Google Scholar] [CrossRef]
- Batra, A.; Barowski, J.; Damyanov, D.; Wiemeler, M.; Rolfes, I.; Schultze, T.; Balzer, J.C.; Göhringer, D.; Kaiser, T. Short-Range SAR Imaging From GHz to THz Waves. IEEE J. Microwaves 2021, 1, 574–585. [Google Scholar] [CrossRef]
- Yi, L.; Nishida, Y.; Sagisaka, T.; Kaname, R.; Mizuno, R.; Fujita, M.; Nagatsuma, T. Towards Practical Terahertz Imaging System With Compact Continuous Wave Transceiver. J. Light. Technol. 2021, 39, 7850–7861. [Google Scholar] [CrossRef]
- Tratnik, J.; Lemut, P.; Vidmar, M. Time-transfer and synchronization equipment for high-performance particle accelerators. J. Microelectron. Electron. Components Mater. 2012, 42, 115–122. [Google Scholar]
- Koala, R.A.S.D.; Fujita, M.; Nagatsuma, T. Nanophotonics-inspired all-silicon waveguide platforms for terahertz integrated systems. Nanophotonics 2022, 11, 1741–1759. [Google Scholar] [CrossRef]
- Strömbeck, F.; Yan, Y.; Zirath, H. A Beyond 100-Gbps Polymer Microwave Fiber Communication Link at D-Band. IEEE Trans. Circuits Syst. I Regul. Pap. 2023, 70, 3017–3028. [Google Scholar] [CrossRef]
- Samarasekera, A.C.J.; Fernández, S.L.; Feger, R.; Hüttner, R.; Gruson, F.; Krainer, S.; Stelzer, A. Distributed Radar Network with Polymer Microwave Fiber (PMF) Based Synchronization. In Proceedings of the 2024 IEEE Topical Conference on Wireless Sensors and Sensor Networks (WiSNeT), San Antonio, TX, USA, 21–24 January 2024; pp. 1–4. [Google Scholar] [CrossRef]
- Reynaert, P.; Dens, K.; D’heer, C.; Simic, D.; Vaes, J.; Philippe, B.; Ooms, S. Polymer Microwave Fiber: A New Communication Concept That Blends Wireless, Wireline and Optical Communication. In Proceedings of the 2019 26th IEEE International Conference on Electronics, Circuits and Systems (ICECS), Genoa, Italy, 27–29 November 2019; pp. 755–758. [Google Scholar] [CrossRef]
- Dragonja, U.; Tratnik, J.; Batagelj, B. Use of copper-coated fiber as a tunable optical time-delay line in precise timing systems. Opt. Quantum Electron. 2013, 45, 1229–1235. [Google Scholar] [CrossRef]
- Podbregar, L.; Dragonja, U.; Krč, J.; Czermann, M.; Blatnik, A.; Batagelj, B. Sensitivity of radio frequency phase stabilization system to temperature changes in a fiber optic link. In Proceedings of the 2024 7th International Balkan Conference on Communications and Networking (BalkanCom), Ljubljana, Slovenia, 3–6 June 2024; pp. 143–147. [Google Scholar] [CrossRef]
- Wang, K.; Wei, W.; Wang, D.; Wang, P.; Xie, W.; Dong, Y. Distributed receiving system with local digitization and combination for SNR enhancement. Opt. Express 2023, 31, 1014–1024. [Google Scholar] [CrossRef]
- Hu, C.; Luo, B.; Bai, W.; Pan, W.; Yan, L.; Zou, X. Stable Radio Frequency Transmission of Single Optical Source Over Fiber Based on Passive Phase Compensation. IEEE Photonics J. 2021, 13, 7200607. [Google Scholar] [CrossRef]
- Tratnik, J.; Dragonja, U.; Batagelj, B. Multi-purpose constant-delay optical link. In Proceedings of the 2014 European Frequency and Time Forum (EFTF), Neuchatel, Switzerland, 23–26 June 2014; pp. 333–335. [Google Scholar] [CrossRef]
- Ben-Amram, A.; Stern, Y.; London, Y.; Antman, Y.; Zadok, A. Stable closed-loop fiber-optic delay of arbitrary radio-frequency waveforms. Opt. Express 2015, 23, 28244–28257. [Google Scholar] [CrossRef]
- Sun, S.; Petropulu, A.P.; Poor, H.V. MIMO Radar for Advanced Driver-Assistance Systems and Autonomous Driving: Advantages and Challenges. IEEE Signal Process. Mag. 2020, 37, 98–117. [Google Scholar] [CrossRef]
- Kruse, S.; Gudyriev, S.; Schwabe, T.; Kneuper, P.; Kurz, H.G.; Scheytt, J.C. Silicon Photonic Radar Transmitter IC for mm-Wave Large Aperture MIMO Radar Using Optical Clock Distribution. IEEE Microw. Wirel. Components Lett. 2021, 31, 783–786. [Google Scholar] [CrossRef]
- Kruse, S.; Gudyriev, S.; Kneuper, P.; Schwabe, T.; Meinecke, M.M.; Kurz, H.G.; Scheytt, J.C. Silicon Photonic Radar Receiver IC for mm-Wave Large Aperture MIMO Radar Using Optical Clock Distribution. IEEE Microw. Wirel. Components Lett. 2022, 32, 1447–1450. [Google Scholar] [CrossRef]
- Ishio, H.; Minowa, J.; Nosu, K. Review and status of wavelength-division-multiplexing technology and its application. J. Light. Technol. 1984, 2, 448–463. [Google Scholar] [CrossRef]
- Cvijetic, N.; Qian, D.; Yu, J.; Huang, Y.K.; Wang, T. Polarization-Multiplexed Optical Wireless Transmission With Coherent Detection. J. Light. Technol. 2010, 28, 1218–1227. [Google Scholar] [CrossRef]
- Kikuchi, K. Performance analyses of polarization demultiplexing based on constant-modulus algorithm in digital coherent optical receivers. Opt. Express 2011, 19, 9868–9880. [Google Scholar] [CrossRef]
- Chen, Z.Y.; Yan, L.S.; Pan, Y.; Jiang, L.; Yi, A.L.; Pan, W.; Luo, B. Use of polarization freedom beyond polarization-division multiplexing to support high-speed and spectral-efficient data transmission. Light. Sci. Appl. 2017, 6, e16207. [Google Scholar] [CrossRef]
- Badraoui, N.; Berceli, T. Enhancing capacity of optical links using polarization multiplexing. Opt. Quantum Electron. 2019, 51, 310. [Google Scholar] [CrossRef]
- Puttnam, B.J.; Rademacher, G.; Luís, R.S. Space-division multiplexing for optical fiber communications. Optica 2021, 8, 1186–1203. [Google Scholar] [CrossRef]
- Majumder, S.P.; Hossain, A. Performance analysis of an SDM-WDM multicore optical fiber link. Opt. Contin. 2023, 2, 600–615. [Google Scholar] [CrossRef]
- Berdagué, S.; Facq, P. Mode division multiplexing in optical fibers. Appl. Opt. 1982, 21, 1950–1955. [Google Scholar] [CrossRef] [PubMed]
- Hanzawa, N.; Saitoh, K.; Sakamoto, T.; Matsui, T.; Tomita, S.; Koshiba, M. Demonstration of mode-division multiplexing transmission over 10 km two-mode fiber with mode coupler. In Proceedings of the 2011 Optical Fiber Communication Conference and Exposition and the National Fiber Optic Engineers Conference, Los Angeles, CA, USA, 6–10 March 2011; pp. 1–3. [Google Scholar]
- Ryf, R.; Randel, S.; Gnauck, A.H.; Bolle, C.; Sierra, A.; Mumtaz, S.; Esmaeelpour, M.; Burrows, E.C.; Essiambre, R.J.; Winzer, P.J.; et al. Mode-Division Multiplexing Over 96 km of Few-Mode Fiber Using Coherent 6 ×6 MIMO Processing. J. Light. Technol. 2012, 30, 521–531. [Google Scholar] [CrossRef]
- Sillard, P.; Bigot-Astruc, M.; Molin, D. Few-Mode Fibers for Mode-Division-Multiplexed Systems. J. Light. Technol. 2014, 32, 2824–2829. [Google Scholar] [CrossRef]
- Rademacher, G.; Puttnam, B.J.; Luís, R.S.; Sakaguchi, J.; Klaus, W.; Eriksson, T.A.; Awaji, Y.; Hayashi, T.; Nagashima, T.; Nakanishi, T.; et al. 10.66 Peta-Bit/s Transmission over a 38-Core-Three-Mode Fiber. In Proceedings of the 2020 Optical Fiber Communications Conference and Exhibition (OFC), San Diego, CA, USA, 8–12 March 2020; pp. 1–3. [Google Scholar]
- Maher, R.; Xu, T.; Galdino, L.; Sato, M.; Alvarado, A.; Shi, K.; Savory, S.J.; Thomsen, B.C.; Killey, R.I.; Bayvel, P. Spectrally Shaped DP-16QAM Super-Channel Transmission with Multi-Channel Digital Back-Propagation. Sci. Rep. 2015, 5, 8214. [Google Scholar] [CrossRef]
- Luo, L.W.; Ophir, N.; Chen, C.P.; Gabrielli, L.H.; Poitras, C.B.; Bergmen, K.; Lipson, M. WDM-compatible mode-division multiplexing on a silicon chip. Nat. Commun. 2014, 5, 3069. [Google Scholar] [CrossRef]
- Yao, J. Microwave Photonics: Photonic Generation of Microwave and Millimeter-wave Signals. Int. J. Microw. Opt. Technol. 2010, 5. [Google Scholar]
- Wei, J.; Zhang, S.; Kim, J.; Pan, S. Compact Phase Detector for Optical-Microwave Synchronization Using Polarization Modulation. J. Light. Technol. 2018, 36, 4267–4272. [Google Scholar] [CrossRef]
- Ponnampalam, L.; Fice, M.J.; Pozzi, F.; Renaud, C.C.; Rogers, D.C.; Lealman, I.F.; Moodie, D.G.; Cannard, P.J.; Lynch, C.; Johnston, L.; et al. Monolithically Integrated Photonic Heterodyne System. J. Light. Technol. 2011, 29, 2229–2234. [Google Scholar] [CrossRef]
- Steed, R.J.; Ponnampalam, L.; Fice, M.J.; Renaud, C.C.; Rogers, D.C.; Moodie, D.G.; Maxwell, G.D.; Lealman, I.F.; Robertson, M.J.; Pavlovic, L.; et al. Hybrid Integrated Optical Phase-Lock Loops for Photonic Terahertz Sources. IEEE J. Sel. Top. Quantum Electron. 2011, 17, 210–217. [Google Scholar] [CrossRef]
- Zhang, F.; Pan, S. Microwave photonic signal generation for radar applications. In Proceedings of the 2016 IEEE International Workshop on Electromagnetics: Applications and Student Innovation Competition (iWEM), Nanjing, China, 16–18 May 2016; pp. 1–3. [Google Scholar] [CrossRef]
- Zhou, W.; Blasche, G. Injection-locked dual opto-electronic oscillator with ultra-low phase noise and ultra-low spurious level. IEEE Trans. Microw. Theory Tech. 2005, 53, 929–933. [Google Scholar] [CrossRef]
- Hao, T.; Liu, Y.; Tang, J.; Cen, Q.; Li, W.; Zhu, N.; Dai, Y.; Capmany, J.; Yao, J.; Li, M. Recent advances in optoelectronic oscillators. Adv. Photonics 2020, 2, 044001. [Google Scholar] [CrossRef]
- Bogataj, L.; Vidmar, M.; Batagelj, B. A Feedback Control Loop for Frequency Stabilization in an Opto-Electronic Oscillator. J. Light. Technol. 2014, 32, 3690–3694. [Google Scholar] [CrossRef]
- Batagelj, B.; Bogataj, L.; Vidmar, M. Key properties and design issues for an opto-electronic oscillator. In Proceedings of the 2015 17th International Conference on Transparent Optical Networks (ICTON), Budapest, Hungary, 5–9 July 2015; pp. 1–4. [Google Scholar] [CrossRef]
- Bogataj, L.; Vidmar, M.; Batagelj, B. Improving the Side-mode Suppression Ratio and Reducing the Frequency Drift in an Opto-Electronic Oscillator With a Feedback Control Loop and Additional Phase Modulation. J. Light. Technol. 2016, 34, 885–890. [Google Scholar] [CrossRef]
- Bogataj, L.; Vidmar, M.; Batagelj, B. Opto-Electronic Oscillator With Quality Multiplier. IEEE Trans. Microw. Theory Tech. 2016, 64, 663–668. [Google Scholar] [CrossRef]
- Li, M.; Hao, T.; Yang, Y.; Shi, N.; Li, W. Recent advances in optoelectronic oscillators and quantum microwave photonics. In Proceedings of the 2021 International Topical Meeting on Microwave Photonics (MWP), Pisa, Italy, 15–17 November 2021; pp. 1–3. [Google Scholar] [CrossRef]
- Ilgaz, M.A.; Batagelj, B. Opto-Electronic Oscillators for Micro- and Millimeter Wave Signal Generation. Electronics 2021, 10, 857. [Google Scholar] [CrossRef]
- Fu, Z.; Ma, Y.; Zeng, Z.; Zhang, L.; Tian, H.; Lyu, W.; Zhang, Y.; Zhang, Z.; Zhang, S.; Li, H.; et al. Microwave local oscillator signal generation with low near-carrier phase noise based on cascaded optoelectronic oscillators. Opt. Laser Technol. 2025, 181, 111628. [Google Scholar] [CrossRef]
- Liu, Q.; Peng, J.; Yan, J. Optoelectronic Oscillators: Progress from Classical Designs to Integrated Systems. Photonics 2025, 12, 120. [Google Scholar] [CrossRef]
- Qi, G.; Yao, J.; Seregelyi, J.; Paquet, S.; Belisle, C. Generation and distribution of a wide-band continuously tunable millimeter-wave signal with an optical external modulation technique. IEEE Trans. Microw. Theory Tech. 2005, 53, 3090–3097. [Google Scholar] [CrossRef]
- Lavrič, A.; Batagelj, B. Phase Noise Measurement for Improving the Performance of High-Order Modulation Scheme Wireless Links. In Proceedings of the 2024 7th International Balkan Conference on Communications and Networking (BalkanCom), Ljubljana, Slovenia, 3–6 June 2024; pp. 148–152. [Google Scholar] [CrossRef]
- Stöhr, A.; Babiel, S.; Cannard, P.J.; Charbonnier, B.; van Dijk, F.; Fedderwitz, S.; Moodie, D.; Pavlovic, L.; Ponnampalam, L.; Renaud, C.C.; et al. Millimeter-Wave Photonic Components for Broadband Wireless Systems. IEEE Trans. Microw. Theory Tech. 2010, 58, 3071–3082. [Google Scholar] [CrossRef]
- Luo, H.; Yu, J.; Wang, J.; Ma, C.; Han, X.; Su, X.; Gao, Y.; Jia, S. Microwave Photonic Frequency Multiplier with Low Phase Noise Based on an Optoelectronic Oscillator. Photonics 2024, 11, 588. [Google Scholar] [CrossRef]
- Peng, M.Y.; Kalaydzhyan, A.; Kärtner, F.X. Balanced optical-microwave phase detector for sub-femtosecond optical-RF synchronization. Opt. Express 2014, 22, 27102–27111. [Google Scholar] [CrossRef] [PubMed]
- Hasanuzzaman, G.K.M.; Iezekiel, S.; Kanno, A. W-Band Optoelectronic Oscillator. IEEE Photonics Technol. Lett. 2020, 32, 771–774. [Google Scholar] [CrossRef]
- Luchinin, A.; Malygin, I. Optoelectronic Microwave Oscillator. Advantages and Disadvantages. Noise Sources in an OEO. In Proceedings of the 2024 IEEE Ural-Siberian Conference on Biomedical Engineering, Radioelectronics and Information Technology (USBEREIT), Yekaterinburg, Russia, 13–15 May 2024; pp. 333–337. [Google Scholar] [CrossRef]
- Kaba, M.; Li, H.W.; Daryoush, A.; Vilcot, J.P.; Decoster, D.; Chazelas, J.; Bouwmans, G.; Quiquempois, Y.; Deborgies, F. Improving thermal stability of opto-electronic oscillators. IEEE Microw. Mag. 2006, 7, 38–47. [Google Scholar] [CrossRef]
- Zhu, X.; Wei, W.; Xie, W.; Dong, Y. Long-Term Stable Optoelectronic Oscillator Based on Phase-Locked Loop. In Proceedings of the 2023 IEEE 7th International Symposium on Electromagnetic Compatibility (ISEMC), Hangzhou, China, 20–23 October 2023; pp. 1–3. [Google Scholar] [CrossRef]
- Eliyahu, D.; Sariri, K.; Kamran, A.; Tokhmakhian, M. Improving short and long term frequency stability of the opto-electronic oscillator. In Proceedings of the 2002 IEEE International Frequency Control Symposium and PDA Exhibition (Cat. No.02CH37234), New Orleans, LA, USA, 31 May 2002; pp. 580–583. [Google Scholar] [CrossRef]
- Wang, C.; Yao, J. Photonic Generation of Chirped Microwave Pulses Using Superimposed Chirped Fiber Bragg Gratings. IEEE Photonics Technol. Lett. 2008, 20, 882–884. [Google Scholar] [CrossRef]
- Li, M.; Shao, L.Y.; Albert, J.; Yao, J. Tilted Fiber Bragg Grating for Chirped Microwave Waveform Generation. IEEE Photonics Technol. Lett. 2011, 23, 314–316. [Google Scholar] [CrossRef]
- Rashidinejad, A.; Weiner, A.M. Photonic Radio-Frequency Arbitrary Waveform Generation With Maximal Time-Bandwidth Product Capability. J. Light. Technol. 2014, 32, 3383–3393. [Google Scholar] [CrossRef]
- Zhou, P.; Zhang, F.; Guo, Q.; Pan, S. Linearly chirped microwave waveform generation with large time-bandwidth product by optically injected semiconductor laser. Opt. Express 2016, 24, 18460–18467. [Google Scholar] [CrossRef]
- Zhou, P.; Zhang, F.; Guo, Q.; Li, S.; Pan, S. Reconfigurable Radar Waveform Generation Based on an Optically Injected Semiconductor Laser. IEEE J. Sel. Top. Quantum Electron. 2017, 23, 1801109. [Google Scholar] [CrossRef]
- Nakarmi, B.; Chen, H.; Ukaegbu, I.A.; Gaudel, B.; Nakarmi, U.; Muthaiyah, S.; Ng, A.; Wang, X.; Pan, S. Linear Frequency Modulated Photonics RADAR using Injection Locking in Semiconductor Laser. In Proceedings of the 2021 International Conference on Electronics, Communications and Information Technology (ICECIT), Khulna, Bangladesh, 14–16 September 2021; pp. 1–4. [Google Scholar] [CrossRef]
- Kumar, C.; Raghuwanshi, S.K.; Yadav, R.K. A review on photonic-assisted dual-chirp microwave waveform generation methods. Microw. Opt. Technol. Lett. 2024, 66, e34266. [Google Scholar] [CrossRef]
- Yao, Y.; Zhang, F.; Zhang, Y.; Ye, X.; Zhu, D.; Pan, S. Demonstration of Ultra-high-resolution Photonics-based Kaband Inverse Synthetic Aperture Radar Imaging. In Proceedings of the 2018 Optical Fiber Communications Conference and Exposition (OFC), San Diego, CA, USA, 11–15 March 2018; pp. 1–3. [Google Scholar]
- Guo, Q.; Zhang, F.; Zhou, P.; Pan, S. Dual-Band LFM Signal Generation by Optical Frequency Quadrupling and Polarization Multiplexing. IEEE Photonics Technol. Lett. 2017, 29, 1320–1323. [Google Scholar] [CrossRef]
- Zhang, F.; Gao, B.; Pan, S. Arbitrary waveform generation by a 4-bit photonic digital-to-analog converter with 3.49 effective number of bits. In Proceedings of the 2016 IEEE International Topical Meeting on Microwave Photonics (MWP), Long Beach, CA, USA, 31 October–3 November 2016; pp. 137–140. [Google Scholar] [CrossRef]
- Peng, S.; Li, S.; Xue, X.; Xiao, X.; Wu, D.; Zheng, X.; Zhou, B. High-resolution W-band ISAR imaging system utilizing a logic-operation-based photonic digital-to-analog converter. Opt. Express 2018, 26, 1978–1987. [Google Scholar] [CrossRef]
- Li, J.; Xue, X.; Zha, Y.; Wu, D.; Li, S.; Zheng, X. A Segmented Photonic Digital-to-analog Converter with a High Effective Number of Bits. In Proceedings of the 2019 International Topical Meeting on Microwave Photonics (MWP), Ottawa, ON, Canada, 7–10 October 2019; pp. 1–3. [Google Scholar] [CrossRef]
- García, S.; Ureña, M.; Gasulla, I. Photonic-Assisted Analog-to-Digital Conversion Based on a Dispersion-Diversity Multicore Fiber. IEEE J. Sel. Top. Quantum Electron. 2023, 29, 4300108. [Google Scholar] [CrossRef]
- Liu, Z.; Slavík, R. Optical Injection Locking: From Principle to Applications. J. Light. Technol. 2020, 38, 43–59. [Google Scholar] [CrossRef]
- Won, Y.S.; Kim, C.H.; Lee, S.G. Range Resolution Improvement of a 24 GHz ISM Band Pulse Radar—A Feasibility Study. IEEE Sens. J. 2015, 15, 7142–7149. [Google Scholar] [CrossRef]
- Vokić, N.; Milovančev, D. Photomixing Techniques for mm-Wave Carrier Generation. In Proceedings of the 2024 47th MIPRO ICT and Electronics Convention (MIPRO), Opatija, Croatia, 20–24 May 2024; pp. 1671–1676. [Google Scholar] [CrossRef]
- Minasian, R.A.; Chan, E.H.W.; Yi, X. Microwave photonic signal processing. Opt. Express 2013, 21, 22918–22936. [Google Scholar] [CrossRef] [PubMed]
- Zhou, Y.; Kong, J.; Zhang, F.; Pan, S. Microwave photonic I/Q mixer for wideband frequency downconversion with serial electro-optical modulations. Opt. Lett. 2024, 49, 65–68. [Google Scholar] [CrossRef]
- Tang, Z.; Li, Y.; Yao, J.; Pan, S. Photonics-Based Microwave Frequency Mixing: Methodology and Applications. Laser Photonics Rev. 2020, 14, 1800350. [Google Scholar] [CrossRef]
- Kittlaus, E.A.; Eliyahu, D.; Ganji, S.; Williams, S.; Matsko, A.B.; Cooper, K.B.; Forouhar, S. A low-noise photonic heterodyne synthesizer and its application to millimeter-wave radar. Nat. Commun. 2021, 12, 4397. [Google Scholar] [CrossRef]
- Yao, J. Microwave Photonics. J. Light. Technol. 2009, 27, 314–335. [Google Scholar] [CrossRef]
- Zhu, D.; Pan, S. Photonics-Based Microwave Image-Reject Mixer. Photonics 2018, 5, 6. [Google Scholar] [CrossRef]
- Capmany, J.; Mora, J.; Gasulla, I.; Sancho, J.; Lloret, J.; Sales, S. Microwave Photonic Signal Processing. J. Light. Technol. 2013, 31, 571–586. [Google Scholar] [CrossRef]
- Han, X.; Huo, B.; Shao, Y.; Wang, C.; Zhao, M. RF Self-Interference Cancellation Using Phase Modulation and Optical Sideband Filtering. IEEE Photonics Technol. Lett. 2017, 29, 917–920. [Google Scholar] [CrossRef]
- Chen, Y.; Pan, S. Photonics-Assisted Radio-Frequency Self-Interference Cancellation and Fiber Transmission Using a DP-QPSK modulator. In Proceedings of the 2018 International Topical Meeting on Microwave Photonics (MWP), Toulouse, France, 22–25 October 2018; pp. 1–4. [Google Scholar] [CrossRef]
- Zhou, Y.; Wang, L.; Liu, Y.; Yu, Y.; Zhang, X. Microwave Photonic Filters and Applications. Photonics 2023, 10, 1110. [Google Scholar] [CrossRef]
- Tao, Z.; Tao, Y.; Jin, M.; Qin, J.; Chen, R.; Shen, B.; Wu, Y.; Shu, H.; Yu, S.; Wang, X. Highly reconfigurable silicon integrated microwave photonic filter towards next-generation wireless communication. Photon. Res. 2023, 11, 682–694. [Google Scholar] [CrossRef]
- Porzi, C.; Serafino, G.; Velha, P.; Ghelfi, P.; Bogoni, A. Integrated SOI High-Order Phase-Shifted Bragg Grating for Microwave Photonics Signal Processing. J. Light. Technol. 2017, 35, 4479–4487. [Google Scholar] [CrossRef]
- Tu, Z.; Wen, A.; Li, X.; Zhang, H. A Photonic Pre-Distortion Technique for RF Self-Interference Cancellation. IEEE Photonics Technol. Lett. 2018, 30, 1297–1300. [Google Scholar] [CrossRef]
- Shi, N.; Song, Q.; Tang, J.; Li, W.; Zhu, N.; Li, M. A switchable self-interference cancellation system for dual-band IBFD system using a monolithic integrated DML array. Opt. Commun. 2019, 447, 55–60. [Google Scholar] [CrossRef]
- Wang, H.; Wen, A.; Men, Y.; Wang, Y. Photonics-Based Radar Jamming Signal Generation and Self-Interference Cancellation. J. Light. Technol. 2023, 41, 5922–5929. [Google Scholar] [CrossRef]
- Bonjour, R.; Singleton, M.; Leuchtmann, P.; Leuthold, J. Comparison of steering angle and bandwidth for various phased array antenna concepts. Opt. Commun. 2016, 373, 35–43, SI: Microwave photonics. [Google Scholar] [CrossRef]
- Abdalrazak, M.Q.; Majeed, A.H.; Abd-Alhameed, R.A. A Critical Examination of the Beam-Squinting Effect in Broadband Mobile Communication: Review Paper. Electronics 2023, 12, 400. [Google Scholar] [CrossRef]
- Cheng, Q.; Zheng, S.; Zhang, Q.; Ji, J.; Yu, H.; Zhang, X. An integrated optical beamforming network for two-dimensional phased array radar. Opt. Commun. 2021, 489, 126809. [Google Scholar] [CrossRef]
- Duan, F.; Guo, Y.; Gu, Z.; Yin, Y.; Wu, Y.; Chen, T. Optical Beamforming Networks for Millimeter-Wave Wireless Communications. Appl. Sci. 2023, 13, 8346. [Google Scholar] [CrossRef]
- Ritoša, P.; Batagelj, B.; Vidmar, M. Optically steerable antenna array for radio over fibre transmission. Electron. Lett. 2005, 41, 917–918. [Google Scholar] [CrossRef]
- Ritosa, P.; Vidmar, M. Remote optically controllable antenna array using a single optical fiber for RoF reception. Microw. Opt. Technol. Lett. 2007, 49, 1349–1353. [Google Scholar] [CrossRef]
- Shin, J.D.; Lee, B.S.; Kim, B.G. Optical true time-delay feeder for X-band phased array antennas composed of 2/spl times/2 optical MEMS switches and fiber delay lines. IEEE Photonics Technol. Lett. 2004, 16, 1364–1366. [Google Scholar] [CrossRef]
- Matthews, P.; Liu, P.L.; Medberry, J.; Franekl, M.; Esman, R. Demonstration of a wide-band fiber-optic nulling system for array antennas. IEEE Trans. Microw. Theory Tech. 1999, 47, 1327–1331. [Google Scholar] [CrossRef]
- Ye, X.; Zhang, F.; Pan, S. Compact optical true time delay beamformer for a 2D phased array antenna using tunable dispersive elements. Opt. Lett. 2016, 41, 3956–3959. [Google Scholar] [CrossRef]
- Luan, Y.; Yang, T.; Ren, J.; Li, R.; Zhang, Z. Broadband Beam-Scanning Phased Array Based on Microwave Photonics. Electronics 2024, 13, 1278. [Google Scholar] [CrossRef]
- Yi, X.; Li, L.; Huang, T.X.H.; Minasian, R.A. Programmable multiple true-time-delay elements based on a Fourier-domain optical processor. Opt. Lett. 2012, 37, 608–610. [Google Scholar] [CrossRef]
- Cardenas, J.; Foster, M.A.; Sherwood-Droz, N.; Poitras, C.B.; Lira, H.L.R.; Zhang, B.; Gaeta, A.L.; Khurgin, J.B.; Morton, P.; Lipson, M. Wide-bandwidth continuously tunable optical delay line using silicon microring resonators. Opt. Express 2010, 18, 26525–26534. [Google Scholar] [CrossRef]
- Hong, S.; Zhang, L.; Wang, Y.; Zhang, M.; Xie, Y.; Dai, D. Ultralow-loss compact silicon photonic waveguide spirals and delay lines. Photon. Res. 2022, 10, 1–7. [Google Scholar] [CrossRef]
- Hong, S.; Zhang, L.; Wu, J.; Peng, Y.; Lyu, L.; Hu, Y.; Xie, Y.; Dai, D. Multimode-enabled silicon photonic delay lines: Break the delay-density limit. Light Sci. Appl. 2015, 14, 145. [Google Scholar] [CrossRef] [PubMed]
- Jannson, T. Real-time Fourier transformation in dispersive optical fibers. Opt. Lett. 1983, 8, 232–234. [Google Scholar] [CrossRef] [PubMed]
- van Howe, J.; Xu, C. Ultrafast Optical Signal Processing Based Upon Space-Time Dualities. J. Light. Technol. 2006, 24, 2649. [Google Scholar] [CrossRef]
- Malacarne, A.; Park, Y.; Li, M.; LaRochelle, S.; Azaña, J. Real-time Fourier transformation of lightwave spectra and application in optical reflectometry. Opt. Express 2015, 23, 32516–32527. [Google Scholar] [CrossRef]
- Zheng, Y.; Li, J.; Dai, Y.; Yin, F.; Xu, K. Real-time Fourier transformation based on the bandwidth magnification of RF signals. Opt. Lett. 2018, 43, 194–197. [Google Scholar] [CrossRef]
- Li, J.; Fu, S.; Xie, X.; Xiang, M.; Dai, Y.; Yin, F.; Qin, Y. Low-Latency Short-Time Fourier Transform of Microwave Photonics Processing. J. Light. Technol. 2023, 41, 6149–6156. [Google Scholar] [CrossRef]
- Wang, C. Dispersive Fourier Transformation for Versatile Microwave Photonics Applications. Photonics 2014, 1, 586–612. [Google Scholar] [CrossRef]
- Akca, B.I. Design of a compact and ultrahigh-resolution Fourier-transform spectrometer. Opt. Express 2017, 25, 1487–1494. [Google Scholar] [CrossRef]
- Souza, M.C.M.M.; Grieco, A.; Frateschi, N.C.; Fainman, Y. Fourier transform spectrometer on silicon with thermo-optic non-linearity and dispersion correction. Nat. Commun. 2018, 9, 665. [Google Scholar] [CrossRef]
- Li, A.; Yao, C.; Xia, J.; Wang, H.; Cheng, Q.; Penty, R.; Fainman, Y.; Pan, S. Advances in cost-effective integrated spectrometers. Light Sci .Appl. 2022, 11, 174. [Google Scholar] [CrossRef] [PubMed]
- Salem, R.; Foster, M.A.; Gaeta, A.L. Application of space–time duality to ultrahigh-speed optical signal processing. Adv. Opt. Photon. 2013, 5, 274–317. [Google Scholar] [CrossRef]
- Yang, D.; Kumar, S. Realization of optical OFDM using time lenses and its comparison with optical OFDM using FFT. Opt. Express 2009, 17, 17214–17226. [Google Scholar] [CrossRef] [PubMed]
- Li, M.; Wang, C.; Li, W.; Yao, J. An Unbalanced Temporal Pulse-Shaping System for Chirped Microwave Waveform Generation. IEEE Trans. Microw. Theory Tech. 2010, 58, 2968–2975. [Google Scholar] [CrossRef]
- de Chatellus, H.G.; Cortés, L.R.; Azaña, J. Optical real-time Fourier transformation with kilohertz resolutions. Optica 2016, 3, 1–8. [Google Scholar] [CrossRef]
- Valley, G.C. Photonic analog-to-digital converters. Opt. Express 2007, 15, 1955–1982. [Google Scholar] [CrossRef] [PubMed]
- Masnad, M.M.; Safaee, S.M.R.; Najeeb, N.; Mojaver, K.R.; Fouda, M.; Peinke, E.; Liboiron-Ladouceur, O. Scalable Photonic Digital-to-Analog Converters. Photonics 2024, 11, 112. [Google Scholar] [CrossRef]
- Han, Y.; Guo, Y.; Gao, B.; Ma, C.; Zhang, R.; Zhang, H. Generation, optimization, and application of ultrashort femtosecond pulse in mode-locked fiber lasers. Prog. Quantum Electron. 2020, 71, 100264. [Google Scholar] [CrossRef]
- Laghezza, F.; Scotti, F.; Ghelfi, P.; Bogoni, A.; Pinna, S. Jitter-limited photonic analog-to-digital converter with 7 effective bits for wideband radar applications. In Proceedings of the 2013 IEEE Radar Conference (RadarCon13), Ottawa, ON, Canada, 29 April–3 May 2013; pp. 1–5. [Google Scholar] [CrossRef]
- Ghelfi, P.; Laghezza, F.; Scotti, F.; Serafino, G.; Capria, A.; Pinna, S.; Onori, D.; Porzi, C.; Scaffardi, M.; Malacarne, A.; et al. A fully photonics-based coherent radar system. Nature 2014, 507, 341–345. [Google Scholar] [CrossRef]
- Fard, A.M.; Gupta, S.; Jalali, B. Photonic time-stretch digitizer and its extension to real-time spectroscopy and imaging. Laser Photonics Rev. 2013, 7, 207–263. [Google Scholar] [CrossRef]
- Zou, W.; Qian, N.; Qin, R.; Wang, J.; Xu, S.; Zou, X.; Zhou, D. Integrated Photonic Analog-to-Digital Converter and Its Applications. In Proceedings of the 2024 International Topical Meeting on Microwave Photonics (MWP), Pisa, Italy, 17–20 September 2024; pp. 1–4. [Google Scholar] [CrossRef]
- Fang, D.; Zazzi, A.; Müller, J.; Drayss, D.; Füllner, C.; Marin-Palomo, P.; Tabatabaei Mashayekh, A.; Dipta Das, A.; Weizel, M.; Gudyriev, S.; et al. Optical Arbitrary Waveform Measurement (OAWM) Using Silicon Photonic Slicing Filters. J. Light. Technol. 2022, 40, 1705–1717. [Google Scholar] [CrossRef]
- Fang, D.; Drayss, D.; Chen, Y.; Lauermann, M.; Peng, H.; Lihachev, G.; Quint, A.; Valenziano, L.; Randel, S.; Zwick, T.; et al. Spectrally Sliced Optical Arbitrary Waveform Measurement (OAWM) Using a Photonic Multi-Chip Receiver Assembly. In Proceedings of the 2024 Optical Fiber Communications Conference and Exhibition (OFC), San Diego, CA, USA, 24–28 March 2024; pp. 1–3. [Google Scholar]
- Li, Z.; Wang, X.; Zhang, Y.; Shang, C.; Lyu, W.; Lyu, Y.; Zeng, C.; Zhang, Z.; Zhang, S.; Li, H.; et al. Photonic sampling analog-to-digital conversion based on time and wavelength interleaved ultra-short optical pulse train generated by using monolithic integrated LNOI intensity and phase modulator. Opt. Express 2022, 30, 29611–29620. [Google Scholar] [CrossRef] [PubMed]
- Wang, X.; Zhou, G.; Guo, Y.; Lu, L.; Nisar, M.S.; Chen, J.; Zhou, L. Integrated High-Repetition-Rate Optical Sampling Chip Exploiting Wavelength and Mode Multiplexing. J. Light. Technol. 2021, 39, 5548–5557. [Google Scholar] [CrossRef]
- Lembo, L.; Maresca, S.; Serafino, G.; Scotti, F.; Amato, F.; Ghelfi, P.; Bogoni, A. In-Field Demonstration of a Photonic Coherent MIMO Distributed Radar Network. In Proceedings of the 2019 IEEE Radar Conference (RadarConf), Boston, MA, USA, 22–26 April 2019; pp. 1–6. [Google Scholar] [CrossRef]
- Scotti, F.; Laghezza, F.; Serafino, G.; Pinna, S.; Onori, D.; Ghelfi, P.; Bogoni, A. In-Field Experiments of the First Photonics-Based Software-Defined Coherent Radar. J. Light. Technol. 2014, 32, 3365–3372. [Google Scholar] [CrossRef]
- Zhou, Y.; Zhang, F.; Kong, J.; Wang, Y.; Li, J.; Chen, K.; Sun, G.; He, Y.; Pan, S. Field Trial of Cluster Target Detection by Broadband Microwave Photonic MIMO Radar. IEEE J. Microwaves 2025, 5, 631–639. [Google Scholar] [CrossRef]



Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Podbregar, L.; Batagelj, B.; Blatnik, A.; Lavrič, A. Advances in and Applications of Microwave Photonics in Radar Systems: A Review. Photonics 2025, 12, 529. https://doi.org/10.3390/photonics12060529
Podbregar L, Batagelj B, Blatnik A, Lavrič A. Advances in and Applications of Microwave Photonics in Radar Systems: A Review. Photonics. 2025; 12(6):529. https://doi.org/10.3390/photonics12060529
Chicago/Turabian StylePodbregar, Luka, Boštjan Batagelj, Aljaž Blatnik, and Andrej Lavrič. 2025. "Advances in and Applications of Microwave Photonics in Radar Systems: A Review" Photonics 12, no. 6: 529. https://doi.org/10.3390/photonics12060529
APA StylePodbregar, L., Batagelj, B., Blatnik, A., & Lavrič, A. (2025). Advances in and Applications of Microwave Photonics in Radar Systems: A Review. Photonics, 12(6), 529. https://doi.org/10.3390/photonics12060529





