Design and Simulation of Optical Waveguide Digital Adjustable Delay Lines Based on Optical Switches and Archimedean Spiral Structures
Abstract
1. Introduction
2. Theoretical Analysis
2.1. Optical True Time Delay
2.2. Time Delay Principle in Optical Waveguides
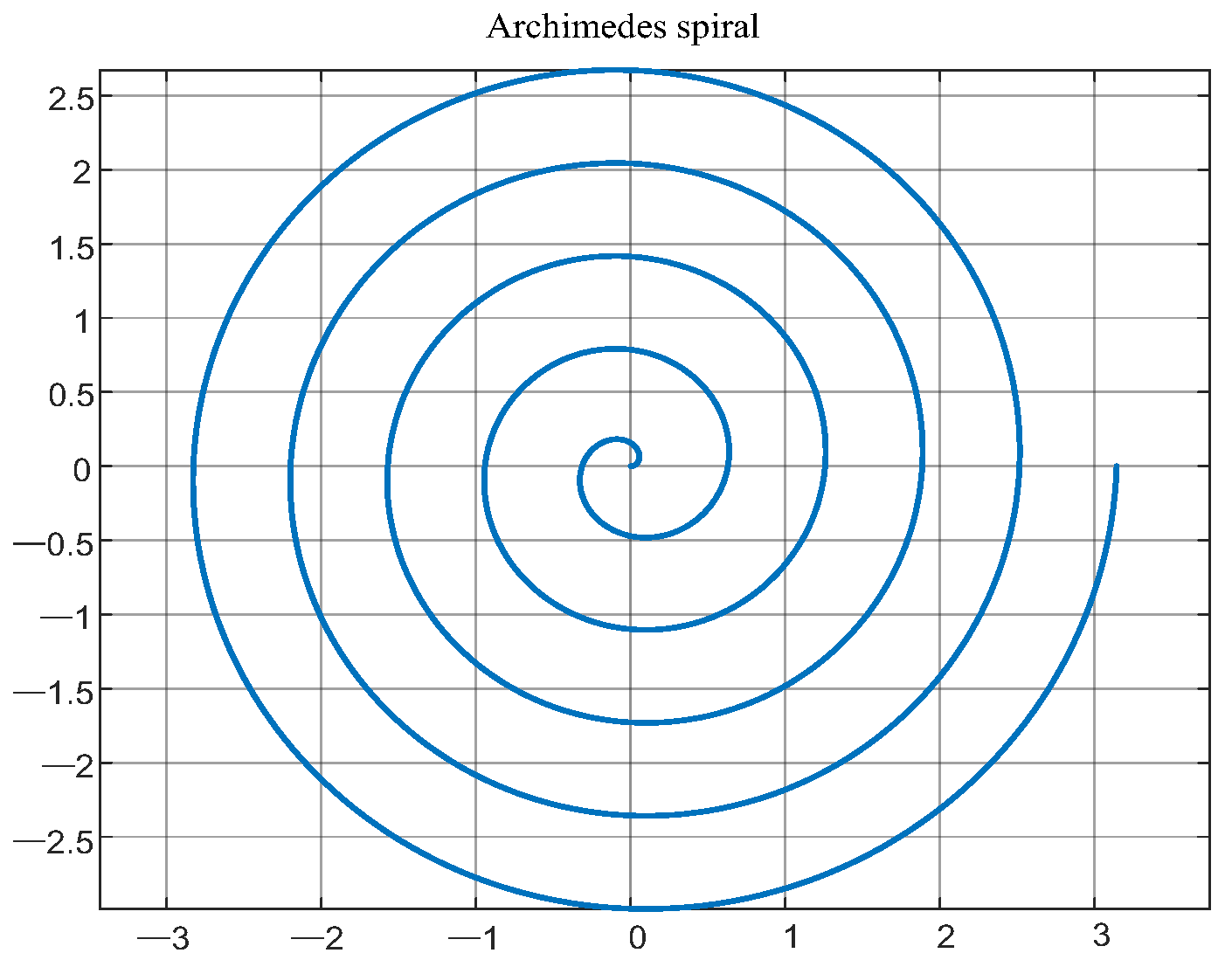
2.3. Basic Principle of Archimedes’ Spiral Optical Waveguide
2.4. Digital Tunable Technology Based on Optical Switch
3. Design and Simulation of Optical Waveguide Digital Adjustable Delay Lines Based on Optical Switches and Archimedean Spiral Structures
3.1. Design Idea of Optical True Delay Line
3.2. Specific Design
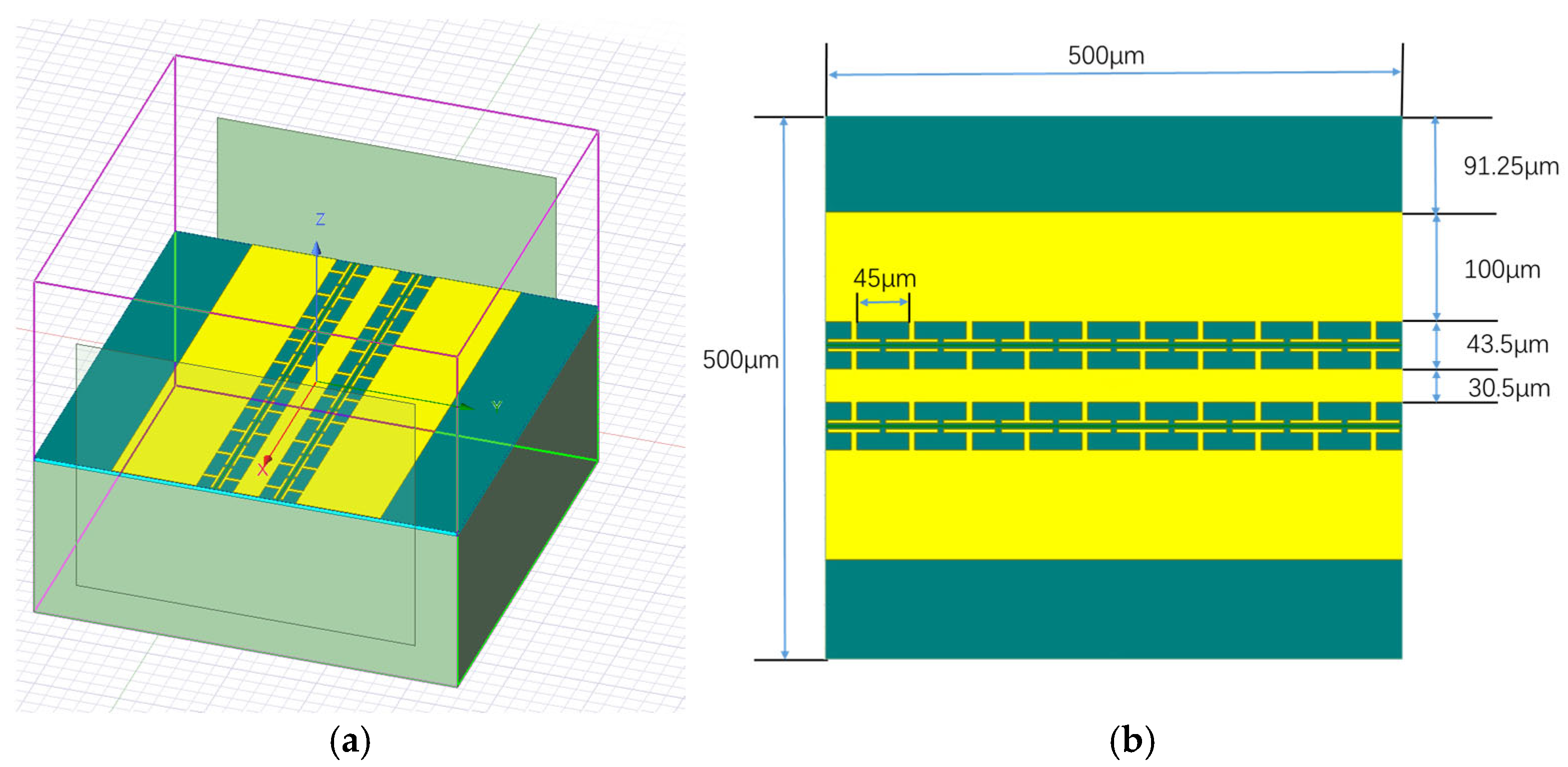
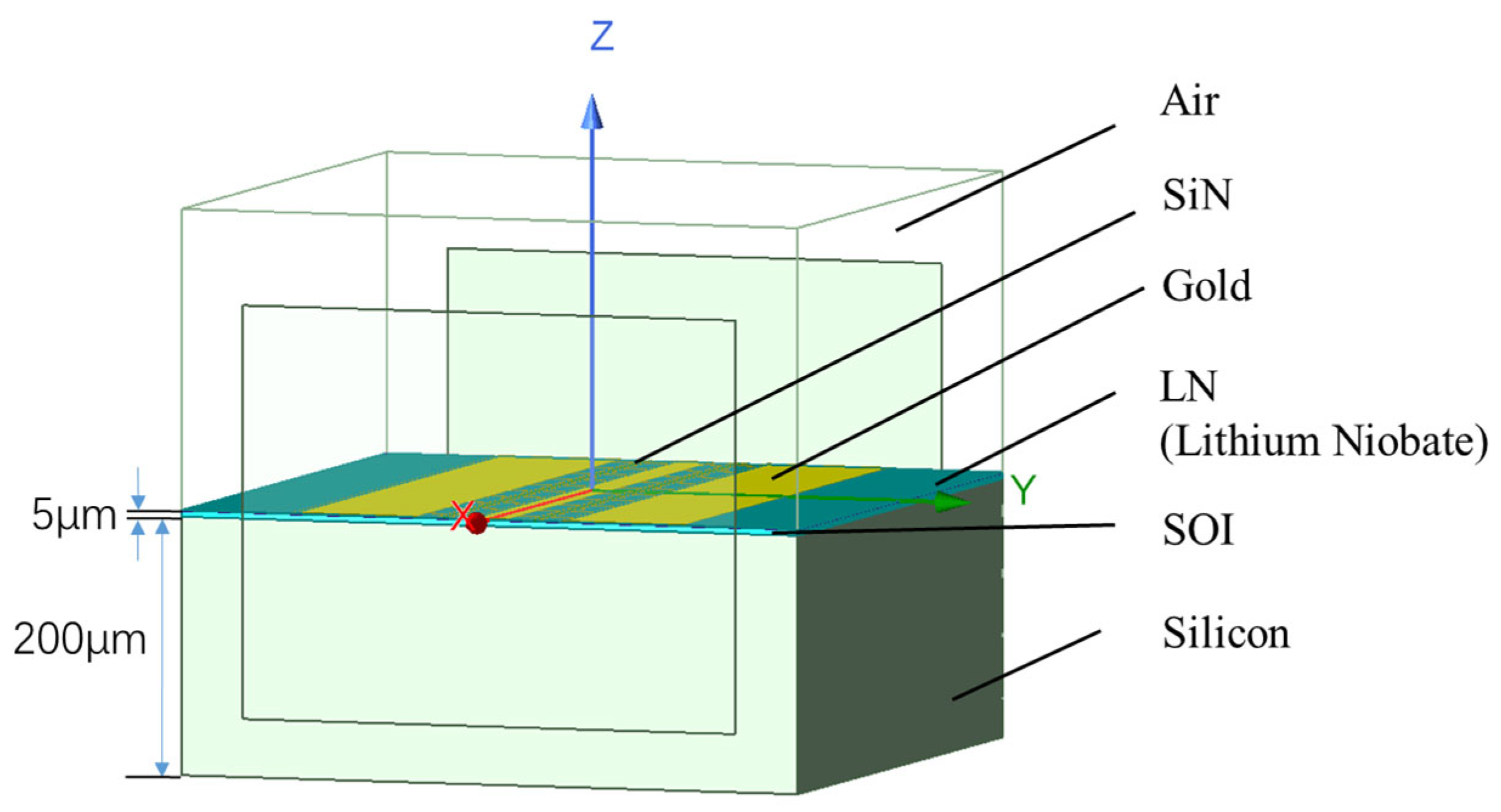
3.2.1. Design of SiN-LiNbO3 Optical Switch
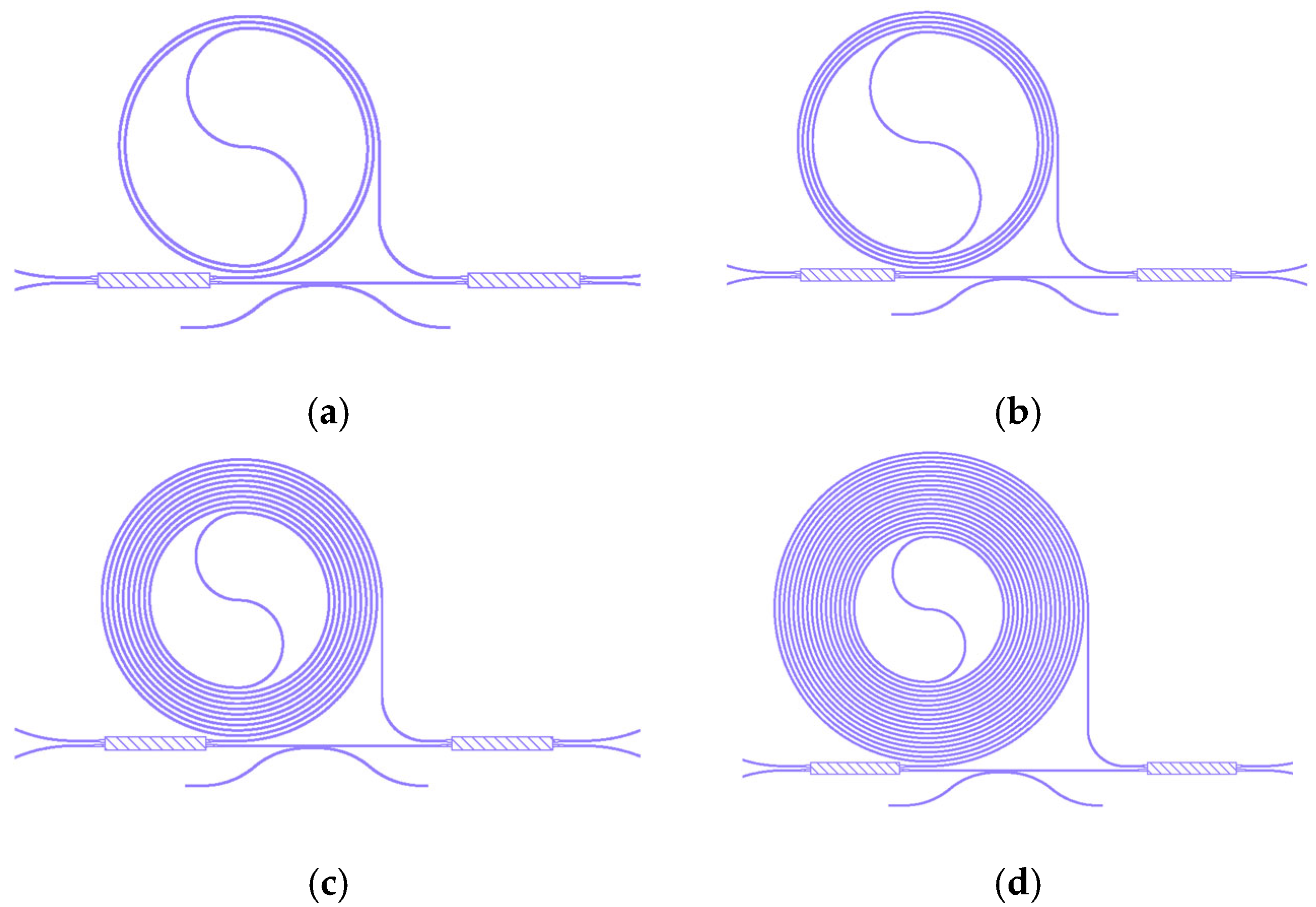
3.2.2. Archimedes’ Spiral Waveguide Delay Line
3.2.3. Design and Simulation of Electrode
4. Result Analysis
4.1. Analysis of Delay Losses in Different Delay Times
4.2. Analysis of the Overall Performance of Digital Dimmable True Delay Line
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Wang, Y.; Dong, Z.; Ding, J.; Li, W.; Wang, M.; Zhao, F.; Yu, J. Photonics-assisted joint high-speed communication and high resolution radar detection system. Opt. Lett. 2021, 46, 6103–6106. [Google Scholar] [CrossRef] [PubMed]
- Shi, S.; Niu, H.; Shi, W.; Lin, D.; Li, S.; Pan, S.; Yun, B. Integrated Optical Tunable Delay Line and Microwave Photonic Beamforming Chip: A Review. Laser Photonics Rev. 2024, 19, 202400663. [Google Scholar] [CrossRef]
- Capmany, J.; Novak, D. Microwave photonics combines two worlds. Nat. Photonics 2007, 1, 319–330. [Google Scholar] [CrossRef]
- Zhang, M.Y. Optically Controlled Phased Array Radar; National Defense Industry Press: Beijing, China, 2008; pp. 1–4. [Google Scholar]
- Pan, S.L.; Zhang, Y.M. Microwave Photon radar and key technologies. Sci. Technol. Rev. 2017, 35, 36–52. [Google Scholar]
- Pan, S.L.; Zhang, Y.M. Microwave Photonic Radar. J. Light. Technol. 2020, 38, 5450–5484. [Google Scholar] [CrossRef]
- Sun, H.B.; Li, S.L.; Wang, Q.; Li, X.K. Development of phased array radar antenna delay technology. J. Microw. 2021, 37, 9–15. [Google Scholar]
- Hu, C.; Luo, B.; Bai, W.L.; Pan, W.; Yan, L.; Zou, X. Stable radio frequency transmission of single optical source over fiber based on passive hase compensation. IEEE Photonics J. 2021, 13, 7200607. [Google Scholar] [CrossRef]
- Lenz, G.; Eggleton, B.J.; Madsen, C.K.; Slusher, R.E. Optical delay lines based on optical filters. IEEE J. Quantum Electron. 2001, 37, 525–532. [Google Scholar] [CrossRef]
- Liang, H.; Wang, K.; Han, S.; Mei, L.; Tian, Z.; Zhang, J.; Chong, M. Research on Delay and Bandwidth Expansion of Discrete Dispersive Fourier Transform in the Optical Domain. Semicond. Optoelectron. 2024, 45, 1–7. [Google Scholar]
- Wang, H.; Chen, L.; Qi, Y.; Ba, D.; Dong, Y. Ultrafast microwave photonics frequency measurement technology. Laser Optoelectron. Prog. 2024, 61, 0112003. [Google Scholar]
- Subha Priyadharshini, C.; Rajeswari, A. High-Capacity Optical Communication Systems using 4D Spatial-Wavelength-Zero Cross Correlation Encoding. IETE J. Res. 2025, 1, 1–13. [Google Scholar] [CrossRef]
- Yessenov, M.; Bhaduri, B.; Delfyett, P.J.; Abouraddy, A.F. Free-space optical delay line using space-time wave packets. Nat. Commun. 2020, 11, 5782. [Google Scholar] [CrossRef]
- Wu, Y.L.; Bao, W.S.; Cao, S.R.; Chen, F.; Chen, M.-C.; Chen, X.; Chung, T.-H.; Deng, H.; Du, Y. Strong quantum computational advantage using a superconducting quantum processor. Phys. Rev. Lett. 2021, 127, 180501. [Google Scholar] [CrossRef]
- Jurcevic, P.; Jacadi-Abhari, A.; Bishop, L.S.; Lauer, I.; Bogorin, D.F.; Brink, M. Demonstration of quantum volume 64 on a superconducting quantum computing system. Quantum Sci. Technol. 2021, 6, 025020. [Google Scholar] [CrossRef]
- Bliek, L.; Wahls, S.; Visscher, I.; Taddei, C.; Timens, R.B.; Oldenbeuving, R.M.; Roeloffzen, C.G.H.; Verhaegen, M. Automatic Delay Tuning of a Novel Ring Resonator-Based Photonic Beamformer for a Transmit Phased Array Antenna. J. Light. Technol. 2019, 37, 346–348. [Google Scholar] [CrossRef]
- Xiang, C.; Davenport, M.L.; Khurgin, J.B.; Morton, P.A.; Bowers, J.E. Low-Loss continuously tunable optical true time delay based on Si3N4 ring resonators. IEEE J. Sel. Top. Quantum Electron. 2018, 24, 1–9. [Google Scholar] [CrossRef]
- Shan, W.; Lu, L.; Wang, X.; Zhou, G.; Liu, Y.; Chen, J.; Zhou, L. Broadband continuously tunable microwave photonic delay line based on cascaded silicon microrings. Opt. Express 2021, 29, 3375. [Google Scholar] [CrossRef] [PubMed]
- Xue, X.X.; Xuan, Y.; Bao, C.Y.; Li, S.; Zheng, X.; Zhou, B. Microcomb-based true-time delay network for microwave beamforming with arbitrary beam pattern control. J. Light. Technol. 2018, 36, 2312–2321. [Google Scholar] [CrossRef]
- Sun, H.; Wang, Y.; Chen, L.R. Integrated discretely tunable optical delay line based on step-chirped subwavelength grating waveguide bragg gratings. J. Light. Technol. 2020, 38, 5551–5560. [Google Scholar] [CrossRef]
- Srivastava, N.K.; Parihar, R.; Raghuwanshi, S.K. Efficient photonic beamforming system incorporating a unique featured tunable chirped fiber Bragg grating for application extended to the ku-band. IEEE Trans. Microw. Theory Tech. 2020, 68, 1851–1857. [Google Scholar] [CrossRef]
- Perez-lopez, D.; Sanchez, E.; Capmany, J. Programmable true time delay lines using integrated waveguide meshes. J. Light. Technol. 2018, 36, 4591–4601. [Google Scholar] [CrossRef]
- Zhu, C.; Lu, L.; Shan, W.; Xu, W.; Zhou, G.; Zhou, L.; Chen, J. Silicon integrated microwave photonic beamformer. Optica 2020, 7, 1162. [Google Scholar] [CrossRef]
- Sun, X.H. True Time-Delay Optical Beamforming Technology with Optic Switched Differential Structure and its Application in Radar Target Direction Finding. Master’s Thesis, Zhejiang University, Hangzhou, China, 2022; pp. 41–48. [Google Scholar]
- Duan, X.; Zhang, S.T.; Jiang, Y.Y. Improvement and implementation of a multi-channel programmable optical controlled true time delay network. Opt. Commun. Technol. 2017, 41, 1–4. [Google Scholar]
- Niu, X.Y.; Gu, Y.R.; Chu, X.; Yao, J.; Yao, J.; Yi, M.; Wang, L. Primary study on time control technology of active phasedarray based on photoconductive microwave source. High Power Laser Partical Beams 2023, 36, 1–6. [Google Scholar]
- Tessema, N.M.; Cao, Z.; Zantvoort, J.H.C.V.; Mekonnen, K.A.; Trinidad, A.M.; Tangdiongga, E.; Smolders, A.B.; Koonen, A.M.J. Wavelength-dependent Continuous Delay Based on a Si3N4 Optical Ring Resonator for K-band Radio Beamformer. In Proceedings of the IEEE International Topical Meeting on Microwave Photonics, California, CA, USA, 31 October–3 November 2016; IEEE: Piscataway, NJ, USA, 2016; pp. 305–308. [Google Scholar]
- Xie, J.; Zhou, L.; Li, Z.; Wang, J.; Chen, J. Seven-bit reconfigurable optical true time delay line based on silicon integration: Erratum. Opt. Express 2014, 22, 25516. [Google Scholar] [CrossRef]
- Zheng, P.F.; Wang, C.Q.; Xu, X.M.; Li, J.; Lin, D.D.; Hu, G.H. A Seven Bit Silicon Optical True Time Delay Line for Ka-Band Phased Array Antenna. IEEE Photonics J. 2019, 11, 1–9. [Google Scholar] [CrossRef]
- Zheng, P.F.; Xu, X.M.; Lin, D.D.; Liu, P.C.; Hu, G.H.; Yun, B.F. A wideband 1 × 4 optical beam-forming chip based on switchable optical delay lines for Ka-band phased array. Opt. Commun. 2021, 488, 126842. [Google Scholar] [CrossRef]
- Zhang, L.; Hong, S.H.; Wang, Y.; Yan, H.; Xie, Y.; Chen, T.; Zhang, M.; Yu, Z.; Shi, Y.; Liu, L.; et al. Ultralow-Loss Silicon Photonics beyond the Singlemode Regime. Laser Photonics Rev. 2022, 16, 2100292. [Google Scholar] [CrossRef]
- Shi, S.Q.; Hu, G.H.; Lin, D.D.; Zhang, J.Y.; Liu, P.C.; Lu, M.J.; Cheng, W.; Lin, T.; Yun, B.F.; Cui, Y.P. Performance comparison of integrated optical switching delay lines on three typical photonic integration pilot lines. Opt. Laser Technol. 2023, 159, 109016. [Google Scholar] [CrossRef]
- Xie, Y.W.; Hong, S.H.; Yan, H.; Zhang, C.P.; Zhang, L.; Zhuang, L.M.; Dai, D.X. Low-loss chip-scale programmable silicon photonic processor. Opto-Electron. Adv. 2023, 6, 220030. [Google Scholar] [CrossRef]
- Fathpour, S.; Riza, N. Silicon-photonics-based wideband radar beamforming: Basic design, Optical. Engineering 2010, 49, 018201. [Google Scholar] [CrossRef]
- Moreira, R.L.; Garcia, J.; Li, W.; Bauters, J.; Barton, J.S.; Heck, M.J.R.; Bowers, J.E.; Blumenthal, D.J. Integrated Ultra-Low-Loss 4-Bit Tunable Delay for Broadband Phased Array Antenna Applications. IEEE Photonics Technol. Lett. 2013, 25, 1165–1168. [Google Scholar] [CrossRef]
- Lin, D.; Shi, S.; Liu, P.; Cheng, W.; Lu, M.; Lin, T.; Hu, G.; Yun, B.; Cui, Y. Low loss silicon nitride 1 × 4 microwave photonic beamforming chip. Opt. Express 2022, 30, 30672–30683. [Google Scholar] [CrossRef]
- Song, Q.Q.; Hu, Z.F.; Chen, K.X. Scalable and reconfigurable true time delay line based on an ultra-low-loss silica waveguide. Appl. Opt. 2018, 57, 4434–4439. [Google Scholar] [CrossRef] [PubMed]
- Liu, D.P.; Sun, S.Q.; Yin, X.; Sun, B.; Sun, J.; Liu, Y.; Li, W.; Zhu, N.; Li, M. Large-capacity and low-loss integrated optical buffer. Opt. Express 2019, 27, 11585–11593. [Google Scholar] [CrossRef]
- Howley, B.; Wang, X.; Chen, M.; Chen, R.T. Reconfigurable Delay Time Polymer Planar Lightwave Circuit for an X-band Phased-Array Antenna Demonstration. J. Light. Technol. 2007, 25, 883–890. [Google Scholar] [CrossRef]
- Wang, X.L.; Howley, B.; Chen, M.Y.; Chen, R.T. Phase error corrected 4-bit true time delay module using a cascaded 2 × 2 polymer waveguide switch array. Appl. Opt. 2007, 46, 379–383. [Google Scholar] [CrossRef]
- Pan, Z.; Subbaraman, H.; Lin, X.; Li, Q.; Zhang, C.; Ling, T.; Guo, L.J.; Chen, R.T. Laser Science to Photonic Applications. In Proceedings of the Conference on Lasers and Electro-Optics (CLEO), San Jose, CA, USA, 8–13 June 2014. [Google Scholar]
- Ke, W.; Lin, Y.; He, M.; Xu, M.; Zhang, J.; Lin, Z.; Yu, S.; Cai, X. Digitally tunable optical delay line based on thin-film lithium niobate featuring high switching speed and low optical loss. Photonics Res. 2022, 10, 2575–2583. [Google Scholar] [CrossRef]
- Chen, R.T. Polymer-based photonic integrated circuits. Opt. Laser Technol. 1993, 25, 347–365. [Google Scholar] [CrossRef]
- Hong, S.; Zhang, L.; Wu, J.; Peng, Y.; Lyu, L.; Hu, Y.; Xie, Y.; Dai, D. Multimode-enabled silicon photonic delay lines: Break the delay-density limit. Light Sci. Appl. 2025, 14, 145. [Google Scholar] [CrossRef]
- Wang, X.; Zhou, L.; Li, R.; Xie, J.; Lu, L.; Wu, K.; Chen, J. Continuously tunable ultra-thin silicon waveguide optical delay line. Optica 2017, 4, 507–515. [Google Scholar] [CrossRef]
- Hong, S.H.; Zhang, L.; Wang, Y.; Zhang, M.; Xie, Y.; Dai, D. Ultralow-loss compact silicon photonic waveguide spirals and delay lines. Photonics Res. 2022, 10, 1–7. [Google Scholar] [CrossRef]
- Ma, T.; Ma, M.; Guo, L.J. Optical multilayer thin film structure inverse design: From optimization to deep learning. iScience 2025, 28, 112222. [Google Scholar] [CrossRef]
- Trager, F. Modern Optics and Photonics Technology; Springer: Berlin/Heidelberg, Germany, 2012. [Google Scholar]
- Liu, S.; Li, C. Photonics Technology and Application; Guangdong Science and Technology Press: Guangzhou, China, 2006. [Google Scholar]
- Wang, Z.Z.; Li, X.Y.; Ji, J.T.; Sun, Z.; Sun, J.; Fang, B.; Lu, J.; Li, S.; Ma, X.; Chen, X.; et al. Fast-speed and low-power-consumption optical phased array based on lithium niobate waveguides. Nanophotonics 2024, 13, 2429–2436. [Google Scholar] [CrossRef]




| Switch 1 | Switch 2 | Switch 3 | Switch 4 | Switch 5 | Delay Value |
|---|---|---|---|---|---|
| through | cross | through | through | through | 10 ps |
| cross | cross | cross | through | through | 20 ps |
| through | through | cross | through | through | 30 ps |
| cross | through | cross | cross | through | 40 ps |
| through | cross | cross | cross | through | 50 ps |
| cross | cross | through | cross | through | 60 ps |
| through | through | through | cross | through | 70 ps |
| cross | through | through | cross | cross | 80 ps |
| through | cross | through | cross | cross | 90 ps |
| cross | cross | cross | cross | cross | 100 ps |
| through | through | cross | cross | cross | 110 ps |
| cross | through | cross | through | cross | 120 ps |
| through | cross | cross | through | cross | 130 ps |
| cross | cross | through | through | cross | 140 ps |
| through | through | through | through | cross | 150 ps |
| cross | through | through | through | cross | 160 ps |
| through | cross | through | through | cross | 170 ps |
| cross | cross | cross | through | cross | 180 ps |
| cross | through | cross | cross | cross | 190 ps |
| cross | through | cross | cross | cross | 200 ps |
| through | cross | cross | cross | cross | 210 ps |
| cross | cross | through | cross | cross | 220 ps |
| through | through | through | cross | cross | 230 ps |
| cross | through | through | cross | through | 240 ps |
| through | cross | through | cross | cross | 250 ps |
| cross | cross | cross | cross | through | 260 ps |
| through | through | cross | cross | through | 270 ps |
| cross | through | cross | through | through | 280 ps |
| through | cross | cross | through | through | 290 ps |
| cross | cross | through | through | through | 300 ps |
| through | through | through | through | through | 310 ps |
| Component | Dimensions/Position | Thickness | Type |
|---|---|---|---|
| MMI | 76 μm × 10 μm × 0.5 μm/(10 μm × 1 μm × 0.5 μm) | 0.5 μm | Rectangle |
| Input waveguide_up | 10 μm × 1 μm × 0.5 μm/(−15 μm, −1.75 μm, 0.15 μm) | 0.5 μm | Rectangle |
| Input waveguide_down | 10 μm × 1 μm × 0.5 μm/(−15 μm, −1.75 μm, 0.15 μm) | 0.5 μm | Rectangle |
| Output waveguide_up | 10 μm × 1 μm × 0.5 μm/(91 μm, 1.75 μm, 0.15 μm) | 0.5 μm | Rectangle |
| Output waveguide_down | 10 μm × 1 μm × 0.5 μm/(91 μm, −1.75 μm, 0.15 μm) | 0.5 μm | Rectangle |
| Taper 1 | (0 μm, 1.75 μm, 0.15 μm) | 0.5 μm | Polygon |
| Taper 2 | (0 μm, −1.75 μm, 0.15 μm) | 0.5 μm | Polygon |
| Taper 3 | (0 μm, 1.75 μm, 0.15 μm) | 0.5 μm | Polygon |
| Taper 4 | (0 μm, −1.75 μm, 0.15 μm) | 0.5 μm | Polygon |
| Material | Radius of Curvature | Waveguide Spacing |
|---|---|---|
| Silicon nitride | Spiral center: R0 = 88.6 μm | Reverse waveguide spacing 4 μm |
| Outside the center: R(θ) = 88.6 + 0.637θ (μm) | Co-directional waveguide spacing 4 μm |
| Delay Time [ps] | Waveguide Length [cm] | Transmission Loss [dB] | Bending Times | Bending Loss [dB] | Optical Switch Loss [dB] | Coupling Loss [dB] | Total Loss [dB] |
|---|---|---|---|---|---|---|---|
| 10 | 0.089 | 0.0445 | 9 | 0.09 | 1 | 1 | 2.1345 |
| 20 | 0.178 | 0.0890 | 17 | 0.17 | 1 | 1 | 2.2590 |
| 30 | 0.267 | 0.1335 | 26 | 0.26 | 1 | 1 | 2.3935 |
| 40 | 0.356 | 0.1780 | 34 | 0.34 | 1 | 1 | 2.5180 |
| 50 | 0.445 | 0.2225 | 43 | 0.43 | 1 | 1 | 2.6550 |
| 60 | 0.534 | 0.2670 | 51 | 0.51 | 1 | 1 | 2.7770 |
| 70 | 0.623 | 0.3115 | 60 | 0.60 | 1 | 1 | 2.9115 |
| 80 | 0.712 | 0.3560 | 69 | 0.69 | 1 | 1 | 3.0460 |
| 90 | 0.801 | 0.4005 | 78 | 0.78 | 1 | 1 | 3.1805 |
| 100 | 0.890 | 0.4450 | 86 | 0.86 | 1 | 1 | 3.3050 |
| 110 | 0.979 | 0.4895 | 95 | 0.95 | 1 | 1 | 3.4395 |
| 120 | 1.068 | 0.5340 | 103 | 1.03 | 1 | 1 | 3.5640 |
| 130 | 1.157 | 0.5785 | 112 | 1.12 | 1 | 1 | 3.6985 |
| 140 | 1.246 | 0.6230 | 120 | 1.20 | 1 | 1 | 3.8230 |
| 150 | 1.335 | 0.6675 | 129 | 1.29 | 1 | 1 | 3.9575 |
| 160 | 1.424 | 0.7120 | 137 | 1.37 | 1 | 1 | 4.0820 |
| 170 | 1.513 | 0.7565 | 146 | 1.46 | 1 | 1 | 4.2165 |
| 180 | 1.602 | 0.8010 | 154 | 1.54 | 1 | 1 | 4.3410 |
| 190 | 1.691 | 0.8455 | 163 | 1.63 | 1 | 1 | 4.4755 |
| 200 | 1.780 | 0.8900 | 171 | 1.71 | 1 | 1 | 4.6000 |
| 210 | 1.869 | 0.9345 | 180 | 1.80 | 1 | 1 | 4.7345 |
| 220 | 1.958 | 0.9790 | 188 | 1.88 | 1 | 1 | 4.8590 |
| 230 | 2.047 | 1.0235 | 197 | 1.97 | 1 | 1 | 4.9935 |
| 240 | 2.136 | 1.0680 | 206 | 2.06 | 1 | 1 | 5.1280 |
| 250 | 2.225 | 1.1125 | 215 | 2.15 | 1 | 1 | 5.2625 |
| 260 | 2.314 | 1.1570 | 223 | 2.23 | 1 | 1 | 5.3870 |
| 270 | 2.403 | 1.2015 | 232 | 2.32 | 1 | 1 | 5.5215 |
| 280 | 2.492 | 1.2460 | 240 | 2.40 | 1 | 1 | 5.6460 |
| 290 | 2.581 | 1.2905 | 249 | 2.49 | 1 | 1 | 5.7805 |
| 300 | 2.670 | 1.3350 | 257 | 2.57 | 1 | 1 | 5.9050 |
| 310 | 2.759 | 1.3795 | 266 | 2.66 | 1 | 1 | 6.0398 |
| Literature | Platform | Delay Tuning Step [ps] | Maximum Delay Tunable Range [ps] | Loss Delay Ratio [dB ns−1] | Footprint [mm2] |
|---|---|---|---|---|---|
| [29] | SOI | 1.52 | 191.37 | 17.81 | 13.32 |
| [36] | Si3N4 | 4.2 | 130 | 1.8 | 35 |
| [37] | SiO2 | 6 | 90.2 | 5.5 | 602 |
| [38] | SiO2 | 10,000 | 100,000 | 0.22 | 4166 |
| [42] | TFLN | 10 | 150 | 23 | 50 |
| This work | SiN-LiNbO3 | 10 | 310 | 13 | 120 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
An, T.; Liu, L.; Lv, G.; Han, C.; Meng, Y.; Zhu, S.; Niu, Y.; Jiang, Y. Design and Simulation of Optical Waveguide Digital Adjustable Delay Lines Based on Optical Switches and Archimedean Spiral Structures. Photonics 2025, 12, 679. https://doi.org/10.3390/photonics12070679
An T, Liu L, Lv G, Han C, Meng Y, Zhu S, Niu Y, Jiang Y. Design and Simulation of Optical Waveguide Digital Adjustable Delay Lines Based on Optical Switches and Archimedean Spiral Structures. Photonics. 2025; 12(7):679. https://doi.org/10.3390/photonics12070679
Chicago/Turabian StyleAn, Ting, Limin Liu, Guizhou Lv, Chunhui Han, Yafeng Meng, Sai Zhu, Yuandong Niu, and Yunfeng Jiang. 2025. "Design and Simulation of Optical Waveguide Digital Adjustable Delay Lines Based on Optical Switches and Archimedean Spiral Structures" Photonics 12, no. 7: 679. https://doi.org/10.3390/photonics12070679
APA StyleAn, T., Liu, L., Lv, G., Han, C., Meng, Y., Zhu, S., Niu, Y., & Jiang, Y. (2025). Design and Simulation of Optical Waveguide Digital Adjustable Delay Lines Based on Optical Switches and Archimedean Spiral Structures. Photonics, 12(7), 679. https://doi.org/10.3390/photonics12070679





