A Residual Optronic Convolutional Neural Network for SAR Target Recognition
Abstract
1. Introduction
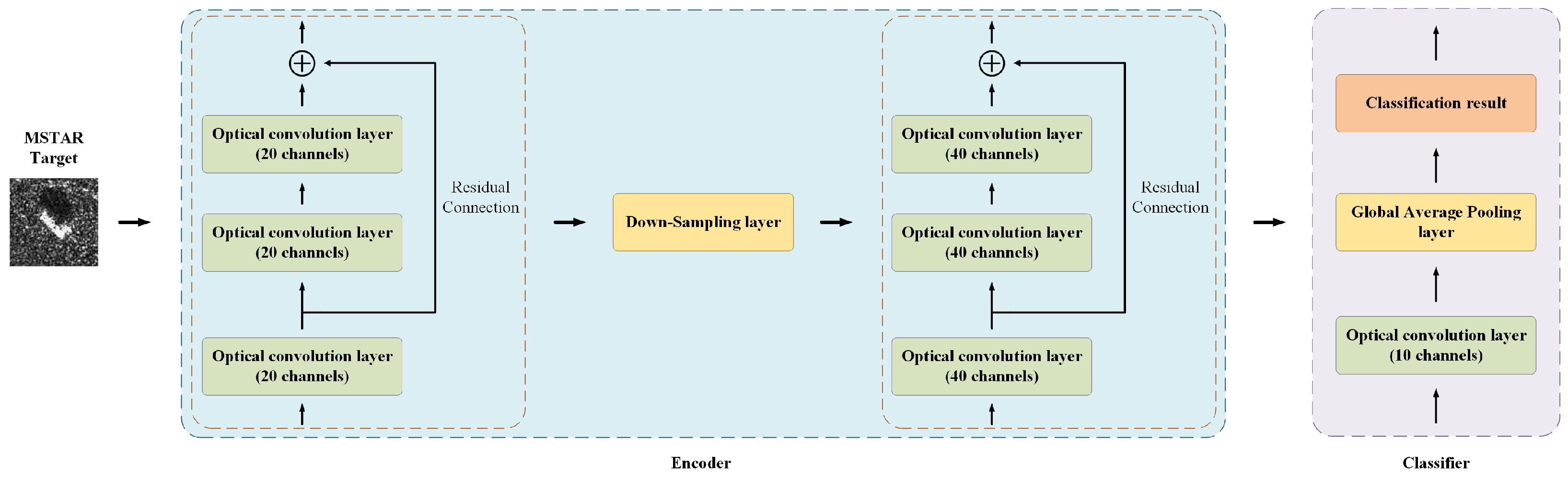
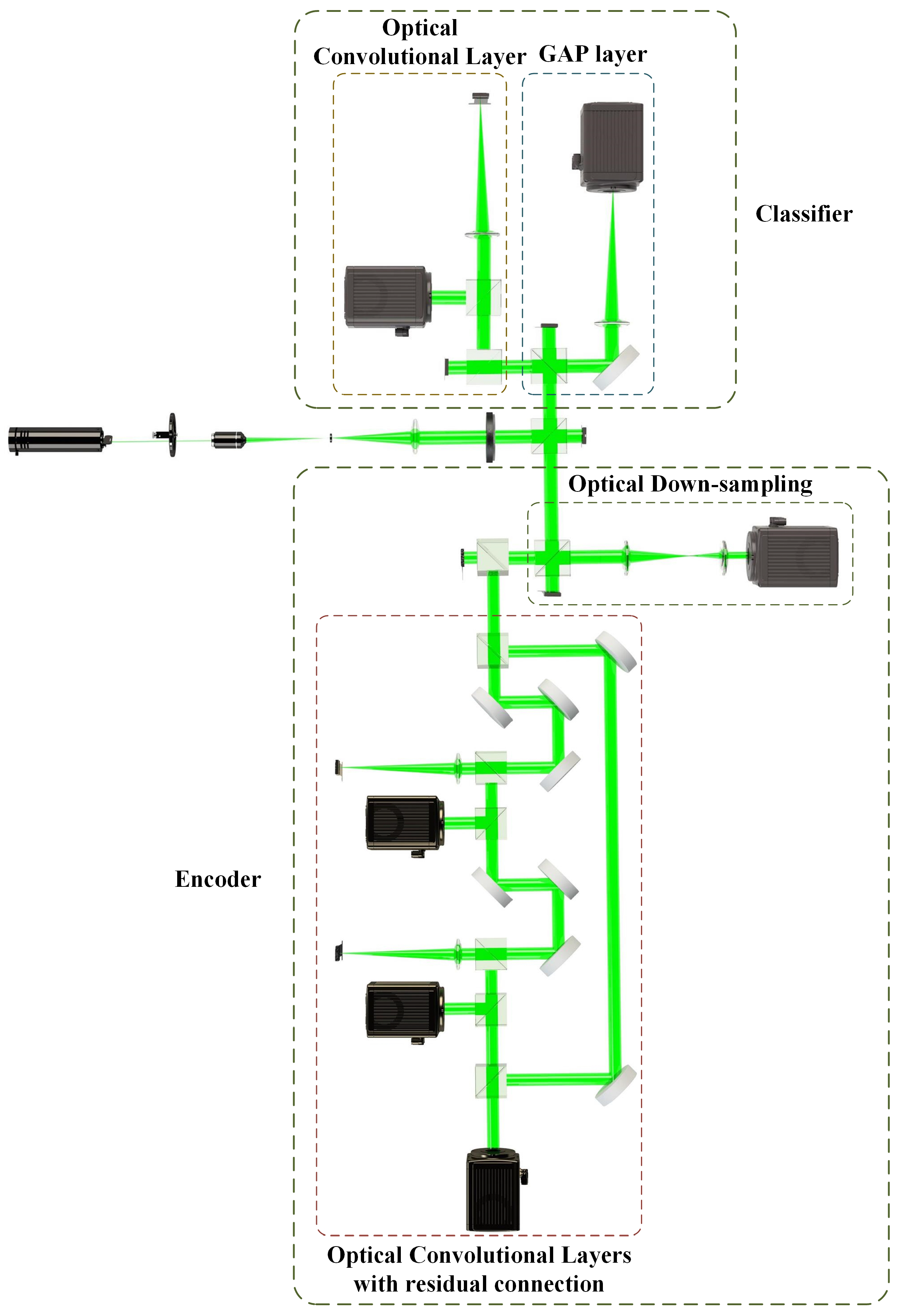
2. Method
2.1. The Encoder
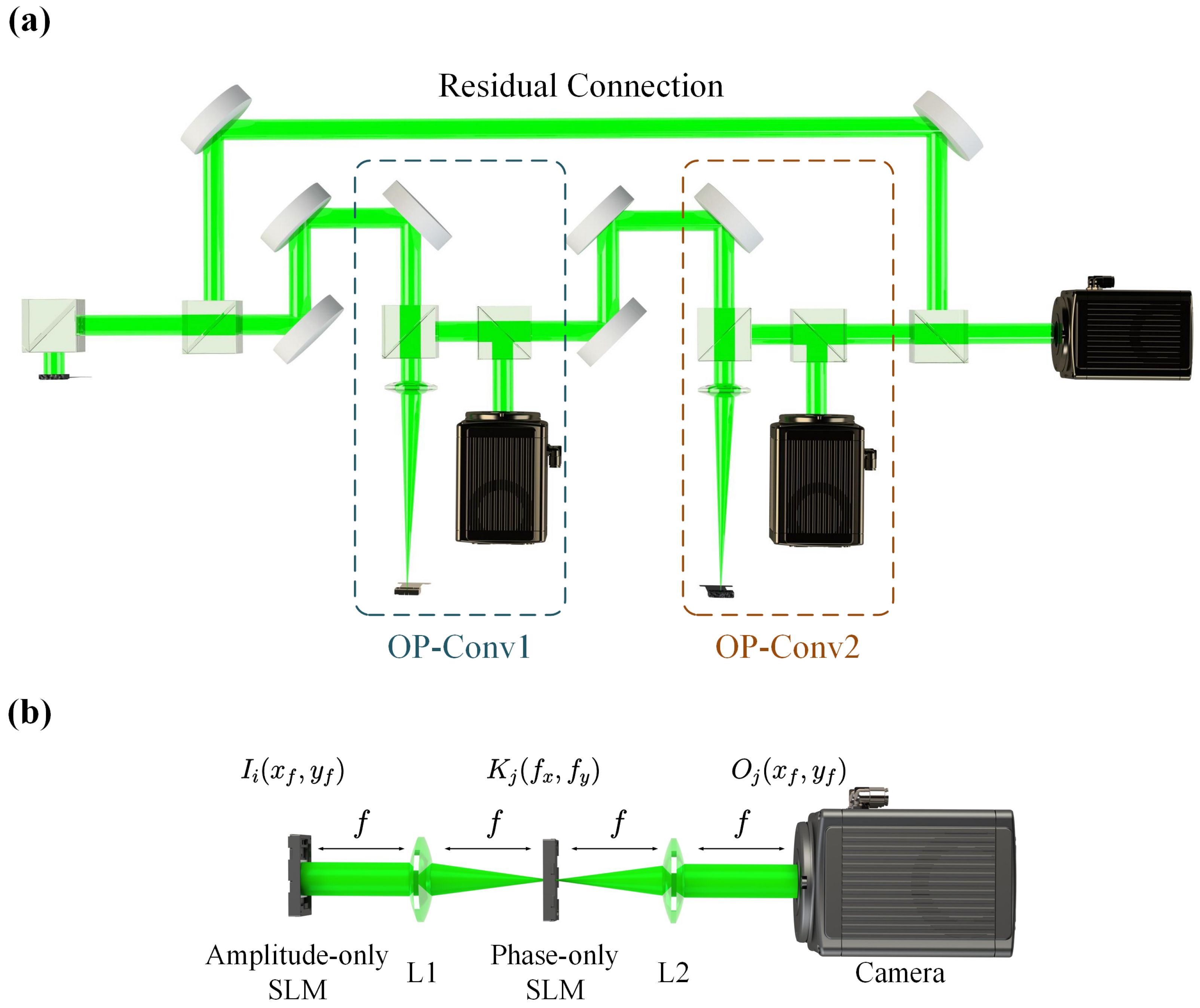
2.1.1. Optical Convolutional Layer with Residual Connection
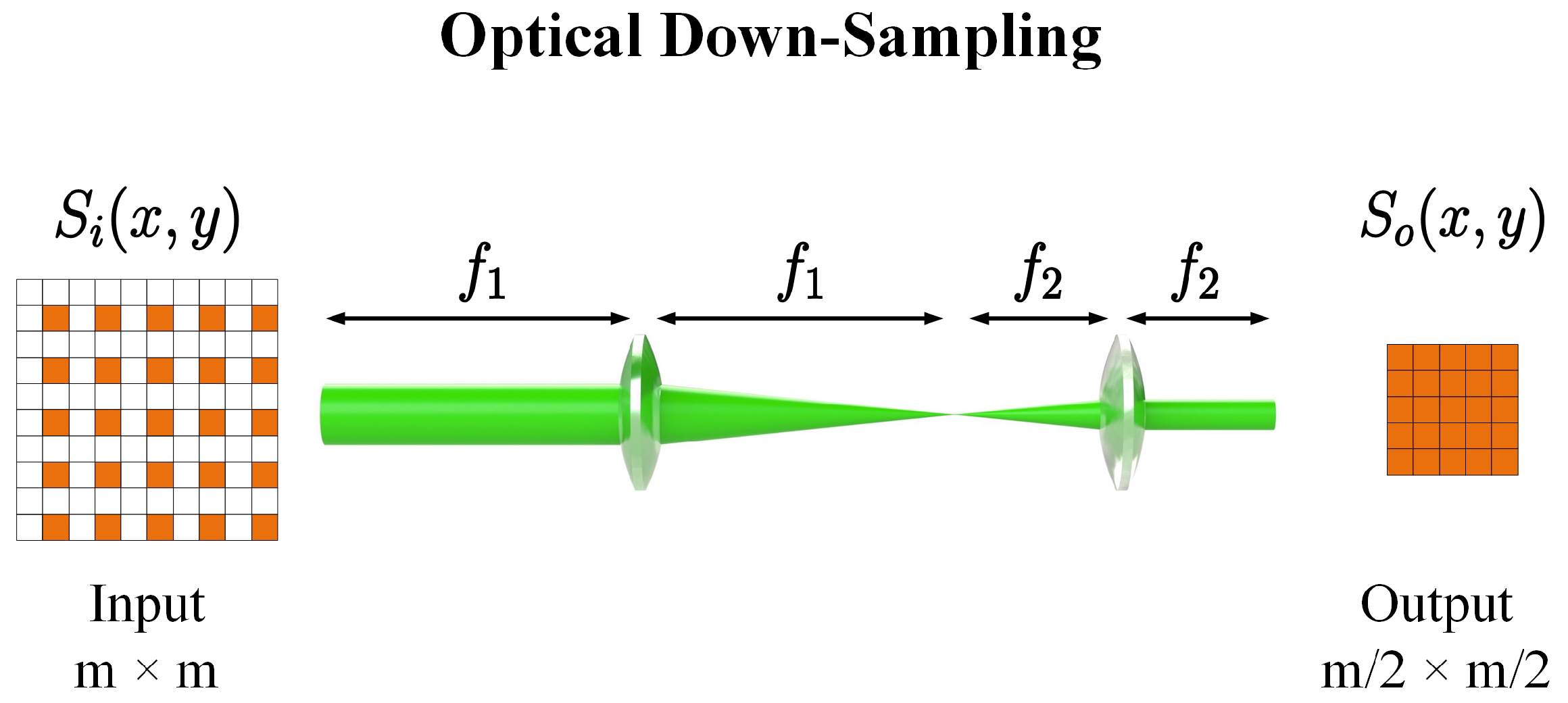
2.1.2. Optical Down-Sampling Layer
2.2. The Classifier
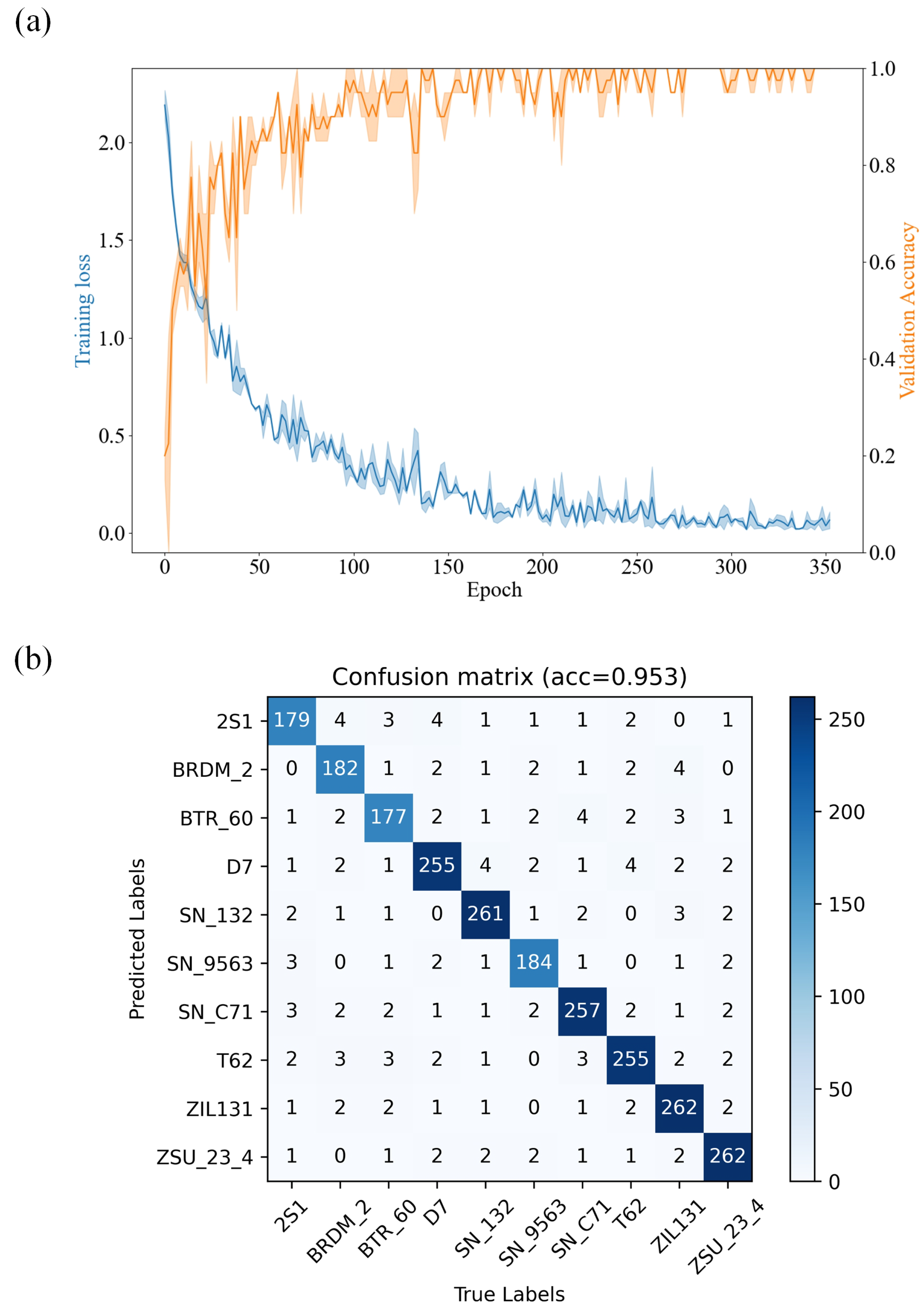
3. Experimental Results
4. Conclusions and Discussion
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Chen, Y.; Lin, Z.; Zhao, X.; Wang, G.; Gu, Y. Deep learning-based classification of hyperspectral data. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2014, 7, 2094–2107. [Google Scholar] [CrossRef]
- Shi, M.; Gao, Y.; Chen, L.; Liu, X. Dual-Branch Multiscale Channel Fusion Unfolding Network for Optical Remote Sensing Image Super-Resolution. IEEE Geosci. Remote Sens. Lett. 2022, 19, 6519105. [Google Scholar] [CrossRef]
- Shi, M.; Gao, Y.; Chen, L.; Liu, X. Dual-Resolution Local Attention Unfolding Network for Optical Remote Sensing Image Super-Resolution. IEEE Geosci. Remote Sens. Lett. 2022, 19, 6016105. [Google Scholar] [CrossRef]
- Shi, M.; Gao, Y.; Chen, L.; Liu, X. Double Prior Network for Multidegradation Remote Sensing Image Super-Resolution. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2023, 16, 3131–3147. [Google Scholar] [CrossRef]
- Krizhevsky, A.; Sutskever, I.; Hinton, G.E. Imagenet classification with deep convolutional neural networks. In Proceedings of the Advances in Neural Information Processing Systems 25, Lake Tahoe, NV, USA, 3–6 December 2012. [Google Scholar]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep residual learning for image recognition. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Vancouver, BC, Canada, 17–24 June 2023; pp. 770–778. [Google Scholar]
- Jouppi, N.P.; Young, C.; Patil, N.; Patterson, D.; Agrawal, G.; Bajwa, R.; Bates, S.; Bhatia, S.; Boden, N.; Borchers, A.; et al. In-datacenter performance analysis of a tensor processing unit. In Proceedings of the 44th Annual International Symposium on Computer Architecture, Toronto, ON, Canada, 24–28 June 2017; pp. 1–12. [Google Scholar]
- Chen, T.; Du, Z.; Sun, N.; Wang, J.; Wu, C.; Chen, Y.; Temam, O. Diannao: A small-footprint high-throughput accelerator for ubiquitous machine-learning. Acm Sigarch Comput. Archit. News 2014, 42, 269–284. [Google Scholar] [CrossRef]
- Zhang, S.; Du, Z.; Zhang, L.; Lan, H.; Liu, S.; Li, L.; Guo, Q.; Chen, T.; Chen, Y. Cambricon-X: An accelerator for sparse neural networks. In Proceedings of the 2016 49th Annual IEEE/ACM International Symposium on Microarchitecture (MICRO), IEEE, Taipei, Taiwan, 15–19 October 2016; pp. 1–12. [Google Scholar]
- Pei, J.; Deng, L.; Song, S.; Zhao, M.; Zhang, Y.; Wu, S.; Wang, G.; Zou, Z.; Wu, Z.; He, W.; et al. Towards artificial general intelligence with hybrid Tianjic chip architecture. Nature 2019, 572, 106–111. [Google Scholar] [CrossRef]
- Merolla, P.A.; Arthur, J.V.; Alvarez-Icaza, R.; Cassidy, A.S.; Sawada, J.; Akopyan, F.; Jackson, B.L.; Imam, N.; Guo, C.; Nakamura, Y.; et al. A million spiking-neuron integrated circuit with a scalable communication network and interface. Science 2014, 345, 668–673. [Google Scholar] [CrossRef]
- Waldrop, M.M. More than moore. Nature 2016, 530, 144–148. [Google Scholar] [CrossRef]
- Moore, J.F. Predators and prey: A new ecology of competition. Harv. Bus. Rev. 1993, 71, 75–86. [Google Scholar]
- Lin, X.; Yang, W.; Wang, K.L.; Zhao, W. Two-dimensional spintronics for low-power electronics. Nat. Electron. 2019, 2, 274–283. [Google Scholar] [CrossRef]
- Goodman, J.W.; Dias, A.R.; Woody, L.M. Fully parallel, high-speed incoherent optical method for performing discrete Fourier transforms. Opt. Lett. 1978, 2, 1–3. [Google Scholar] [CrossRef] [PubMed]
- Lin, X.; Rivenson, Y.; Yardimci, N.T.; Veli, M.; Luo, Y.; Jarrahi, M.; Ozcan, A. All-optical machine learning using diffractive deep neural networks. Science 2018, 361, 1004–1008. [Google Scholar] [CrossRef] [PubMed]
- Mengu, D.; Luo, Y.; Rivenson, Y.; Ozcan, A. Analysis of diffractive optical neural networks and their integration with electronic neural networks. IEEE J. Sel. Top. Quantum Electron. 2019, 26, 1–14. [Google Scholar] [CrossRef] [PubMed]
- Li, J.; Mengu, D.; Luo, Y.; Rivenson, Y.; Ozcan, A. Class-specific differential detection in diffractive optical neural networks improves inference accuracy. Adv. Photonics 2019, 1, 046001. [Google Scholar] [CrossRef]
- Yan, T.; Wu, J.; Zhou, T.; Xie, H.; Xu, F.; Fan, J.; Fang, L.; Lin, X.; Dai, Q. Fourier-space diffractive deep neural network. Phys. Rev. Lett. 2019, 123, 023901. [Google Scholar] [CrossRef]
- Zuo, Y.; Li, B.; Zhao, Y.; Jiang, Y.; Chen, Y.-C.; Chen, P.; Jo, G.-B.; Liu, J.; Du, S. All-optical neural network with nonlinear activation functions. Optica 2019, 6, 1132–1137. [Google Scholar] [CrossRef]
- Tait, A.N.; De Lima, T.F.; Zhou, E.; Wu, A.X.; Nahmias, M.A.; Shastri, B.J.; Prucnal, P.R. Neuromorphic photonic networks using silicon photonic weight banks. Sci. Rep. 2017, 7, 7430. [Google Scholar] [CrossRef]
- Zhang, H.; Gu, M.; Jiang, X.D.; Thompson, J.; Cai, H.; Paesani, S.; Santagati, R.; Laing, A.; Zhang, Y.; Yung, M.H.; et al. An optical neural chip for implementing complex-valued neural network. Nat. Commun. 2021, 12, 457. [Google Scholar] [CrossRef] [PubMed]
- Tahersima, M.H.; Kojima, K.; Koike-Akino, T.; Jha, D.; Wang, B.; Lin, C.; Parsons, K. Deep neural network inverse design of integrated photonic power splitters. Sci. Rep. 2019, 9, 1368. [Google Scholar] [CrossRef]
- Shen, Y.; Harris, N.C.; Skirlo, S.; Prabhu, M.; Baehr-Jones, T.; Hochberg, M.; Sun, X.; Zhao, S.; Larochelle, H.; Englund, D.; et al. Deep learning with coherent nanophotonic circuits. Nat. Photonics 2017, 11, 441–446. [Google Scholar] [CrossRef]
- Hughes, T.W.; Minkov, M.; Shi, Y.; Fan, S. Training of photonic neural networks through in situ backpropagation and gradient measurement. Optica 2018, 5, 864–871. [Google Scholar] [CrossRef]
- Jiao, S.; Liu, J.; Zhang, L.; Yu, F.; Zuo, G.; Zhang, J.; Zhao, F.; Lin, W.; Shao, L. All-optical logic gate computing for high-speed parallel information processing. Opto-Electron. Sci. 2022, 1, 220010. [Google Scholar] [CrossRef]
- Qiu, C.; Xiao, H.; Wang, L.; Tian, T. Recent advances in integrated optical directed logic operations for high performance optical computing: A review. Front. Optoelectron. 2022, 15, 1. [Google Scholar] [CrossRef] [PubMed]
- Gu, Z.; Huang, Z.; Gao, Y.; Liu, X. Training optronic convolutional neural networks on an optical system through backpropagation algorithms. Optics Express 2022, 30, 19416–19440. [Google Scholar] [CrossRef]
- Gu, Z.; Shi, M.; Huang, Z.; Gao, Y.; Liu, X. In-Situ Training Optronic Convolutional Neural Network for SAR Target Recognition. In Proceedings of the IGARSS 2022-2022 IEEE International Geoscience and Remote Sensing Symposium, Kuala Lumpur, Malaysia, 17–22 July 2022; pp. 3363–3366. [Google Scholar]
- Dou, H.; Deng, Y.; Yan, T.; Wu, H.; Lin, X.; Dai, Q. Residual D2NN: Training diffractive deep neural networks via learnable light shortcuts. Opt. Lett. 2020, 45, 2688–2691. [Google Scholar] [CrossRef]
- Gu, Z.; Gao, Y.; Liu, X. Position-robust optronic convolutional neural networks dealing with images position variation. Opt. Commun. 2022, 505, 127505. [Google Scholar] [CrossRef]

| Method | Power Consumption | Computational Complexity | Accuracy |
|---|---|---|---|
| Digital CNN | 1000 W | 18.56 MMac | 95.1% |
| res-OPCNN | 250 W | 748.6 KMac | 95.3% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gu, Z.; Huang, Z.; Lu, X.; Zhang, H.; Kuang, H. A Residual Optronic Convolutional Neural Network for SAR Target Recognition. Photonics 2025, 12, 678. https://doi.org/10.3390/photonics12070678
Gu Z, Huang Z, Lu X, Zhang H, Kuang H. A Residual Optronic Convolutional Neural Network for SAR Target Recognition. Photonics. 2025; 12(7):678. https://doi.org/10.3390/photonics12070678
Chicago/Turabian StyleGu, Ziyu, Zicheng Huang, Xiaotian Lu, Hongjie Zhang, and Hui Kuang. 2025. "A Residual Optronic Convolutional Neural Network for SAR Target Recognition" Photonics 12, no. 7: 678. https://doi.org/10.3390/photonics12070678
APA StyleGu, Z., Huang, Z., Lu, X., Zhang, H., & Kuang, H. (2025). A Residual Optronic Convolutional Neural Network for SAR Target Recognition. Photonics, 12(7), 678. https://doi.org/10.3390/photonics12070678




