Next Article in Journal
A Residual Optronic Convolutional Neural Network for SAR Target Recognition
Next Article in Special Issue
Burst-Mode Operation of End-Pumped, Passively Q-Switched (Er/Yb):Glass Lasers
Previous Article in Journal
The Cone Optoretinogram as a Function of Retinal Eccentricity
Previous Article in Special Issue
Orthogonally Polarized Green Dual-Wavelength Pr3+:LiLuF4 Laser at 523 and 538 nm with the Power Ratio of 1:1
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Photonics
Volume 12
Issue 7
10.3390/photonics12070677
photonics-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Review

Self-Mode-Locking and Frequency-Modulated Comb Semiconductor Disk Lasers

by
Arash Rahimi-Iman
I. Physikalisches Institut and Center for Materials Research, Justus-Liebig-Universität Gießen, D-35392 Giessen, Germany
Photonics 2025, 12(7), 677; https://doi.org/10.3390/photonics12070677
Submission received: 16 May 2025 / Revised: 25 June 2025 / Accepted: 30 June 2025 / Published: 5 July 2025
(This article belongs to the Special Issue Laser Technology and Applications)
Browse Figures
Versions Notes

Abstract

Optically pumped semiconductor disk lasers—known as vertical-external-cavity surface-emitting lasers (VECSELs)—are promising devices for ultrashort pulse formation. For it, a “SESAM-free” approach labeled “self-mode-locking” received considerable attention in the past decade, relying solely on a chip-related nonlinear optical property which can establish adequate pulsing conditions—thereby suggesting a reduced reliance on a semiconductor saturable-absorber mirror (the SESAM) in the cavity. Self-mode-locked (SML) VECSELs with sub-ps pulse durations were reported repeatedly. This motivated investigations on a Kerr-lensing type effect acting as an artificial saturable absorber. So-called Z-scan and ultrafast beam-deflection experiments were conducted to emphasize the role of nonlinear lensing in the chip for pulse formation. Recently, in addition to allowing stable ultrashort pulsed operation, self-starting mode-locked operation gave rise to another emission regime related to frequency comb formation. While amplitude-modulated combs relate to signal peaks in time, providing a so-called pulse train, a frequency-modulated comb is understood to cause quasi continuous-wave output with its sweep of instantaneous frequency over the range of phase-locked modes. With gain-bandwidth-enhanced chips, as well as with an improved understanding of the impacts of dispersion and nonlinear lensing properties and cavity configurations on the device output, an enhanced employment of SML VECSELs is to be expected.

1. Introduction

Mode-locked (ML) VECSELs/semiconductor disk lasers (SDLs) [1,2] are a class of lasers with great potential for science and industry applications owing to their remarkable and promising features [3,4,5], among them their brightness, beam quality and competitiveness in terms of size, price, and pulse durations.
Ultrafast optical pulse generation remains a key topic in the laser community and has opened the door for a wide range of different applications in biology, medicine, manufacturing, and metrology. With ultrashort pulse durations obtainable from advanced solid-state lasers since the end of the past century [6,7], similar trends are observable for VECSELs [8,9,10]. In the past decade, advances on pulsed VECSELs were regularly accompanied by both experimental milestones and corresponding design considerations [11,12,13,14,15,16] as well as theoretical knowhow generation [17,18,19].

1.1. Towards Self-Mode-Locking

Since the early 2000s, VECSELs have been gaining popularity not only for their continuous-wave (cw) high power output, but also for their design flexibility [20] and capability to deliver sub-ps pulses with peak powers up to the few-kW range [11]. With repetition rates typically of the order of 1 GHz, VECSELs even became attractive as a pump device in the field of ultrafast quantum communication [21]. Thus, for many years, VECSELs have been seen as an ideal platform for the realization of compact, robust, and cost-efficient fs-pulsed lasers [3,5].
The aim to harness on self-mode-locking for ultrashort-pulse or comb formation is understandable, as the “extra” saturable-absorber mirrors (SAMs, usually SESAMs) in the laser cavity must be individually designed concerning different parameters and produced for the targeted operation wavelength. Self-mode-locked SDLs are expected to circumvent certain restrictions inherently set by saturable-absorber based devices—other than an additional design, optimization and growth process. Such could be the needed attention to the proper thermal management of SAMs (nonradiative absorption), degradation issues at high powers (spot-wise strong irradiances) and thereby peak-power limitations (possible cap for power-scaling approaches); or, the extra costs and space for the implementation of SESAM chips in VECSELs.
The phenomenon first reported in 2011 for SDLs [22] has become a well-tested concept for VECSELs [9,12,19,23,24,25,26,27,28,29,30,31,32,33,34,35], even when the mechanisms behind still remain not “fully” explained or examined. Typically, Kerr lensing has been the underlying hypothesis for self-starting ultrashort-pulse operation. The results achieved usually have relied either on an adjustable hard or soft aperture inside the cavity (e.g., a spatially beam-truncating physical object or pump spot size on gain chip, respectively; cf. sketch in Figure 1). Additionally, the laser cavity has often been set near the edge of its stable region. Then, owing to the assumed Kerr lensing effect in the gain chip, the pulsing regime of the laser could benefit from an intensity-dependent defocusing or focusing phenomenon and suffer smaller cavity loss (per roundtrip) from the aperture’s truncation effect (cf. initial reports [9,23,24]).
However, notice that works reporting ultrashort pulses based on SESAM-free ML at a very early stage were met with skepticism by different actors of the ML VECSEL community. In 2013, scholars from different groups led a discussion about the correctness or incompleteness of reported characteristics [36,37], known as the “controversy” regarding SML demonstrations—also referred to in more detail in refs. [5,9,38]). Additionally, wider skepticism seems to be fueled by the perceivably nonuniform interpretation of the underlying (S)ML principles in the semiconductor laser community across different works when it comes to pulse/comb formation (cf. Table 1, right column). Note that the causes can differ for the formation of the below-mentioned distinct comb regimes and may need further clarification through supplementary meticulous studies. Table 1 summarizes some of the author-known and prominent SML achievements, and more details on the subject can be found in, e.g., ref. [38].
While a chip’s nonlinear lensing properties such as sign and focal lengths can be at the core of theoretical considerations made in the past with regard to the VECSEL’s resonator design (cf. [24,28]), one should note the following. In many cases, neither the assumed nonlinear lensing feature of the chips has been even up to now deliberately shaped for SML operation by design—although markedly affected by the properties of the chip [39]—nor the influential higher-order dispersion properties (mainly group-delay, short GDD) (cf. [30,35]) have been notably tailored on the chip-side for breakthrough SML results yet. It is also worth noting that a frequency chirp is often present in SML-generated laser pulses and hardly actively compensated in many reported SML devices.
Unlike in explicit studies on the impact of adjustable group-velocity dispersion on the pulse properties of SML VECSELs, such as in ref. [24], there are usually no other elements present in a basic VECSEL cavity (with commonly “chirp-free” optics) that could cause the frequency chirp other than the semiconductor gain mirror itself. For those SML works assuming a Kerr nonlinearity acting as the pulse-shaping mechanism in a semiconductor gain medium, the frequency chirp would be generated inherently [19], because the Kerr effect exists not only in the spatial but also temporal domains. The typically Gaussian spatial distribution of irradiance may act as the so-to-say chip-integrated Kerr lens and accordingly start the mode-locking process (with a soft or hard aperture in the cavity). Concurrently, the time-varying light intensity I(t) of a propagating cavity pulse implies a temporal Kerr effect. The temporal variation of the nonlinear refractive index n(t) = n0 + n2I(t) can alter the phase of a pulse and produce new frequency components, thus generating the frequency chirp [19]. In addition to intracavity chirp, SML-VECSEL performance is prone to power-dependencies or cavity-length-dependencies, such as switching between fundamental and harmonic mode-locking (cf. refs. [12,35]) or between the regimes of instable, Q-switched, and stable mode-locking (cf. refs. [18,19]). Similarly, a VECSEL can experience switching between fundamental-mode and high-order-transverse-modes pulse trains by the adjustment of resonator optics or power levels (cf. refs. [25,33]), and the SML operation onset was once reported to coincide with the threshold power for high-order transverse mode emission [27].
In recent theoretical work, the parameters for the saturable-absorber equivalent composed of an effective Kerr lens and a soft aperture (defined by the pump spot’s overlapping area with the laser spot) in the SML VECSEL’s cavity were analyzed [18]. This is aimed at understanding how applied pump power—acting as the tuning knob for the given focal length of the chip-internal Kerr lens—and intracavity aperture affect mode-locking. The latter’s aperture size acts as the primary means to change the modulation depth of the artificial saturable absorber. With the help of calculated loss difference for the laser beam per round-trip between the cases of acting and absent Kerr lens, operation conditions were discussed for a facilitated start of mode-locking, which is pump-dependent. Generally, the greater the loss difference, the higher the modulation depth of the SESAM equivalent. But due to the possible change of sign of the effective n2 with increasing pump density, the preferred spot size may be on the larger side of diameters before the sign flip, according to considerations in ref. [18]. Furthermore, within that theory framework, the operation regimes “Q-Switched ML”, “CW ML” (i.e., steady pulse train) and “Harmonic ML” were compared: Undersaturation of the absorber-equivalent (i.e., of the process of saturable absorption) was attributed to Q-switched ML operation. But with adequate intracavity circulating power (providing signal noise peak powers sufficient to generate any Kerr effect) and appropriate aperture size (difference between round-trip losses for ML and cw operation), regular fundamental (“CW”) ML was deemed achievable. Mode-locking behavior in previously reported experimental results with fundamental, 2nd, and 3rd harmonic SML [12] was explained to be consistent with the reported simulation findings [18]—with higher harmonics requiring more saturable absorption and higher pump intensity. Note that some predictions for the pulse width behavior for altered saturation parameters for gain and absorption are given, too.
To achieve a kind of Kerr-lens integrated analog to the saturable-absorber integrated ultrafast MIXSEL (abbreviation for mode-locked integrated external-cavity surface emitting laser, cf. [14]), the combination of tailored nonlinear lensing and phase modulation features in the chip appears crucial. Recent investigations on gain dynamics and nonlinear lensing [40] as well as on the role of noise and GDD [35] and follow-up studies may all together facilitate the design of cost-effective, compact, and reliable SML (comb) devices.
Interestingly, a new possible mechanism for SML/comb occurrence in semiconductor lasers has been recently introduced and examined, referred to as “phase turbulence” in the discussion of frequency combs induced in QCL ring lasers [41] and revisited for SDLs [35] (also see refs. [42,43] therein on phase instabilities). This generally motivates a deeper examination and discussion with respect to the phenomena and features observable for SML SDLs which may result in more matured design principles concerning comb generation with VECSELs.

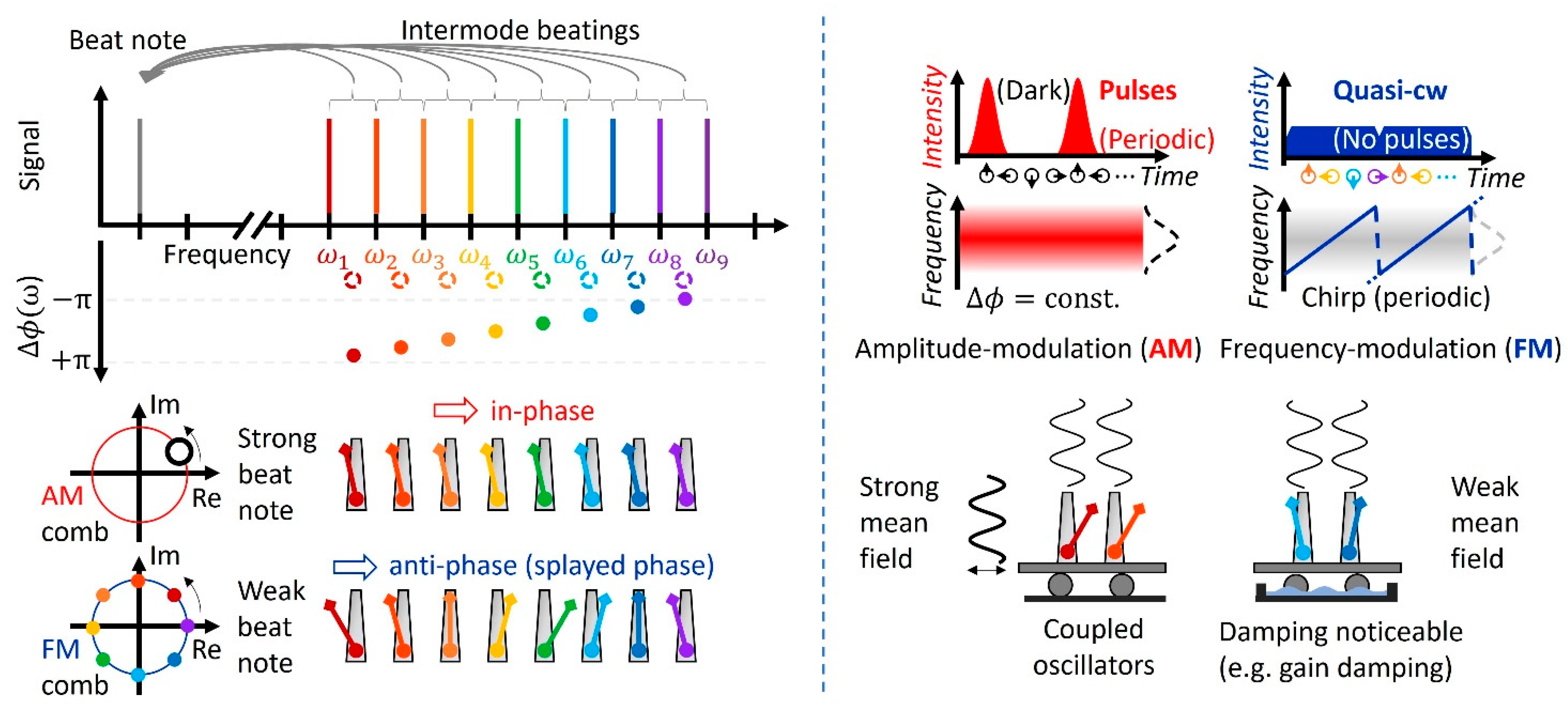
1.2. From Self-Mode-Locking to a Frequency-Modulated Comb

In brief, recent advances in VECSEL technology clearly indicate new trends such as self-starting ultrashort-pulse or self-starting optical-comb generation [5,30,35] and their potential for applications in spectroscopy, sensing and metrology [44,45]. Figure 2a–g show experimental signatures of SML-based sub-ps pulsing from a quantum-dot VECSEL [26] and FM-comb formation in a quantum-well VECSEL [30], respectively.
Intrinsically, (self-)mode-locking is related to frequency-comb generation. To enter and maintain the regime of an optical frequency comb, a locking mechanism is needed. Such a mechanism should compensate for dispersion and noise in VECSELs which otherwise prevent the equidistance and phase coherence, respectively, of the modes. Equidistantly spaced laser lines and a fixed phase relationship between adjacent longitudinal modes oscillating in the resonator can characterize a frequency comb. It is nowadays understood that a comb state in semiconductor lasers can occur in the absence of a saturable absorber [46,47] and can exhibit an interesting characteristic linear frequency chirp—“frequency modulation” (FM)—in the time domain [48,49].
A common approach to achieve mode-locking is based on nonlinear optics in the laser cavity, where (a medium’s) saturable absorption typically provides a coupling mechanism between laser modes. Both the FM comb and the commonly considered amplitude-modulated (AM) comb arise from the locking of the modes. AM comb formation typically results in ultrashort pulses in the time domain and the underlying mode-locking regime can be understood as in-phase synchronization of laser modes [50,51]. In the FM comb case, the beating of different laser modes leads to oscillations of the carrier density in the gain medium at multiples of the laser repetition rate (i.e., the longitudinal mode frequency spacing). In turn, these oscillations again couple with the laser modes. In sum, this provides the locking mechanism and has been discussed primarily for interband-cascade and quantum-cascade lasers and later also in interband diode lasers. Theoretical considerations have suggested that the interplay of group-delay dispersion (GDD) and carrier-induced refractive-index changes lead to soliton-like states. This principally leads to the FM comb formation observed in these edge emitting semiconductor laser diodes [51], as sketched in Figure 3.
Figure 3 represents a schematic comparison of the two synchronization states for the oscillating laser modes. To be more specific, the one state attributed to AM comb formation is the “in-phase” state, the other state related to FM combs is referred to as the “splayed phase” (or antiphase) state. The former type yields a strong mean field because intermode beat notes can have the same phase, whereas the latter exhibits phases between the intermode beat notes across the laser spectrum spanning a range from 0 to 2π, with a weak mean field [51]. In other words, such antiphase states feature for each intermode beat note another one that is π out of phase with it (see bottom left diagram in Figure 3). Corresponding FM-comp emission was reported in various types of (free-running) semiconductor lasers, with both interband laser transitions [30,51,52,53], including cascaded [54], and intraband (quantum) cascaded [55,56,57]. A detailed discussion of quasi-cw FM-type and pulsed AM-type frequency combs (cf. Figure 3) can be found for instance in ref. [51]. It is noteworthy that FM mode-locking is, however, not a new phenomenon and was discussed in the past also for solid state lasers [58].
Figure 4 furthermore indicates the difference in temporal evolution between an amplitude-modulated (AM) and FM comb signal. The example time trace for the stable AM comb as well as instable multimode output on the right side of Figure 4 is sketched after recorded traces for a VECSEL in a Streak-camera experiment in ref. [35]. An additional diagram for the FM comb indicates the periodic sweep in the instantaneous frequency (the single mode of the multimode system “on”, i.e., emitting, at the given-time)—like in a traffic light. Apparently, it would be a highlight to obtain experimental demonstrations of such a time-dependent emission signature of the FM-comb state with a system capable of resolving such a temporal and spectral pattern (spatially on a detector screen with time-tagged events, such as with a Streak camera system).
It was discovered that such an FM comb state can also arise in the optically pumped semiconductor disk lasers, the VECSELs [30]. That is, such a comb state was established from a gain mirror disk with a vertical external resonator. These lasers typically feature a gain-recovery time and round-trip time of similar magnitude. Yet, two key differences to the edge emitting counterparts would be the absence of a noticeable spatial hole burning process, which typically triggers multi-mode operation in edge emitters, and the storage of optical power away from the gain medium in a centimeters-long external cavity.
The recently reported FM comb strongly encourages further investigations on the basic properties of and the requirements for comb operation in SDLs, as well as the exploration of its utilization. Its demonstration for VECSELs in addition to that for edge-emitting diode lasers and QCLs indicates how general the phenomenon of FM combs is. Owing to the high optical power per comb line and consequently increased signal-to-noise ratio (SNR) in possible applications such as dual-comb spectroscopy [45], FM combs in VECSELs might be very practical. In terms of high-power operation with desirable spectral and beam properties, VECSELs can outperform edge emitters as discussed widely [2].
What appears most intriguing about FM combs in contrast to the more widely known amplitude-modulated combs is that their average power per time is relatively constant. The modes are locked, while a 2π phase difference exists over the span of the coherent laser emission spectrum. But not a pulse train is formed through interference in the time domain, instead the laser’s instantaneous frequency changes periodically with the round-trip time. Thus, at a single instance in time during a full repetition cycle, the laser is “ON” only with one longitudinal mode, resulting in the quasi cw output.
Challenges regarding peak and average power achievements for ultrashort pulsed VECSELs undercutting pulse durations of 100 fs [10] were attributed to fundamental non-equilibrium carrier dynamics such as kinetic hole burning [59]. With the idea of dual-comb spectroscopy in mind [45], an increased average power and consequently more power per comb line would require the increase in pulse duration by means of generating chirped pulses for a given bandwidth. In contrast, an FM comb, which can be considered the extreme case of a maximally linearly chirped “pulse”, offers quasi-cw operation (cf. Figure 4) and thus the highest average power.
It is noteworthy that the existence of FM combs in lasers with fast gain media was explained in the literature with the so-called maximum-emission principle. This principle states that the phase–amplitude relations of the laser modes will organize themselves in a way to extract the maximum amount of power from the gain medium, which corresponds to the FM state [60]. It is imaginable that the FM-comb state has remained hidden for some of the previously studied SML VECSELs and has merely awaited experimental verification. A suitable technique to accomplish the task utilizing interferometry is summarized in the next section.
Compact comb sources are promising for dual-comb spectroscopy. It enables the realization of a simple absorption spectrometer, which comes without any moving parts, as is the case for Fourier-transform or grating-based spectrometers. Furthermore, it gives the ability to evaluate spectral signatures of a specimen via the comb’s beat frequencies in the radio-frequency region (e.g., GHz) for easier signal acquisition. This concept has for instance widespread use in gas sensing, such as in industrial process monitoring [44].

2. Methodology and Outcomes Summarized

2.1. Mechanism Behind Self-Mode-Locking in VECSELs

In short, the early working hypothesis of Kerr lens mode-locking in the VECSEL community has triggered a wave of nonlinear-refractive index studies for SDL chips, as SESAM-free VECSELs with an inserted slit in the external cavity resemble coarsely the design of commonly used ultrashort-pulsed Ti:Sa lasers. Nonetheless, despite the analogy to SML solid-state lasers, those pulsing SDLs mostly do not exhibit comprehensive measures for dispersion management or profound control of Kerr-lens-assisted SML achievement at the current stage. However, care has to be taken with the assumption of Kerr lensing (KL), since nonlinear lensing effects are not necessarily based on a Kerr nonlinearity in the VECSEL chip (gain medium) but can be free-carrier related, and since mode-locking (even when such a Kerr medium may contribute to it) can result as an interplay of different (nonlinear) pulse-shaping mechanisms. Those mechanisms could be gain dynamics, four-wave mixing, self-phase modulation. and the lensing behaviors supported inside the laser. Thus, a constructive scientific discussion arose among experts in this field after initial reports on self-mode-locked (or KL-ML) VECSELs [5].
Numerous works of the past decade demonstrated self-starting ML VECSELs with different chip types and explanations [9,12,22,23,24,26,29]. A particularly clear demonstration of mode-locking in an SML device [9] included using nonlinear frequency conversion and long-time-span autocorrelation measurements to evidence pulsing, as well as side-mode free RF spectra and beam-profile measurements to reveal stable and fundamental transverse-mode operation with excellent M2 values, respectively.
Furthermore, a few specific works were conducted shortly after, which could support the claim of nonlinear lensing, i.e., the involvement of a chip-based lensing phenomenon [39,61,62,63,64], and even inferred ultrafast Kerr lensing [40] and four-wave-mixing [30] as reasonable candidates behind pulse and comb formation, respectively. While no community-wide consent exists on what mechanism (exactly) causes such SML behaviors, a strongly improved understanding has been established so far together with the wider academic belief that the lensing-induced perturbation in the cavity can be sufficient.
Nonetheless, key questions remain, such as to what extent the magnitude and sign of the (Kerr) lens affects the operation regime and cavity design aspects, or such as whether there can be a tuning knob exploited among the design parameters of the chip itself. That is, to facilitate, trigger, stabilize or even enhance/adjust ultrashort pulse formation, or, similarly, suppress it in favor of a frequency-modulated comb state.
Whether the near future brings up a “Kerr-lens integrated” chip version of the VECSEL, or a “(FM-)comb integrated” one, remains to be seen. It may critically depend on the matured view on the mode-locking mechanisms possible and involved. Because a nonlinear lens acting as an artificial saturable absorber does not necessarily equate to a mechanism establishing phase coherence across the oscillating modes in the laser emission, such as for the FM-comb state.
Further studies are motivated to unravel the interplay of different effects behind the SML regimes obtainable. The involvement in SML as well as nonlinearity studies of DBR-free SDL membrane gain chips, as developed among others by pioneering research groups worldwide (referred to as MECSEL, MEXL or similar), additionally promises to contribute to the advantages of those possible bandwidth and flexibility benefits expected from a DBR-free design. It should be noted that for designs with intracavity transparent heat spreaders, basically the (Kerr-lensing) nonlinearity of this thin element should add up to that of the gain chip to reach the “black-box” VECSEL core element’s effective nonlinear lensing capability. For example, the used intracavity SiC heat spreader in the (pumped chip’s) Z-scan examination of close-to-operation conditions was measured to exhibit 0.001 × 10−16 m2/W [64].
The collaborative activities of the author’s VECSEL team previously at the University of Marburg together with regional and international partners focused mainly on two aspects. Firstly, one aim was to render (Kerr lens) self-mode-locking an appealing pathway towards ultrashort pulses. Gaafar et al. demonstrated and characterized SML VECSELs based on quantum-well [9,12] or quantum-dot [26] gain media in the infrared and for visible light [29]. Secondly, nonlinear optics studies followed for VECSEL chips, i.e., the single intracavity element, which can introduce a pulse-shaping mechanism to the device, to unravel the mechanisms behind the SML phenomenon. The nonlinearity studies by Kriso et al. comprised time-integrating Z-scan (Figure 5) and later time-resolving beam-deflection experiments [39,40,64], complemented by considerations regarding the group-delay dispersion (GDD), pulse durations, and the microcavity effect in the chip. Experiments were conducted with and without optical carrier excitation (pumping).
Typical VECSEL chips indeed exhibit an intensity-dependent lensing (i.e., nonlinear refraction) and show rather a minor influence of the typical optical pumping situation on it, as demonstrated so far by different Z-scan experiments (see early measurements [61,62,63] and detailed spectrally- and time-resolved studies [39,40,64]). Correspondingly, one can already deduce an effective nonlinear refractive index value for a given “black-box” VECSEL chip to be of the order of negative 10−16 m2/W. It was shown that the microcavity strongly affects the measured effective nonlinear refraction as well as absorption of the (unpumped) gain mirror [39]. When accounting for a thermal shift of the lasing wavelength of the pumped VECSEL chip, the effective n2 decreases for the probe pulses of 150-fs duration with increasing optical excitation density [64]. Whereas, for an optically excited DBR-free VECSEL, it was recently reported that the sign of the effective n2 (initially negative) can become opposite (positive) for higher chip-excitation fluences and longer pulse lengths [40].
Only time-resolved measurements of the nonlinearity seemingly provide the bigger picture regarding the origin of nonlinear lensing that can be attributed to either an ultrafast bound-electronic Kerr effect (BEKE)—if taking place on the fs scale—or to free-carrier nonlinearities (FCN)—on the ps scale. In fact, the interplay of both effects, BEKE and FCN, had been assumed as the reason behind stable self-mode-locking, acting as both an ultrafast and slow artificial saturable absorber, respectively (see discussion in ref. [39]).
An important step forward was delivered by the follow-up study with the ultrafast beam-deflection technique [40]. Such a beam-deflection experiment enabled to probe the gain dynamics and the pulse-length differences of the nonlinear lensing. A time-resolved refractive index response of a MECSEL chip (i.e., DBR-free gain membrane) as a function of different excitation fluences was probed. This allowed calculating that the effective n2 (initially negative for sub-ps pulses and low carrier excitation) became positive for high excitation fluences and for pulse lengths larger than 1 ps. In this context, the unexpected n2 sign change from negative to positive hinted at the respective nature of the lensing. While for ultrashort times, a Kerr (lensing) effect appears to be the key (plausible) effect, thus remaining a very reasonable starting mechanism for VECSELs by sufficiently perturbing the intracavity beam, it is the free charge-carrier effects which play a dominant role above ps pulse durations. Thus, for long pulses the free-carrier dynamics become additionally important.
It is worth noting that the DBR-free VECSEL structure does not exhibit any pronounced microcavity effect at the lasing wavelength due to the lack of the incidence-angle and wavelength-sensitive Bragg mirror (planar layered structure) in typical gain chips (cf. ref. [16]). In most VECSEL chips, the microcavity effect governs the emission behavior significantly, and similarly, the longitudinal confinement factor (LCF) shapes the strength of the nonlinear lensing behavior [39] (cf. Figure 6). Thus, the spectral positions, at which the quantum wells (QWs) emit and where the maximum photoluminescence (PL) from the surface of the chip lies, differ. For resonant designs, microcavity enhancement is desired at the cost of temporal pulse lengths, and for antiresonant designs the reduced overlap with the QWs broadens the spectrum at the cost of power extraction (cf. refs. [2,3]). The less microcavity effect present, the more material properties matter. For bulk GaAs, the literature value n2 at 1060 nm is about 0.3 × 10−16 m2/W according to ref. [65]. In contrast, for the QW material InGaAsP in ref. [58], n2 ~ 5 × 10−16 m2/W close to the lasing wavelength was calculated. Table 2 summarizes the main nonlinear-lensing findings from these six prominent VECSEL experiments.

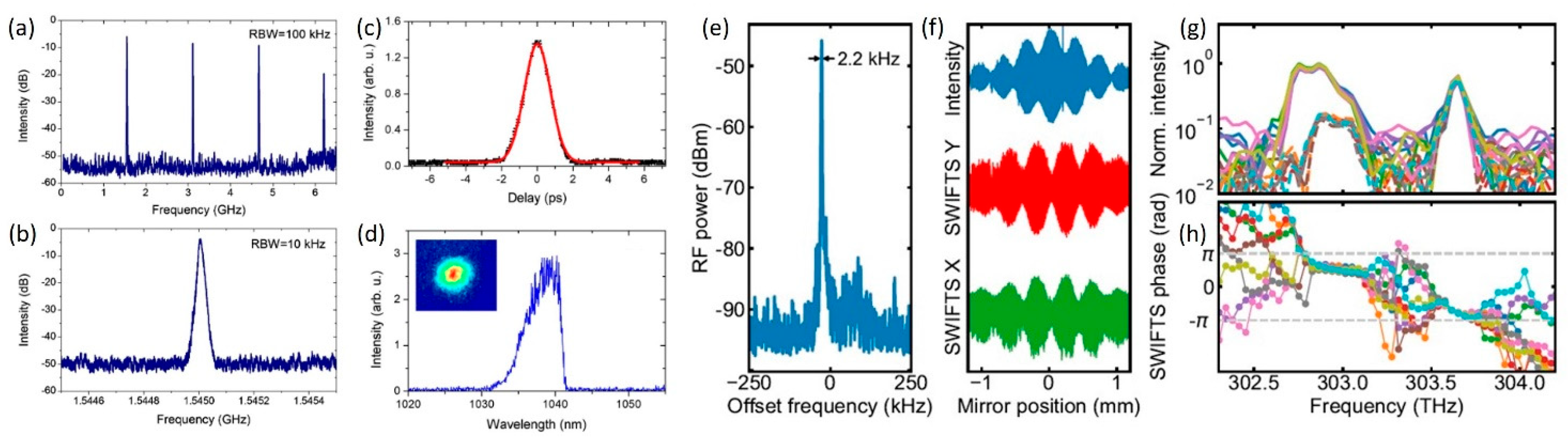
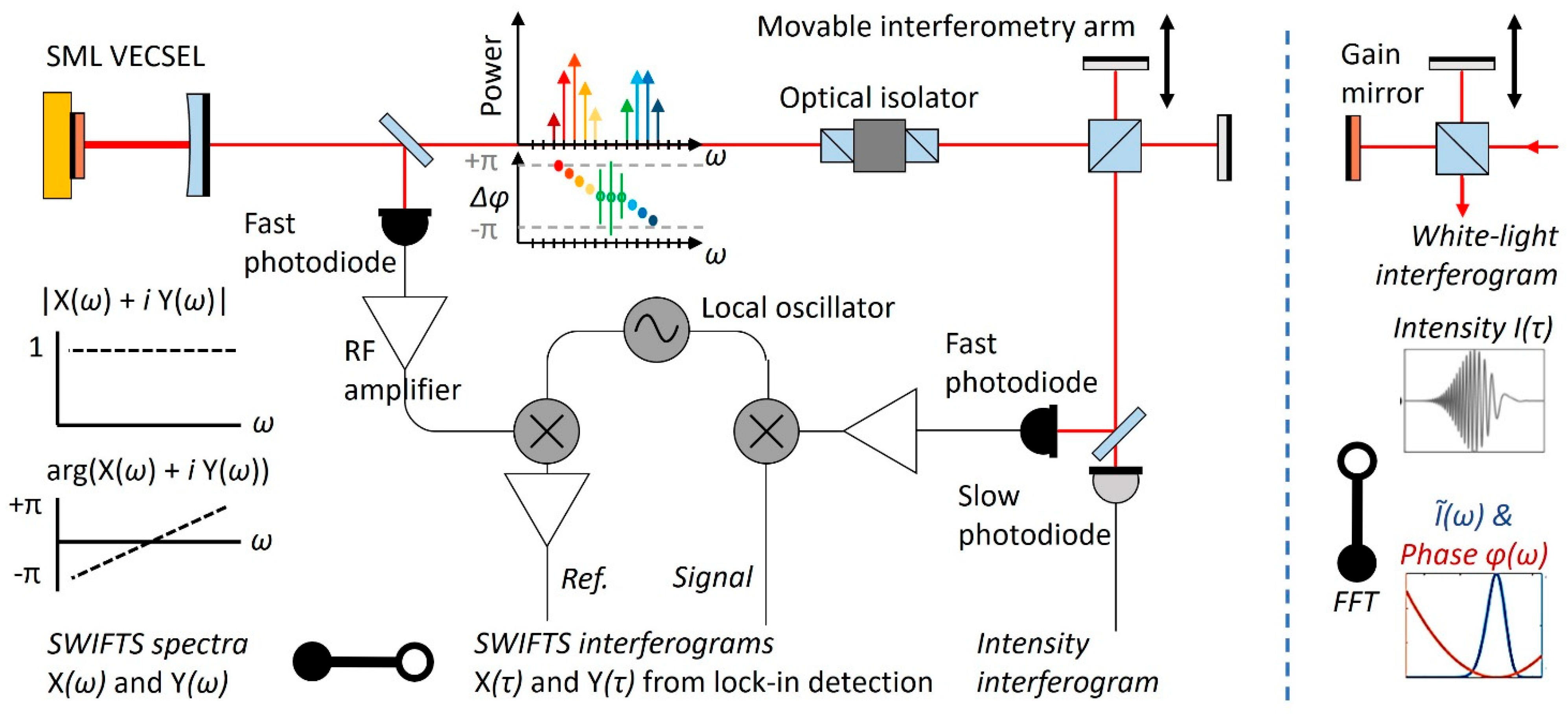
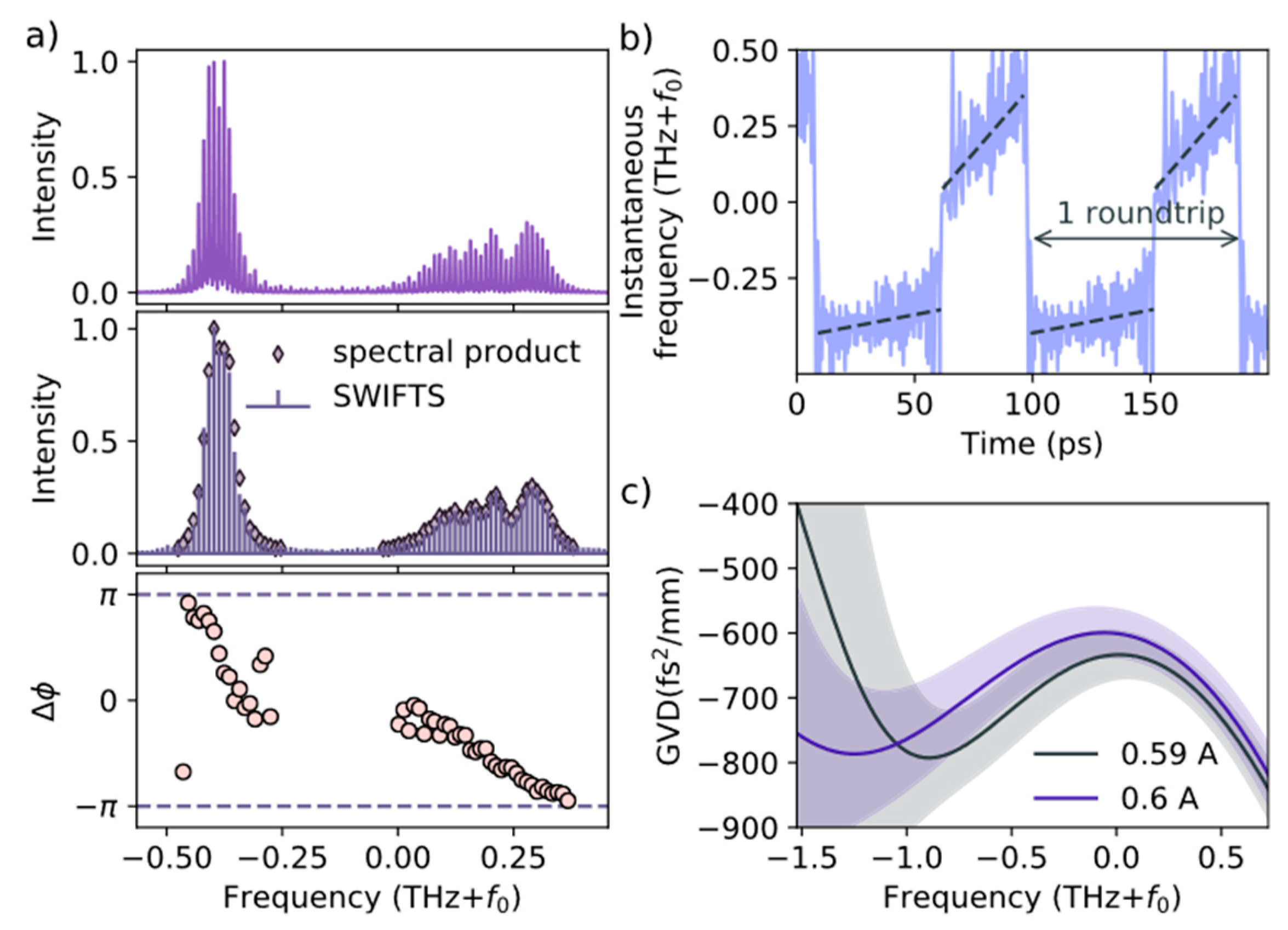
2.2. FM-Comb SML VECSEL and Shifted-Wave-Interference Fourier-Transform Spectroscopy (SWIFTS)

Ultimately, measurements regarding the phase information of the optical so-to-say “pulses” in VECSELs with detectable self-mode-locking signatures (imminent stable pulse trains) revealed a self-starting FM-comb state, which was characterized in a foundational study [30]. This followed the implementation of a so-called “SWIFTS” experiment for ML VECSELs, employing an antiresonant 970-nm VECSEL for the characterization of its (phase-coherent) output.
SWIFTS is a technique which allows the measuring of the intermode phase relation of a laser without requiring high peak powers and can reveal the coherence within the laser spectrum (or parts thereof) [66]. It rendered itself well suited for the characterization of laser sources with GHz repetition rates and FM comb emission, or with long pulses. It is a coherent beat-note spectroscopy technique previously employed to investigate comb states in quantum-cascade lasers (see ref. [66]). While it could also be theoretically used to measure the pulse width and chirp of ultrashort pulses, the Signal-to-Noise Ratio (SNR) of the measurement according to ref. [67] would usually shrink a lot for very short pulse lengths (<1 ps) and for relatively low repetition rates, e.g., of the order of MHz. For (S)ML VECSELs with pulse durations above ps and repetition rates above 500 MHz, the SWIFTS technique may actually offer an alternative versatile means of emission characterization, including the probing of phase stability (coherence) over the laser spectrum. Otherwise, pulse characterization typically relies on a sufficient second-harmonic signal in intensity-autocorrelation-type experiments. Particularly linear cavities with their commonly shorter resonators and typically GHz repetition rates could be used in combination with chirped out-coupling mirrors for GDD compensation for stable pulsed or FM-comb emission, which would be analyzable with SWIFTS. For the FM comb state, an intermode phase spanning 2π over the whole laser spectrum is a characteristic result obtained from the phase-sensitive SWIFTS measurements of such mode-locked laser’s emission. Self-starting FM-comb operation of a VECSEL was demonstrated accordingly [30]. Figure 7 shows a schematic drawing of the experiment.

3. Applications and Outlook Comb V(E)CSEL

3.1. Dual-Comb Spectroscopy, Quantum Metrology, and More

Semiconductor lasers remain a practical and attractive platform for application-oriented device development due to their compact nature, design flexibility, and not seldom turn-key small-footprint architectures. Additional research interest in semiconductor lasers emerged recently due to their capacity to emit FM combs.
The optical AM combs produced by VECSELs have already been proposed for spectroscopic applications, such as dual comb spectroscopy with a single ML semiconductor disk laser (of MIXSEL-design type) [45]. High-precision sensing with RF frequencies (i.e., MHz-GHz offset in the repetition rates of the two optical combs employed) can be attractive for the chemical analysis of gases in industrial applications. Application potential lies for instance in dual-comb hyperspectral imaging promising spatial information when doing molecular fingerprinting with ultra-high spectral resolution, such as pursued with other laser types [70].
While for or QCLs and diode lasers, the FM-comb state appears as a fundamental operation regime utilizable for applications such as dual comb spectroscopy [51,71], the possibility to yield high-power, compact dual comb sources based on FM-comb VECSELs, where the device could deliver high-power comb lines in a frequency-sweeping quasi-cw regime to the experiment, and where the wavelength could be designed by semiconductor technology, is attractive. However, spectrally dependent dispersion has been identified to be detrimental for comb performance and leads to a decreased comb bandwidth and the appearance of spectral holes [72]: It is deemed responsible for nonuniform comb spectra, nonlinear frequency chirp, and spectral narrowing. To overcome such limitations for FM-comb deployment to applications, accordingly, compensation of higher-order dispersion in the VECSEL chip may become an essential aspect for the design optimization towards improving FM comb operation. An experimental study by Opačak and coworkers [72] on the impact of group velocity dispersion (GVD, equals GDD per unit length) for a semiconductor laser platform with FM-comb emission is summarized in Figure 8. Accordingly, such wavelength-dependent dispersion in the optical system (e.g., the VECSEL chip’s GDD, also known as second-order dispersion) could cause the observation of imperfect combs, e.g., with a split emission spectrum, or partial coherence, such as discussed in the literature (cf. [73]).
While unstable (S)ML pulses feature a so-called “coherent artifact” in intensity autocorrelation traced on top of a so-called “pedestal” indicating partial mode-locking (cf. Chapters on mode-locking in ref. [2]), the autocorrelation measurement has commonly not been accomplished for such quasi-cw operation with the FM-comb state. This is—one recalls—because an efficient optical gating (frequency conversion) process in the autocorrelator usually relies on peak power and relatively short pulses, what renders SWIFTS the platform of choice for low-intensity ML characterization. Moreover, note that the topic of partial coherence, mode-locking stability, and the possible lack of a coherent wavefront from all portions of the output spectrum can be regarded as a subject of ongoing and following studies in this community.
FM-comb VECSELs can be particularly appealing for the study of physical properties of partially coherent combs and cluster synchronization phenomena in coupled-oscillator populations [73]. For instance, occurring beat notes within two families can be synchronized in opposite configurations—in-phase and antiphase, as recent studies on the so-called “cluster synchronization state” with the coherent beat note detection scheme on a quantum cascade laser (QCL) demonstrated (see SWIFTS technique). In such a state, both synchronization states, that are the FM-comb and the AM-comb state, occurred simultaneously in their Fabry–Pérot QCL [73]. According to Kazakov et al., this cluster state is seemingly inherent to Fabry–Pérot cavities, which give the class of resonators basically characteristic for V(E)CSELs, as well as for edge-emitting diode lasers.
The further investigation of the aforementioned effects and scenarios for VECSELs—some apparently related to recent studies on cluster synchronization summarized above—promise better control of the spectral and temporal properties of FM-comb VECSELs through possible design optimization. According to the literature (cf. ref. [72] and refs. therein), the particular modal phase arrangement of FM combs originates purely from a Kerr third-order optical nonlinearity or a GVD present in the laser system with optical losses through a finite resonator quality. Thus, with chip-internal dispersion and Kerr nonlinearity as tunable properties at one’s disposal, further knowhow on GDD and χ(3) properties can enable a new generation of comb VECSELs. The important studies towards such are directly linked to characterization work with the techniques and tools described in the context of SML (AM/FM-comb) VECSEL discoveries above.
Also, ultrashort pulse generation with VECSELs can benefit from developments in the domain of (generally) self-mode-locking and (more specifically) comb studies with QCLs, such as those looking into giant ultrafast optical nonlinearities [74] and transitions between mode-locking states (e.g., FM comb to dissipative Kerr soliton) [75], respectively. One may recall that regarding the FM-comb mode-locked regime the Kerr nonlinearity does not act as the pulse-forming “artificial saturable absorber” via self-focusing, but as a nonlinear mechanism which “tunes” the modes into the anti-phase state (splayed-phase synchronization) with the resulting characteristic (linear) chirp for the saturable-absorber-free QCLs.
Besides spectroscopy, comb lasers are attractive for quantum metrology, quantum optics and photonic computing. Nanophotonic comb devices can even become part of (optical) artificial neural networks for speedy and powerful information processing devices in the field of artificial intelligence with light. For instance, such combs—so far obtained from chip-integrated micro-size light sources [76]—can be used for wavelength multiplexing in matrix vector multiplication units enabling highly parallel data processing via noninteracting photons of different wavelengths.
For the interested reader, beyond VECSELs and QCLs, a broadband quantum-dot FM-comb laser is reported in a work by Dong et al., where the authors demonstrate an electrically driven 60 GHz mode-locked laser in which both the AM comb and the FM comb can be generated independently [77]. Additionally, the authors of the study state that the Kerr nonlinearity can be practically engineered to improve the FM comb bandwidth without the need for GVD engineering.
Furthermore, interesting details and the current status of FM combs in semiconductor lasers based on Fabry–Pérot cavities can be discovered through the recently published Perspective article “Self-frequency-modulated laser combs”, by Roy, Zeng, and Burghoff, which focuses on the physical origin, modeling, characterization, bandwidth enhancement, and application potentials [78].

3.2. Further Advances on Self-Mode-Locked VECSELs

Note that during the preparation time of this review, ongoing efforts in the VECSEL research community have led to further reports which are briefly highlighted in this appended subsection. Because mode-locking achievements based on SESAM-free devices can benefit both FM-comb and AM-comb VECSEL applications, this subject has been receiving further attention since its early days one decade ago.
A synchronized dual-pulse self-mode-locked VECSEL at around 980 nm with 890-fs-short pulses was reported by Mao et al. recently [79]: The 1-ns separated dual-pulses were examined at VECSEL output levels of 2 W, whereas the authors’ device could be also operated in single-pulse fundamental mode-locking state with 1.2 ps pulse duration at a repetition rate of 416 MHz.
At longer wavelengths, a self-mode-locked 2-µm GaSb-based device was reported by Feng et al. with about 255-ps-long pulses at a repetition rate of 404 MHz at VECSEL output levels of approximately 0.2 W [80].
Since early reports on self-mode-locking discussed higher-order modes as a possible element in the mechanisms behind the self-starting effect (see Table 1, ref. [25]), a recent work in this context was published and demonstrated “robust mode-locking with high-order transverse mode in a Kerr-lens mode-locked” VECSEL [81].

4. Conclusions

To summarize, self-mode-locking has emerged as a noteworthy and believable pathway towards ultrashort pulse generation from VECSELs, and nonlinear lensing for the semiconductor disk laser’s chip is recognized as one likely intracavity pulse forming mechanism according to independent as well as consecutive investigations. The term “SESAM-free” became synonymous with “self-starting” or “magic” mode-locking in the past. Among the achievable self-starting mode-locking states in semiconductor lasers, the FM-comb state attracts particular attention due to the possible applications of high-power-per-line quasi-cw light sources with phase coherent output and the interesting peculiarities associated with phase and anti-phase synchronization of longitudinal laser modes in optical comb-producing semiconductor lasers.
Expectedly, existing testbed ML-SDL platforms can be beneficial for a deeper investigation of (self-)mode-locking with the SWIFTS technique, supported by the conventional method of phase and pulse-duration mapping such as by the Frequency-Resolved-Optical-Gating (FROG) method. In addition, novel computer-based optimization, classification, and inference tools (which were recently highlighted for ultrafast photonics [82]) can be utilized towards tailoring VECSEL output with exquisite mode-locking properties. Also, the role of GDD in the occurrence of different emission regimes should be further considered, particularly with eyes towards a transition between an ultrashort-pulsed and a quasi-cw mode-locked regime.

Funding

Funding by the Deutsche Forschungsgemeinschaft (DFG, the German Research Foundation) through grants RA2841/1-1 & 1-3 (ID 290461173), and RA2841/12-1 (ID 456700276) is acknowledged.

Acknowledgments

Many thanks are devoted to C. Kriso, the author’s former team member and project staff member, for joint VECSEL investigations with a focus on the mechanisms behind self-mode-locking during his PhD studies [83] and literature suggestions, as well as to M. Gaafar, likewise a former team member, for his achievements on self-mode-locked VECSELs during his PhD studies [84]. The author is also grateful to all the VECSEL team members during the past decade, for their help and contributions, as well as to the Semiconductor Photonics Group in Marburg and cooperation partners worldwide for fruitful research opportunities.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Hoogland, S.; Dhanjal, S.; Tropper, A.C.; Roberts, S.J.; Häring, R.; Paschotta, R.; Keller, U. Passively mode-locked diode-pumped surface-emitting semiconductor laser. IEEE Photonics Technol. Lett. 2000, 12, 1135–1137. [Google Scholar] [CrossRef]
  2. Jetter, M.; Michler, P. Vertical External Cavity Surface Emitting Lasers: VECSEL Technology and Applications; Wiley-VCH: Weinheim, Germany, 2021; ISBN 978-3-527-41362-1. [Google Scholar] [CrossRef]
  3. Keller, U.; Tropper, A.C. Passively modelocked surface-emitting semiconductor lasers. Phys. Rep. 2006, 429, 67–120. [Google Scholar] [CrossRef]
  4. Tilma, B.W.; Mangold, M.; Zaugg CALink, S.M.; Waldburger, D.; Klenner, A.; Mayer, A.S.; Gini, E.; Golling, M.; Keller, U. Mode-locked semiconductor disk lasers. Light Sci. Appl. 2015, 4, e310. [Google Scholar] [CrossRef]
  5. Gaafar, M.A.; Rahimi-Iman, A.; Fedorova, K.A.; Stolz, W.; Rafailov, E.U.; Koch, M. Mode-locked semiconductor disk lasers. Adv. Opt. Photonics 2016, 8, 370–400. [Google Scholar] [CrossRef]
  6. Spence, D.E.; Kean, P.N.; Sibbett, W. 60-fsec pulse generation from a self-mode-locked Ti: Sapphire laser. Opt. Lett. 1991, 16, 42–44. [Google Scholar] [CrossRef]
  7. Keller, U.; ’tHooft, G.W.; Knox, W.H.; Cunningham, J.E. Femtosecond pulses from a continuously self-starting passively mode-locked Ti:sapphire laser. Opt. Lett. 1991, 16, 1022–1024. [Google Scholar] [CrossRef]
  8. Klopp, P.; Griebner, U.; Zorn Mund Weyers, M. Pulse repetition rate up to 92 GHz or pulse duration shorter than 110 fs from a mode-locked semiconductor disk laser. Appl. Phys. Lett. 2011, 98, 071103. [Google Scholar] [CrossRef]
  9. Gaafar, M.; Richter, P.; Keskin, H.; Möller, C.; Wichmann, M.; Stolz, W.; Rahimi-Iman, A.; Koch, M. Self-mode-locking semiconductor disk laser. Opt. Express 2014, 22, 28390–28399. [Google Scholar] [CrossRef]
  10. Waldburger, D.; Link, S.M.; Mangold, M.; Alfieri, C.G.E.; Gini, E.; Golling, M.; Tilma, B.W.; Keller, U. High-power 100 fs semiconductor disk lasers. Optica 2016, 3, 844–852. [Google Scholar] [CrossRef]
  11. Wilcox, K.G.; Tropper, A.C.; Beere, H.E.D.A.; Ritchie, B.; Kunert, B.; Heinen Stolz, W. 4.35 kW peak power femtosecond pulse mode-locked VECSEL for supercontinuum generation. Opt. Express 2013, 21, 1599–1605. [Google Scholar]
  12. Gaafar, M.; Möller, C.; Wichmann, M.; Heinen, B.; Kunert, B.; Rahimi-Iman, A.; Stolz, W.; Koch, M. Harmonic self-mode-locking of optically pumped semiconductor disc laser. Electron. Lett. 2014, 50, 542–543. [Google Scholar] [CrossRef]
  13. Husaini, S.; Bedford, R.G. Graphene saturable absorber for high power semiconductor disk laser mode-locking. Appl. Phys. Lett. 2014, 104, 161107. [Google Scholar] [CrossRef]
  14. Mangold, M.; Golling, M.; Gini, E.; Tilma, B.W.; Keller, U. Sub-300-femtosecond operation from a MIXSEL. Opt. Express 2015, 23, 22043–22059. [Google Scholar] [CrossRef]
  15. Laurain, A.; Kilen, I.; Hader, J.; Perez, A.R.; Ludewig, P.; Stolz, W.; Balakrishnan, G.; Koch, S.W.; Moloney, J.V. Modeling and experimental realization of modelocked VECSEL producing high power sub-100 fs pulses. Appl. Phys. Lett. 2018, 113, 121113. [Google Scholar] [CrossRef]
  16. Zhang, M.; Albrecht, A.R.; Nguyen, C.; Follman, D.; Cole, G.D.; Sheik-Bahae, M. Hybrid membrane-external-cavity surface-emitting laser. Opt. Express 2022, 30, 42470. [Google Scholar] [CrossRef]
  17. Kilen, I.; Koch, S.W.; Hader, J.; Moloney, J.V. Fully microscopic modeling of mode locking in microcavity lasers. JOSAB 2015, 33, 75–80. [Google Scholar] [CrossRef]
  18. Wang, T.; Zhu, R.; Tong, C.; Liu, Y.; Zhang, P. Dynamics Simulation of Self-Mode-Locking in a Semiconductor Disk Laser Using Delay Differential Equations. Photonics 2022, 9, 859. [Google Scholar] [CrossRef]
  19. Zhang, P.; Zhu, R.; Wang, T.; Wu, Y.; Tong, C.; Wang, L.; Song, Y. Dynamics Simulation and Experimental Investigation of Q-Switching in a Self-Mode-Locked Semiconductor Disk Laser. IEEE Photonics J. 2022, 14, 1548808. [Google Scholar] [CrossRef]
  20. Tropper, C.; Hoogland, S. Extended cavity surface-emitting semiconductor lasers. Prog. Quantum Electron. 2006, 30, 1–43. [Google Scholar] [CrossRef]
  21. Schlehahn, A.; Gaafar, M.; Vaupel, M.; Gschrey, M.; Schnauber, P.; Schulze, J.-H.; Rodt, S.; Strittmatter, A.; Stolz, W.; Rahimi-Iman, A.; et al. Single-photon emission at a rate of 143MHz from a deterministic quantum-dot microlens triggered by a mode-locked vertical-external-cavity surface-emitting laser. Appl. Phys. Lett. 2015, 107, 041105. [Google Scholar] [CrossRef]
  22. Chen, Y.F.; Lee, Y.C.; Liang, H.C.; Lin, K.Y.; Su, K.W.; Huang, K.F. Femtosecond high-power spontaneous mode-locked operation in vertical-external cavity surface-emitting laser with gigahertz oscillation. Opt. Lett. 2011, 36, 4581–4583. [Google Scholar] [CrossRef] [PubMed]
  23. Kornaszewski, L.; Maker, G.; Malcolm, G.P.A.; Butkus, M.; Rafailov, E.U.; Hamilton, C.J. SESAM-free mode-locked semiconductor disk laser. Laser Photonics Rev. 2012, 6, L20–L23. [Google Scholar] [CrossRef]
  24. Albrecht, A.R.; Wang, Y.; Ghasemkhani, M.; Seletskiy, D.V.; Cederberg, J.G.; Sheik-Bahae, M. Exploring ultrafast negative Kerr effect for mode-locking vertical external-cavity surface-emitting lasers. Opt. Express 2013, 21, 28801–28808. [Google Scholar] [CrossRef] [PubMed]
  25. Liang, H.C.; Tsou, C.H.; Lee, Y.C.; Huang, K.F.; Chen, Y.F. Observation of self-mode-locking assisted by high-order transverse modes in optically pumped semiconductor lasers. Laser Phys. Lett. 2014, 11, 105803. [Google Scholar] [CrossRef]
  26. Gaafar, M.; Al Nakdali, D.; Möller, C.; Fedorova, K.A.; Wichmann, M.; Shakfa, M.K.; Zhang, F.; Rahimi-Iman, A.; Rafailov, E.U.; Koch, M. Self-mode-locked quantum-dot vertical-external-cavity surface-emitting laser. Opt. Lett. 2014, 39, 4623–4626. [Google Scholar] [CrossRef] [PubMed]
  27. Tsou, C.H.; Liang, H.C.; Wen, C.P.; Su, K.W.; Huang, K.F.; Chen, Y.F. Exploring the influence of high order transverse modes on the temporal dynamics in an optically pumped mode-locked semiconductor disk laser. Opt. Express 2015, 23, 16339–16347. [Google Scholar] [CrossRef]
  28. Rahimi-Iman, A.; Gaafar, M.; Möller, C.; Vaupel, M.; Zhang, F.; Al-Nakdali, D.; Fedorova, K.A.; Stolz, W.; Rafailov, E.U.; Koch, M. Self-mode-locked vertical-external-cavity surface-emitting laser. Proc. SPIE 2016, 9734, 90–95. [Google Scholar] [CrossRef]
  29. Bek, R.; Großmann, M.; Kahle, H.; Koch, M.; Rahimi-Iman, A.; Jetter, M.; Michler, P. Self-mode-locked AlGaInP-VECSEL. Appl. Phys. Lett. 2017, 111, 182105. [Google Scholar] [CrossRef]
  30. Kriso, C.; Barua, A.; Mohiuddin, O.; Möller, C.; Ruiz-Perez, A.; Stolz, W.; Koch, M.; Rahimi-Iman, A. Signatures of a frequency-modulated comb in a VECSEL. Optica 2021, 8, 458–463. [Google Scholar] [CrossRef]
  31. Li, C.; Cheng, J.; Zhu, R.; Wang, T.; Jiang, L.; Tong, C.; Song, Y.; Zhang, P. Intracavity third-harmonic generation in a continuous-wave/self-mode-locked semiconductor disk laser. Chin. Opt. Lett. 2023, 21, 051404. [Google Scholar] [CrossRef]
  32. Mao, L.; Hua, L.; Zhuang, B.; Tian, J.; Zhang, P.; Song, Y. Wavelength tunable self-mode locking semiconductor disk laser. In Proceedings of the International Conference on Optical and Photonic Engineering (icOPEN 2022), Online, 24–27 November 2022; p. 125502D. [Google Scholar] [CrossRef]
  33. Zhuang, B.; Hua, L.; Tian, J.; Mao, L.; Song, Y. Switching of several self-mode-locking states in an optically pumped semiconductor disk laser. Laser Phys. Lett. 2023, 20, 115801. [Google Scholar] [CrossRef]
  34. Yan, R.; Zhu, R.; Wu, Y.; Wang, T.; Jiang, L.; Lu, H.; Song, Y.; Zhang, Z. Power scaling of a self-mode-locked vertical-external-cavity surface-emitting laser. Appl. Phys. Lett. 2023, 123, 011106. [Google Scholar] [CrossRef]
  35. Chormet, B.; Blin, S.; Beaudoin, G.; Pantzas, K.; Sagnes, I.; Denet, S.; Garnache, A. Spontaneous mode locking of a multimode semiconductor laser under continuous wave operation. Front. Photonics 2023, 4, 1160251. [Google Scholar]
  36. Wilcox, K.G.; Tropper, A.C. Comment on SESAM-free mode-locked semiconductor disk laser. Laser Photonics Rev. 2013, 7, 422–423. [Google Scholar] [CrossRef]
  37. Kornaszewski, L.; Maker, G.; Malcolm, G.P.A.; Butkus, M.; Rafailov, E.U.; Hamilton, C.J. Reply to comment on SESAM-free mode-locked semiconductor disk laser. Laser Photonics Rev. 2013, 7, 555–556. [Google Scholar] [CrossRef]
  38. Rahimi-Iman, A. Self-mode-locked vertical-external-cavity surface-emitting laser, Chap. 12. In Vertical External Cavity Surface Emitting Lasers: VECSEL Technology and Applications; Jetter, M., Michler, P., Eds.; Wiley-VCH: Weinheim, Germany, 2021; ISBN 978-3527413621. [Google Scholar] [CrossRef]
  39. Kriso, C.; Kress, S.; Munshi, T.; Grossmann, M.; Bek, R.; Jetter, M.; Michler, P.; Stolz, W.; Koch, M.; Rahimi-Iman, A. Microcavity-enhanced Kerr nonlinearity in a vertical-external-cavity surface-emitting laser. Opt. Express 2019, 27, 11914–11929, Erratum in Opt. Express 2021, 29, 23290. [Google Scholar] [CrossRef]
  40. Kriso, C.; Bergmeier, T.; Giannini, N.; Albrecht, A.R.; Sheik-Bahae, M.; Benis, S.; Faryadras, S.; Van Stryland, E.W.; Hagan, D.J.; Koch, M.; et al. Probing the ultrafast gain and refractive index dynamics of a VECSEL. Appl. Phys. Lett. 2021, 119, 191105. [Google Scholar] [CrossRef]
  41. Piccardo, M.; Schwarz, B.; Kazakov, D.; Beiser, M.; Opacak, N.; Wang, Y.; Jha, S.; Hillbrand, J.; Tamagnone, M.; Chen, W.T.; et al. Frequency combs induced by phase turbulence. Nature 2020, 582, 360–364. [Google Scholar] [CrossRef]
  42. Gil, L.; Lippi, G.L. Phase instabilities in semiconductor lasers: A codimension-2 analysis. Phys. Rev. A 2014, 90, 05383. [Google Scholar] [CrossRef]
  43. Gil, L.; Lippi, G.L. Phase Instability in Semiconductor Lasers. Phys. Rev. Lett. 2014, 113, 213902. [Google Scholar] [CrossRef]
  44. Coddington, I.; Newbury, N.; Swann, W. Dual-comb spectroscopy. Optica 2016, 3, 414–426. [Google Scholar] [CrossRef] [PubMed]
  45. Link, S.M.; Maas, D.J.H.C.; Waldburger, D.; Keller, U. Dual-comb spectroscopy of water vapor with a free-running semiconductor disk laser. Science 2017, 356, 1164–1168. [Google Scholar] [CrossRef]
  46. Hugi, A.; Villares, G.; Blaser, S.; Liu, H.C.; Faist, J. Mid-infrared frequency comb based on a quantum cascade laser. Nature 2012, 492, 229–233. [Google Scholar] [CrossRef] [PubMed]
  47. Escoto, E.; Steinmeyer, G. Cage Solitons. Proc. SPIE 2020, 11263, 1126306. [Google Scholar] [CrossRef]
  48. Opacak, N.; Schwarz, B. Theory of frequency-modulated combs in lasers with spatial hole burning, dispersion, and Kerr nonlinearity. Phys. Rev. Lett. 2019, 123, 243902. [Google Scholar] [CrossRef]
  49. Burghoff, D. Unraveling the origin of frequency modulated combs using active cavity mean-field theory. Optica 2020, 7, 1781–1787. [Google Scholar] [CrossRef]
  50. Haus, H.A. Mode-locking of lasers. J. Sel. Top. Quantum Electron. 2000, 6, 1173–1185. [Google Scholar] [CrossRef]
  51. Hillbrand, J.; Auth, D.; Piccardo, M.; Opačak, N.; Gornik, E.; Strasser, G.; Capasso, F.; Breuer, S.; Schwarz, B. In-Phase and Anti-Phase Synchronization in a Laser Frequency Comb. Phys. Rev. Lett. 2020, 124, 023901. [Google Scholar] [CrossRef]
  52. Rosales, R.; Murdoch, S.G.; Watts, R.T.; Merghem, K.; Martinez, A.; Lelarge, F.; Accard, A.; Barry, L.P.; Ramdane, A. High performance mode locking characteristics of single section quantum dash lasers. Opt. Express 2012, 20, 8649–8657. [Google Scholar] [CrossRef]
  53. Sterczewski, L.A.; Frez, C.; Forouhar, S.; Burghoff, D.; Bagheri, M. Frequency-modulated diode laser frequency combs at 2 μm wavelength. APL Photonics 2020, 5, 076111. [Google Scholar] [CrossRef]
  54. Schwarz, B.; Hillbrand, J.; Beiser, M.; Andrews, A.M.; Strasser, G.; Detz, H.; Schade, A.; Weih, R.; Höfling, S. Monolithic frequency comb platform based on interband cascade lasers and detectors. Optica 2019, 6, 890–895. [Google Scholar] [CrossRef]
  55. Singleton, M.; Jouy, P.; Beck, M.; Faist, J. Evidence of linear chirp in mid-infrared quantum cascade lasers. Optica 2018, 5, 948–953. [Google Scholar] [CrossRef]
  56. Hillbrand JAndrews AMDetz HStrasser, G.; Schwarz, B. Coherent injection locking of quantum cascade laser frequency combs. Nat. Photonics 2018, 13, 101–104. [Google Scholar]
  57. Täschler, P.; Forrer ABertrand, M.; Kapsalidis, F.; Beck, M.; Faist, J. Asynchronous upconversion sampling of frequency modulated combs. Laser Photonics Rev. 2023, 17, 220063. [Google Scholar] [CrossRef]
  58. Sweetser, J.; Dunn, T.J.; Walmsley, I.A.; Radzewicz, C.; Palese, S.; Miller, R.J.D. Characterization of an FM mode-locked Nd: YLF laser synchronized with a passively mode-locked dye laser. Opt. Commun. 1993, 97, 379–387. [Google Scholar] [CrossRef]
  59. Kilen, I.; Hader, J.; Moloney, J.V.; Koch, S.W. Ultrafast nonequilibrium carrier dynamics in semiconductor laser mode locking. Optica 2014, 1, 192–197. [Google Scholar] [CrossRef]
  60. Piccardo, M.; Chevalier, P.; Schwarz, B.; Kazakov, D.; Wang, Y.; Belyanin, A.; Capasso, F. Frequency-Modulated Combs Obey a Variational Principle. Phys. Rev. Lett. 2019, 122, 253901. [Google Scholar] [CrossRef]
  61. Quarterman, A.H.; Tyrk, M.A.; Wilcox, K.G. Z-scan measurements of the nonlinear refractive index of a pumped semiconductor disk laser gain medium. Appl. Phys. Lett. 2015, 106, 011105. [Google Scholar] [CrossRef]
  62. Shaw, E.A.; Quarterman, A.H.; Turnbull, A.P.; Sverre, T.C.; Head CRTropper, A.C.; Wilcox, K.G. Nonlinear lensing in an unpumped antiresonant semiconductor disk laser gain structure. IEEE Photonics Technol. Lett. 2016, 28, 1395–1398. [Google Scholar] [CrossRef]
  63. Quarterman, A.H.; Mirkhanov, S.; Smyth, C.J.C.; Wilcox, K.G. Measurements of nonlinear lensing in a semiconductor disk laser gain sample under optical pumping and using a resonant femtosecond probe laser. Appl. Phys. Lett. 2016, 109, 121113. [Google Scholar] [CrossRef]
  64. Kriso, C.; Kress, S.; Munshi, T.; Grossmann, M.; Bek, R.; Jetter, M.; Michler, P.; Stolz, W.; Koch, M.; Rahimi-Iman, A. Wavelength and pump-power dependent nonlinear refraction and absorption in a semiconductor disk laser. Photon. Technol. Lett. 2020, 32, 85–88. [Google Scholar] [CrossRef]
  65. Sheik-Bahae, M.; Hutchings, D.; Hagan, D.; Van Stryland, E. Dispersion of bound electron nonlinear refraction in solids. IEEE J. Quantum Electron. 1991, 27, 1296–1309. [Google Scholar] [CrossRef]
  66. Burghoff, D.; Yang, Y.; Hayton, D.J.; Gao, J.-R.; Reno, J.L.; Hu, Q. Evaluating the coherence and time-domain profile of quantum cascade laser frequency combs. Opt. Express 2015, 23, 1190–1202. [Google Scholar] [CrossRef]
  67. Han, Z.; Ren, D.; Burghoff, D. Sensitivity of SWIFT spectroscopy. Opt. Express 2020, 28, 6002–6017. [Google Scholar] [CrossRef]
  68. Diddams, S.; Diels, J.-C. Dispersion measurements with white-light interferometry. J. Opt. Soc. Am. B 1996, 13, 1120–1129. [Google Scholar] [CrossRef]
  69. Gosteva, A.; Haiml, M.; Paschotta, R.; Keller, U. Noise-related resolution limit of dispersion measurements with white-light interferometers. J. Opt. Soc. Am. B 2005, 22, 1868–1874. [Google Scholar] [CrossRef]
  70. Voumard TWildi, T.; Brasch, V.; Álvarez, R.G.; Ogando, G.V.; Herr, T. AI-enabled real-time dual-comb molecular fingerprint imaging. Opt. Lett. 2020, 45, 6583–6586. [Google Scholar] [CrossRef] [PubMed]
  71. Villares, G.; Hugi, A.; Blaser, S.; Faist, J. Dual-comb spectroscopy based on quantum-cascade-laser frequency combs. Nat. Commun. 2014, 5, 5192. [Google Scholar] [CrossRef]
  72. Opačak, N.; Schneider, B.; Faist, J.; Schwarz, B. Impact of higher-order dispersion on frequency-modulated combs. Opt. Lett. 2024, 49, 794–797. [Google Scholar] [CrossRef]
  73. Kazakov, D.; Opačak, N.; Pilat, F.; Wang, Y.; Belyanin, A.; Schwarz, B.; Capasso, F. Cluster synchronization in a semiconductor laser. APL Photonics 2024, 9, 026104. [Google Scholar] [CrossRef]
  74. Paiella, R.; Capasso, F.; Gmachl, C.; Sivco, D.L.; Baillargeon, J.N.; Hutchinson, A.L.; Cho, A.Y.; Liu, H.C. Self-Mode-Locking of Quantum Cascade Lasers with Giant Ultrafast Optical Nonlinearities. Science 2000, 290, 1739–1742. [Google Scholar] [CrossRef] [PubMed]
  75. Khurgin, J.B.; Dikmelik, Y.; Hugi, A.; Faist, J. Coherent frequency combs produced by self frequency modulation in quantum cascade lasers. Appl. Phys. Lett. 2014, 104, 081118. [Google Scholar] [CrossRef]
  76. Feldmann, J.; Youngblood, N.; Karpov, M.; Gehring, H.; Li, X.; Stappers, M.; Le Gallo, M.; Fu, X.; Lukashchuk, A.; Raja, A.S.; et al. Parallel convolutional processing using an integrated photonic tensor core. Nature 2021, 589, 52–58. [Google Scholar] [CrossRef]
  77. Dong, B.; Dumont, M.; Terra, O.; Wang, H.; Netherton, A.; Bowers, J.E. Broadband quantum-dot frequency-modulated comb laser. Light Sci. Appl. 2023, 12, 182. [Google Scholar] [CrossRef]
  78. Roy, M.; Zeng, T.; Burghoff, D. Self-frequency-modulated laser combs. Appl. Phys. Lett. 2024, 125, 070503. [Google Scholar] [CrossRef]
  79. Mao, L.; Wang, D.; Zhang, P.; Zhang, Z.; Tian, J.; Song, Y. Synchronized Dual-Pulse Self-Mode-Locked VECSELs. J. Light. Technol. 2025, 1–6. [Google Scholar] [CrossRef]
  80. Feng, J.; Meng, B.; Shang, J.; Zhang, X.; Tong, C.; Zhang, Y.; Niu, Z.; Wang, L. Self−Mode−Locked 2−μm GaSb−Based Optically Pumped Semiconductor Disk Laser. Appl. Sci. 2023, 13, 6873. [Google Scholar] [CrossRef]
  81. Wang, T.; Liu, Y.; Zhu, R.; Jiang, L.; Lu, H.; Song, Y.; Zhang, P. Mode-Locked Operation of High-Order Transverse Modes in a Vertical-External-Cavity Surface-Emitting Laser. Sensors 2024, 24, 2839. [Google Scholar] [CrossRef]
  82. Genty, G.; Salmela, L.; Dudley, J.M.; Brunner, D.; Kokhanovskiy, A.; Kobtsev, S.; Turitsyn, S.K. Machine learning and applications in ultrafast photonics. Nat. Photonics 2021, 15, 91–101. [Google Scholar] [CrossRef]
  83. Kriso, C.D. Investigating Self-Mode-Locking in VECSELs: Nonlinear Lensing and Frequency-Modulated Combs; Philipps-Universitaet Marburg: Marburg, Germany, 2021; Available online: https://archiv.ub.uni-marburg.de/diss/z2021/0495 (accessed on 23 May 2024).
  84. Gaafar, M.A. Realization of a Kerr-Lens Mode-Locked Vertical-External-Cavity Surface-Emitting Laser; Philipps-Universitaet Marburg: Marburg, Germany, 2015; Available online: https://archiv.ub.uni-marburg.de/diss/z2015/0403 (accessed on 23 May 2024).
Photonics 12 00677 g001
Figure 1. Top: Schematic drawing of a VECSEL with optically pumped gain mirror comprising an active region made of multiple quantum wells distributed over the consecutive antinode positions of the standing wave electric-field in a typically resonant microcavity configuration. For ultrashort-pulse VECSELs, chip designs with more attention to the gain mirror’s subcavity configuration are used to optimize dispersion [20] and dynamics [15] by utilizing antiresonant light–matter interaction conditions. Additionally, V-shaped and Z-shaped device configurations are shown. In the SESAM ML version, pulses are shaped by nonlinear absorption properties in an extra passive intracavity element, whereas a soft/hard aperture addressing low-intensity circulating cavity light is utilized to trigger Kerr lens ML operation for temporal pulse train generation. Self-drawn example figures not to scale.
Figure 1. Top: Schematic drawing of a VECSEL with optically pumped gain mirror comprising an active region made of multiple quantum wells distributed over the consecutive antinode positions of the standing wave electric-field in a typically resonant microcavity configuration. For ultrashort-pulse VECSELs, chip designs with more attention to the gain mirror’s subcavity configuration are used to optimize dispersion [20] and dynamics [15] by utilizing antiresonant light–matter interaction conditions. Additionally, V-shaped and Z-shaped device configurations are shown. In the SESAM ML version, pulses are shaped by nonlinear absorption properties in an extra passive intracavity element, whereas a soft/hard aperture addressing low-intensity circulating cavity light is utilized to trigger Kerr lens ML operation for temporal pulse train generation. Self-drawn example figures not to scale.
Photonics 12 00677 g001
Photonics 12 00677 g002
Figure 2. QD VECSEL’s RF spectrum (a,b), intensity autocorrelation trace (c), and spectrum (d) during room-temperature SML operation, exhibiting sub-ps pulse duration and few-nm emission band width, respectively. (a–d) Reused from ref. [26] with permission from the Optical Society of America OPTICA© 2014. For FM-comb investigations, the RF power spectrum (e) and interferometric traces from a coherent beat note measurement technique (SWIFTS) (f) can provide insights into the narrow beat note and intermodal phase relationship of the nearly linear frequency-chirped laser signal, respectively. (g) Semilogarithmic plot of amplitude spectra (Fourier-transforms of interferograms) obtained from ten subsequently recorded intensity interferograms (solid lines) and combined SWIFTS interferograms (dashed lines). (h) Experimental SWIFTS phase obtained for a VECSEL as FM-comb signature. Same arbitrary color-code used in both data plots (g,h) for the individual measurements. (e–h) Reused from ref. [30] with permission from the Optical Society of America OPTICA© 2021.
Figure 2. QD VECSEL’s RF spectrum (a,b), intensity autocorrelation trace (c), and spectrum (d) during room-temperature SML operation, exhibiting sub-ps pulse duration and few-nm emission band width, respectively. (a–d) Reused from ref. [26] with permission from the Optical Society of America OPTICA© 2014. For FM-comb investigations, the RF power spectrum (e) and interferometric traces from a coherent beat note measurement technique (SWIFTS) (f) can provide insights into the narrow beat note and intermodal phase relationship of the nearly linear frequency-chirped laser signal, respectively. (g) Semilogarithmic plot of amplitude spectra (Fourier-transforms of interferograms) obtained from ten subsequently recorded intensity interferograms (solid lines) and combined SWIFTS interferograms (dashed lines). (h) Experimental SWIFTS phase obtained for a VECSEL as FM-comb signature. Same arbitrary color-code used in both data plots (g,h) for the individual measurements. (e–h) Reused from ref. [30] with permission from the Optical Society of America OPTICA© 2021.
Photonics 12 00677 g002
Photonics 12 00677 g003
Figure 3. Schematic of the phase relationship between individual oscillators in a frequency comb with two opposing mode-locking regimes, the in-phase and the anti-phase state corresponding to the establishment of an amplitude-modulated and frequency-modulated comb, respectively. The AM state exhibits a strong beat note as a consequence of synchronization and leads to a pulse train. In contrast, a (periodic, linear) chirp of the instantaneous frequency is obtained for a FM-comb regime, with the comb source emitting with quasi-constant intensity. Spectral as well as temporal signal profiles are sketched together with small auxiliary pointer icons (like clocks) visualizing phase evolution for both regimes at different moments in time. Freely drawn after ref. [51].
Figure 3. Schematic of the phase relationship between individual oscillators in a frequency comb with two opposing mode-locking regimes, the in-phase and the anti-phase state corresponding to the establishment of an amplitude-modulated and frequency-modulated comb, respectively. The AM state exhibits a strong beat note as a consequence of synchronization and leads to a pulse train. In contrast, a (periodic, linear) chirp of the instantaneous frequency is obtained for a FM-comb regime, with the comb source emitting with quasi-constant intensity. Spectral as well as temporal signal profiles are sketched together with small auxiliary pointer icons (like clocks) visualizing phase evolution for both regimes at different moments in time. Freely drawn after ref. [51].
Photonics 12 00677 g003
Photonics 12 00677 g004
Figure 4. Sketch of the light-field amplitude evolution of frequency-modulated (FM) and amplitude-modulated (AM) output of a laser as a function of time over round-trip time (numerically obtained curves within works in the author’s team, based on the addition of 50 sine functions with equal amplitude; calculation data courtesy of C. Kriso). A pulse train signal (AM case) in contrast to a quasi-continuous emission with chirped instantaneous frequency (FM). Schematically, the two stable cases of mode locking (AM and FM comb signature) are compared to the unstable multimode operation. Drawings are not to scale and merely for visualization of the basic output features.
Figure 4. Sketch of the light-field amplitude evolution of frequency-modulated (FM) and amplitude-modulated (AM) output of a laser as a function of time over round-trip time (numerically obtained curves within works in the author’s team, based on the addition of 50 sine functions with equal amplitude; calculation data courtesy of C. Kriso). A pulse train signal (AM case) in contrast to a quasi-continuous emission with chirped instantaneous frequency (FM). Schematically, the two stable cases of mode locking (AM and FM comb signature) are compared to the unstable multimode operation. Drawings are not to scale and merely for visualization of the basic output features.
Photonics 12 00677 g004
Photonics 12 00677 g005
Figure 5. (a) Sketch of a typical Z-scan apparatus used for characterizing a gain mirror chip (upper part) and gain membrane chip (lower part) in reflection and transmission geometry, respectively (cf. refs. [40,64]). A normalized transmission Z-scan trace (from time-integrated acquisition) as a result of combining “open” and “closed” detector signals for a given probe fluence setting is sketched—here for a negative n2. For the investigation of a nonlinear lensing effect in a VECSEL chip (“black box” effective n2, similarly effective nonlinear absorption), the sample is step-wise displaced in z-direction along the optical axis (irradiance with ~0.1 ps probe pulses, with Gaussian beam profile) to obtain the typical beam transmission variations as a function of the z position. For opaque chip structures, as is the case for most VECSELs, the incident and reflected beam part defines a small opening angle (2α), which can be varied to tune the microcavity properties (cf. ref. [39]). Optional cw optical pumping similar to laser operation conditions, or a pulsed excitation of free-charge carriers, can be applied to study their role in the effective n2. (b) Schematic drawing of an ultrafast beam deflection setup for the direct measurement of the Kerr nonlinearity and gain dynamics on sub-ps time scales (cf. ref. [40]). The probe beam spot located on the falling slope of the Gaussian pump irradiance gradient will experience a nonlinearity-dependent deflection, which is detected with the help of a quadcell photodetector—with temporal features of the transmission accessible through time delay settings. Author drawings after the respective literature examples.
Figure 5. (a) Sketch of a typical Z-scan apparatus used for characterizing a gain mirror chip (upper part) and gain membrane chip (lower part) in reflection and transmission geometry, respectively (cf. refs. [40,64]). A normalized transmission Z-scan trace (from time-integrated acquisition) as a result of combining “open” and “closed” detector signals for a given probe fluence setting is sketched—here for a negative n2. For the investigation of a nonlinear lensing effect in a VECSEL chip (“black box” effective n2, similarly effective nonlinear absorption), the sample is step-wise displaced in z-direction along the optical axis (irradiance with ~0.1 ps probe pulses, with Gaussian beam profile) to obtain the typical beam transmission variations as a function of the z position. For opaque chip structures, as is the case for most VECSELs, the incident and reflected beam part defines a small opening angle (2α), which can be varied to tune the microcavity properties (cf. ref. [39]). Optional cw optical pumping similar to laser operation conditions, or a pulsed excitation of free-charge carriers, can be applied to study their role in the effective n2. (b) Schematic drawing of an ultrafast beam deflection setup for the direct measurement of the Kerr nonlinearity and gain dynamics on sub-ps time scales (cf. ref. [40]). The probe beam spot located on the falling slope of the Gaussian pump irradiance gradient will experience a nonlinearity-dependent deflection, which is detected with the help of a quadcell photodetector—with temporal features of the transmission accessible through time delay settings. Author drawings after the respective literature examples.
Photonics 12 00677 g005
Photonics 12 00677 g006
Figure 6. Spectrally resolved typical nonlinear lensing strength in the vicinity of the VECSEL operation wavelength for three on-chip incidence angles, as deduced from experimental data in ref. [39] (see right axis). The ratio of the real and imaginary part of the measured third-order nonlinearity χ(3) is displayed (see left side) with error bars according to the limited precision in nonlinear absorption and refraction determination as depicted in Figure 4 of the original publication. Reused with permission from the Optical Society of America OPTICA© 2021 [39]. Inset: Four recorded Z-scan traces (data points) with indicated upper/lower bounds (dashed lines) for increasing probe beam irradiances (peak intensity levels), from yellow to red colored [39]; reused with permission from the Optical Society of America OPTICA© 2019.
Figure 6. Spectrally resolved typical nonlinear lensing strength in the vicinity of the VECSEL operation wavelength for three on-chip incidence angles, as deduced from experimental data in ref. [39] (see right axis). The ratio of the real and imaginary part of the measured third-order nonlinearity χ(3) is displayed (see left side) with error bars according to the limited precision in nonlinear absorption and refraction determination as depicted in Figure 4 of the original publication. Reused with permission from the Optical Society of America OPTICA© 2021 [39]. Inset: Four recorded Z-scan traces (data points) with indicated upper/lower bounds (dashed lines) for increasing probe beam irradiances (peak intensity levels), from yellow to red colored [39]; reused with permission from the Optical Society of America OPTICA© 2019.
Photonics 12 00677 g006
Photonics 12 00677 g007
Figure 7. Sketch of a SWIFTS apparatus used for characterizing signatures of a self-starting FM comb in a VECSEL [30] with phase-sensitive lock-in detection, transforming traces from a Michelson interferometer into in-phase (“SWIFTS X”) and quadrature component (“SWIFTS Y”), next to a slow-photodiode recorded (regular) intensity interferogram. Such a setup can furthermore be used for dispersion characterization via white-light interferometry (cf. Supplementary Information refs. [30,68]; here, indicated on the right side of the dashed vertical line), when employing the chip as a phase-altering element in one of the two arms, like in an unbalanced interferometer, and irradiating broadband light onto it for group-delay dispersion extraction from the frequency-dependent phase (cf. ref. [69]).
Figure 7. Sketch of a SWIFTS apparatus used for characterizing signatures of a self-starting FM comb in a VECSEL [30] with phase-sensitive lock-in detection, transforming traces from a Michelson interferometer into in-phase (“SWIFTS X”) and quadrature component (“SWIFTS Y”), next to a slow-photodiode recorded (regular) intensity interferogram. Such a setup can furthermore be used for dispersion characterization via white-light interferometry (cf. Supplementary Information refs. [30,68]; here, indicated on the right side of the dashed vertical line), when employing the chip as a phase-altering element in one of the two arms, like in an unbalanced interferometer, and irradiating broadband light onto it for group-delay dispersion extraction from the frequency-dependent phase (cf. ref. [69]).
Photonics 12 00677 g007
Photonics 12 00677 g008
Figure 8. Literature example for an FM-comb semiconductor laser with a spectral hole in the middle of the laser spectrum (a) and accordingly piecewise-linear modulation of the instantaneous frequency (b) resulting from higher-order dispersion contributions to the group velocity dispersion (c). The intermodal phase splayed in total over 2π (bottom left plot) indicates the split nature of the comb spectrum, with intensity and SWIFTS spectra in good agreement with each other (top and middle row of (a), respectively). Correspondingly, the temporal frequency modulation exhibits discontinuity and two slopes (different linear chirp) during one photon roundtrip (duty cycle) indicated by dashed lines. Reused from [72] with permission from the Optical Society of America OPTICA© 2024.
Figure 8. Literature example for an FM-comb semiconductor laser with a spectral hole in the middle of the laser spectrum (a) and accordingly piecewise-linear modulation of the instantaneous frequency (b) resulting from higher-order dispersion contributions to the group velocity dispersion (c). The intermodal phase splayed in total over 2π (bottom left plot) indicates the split nature of the comb spectrum, with intensity and SWIFTS spectra in good agreement with each other (top and middle row of (a), respectively). Correspondingly, the temporal frequency modulation exhibits discontinuity and two slopes (different linear chirp) during one photon roundtrip (duty cycle) indicated by dashed lines. Reused from [72] with permission from the Optical Society of America OPTICA© 2024.
Photonics 12 00677 g008
Table 1. On the SML operation of VECSELs in the literature. References listed chronologically and with a focus on pulse width, time-bandwidth product (TBP, optimum, i.e., Fourier limit, for sech2/Gaussian pulse shape is 0.315/0.441), laser cavity design ([*] chip as resonator-folding mirror, [**] intracavity nonlinear crystal inserted for third-harmonic generation), assumed intracavity pulsing trigger, and main working hypothesis, to the best of the author’s knowledge, as extracted from these selected publications. These may represent the majority of past SML reports, with no claim to completeness. Values rounded to two digits. Where applicable, Kerr lens sign n2 > 0 displayed, else negative sign (extracted or assumed/deduced); and as possible, TBP listed.
Table 1. On the SML operation of VECSELs in the literature. References listed chronologically and with a focus on pulse width, time-bandwidth product (TBP, optimum, i.e., Fourier limit, for sech2/Gaussian pulse shape is 0.315/0.441), laser cavity design ([*] chip as resonator-folding mirror, [**] intracavity nonlinear crystal inserted for third-harmonic generation), assumed intracavity pulsing trigger, and main working hypothesis, to the best of the author’s knowledge, as extracted from these selected publications. These may represent the majority of past SML reports, with no claim to completeness. Values rounded to two digits. Where applicable, Kerr lens sign n2 > 0 displayed, else negative sign (extracted or assumed/deduced); and as possible, TBP listed.
Ref.Pulse Length (ps), [TBP]Resonator LayoutPulse Shaping SupportPresumed Key
[22]0.65LinearNoneSaturable absorption (in gain mirror)
[23]0.93/1.5Z-shape [*] Hard aperture/Soft apertureKerr lensing
[24]1.3, 1.0, 0.76, and 0.48, in order of increasing pump power, V-cavity
(~0.9 to 1.8 by dispersion adjustment for lowest pump, V-cavity)		V-shape [*]/LinearHard aperture/Soft aperture (additionally, intracavity dispersion adjustment for pulse length tuning)Kerr lensing
[25]0.93 [~0.45 (Gaussian)]LinearNone (pump-to-mode size ratio)Higher-order transverse modes (pump-power dependent onset)
[9,12]0.86 (~1 for 2nd, 3rd harmonic)
[0.69/0.73/0.72 (sech21st/2nd/3rd)]		Z-shape [*]Hard apertureKerr lensing
[26]0.83 at 30 °C (0.95 at 5 °C)
[0.94/1.08 at 30°/5 °C (sech2)]		LinearHard apertureKerr lensing (n2 > 0)
[27]2.4LinearHard apertureKerr lensing (n2 > 0)
[28]3.5LinearHard apertureKerr lensing (n2 > 0)
[29]22 [0.33 (sech2)]LinearSoft apertureKerr lensing
[30]-Linear(Soft aperture for pulsing, not part of article)Four-wave mixing for frequency-modulated comb state (nonlinear lensing for pulsing, not part of article)
[19]~5 [~1.5 (Gaussian)]LinearSoft apertureKerr lensing
[31]~5 [~2.5 (Gaussian)]V-shape [**]Soft apertureKerr lensing
[32]4.3LinearSoft apertureKerr lensing
[33]2.0, 2.0, 1.9, 1.7, 1.6, in order of increasing pump power (and 1.7, 1.6, 1.4, 1.4, 1.3 for high-order TM SML)LinearSoft aperture (outcoupler, for high-order-transverse-mode SML)Kerr lensing
[34]1.9 [~0.82 (Gaussian)]V-shapeSoft-apertureKerr lensing
[35]~2LinearDispersive cavityPhase turbulence and mode–mode coupling through self-phase modulation and anomalous dispersion, together with time symmetry breaking (slow light-matter interaction compared to round-trip time)
Table 2. On the VECSEL chip’s nonlinear lensing strength in the literature. References listed chronologically. For comparison, typically relevant experimental details are summarized, such as wavelengths of chip and probe beam, effective nonlinear refraction (whole chip acting as “black box” optical element) and accessible time scales, to the best of the author’s knowledge, as extracted from these selected publications, with no claim to completeness. In the case of (diode-pumped or [*] unpumped) time-integrated Z-scan n2 measurements, the pulse duration of the probe laser is listed in parentheses. Wavelengths as provided in the original publication, n2 rounded to one digit. For incidence angles not stated in the report from a similar author group, the assumed value is placed in brackets. [**] Calculated data showed transition of n2 sign from negative to positive for higher chip-excitation fluences and longer pulse lengths.
Table 2. On the VECSEL chip’s nonlinear lensing strength in the literature. References listed chronologically. For comparison, typically relevant experimental details are summarized, such as wavelengths of chip and probe beam, effective nonlinear refraction (whole chip acting as “black box” optical element) and accessible time scales, to the best of the author’s knowledge, as extracted from these selected publications, with no claim to completeness. In the case of (diode-pumped or [*] unpumped) time-integrated Z-scan n2 measurements, the pulse duration of the probe laser is listed in parentheses. Wavelengths as provided in the original publication, n2 rounded to one digit. For incidence angles not stated in the report from a similar author group, the assumed value is placed in brackets. [**] Calculated data showed transition of n2 sign from negative to positive for higher chip-excitation fluences and longer pulse lengths.
Ref.ExperimentWavelengths (nm)Effective n2 (10−16 m2/W)Incidence Angle to NormalTime Scales
(Pulse Duration)
[61]Z-scan
(t-integrated, in reflection)		chip design 1040,
lasing ~1050,
probe 1064		−1.5 [*],
+0.5 (pump ~60 kW/cm2)
up to +1.4 (highest pump ~90 kW/cm2)		~10°–
(~10 ps pulses)
[62]Z-scan
(t-int., in refl.)		chip design 1035,
lasing ~1025–1040,
probe 1035		~−0.4 [*][~10°]–
(~0.23 ps pulses)
[63]Z-scan
(t-int., in refl.)		chip design 1040,
probe 1035		~−0.6 [*],
−0.7 (pump ~60 kW/cm2)
−0.6 (highest pump ~75 kW/cm2)		[~10°]–
(~0.34 ps pulses)
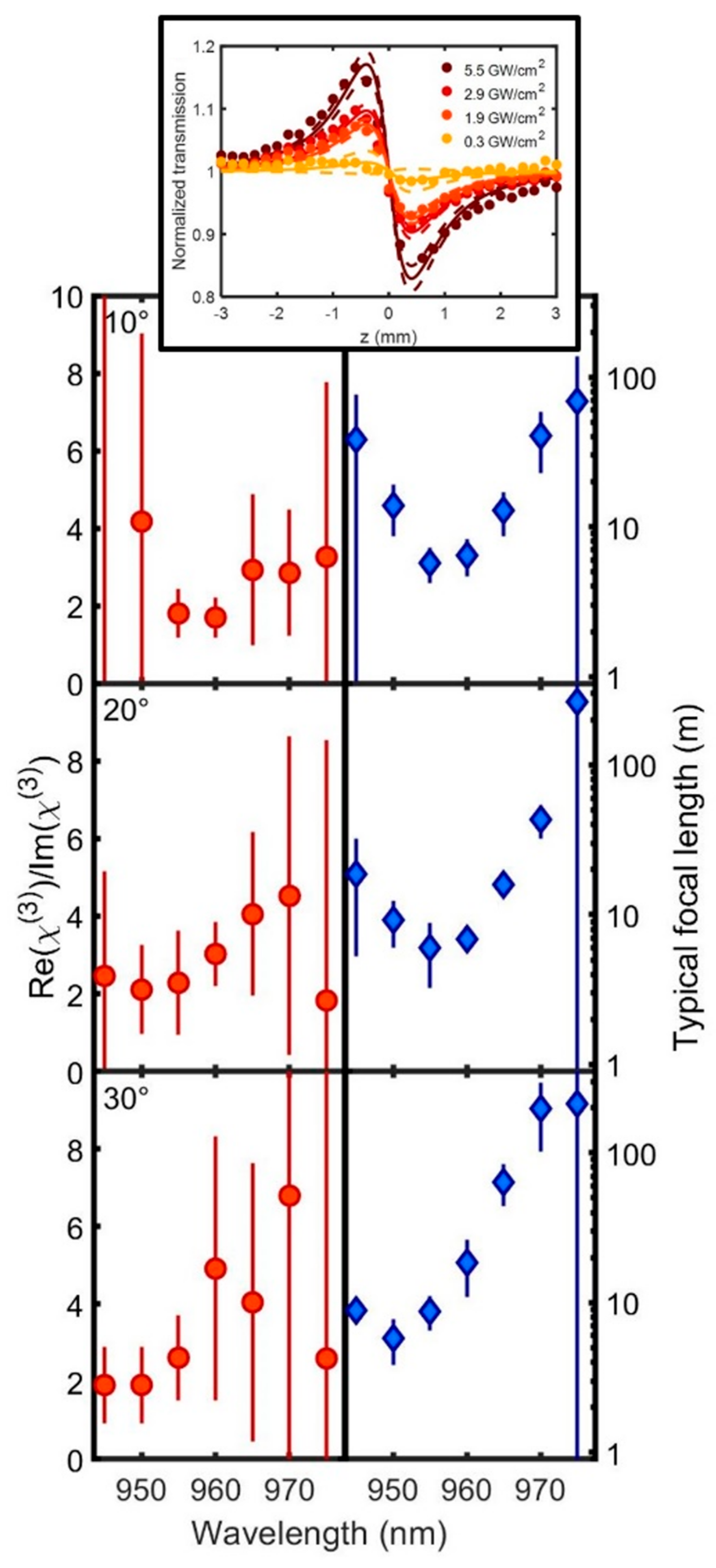
[39]Z-scan
(t-int., in refl.)		chip design 960 (0°), ~960, 955, 950 for 10°, 20°, 30°,
probe 930–975		~−4.5 to −5 [*] (at microcavity preference wavelength, PL peak position, LCF shaped)
~−0.5 to 1.5 [*] (at QW PL wavelength) 		10°, 20°, 30°–
(~0.15 ps pulses)
[64]Z-scan
(t-int., in refl.)		chip design 960
(0°, intracavity SiC on gain mirror)
lasing ~960–970,
probe 955–970		~−0.8 [*] (960 nm)
~−0.5 [*] (970 nm)
−0.6 (above threshold pump ~4 kW/cm2)
−0.3 (highest pump ~9 kW/cm2)		[~10°]–
(~0.15 ps pulses)
[40]Beam-deflection (ultrafast) & Z-scan (t-int.)chip design 1150
(0°, gain membrane on SiC),
probe ~1150		~−1.2 [*] (Z-scan) corresponding to ~−3 calculated from beam-deflection meas. data [**]0° probe,
all transmission geometry		0.01–2.5 ps,
pulses ~0.13 ps for pump/probe
(~0.12 ps pulses)
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

Share and Cite

MDPI and ACS Style

Rahimi-Iman, A. Self-Mode-Locking and Frequency-Modulated Comb Semiconductor Disk Lasers. Photonics 2025, 12, 677. https://doi.org/10.3390/photonics12070677

AMA Style

Rahimi-Iman A. Self-Mode-Locking and Frequency-Modulated Comb Semiconductor Disk Lasers. Photonics. 2025; 12(7):677. https://doi.org/10.3390/photonics12070677

Chicago/Turabian Style

Rahimi-Iman, Arash. 2025. "Self-Mode-Locking and Frequency-Modulated Comb Semiconductor Disk Lasers" Photonics 12, no. 7: 677. https://doi.org/10.3390/photonics12070677

APA Style

Rahimi-Iman, A. (2025). Self-Mode-Locking and Frequency-Modulated Comb Semiconductor Disk Lasers. Photonics, 12(7), 677. https://doi.org/10.3390/photonics12070677

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop