Analysis and Suppression of Pump Beam Alignment Error in SERF Co-Magnetometer
Abstract
1. Introduction
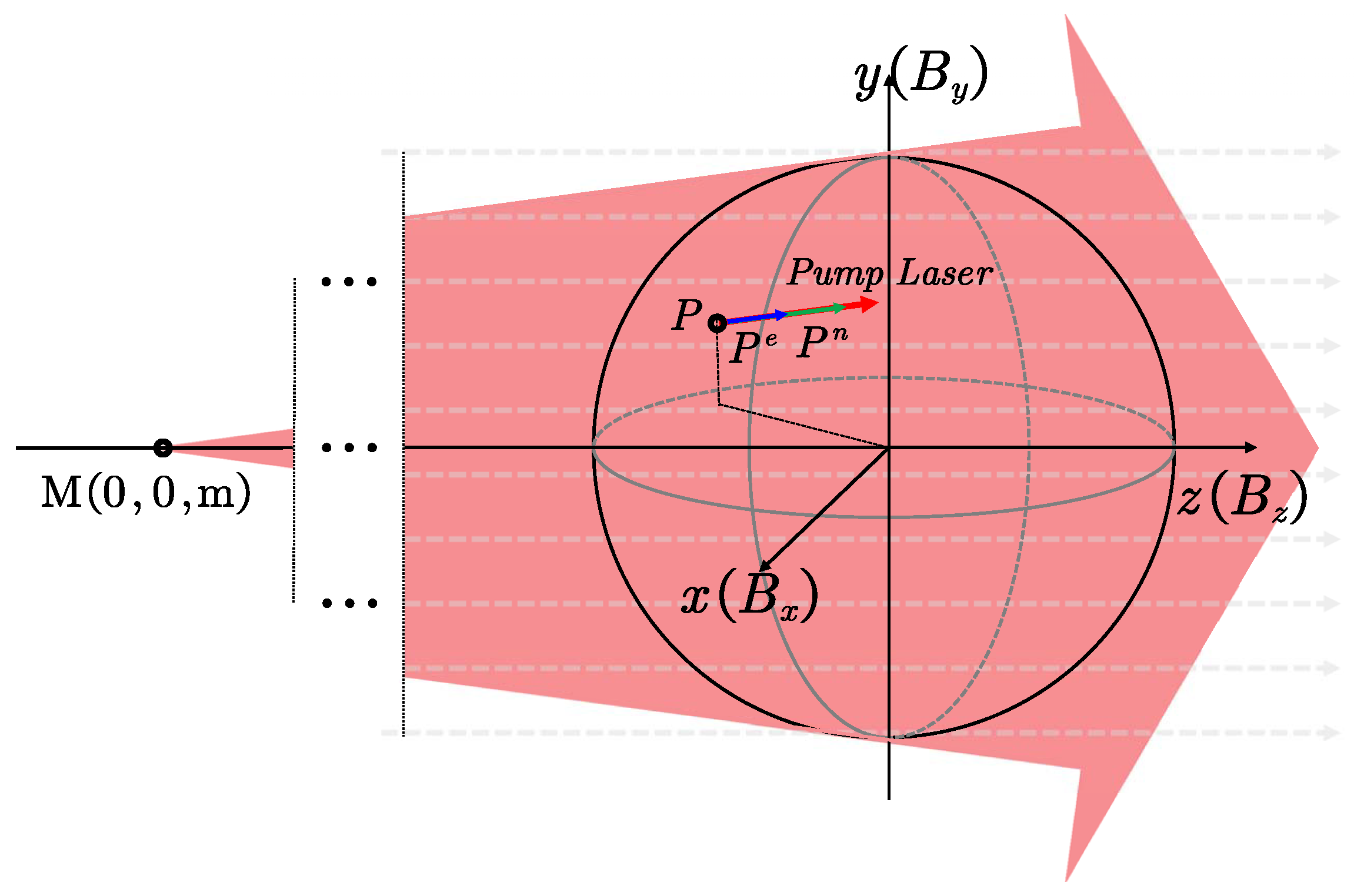
2. Theoretical Principles
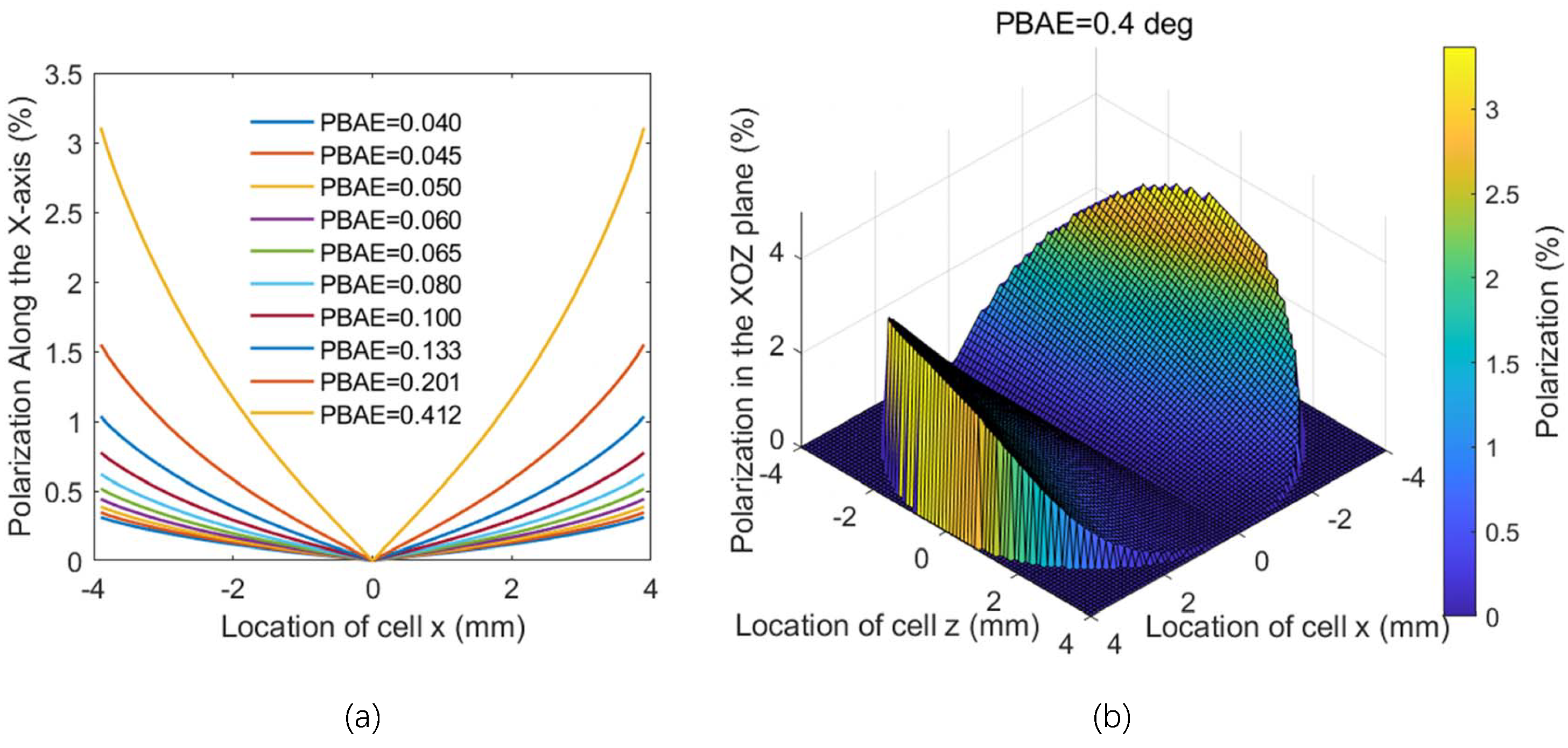
2.1. Mathematical Model
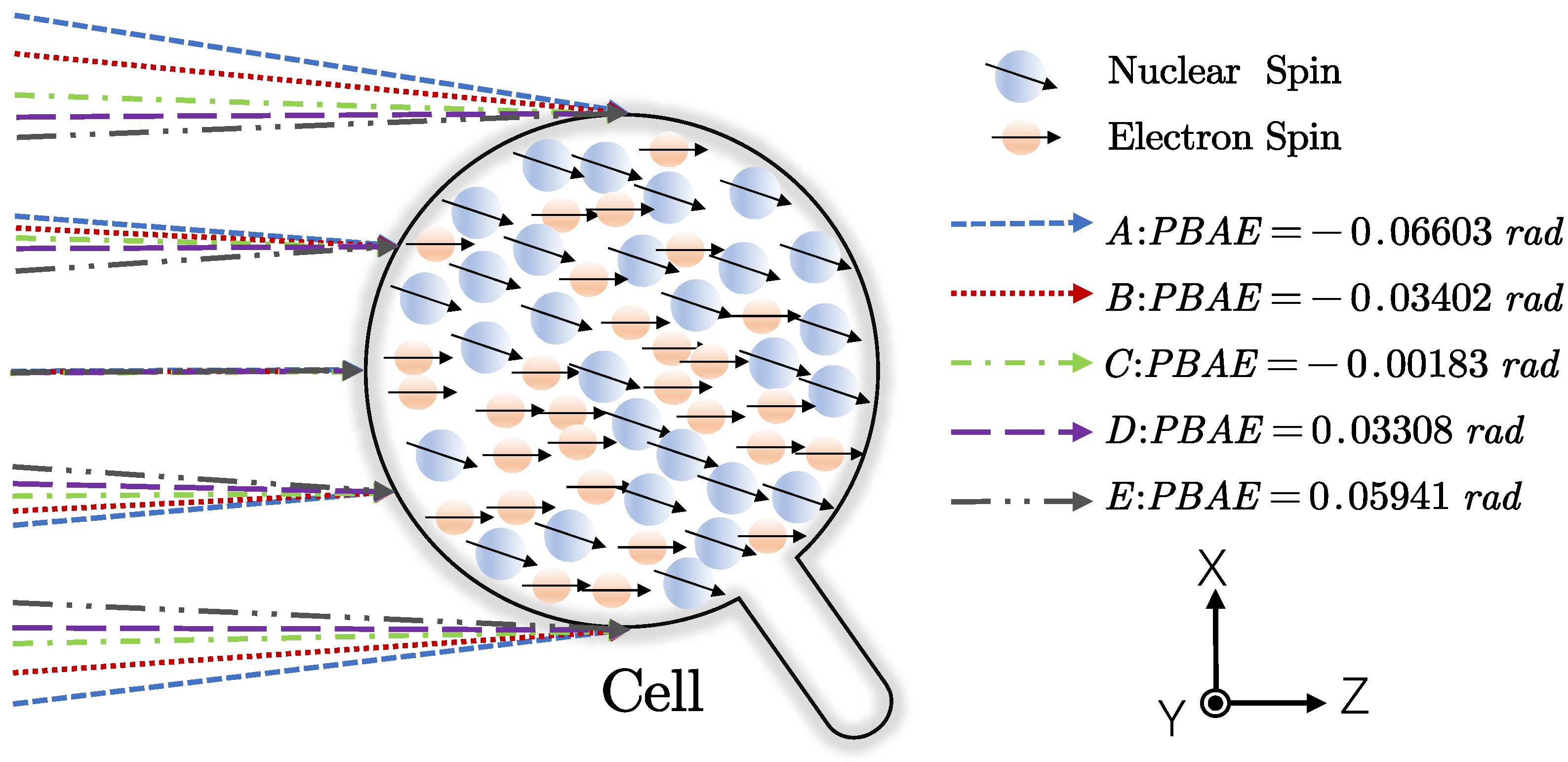
2.2. In Situ Suppression Method for PBAE
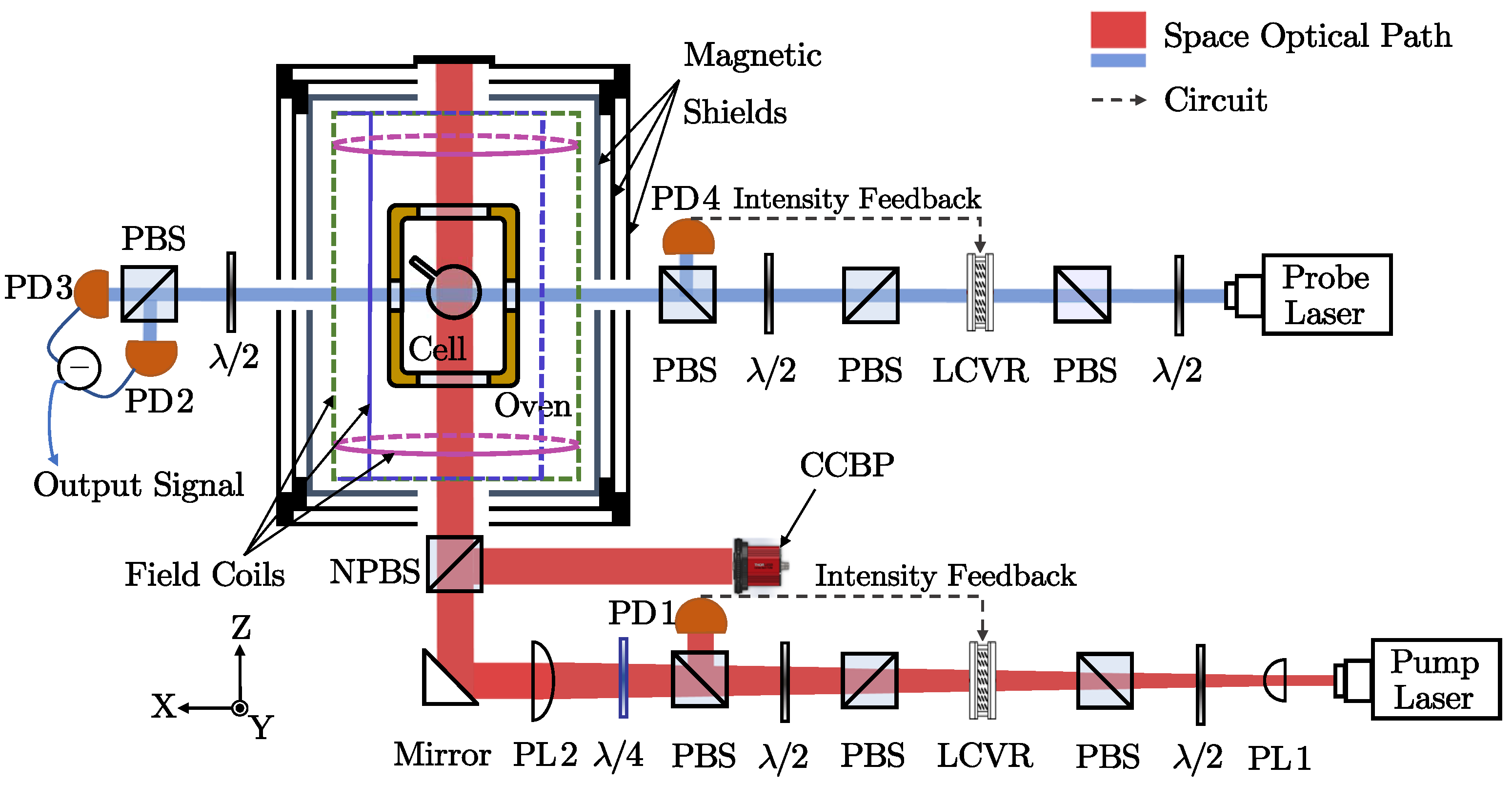
3. Experimental Setup of SERFCM
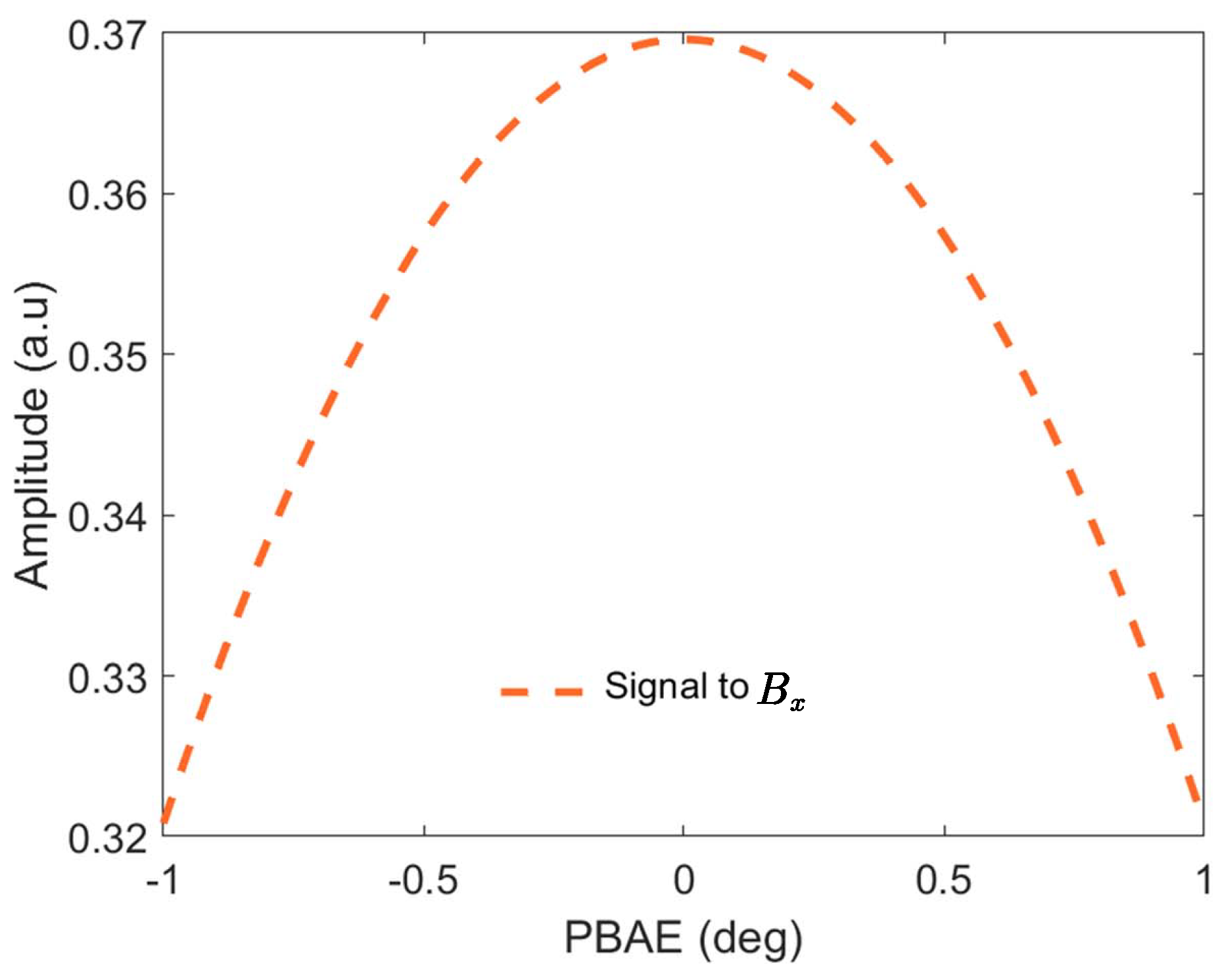
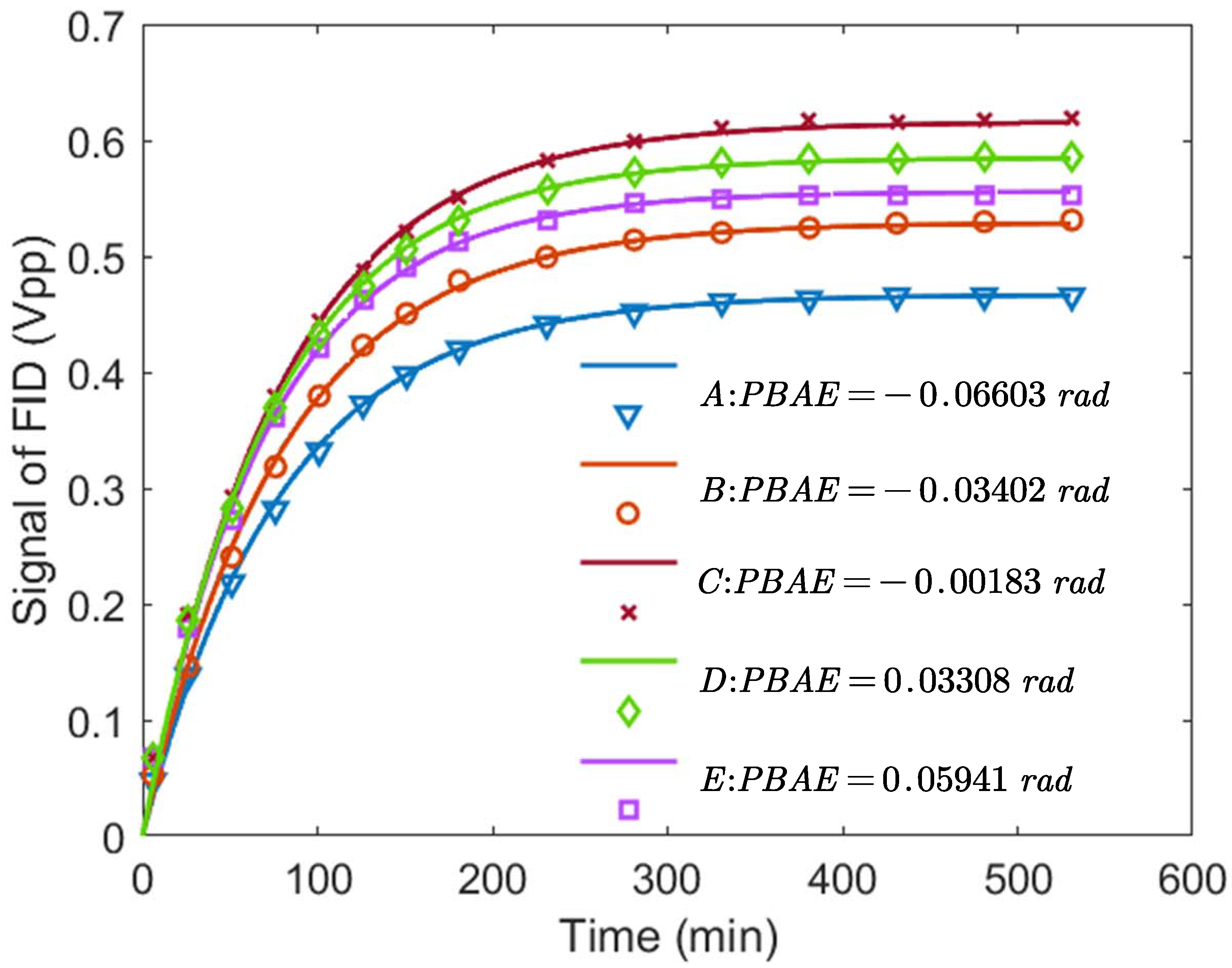
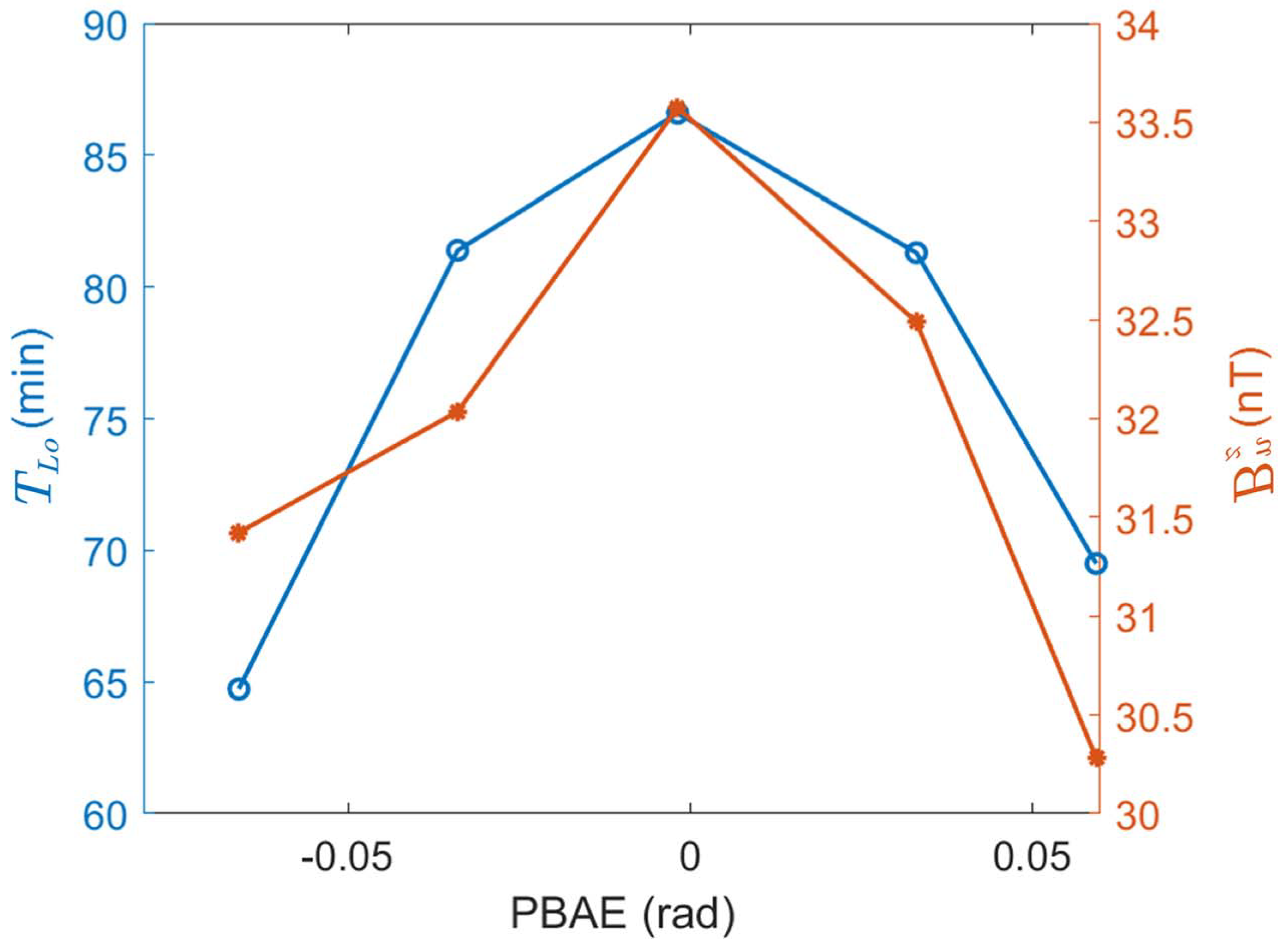
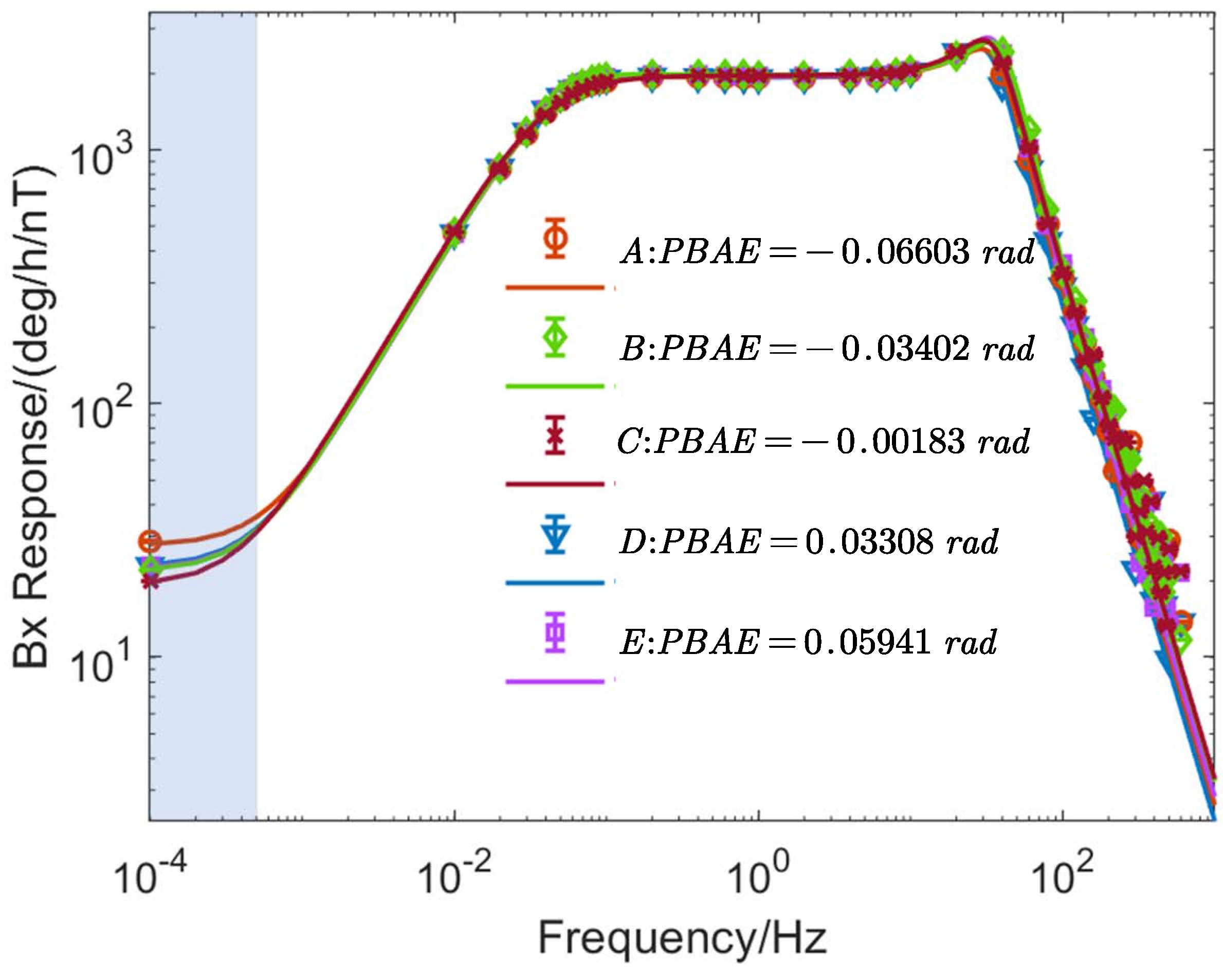
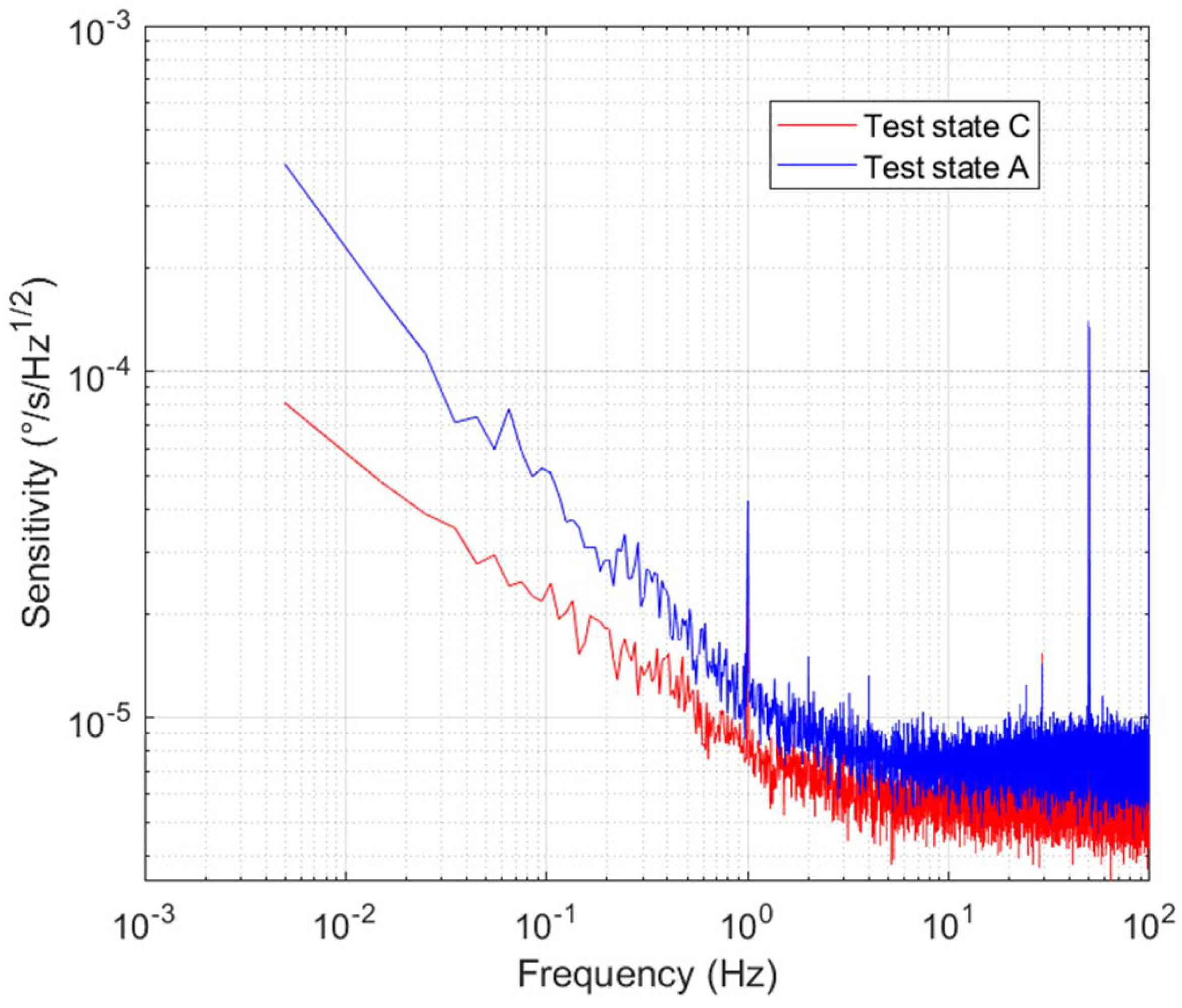
4. Experimental Results and Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Smiciklas, M.; Brown, J.; Cheuk, L.; Smullin, S.; Romalis, M. New Test of Local Lorentz Invariance Using a 21Ne-Rb-K Comagnetometer. Phys. Rev. Lett. 2011, 107, 171604. [Google Scholar] [CrossRef]
- Kornack, T.; Ghosh, R.; Romalis, M. Nuclear spin gyroscope based on an atomic comagnetometer. Phys. Rev. Lett. 2005, 95, 230801. [Google Scholar] [CrossRef]
- Pei, H.; Pang, H.; Quan, W.; Fan, W.; Yuan, L.; Zhang, K.; Fang, C. Pulsed optical pumping in electron spin vapor. Measurement 2024, 231, 114619. [Google Scholar] [CrossRef]
- Li, F.; Pang, H.; Wang, Z.; Fan, W.; Zhang, M.; Liu, Z.; Li, J.; Qin, B.; Zhou, X.; Lei, X.; et al. In situ real-time measurement for electron spin polarization in atomic spin gyroscopes. iScience 2025, 28, 111757. [Google Scholar] [CrossRef]
- Zheng, W.; Su, S.; Zhang, G.; Bi, X.; Lin, Q. Vector magnetocardiography measurement with a compact elliptically polarized laser-pumped magnetometer. Biomed. Opt. Express 2020, 11, 649–659. [Google Scholar] [CrossRef]
- Flambaum, V.; Romalis, M. Limits on lorentz invariance violation from coulomb interactions in nuclei and atoms. Phys. Rev. Lett. 2017, 118, 142501. [Google Scholar]
- Wei, K.; Zhao, T.; Fang, X.; Xu, Z.; Liu, C.; Cao, Q.; Wickenbrock, A.; Hu, Y.; Ji, W.; Fang, J.; et al. Ultrasensitive atomic comagnetometer with enhanced nuclear spin coherence. Phys. Rev. Lett. 2023, 130, 063201. [Google Scholar] [CrossRef]
- Kornack, T.; Romalis, M. Dynamics of two overlapping spin ensembles interacting by spin exchange. Phys. Rev. Lett. 2002, 89, 253002. [Google Scholar] [CrossRef]
- Chann, B.; Babcock, E.; Anderson, L.; Walker, T. Skew light propagation in optically thick optical pumping cells. Phys. Rev. A 2002, 66, 033406. [Google Scholar] [CrossRef]
- Wu, Z.; Jia, Y.; Chai, Z.; Liu, Z. Influence of skew light propagation on electron spin polarization in an atomic magnetometer. In Proceedings of the First Optics Frontier Conference, SPIE, Hangzhou, China, 24–26 April 2021; Volume 11850, pp. 36–41. [Google Scholar]
- Zhao, J.; Liu, G.; Lu, J.; Ding, M.; Ma, Y.; Ji, J.; Yang, K.; Ma, D.; Xing, B.; Zhang, N.; et al. Improvement of spin polarization spatial uniformity in optically pumped atomic magnetometers based on counter-propagating pump beams and atomic diffusion. Meas. Sci. Technol. 2020, 32, 035902. [Google Scholar] [CrossRef]
- Jia, Y.; Liu, Z.; Zhou, B.; Liang, X.; Wu, W.; Peng, J.; Ding, M.; Zhai, Y.; Fang, J. Pump beam influence on spin polarization homogeneity in the nuclear magnetic resonance gyroscope. J. Phys. Appl. Phys. 2019, 52, 355001. [Google Scholar] [CrossRef]
- Kornack, T.W. A Test of CPT and Lorentz Symmetry Using a Potassium-Helium-3 co-Magnetometer. Ph.D. Thesis, Princeton University, Princeton, NJ, USA, 2005. [Google Scholar]
- Xing, L.; Quan, W.; Fan, W.; Zhang, W.; Fu, Y.; Song, T. The method for measuring the non-orthogonal angle of the magnetic field coils of a K-Rb-21 Ne co-magnetometer. IEEE Access 2019, 7, 63892–63899. [Google Scholar] [CrossRef]
- Huang, J.; Fan, W.; Wang, Z.; Yuan, L.; Zhang, K.; Pei, H.; Pang, H.; Quan, W. Analysis and suppression of the misalignment error for the pumping laser in the atomic comagnetometer. Opt. Express 2022, 30, 6374–6387. [Google Scholar] [CrossRef]
- Chen, Y.; Quan, W.; Duan, L.; Lu, Y.; Jiang, L.; Fang, J. Spin-exchange collision mixing of the K and Rb ac Stark shifts. Phys. Rev. A 2016, 94, 052705. [Google Scholar] [CrossRef]
- Wang, X.; Chen, Y.; Quan, W.; Fan, W.; Fang, J. A rapid spin exchange tightly bound alkali metal hybrid optical pumping system. J. Phys. At. Mol. Opt. Phys. 2018, 51, 045001. [Google Scholar] [CrossRef]
- Babcock, E.; Nelson, I.; Kadlecek, S.; Driehuys, B.; Anderson, L.; Hersman, F.; Walker, T. Hybrid Spin-Exchange Optical Pumping of 3He. Phys. Rev. Lett. 2003, 91, 123003. [Google Scholar] [CrossRef] [PubMed]
- Wei, K.; Zhao, T.; Fang, X.; Xu, Z.; Zhai, Y.; Quan, W. Accurate polarimetry of hybrid K-Rb and 21Ne atoms based on spin-exchange interactions. IEEE Sens. J. 2020, 21, 5879–5885. [Google Scholar] [CrossRef]
- Savukov, I.; Romalis, M. Effects of spin-exchange collisions in a high-density alkali-metal vapor in low magnetic fields. Phys. Rev. A 2005, 71, 023405. [Google Scholar] [CrossRef]
- Cates, G.; Schaefer, S.; Happer, W. Relaxation of spins due to field inhomogeneities in gaseous samples at low magnetic fields and low pressures. Phys. Rev. A 1988, 37, 2877. [Google Scholar] [CrossRef]
- Fang, X.; Wei, K.; Zhai, Y.; Zhao, T.; Chen, X.; Zhou, M.; Liu, Y.; Ma, D.; Xiao, Z. Analysis of effects of magnetic field gradient on atomic spin polarization and relaxation in optically pumped atomic magnetometers. Opt. Express 2022, 30, 3926–3940. [Google Scholar] [CrossRef]
- Zhao, T.; Zhai, Y.; Liu, C.; Xie, H.; Cao, Q.; Fang, X. Spin polarization characteristics of hybrid optically pumped comagnetometers with different density ratios. Opt. Express 2022, 30, 28067–28078. [Google Scholar] [CrossRef]
- Fang, J.; Wan, S.; Yuan, H. Dynamics of an all-optical atomic spin gyroscope. Appl. Opt. 2013, 52, 7220–7227. [Google Scholar] [CrossRef] [PubMed]
- Pang, H.; Liu, F.; Fan, W.; Wu, Z.; Yuan, Q.; Quan, W. Comprehensive analysis of the effects of magnetic field gradient on the performance of the SERF co-magnetometer. Opt. Express 2023, 31, 5215–5228. [Google Scholar] [CrossRef] [PubMed]
- Fang, J.; Wan, S.; Chen, Y.; Li, R. Light-shift measurement and suppression in atomic spin gyroscope. Appl. Opt. 2012, 51, 7714–7717. [Google Scholar] [CrossRef]
- Wyllie, R.; Kauer, M.; Smetana, G.; Wakai, R.; Walker, T. Magnetocardiography with a modular spin-exchange relaxation-free atomic magnetometer array. Phys. Med. Biol. 2012, 57, 2619. [Google Scholar] [CrossRef]
- Savukov, I.; Kim, Y.; Shah, V.; Boshier, M. High-sensitivity operation of single-beam optically pumped magnetometer in a kHz frequency range. Meas. Sci. Technol. 2017, 28, 035104. [Google Scholar] [CrossRef]
- Eklund, E.J. Microgyroscope Based on Spin-Polarized Nuclei; University of California: Irvine, CA, USA, 2008. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yuan, Q.; Fan, W.; Pang, H.; Han, X.; Wang, Z.; Quan, W. Analysis and Suppression of Pump Beam Alignment Error in SERF Co-Magnetometer. Photonics 2025, 12, 550. https://doi.org/10.3390/photonics12060550
Yuan Q, Fan W, Pang H, Han X, Wang Z, Quan W. Analysis and Suppression of Pump Beam Alignment Error in SERF Co-Magnetometer. Photonics. 2025; 12(6):550. https://doi.org/10.3390/photonics12060550
Chicago/Turabian StyleYuan, Qi, Wenfeng Fan, Haoying Pang, Xue Han, Zhuo Wang, and Wei Quan. 2025. "Analysis and Suppression of Pump Beam Alignment Error in SERF Co-Magnetometer" Photonics 12, no. 6: 550. https://doi.org/10.3390/photonics12060550
APA StyleYuan, Q., Fan, W., Pang, H., Han, X., Wang, Z., & Quan, W. (2025). Analysis and Suppression of Pump Beam Alignment Error in SERF Co-Magnetometer. Photonics, 12(6), 550. https://doi.org/10.3390/photonics12060550




