Subtraction Method for Subpixel Stitching: Synthetic Aperture Holographic Imaging
Abstract
1. Introduction
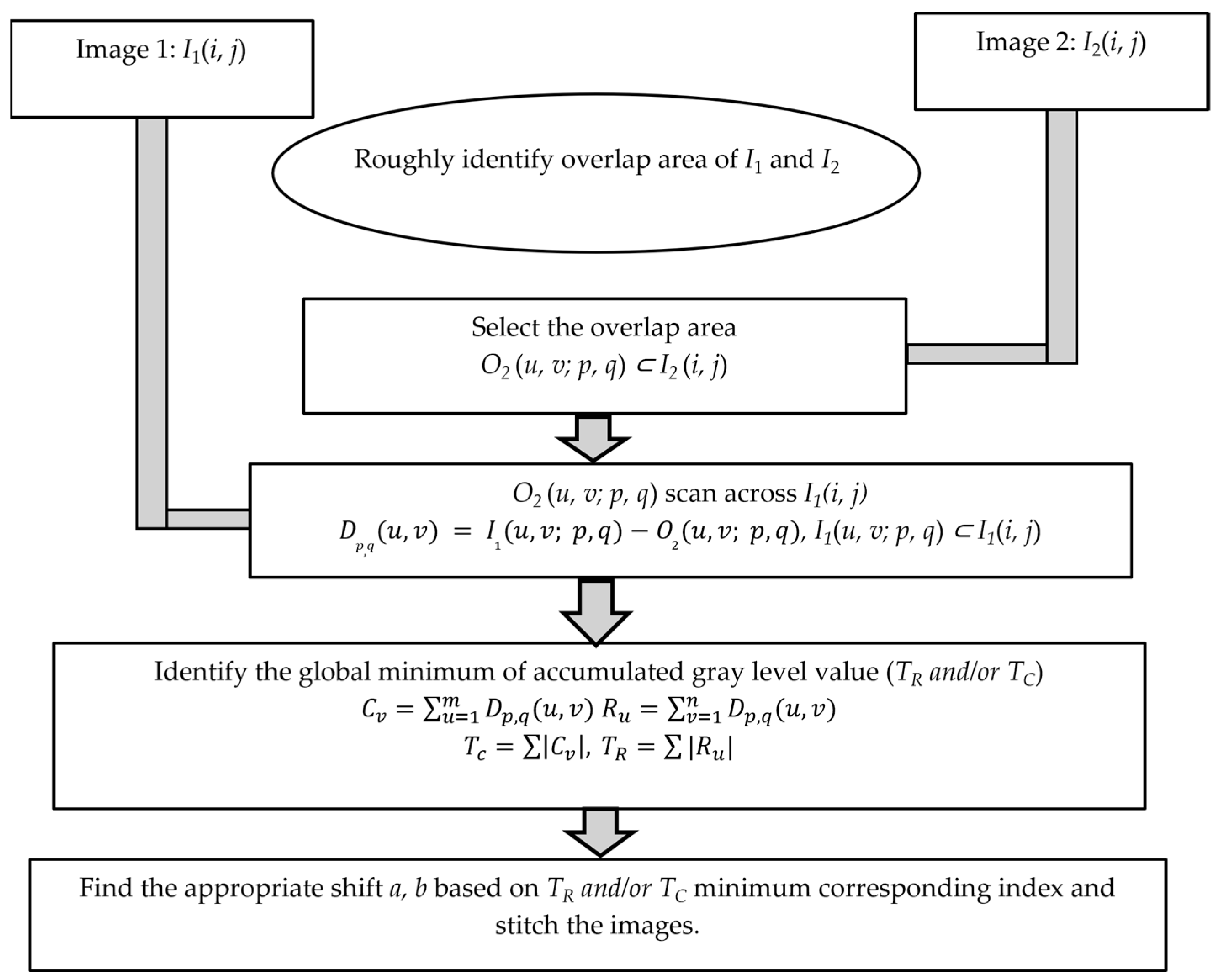
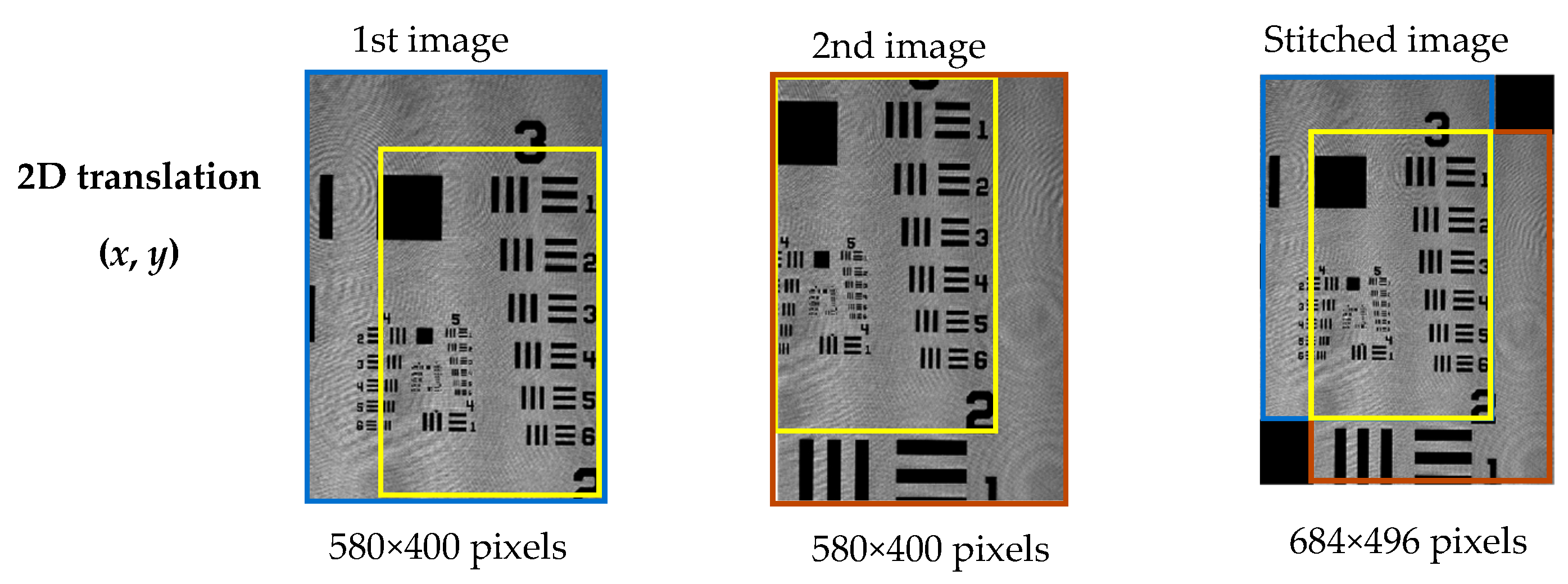
2. SM on Image Registration
2.1. Pixel Level Image Registration
2.2. Subpixel-Level Image Registration
3. Holographic Imaging Stitching
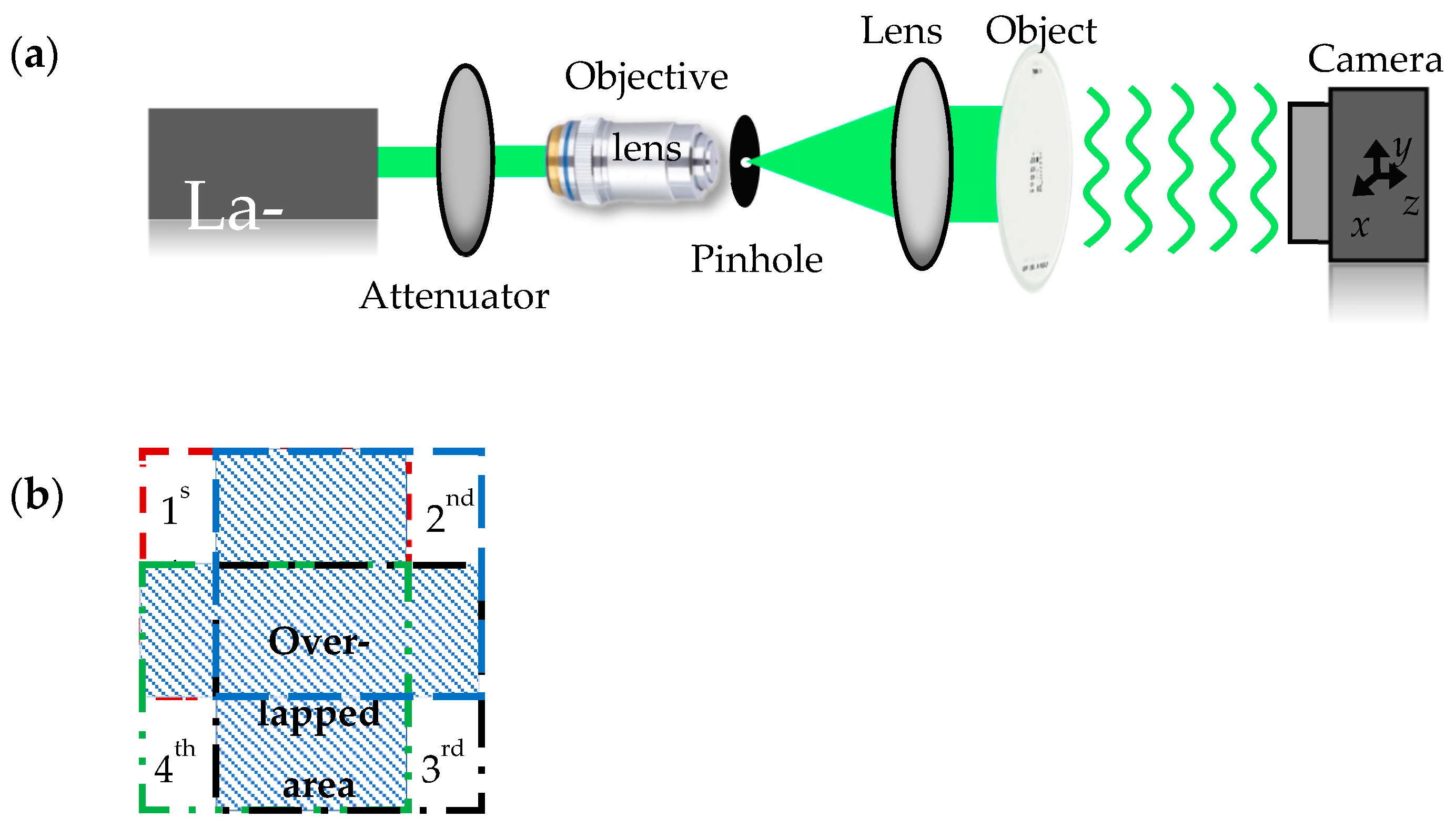
3.1. System Setup
3.2. Time Complexity Analysis
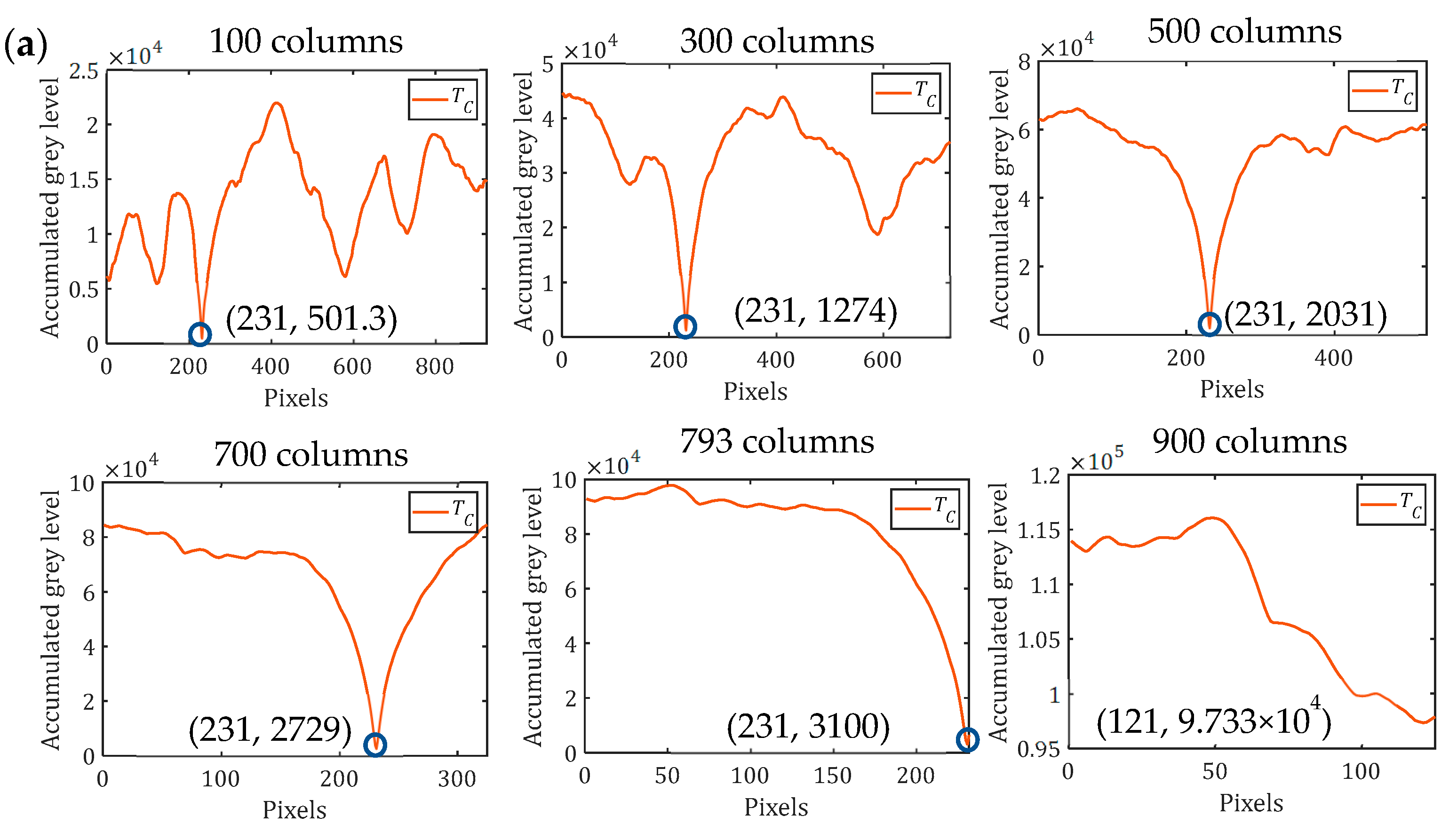
3.3. Pixel-Level Registration
3.4. Subpixel-Level Registration
| Interpolation Factor | RMSD | PSNR | E | |||
|---|---|---|---|---|---|---|
| Single | Synthetic | Single | Synthetic | Single | Synthetic | |
| 1 | 0.2766 | 0.2388 | 25.70 | 28.64 | 2.327 | 0.9938 |
| 2 | 0.2698 | 0.2367 | 26.20 | 28.81 | 2.316 | 0.9601 |
| 4 | 0.2681 | 0.2383 | 26.32 | 28.68 | 2.319 | 0.9582 |
| 8 | 0.2673 | 0.2401 | 26.38 | 28.50 | 2.310 | 0.9565 |
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Szeliski, R. Image Alignment and Stitching: A Tutorial. Found. Trends Comput. Graph. Vis. 2007, 2, 1–104. [Google Scholar] [CrossRef]
- Brown, L.G. A Survey of Image Registration Techniques. ACM Comput. Surv. 1992, 24, 325–376. [Google Scholar] [CrossRef]
- Adel, E.; Elmogy, M.; Elbakry, H. Image Stitching Based on Feature Extraction Techniques: A Survey. Int. J. Comput. Appl. 2014, 99, 1–8. [Google Scholar] [CrossRef]
- Levin, A.; Zomet, A.; Peleg, S.; Weiss, Y. Seamless Image Stitching in the Gradient Domain. Computer Vision—ECCV. 2004, 3024, 377–389. [Google Scholar]
- Megha, V.; Rajkumar, K.K. A Comparative Study on Different Image Stitching Techniques. Int. J. Eng. Trends Technol. 2022, 70, 44–58. [Google Scholar]
- Xiong, Y.; Turkowski, K. Registration, Calibration and Blending in Creating High-Quality Panoramas. In Proceedings of the Fourth IEEE Workshop on Applications of Computer Vision (WACV’98), Princeton, NJ, USA, 19–21 October 1998; pp. 69–74. [Google Scholar]
- Rankov, V.; Locke, R.J.; Edens, R.J.; Barber, P.R.; Vojnovic, B. An Algorithm for Image Stitching and Blending. In Proceedings of the SPIE in Three-Dimensional and Multidimensional Microscopy, San Jose, CA, USA, 22–27 January 2005; Volume 5701, pp. 190–199. [Google Scholar]
- Wan, M.; Healy, J.J.; Sheridan, J.T. Fast 2D Subpixel Displacement Estimation. Photonics 2024, 11, 625. [Google Scholar] [CrossRef]
- Goodman, J.W. Introduction to Fourier Optics, 3rd ed.; Roberts and Company: Greenwood Village, CO, USA, 2005. [Google Scholar]
- Schnars, U.; Falldorf, C.; Watson, J.; Jüptner, W. Digital Holography and Wavefront Sensing: Digital Holography; Springer: Berlin/Heidelberg, Germany, 2015; pp. 39–68. [Google Scholar]
- Rivenson, Y.; Wu, Y.; Ozcan, A. Deep Learning in Holography and Coherent Imaging. Light Sci. Appl. 2019, 8, 85. [Google Scholar] [CrossRef]
- Zhang, W.; Cao, L.; Jin, G. Review on High Resolution and Large Field of View Digital Holography. Infrared Laser Eng. 2019, 48, 603008. [Google Scholar]
- Wan, M.; Healy, J.J.; Sheridan, J.T. Fast, Sub-Pixel Accurate, Displacement Measurement Method: Optical and Terahertz Systems. Opt. Lett. 2020, 45, 6611–6614. [Google Scholar] [CrossRef]
- Wan, M.; Healy, J.J.; Sheridan, J.T. Fast subpixel displacement measurement, part 1: One-dimensional analysis, simulation, and experiment. Opt. Eng. 2022, 61, 043105. [Google Scholar] [CrossRef]
- Nocedal, J.; Wright, S.J. Numerical Optimization; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2006. [Google Scholar]
- Ahmadianfar, O.; Bozorg-Haddad, O.; Chu, X. Gradient-Based Optimizer: A New Metaheuristic Optimization Algorithm. Inf. Sci. 2020, 540, 131–159. [Google Scholar] [CrossRef]
- Standford AAA222 Lecture 3 Note. Available online: https://office365stanford-my.sharepoint.com/ (accessed on 19 March 2025).
- Why Your Loops Are So Slow. Available online: https://medium.com/data-science/why-your-loops-are-so-slow-166ec67db47d (accessed on 19 March 2025).
- Cooper, K.; Torczon, L. Engineering a Compiler: Introduction to Optimization; Elsevier: Amsterdam, The Netherlands, 2011; Chapter 8. [Google Scholar]
- RQDS1P-Positive 1951 USAF Test Target Groups 2–7. Available online: https://www.thorlabs.com/thorproduct.cfm?partnumber=R1DS1P (accessed on 19 March 2025).
- MATLAB 2018a. Available online: https://nl.mathworks.com/downloads/ (accessed on 26 May 2025).
- Wan, M.; Yuan, H.; Čibiraitė, D.; Cassidy, D.; Lisauskas, A.; Healy, J.J.; Roskos, H.G.; Krozer, V.; Sheridan, J.T. Terahertz Quantitative Metrology Using 300 GHz In-Line Digital Holography. Proc. SPIE 2019, 11030, 110300R. [Google Scholar]
- 8MT167-100—Motorized Translation Stage. Available online: http://www.standa.lt/products/catalog/motorised_positioners?item=64 (accessed on 19 March 2025).
- LabVIEW. Available online: https://www.ni.com/en-ie/support/downloads/software-products/download.labview.html#411240 (accessed on 19 March 2025).
- Sundararajan, D. Digital Image Processing: A Signal Processing and Algorithmic Approach; Springer: Singapore, 2017; Chapter 3.3. [Google Scholar]
- Kirkpatrick, S.; Gelatt, C.D.J.; Vecchi, M.P. Optimization by Simulated Annealing. Science 1983, 220, 671–680. [Google Scholar] [CrossRef]
- Lyu, M.; Yuan, C.; Li, D.; Situ, G. Fast Autofocusing in Digital Holography Using the Magnitude Differential. Appl. Opt. 2017, 56, F152–F157. [Google Scholar] [CrossRef]
- Latychevskaia, T. Iterative Phase Retrieval for Digital Holography: Tutorial. JOSA A 2019, 36, D31–D40. [Google Scholar] [CrossRef]
- Wikipedia. Root-Mean-Square Deviation. Available online: https://en.wikipedia.org/wiki/Root-mean-square_deviation (accessed on 19 March 2025).
- Wikipedia. Peak Signal-to-Noise Ratio. Available online: https://en.wikipedia.org/wiki/Peak_signal-to-noise_ratio (accessed on 19 March 2025).
- Tsai, D.Y.; Lee, Y.; Matsuyama, E. Information Entropy Measure for Evaluation of Image Quality. J. Digit. Imaging 2008, 21, 338–347. [Google Scholar] [CrossRef]
- Entropy. Available online: https://uk.mathworks.com/help/images/ref/entropy.html (accessed on 19 March 2025).
- Kolonko, M. Some New Results on Simulated Annealing Applied to the Job Shop Scheduling Problem. Eur. J. Oper. Res. 1999, 113, 123–136. [Google Scholar] [CrossRef]
- Memmolo, P.; Miccio, L.; Paturzo, M.; Di Caprio, G.; Coppola, G.; Netti, P.A.; Ferraro, P. Recent Advances in Holographic 3D Particle Tracking. Adv. Opt. Photon. 2015, 7, 713–755. [Google Scholar] [CrossRef]
- Paul, M.; Lin, W.; Lau, C.T.; Lee, B.S. Direct Intermode Selection for H.264 Video Coding Using Phase Correlation. IEEE Trans. Image Process. 2010, 20, 461–473. [Google Scholar] [CrossRef]
- Baqersad, J.; Poozesh, P.; Niezrecki, C.; Avitabile, P. Photogrammetry and Optical Methods in Structural Dynamics—A Review. Mech. Syst. Signal Process. 2017, 86, 17–34. [Google Scholar] [CrossRef]
- Li, J.; Thakur, P.; Fok, A.S.L. Shrinkage of Dental Composite in Simulated Cavity Measured with Digital Image Correlation. JoVE J. Vis. Exp. 2014, 89, 51191. [Google Scholar]
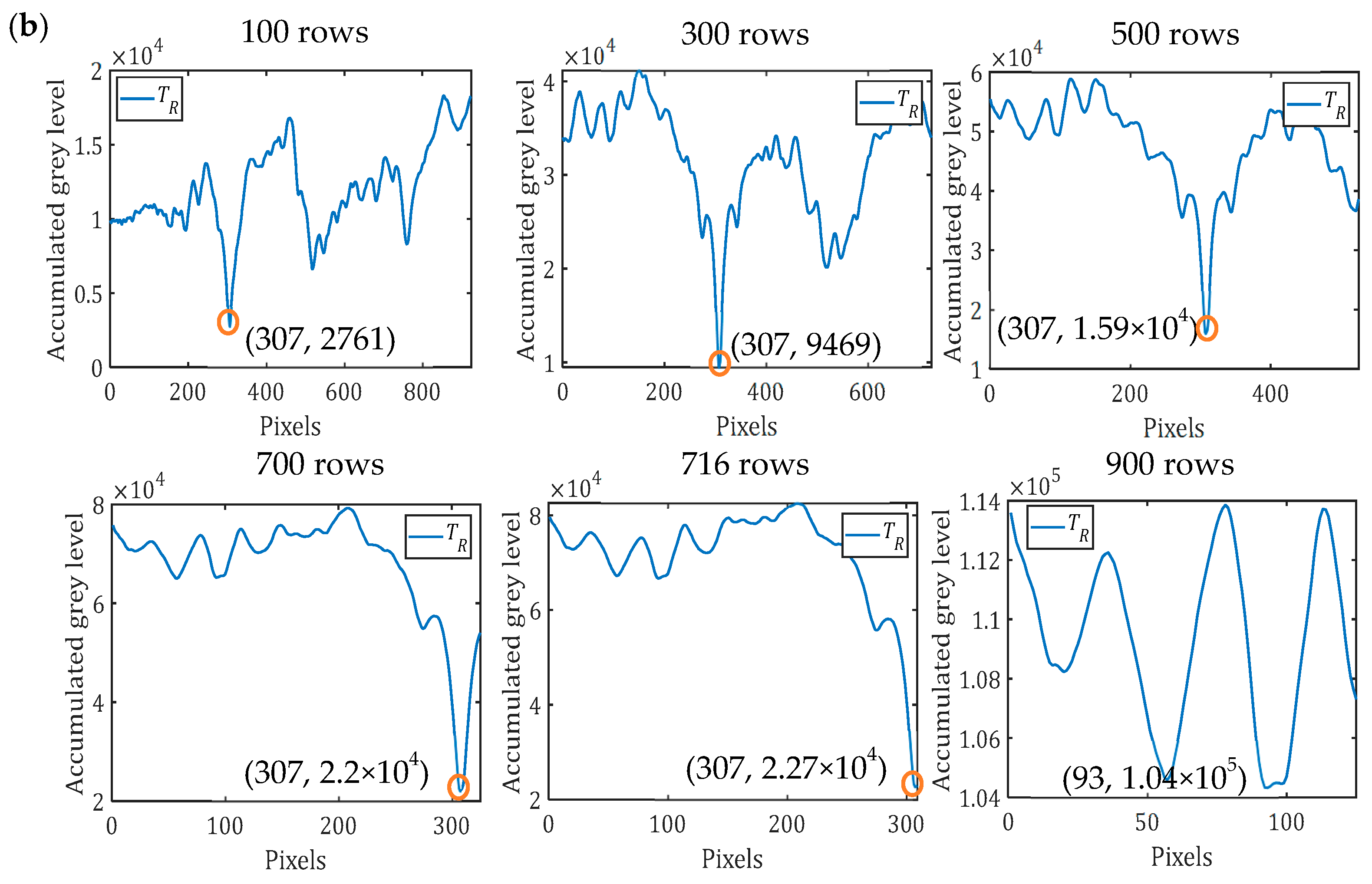
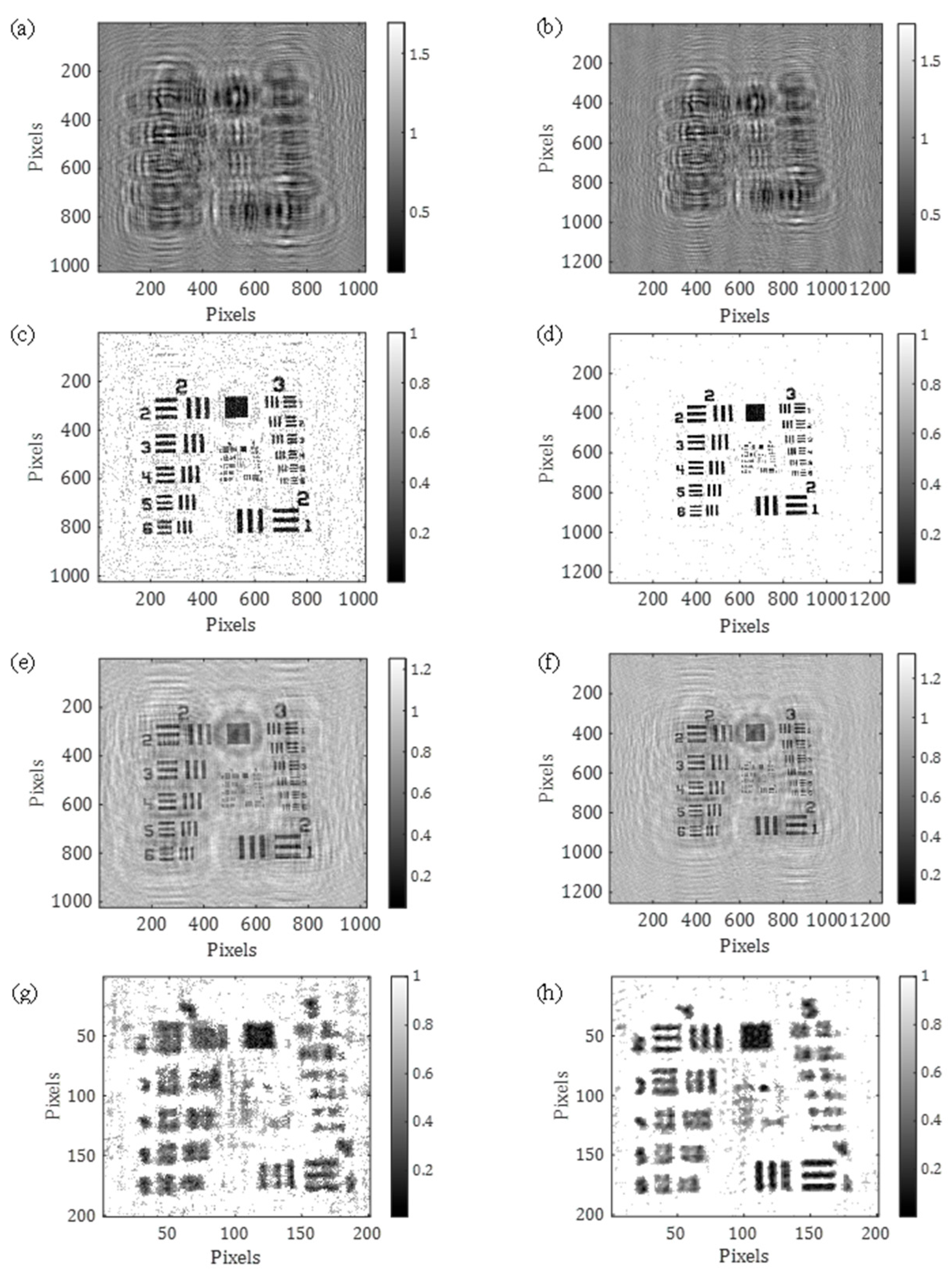
| CM (ms) | SM (ms) | SMSA (ms) | |
|---|---|---|---|
| m = 100 | / | 117 | 10.1 |
| m = 300 | / | 138 | 12.2 |
| m = 500 | 22.9 | 195 | 26.9 |
| m = 700 | / | 169 | 37.3 |
| m = 715 | / | 168 | 38.4 |
| m = 900 | / | 96 | 55.2 |
| Interpolation Factor | CM (ms) | SM (ms) | SMSA (ms) |
|---|---|---|---|
| 2 | 6.927 | 20.71 | 3.842 |
| 4 | 23.78 | 147.2 | 12.74 |
| 8 | 101.2 | 843.6 | 31.23 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wei, Z.; Healy, J.J.; Wan, M. Subtraction Method for Subpixel Stitching: Synthetic Aperture Holographic Imaging. Photonics 2025, 12, 551. https://doi.org/10.3390/photonics12060551
Wei Z, Healy JJ, Wan M. Subtraction Method for Subpixel Stitching: Synthetic Aperture Holographic Imaging. Photonics. 2025; 12(6):551. https://doi.org/10.3390/photonics12060551
Chicago/Turabian StyleWei, Zhangyue, John J. Healy, and Min Wan. 2025. "Subtraction Method for Subpixel Stitching: Synthetic Aperture Holographic Imaging" Photonics 12, no. 6: 551. https://doi.org/10.3390/photonics12060551
APA StyleWei, Z., Healy, J. J., & Wan, M. (2025). Subtraction Method for Subpixel Stitching: Synthetic Aperture Holographic Imaging. Photonics, 12(6), 551. https://doi.org/10.3390/photonics12060551





