A Comprehensive Review of Rubidium Two-Photon Vapor Cell Optical Clock: Long-Term Performance Limitations and Potential Improvements
Abstract
1. Introduction
2. Two-Photon Excitation Principle in Vapor Cell Optical Clocks
3. Conventional Vapor Cell Optical Clocks
3.1. Rubidium Two-Photon Optical Clock
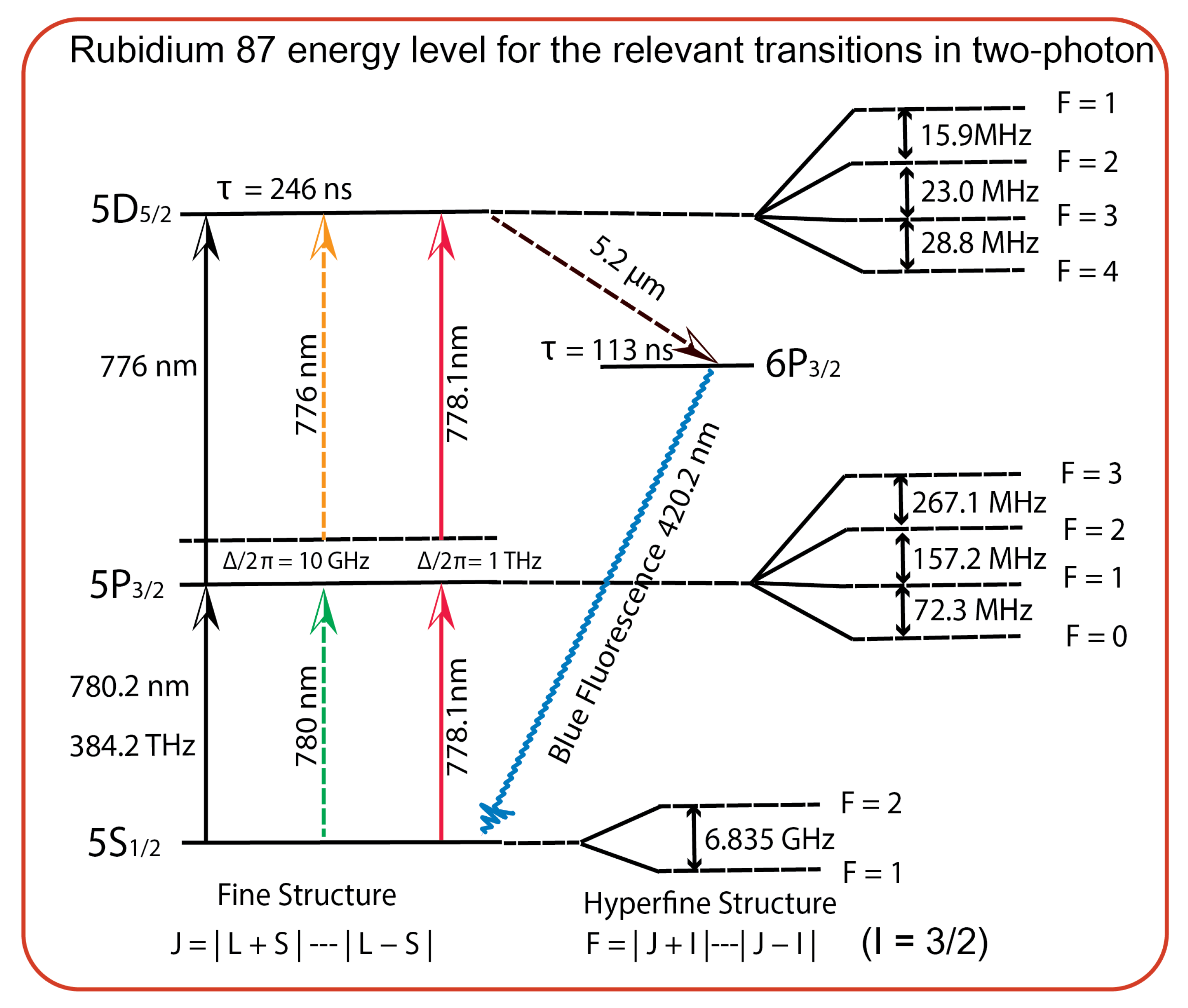
3.1.1. Two-Photon Single-Color Excitation
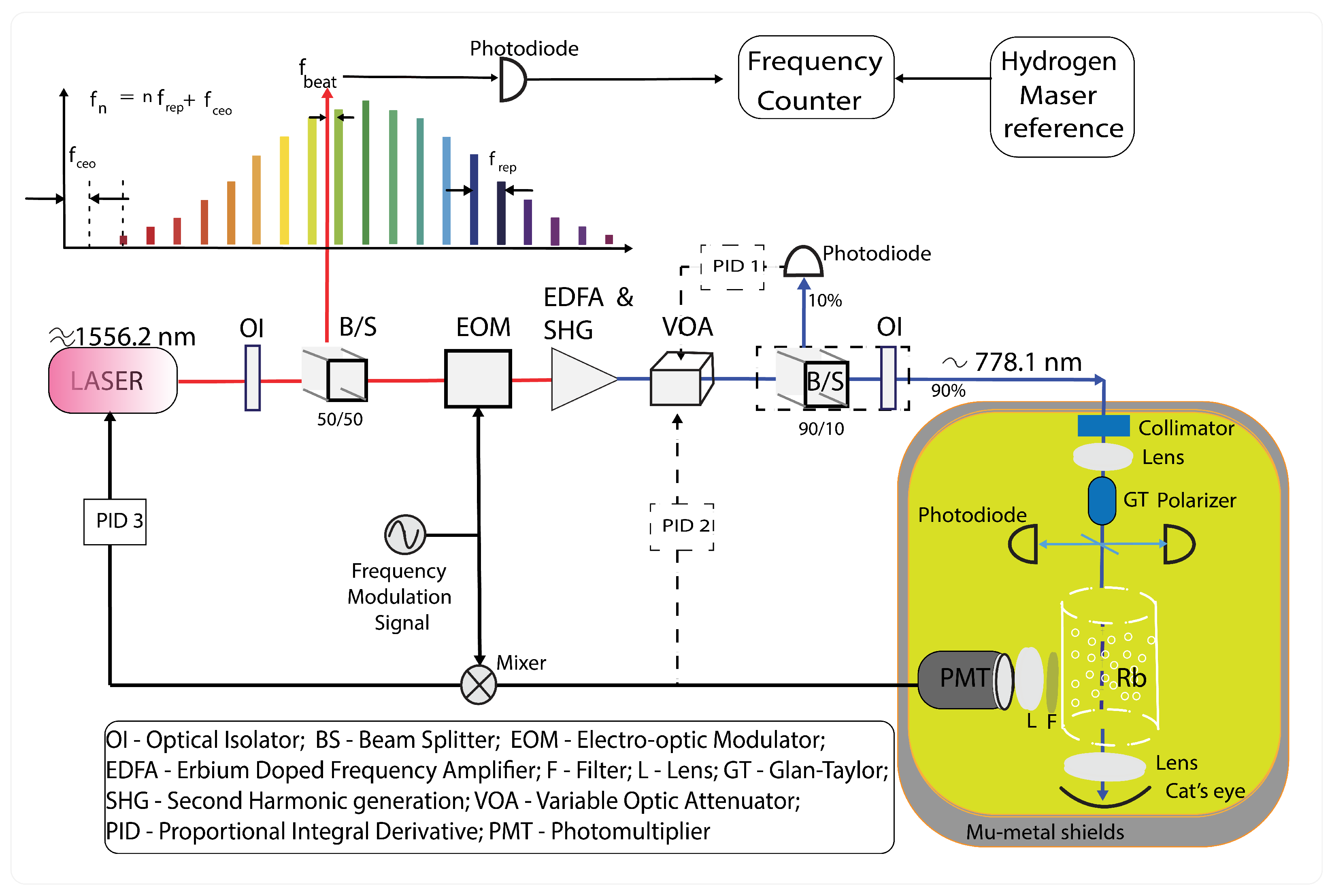
3.1.2. Difference in Experimental Schemes
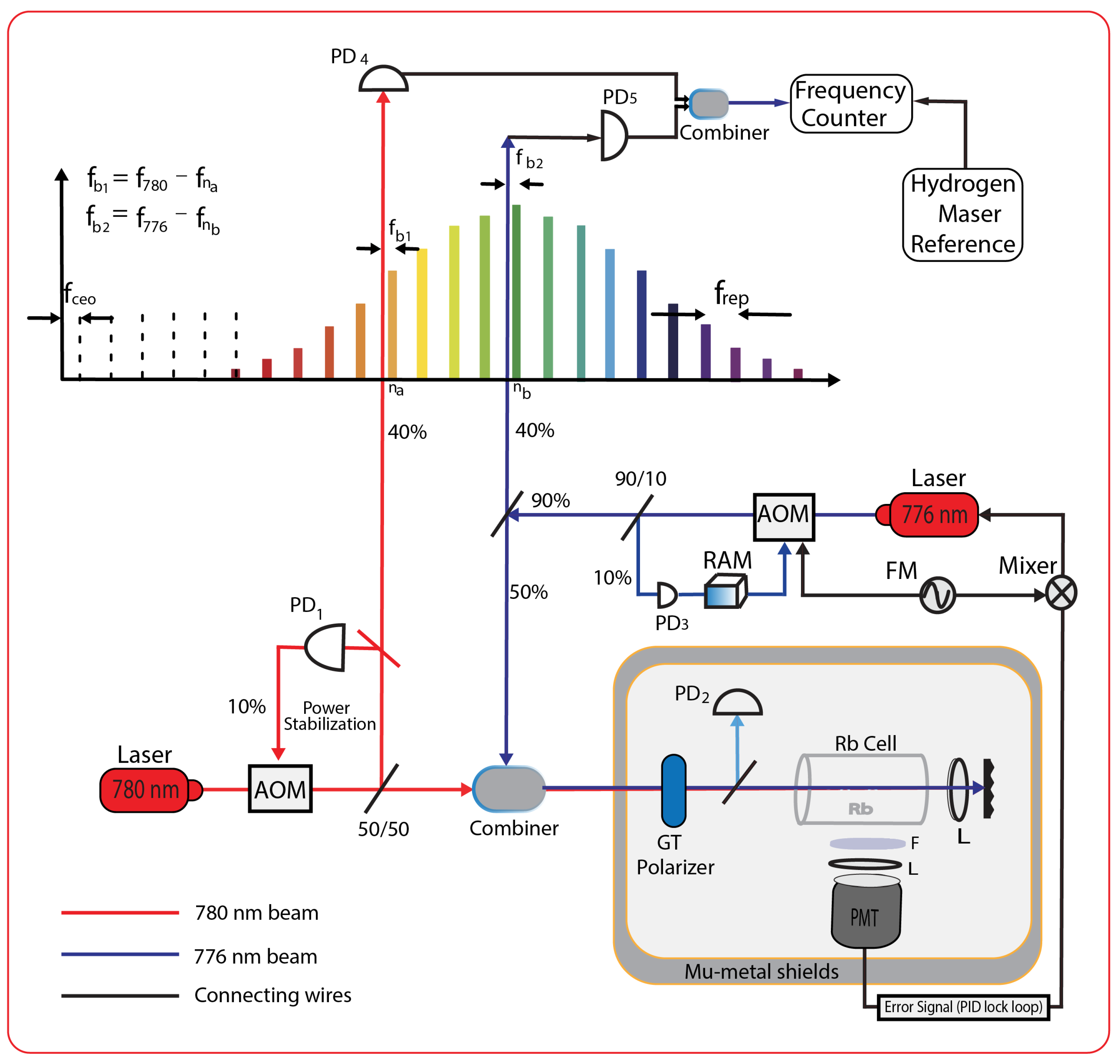
3.1.3. Two-Photon Two-Color Excitation
3.1.4. Experimental Schemes Discussion
3.2. Comparison and Drawbacks of the Single-Color and Two-Color Rb Schemes
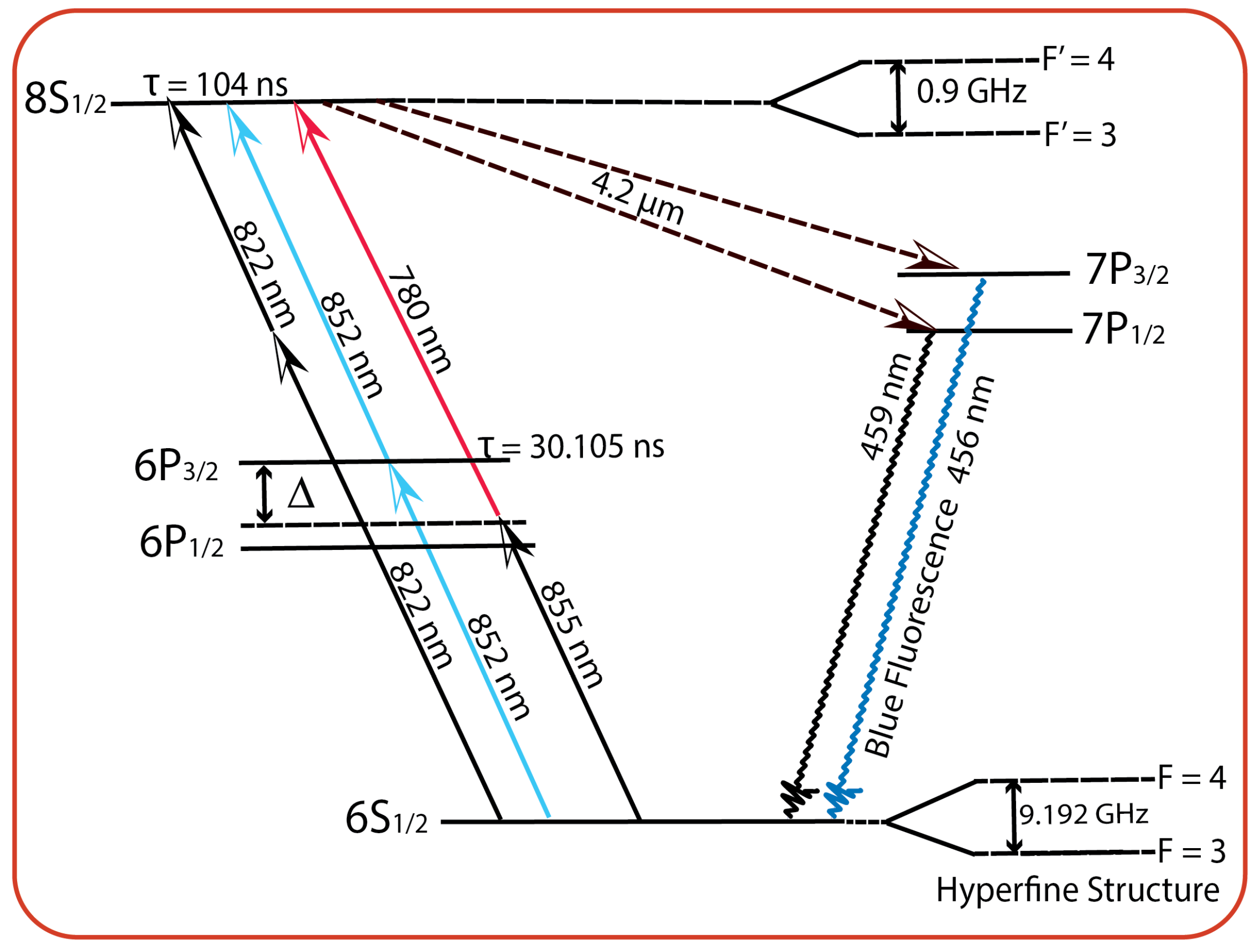
3.3. Cesium Two-Photon Vapor Cell Optical Clock
Experimental Procedure
3.4. Microcell-Based Optical Frequency Standards
4. Short-Term-Performance Metrics and Limitations
4.1. Photon Shot-Noise
4.2. Intermodulation Effect
Background Noise
5. Long-Term Performance Limiting Effects
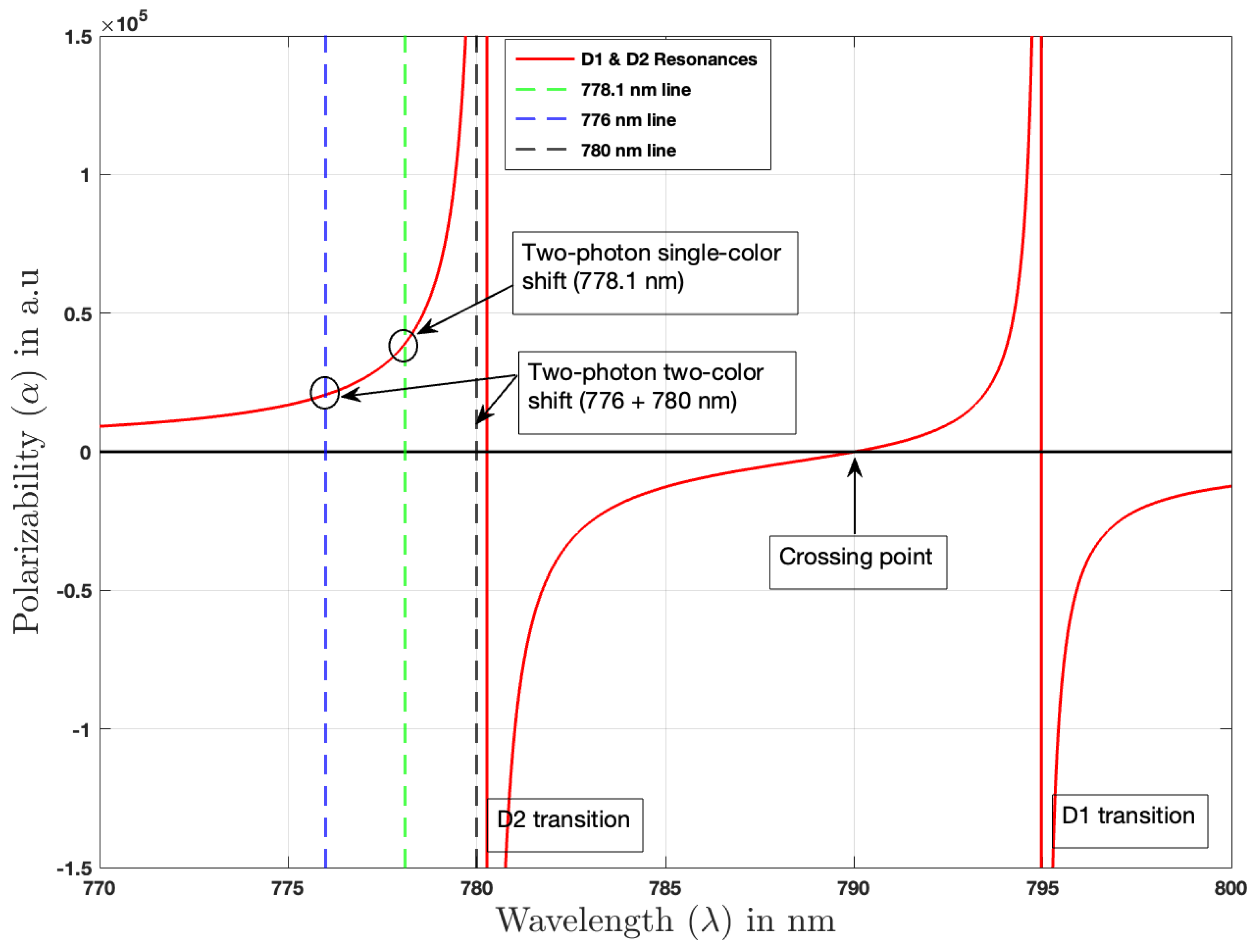
5.1. Light Shift Theory and Discussion
Beyond Two-Level System
5.2. Vapor Cell Temperature Fluctuation and Drift
6. Other Performance-Limiting Effects
6.1. The Stochastic Nature of the Laser Field
6.2. Vapor Cell Design and Functionality
The Signal Detection System
6.3. Density Effects and Impact Due to Spatial Inhomogeneities
6.4. Geometrical Broadening
6.5. Power Broadening
6.6. Second-Order Doppler Effect
6.7. Blackbody Radiation (BBR) Shift
6.8. Atomic Collisions
6.9. DC Stark Shift Contribution
7. Methods for Suppressing the Light-Shift Effects
7.1. Resonance-Offset Locking (ROL)
7.2. Combined Error Signal Method
7.3. Counter-Propagating Beam Approach
8. Conclusions and Prospects
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Essen, L.; Parry, J.V. An atomic standard of frequency and time interval: A cesium resonator. Nature 1955, 176, 280–282. [Google Scholar] [CrossRef]
- Lombardi, M.A. A Historical Review of US Contributions to the Atomic Redefinition of the SI Second in 1967. J. Res. Natl. Inst. Stand. Technol. 2017, 122, 1. [Google Scholar] [CrossRef]
- Ramsey, N.F. History of early atomic clocks. Metrologia 2005, 42, S1. [Google Scholar] [CrossRef]
- Riley, W.J. A History of the Rubidium Frequency Standard; IEEE UFFC-S: Knoxville, TN, USA, 2019; p. 2. [Google Scholar]
- Gill, P. When should we change the definition of the second? Philos. Trans. R. Soc. A Math. Phys. Eng. Sci. 2011, 369, 4109–4130. [Google Scholar] [CrossRef] [PubMed]
- Margolis, H. Optical frequency standards and clocks. Contemp. Phys. 2010, 51, 37–58. [Google Scholar] [CrossRef]
- Aeppli, A.; Kim, K.; Warfield, W.; Safronova, M.S.; Ye, J. Clock with 8 × 10−19 systematic uncertainty. Phys. Rev. Lett. 2024, 133, 023401. [Google Scholar] [CrossRef]
- National Institute of Standards and Technology (NIST). World’s Most Precise and Accurate Atomic Clock Pushes New Frontiers in Physics. Available online: https://www.nist.gov/news-events/news (accessed on 18 May 2025).
- Wang, B.; Li, B.; Xiao, Q.; Mo, G.; Cai, Y.F. Space-based optical lattice clocks as gravitational wave detectors in search for new physics. Sci. China Phys. Mech. Astron. 2025, 68, 249512. [Google Scholar] [CrossRef]
- Bothwell, T.; Hunt, B.D.; Siegel, J.L.; Hassan, Y.S.; Grogan, T.; Kobayashi, T.; Gibble, K.; Porsev, S.G.; Safronova, M.S.; Brown, R.C.; et al. Lattice Light Shift Evaluations in a Dual-Ensemble Yb Optical Lattice Clock. Phys. Rev. Lett. 2025, 134, 033201. [Google Scholar] [CrossRef]
- Bothwell, T.; Brand, W.; Fasano, R.; Akin, T.; Whalen, J.; Grogan, T.; Chen, Y.J.; Pomponio, M.; Nakamura, T.; Rauf, B.; et al. Deployment of a transportable Yb optical lattice clock. Opt. Lett. 2025, 50, 646–649. [Google Scholar]
- Liao, T.Y.; Liu, H.; Meng, F.; Wang, Q.; Yang, T.; Tian, H.C.; Lu, B.K.; Zhu, L.; Li, Y.; Lin, B.K.; et al. Remote comparison of two Sr optical lattice clocks through a 58 km fiber link. Chin. Phys. Lett. 2025, 42, 034201. [Google Scholar] [CrossRef]
- Shinkai, H.; Takamoto, M.; Katori, H. Transportable optical lattice clocks and general relativity. Int. J. Mod. Phys. D 2025, 34, 2540012. [Google Scholar] [CrossRef]
- Kale, Y.B.; Singh, A.; Gellesch, M.; Jones, J.M.; Morris, D.; Aldous, M.; Bongs, K.; Singh, Y. Field deployable atomics package for an optical lattice clock. Quantum Sci. Technol. 2022, 7, 045004. [Google Scholar] [CrossRef]
- Ohmae, N.; Takamoto, M.; Takahashi, Y.; Kokubun, M.; Araki, K.; Hinton, A.; Ushijima, I.; Muramatsu, T.; Furumiya, T.; Sakai, Y.; et al. Transportable strontium optical lattice clocks operated outside laboratory at the level of 10−18 uncertainty. Adv. Quantum Technol. 2021, 4, 2100015. [Google Scholar] [CrossRef]
- Hobson, R.; Bowden, W.; Vianello, A.; Silva, A.; Baynham, C.F.; Margolis, H.S.; Baird, P.E.; Gill, P.; Hill, I.R. A strontium optical lattice clock with 1 × 10−17 uncertainty and measurement of its absolute frequency. Metrologia 2020, 57, 065026. [Google Scholar] [CrossRef]
- Kong, D.H.; Wang, Z.H.; Guo, F.; Zhang, Q.; Lu, X.T.; Wang, Y.B.; Chang, H. A transportable optical lattice clock at the National Time Service Center. Chin. Phys. B 2020, 29, 070602. [Google Scholar] [CrossRef]
- Bothwell, T.; Kedar, D.; Oelker, E.; Robinson, J.M.; Bromley, S.L.; Tew, W.L.; Ye, J.; Kennedy, C.J. JILA SrI optical lattice clock with uncertainty of 2.0 × 10−18. Metrologia 2019, 56, 065004. [Google Scholar] [CrossRef]
- Bloom, B.; Nicholson, T.; Williams, J.; Campbell, S.; Bishof, M.; Zhang, X.; Zhang, W.; Bromley, S.; Ye, J. An optical lattice clock with accuracy and stability at the 10−18 level. Nature 2014, 506, 71–75. [Google Scholar] [CrossRef]
- Poli, N.; Schioppo, M.; Vogt, S.; Falke, S.; Sterr, U.; Lisdat, C.; Tino, G. A transportable strontium optical lattice clock. Appl. Phys. B 2014, 117, 1107–1116. [Google Scholar] [CrossRef]
- Takamoto, M.; Hong, F.L.; Higashi, R.; Katori, H. An optical lattice clock. Nature 2005, 435, 321–324. [Google Scholar] [CrossRef]
- McGrew, W.F.; Zhang, X.; Fasano, R.J.; Schäffer, S.A.; Beloy, K.; Nicolodi, D.; Brown, R.C.; Hinkley, N.; Milani, G.; Schioppo, M.; et al. Atomic clock performance enabling geodesy below the centimetre level. Nature 2018, 564, 87–90. [Google Scholar] [CrossRef]
- Koller, S.; Grotti, J.; Vogt, S.; Al-Masoudi, A.; Dörscher, S.; Häfner, S.; Sterr, U.; Lisdat, C. Transportable optical lattice clock with 7 × 10−17 uncertainty. Phys. Rev. Lett. 2017, 118, 073601. [Google Scholar] [CrossRef] [PubMed]
- Origlia, S.; Pramod, M.S.; Schiller, S.; Singh, Y.; Bongs, K.; Schwarz, R.; Al-Masoudi, A.; Dörscher, S.; Herbers, S.; Häfner, S.; et al. Towards an optical clock for space: Compact, high-performance optical lattice clock based on bosonic atoms. Phys. Rev. A 2018, 98, 053443. [Google Scholar] [CrossRef]
- Vogt, S.; Häfner, S.; Grotti, J.; Koller, S.; Al-Masoudi, A.; Sterr, U.; Lisdat, C. A transportable optical lattice clock. J. Phys. Conf. Ser. IOP Publ. 2016, 723, 012020. [Google Scholar] [CrossRef]
- Hausser, H.; Keller, J.; Nordmann, T.; Bhatt, N.; Kiethe, J.; Liu, H.; Richter, I.; von Boehn, M.; Rahm, J.; Weyers, S.; et al. In+ 115-Yb+ 172 Coulomb Crystal Clock with 2.5 × 10−18 Systematic Uncertainty. Phys. Rev. Lett. 2025, 134, 023201. [Google Scholar] [CrossRef]
- King, S.A.; Spieß, L.J.; Micke, P.; Wilzewski, A.; Leopold, T.; Benkler, E.; Lange, R.; Huntemann, N.; Surzhykov, A.; Yerokhin, V.A.; et al. An optical atomic clock based on a highly charged ion. Nature 2022, 611, 43–47. [Google Scholar] [CrossRef]
- Gao, K. The 40Ca+ ion optical clock. Natl. Sci. Rev. 2020, 7, 1799–1801. [Google Scholar] [CrossRef]
- Zhang, B.; Huang, Y.; Zhang, H.; Hao, Y.; Zeng, M.; Guan, H.; Gao, K. Progress on the 40Ca+ ion optical clock. Chin. Phys. B 2020, 29, 074209. [Google Scholar] [CrossRef]
- Diddams, S.A.; Udem, T.; Bergquist, J.; Curtis, E.; Drullinger, R.; Hollberg, L.; Itano, W.M.; Lee, W.; Oates, C.; Vogel, K.; et al. An optical clock based on a single trapped 199Hg+ ion. Science 2001, 293, 825–828. [Google Scholar] [CrossRef] [PubMed]
- Zeng, M.; Huang, Y.; Zhang, B.; Hao, Y.; Ma, Z.; Hu, R.; Zhang, H.; Chen, Z.; Wang, M.; Guan, H.; et al. Toward a transportable Ca+ optical clock with a systematic uncertainty of 4.8 × 10−18. Phys. Rev. Appl. 2023, 19, 064004. [Google Scholar] [CrossRef]
- Huntemann, N.; Sanner, C.; Lipphardt, B.; Tamm, C.; Peik, E. Single-ion atomic clock with 3 × 10−18 systematic uncertainty. Phys. Rev. Lett. 2016, 116, 063001. [Google Scholar] [CrossRef]
- Huang, Y.; Zhang, B.; Zeng, M.; Hao, Y.; Ma, Z.; Zhang, H.; Guan, H.; Chen, Z.; Wang, M.; Gao, K. Liquid-nitrogen-cooled Ca+ optical clock with systematic uncertainty of 3 × 10−18. Phys. Rev. Appl. 2022, 17, 034041. [Google Scholar] [CrossRef]
- Marshall, M.; Castillo, D.R.; Dworschack, W.; Aeppli, A.; Kim, K.; Lee, D.; Warfield, W.; Nardelli, N.; Fortier, T.; Ye, J.; et al. High-Stability Single-Ion Clock with 5.5 × 10−19 Systematic Uncertainty. arXiv 2025, arXiv:2504.13071. [Google Scholar]
- Huntemann, N.; Okhapkin, M.; Lipphardt, B.; Weyers, S.; Tamm, C.; Peik, E. High-accuracy optical clock based on the octupole transition in Yb+ 171. Phys. Rev. Lett. 2012, 108, 090801. [Google Scholar] [CrossRef]
- Beeks, K.; Sikorsky, T.; Schumm, T.; Thielking, J.; Okhapkin, M.V.; Peik, E. The thorium-229 low-energy isomer and the nuclear clock. Nat. Rev. Phys. 2021, 3, 238–248. [Google Scholar] [CrossRef]
- Kraemer, S.; Moens, J.; Athanasakis-Kaklamanakis, M.; Bara, S.; Beeks, K.; Chhetri, P.; Chrysalidis, K.; Claessens, A.; Cocolios, T.E.; Correia, J.G.; et al. Observation of the radiative decay of the 229Th nuclear clock isomer. Nature 2023, 617, 706–710. [Google Scholar] [CrossRef] [PubMed]
- Zhang, C.; von der Wense, L.; Doyle, J.F.; Higgins, J.S.; Ooi, T.; Friebel, H.U.; Ye, J.; Elwell, R.; Terhune, J.; Morgan, H.; et al. 229ThF4 thin films for solid-state nuclear clocks. Nature 2024, 636, 603–608. [Google Scholar] [CrossRef]
- Thirolf, P. Shedding Light on the Thorium-229 Nuclear Clock Isomer. Physics 2024, 17, 71. [Google Scholar] [CrossRef]
- Scott, J.P.; Potvliege, R.; Carty, D.; Jones, M.P. Trap induced broadening in a potential hydrogen lattice clock. Metrologia 2024, 61, 025001. [Google Scholar] [CrossRef]
- Baker, C.; Bertsche, W.; Capra, A.; Carruth, C.; Cesar, C.; Charlton, M.; Christensen, A.; Collister, R.; Mathad, A.C.; Eriksson, S.; et al. Laser cooling of antihydrogen atoms. Nature 2021, 592, 35–42. [Google Scholar] [CrossRef]
- Lane, I.C. Production of ultracold hydrogen and deuterium via Doppler-cooled Feshbach molecules. Phys. Rev. A 2015, 92, 022511. [Google Scholar] [CrossRef]
- Gabrielse, G.; Glowacz, B.; Grzonka, D.; Hamley, C.; Hessels, E.; Jones, N.; Khatri, G.; Lee, S.; Meisenhelder, C.; Morrison, T.; et al. Lyman-α source for laser cooling antihydrogen. Opt. Lett. 2018, 43, 2905–2908. [Google Scholar] [CrossRef] [PubMed]
- Burkley, Z.; Yost, D. Proposal for loading hydrogen into a magic wavelength optical lattice. Bull. Am. Phys. Soc. 2018, 63, 16. [Google Scholar]
- Liu, Y.; Zhu, X.; Chen, C. Millisecond pulsar augmented atomic clock ensemble timescale algorithm. Measurement 2025, 250, 117033. [Google Scholar] [CrossRef]
- Zheng, Z.H.; Liu, Y.; Shen, D.; Feng, F.; Liu, J.L.; Ma, Y.X.; Zhu, X.W. Research on Pulsar Time Steered Atomic Time Algorithm Based on DPLL. Res. Astron. Astrophys. 2024, 24, 035019. [Google Scholar] [CrossRef]
- Zhu, X.; Zhang, Z.; Zhao, C.; Li, B.; Tong, M.; Gao, Y.; Yang, T. Research on establishing a joint time-scale of pulsar time and atomic time based on a wavelet analysis method. Mon. Not. R. Astron. Soc. 2024, 529, 1082–1090. [Google Scholar] [CrossRef]
- Critchley-Marrows, J.; Wu, X.; Ambatali, C.; Nakasuka, S. Pulsar Timing for Clock Stability–Exploring an Autonomous and Resilient Approach to Timing Using Radio Pulsars. In Proceedings of the 36th International Technical Meeting of the Satellite Division of The Institute of Navigation (ION GNSS+ 2023), Denver, CO, USA, 11–15 September 2023; pp. 3175–3189. [Google Scholar]
- Hobbs, G.; Guo, L.; Caballero, R.; Coles, W.; Lee, K.; Manchester, R.; Reardon, D.; Matsakis, D.; Tong, M.; Arzoumanian, Z.; et al. A pulsar-based time-scale from the International Pulsar Timing Array. Mon. Not. R. Astron. Soc. 2020, 491, 5951–5965. [Google Scholar] [CrossRef]
- Taylor, J.H. Millisecond pulsars: Nature’s most stable clocks. Proc. IEEE 1991, 79, 1054–1062. [Google Scholar] [CrossRef]
- Kim, M. Design and Analysis of High-Stability THz Molecular Clock System. Ph.D. Thesis, Massachusetts Institute of Technology, Cambridge, MA, USA, 2022. [Google Scholar]
- Leung, K.; Iritani, B.; Tiberi, E.; Majewska, I.; Borkowski, M.; Moszynski, R.; Zelevinsky, T. Terahertz vibrational molecular clock with systematic uncertainty at the 10−14 level. Phys. Rev. X 2023, 13, 011047. [Google Scholar] [CrossRef]
- Hanneke, D.; Kuzhan, B.; Lunstad, A. Optical clocks based on molecular vibrations as probes of variation of the proton-to-electron mass ratio. Quantum Sci. Technol. 2020, 6, 014005. [Google Scholar] [CrossRef]
- Roslund, J.D.; Cingöz, A.; Lunden, W.D.; Partridge, G.B.; Kowligy, A.S.; Roller, F.; Sheredy, D.B.; Skulason, G.E.; Song, J.P.; Abo-Shaeer, J.R.; et al. Optical clocks at sea. Nature 2024, 628, 736–740. [Google Scholar] [CrossRef]
- Döringshoff, K.; Gutsch, F.B.; Schkolnik, V.; Kürbis, C.; Oswald, M.; Pröbster, B.; Kovalchuk, E.V.; Bawamia, A.; Smol, R.; Schuldt, T.; et al. Iodine frequency reference on a sounding rocket. Phys. Rev. Appl. 2019, 11, 054068. [Google Scholar] [CrossRef]
- Ye, J.; Ma, L.S.; Hall, J.L. Molecular iodine clock. Phys. Rev. Lett. 2001, 87, 270801. [Google Scholar] [CrossRef]
- Day, C. New Accuracy Record for Molecular Lattice Clock. Physics 2023, 16, 36. [Google Scholar] [CrossRef]
- Mawdsley, J.P. Terahertz Frequency Synthesis in CMOS for a Chip-Scale Molecular Clock. Ph.D. Thesis, Massachusetts Institute of Technology, Cambridge, MA, USA, 2019. [Google Scholar]
- Wang, C.; Yi, X.; Mawdsley, J.; Kim, M.; Hu, Z.; Zhang, Y.; Perkins, B.; Han, R. Chip-scale molecular clock. IEEE J. Solid-State Circuits 2018, 54, 914–926. [Google Scholar] [CrossRef]
- Fortier, T.; Baumann, E. 20 years of developments in optical frequency comb technology and applications. Commun. Phys. 2019, 2, 153. [Google Scholar] [CrossRef]
- Hall, J.L. Optical frequency measurement: 40 years of technology revolutions. IEEE J. Sel. Top. Quantum Electron. 2000, 6, 1136–1144. [Google Scholar] [CrossRef]
- Sinclair, L.C.; Coddington, I.; Swann, W.C.; Rieker, G.B.; Hati, A.; Iwakuni, K.; Newbury, N.R. Operation of an optically coherent frequency comb outside the metrology lab. Opt. Express 2014, 22, 6996–7006. [Google Scholar] [CrossRef]
- Jana, S.; Sahoo, B.; Sharma, A. Progress towards the development of a portable all-optical atomic clock based on a two-photon transition in warm atomic vapor. In Proceedings of the 2022 URSI Regional Conference on Radio Science (USRI-RCRS), Indore, India, 1–4 December 2022; IEEE: Piscataway, NJ, USA, 2022; pp. 1–4. [Google Scholar]
- Gill, P. Optical frequency standards. Metrologia 2005, 42, S125–S137. [Google Scholar] [CrossRef]
- Bandi, T.N. A comprehensive overview of atomic clocks and their applications. Demo J. 2024, 1, 40–50. [Google Scholar] [CrossRef]
- Strangfeld, A.; Kanthak, S.; Schiemangk, M.; Wiegand, B.; Wicht, A.; Ling, A.; Krutzik, M. Prototype of a compact rubidium-based optical frequency reference for operation on nanosatellites. J. Opt. Soc. Am. B 2021, 38, 1885–1891. [Google Scholar] [CrossRef]
- Morley, P.D.; Buettner, D.J. Atomic-Clock Detection of CNO-Based Dark Matter; IntechOpen: London, UK, 2024. [Google Scholar]
- Safronova, M.; Budker, D.; DeMille, D.; Kimball, D.F.J.; Derevianko, A.; Clark, C.W. Search for new physics with atoms and molecules. Rev. Mod. Phys. 2018, 90, 025008. [Google Scholar] [CrossRef]
- Dimarcq, N.; Gertsvolf, M.; Mileti, G.; Bize, S.; Oates, C.; Peik, E.; Calonico, D.; Ido, T.; Tavella, P.; Meynadier, F.; et al. Roadmap towards the redefinition of the second. Metrologia 2024, 61, 012001. [Google Scholar] [CrossRef]
- Lodewyck, J. On a definition of the SI second with a set of optical clock transitions. Metrologia 2019, 56, 055009. [Google Scholar] [CrossRef]
- Kristen Cote, S.J.; Ryan Zazo, L.M.; Vutha, A.C. The Stratospheric Optical Rubidium Clock Experiment. In Proceedings of the 70th International Astronautical Congress (IAC), Washington, DC, USA, 21–25 October 2019. [Google Scholar]
- Jackson, S.; Vutha, A.C. Magic polarization for cancellation of light shifts in two-photon optical clocks. Phys. Rev. A 2019, 99, 063422. [Google Scholar] [CrossRef]
- Riehle, F. Towards a redefinition of the second based on optical atomic clocks. Comptes Rendus. Phys. 2015, 16, 506–515. [Google Scholar] [CrossRef]
- Yasuda, M.; Inaba, H.; Kohno, T.; Tanabe, T.; Nakajima, Y.; Hosaka, K.; Akamatsu, D.; Onae, A.; Suzuyama, T.; Amemiya, M.; et al. Improved absolute frequency measurement of the 171Yb optical lattice clock towards a candidate for the redefinition of the second. Appl. Phys. Express 2012, 5, 102401. [Google Scholar] [CrossRef]
- McGrew, W.F.; Zhang, X.; Leopardi, H.; Fasano, R.; Nicolodi, D.; Beloy, K.; Yao, J.; Sherman, J.A.; Schaeffer, S.A.; Savory, J.; et al. Towards the optical second: Verifying optical clocks at the SI limit. Optica 2019, 6, 448–454. [Google Scholar] [CrossRef]
- Yadav, S.; Aswal, D.K. Redefined SI units and their implications. Mapan 2020, 35, 1–9. [Google Scholar] [CrossRef]
- Le Targat, R.; Lorini, L.; Le Coq, Y.; Zawada, M.; Guéna, J.; Abgrall, M.; Gurov, M.; Rosenbusch, P.; Rovera, D.; Nagórny, B.; et al. Experimental realization of an optical second with strontium lattice clocks. Nat. Commun. 2013, 4, 2109. [Google Scholar] [CrossRef]
- Ludlow, A.D.; Boyd, M.M.; Ye, J.; Peik, E.; Schmidt, P.O. Optical atomic clocks. Rev. Mod. Phys. 2015, 87, 637–701. [Google Scholar] [CrossRef]
- Kitching, J. Chip-scale atomic devices. Appl. Phys. Rev. 2018, 5, 031302. [Google Scholar] [CrossRef]
- Arimondo, E. V coherent population trapping in laser spectroscopy. In Progress in Optics; Elsevier: Amsterdam, The Netherlands, 1996; Volume 35, pp. 257–354. [Google Scholar]
- Shah, V.; Kitching, J. Advances in coherent population trapping for atomic clocks. In Advances in Atomic, Molecular, and Optical Physics; Elsevier: Amsterdam, The Netherlands, 2010; Volume 59, pp. 21–74. [Google Scholar]
- Petit, G.; Wolf, P.; Delva, P. Atomic time, clocks, and clock comparisons in relativistic spacetime: A review. Front. Relativ. Celest. Mech. 2014, 2, 249–279. [Google Scholar]
- Kang, S.; Gharavipour, M.; Affolderbach, C.; Gruet, F.; Mileti, G. Demonstration of a high-performance pulsed optically pumped Rb clock based on a compact magnetron-type microwave cavity. J. Appl. Phys. 2015, 117, 104510. [Google Scholar] [CrossRef]
- Kang, S.; Gharavipour, M.; Gruet, F.; Affolderbach, C.; Mileti, G. Compact and high-performance Rb clock based on pulsed optical pumping for industrial application. In Proceedings of the 2015 Joint Conference of the IEEE International Frequency Control Symposium & the European Frequency and Time Forum, Denver, CO, USA, 12–16 April 2015; IEEE: Piscataway, NJ, USA, 2015; pp. 800–803. [Google Scholar]
- Godone, A.; Micalizio, S.; Levi, F. Pulsed optically pumped frequency standard. Phys. Rev. A—At. Mol. Opt. Phys. 2004, 70, 023409. [Google Scholar] [CrossRef]
- Gozzelino, M.; Micalizio, S.; Calosso, C.E.; Belfi, J.; Sapia, A.; Gioia, M.; Levi, F. Realization of a pulsed optically pumped Rb clock with a frequency stability below 10−15. Sci. Rep. 2023, 13, 12974. [Google Scholar] [CrossRef]
- Pei, H.; Pang, H.; Quan, W.; Fan, W.; Yuan, L.; Zhang, K.; Fang, C. Pulsed optical pumping in electron spin vapor. Measurement 2024, 231, 114619. [Google Scholar] [CrossRef]
- Hao, Q.; Yang, S.; Zheng, S.; Yun, P.; Ruan, J.; Zhang, S. A 44-cm3 physics package for the high-performance pulsed optically pumped atomic clock. Rev. Sci. Instrum. 2024, 95. [Google Scholar] [CrossRef]
- Hao, Q.; Yang, S.; Ruan, J.; Yun, P.; Zhang, S. Integrated pulsed optically pumped Rb atomic clock with frequency stability of 10−15. Phys. Rev. Appl. 2024, 21, 024003. [Google Scholar] [CrossRef]
- Micalizio, S.; Levi, F.; Godone, A.; Calosso, C.; Francois, B.; Boudot, R.; Affolderbach, C.; Kang, S.; Gharavipour, M.; Gruet, F.; et al. Pulsed optically pumped Rb clock. J. Phys. Conf. Ser. IOP Publ. 2016, 723, 012015. [Google Scholar] [CrossRef]
- Micalizio, S.; Godone, A.; Calosso, C.; Levi, F.; Affolderbach, C.; Gruet, F. Pulsed optically pumped rubidium clock with high frequency-stability performance. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2012, 59, 457–462. [Google Scholar] [CrossRef]
- Dong, G.; Deng, J.; Lin, J.; Zhang, S.; Lin, H.; Wang, Y. Recent improvements on the pulsed optically pumped rubidium clock at SIOM. Chin. Opt. Lett. 2017, 15, 040201. [Google Scholar] [CrossRef]
- Shen, Q.; Lin, H.; Deng, J.; Wang, Y. Pulsed optically pumped atomic clock with a medium-to long-term frequency stability of 10−15. Rev. Sci. Instrum. 2020, 91. [Google Scholar] [CrossRef]
- Wang, K.M.; Du, Z.J.; Liu, Y.Y.; Yu, Z.J.; Yan, S.B.; Liu, T.; Dong, R.F.; Zhang, S.G. Pulsed vapor cell atomic clock with a differential Faraday rotation angle detection. Opt. Express 2021, 29, 38527–38539. [Google Scholar] [CrossRef]
- Baryshev, V.N.; Aleynikov, M.S.; Osipenko, G.V.; Blinov, I.Y. Technique of pulsed optical pumping and pulsed excitation of microwave resonances using the Ramsey scheme in a 87Rb cell with a buffer gas. Quantum Electron. 2018, 48, 443. [Google Scholar] [CrossRef]
- Choi, I.; Lee, S.; Kwon, T.; Park, S. Improvement of short-term stability of pulsed optically pumped rubidium atomic clock. In Proceedings of the CPEM 2010, Daejeon, Republic of Korea, 13–18 June 2010; IEEE: Piscataway, NJ, USA, 2010; pp. 432–433. [Google Scholar]
- Lin, H.; Deng, J.; Lin, J.; Zhang, S.; Wang, Y. Frequency stability of a pulsed optically pumped atomic clock with narrow Ramsey linewidth. Appl. Opt. 2018, 57, 3056–3060. [Google Scholar] [CrossRef]
- Knappe, S.; Shah, V.; Schwindt, P.D.; Hollberg, L.; Kitching, J.; Liew, L.A.; Moreland, J. A microfabricated atomic clock. Appl. Phys. Lett. 2004, 85, 1460–1462. [Google Scholar] [CrossRef]
- Venkatraman, V.; Kang, S.; Affolderbach, C.; Shea, H.; Mileti, G. Optical pumping in a microfabricated Rb vapor cell using a microfabricated Rb discharge light source. Appl. Phys. Lett. 2014, 104, 054104. [Google Scholar] [CrossRef]
- Liew, L.A.; Knappe, S.; Moreland, J.; Robinson, H.; Hollberg, L.; Kitching, J. Microfabricated alkali atom vapor cells. Appl. Phys. Lett. 2004, 84, 2694–2696. [Google Scholar] [CrossRef]
- Abdullah, S.; Affolderbach, C.; Gruet, F.; Mileti, G. Aging studies on micro-fabricated alkali buffer-gas cells for miniature atomic clocks. Appl. Phys. Lett. 2015, 106, 163505. [Google Scholar] [CrossRef]
- Nishino, H.; Hara, M.; Yano, Y.; Toda, M.; Kanamori, Y.; Kajita, M.; Ido, T.; Ono, T. A reflection-type vapor cell using anisotropic etching of silicon for micro atomic clocks. Appl. Phys. Express 2019, 12, 072012. [Google Scholar] [CrossRef]
- Maurice, V.; Rutkowski, J.; Kroemer, E.; Bargiel, S.; Passilly, N.; Boudot, R.; Gorecki, C.; Mauri, L.; Moraja, M. Microfabricated vapor cells filled with a cesium dispensing paste for miniature atomic clocks. Appl. Phys. Lett. 2017, 110, 164103. [Google Scholar] [CrossRef]
- Knappe, S.; Schwindt, P.; Gerginov, V.; Shah, V.; Liew, L.; Moreland, J.; Robinson, H.; Hollberg, L.; Kitching, J. Microfabricated atomic clocks and magnetometers. J. Opt. A Pure Appl. Opt. 2006, 8, S318. [Google Scholar] [CrossRef]
- Kitching, J.; Knappe, S.; Shah, V.; Schwindt, P.; Griffith, C.; Jimenez, R.; Preusser, J.; Liew, L.A.; Moreland, J. Microfabricated atomic magnetometers and applications. In Proceedings of the 2008 IEEE International Frequency Control Symposium, Honolulu, HI, USA, 19–21 May 2008; IEEE: Piscataway, NJ, USA, 2008; pp. 789–794. [Google Scholar]
- Hollberg, L.; Kitching, J. Microfabricated atomic clocks and magnetometers. In Laser Spectroscopy PY; World Scientific: Singapore, 2005; p. 337. [Google Scholar]
- Venkatraman, V.; Pétremand, Y.; de Rooij, N.; Shea, H. Reliability characteristics of microfabricated Rb mini-lamps for optical pumping in miniature atomic clocks and magnetometers. In Reliability, Packaging, Testing, and Characterization of MOEMS/MEMS and Nanodevices XII; SPIE: Bellingham, WA, USA, 2013; Volume 8614, pp. 27–33. [Google Scholar]
- Carlé, C.; Callejo, M.; Mursa, A.; Hafiz, M.A.; Tanguy, Q.; Vicarini, R.; Millo, J.; Maurice, V.; Klinger, E.; Passilly, N.; et al. Microfabricated vapor cell atomic clocks at FEMTO-ST. In Proceedings of the Hot Vapor Workshop, Stuttgart, Germany, 30 September–2 October 2024. [Google Scholar]
- Maurice, V.; Newman, Z.L.; Dickerson, S.; Rivers, M.; Hsiao, J.; Greene, P.; Mescher, M.; Kitching, J.; Hummon, M.T.; Johnson, C. Miniaturized optical frequency reference for next-generation portable optical clocks. Opt. Express 2020, 28, 24708–24720. [Google Scholar] [CrossRef]
- Newman, Z.L.; Maurice, V.; Drake, T.; Stone, J.R.; Briles, T.C.; Spencer, D.T.; Fredrick, C.; Li, Q.; Westly, D.; Ilic, B.R.; et al. Architecture for the photonic integration of an optical atomic clock. Optica 2019, 6, 680–685, Also see supplementary material. [Google Scholar] [CrossRef]
- Gellesch, M.; Jones, J.; Barron, R.; Singh, A.; Sun, Q.; Bongs, K.; Singh, Y. Transportable optical atomic clocks for use in out-of-the-lab environments. Adv. Opt. Technol. 2020, 9, 313–325. [Google Scholar] [CrossRef]
- Takamoto, M.; Ushijima, I.; Ohmae, N.; Yahagi, T.; Kokado, K.; Shinkai, H.; Katori, H. Test of general relativity by a pair of transportable optical lattice clocks. Nat. Photonics 2020, 14, 411–415. [Google Scholar] [CrossRef]
- Grotti, J.; Koller, S.; Vogt, S.; Häfner, S.; Sterr, U.; Lisdat, C.; Denker, H.; Voigt, C.; Timmen, L.; Rolland, A.; et al. Geodesy and metrology with a transportable optical clock. Nat. Phys. 2018, 14, 437–441. [Google Scholar] [CrossRef]
- Callejo, M.; Mursa, A.; Vicarini, R.; Klinger, E.; Tanguy, Q.; Millo, J.; Passilly, N.; Boudot, R. Short-term stability of a microcell optical reference based on the Rb atom two-photon transition at 778 nm. J. Opt. Soc. Am. B 2024, 42, 151–159. [Google Scholar] [CrossRef]
- Erickson, S.E.; Tooley, D.P.; Weerasinghe, K.; Zhu, X.; Chavez-Pirson, A.; Jason Jones, R. Atomic frequency standard based on direct frequency comb spectroscopy. Opt. Lett. 2024, 49, 5340–5343. [Google Scholar] [CrossRef] [PubMed]
- Beard, R.; Martin, K.W.; Elgin, J.D.; Kasch, B.L.; Krzyzewski, S.P. Two-photon rubidium clock detecting 776 nm fluorescence. Opt. Express 2024, 32, 7417–7425. [Google Scholar] [CrossRef] [PubMed]
- Lemke, N.D.; Martin, K.W.; Beard, R.; Stuhl, B.K.; Metcalf, A.J.; Elgin, J.D. Measurement of optical rubidium clock frequency spanning 65 days. Sensors 2022, 22, 1982. [Google Scholar] [CrossRef] [PubMed]
- Gerginov, V.; Beloy, K. Two-photon optical frequency reference with active ac Stark shift cancellation. Phys. Rev. Appl. 2018, 10, 014031. [Google Scholar] [CrossRef]
- Martin, K.W.; Phelps, G.; Lemke, N.D.; Bigelow, M.S.; Stuhl, B.; Wojcik, M.; Holt, M.; Coddington, I.; Bishop, M.W.; Burke, J.H. Compact optical atomic clock based on a two-photon transition in rubidium. Phys. Rev. Appl. 2018, 9, 014019. [Google Scholar] [CrossRef]
- Poulin, M.; Latrasse, C.; Touahri, D.; Têtu, M. Frequency stability of an optical frequency standard at 192.6 THz based on a two-photon transition of rubidium atoms. Opt. Commun. 2002, 207, 233–242. [Google Scholar] [CrossRef]
- Ahern, E.J.; Scholten, S.K.; Locke, C.; Hébert, N.B.; White, B.; Luiten, A.N.; Perrella, C. Tailoring the stability of a two-color, two-photon rubidium frequency standard. Phys. Rev. Appl. 2025, 23, 044025. [Google Scholar] [CrossRef]
- Perrella, C.; Light, P.; Anstie, J.; Baynes, F.; White, R.; Luiten, A. Dichroic two-photon rubidium frequency standard. Phys. Rev. Appl. 2019, 12, 054063. [Google Scholar] [CrossRef]
- QuantX Lab. Tempo Compact Rubidium Optical Clock. Available online: https://quantxlabs.com/wp-content/uploads/2024/09/TEMPO.pdf (accessed on 18 May 2025).
- Quantum Computing Report. Infleqtion Sells First Tiqker Quantum Clock in the UK. Available online: https://quantumcomputingreport.com/infleqtion-sells-first-tiqker-quantum-clock-in-the-uk/ (accessed on 18 May 2025).
- McGuyer, B.H. Atomic Physics with Vapor-Cell Clocks. Ph.D. Thesis, Princeton University, Princeton, NJ, USA, 2012. [Google Scholar]
- Camparo, J. The rubidium atomic clock and basic research. Phys. Today 2007, 60, 33–39. [Google Scholar] [CrossRef]
- McGuyer, B.; Jau, Y.Y.; Happer, W. Simple method of light-shift suppression in optical pumping systems. Appl. Phys. Lett. 2009, 94, 251110. [Google Scholar] [CrossRef]
- Affolderbach, C.; Breschi, E.; Schori, C.; Mileti, G. Gas-cell atomic clocks for space: New results and alternative schemes. In Proceedings of the International Conference on Space Optics—ICSO 2006, Noordwijk, The Netherlands, 27–30 June 2006; SPIE: Bellingham, WA, USA, 2017; Volume 10567, pp. 694–700. [Google Scholar]
- Göppert-Mayer, M. Über elementarakte mit zwei quantensprüngen. Ann. der Phys. 1931, 401, 273–294. [Google Scholar] [CrossRef]
- Biraben, F. The first decades of Doppler-free two-photon spectroscopy. Comptes Rendus. Phys. 2019, 20, 671–681. [Google Scholar] [CrossRef]
- Abella, I. Optical double-photon absorption in cesium vapor. Phys. Rev. Lett. 1962, 9, 453. [Google Scholar] [CrossRef]
- Roy, R.; Condylis, P.C.; Johnathan, Y.J.; Hessmo, B. Atomic frequency reference at 1033 nm for ytterbium (Yb)-doped fiber lasers and applications exploiting a rubidium (Rb) 5S1/2 to 4D5/2 one-colour two-photon transition. Opt. Express 2017, 25, 7960–7969. [Google Scholar] [CrossRef]
- Khripunov, S.; Radnatarov, D.; Kobtsev, S. Atomic clock based on a coherent population trapping resonance in 87Rb with improved high-frequency modulation parameters. In Proceedings of the Slow Light, Fast Light, and Opto-Atomic Precision Metrology VIII, San Francisco, CA, USA, 8–12 February 2015; SPIE: Bellingham, WA, USA, 2015; Volume 9378, pp. 8–13. [Google Scholar]
- Sharma, A.; Kolkowitz, S.; Saffman, M. Analysis of a cesium lattice optical clock. arXiv 2022, arXiv:2203.08708. [Google Scholar]
- Zameroski, N.D.; Hager, G.D.; Erickson, C.J.; Burke, J.H. Pressure broadening and frequency shift of the 5S1/2–5D5/2 and 5S1/2–7S1/2 two photon transitions in 85Rb by the noble gases and N2. J. Phys. B At. Mol. Opt. Phys. 2014, 47, 225205. [Google Scholar] [CrossRef]
- Nguyen, T.N.; Schibli, T.R. Temperature-shift-suppression scheme for two-photon two-color rubidium vapor clocks. Phys. Rev. A 2022, 106, 053104. [Google Scholar] [CrossRef]
- Hassanin, K.; Federsel, P.; Karlewski, F.; Zimmermann, C. 5S–5D two-photon transition in rubidium vapor at high densities. Phys. Rev. A 2023, 107, 043104. [Google Scholar] [CrossRef]
- Nez, F.; Biraben, F.; Felder, R.; Millerioux, Y. Optical frequency determination of the hyperfine components of the 5S1/2–5D3/2 two-photon transitions in rubidium. Opt. Commun. 1993, 102, 432–438. [Google Scholar] [CrossRef]
- Kiran Kumar, P.; Suryanarayana, M. Precision two-photon spectroscopy of alkali elements. Pramana 2014, 83, 189–219. [Google Scholar] [CrossRef]
- Martin, K.W.; Lemke, N.D.; Phelps, G.; Burke, J.H.; Stuhl, B. The Optical Stark Shift on a Two-Photon Transition in Rubidium. In Proceedings of the 2018 IEEE International Frequency Control Symposium (IFCS), Flagship Olympic Valley, CA, USA, 21–24 May 2018; IEEE: Piscataway, NJ, USA, 2018; pp. 1–2. [Google Scholar]
- Nguyen, T.N. Degenerate and Non-Degenerate Two-Photon Rubidium Frequency Standard. Ph.D. Thesis, University of Colorado at Boulder, Boulder, CO, USA, 2024. [Google Scholar]
- Gusching, A.; Petersen, M.; Passilly, N.; Brazhnikov, D.; Abdel Hafiz, M.; Boudot, R. Short-term stability of Cs microcell-stabilized lasers using dual-frequency sub-Doppler spectroscopy. J. Opt. Soc. Am. B 2021, 38, 3254–3260. [Google Scholar] [CrossRef]
- Shi, T.; Wei, Q.; Qin, X.; Liu, Z.; Chen, K.; Cao, S.; Shi, H.; Liu, Z.; Chen, J. Dual-frequency optical-microwave atomic clocks based on cesium atoms. Photonics Res. 2024, 12, 1972–1980. [Google Scholar] [CrossRef]
- Kitching, J.; Knappe, S.; Hollberg, L. Miniature vapor-cell atomic-frequency references. Appl. Phys. Lett. 2002, 81, 553–555. [Google Scholar] [CrossRef]
- Kazakov, G.; Matisov, B.; Litvinov, A.; Mazets, I. Coherent population trapping in a finite-size buffer-less cell. J. Phys. B At. Mol. Opt. Phys. 2007, 40, 3851. [Google Scholar] [CrossRef]
- Erhard, M.; Helm, H. Buffer-gas effects on dark resonances: Theory and experiment. Phys. Rev. A 2001, 63, 043813. [Google Scholar] [CrossRef]
- Khan, S.; Kumar, M.P.; Bharti, V.; Natarajan, V. Coherent population trapping (CPT) versus electromagnetically induced transparency (EIT). Eur. Phys. J. D 2017, 71, 1–9. [Google Scholar] [CrossRef]
- Batori, E.; Affolderbach, C.; Pellaton, M.; Gruet, F.; Violetti, M.; Su, Y.; Skrivervik, A.K.; Mileti, G. μ POP clock: A microcell atomic clock based on a double-resonance Ramsey scheme. Phys. Rev. Appl. 2022, 18, 054039. [Google Scholar] [CrossRef]
- Knappe, S.; Schwindt, P.; Shah, V.; Hollberg, L.; Kitching, J.; Liew, L.; Moreland, J. A chip-scale atomic clock based on 87Rb with improved frequency stability. Opt. Express 2005, 13, 1249–1253. [Google Scholar] [CrossRef]
- Bandi, T.; Affolderbach, C.; Stefanucci, C.; Merli, F.; Skrivervik, A.K.; Mileti, G. Compact high-performance continuous-wave double-resonance rubidium standard with 1.4 × 10−13 τ−1/2 stability. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2014, 61, 1769–1778. [Google Scholar] [CrossRef]
- Gharavipour, M.; Affolderbach, C.; Kang, S.; Bandi, T.; Gruet, F.; Pellaton, M.; Mileti, G. High performance vapour-cell frequency standards. J. Phys. Conf. Ser. Iop Publ. 2016, 723, 012006. [Google Scholar] [CrossRef]
- Affolderbach, C.; Droz, F.; Mileti, G. Experimental demonstration of a compact and high-performance laser-pumped rubidium gas cell atomic frequency standard. IEEE Trans. Instrum. Meas. 2006, 55, 429–435. [Google Scholar] [CrossRef]
- Chen, K.H.; Wu, C.M.; Wu, S.R.; Yu, H.H.; Liu, T.W.; Cheng, W.Y. Influence of atmospheric helium on secondary clocks. Opt. Lett. 2020, 45, 4088–4091. [Google Scholar] [CrossRef]
- Moreno, W. Rubidium Vapour-cell Frequency Standards: Metrology of Optical and Microwave Frequency References. Ph.D. Thesis, Université de Neuchâtel, Neuchâtel, Switzerland, 2019. [Google Scholar]
- Terra, O.; Hussein, H. An ultra-stable optical frequency standard for telecommunication purposes based upon the 5S1/2–5D5/2 two-photon transition in Rubidium. Appl. Phys. B 2016, 122, 1–12. [Google Scholar] [CrossRef]
- Martin, K.W. Compact Optical Frequency Standards for Future Applications Beyond the Laboratory. Ph.D. Thesis, The University of New Mexico, Albuquerque, NM, USA, 2019. [Google Scholar]
- Li, D.; Liu, K.; Wang, P.; Kang, S. Dual-interrogation method for suppressing light shift in Rb 778 nm two-photon transition optical frequency standard. Opt. Express 2024, 32, 2766–2773. [Google Scholar] [CrossRef]
- Edwards, C.; Barwood, G.; Margolis, H.; Gill, P.; Rowley, W. Development and absolute frequency measurement of a pair of 778 nm two-photon rubidium standards. Metrologia 2005, 42, 464. [Google Scholar] [CrossRef]
- Newman, Z.L.; Maurice, V.; Fredrick, C.; Fortier, T.; Leopardi, H.; Hollberg, L.; Diddams, S.A.; Kitching, J.; Hummon, M.T. High-performance, compact optical standard. Opt. Lett. 2021, 46, 4702–4705. [Google Scholar] [CrossRef]
- Erickson, S.E. An Optical Atomic Clock Based on Frequency Comb Spectroscopy. Ph.D. Thesis, The University of Arizona, Tucson, AZ, USA, 2024. [Google Scholar]
- Li, D.; Liu, K.; Zhao, L.; Kang, S. A frequency shift compensation method for light shift and vapor-cell temperature shift in atomic clocks. arXiv 2024, arXiv:2405.14281. [Google Scholar]
- Perrella, C. Demonstration of a Two-Photon Atomic Clock with Light Shift Suppression Using Two-Colour Magic Wavelengths; Technical Report; The University of Adelaide North Terrace: Adelaide, Australia, 2022. [Google Scholar]
- Phelps, G.; Lemke, N.; Erickson, C.; Burke, J.; Martin, K. Compact optical clock with 5 × 10−13 instability at 1 s. Navig. J. Inst. Navig. 2018, 65, 49–54. [Google Scholar] [CrossRef]
- Olson, A.J.; Carlson, E.J.; Mayer, S.K. Two-photon spectroscopy of rubidium using a grating-feedback diode laser. Am. J. Phys. 2006, 74, 218–223. [Google Scholar] [CrossRef]
- Bigelow, M.S.; Martin, K.W.; Phelps, G.; Lemke, N.D. A high performance clock laser for two-photon frequency stabilized optical clocks. In Proceedings of the CLEO: Science and Innovations, San Jose, CA, USA, 13–18 May 2018; Optica Publishing Group: Washington, DC, USA, 2018; p. JW2A-163. [Google Scholar]
- Manurkar, P.; Perez, E.F.; Hickstein, D.D.; Carlson, D.R.; Chiles, J.; Westly, D.A.; Baumann, E.; Diddams, S.A.; Newbury, N.R.; Srinivasan, K.; et al. Fully self-referenced frequency comb consuming 5 watts of electrical power. OSA Contin. 2018, 1, 274–282. [Google Scholar] [CrossRef]
- Xu, D.R. White Paper: Non-linear Optical Crystals Used for Quantum Technology. 2022. Available online: https://covesion.com/knowledge-hub/white-paper-non-linear-optical-crystals-used-for-quantum-technology/ (accessed on 18 May 2025).
- Terra, O. Absolute frequency measurement of the hyperfine structure of the 5S1/2–5D3/2 two-photon transition in rubidium using femtosecond frequency comb. Measurement 2019, 144, 83–87. [Google Scholar] [CrossRef]
- Nikogosyan, D.N. Nonlinear Optical Crystals: A Complete Survey; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2006. [Google Scholar]
- Cutler, T.F.; Hamlyn, W.J.; Renger, J.; Whittaker, K.A.; Pizzey, D.; Hughes, I.G.; Sandoghdar, V.; Adams, C.S. Nanostructured alkali-metal vapor cells. Phys. Rev. Appl. 2020, 14, 034054. [Google Scholar] [CrossRef]
- Plocki, A.; Nguyen, T.N.; Schibli, T. Two-color Rubidium clock with AC Stark Shift Suppression. Bull. Am. Phys. Soc. 2023. Available online: https://scholar.colorado.edu/concern/undergraduate_honors_theses/d504rn15n (accessed on 18 May 2025).
- Martin, K.W.; Stuhl, B.; Eugenio, J.; Safronova, M.S.; Phelps, G.; Burke, J.H.; Lemke, N.D. Frequency shifts due to Stark effects on a rubidium two-photon transition. Phys. Rev. A 2019, 100, 023417. [Google Scholar] [CrossRef]
- Bjorkholm, J.; Liao, P. Line shape and strength of two-photon absorption in an atomic vapor with a resonant or nearly resonant intermediate state. Phys. Rev. A 1976, 14, 751. [Google Scholar] [CrossRef]
- Egidi, A. Review of main optical retroreflectors. Ist. Naz. Ric. Metrol. Turin Italy Tech. Rep. RT 31 2018, 31, 2018. [Google Scholar] [CrossRef]
- Mungan, C. The cat’s Eye Retroreflector; Technical Report; United States Naval Academy: Naval Academy, MD, USA, 2001. [Google Scholar]
- Snyder, J. Paraxial ray analysis of a cat’s-eye retroreflector. Appl. Opt. 1975, 14, 1825–1828. [Google Scholar] [CrossRef]
- Hamilton, R.; Roberts, B.M.; Scholten, S.K.; Locke, C.; Luiten, A.N.; Ginges, J.S.; Perrella, C. Experimental and Theoretical Study of Dynamic Polarizabilities in the 5S1/2–5D5/2 Clock Transition in Rubidium-87 and Determination of Electric Dipole Matrix Elements. Phys. Rev. Appl. 2023, 19, 054059. [Google Scholar] [CrossRef]
- Hilico, L.; Felder, R.; Touahri, D.; Acef, O.; Clairon, A.; Biraben, F. Metrological features of the rubidium two-photon standards of the BNM-LPTF and Kastler Brossel Laboratories. Eur. Phys. J.-Appl. Phys. 1998, 4, 219–225. [Google Scholar] [CrossRef]
- Perrella, C.; Light, P.; Anstie, J.; Baynes, F.; Benabid, F.; Luiten, A.N. Two-color rubidium fiber frequency standard. Opt. Lett. 2013, 38, 2122–2124. [Google Scholar] [CrossRef]
- Locke, C.; Ng, S.; Scarabel, J.; O’Connor, M.; Luiten, A.; Scholten, S.; Ahern, E.; Hebert, N.; Perrella, C. Portable Optical Atomic Clock Based on a Dichroic Two-Photon Transition in Rubidium. In Proceedings of the 2023 Joint Conference of the European Frequency and Time Forum and IEEE International Frequency Control Symposium (EFTF/IFCS), Toyama, Japan, 15–19 May 2023; IEEE: Piscataway, NJ, USA, 2023; pp. 1–2. [Google Scholar]
- Miao, J.; Chen, J.; Yu, D.; Yang, Q.; Pan, D.; Chen, J. Single-Atomic-Ensemble Dual-Wavelength Optical Standard. arXiv 2024, arXiv:2411.02107. [Google Scholar]
- Kulatunga, P.; Busch, H.; Andrews, L.; Sukenik, C. Two-color polarization spectroscopy of rubidium. Opt. Commun. 2012, 285, 2851–2853. [Google Scholar] [CrossRef]
- True, T.M.; Pitz, G.A.; Rice, C.A.; Perram, G.P. Resonant enhancement of two-photon absorption in rubidium with crossed polarizations. Opt. Commun. 2022, 510, 127943. [Google Scholar] [CrossRef]
- Perrella, C.; Light, P.; Anstie, J.; Stace, T.; Benabid, F.; Luiten, A.N. High-resolution two-photon spectroscopy of rubidium within a confined geometry. Phys. Rev. A—At. Mol. Opt. Phys. 2013, 87, 013818. [Google Scholar] [CrossRef]
- Caracas Núñez, M.; Gonzalez, M.A.; Núñez Portela, M. Theoretical and experimental study of the 6S-8S two-photon absorption cross-section in cesium atoms. Opt. Express 2023, 31, 31749–31759. [Google Scholar] [CrossRef]
- Uehara, T.; Sugiyama, K.; Kitano, M. Frequency measurement of the 6S-8S two-photon transition in cesium. In Proceedings of the Conference on Lasers and Electro-Optics/Pacific Rim, Kyoto, Japan, 30 June–4 July 2013; Optica Publishing Group: Washington, DC, USA, 2013; p. WPF_3. [Google Scholar]
- Wu, C.M.; Liu, T.W.; Wu, M.H.; Lee, R.K.; Cheng, W.Y. Absolute frequency of cesium 6S–8S 822 nm two-photon transition by a high-resolution scheme. Opt. Lett. 2013, 38, 3186–3189. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Chen, Y.H.; Liu, T.W.; Wu, C.M.; Lee, C.C.; Lee, C.K.; Cheng, W.Y. High-resolution 133Cs 6 S–6 D, 6 S–8 S two-photon spectroscopy using an intracavity scheme. Opt. Lett. 2011, 36, 76–78. [Google Scholar] [CrossRef]
- Wu, C.M.; Cheng, W.Y.; Lee, R.K. Cesium 6S1/2→8S1/2 two photon-transition stabilized 822.5 nm diode laser. In Proceedings of the 2008 Conference on Precision Electromagnetic Measurements Digest, Broomfield, CO, USA, 8–13 June 2008; IEEE: Piscataway, NJ, USA, 2008; pp. 318–319. [Google Scholar]
- Cheng, C.Y.; Wu, C.M.; Liao, G.B.; Cheng, W.Y. Cesium 6S1/2→8S1/2 two-photon-transition-stabilized 822.5 nm diode laser. Opt. Lett. 2007, 32, 563–565. [Google Scholar] [CrossRef]
- Hagel, G.; Nesi, C.; Jozefowski, L.; Schwob, C.; Nez, F.; Biraben, F. Accurate measurement of the frequency of the 6S–8S two-photon transitions in cesium. Opt. Commun. 1999, 160, 1–4. [Google Scholar] [CrossRef]
- Lee, Y.C.; Chui, H.C.; Chen, Y.Y.; Chang, Y.H.; Tsai, C.C. Effects of light on cesium 6S–8S two-photon transition. Opt. Commun. 2010, 283, 1788–1791. [Google Scholar] [CrossRef]
- Sieradzan, A.; Havey, M.; Safronova, M. Combined experimental and theoretical study of the 6p2Pj→8s2S1/2 relative transition matrix elements in atomic Cs. Phys. Rev. A 2004, 69, 022502. [Google Scholar] [CrossRef]
- Kim, K.t.; Ahn, J. Direct frequency-comb spectroscopy of 6S1/2–8S1/2 transitions of atomic cesium. arXiv 2017, arXiv:1707.06424. [Google Scholar]
- Fendel, P.; Bergeson, S.; Udem, T.; Hänsch, T. Two-photon frequency comb spectroscopy of the 6s–8s transition in cesium. Opt. Lett. 2007, 32, 701–703. [Google Scholar] [CrossRef] [PubMed]
- Bertinetto, F.; Cordiale, P.; Galzerano, G.; Bava, E. Frequency stabilization of DBR diode laser against Cs absorption lines at 852 nm using the modulation transfer method. IEEE Trans. Instrum. Meas. 2001, 50, 490–492. [Google Scholar] [CrossRef]
- Nakazawa, M.; Suzuki, K. Cesium optical atomic clock: An optical pulse that tells the time. Opt. Lett. 2001, 26, 635–637. [Google Scholar] [CrossRef] [PubMed]
- Ohtsuka, T.; Nishimiya, N.; Fukuda, T.; Suzuki, M. Doppler-Free Two-Photon Spectroscopy of 6S1/2–6D3/2,5/2 Transition in Cesium. J. Phys. Soc. Jpn. 2005, 74, 2487–2491. [Google Scholar] [CrossRef]
- Bandi, T.; Affolderbach, C.; Mileti, G. Laser-pumped paraffin-coated cell rubidium frequency standard. J. Appl. Phys. 2012, 111, 124906. [Google Scholar] [CrossRef]
- Pétremand, Y.; Affolderbach, C.; Straessle, R.; Pellaton, M.; Briand, D.; Mileti, G.; de Rooij, N.F. Microfabricated rubidium vapour cell with a thick glass core for small-scale atomic clock applications. J. Micromech. Microeng. 2012, 22, 025013. [Google Scholar] [CrossRef]
- Knappe, S.; Gerginov, V.; Schwindt, P.; Shah, V.; Robinson, H.; Hollberg, L.; Kitching, J. Atomic vapor cells for chip-scale atomic clocks with improved long-term frequency stability. Opt. Lett. 2005, 30, 2351–2353. [Google Scholar] [CrossRef]
- Kazakin, A.; Kleimanov, R.; Komarevtsev, I.; Kondrateva, A.; Enns, Y.; Shashkin, A.; Glukhovskoy, A. Microfabrication of Alkali Vapor MEMS Cells for chip-scale atomic clock. J. Phys. Conf. Ser. IOP Publ. 2021, 2103, 012188. [Google Scholar] [CrossRef]
- Di Gaetano, E.; Keliehor, B.; Gallacher, K.; Griffin, P.; Sorel, M.; Riis, E.; Paul, D. 778.1 nm distributed feedback lasers for Rb two-photon atomic systems with sub-4 kHz linewidths. APL Photonics 2024, 9, 056114. [Google Scholar] [CrossRef]
- Hou, D.; Wu, J.; Zhang, S.; Ren, Q.; Zhang, Z.; Zhao, J. A stable frequency comb directly referenced to rubidium electromagnetically induced transparency and two-photon transitions. Appl. Phys. Lett. 2014, 104, 111104. [Google Scholar] [CrossRef]
- Abdel Hafiz, M.; Carlé, C.; Passilly, N.; Danet, J.; Calosso, C.; Boudot, R. Light-shift mitigation in a microcell-based atomic clock with symmetric auto-balanced Ramsey spectroscopy. Appl. Phys. Lett. 2022, 120, 064101. [Google Scholar] [CrossRef]
- Lin, J.; Deng, J.; Ma, Y.; He, H.; Wang, Y. Detection of ultrahigh resonance contrast in vapor-cell atomic clocks. Opt. Lett. 2012, 37, 5036–5038. [Google Scholar] [PubMed]
- Camparo, J.; Frueholz, R. Fundamental stability limits for the diode-laser-pumped rubidium atomic frequency standard. J. Appl. Phys. 1986, 59, 3313–3317. [Google Scholar] [CrossRef]
- Audoin, C.; Candelier, V.; Dimarcq, N. A limit to the frequency stability of passive frequency standards due to an intermodulation effect. IEEE Trans. Instrum. Meas. 1991, 40, 121–125. [Google Scholar] [CrossRef]
- Brezinski, M. Noise and system performance with td-oct and sd-oct. In Optical Coherence Tomography; Academic Press: Burlington, ON, Canada, 2006; pp. 175–195. [Google Scholar]
- Duspayev, A.; Owens, C.; Dash, B.; Raithel, G. An optical atomic clock using 4DJ states of rubidium. Quantum Sci. Technol. 2024, 9, 045046. [Google Scholar] [CrossRef]
- Haas, M.; Jentschura, U.D.; Keitel, C.H. Comparison of classical and second quantized description of the dynamic Stark shift. Am. J. Phys. 2006, 74, 77–81. [Google Scholar] [CrossRef]
- Kaplan, A.; Andersen, M.F.; Davidson, N. Suppression of inhomogeneous broadening in rf spectroscopy of optically trapped atoms. Phys. Rev. A 2002, 66, 045401. [Google Scholar] [CrossRef]
- Grynberg, G.; Cagnac, B. Doppler-free multiphotonic spectroscopy. Rep. Prog. Phys. 1977, 40, 791. [Google Scholar] [CrossRef]
- Levi, F.; Camparo, J.; Francois, B.; Calosso, C.; Micalizio, S.; Godone, A. Precision test of the ac Stark shift in a rubidium atomic vapor. Phys. Rev. A 2016, 93, 023433. [Google Scholar] [CrossRef]
- Miletic, D.; Bandi, T.; Affolderbach, C.; Mileti, G. ac Stark shift in double resonance and coherent population trapping in a wall-coated cell for compact Rb atomic clocks. Phys. Scr. 2012, 2012, 014012. [Google Scholar] [CrossRef]
- Camparo, J.; Frueholz, R.; Volk, C. Inhomogeneous light shift in alkali-metal atoms. Phys. Rev. A 1983, 27, 1914. [Google Scholar] [CrossRef]
- Radnatarov, D.A.; Kobtsev, S.M.; Andryushkov, V.A.; Basalaev, M.Y.; Taichenachev, A.V.; Radchenko, M.D.; Yudin, V.I. Active Suppression of the Light Shift in an Atomic Clock Based on Coherent Population Trapping in 87Rb Vapor Using the Phase Jump Technique. JETP Lett. 2023, 117, 504–508. [Google Scholar] [CrossRef]
- Bergquist, J.C. Doppler-free spectroscopy. In Experimental Methods in the Physical Sciences; Elsevier: Amsterdam, The Netherlands, 1996; Volume 29, pp. 255–272. [Google Scholar]
- Formichella, V.; Camparo, J.; Tavella, P. Influence of the ac-Stark shift on GPS atomic clock timekeeping. Appl. Phys. Lett. 2017, 110. [Google Scholar] [CrossRef]
- Jones, M. Atom-Light Interactions; Archived Lecture Notes; Durham University: Durham, UK, 2015. [Google Scholar]
- Steck, D.A. Rubidium 87 D Line Data. Available online: http://steck.us/alkalidata/ (accessed on 18 May 2025).
- Arora, B.; Safronova, M.; Clark, C.W. Magic wavelengths for the np-ns transitions in alkali-metal atoms. Phys. Rev. A—At. Mol. Opt. Phys. 2007, 76, 052509. [Google Scholar] [CrossRef]
- Gallagher, J.; Perram, G. Determining the Two-Photon Absorption Cross-Section for the 52S1/2 –> 52D5/2 Transition in Naturally Occurring Rubidium. In Proceedings of the 42nd AIAA Plasmadynamics and Lasers Conference in Conjunction with the 18th International Conference on MHD Energy Conversion (ICMHD), Honolulu, HI, USA, 27–30 June 2011; p. 4005. [Google Scholar]
- Sakurai, J.; Napolitano, J. Modern Quantum Mechanics; Cambridge University Press: Cambridge, UK, 2021. [Google Scholar]
- Le Kien, F.; Schneeweiss, P.; Rauschenbeutel, A. Dynamical polarizability of atoms in arbitrary light fields: General theory and application to cesium. Eur. Phys. J. D 2013, 67, 1–16. [Google Scholar] [CrossRef]
- Mitroy, J.a.; Safronova, M.S.; Clark, C.W. Theory and applications of atomic and ionic polarizabilities. J. Phys. B At. Mol. Opt. Phys. 2010, 43, 202001. [Google Scholar] [CrossRef]
- Sheng, D.; Pérez Galván, A.; Orozco, L. Lifetime measurements of the 5d states of rubidium. Phys. Rev. A—At. Mol. Opt. Phys. 2008, 78, 062506. [Google Scholar] [CrossRef]
- Safronova, M.; Williams, C.J.; Clark, C.W. Relativistic many-body calculations of electric-dipole matrix elements, lifetimes, and polarizabilities in rubidium. Phys. Rev. A 2004, 69, 022509. [Google Scholar] [CrossRef]
- Wang, X.; Jiang, J.; Xie, L.Y.; Zhang, D.H.; Dong, C.Z. Polarizabilities and tune-out wavelengths of the hyperfine ground states of 87,85Rb. Phys. Rev. A 2016, 94, 052510. [Google Scholar] [CrossRef]
- Di Domenico, G.; Schilt, S.; Thomann, P. Simple approach to the relation between laser frequency noise and laser line shape. Appl. Opt. 2010, 49, 4801–4807. [Google Scholar] [CrossRef]
- Zhu, M.; Hall, J.L. Stabilization of optical phase/frequency of a laser system: Application to a commercial dye laser with an external stabilizer. J. Opt. Soc. Am. B 1993, 10, 802–816. [Google Scholar] [CrossRef]
- Camparo, J. Conversion of laser phase noise to amplitude noise in an optically thick vapor. J. Opt. Soc. Am. B 1998, 15, 1177–1186. [Google Scholar] [CrossRef]
- Drullinger, R.E.; Szekely, C.; Camparo, J.C. Diode-laser-pumped, gas-cell atomic clocks. In Proceedings of the 1992 IEEE Frequency Control Symposium, Hershey, PA, USA, 27–29 May 1992; IEEE: Piscataway, NJ, USA, 1992; pp. 104–107. [Google Scholar]
- Robinson, H.; Johnson, C. Narrow 87Rb hyperfine-structure resonances in an evacuated wall-coated cell. Appl. Phys. Lett. 1982, 40, 771–773. [Google Scholar] [CrossRef]
- Knappe, S.; Robinson, H.G. Double-resonance lineshapes in a cell with wall coating and buffer gas. New J. Phys. 2010, 12, 065021. [Google Scholar] [CrossRef]
- Seltzer, S.; Michalak, D.; Donaldson, M.; Balabas, M.; Barber, S.; Bernasek, S.; Bouchiat, M.A.; Hexemer, A.; Hibberd, A.; Kimball, D.; et al. Investigation of antirelaxation coatings for alkali-metal vapor cells using surface science techniques. J. Chem. Phys. 2010, 133, 144703. [Google Scholar] [CrossRef] [PubMed]
- Bandi, T.; Affolderbach, C.; Mileti, G. Study of Rb 0-0 hyperfine double-resonance transition in a wall-coated cell. In Proceedings of the EFTF-2010 24th European Frequency and Time Forum, Noordwijk, The Netherlands, 13–16 April 2010; IEEE: Piscataway, NJ, USA, 2010; pp. 1–8. [Google Scholar]
- Singh, G.; Dilavore, P.; Alley, C.O. A technique for preparing wall coated cesium vapor cells. Rev. Sci. Instrum. 1972, 43, 1388–1389. [Google Scholar] [CrossRef]
- Chu, C.H.; Chang, P.C.; Shih, Y.J.; Luh, D.A.; Chang, M.S.; Liu, T.W.; Lin, Y.T.; Chen, B.W.; Cheng, W.Y. Measurement of the 5S1/2 to 5D5/2 two-photon clock transition frequency of rubidium-85 in high vacuum. Opt. Lett. 2023, 48, 5984–5987. [Google Scholar] [CrossRef]
- Straessle, R.; Pellaton, M.; Affolderbach, C.; Pétremand, Y.; Briand, D.; Mileti, G.; de Rooij, N.F. Microfabricated alkali vapor cell with anti-relaxation wall coating. Appl. Phys. Lett. 2014, 105, 043502. [Google Scholar] [CrossRef]
- Stoicheff, B.; Weinberger, E. Doppler-free two-photon absorption spectrum of rubidium. Can. J. Phys. 1979, 57, 2143–2154. [Google Scholar] [CrossRef]
- Camparo, J. The semiclassical stochastic-field/atom interaction problem. In Frequency Standards and Metrology; World Scientific: Singapore, 2009; pp. 109–117. [Google Scholar]
- Kraft, S.; Deninger, A.; Trück, C.; Fortágh, J.; Lison, F.; Zimmermann, C. Rubidium spectroscopy at 778–780 nm with a distributed feedback laser diode. Laser Phys. Lett. 2004, 2, 71. [Google Scholar] [CrossRef]
- Calosso, C.E.; Godone, A.; Levi, F.; Micalizio, S. Enhanced temperature sensitivity in vapor-cell frequency standards. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2012, 59, 2646–2654. [Google Scholar] [CrossRef] [PubMed]
- Mishra, N.S. Frequency modulation of Rydberg states by radio frequency electromagnetic fields. In Proceedings of the Quantum Sensing and Nano Electronics and Photonics XX, San Francisco, CA, USA, 28 January–1 February 2024; SPIE: Bellingham, WA, USA, 2024; Volume 12895, pp. 193–198. [Google Scholar]
- Delone, N.B.; Krainov, V.P. AC Stark shift of atomic energy levels. Physics-Uspekhi 1999, 42, 669. [Google Scholar] [CrossRef]
- Lodewyck, J.; Bilicki, S.; Bookjans, E.; Robyr, J.L.; Shi, C.; Vallet, G.; Le Targat, R.; Nicolodi, D.; Le Coq, Y.; Guéna, J.; et al. Optical to microwave clock frequency ratios with a nearly continuous strontium optical lattice clock. Metrologia 2016, 53, 1123. [Google Scholar] [CrossRef]
- Rębilas, K. Light-induced atomic desorption dynamics: Theory for a completely illuminated cell. Phys. Rev. A—At. Mol. Opt. Phys. 2009, 80, 014901. [Google Scholar] [CrossRef]
- Talker, E.; Arora, P.; Zektzer, R.; Sebbag, Y.; Dikopltsev, M.; Levy, U. Light-induced atomic desorption in microfabricated vapor cells for demonstrating quantum optical applications. Phys. Rev. Appl. 2021, 15, L051001. [Google Scholar] [CrossRef]
- Graf, M.T.; Kimball, D.F.; Rochester, S.M.; Kerner, K.i.; Wong, C.; Budker, D.; Alexandrov, E.B.; Balabas, M.V.; Yashchuk, V.V. Relaxation of atomic polarization in para+n-coated alkali-metal vapor cells. Phys. Rev. A 2005, 72, 023401. [Google Scholar] [CrossRef]
- Yano, Y.; Gao, W.; Goka, S.; Kajita, M. Theoretical and experimental investigation of the light shift in Ramsey coherent population trapping. Phys. Rev. A 2014, 90, 013826. [Google Scholar] [CrossRef]
- Yudin, V.; Basalaev, M.Y.; Taichenachev, A.; Pollock, J.; Newman, Z.; Shuker, M.; Hansen, A.; Hummon, M.; Boudot, R.; Donley, E.A.; et al. General methods for suppressing the light shift in atomic clocks using power modulation. Phys. Rev. Appl. 2020, 14, 024001. [Google Scholar] [CrossRef]
- Abdel Hafiz, M.; Coget, G.; Petersen, M.; Rocher, C.; Guérandel, S.; Zanon-Willette, T.; de Clercq, E.; Boudot, R. Toward a high-stability coherent population trapping Cs vapor-cell atomic clock using autobalanced Ramsey spectroscopy. Phys. Rev. Appl. 2018, 9, 064002. [Google Scholar] [CrossRef]
- Aumiler, D.; Ban, T.; Pichler, G. High-resolution measurements of the pressure broadening and shift of the rubidium 5 2S1/2–6 2P3/2 line by argon and helium. Phys. Rev. A—At. Mol. Opt. Phys. 2004, 70, 032723. [Google Scholar] [CrossRef]
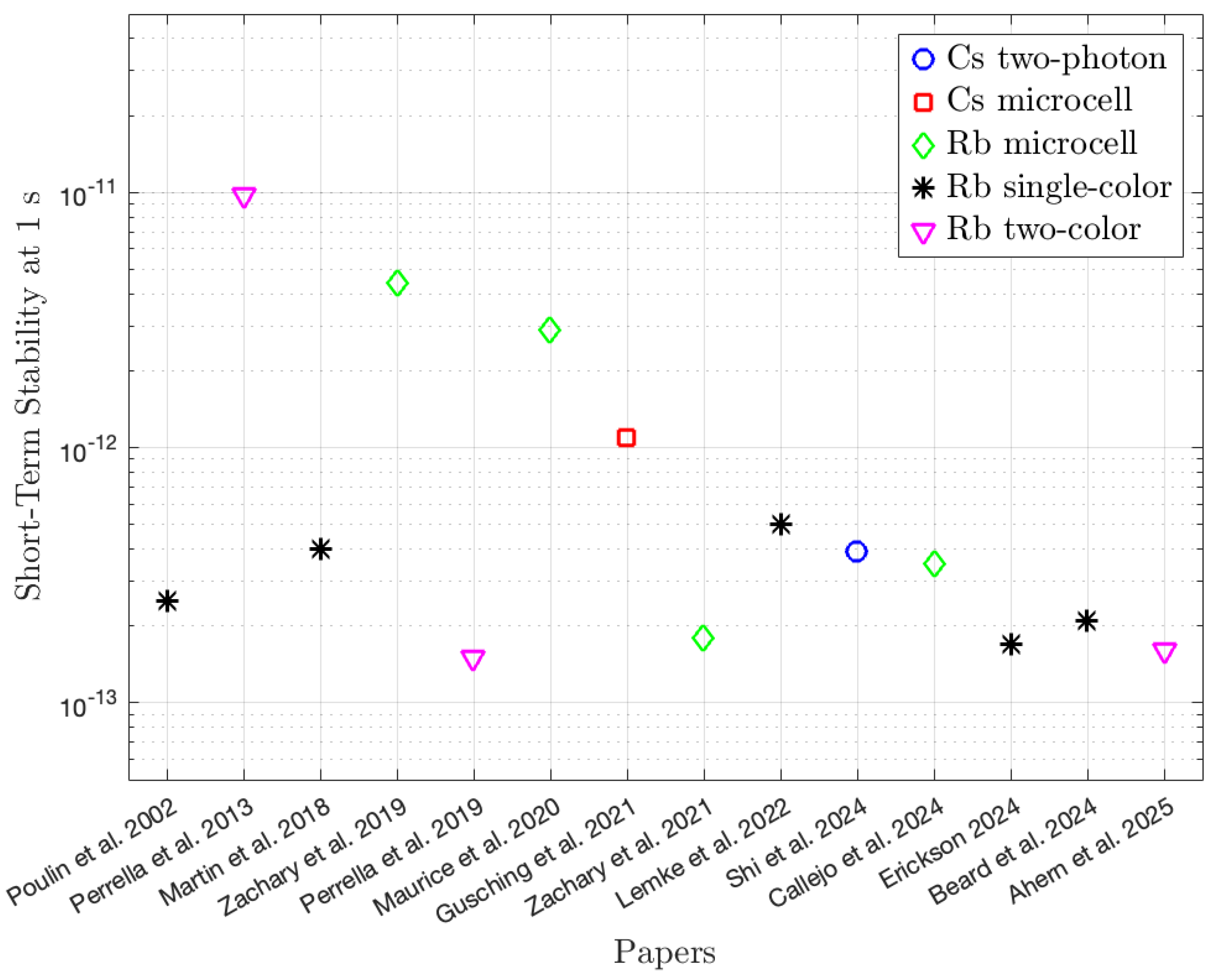


| Articles | Signal Linewidth (kHz) | Cell Temperature (°C) | Vapor Cell Dimension (mm) | Beam Waist (μm) | Fractional Light Shift (per mW) | Reported Fractional Frequency Instability (1/) |
|---|---|---|---|---|---|---|
| Callejo et al., 2024 [114] | 450 | 110 | 25 diameter, 70 length cell | 100 | ||
| Erickson, 2024 [160] | 774 | 100 | 1/2″ diameter, 1/2″ length fill stem, 5 active length | 230 | ||
| Li et al., 2024 [161] | 618 | 100 | ‡ | 800 | † | † |
| Beard et al., 2024 [116] | 106 | 5 length | 490 | |||
| Lemke et al., 2022 [117] | 550 | 100 | 50 diameter, 10 length | 2100 | ||
| Maurice et al., 2020 [109] | 2200 | 80 | ‡ | Horizontal 200, Vertical 100 | ||
| Zachary et al., 2019 [110] | 1000 | 100 | ‡ | |||
| Gerginov et al., 2018 [118] | 795 | 90 | 25 diameter, 25 length | 400 | reported for (1%) laser variation | ** |
| Martin et al., 2018 [119] | 609 | 100 | rectangular prism of | 0.66(5) | ||
| Poulin et al., 2002 [120] | 410 | 90 | ‡ | 420 |
| Authors | Beam Diameter (mm) | Laser Power (mW) | Detuning (GHz) | Signal Linewidth (kHz) | Fractional Frequency Instability | Fractional Light Shift (per mW) | Rb-Rb Shift (kHz) | Cell Temperature (°C) |
|---|---|---|---|---|---|---|---|---|
| Ahern et al., 2025 [121] | ‡ | , | 1.5 | 3470 | at s | at 780 nm, at 776 nm | ‡ | 60 to 70 |
| Hamilton et al., 2023 [177] | 1.5 | , | 3700 | for 50 s | ‡ | ‡ | ||
| Perrella et al., 2019 [122] | 1.5 | , | 1.5 | at s | at 780 nm, at 776 nm | 90 | ||
| Gerginov and Beloy, 2018 [118] | 2 | , | 10 | 3480 | † at 1 s | reported for 1% laser variation | ‡ | 90 |
| Perrella et al., 2013 [179] | ‡ | , | 2 | 10,400 | at 10 s | at 780, at 776 nm | ||
| Nguyen et al., 2022 [136] | 2 | , | 10 | ‡ | ‡ | ‡ | −27/mTorr | 79.5 |
| Perrella et al., 2013 [184] | 1.3 | , | 2 | 10,400 | ‡ | ‡ | ‡ | 22 |
| Article | Signal Linewidth (MHz) | Beam Waist (mm) | Cell Temperature (°C) | Light Shift (Hz/mW) | Pressure Shift (kHz/Pa) | Reported Fractional Frequency Variation |
|---|---|---|---|---|---|---|
| Shi et al., 2024 [143] | 0.03995 | ‡ | 35 | 30,000 | ‡ | at s |
| Gusching et al., 2021 [142] | 14.2 | 2 | 62 | ‡ | ‡ | at s |
| Wu et al., 2013 [187] | 1.398 | 0.2 | 81 | −76.92 | ‡ | for 1 day, and for 10 s |
| Chen et al., 2011 [188] | 1.2 | ‡ | 100 | ‡ | −290 | @ 400 s |
| Cheng et al., 2007 [190] | <6 | 0.15 | 68–85 | −179 | −475 | ** @ 60 s |
| Fendel et al., 2007 [195] | 1.2 | 0.72 | 22 | 12.89 | 75 | @ 1 s |
| Hagel et al., 1999 [191] | 1.89 | 0.38 | <110 | −54 | −90 | ‡ |
| Author | Temperature Shift (K−1) | Helium Collision Shift (Torr)−1 | Second-Order Doppler Shift (K−1) | Quadratic Zeeman Shift (G−2) | Blackbody Radiation (K−1) |
|---|---|---|---|---|---|
| Martin et al., 2018 [119] | |||||
| Zachary et al., 2019 [110] | ‡ |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Obaze-Adeleke, A.C.; Semon, B.; Bandi, T.N. A Comprehensive Review of Rubidium Two-Photon Vapor Cell Optical Clock: Long-Term Performance Limitations and Potential Improvements. Photonics 2025, 12, 513. https://doi.org/10.3390/photonics12050513
Obaze-Adeleke AC, Semon B, Bandi TN. A Comprehensive Review of Rubidium Two-Photon Vapor Cell Optical Clock: Long-Term Performance Limitations and Potential Improvements. Photonics. 2025; 12(5):513. https://doi.org/10.3390/photonics12050513
Chicago/Turabian StyleObaze-Adeleke, Asagwegbe C., Bryan Semon, and Thejesh N. Bandi. 2025. "A Comprehensive Review of Rubidium Two-Photon Vapor Cell Optical Clock: Long-Term Performance Limitations and Potential Improvements" Photonics 12, no. 5: 513. https://doi.org/10.3390/photonics12050513
APA StyleObaze-Adeleke, A. C., Semon, B., & Bandi, T. N. (2025). A Comprehensive Review of Rubidium Two-Photon Vapor Cell Optical Clock: Long-Term Performance Limitations and Potential Improvements. Photonics, 12(5), 513. https://doi.org/10.3390/photonics12050513







