Dynamic Observation of Ultrashort Pulses with Chaotic Features in a Tm-Doped Fiber Laser with a Single Mode Fiber–Grade Index Multimode Fiber–Single Mode Fiber Structure
Abstract
1. Introduction
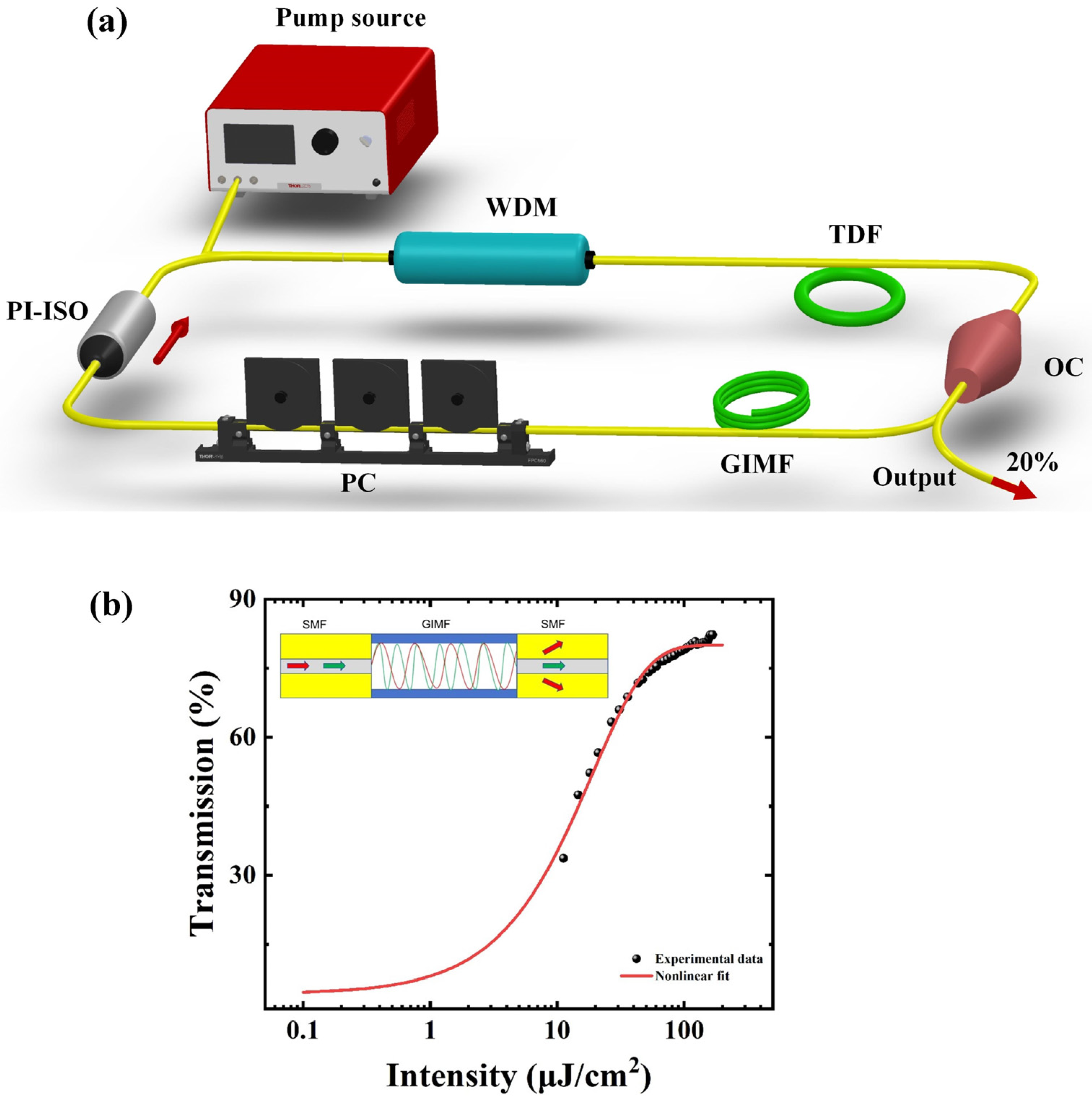
2. Experimental Setup
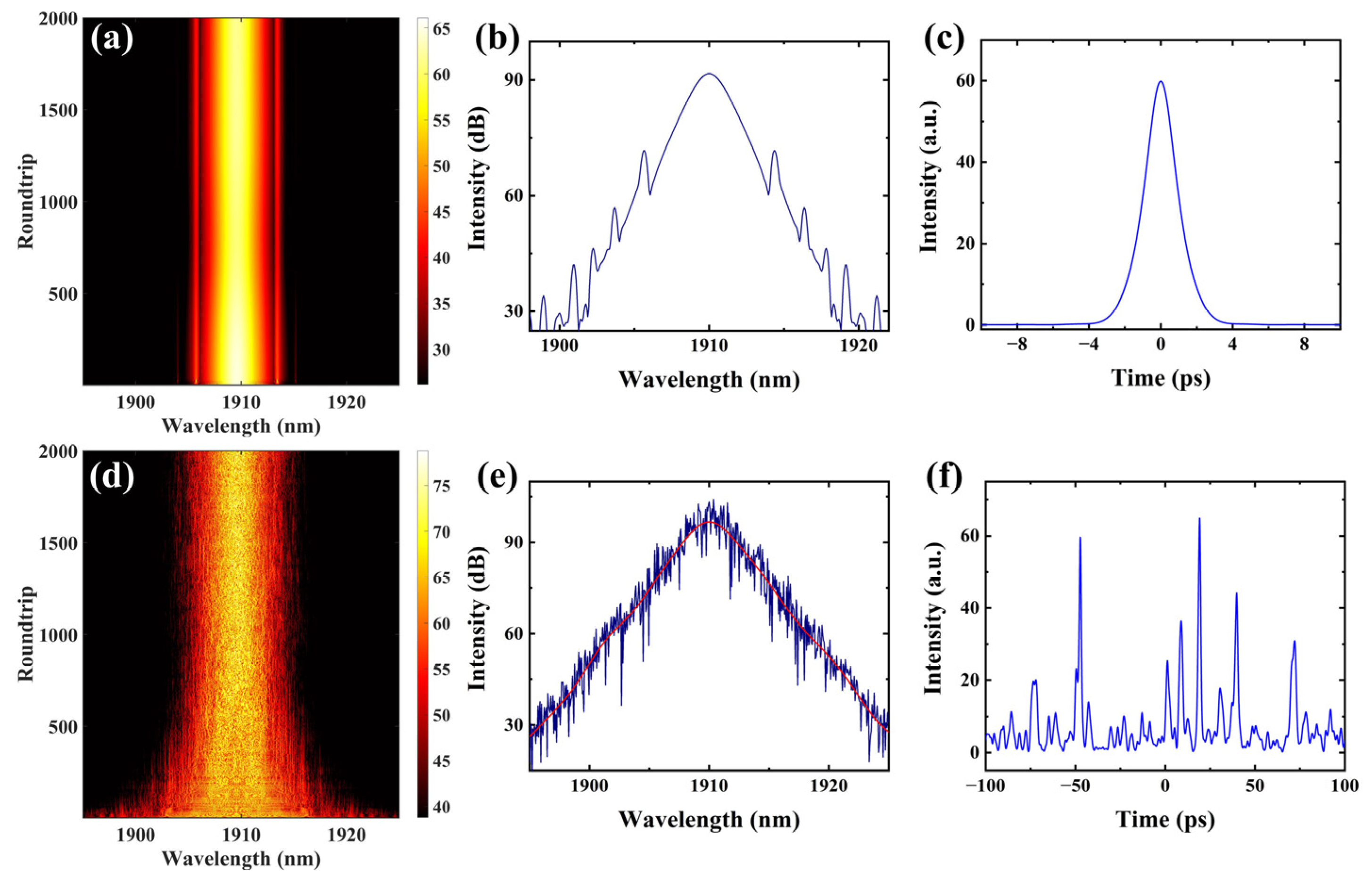
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Huang, J.; Yang, S. Investigation on anisotropic tribological properties of superhydrophobic/superlipophilic lead bronze surface textured by femtosecond laser. Appl. Surf. Sci. 2022, 579, 152223. [Google Scholar] [CrossRef]
- Mihailov, S.J.; Hnatovsky, C.; Abdukerim, N.; Walker, R.B.; Lu, P.; Xu, Y.; Bao, X.; Ding, H.; De Silva, M.; Coulas, D.; et al. Ultrafast Laser Processing of Optical Fibers for Sensing Applications. Sensors 2021, 21, 1447. [Google Scholar] [CrossRef]
- Qi, Y.; Yang, S.; Wang, J.; Li, L.; Bai, Z.; Wang, Y.; Lv, Z. Recent advance of emerging low-dimensional materials for vector soliton generation in fiber lasers. Mater. Today Phys. 2022, 23, 100622. [Google Scholar] [CrossRef]
- Fermann, M.E.; Hartl, I. Ultrafast fibre lasers. Nat. Photon. 2013, 7, 868–874. [Google Scholar] [CrossRef]
- Yang, S.; Zhang, Q.-Y.; Zhu, Z.-W.; Qi, Y.-Y.; Yin, P.; Ge, Y.-Q.; Li, L.; Jin, L.; Zhang, L.; Zhang, H. Recent advances and challenges on dark solitons in fiber lasers. Opt. Laser Technol. 2022, 152, 108116. [Google Scholar] [CrossRef]
- Yang, Y.; Ji, Y.; Xie, Y.; Song, Y.; Wang, K.; Wang, Z. Generation and observation of noise-like pulses in an ultrafast fiber laser at 1.7 μm. Opt. Laser Technol. 2024, 174, 110715. [Google Scholar] [CrossRef]
- Li, W.; Huang, Z.; Xiao, X.; Yan, Z.; Luo, S.; Song, Y.; Jiang, C.; Liu, Y.; Mou, C. 0.017 nm, 143 ps passively mode-locked fiber laser based on nonlinear polarization rotation. Opt. Lett. 2023, 48, 2676–2679. [Google Scholar] [CrossRef]
- Huang, P.L.; Lin, S.-C.; Yeh, C.-Y.; Kuo, H.-H.; Huang, S.-H.; Lin, G.-R.; Li, L.-J.; Su, C.-Y.; Cheng, W.-H. Stable mode-locked fiber laser based on CVD fabricated graphene saturable absorber. Opt. Express 2012, 20, 2460–2465. [Google Scholar] [CrossRef]
- Zhao, W.; Chen, G.; Li, W.; Wang, G.; Zeng, C. All-Fiber Saturable Absorbers for Ultrafast Fiber Lasers. IEEE Photon. J. 2019, 11, 7104019. [Google Scholar] [CrossRef]
- Zhao, J.; Zhou, J.; Jiang, Y.; Li, L.; Shen, D.; Komarov, A.; Su, L.; Tang, D.; Klimczak, M.; Zhao, L. Nonlinear Absorbing-Loop Mirror in a Holmium-Doped Fiber Laser. J. Light. Technol. 2020, 38, 6069–6075. [Google Scholar] [CrossRef]
- Lian, Y.; Wang, J.; Yang, M.; Zhang, Y.; Wang, Y. Multiwavelength Fiber Laser Using Erbium-Doped Twin-Core Fiber and Nonlinear Optical Loop Mirror. IEEE Access 2019, 7, 152478–152482. [Google Scholar] [CrossRef]
- Zhang, Z.X.; Ye, Z.Q.; Sang, M.H.; Nie, Y.Y. Passively mode-locked fiber laser based on symmetrical nonlinear optical loop mirror. Laser Phys. Lett. 2008, 5, 364–366. [Google Scholar] [CrossRef]
- Ji, Y.; Yang, Y.; Song, Y.; Wang, K.; Du, G.; Liu, J.; Tang, D.; Wang, Z. Dynamics of pulsating solitons with chaotic behaviors from a 1.7 μm ultrafast fiber laser. Chaos Solitons Fractals 2024, 187, 115379. [Google Scholar] [CrossRef]
- Zhao, Q.; Pei, L.; Zheng, J.; Tang, M.; Xie, Y.; Li, J.; Ning, T. Tunable and interval-adjustable multi-wavelength erbium-doped fiber laser based on cascaded filters with the assistance of NPR. Opt. Laser Technol. 2020, 131, 106387. [Google Scholar] [CrossRef]
- Lang, J.; Lv, C.; Lu, B.; Bai, J. Mechanism of noise-like pulse in all-normal dispersion all-fiber laser based on nonlinear polarization rotation. Opt. Express 2024, 32, 2392–2404. [Google Scholar] [CrossRef] [PubMed]
- Aguergaray, C.; Broderick, N.G.R.; Erkintalo, M.; Chen, J.S.Y.; Kruglov, V. Mode-locked femtosecond all-normal all-PM Yb-doped fiber laser using a nonlinear amplifying loop mirror. Opt. Express 2012, 20, 10545–10551. [Google Scholar] [CrossRef]
- Liu, W.; Shi, H.; Cui, J.; Xie, C.; Song, Y.; Wang, C.; Hu, M. Single-polarization large-mode-area fiber laser mode-locked with a nonlinear amplifying loop mirror. Opt. Lett. 2018, 43, 2848–2851. [Google Scholar] [CrossRef]
- Łaszczych, Z.; Soboń, G. Dispersion management of a nonlinear amplifying loop mirror-based erbium-doped fiber laser. Opt. Express 2021, 29, 2690–2702. [Google Scholar] [CrossRef]
- Didychenko, D.; Kovalchuk, O.; Uddin, S.; Lee, S.; Song, Y.-W. Chromatic dispersion-tolerant mode-locking of directly synthesized graphene for the control of laser pulse energy. Opt. Mater. 2024, 150, 115259. [Google Scholar] [CrossRef]
- Alghamdi, T.A.; Adwan, S.; Arof, H.; Harun, S.W. Q-switched triple-wavelength erbium-doped fiber laser with black phosphorus absorber. Optik 2024, 311, 171874. [Google Scholar] [CrossRef]
- Li, L.; Pang, L.; Wang, R.; Zhang, X.; Hui, Z.; Han, D.; Zhao, F.; Liu, W. Ternary Transition Metal Dichalcogenides for High Power Vector Dissipative Soliton Ultrafast Fiber Laser. Laser Photon. Rev. 2022, 16, 2100255. [Google Scholar] [CrossRef]
- Liu, J.; Zhao, F.; Wang, H.; Zhang, W.; Hu, X.; Li, X.; Wang, Y. Generation of dark solitons in erbium-doped fiber laser based on black phosphorus nanoparticles. Opt. Mater. 2019, 89, 100–105. [Google Scholar] [CrossRef]
- Cheng, P.; Han, M.; Li, Q.; Shu, X. Generation of different mode-locked states in a Yb-doped fiber laser based on nonlinear multimode interference. Opt. Express 2022, 30, 35911–35922. [Google Scholar] [CrossRef] [PubMed]
- Qi, Y.; Liu, M.; Luan, N.; Yang, S.; Bai, Z.; Yan, B.; Jie, D.; Wang, Y.; Lu, Z. Recent research progress of nonlinear multimode interference mode-locking technology based on multimode fibers. Infrared Phys. Technol. 2022, 121, 104017. [Google Scholar] [CrossRef]
- Zhu, T.; Wang, Z.; Wang, D.N.; Yang, F.; Li, L. Observation of controllable tightly and loosely bound solitons with an all-fiber saturable absorber. Photon. Res. 2019, 7, 61–68. [Google Scholar] [CrossRef]
- Chen, J.; Wang, Z.; Li, L.; Wang, D.N.; Zhu, T.; Gao, F.; Cao, S.; Fang, Z. GIMF-Based SA for Generation of High Pulse Energy Ultrafast Solitons in a Mode-Locked Linear-Cavity Fiber Laser. J. Light. Technol. 2020, 38, 1480–1485. [Google Scholar] [CrossRef]
- Ahmad, H.; Mansor, N.H.; Samion, M.Z.; Reduan, S.A. High power mode-locked erbium–ytterbium doped fiber laser using GIMF–SIMF–GIMF fiber structure as saturable absorber. Opt. Quantum Electron. 2023, 55, 213. [Google Scholar] [CrossRef]
- Li, H.; Wang, Z.; Li, C.; Tian, Y.; Xiao, Z.; Zhang, J.; Xu, S. Self-Starting Mode-Locked Tm-Doped Fiber Laser Using a Hybrid Structure of No Core-Graded Index Multimode Fiber as the Saturable Absorber. Opt. Laser Technol. 2019, 113, 317–321. [Google Scholar] [CrossRef]
- Wang, X.; Zhong, M.; Li, H.; Wang, K.; Li, C.; Zhang, J.; Xu, S. Mode-Locked Thulium-Doped Fiber Laser Using a Stretched Few-Mode Fiber as a Saturable Absorber. Laser Phys. 2024, 34, 045102. [Google Scholar] [CrossRef]
- Smith, N.J.; Blow, K.J.; Andonovic, I. Sideband generation through perturbations to the average soliton model. J. Light. Technol. 1992, 10, 1329–1333. [Google Scholar] [CrossRef]
- Nelson, L.; Jones, D.; Tamura, K.; Haus, H.A.; Ippen, E.P. Ultrashort-pulse fiber ring lasers. Appl. Phys. B 1997, 65, 277–294. [Google Scholar] [CrossRef]
- Goda, K.; Jalali, B. Dispersive Fourier Transformation for Fast Continuous Single-Shot Measurements. Nat. Photon. 2013, 7, 102–112. [Google Scholar] [CrossRef]
- Lecaplain, C.; Grelu, P. Rogue Waves among Noiselike-Pulse Laser Emission: An Experimental Investigation. Phys. Rev. A 2014, 90, 013805. [Google Scholar] [CrossRef]
- Agrawal, G.P. Nonlinear Fiber Optics, 5th ed.; Academic Press: San Diego, CA, USA, 2013. [Google Scholar]
- Tang, D.; Zhao, L.; Zhao, B. Soliton collapse and bunched noise-like pulse generation in a passively mode-locked fiber ring laser. Opt. Express 2005, 13, 2289–2294. [Google Scholar] [CrossRef]
- Chernykh, A.I.; Turitsyn, S.K. Soliton and collapse regimes of pulse generation in passively mode-locking laser systems. Opt. Lett. 1995, 20, 398–400. [Google Scholar] [CrossRef]
- Vazquez-Zuniga, L.A.; Jeong, Y. Super-Broadband Noise-like Pulse Erbium-Doped Fiber Ring Laser with a Highly Nonlinear Fiber for Raman Gain Enhancement. IEEE Photon. Technol. Lett. 2012, 24, 1549–1551. [Google Scholar] [CrossRef]
- Horowitz, M.; Barad, Y.; Silberberg, Y. Noiselike pulses with a broadband spectrum generated from an erbium-doped fiber laser. Opt. Lett. 1997, 22, 799–801. [Google Scholar] [CrossRef]
- Wang, Q.; Chen, T.; Zhang, B.; Li, M.; Lu, Y.; Chen, K.P. All-Fiber Passively Mode-Locked Thulium-Doped Fiber Ring Laser Using Optically Deposited Graphene Saturable Absorbers. Appl. Phys. Lett. 2013, 102, 131117. [Google Scholar] [CrossRef]
- Ahmad, H.; Aidit, S.N.; Yusoff, N.; Ismail, N.N.; Ismail, M.F.; Zamzuri, A.K.; Thambiratnam, K. All-Fiberized, Mode-Locked Laser at 1.95μm Using Copper Chalcogenide Cu2Te-Based Evanescent Field Interaction. Opt. Commun. 2020, 476, 126329. [Google Scholar] [CrossRef]
- Ahmad, H.; Zaini, M.K.A.; Samion, M.Z.; Yusoff, N. Generation of Mode-Locked Thulium-Doped Fiber Laser in 2.0-μm Wavelength Operation by Polymer-Coated Iron Phosphorus Trisulfide (FePS3)-Based Saturable Absorber. IEEE J. Quantum Electron. 2022, 58, 1600208. [Google Scholar] [CrossRef]
- Liu, F.; Zhang, Y.; Wu, X.; Li, J.; Yan, F.; Li, X.; Qyyum, A.; Hu, Z.; Zhu, C.; Liu, Y. Lead Sulfide Saturable Absorber Based Passively Mode-Locked Tm-Doped Fiber Laser. IEEE Photon. J. 2020, 12, 1500910. [Google Scholar] [CrossRef]





| TDF | SMF | SMF-GIMF-SMF SA |
|---|---|---|
| β2 = −69 ps2/km | β2 = −65 ps2/km | ΔT = 75.8% |
| γ = 3 W−1 km−1 | γ = 3 W−1 km−1 | Tns = 20% |
| L = 2 m | L = 30.2 m | Psat = 50 W |
| Wavelength/nm | Material | Width/ps | Repetition/MHz | Output/mW | Energy/nJ | Ref. |
|---|---|---|---|---|---|---|
| 1953 | Graphene | 2.1 | 16.93 | 0.08 | 1.41 | [39] |
| 1951 | Cu2Te | 1.58 | 8.1 | ~3.2 | 0.39 | [40] |
| 1935.7 | FePS3 | 1.47 | 10.95 | 1.28 | 0.117 | [41] |
| 1961.2 | PbS | 1.09 | 43.86 | 9.06 | 0.207 | [42] |
| 1911 | SMF-FMF-SMF | 1.96 | 15.69 | 2.8 | 0.178 | [29] |
| 1910 | SMF-GIMF-SMF | 1.43 | 6.21 | 42.72 | ~6.88 | Our |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, Z.; Zhou, Z.; Ji, Y.; Zeng, Q.; Song, Y.; Du, G.; Li, H. Dynamic Observation of Ultrashort Pulses with Chaotic Features in a Tm-Doped Fiber Laser with a Single Mode Fiber–Grade Index Multimode Fiber–Single Mode Fiber Structure. Photonics 2025, 12, 465. https://doi.org/10.3390/photonics12050465
Wang Z, Zhou Z, Ji Y, Zeng Q, Song Y, Du G, Li H. Dynamic Observation of Ultrashort Pulses with Chaotic Features in a Tm-Doped Fiber Laser with a Single Mode Fiber–Grade Index Multimode Fiber–Single Mode Fiber Structure. Photonics. 2025; 12(5):465. https://doi.org/10.3390/photonics12050465
Chicago/Turabian StyleWang, Zhenhong, Zexin Zhou, Yubo Ji, Qiong Zeng, Yufeng Song, Geguo Du, and Hongye Li. 2025. "Dynamic Observation of Ultrashort Pulses with Chaotic Features in a Tm-Doped Fiber Laser with a Single Mode Fiber–Grade Index Multimode Fiber–Single Mode Fiber Structure" Photonics 12, no. 5: 465. https://doi.org/10.3390/photonics12050465
APA StyleWang, Z., Zhou, Z., Ji, Y., Zeng, Q., Song, Y., Du, G., & Li, H. (2025). Dynamic Observation of Ultrashort Pulses with Chaotic Features in a Tm-Doped Fiber Laser with a Single Mode Fiber–Grade Index Multimode Fiber–Single Mode Fiber Structure. Photonics, 12(5), 465. https://doi.org/10.3390/photonics12050465






