Boundary Integral Equations Approach for a Scattering Problem of a TE-Wave on a Graphene-Coated Slab
Abstract
1. Introduction
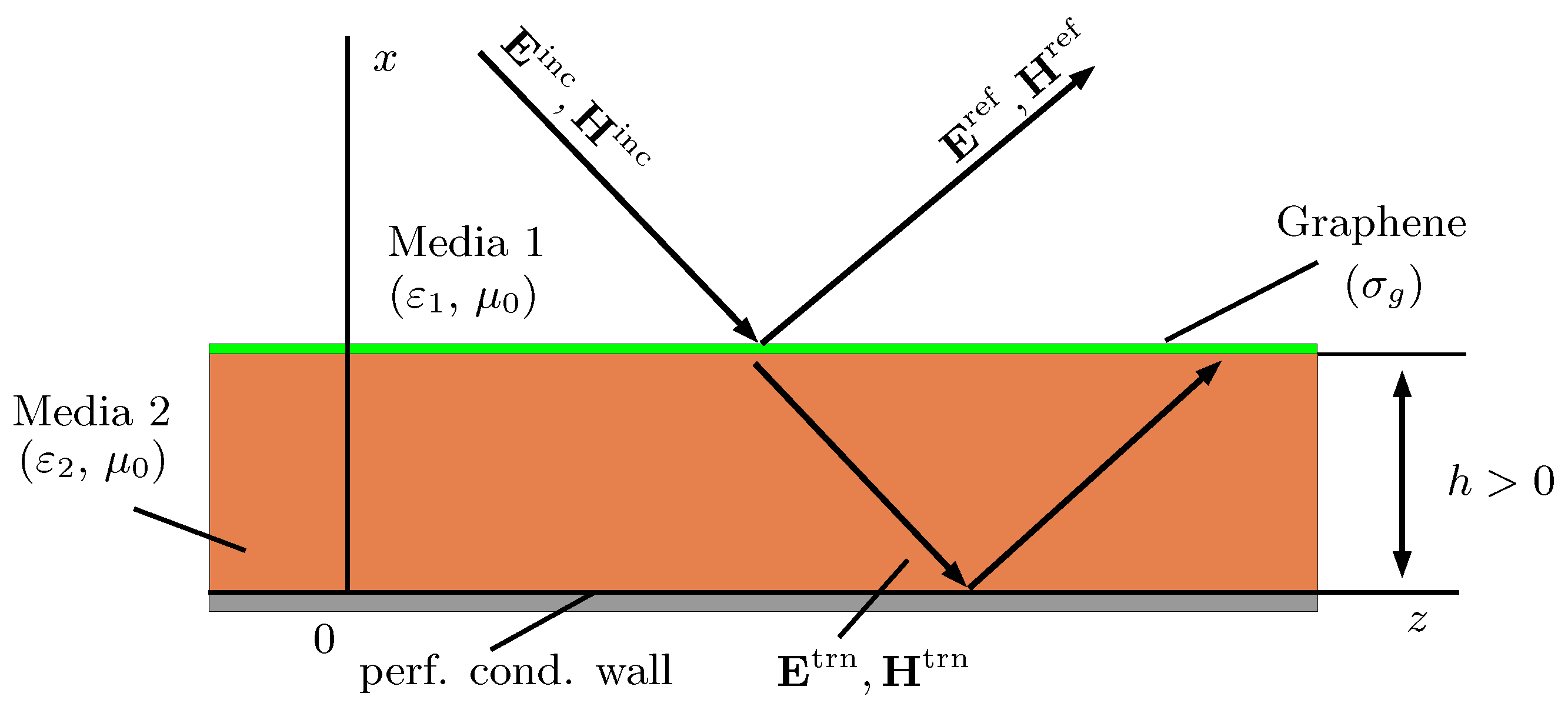
2. Statement of the Problem
3. Methods
3.1. Reduction to a Single Boundary Integral Equation
3.2. Analytical Calculation of Hypersingular Integral Operators
3.3. Collocation Method & Iterative Scheme
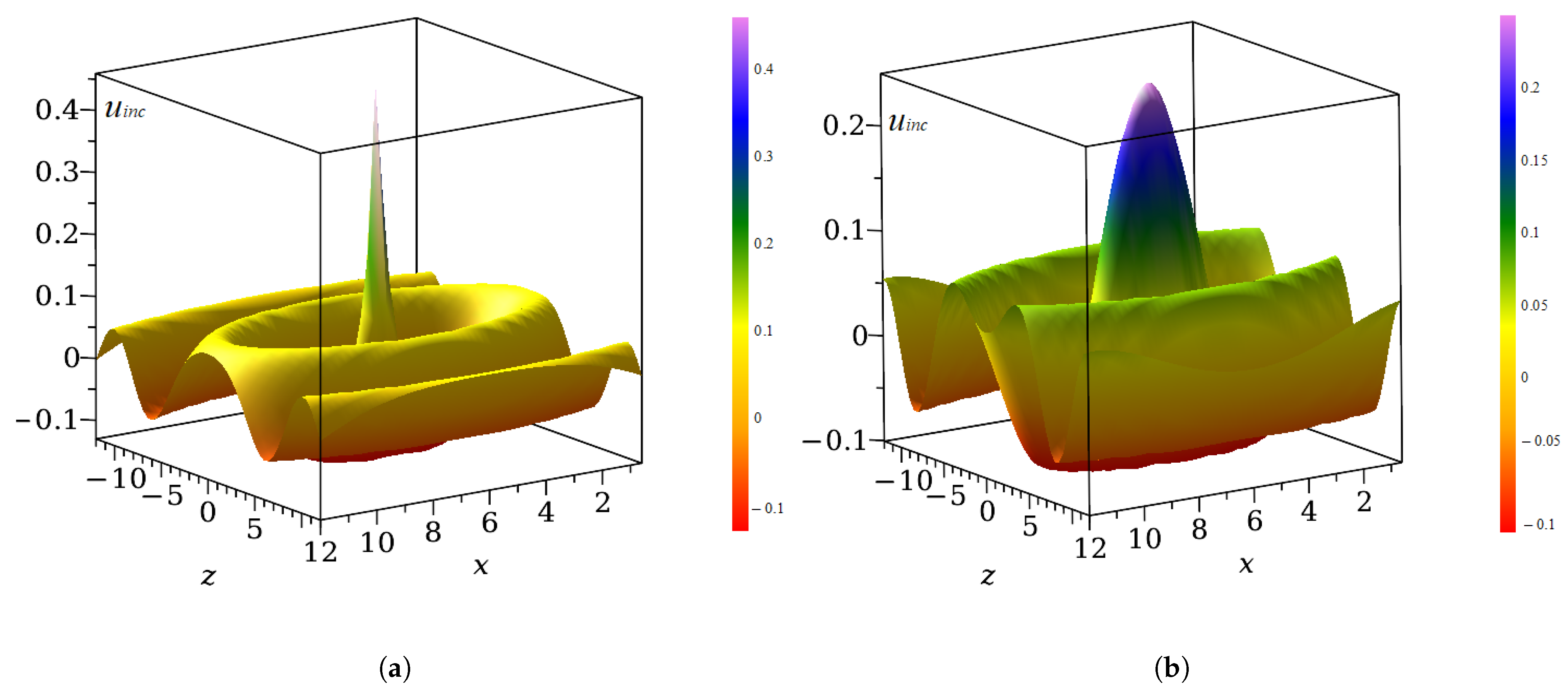
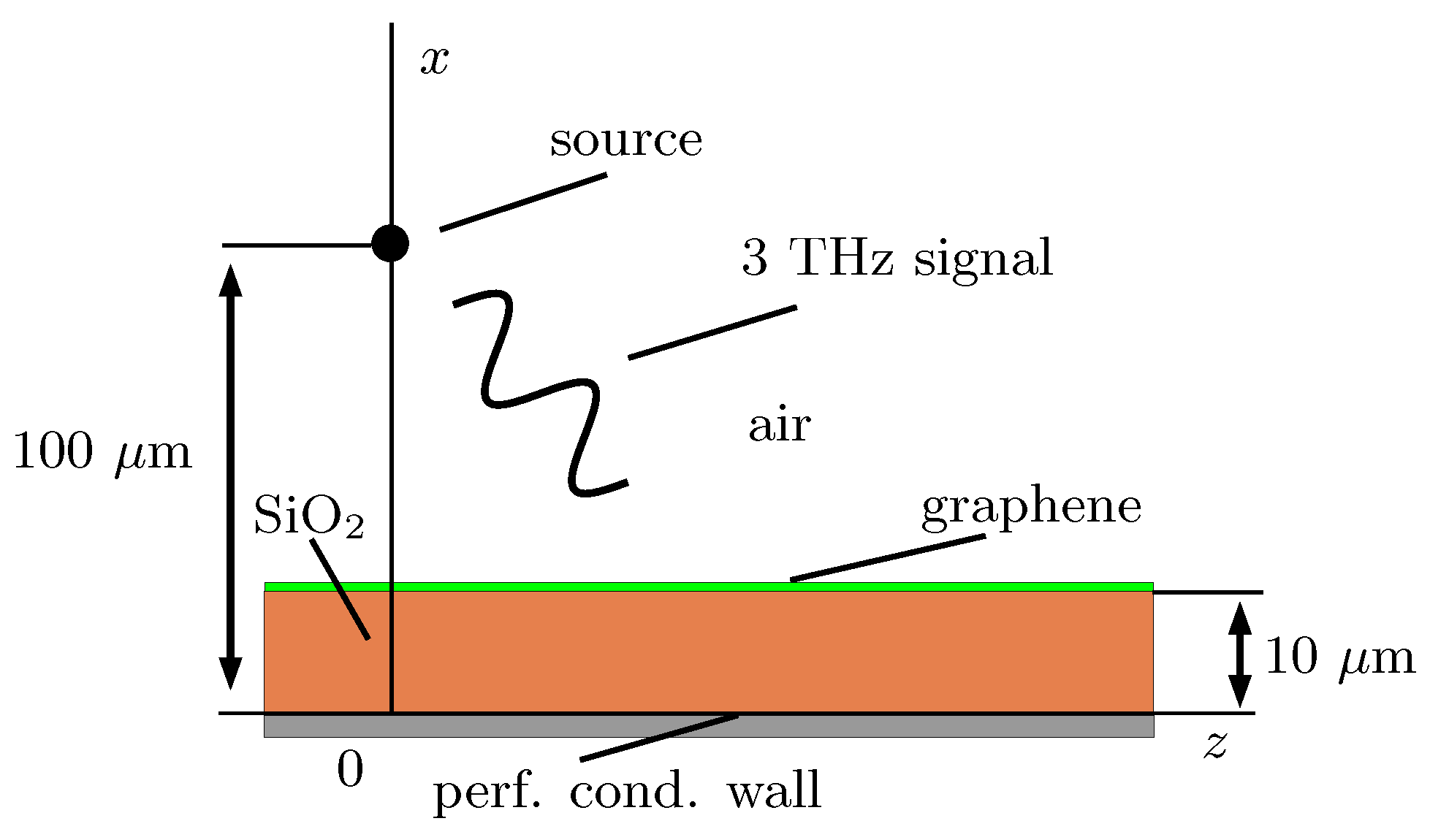
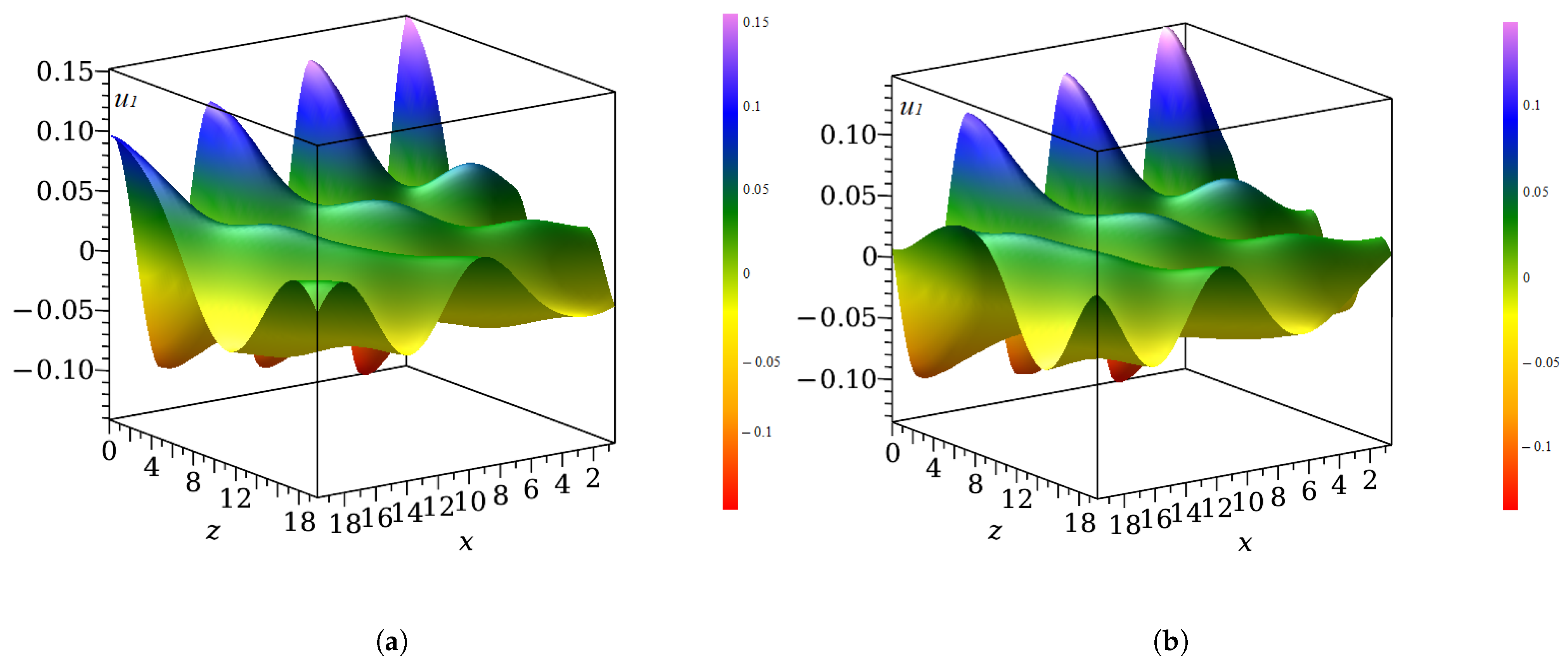
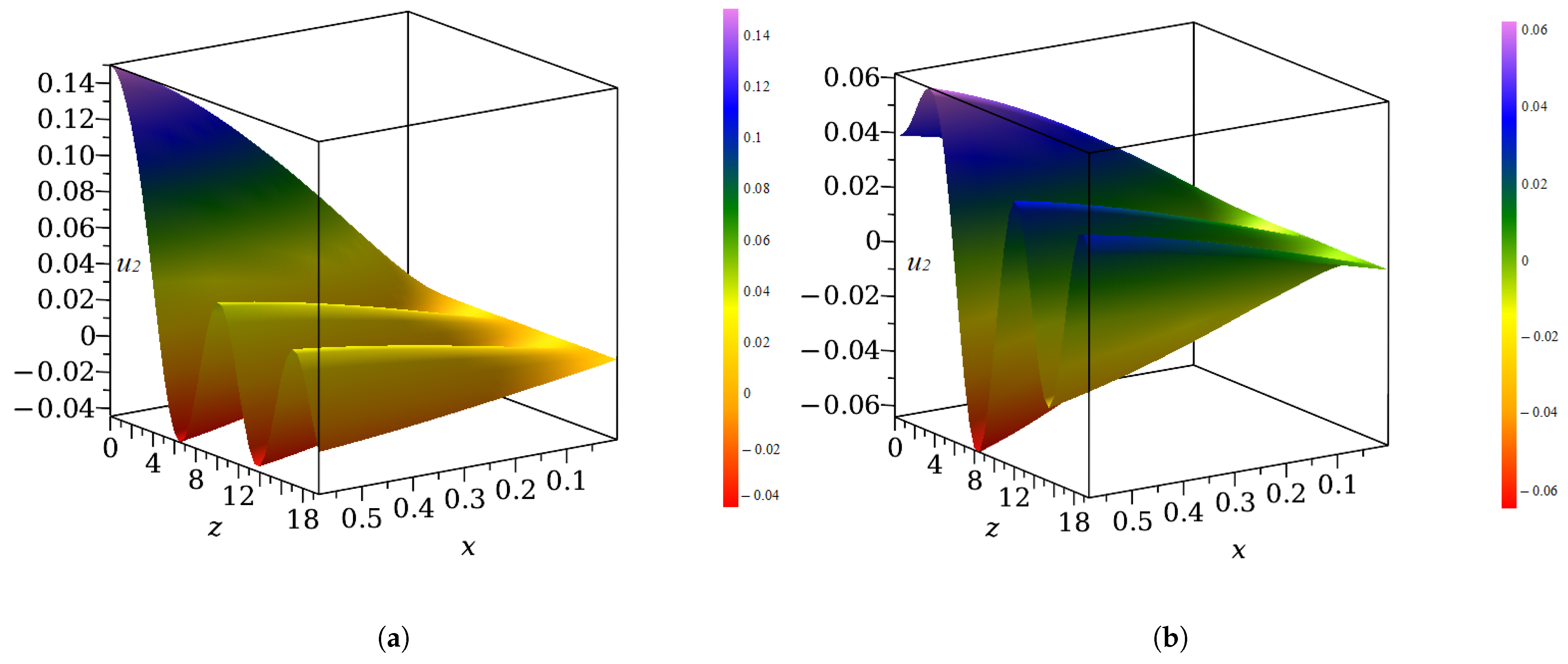
4. Results

5. Discussion
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A. Hypersingular Integral Operator
Appendix B. Hypersingular Integral Operator
Appendix C. Right-Hand Side
References
- Geim, A.K.; Novoselov, K.S. The rise of graphene. Nat. Mater. 2007, 6, 183–191. [Google Scholar] [CrossRef]
- Castro Neto, A.H.; Guinea, F.; Peres, N.M.R.; Novoselov, K.S.; Geim, A.K. The electronic properties of graphene. Rev. Mod. Phys. 2009, 81, 109–162. [Google Scholar] [CrossRef]
- Nair, R.R.; Blake, P.; Grigorenko, A.N.; Novoselov, K.S.; Booth, T.J.; Stauber, T.; Peres, N.M.R.; Geim, A.K. Fine Structure Constant Defines Visual Transparency of Graphene. Science 2008, 320, 1308. [Google Scholar] [CrossRef] [PubMed]
- Mak, K.; Ju, L.; Wang, F.; Heinz, T. Optical spectroscopy of graphene: From the far infrared to the ultraviolet. Solid State Commun. 2012, 152, 1341–1349. [Google Scholar] [CrossRef]
- Wang, F.; Zhang, Y.; Tian, C.; Girit, C.; Zettl, A.; Crommie, M.; Shen, Y.R. Gate-Variable Optical Transitions in Graphene. Science 2008, 320, 206–209. [Google Scholar] [CrossRef] [PubMed]
- Li, Z.Q.; Henriksen, E.A.; Jiang, Z.; Hao, Z.; Martin, M.C.; Kim, P.; Stormer, H.L.; Basov, D.N. Dirac charge dynamics in graphene by infrared spectroscopy. Nat. Phys. 2008, 4, 532–535. [Google Scholar] [CrossRef]
- Liu, M.; Yin, X.; Ulin-Avila, E.; Geng, B.; Zentgraf, T.; Ju, L.; Wang, F.; Zhang, X. A graphene-based broadband optical modulator. Nature 2011, 474, 64–67. [Google Scholar] [CrossRef]
- Xia, F.; Mueller, T.; Lin, Y.m.; Valdes-Garcia, A.; Avouris, P. Ultrafast graphene photodetector. Nat Nanotechnol. 2009, 4, 839–843. [Google Scholar] [CrossRef]
- Pospischil, A.; Humer, M.; Furchi, M.M.; Bachmann, D.; Guider, R.; Fromherz, T.; Mueller, T. CMOS-compatible graphene photodetector covering all optical communication bands. Nat. Photonics 2013, 7, 892–896. [Google Scholar] [CrossRef]
- Gómez-Díaz, J.S.; Perruisseau-Carrier, J. Graphene-based plasmonic switches at near infrared frequencies. Opt. Express 2013, 21, 15490–15504. [Google Scholar] [CrossRef]
- Romagnoli, M.; Sorianello, V.; Midrio, M.; Koppens, F.H.L.; Huyghebaert, C.; Neumaier, D.; Galli, P.; Templ, W.; D’Errico, A.; Ferrari, A.C. Graphene-based integrated photonics for next-generation datacom and telecom. Nat. Rev. Mater. 2018, 3, 392–414. [Google Scholar] [CrossRef]
- Mikhailov, S.A.; Ziegler, K. Nonlinear electromagnetic response of graphene: Frequency multiplication and the self-consistent-field effects. J. Phys.—Condens. Matter 2008, 20, 384204. [Google Scholar] [CrossRef]
- Hendry, E.; Hale, P.J.; Moger, J.; Savchenko, A.K.; Mikhailov, S.A. Coherent Nonlinear Optical Response of Graphene. Phys. Rev. Lett. 2010, 105, 097401. [Google Scholar] [CrossRef] [PubMed]
- Kumar, N.; Kumar, J.; Gerstenkorn, C.; Wang, R.; Chiu, H.Y.; Smirl, A.L.; Zhao, H. Third harmonic generation in graphene and few-layer graphite films. Phys. Rev. B 2013, 87, 121406. [Google Scholar] [CrossRef]
- Cheng, J.L.; Vermeulen, N.; Sipe, J.E. Third order optical nonlinearity of graphene. New J. Phys. 2014, 16, 053014. [Google Scholar] [CrossRef]
- Vermeulen, N.; Castelló-Lurbe, D.; Khoder, M.; Pasternak, I.; Krajewska, A.; Ciuk, T.; Strupinski, W.; Cheng, J.; Thienpont, H.; Van Erps, J. Graphene’s nonlinear-optical physics revealed through exponentially growing self-phase modulation. Nat. Commun. 2018, 9, 2675. [Google Scholar] [CrossRef] [PubMed]
- Hafez, H.A.; Kovalev, S.; Tielrooij, K.J.; Bonn, M.; Gensch, M.; Turchinovich, D. Terahertz Nonlinear Optics of Graphene: From Saturable Absorption to High-Harmonics Generation. Adv. Opt. Mater. 2020, 8, 1900771. [Google Scholar] [CrossRef]
- Bao, Q.; Zhang, H.; Wang, Y.; Ni, Z.; Yan, Y.; Shen, Z.X.; Loh, K.P.; Tang, D.Y. Atomic-Layer Graphene as a Saturable Absorber for Ultrafast Pulsed Lasers. Adv. Funct. Mater. 2009, 19, 3077–3083. [Google Scholar] [CrossRef]
- Ooi, K.J.A.; Cheng, J.L.; Sipe, J.E.; Ang, L.K.; Tan, D.T.H. Ultrafast, broadband, and configurable midinfrared all-optical switching in nonlinear graphene plasmonic waveguides. APL Photonics 2016, 1, 046101. [Google Scholar] [CrossRef]
- Li, J.; Tao, J.; Chen, Z.H.; Huang, X.G. All-optical controlling based on nonlinear graphene plasmonic waveguides. Opt. Express 2016, 24, 22169–22176. [Google Scholar] [CrossRef]
- Vermeulen, N. Perspectives on nonlinear optics of graphene: Opportunities and challenges. APL Photonics 2022, 7, 020901. [Google Scholar] [CrossRef]
- Gorbach, A.V. Nonlinear graphene plasmonics: Amplitude equation for surface plasmons. Phys. Rev. A 2013, 87, 013830. [Google Scholar] [CrossRef]
- Smirnova, D.A.; Gorbach, A.V.; Iorsh, I.V.; Shadrivov, I.V.; Kivshar, Y.S. Nonlinear switching with a graphene coupler. Phys. Rev. B 2013, 88, 045443. [Google Scholar] [CrossRef]
- Gorbach, A.V.; Marini, A.; Skryabin, D.V. Graphene-clad tapered fiber: Effective nonlinearity and propagation losses. Opt. Lett. 2013, 38, 5244–5247. [Google Scholar] [CrossRef]
- Gorbach, A.V. Graphene Plasmonic Waveguides for Mid-Infrared Supercontinuum Generation on a Chip. Photonics 2015, 2, 825–837. [Google Scholar] [CrossRef]
- Savostianova, N.A.; Mikhailov, S.A. Giant enhancement of the third harmonic in graphene integrated in a layered structure. Appl. Phys. Lett. 2015, 107, 181104. [Google Scholar] [CrossRef]
- Savostianova, N.A.; Mikhailov, S.A. Third harmonic generation from graphene lying on different substrates: Optical-phonon resonances and interference effects. Opt. Express 2017, 25, 3268–3285. [Google Scholar] [CrossRef]
- Andreeva, V.; Luskin, M.; Margetis, D. Nonperturbative nonlinear effects in the dispersion relations for TE and TM plasmons on two-dimensional materials. Phys. Rev. B 2018, 98, 195407. [Google Scholar] [CrossRef]
- Cheng, J.L.; Sipe, J.E.; Vermeulen, N.; Guo, C. Nonlinear optics of graphene and other 2D materials in layered structures. J. Phys. Photonics 2018, 1, 015002. [Google Scholar] [CrossRef]
- Smirnov, Y.; Tikhov, S. The Nonlinear Eigenvalue Problem of Electromagnetic Wave Propagation in a Dielectric Layer Covered with Graphene. Photonics 2023, 10, 523. [Google Scholar] [CrossRef]
- Smirnov, Y.G.; Tikhov, S.V. On the Ability of TE- and TM-waves Propagation in a Dielectric Layer Covered with Nonlinear Graphene. Lobachevskii J. Math. 2023, 44, 5057–5071. [Google Scholar] [CrossRef]
- Čtyroký, J.; Petráček, J.; Kwiecien, P.; Richter, I.; Kuzmiak, V. Graphene on an optical waveguide: Comparison of simulation approaches. Opt. Quantum Electron. 2020, 52, 149. [Google Scholar] [CrossRef]
- Kleinman, R.E.; Martin, P.A. On Single Integral Equations for the Transmission Problem of Acoustics. SIAM J. Appl. Math. 1988, 48, 307–325. [Google Scholar] [CrossRef]
- Saillard, M.; Maystre, D. Scattering from metallic and dielectric rough surfaces. J. Opt. Soc. Am. A 1990, 7, 982–990. [Google Scholar] [CrossRef]
- Kaya, A.C.; Erdogan, F. On the solution of integral equations with strongly singular kernels. Q. Appl. Math. 1987, 45, 105–122. [Google Scholar] [CrossRef]
- Ervin, V.; Stephan, E. Collocation with Chebyshev polynomials for a hypersingular integral equation on an interval. J. Comput. Appl. Math. 1992, 43, 221–229. [Google Scholar] [CrossRef]
- Shestopalov, Y.V.; Smirnov, Y.G.; Chernokozhin, E.V. Logarithmic Integral Equations in Electromagnetics; De Gruyter: Berlin, Germany, 2000. [Google Scholar] [CrossRef]
- Mikhailov, S.A.; Ziegler, K. New Electromagnetic Mode in Graphene. Phys. Rev. Lett. 2007, 99, 016803. [Google Scholar] [CrossRef]
- Jablan, M.; Buljan, H.; Soljačić, M. Plasmonics in graphene at infrared frequencies. Phys. Rev. B 2009, 80, 245435. [Google Scholar] [CrossRef]
- Gu, T.; Petrone, N.; McMillan, J.F.; van der Zande, A.; Yu, M.; Lo, G.Q.; Kwong, D.L.; Hone, J.; Wong, C.W. Regenerative oscillation and four-wave mixing in graphene optoelectronics. Nat. Photonics 2012, 6, 554–559. [Google Scholar] [CrossRef]
- Vasić, B.; Isić, G.; Gajić, R. Localized surface plasmon resonances in graphene ribbon arrays for sensing of dielectric environment at infrared frequencies. J. Appl. Phys. 2013, 113, 013110. [Google Scholar] [CrossRef]
- Shapoval, O.V.; Gomez-Diaz, J.S.; Perruisseau-Carrier, J.; Mosig, J.R.; Nosich, A.I. Integral Equation Analysis of Plane Wave Scattering by Coplanar Graphene-Strip Gratings in the THz Range. IEEE Trans. Terahertz Sci. Technol. 2013, 3, 666–674. [Google Scholar] [CrossRef]
- Zinenko, T.L. Scattering and absorption of terahertz waves by a free-standing infinite grating of graphene strips: Analytical regularization analysis. J. Opt. 2015, 17, 055604. [Google Scholar] [CrossRef]
- You, J.; Bongu, S.; Bao, Q.; Panoiu, N. Nonlinear optical properties and applications of 2D materials: Theoretical and experimental aspects. Nanophotonics 2019, 8, 63–97. [Google Scholar] [CrossRef]
- Kumbhakar, P.; Jayan, J.S.; Sreedevi Madhavikutty, A.; Sreeram, P.; Saritha, A.; Ito, T.; Tiwary, C.S. Prospective applications of two-dimensional materials beyond laboratory frontiers: A review. iScience 2023, 26, 106671. [Google Scholar] [CrossRef] [PubMed]
- Polyanin, A.D.; Nazaikinskii, V.E. Handbook of Linear Partial Differential Equations for Engineers and Scientists, 2nd ed.; Chapman and Hall/CRC: Boca Raton, FL, USA, 2016. [Google Scholar] [CrossRef]




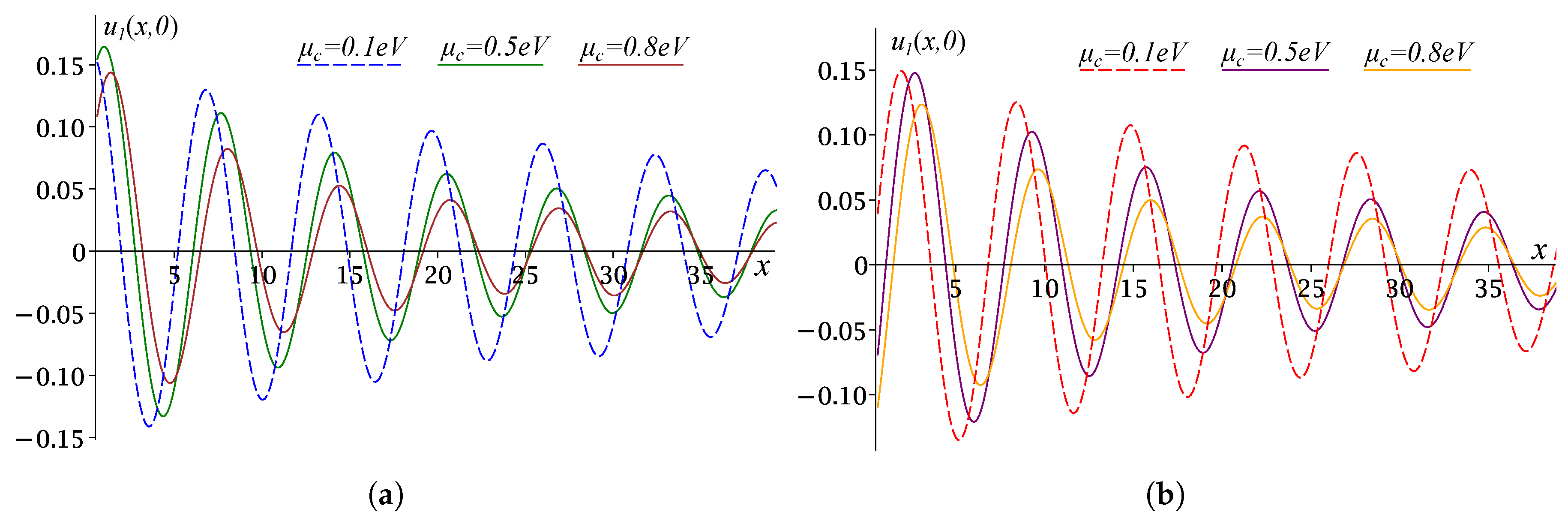
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Smirnov, Y.; Tikhov, S. Boundary Integral Equations Approach for a Scattering Problem of a TE-Wave on a Graphene-Coated Slab. Photonics 2025, 12, 456. https://doi.org/10.3390/photonics12050456
Smirnov Y, Tikhov S. Boundary Integral Equations Approach for a Scattering Problem of a TE-Wave on a Graphene-Coated Slab. Photonics. 2025; 12(5):456. https://doi.org/10.3390/photonics12050456
Chicago/Turabian StyleSmirnov, Yury, and Stanislav Tikhov. 2025. "Boundary Integral Equations Approach for a Scattering Problem of a TE-Wave on a Graphene-Coated Slab" Photonics 12, no. 5: 456. https://doi.org/10.3390/photonics12050456
APA StyleSmirnov, Y., & Tikhov, S. (2025). Boundary Integral Equations Approach for a Scattering Problem of a TE-Wave on a Graphene-Coated Slab. Photonics, 12(5), 456. https://doi.org/10.3390/photonics12050456





