Hybrid Method for Solving the Radiative Transport Equation †
Abstract
1. Introduction
2. Hybrid Method
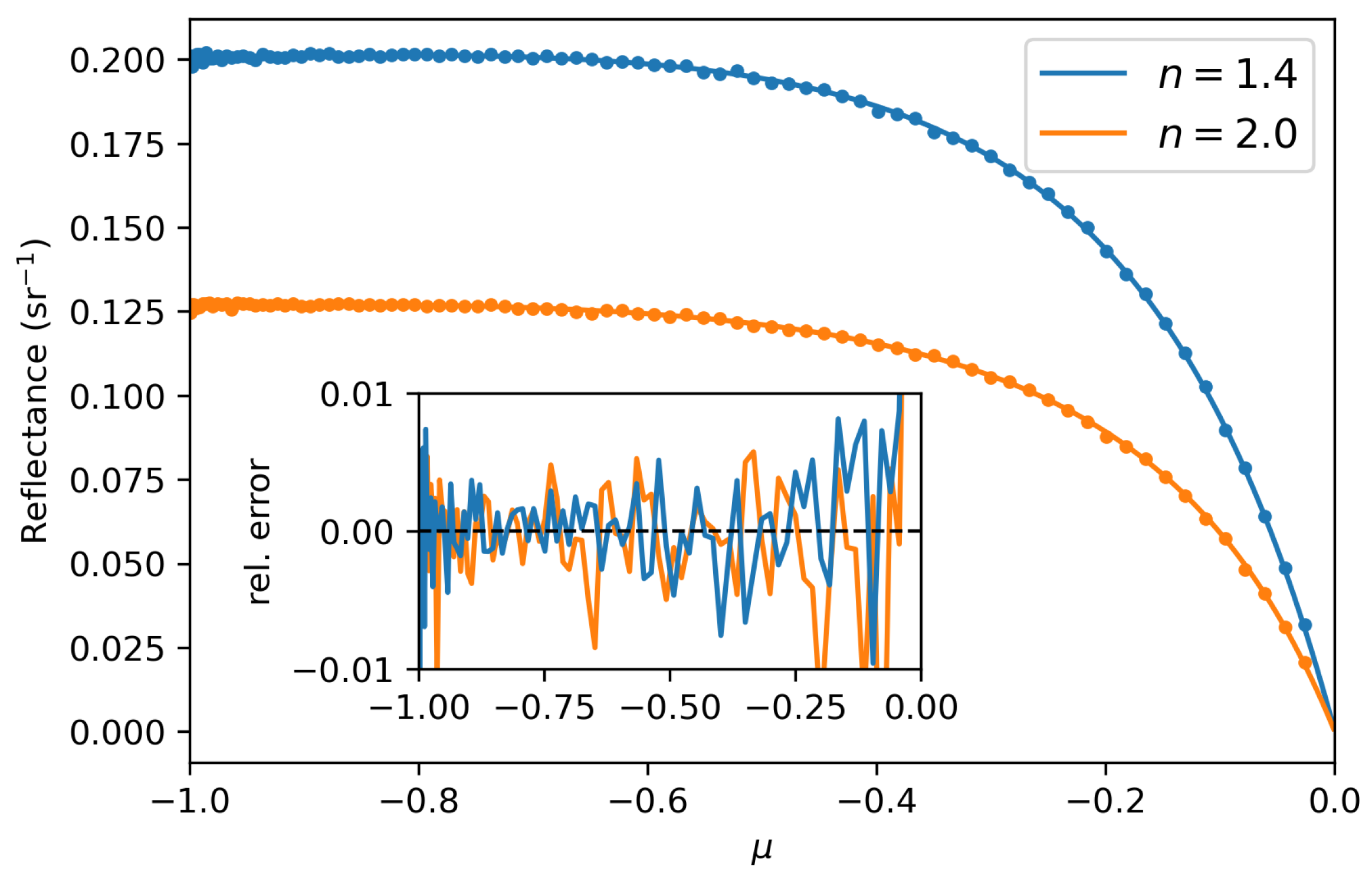
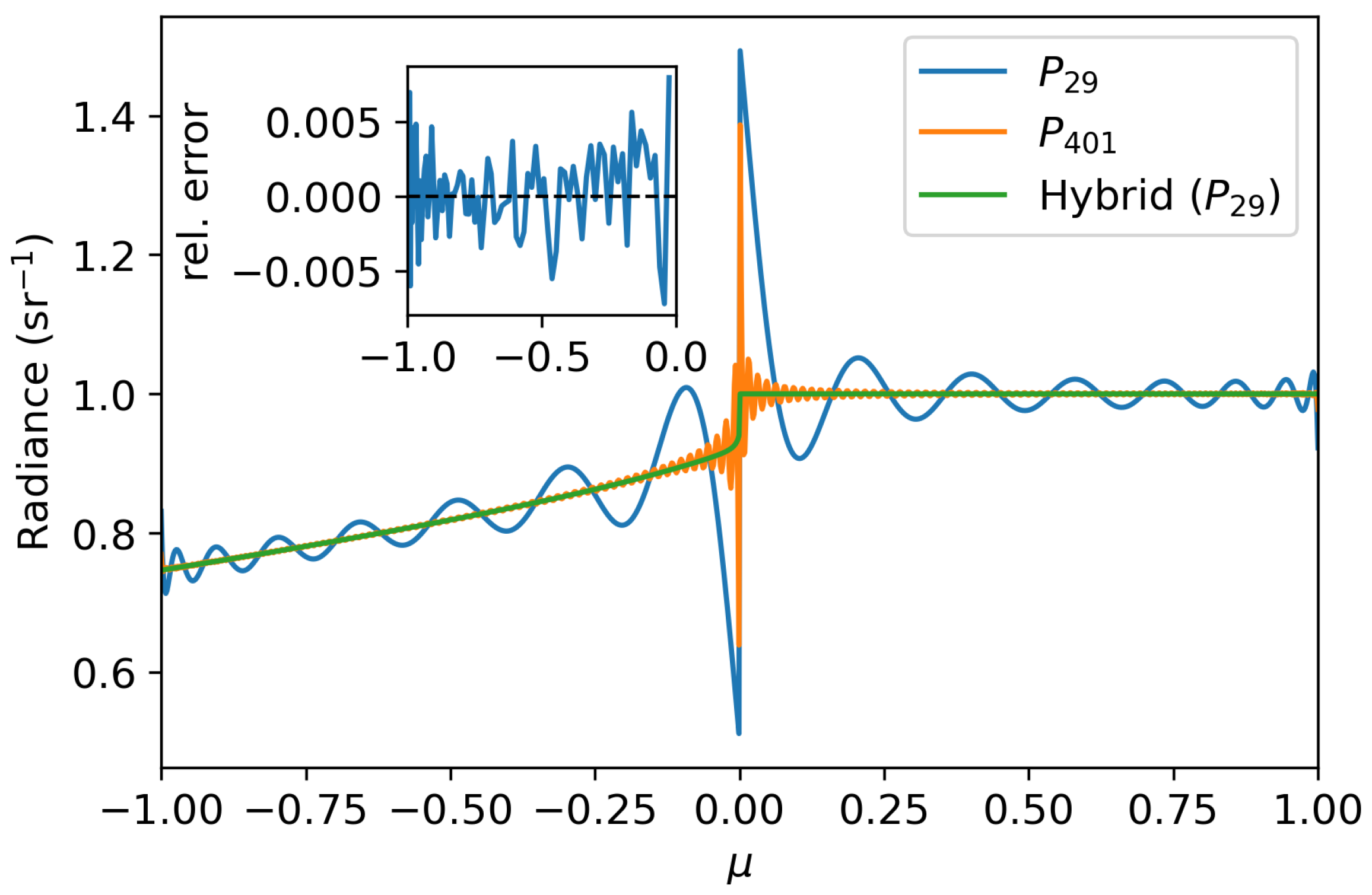
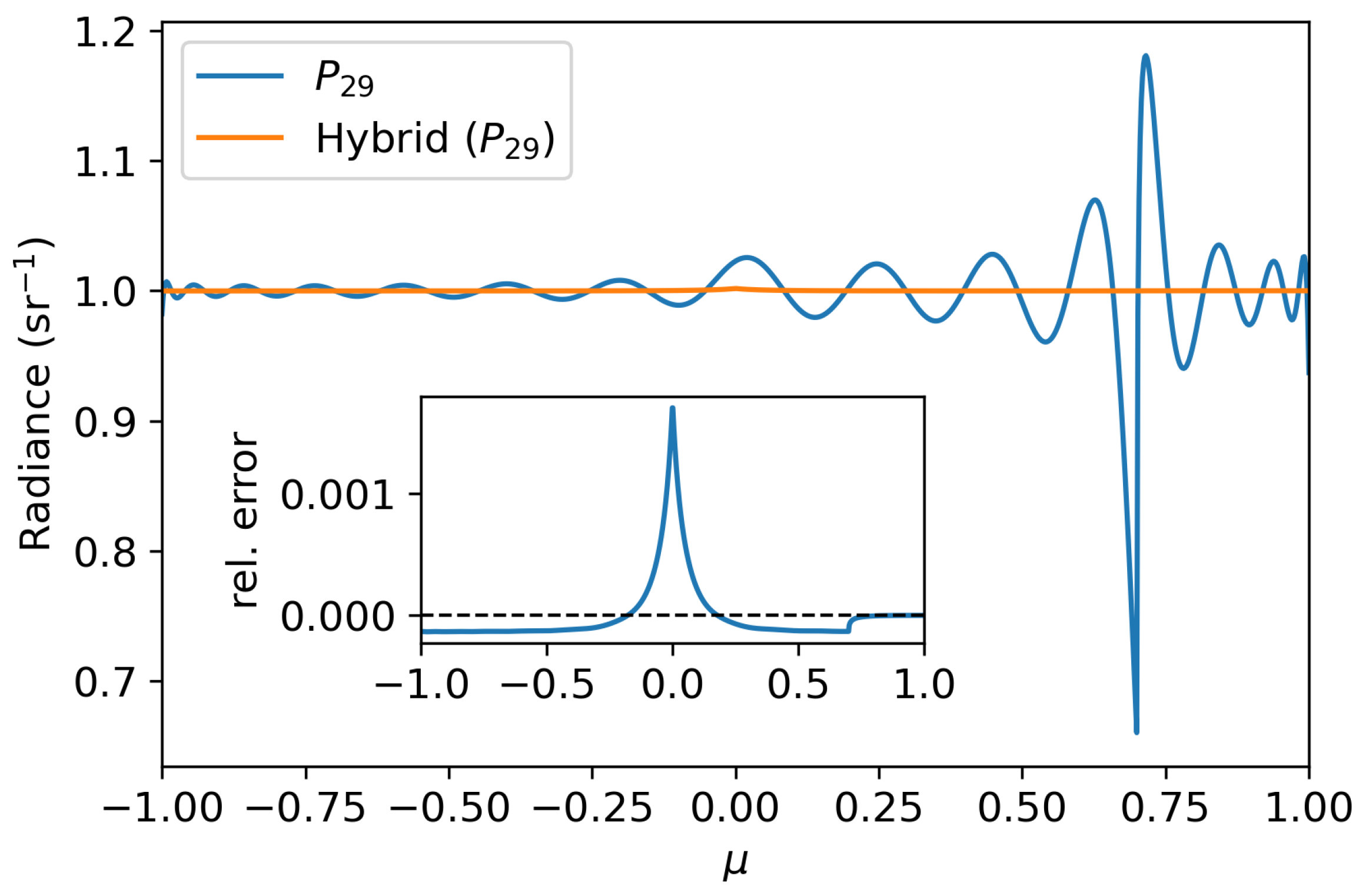
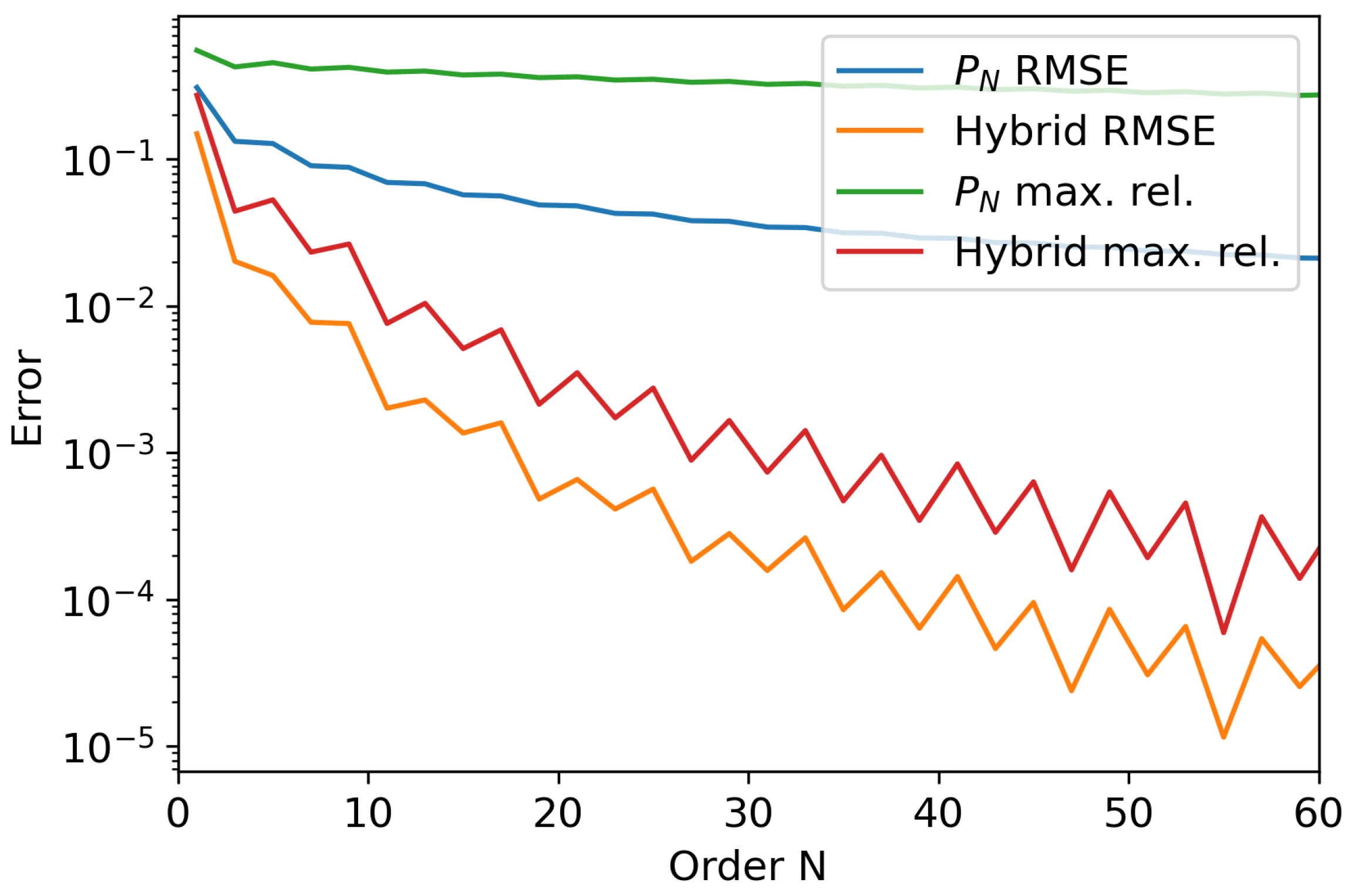
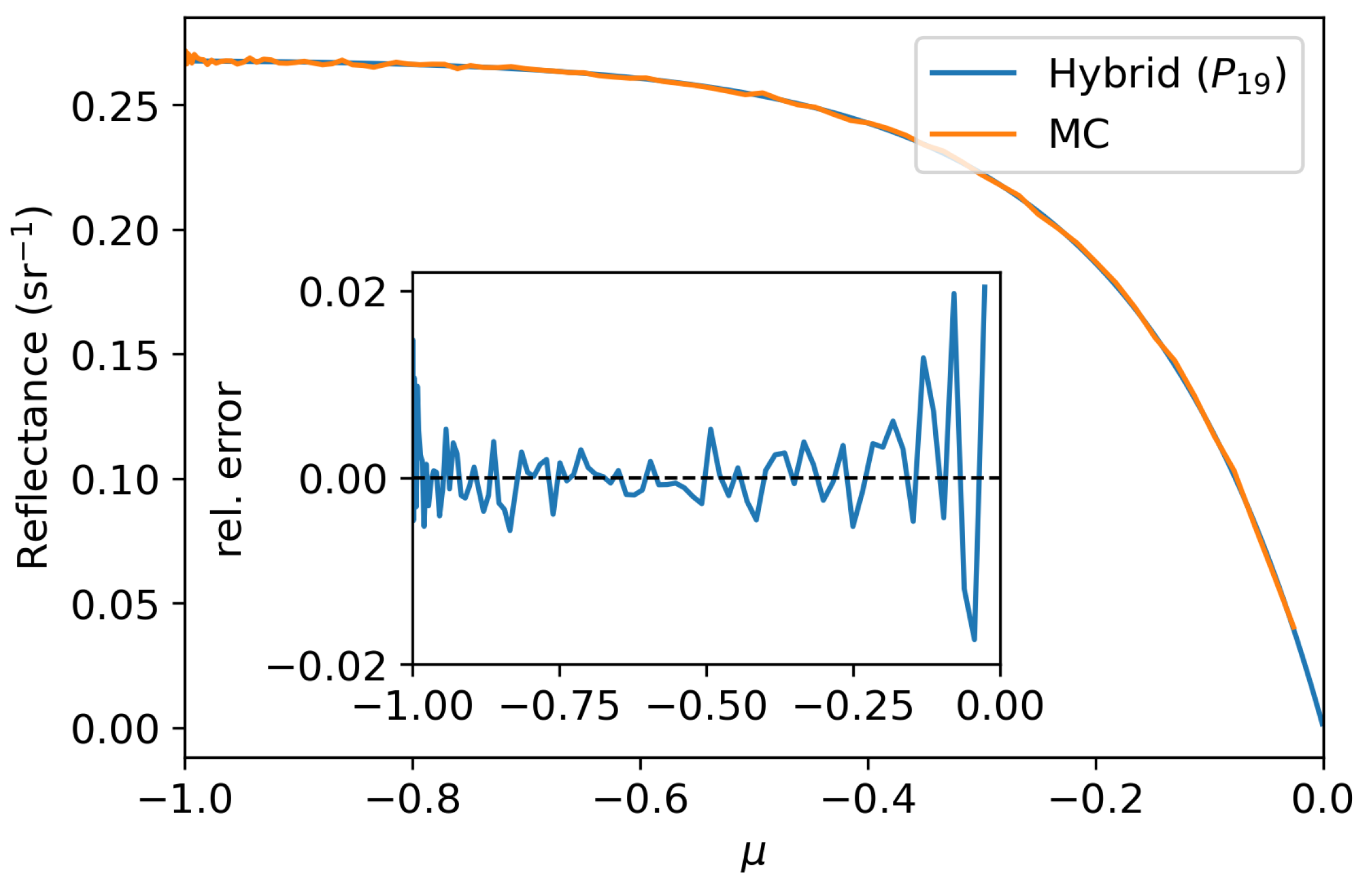
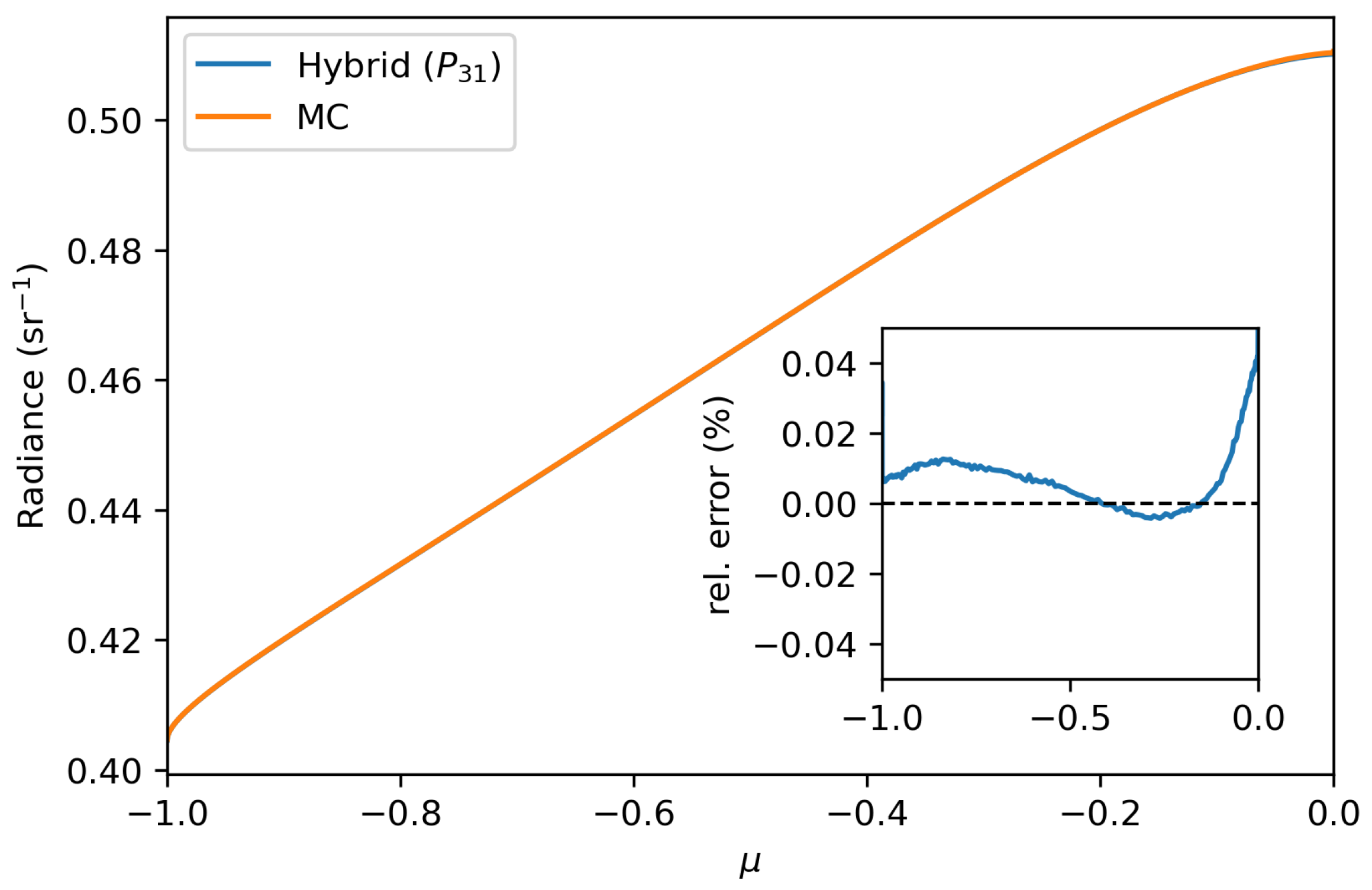
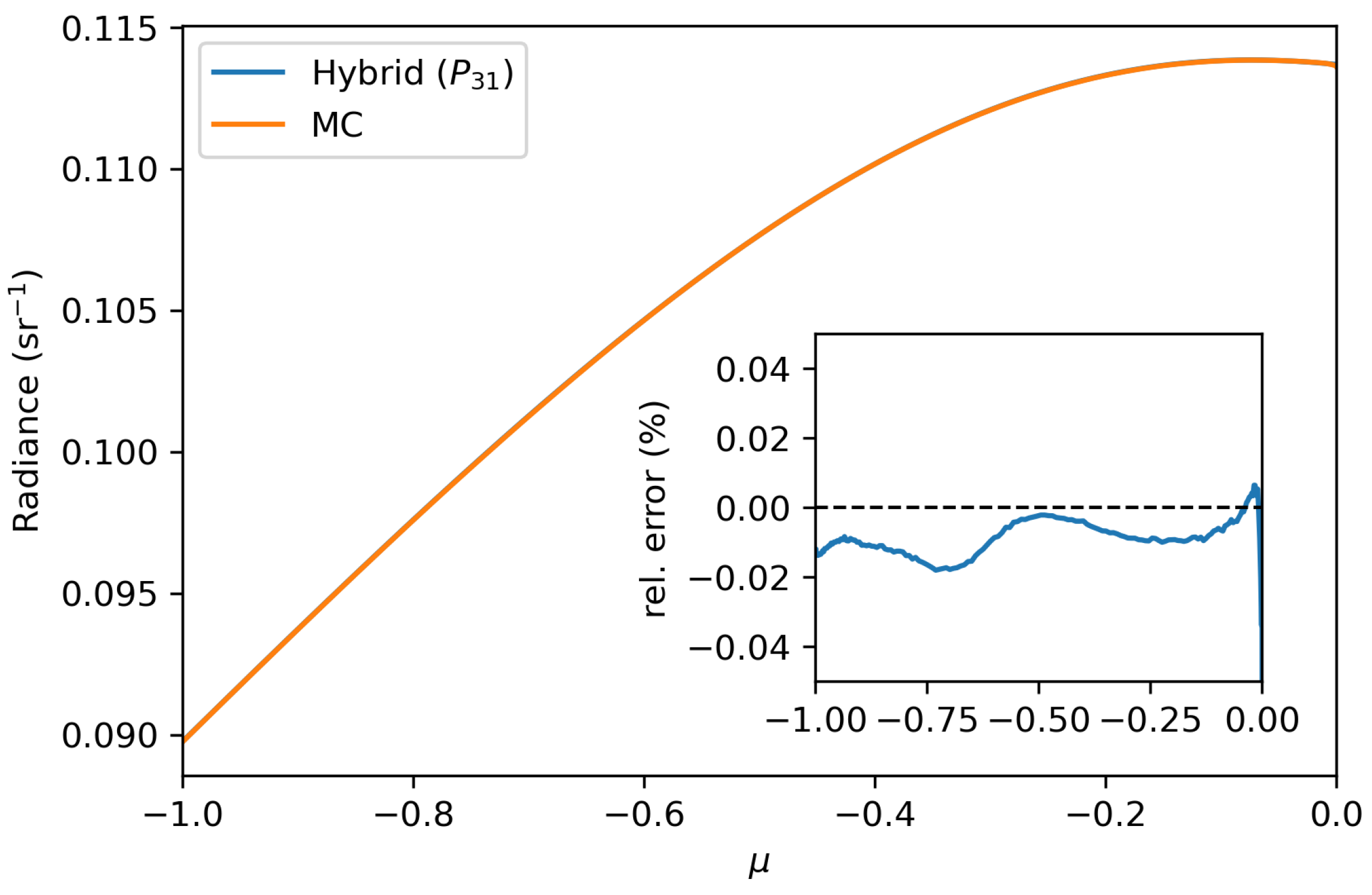
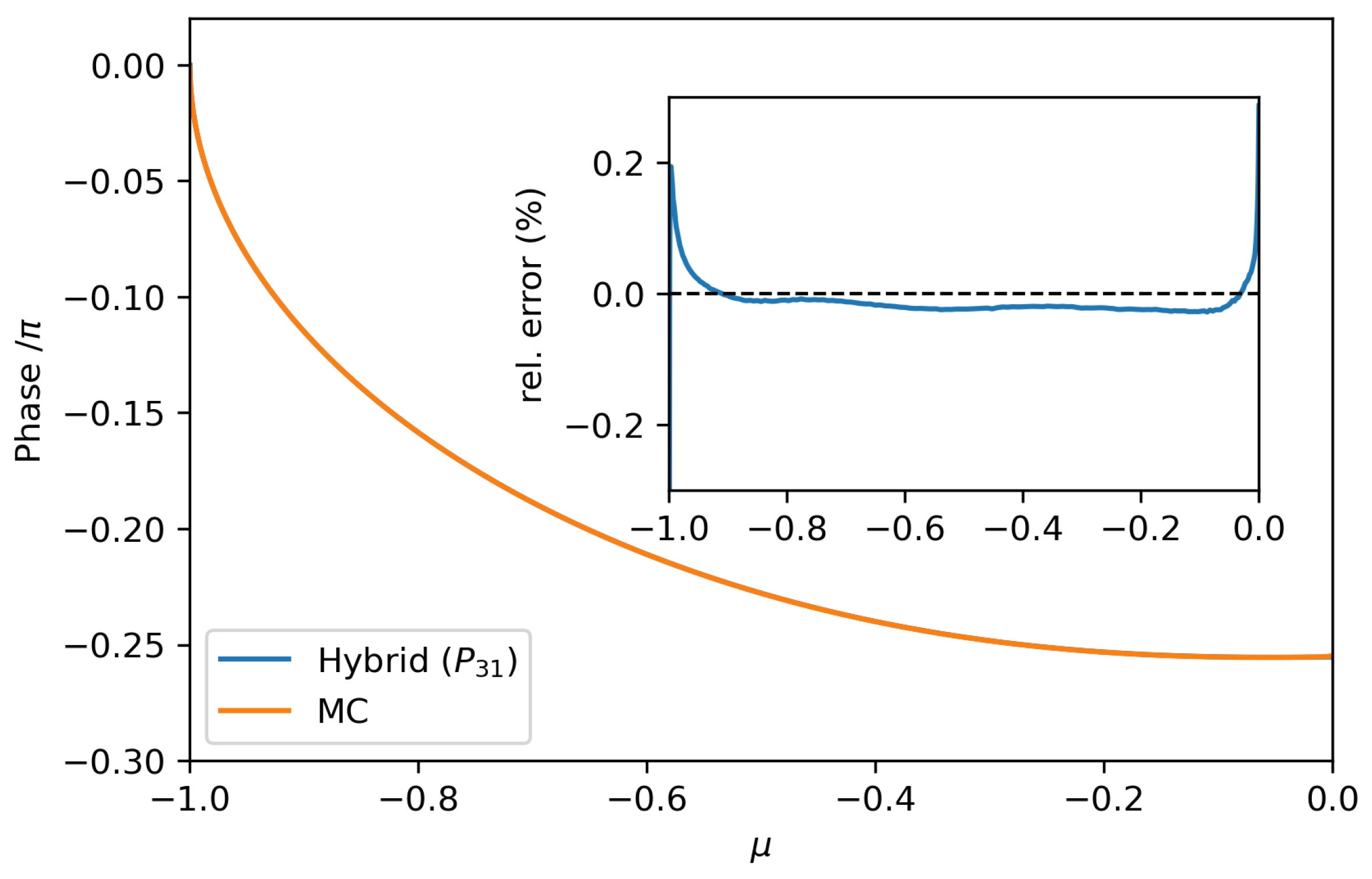
3. Numerical Experiments
4. Concluding Remarks
Author Contributions
Funding
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Ishimaru, A. Wave Propagation and Scattering in Random Media; Academic Press: New York, NY, USA, 1978. [Google Scholar]
- Case, K.M.; Zweifel, P.F. Linear Transport Theory; Addison-Wesley: New York, NY, USA, 1967. [Google Scholar]
- Duderstadt, J.J.; Martin, W.R. Transport Theory; John Wiley & Sons: New York, NY, USA, 1979. [Google Scholar]
- Ganapol, B.D.; Johnson, L.F.; Hammer, P.D.; Hlavka, C.A.; Peterson, D.L. LEAFMOD: A new within-leaf radiative transfer model. Remote Sens. Environ. 1998, 63, 182–193. [Google Scholar] [CrossRef]
- Martelli, F.; Binzoni, T.; Bianco, S.D.; Liemert, A.; Kienle, A. Light Propagation through Biological Tissue and Other Diffusive Media: Theory, Solutions, and Validations; SPIE Press: Bellingham, WA, USA, 2022; pp. 1–698. [Google Scholar]
- d’Eon, E.; Irving, G. A Quantized-Diffusion Model for Rendering Translucent Materials. ACM Trans. Graph. 2011, 30, 56:1–56:12. [Google Scholar]
- Hacker, L.; Wabnitz, H.; Pifferi, A.; Pfefer, T.J.; Pogue, B.W.; Bohndiek, S.E. Criteria for the design of tissue-mimicking phantoms for the standardization of biophotonic instrumentation. Nat. Biomed. Eng. 2022, 6, 541–558. [Google Scholar] [CrossRef]
- Mishchenko, M.I.; Travis, L.D.; Lacis, A.A. Multiple Scattering of Light by Particles; Cambridge University Press: New York, NY, USA, 2006. [Google Scholar]
- Ott, F.; Reitzle, D.; Krüger, B.; Liemert, A.; Kienle, A. Distribution of light inside three-dimensional scattering slabs: Comparison of radiative transfer and electromagnetic theory. J. Quant. Spectrosc. Radiat. Transf. 2022, 277, 107987. [Google Scholar] [CrossRef]
- Ntziachristos, V. Going deeper than microscopy: The optical imaging frontier in biology. Nat. Methods 2010, 7, 603–614. [Google Scholar] [CrossRef] [PubMed]
- Backman, V.; Wallace, M.B.; Perelman, L.T.; Arendt, J.T.; Gurjar, R.; Müller, M.G.; Zhang, Q.; Zonios, G.; Kline, E.; McGillican, T.; et al. Detection of Preinvasive Cancer Cells. Nature 2000, 406, 35–36. [Google Scholar] [CrossRef] [PubMed]
- Weissleder, R.; Ntziachristos, V. Shedding light onto live molecular targets. Nat. Med. 2003, 9, 123–128. [Google Scholar] [CrossRef]
- Wang, L.V. Multiscale photoacoustic microscopy and computed tomography. Nat. Photonics 2009, 3, 503–509. [Google Scholar] [CrossRef]
- Xu, X.; Liu, H.; Wang, L.V. Time-reversed ultrasonically encoded optical focusing into scattering media. Nat. Photonics 2011, 5, 154–157. [Google Scholar] [CrossRef]
- Ntziachristos, V.; Ripoll, J.; Wang, L.V.; Weissleder, R. Looking and listening to light: The evolution of whole-body photonic imaging. Nat. Biotechnol. 2005, 23, 313–320. [Google Scholar] [CrossRef]
- Wang, L.; Jacques, S.L.; Zheng, L. MCML–Monte Carlo modeling of light transport in multi-layered tissues. Comput. Methods Programs Biomed. 1995, 47, 131–146. [Google Scholar] [CrossRef] [PubMed]
- Tarvainen, T.; Vauhkonen, M.; Kolehmainen, V.; Kaipio, J.P. Finite element model for the coupled radiative transfer equation and diffusion approximation. Int. J. Numer. Methods Eng. 2006, 65, 383–405. [Google Scholar] [CrossRef]
- Fedele, F.; Eppstein, M.J.; Laible, J.P.; Godavarty, A.; Sevick-Muraca, E.M. Fluorescence photon migration by the boundary element method. J. Comput. Phys. 2005, 210, 109–132. [Google Scholar] [CrossRef]
- Balsara, D. Fast and accurate discrete ordinates methods for multidimensional radiative transfer. Part I, basic methods. J. Quant. Spectrosc. Radiat. Transf. 2001, 69, 671–707. [Google Scholar] [CrossRef]
- Asllanaj, F.; Fumeron, S. Modified finite volume method applied to radiative transfer in 2D complex geometries and graded index media. J. Quant. Spectrosc. Radiat. Transf. 2010, 111, 274–279. [Google Scholar] [CrossRef]
- Vitkin, E.; Turzhitsky, V.; Qiu, L.; Guo, l.; Itzkan, I.; Hanlon, E.B.; Perelman, L.T. Photon diffusion near the point-of-entry in anisotropically scattering turbid media. Nat. Commun. 2011, 2, 5874. [Google Scholar] [CrossRef]
- Jensen, H.W.; Marschner, S.R.; Levoy, M.; Hanrahan, P. A practical model for subsurface light transport. Comput. Graph. 2001, 35, 511–518. [Google Scholar]
- Patterson, M.S.; Chance, B.; Wilson, B.C. Time resolved reflectance and transmittance for the non-invasive measurement of tissue optical properties. Appl. Opt. 1989, 28, 2331–2336. [Google Scholar] [CrossRef]
- Liemert, A.; Kienle, A. Light diffusion in a radially N-layered cylinder. Phys. Rev. E 2011, 84, 041911. [Google Scholar] [CrossRef]
- Martelli, F.; Sassaroli, A.; Pifferi, A.; Torricelli, A.; Spinelli, L.; Zaccanti, G. Heuristic Green’s function of the time dependent radiative transfer equation for a semi-infinite medium. Opt. Express 2007, 15, 18168–18175. [Google Scholar] [CrossRef]
- Hull, E.L.; Foster, T.H. Steady-state reflectance spectroscopy in the P3 approximation. JOSA A 2001, 18, 584–599. [Google Scholar] [CrossRef]
- Gardner, A.; Kim, A.D.; Venugopalan, V. Radiative transport produced by oblique illumination of turbid media with collimated beams. Phys. Rev. E 2013, 87, 063308. [Google Scholar] [CrossRef] [PubMed]
- Markel, V.A. Modified spherical harmonics method for solving the radiative transport equation. Waves Random Complex Media 2004, 14, 13–19. [Google Scholar] [CrossRef]
- Liemert, A.; Kienle, A. Green’s Function of the Time-Dependent Radiative Transport Equation in Terms of Rotated Spherical Harmonics. Phys. Rev. E 2012, 14, 036603. [Google Scholar] [CrossRef]
- Machida, M.; Panasyuk, G.Y.; Schotland, J.C.; Markel, V.A. The Green’s function for the radiative transport equation in the slab geometry. J. Phys. A Math. Theor. 2010, 43, 065402. [Google Scholar] [CrossRef]
- Machida, M. The Green’s function for the three-dimensional linear Boltzmann equation via Fourier transform. J. Phys. A Math. Theor. 2016, 49, 175001. [Google Scholar] [CrossRef]
- Machida, M.; Hoshi, Y.; Kagawa, K.; Takada, K. Decay behavior and optical parameter identification for spatial-frequency domain imaging by the radiative transport equation. J. Opt. Soc. Am. A 2020, 37, 2020–2031. [Google Scholar] [CrossRef]
- Machida, M. Rotated reference frames in radiative transport theory. Prog. Opt. 2023; in press. [Google Scholar]
- Liemert, A.; Reitzle, D.; Kienle, A. Analytical solutions of the radiative transport equation for turbid and fluorescent layered media. Sci. Rep. 2017, 7, 3819. [Google Scholar] [CrossRef]
- Joseph, J.H.; Wiscombe, W.J. The delta-Eddington approximation for radiative flux transfer. J. Atmos. Sci. 1976, 33, 2452–2459. [Google Scholar] [CrossRef]
- Liemert, A.; Reitzle, D.; Kienle, A. Hybrid method for solving the radiative transport equation. In European Conference on Biomedical Optics; Optica Publishing Group: Washington, DC, USA, 2023; p. 126281G. [Google Scholar]
- Kienle, A.; Lilge, L.; Patterson, M.S.; Hibst, R.; Steiner, R.; Wilson, B.C. Spatially resolved absolute diffuse reflectance measurements for noninvasive determination of the optical scattering and absorption coefficients of biological tissue. Appl. Opt. 1996, 35, 2304–2314. [Google Scholar] [CrossRef]
- Martelli, F.; Tommasi, F.; Fini, L.; Cortese, L.; Sassaroli, A.; Cavalieri, S. Invariance properties of exact solutions of the radiative transfer equation. J. Quant. Spectrosc. Radiat. Transf. 2021, 276, 107887. [Google Scholar] [CrossRef]
- Hevisov, D.; Reitzle, D.; Liemert, A.; Kienle, A. An Integral-Equation-Based Variance Reduction Method for Accelerated Monte Carlo Simulations. Photonics 2023, 11, 5. [Google Scholar] [CrossRef]
- Zhao, Y.; Pilvar, A.; Tank, A.; Peterson, H.; Jiang, J.; Aster, J.C.; Dumas, J.P.; Pierce, M.C.; Roblyer, D. Shortwave-infrared meso-patterned imaging enables label-free mapping of tissue water and lipid content. Nat. Commun. 2020, 11, 5355. [Google Scholar] [CrossRef] [PubMed]
- Cuccia, D.J.; Bevilacqua, F.; Durkin, A.J.; Tromberg, B.J. Modulated imaging: Quantitative analysis and tomography of turbid media in the spatial-frequency domain. Opt. Lett. 2005, 30, 1354–1356. [Google Scholar] [CrossRef] [PubMed]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liemert, A.; Reitzle, D.; Kienle, A. Hybrid Method for Solving the Radiative Transport Equation. Photonics 2025, 12, 409. https://doi.org/10.3390/photonics12050409
Liemert A, Reitzle D, Kienle A. Hybrid Method for Solving the Radiative Transport Equation. Photonics. 2025; 12(5):409. https://doi.org/10.3390/photonics12050409
Chicago/Turabian StyleLiemert, André, Dominik Reitzle, and Alwin Kienle. 2025. "Hybrid Method for Solving the Radiative Transport Equation" Photonics 12, no. 5: 409. https://doi.org/10.3390/photonics12050409
APA StyleLiemert, A., Reitzle, D., & Kienle, A. (2025). Hybrid Method for Solving the Radiative Transport Equation. Photonics, 12(5), 409. https://doi.org/10.3390/photonics12050409



