Dynamically Tunable Singular States Through Air-Slit Control in Asymmetric Resonant Metamaterials
Abstract
1. Introduction
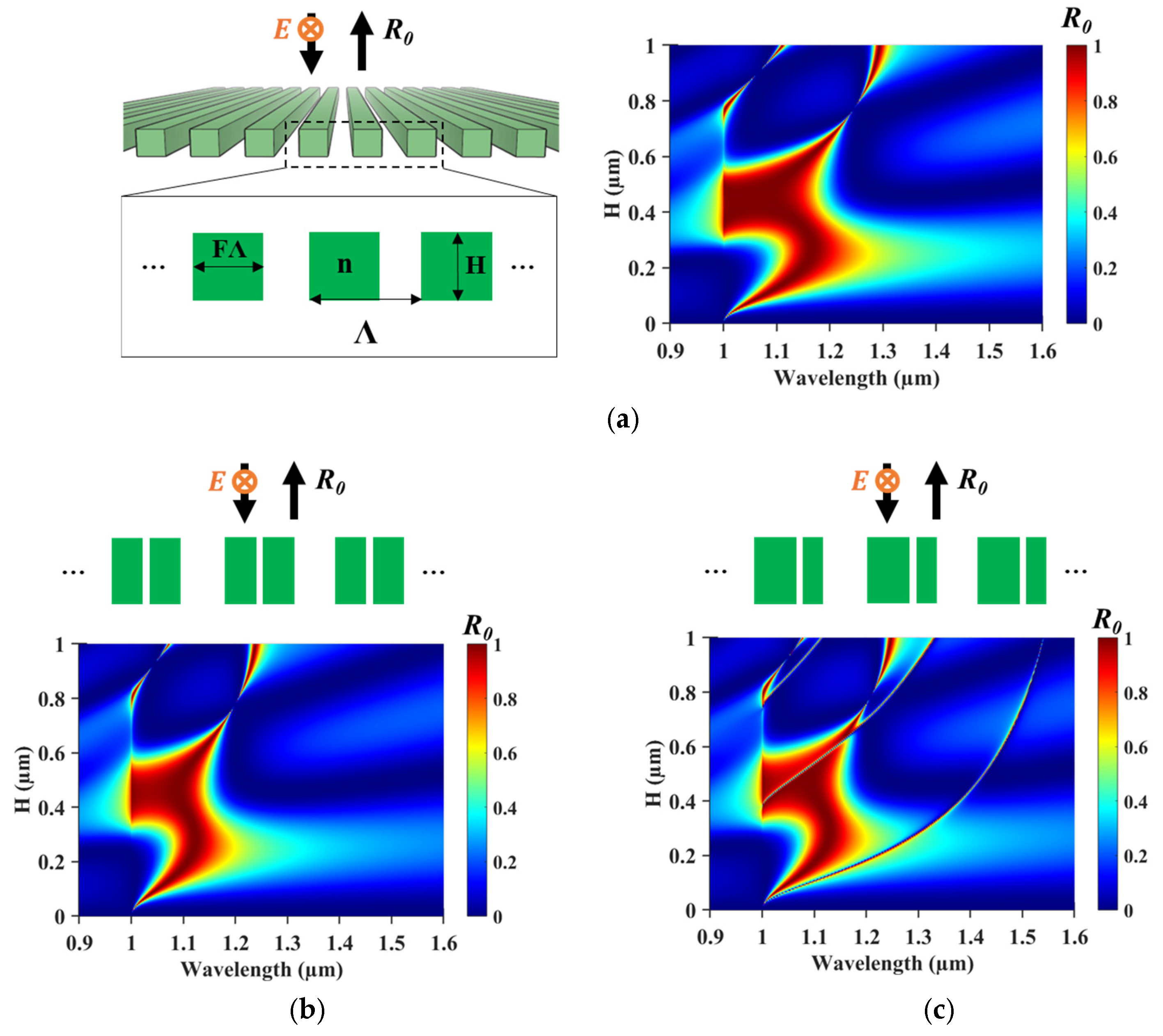
2. Air-Slit-Induced Singular States
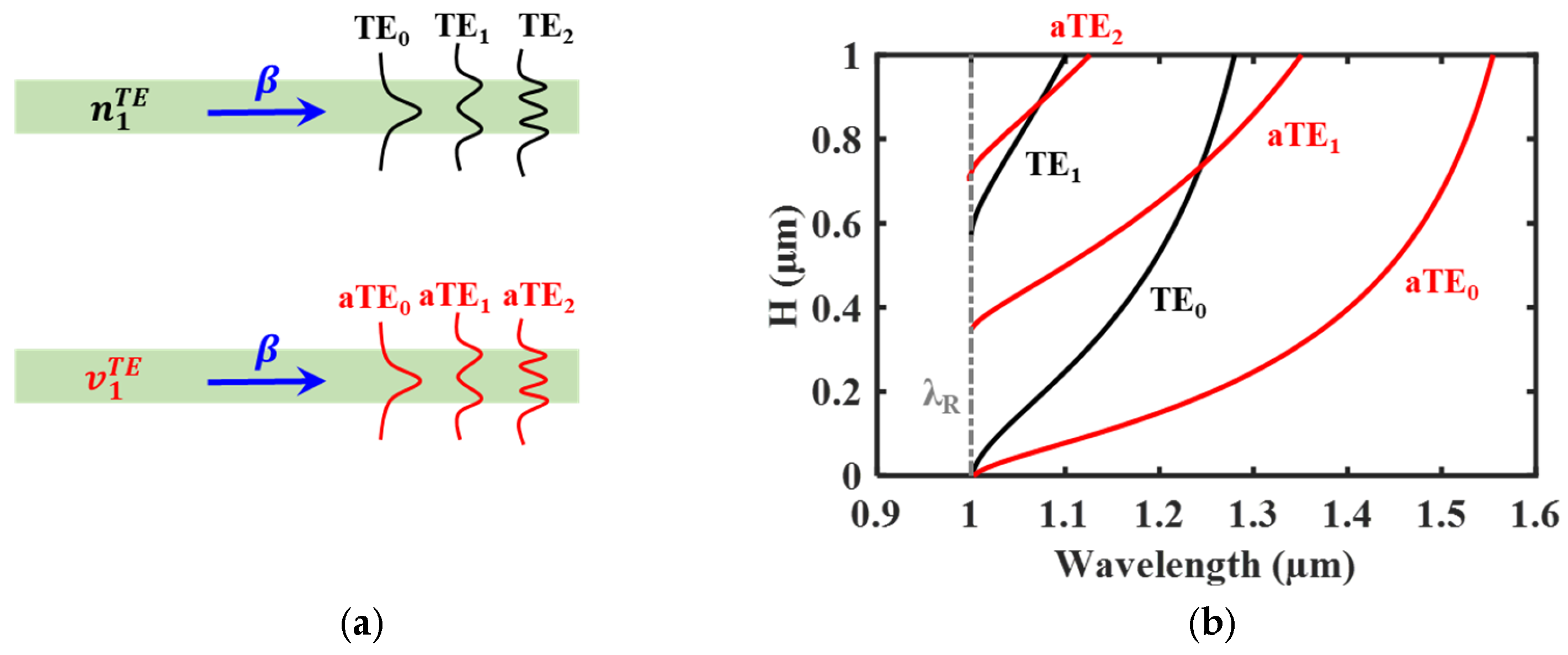
3. Interpretation of Singular States
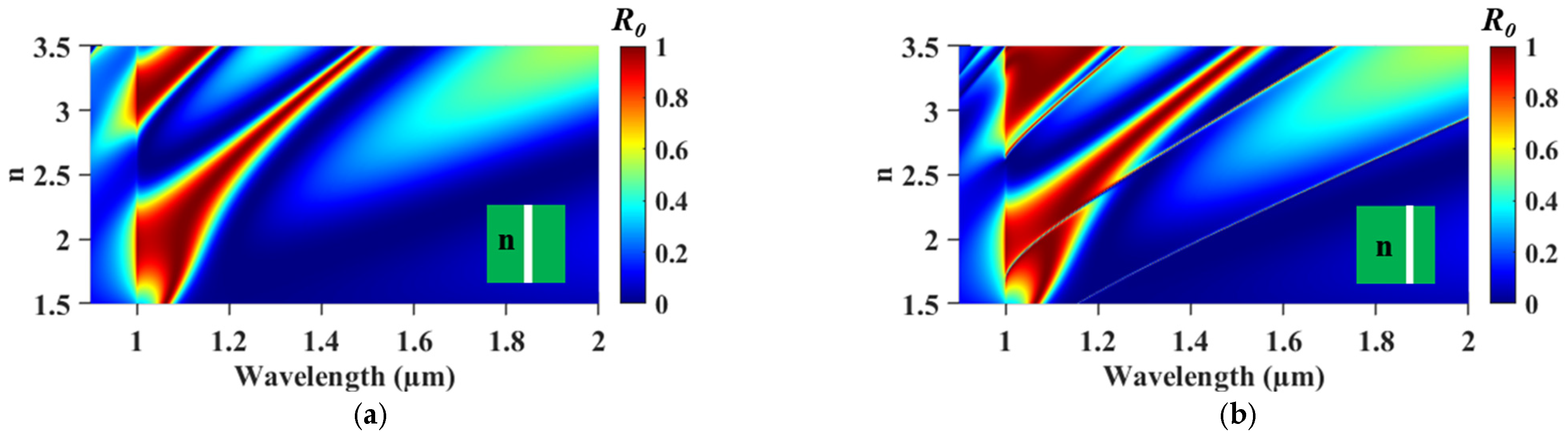
4. Analysis of Air Slit-Induced Singular States
5. Tunable Singular States by Asymmetric Air-Slit 1D Lattice
6. Discussion
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Ji, W.; Chang, J.; Xu, H.-X.; Gao, J.R.; Gröblacher, S.; Urbach, H.P.; Adam, A.J.L. Recent advances in metasurface design and quantum optics applications with machine learning, physics-informed neural networks, and topology optimization methods. Light Sci. Appl. 2023, 12, 169. [Google Scholar] [CrossRef] [PubMed]
- Armelles, G.; Bergamini, L.; Zabala, N.; García, F.; Dotor, M.L.; Torné, L.; Alvaro, R.; Griol, A.; Martínez, A.; Aizpurua, J.; et al. Metamaterial Platforms for Spintronic Modulation of Mid-Infrared Response under Very Weak Magnetic Field. ACS Photonics 2018, 5, 3956–3961. [Google Scholar] [CrossRef]
- Su, V.-C.; Chu, C.H.; Sun, G.; Tsai, D.P. Advances in optical metasurfaces: Fabrication and applications [Invited]. Opt. Express 2018, 26, 13148–13182. [Google Scholar] [CrossRef] [PubMed]
- Jakšić, Z.; Vuković, S.; Matovic, J.; Tanasković, D. Negative Refractive Index Metasurfaces for Enhanced Biosensing. Materials 2011, 4, 1–36. [Google Scholar] [CrossRef]
- Banerji, S.; Meem, M.; Majumder, A.; Vasquez, F.G.; Sensale-Rodriguez, B.; Menon, R. Imaging with flat optics: Metalenses or diffractive lenses? Optica 2019, 6, 805–810. [Google Scholar] [CrossRef]
- Roger, T.; Vezzoli, S.; Bolduc, E.; Valente, J.; Heitz, J.J.F.; Jeffers, J.; Soci, C.; Leach, J.; Couteau, C.; Zheludev, N.I.; et al. Coherent perfect absorption in deeply subwavelength films in the single-photon regime. Nat. Commun. 2015, 6, 7031. [Google Scholar] [CrossRef]
- Overvig, A.C.; Shrestha, S.; Malek, S.C.; Lu, M.; Stein, A.; Zheng, C.; Yu, N. Dielectric metasurfaces for complete and independent control of the optical amplitude and phase. Light Sci. Appl. 2019, 8, 92. [Google Scholar] [CrossRef]
- Chen, J.; Xiao, J.; Lisevych, D.; Shakouri, A.; Fan, Z. Deep-subwavelength control of acoustic waves in an ultra-compact metasurface lens. Nat. Commun. 2018, 9, 4920. [Google Scholar] [CrossRef]
- Luo, X. Subwavelength Optical Engineering with Metasurface Waves. Adv. Opt. Mater. 2018, 6, 1701201. [Google Scholar] [CrossRef]
- Hu, Y.; Luo, X.; Chen, Y.; Liu, Q.; Li, X.; Wang, Y.; Liu, N.; Duan, H. 3D-Integrated metasurfaces for full-colour holography. Light Sci. Appl. 2019, 8, 86. [Google Scholar] [CrossRef]
- Zhang, X.; Wu, Y. Effective medium theory for anisotropic metamaterials. Sci. Rep. 2015, 5, 7892. [Google Scholar] [CrossRef] [PubMed]
- Van de Groep, J.; Polman, A. Designing Dielectric Resonators on Substrates: Combining Magnetic and Electric Resonances. Opt. Express 2013, 21, 26285–26302. [Google Scholar] [CrossRef]
- Genevet, P.; Capasso, F.; Aieta, F.; Khorasaninejad, M.; Devlin, R. Recent Advances in Planar Optics: From Plasmonic to Dielectric Metasurfaces. Optica 2017, 4, 139–152. [Google Scholar] [CrossRef]
- Chen, X.; Grzegorczyk, T.M.; Wu, B.-I.; Pacheco, J.; Kong, J.A. Robust method to retrieve the constitutive effective parameters of metamaterials. Phys. Rev. E 2004, 70, 16608. [Google Scholar] [CrossRef]
- Wang, S.S.; Magnusson, R. Theory and applications of guided-mode resonance filters. Appl. Opt. 1993, 32, 2606–2613. [Google Scholar] [CrossRef] [PubMed]
- Huang, L.; Jin, R.; Zhou, C.; Jiang, Y.; Jia, Y.; Gao, Y.; Xu, L.; Hu, W.; Gao, J.; Song, Q. Ultrahigh-Q guided mode resonances in an All-dielectric metasurface. Nat. Commun. 2023, 14, 3433. [Google Scholar] [CrossRef]
- Magnusson, R.; Wang, S.S. New principle for optical filters. Appl. Phys. Lett. 1992, 61, 1022–1024. [Google Scholar] [CrossRef]
- Murai, S.; Castellanos, G.W.; Raziman, T.V.; Curto, A.G.; Rivas, J.G. Enhanced Light Emission by Magnetic and Electric Resonances in Dielectric Metasurfaces. Adv. Opt. Mater. 2020, 8, 1902024. [Google Scholar] [CrossRef]
- Marinica, D.C.; Borisov, A.G.; Shabanov, S.V. Bound States in the Continuum in Photonics. Phys. Rev. Lett. 2008, 100, 183902. [Google Scholar] [CrossRef]
- Azzam, S.I.; Kildishev, A.V. Photonic Bound States in the Continuum: From Basics to Applications. Adv. Opt. Mater. 2021, 9, 2001469. [Google Scholar] [CrossRef]
- Liu, Y.; Zhang, Q.; Xing, X.; Zou, D.; Mao, B.; Yao, J.; Ouyang, C.; Wang, Z.; Wu, L. Terahertz narrowband filter metasurfaces based on bound states in the continuum. Opt. Express 2023, 31, 35272–35281. [Google Scholar] [CrossRef] [PubMed]
- Che, Y.; Zhang, T.; Shi, T.; Deng, Z.-L.; Cao, Y.; Guan, B.-O.; Li, X. Ultrasensitive Photothermal Switching with Resonant Silicon Metasurfaces at Visible Bands. Nano Lett. 2024, 24, 576–583. [Google Scholar] [CrossRef]
- Liu, B.; Peng, Y.; Jin, Z.; Wu, X.; Gu, H.; Wei, D.; Zhu, Y.; Zhuang, S. Terahertz ultrasensitive biosensor based on wide-area and intense light-matter interaction supported by QBIC. Chem. Eng. J. 2023, 462, 142347. [Google Scholar] [CrossRef]
- Xia, S.-X.; Zhai, X.; Wang, L.-L.; Wen, S.-C. Plasmonically Induced Transparency in Double-Layered Graphene Nanoribbons. Photonics Res. 2018, 6, 692–702. [Google Scholar] [CrossRef]
- Ko, Y.H.; Lee, K.J.; Simlan, F.A.; Magnusson, R. Singular states of resonant nanophotonic lattices. Nanophotonics 2023, 12, 263–272. [Google Scholar] [CrossRef]
- Ko, Y.H.; Hemmati, H.; Magnusson, R. Quantifying bound and leaky states of resonant optical lattices by Rytov-equivalent homogeneous waveguides. Opt. Lett. 2023, 48, 311–314. [Google Scholar] [CrossRef]
- Moharam, M.G.; Grann, E.B.; Pommet, D.A.; Gaylord, T.K. Formulation for Stable and Efficient Implementation of the Rigorous Coupled-Wave Analysis of Binary Gratings. J. Opt. Soc. Am. A 1995, 12, 1068–1076. [Google Scholar] [CrossRef]
- RSoft Products. DiffractMod v2023.12; Synopsys Inc.: Sunnyvale, CA, USA, 2025. [Google Scholar]
- Rytov, S.M. Electromagnetic properties of a finely stratified medium. Sov. Phys. JETP 1956, 2, 466–475. [Google Scholar]
- Hemmati, H.; Magnusson, R. Applicability of Rytov’s Full Effective-Medium Formalism to the Physical Description and Design of Resonant Metasurfaces. ACS Photonics 2020, 7, 3177–3187. [Google Scholar] [CrossRef]
- Adams, M.J. An Introduction to Optical Waveguides; Wiley: Chichester, UK, 1981. [Google Scholar]
- Bin-Alam, M.S.; Reshef, O.; Mamchur, Y.; Alam, M.Z.; Carlow, G.; Upham, J.; Sullivan, B.T.; Ménard, J.-M.; Huttunen, M.J.; Boyd, R.W.; et al. Ultra-high-Q resonances in plasmonic metasurfaces. Nat. Commun. 2021, 12, 974. [Google Scholar] [CrossRef]
- Wang, A.; Cheng, F.; Wang, Y.Z.; Zhang, X.; Nie, Y.N.; Gong, R.Z. Narrow band filter at 1550 nm based on quasi-one-dimensional photonic crystal with a mirror-symmetric heterostructure. Materials 2018, 11, 1099. [Google Scholar] [CrossRef] [PubMed]
- Park, C.G.; Park, K. Tunable dual-wavelength absorption switch with graphene based on an asymmetric guided-mode resonance structure. Opt. Express 2021, 29, 7307–7315. [Google Scholar] [CrossRef] [PubMed]
- Lin, D.Y.-C.; Chou, S.-H.; Hsueh, W.-J. Robust high-Q filter with complete transmission by conjugated topological photonic crystals. Sci. Rep. 2020, 10, 7040. [Google Scholar] [CrossRef] [PubMed]
- Parasuraman, F.A.; Summanwar, A.M.; Marty, F.P.; Basset, P.A.; Angelescu, D.E.B.; Bourouina, T.V. Very high aspect ratio deep reactive ion etching of submicrometer trenches in silicon. J. Microelectromech. Syst. 2012, 21, 1234–1241. [Google Scholar]




Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ko, Y.H.; Magnusson, R. Dynamically Tunable Singular States Through Air-Slit Control in Asymmetric Resonant Metamaterials. Photonics 2025, 12, 403. https://doi.org/10.3390/photonics12050403
Ko YH, Magnusson R. Dynamically Tunable Singular States Through Air-Slit Control in Asymmetric Resonant Metamaterials. Photonics. 2025; 12(5):403. https://doi.org/10.3390/photonics12050403
Chicago/Turabian StyleKo, Yeong Hwan, and Robert Magnusson. 2025. "Dynamically Tunable Singular States Through Air-Slit Control in Asymmetric Resonant Metamaterials" Photonics 12, no. 5: 403. https://doi.org/10.3390/photonics12050403
APA StyleKo, Y. H., & Magnusson, R. (2025). Dynamically Tunable Singular States Through Air-Slit Control in Asymmetric Resonant Metamaterials. Photonics, 12(5), 403. https://doi.org/10.3390/photonics12050403




