Underwater Coherent Optical Wireless Communications with Electronic Beam Steering and Turbulence Compensation Using Adaptive Optics and Aperture Averaging
Abstract
1. Introduction
- OPA antennas for electronic beam steering which accommodates PAT.
- Adaptive optics based on an LC-SLM for wavefront correction, and
- Aperture averaging with a converging lens.
2. Light Propagation in Water
2.1. Absorption and Scattering
2.2. Turbulence
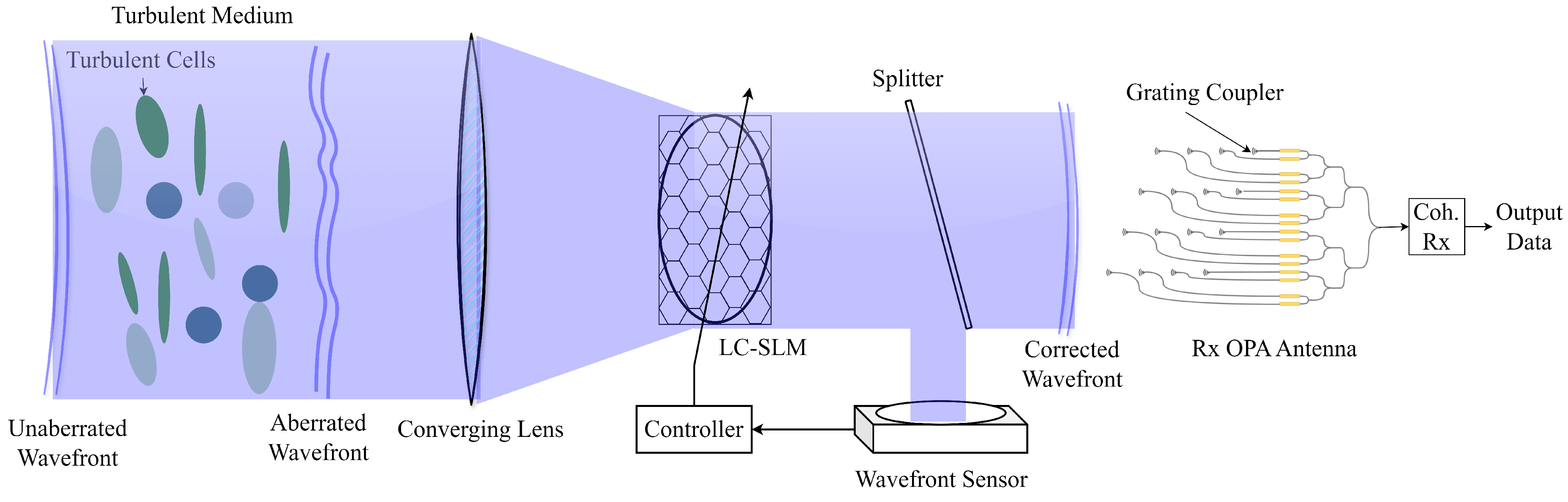
3. Proposed System Concept Architecture
3.1. PAT and Beam Divergence Control
3.2. Turbulence Compensation
3.2.1. Adaptive Optics
3.2.2. Aperture Averaging
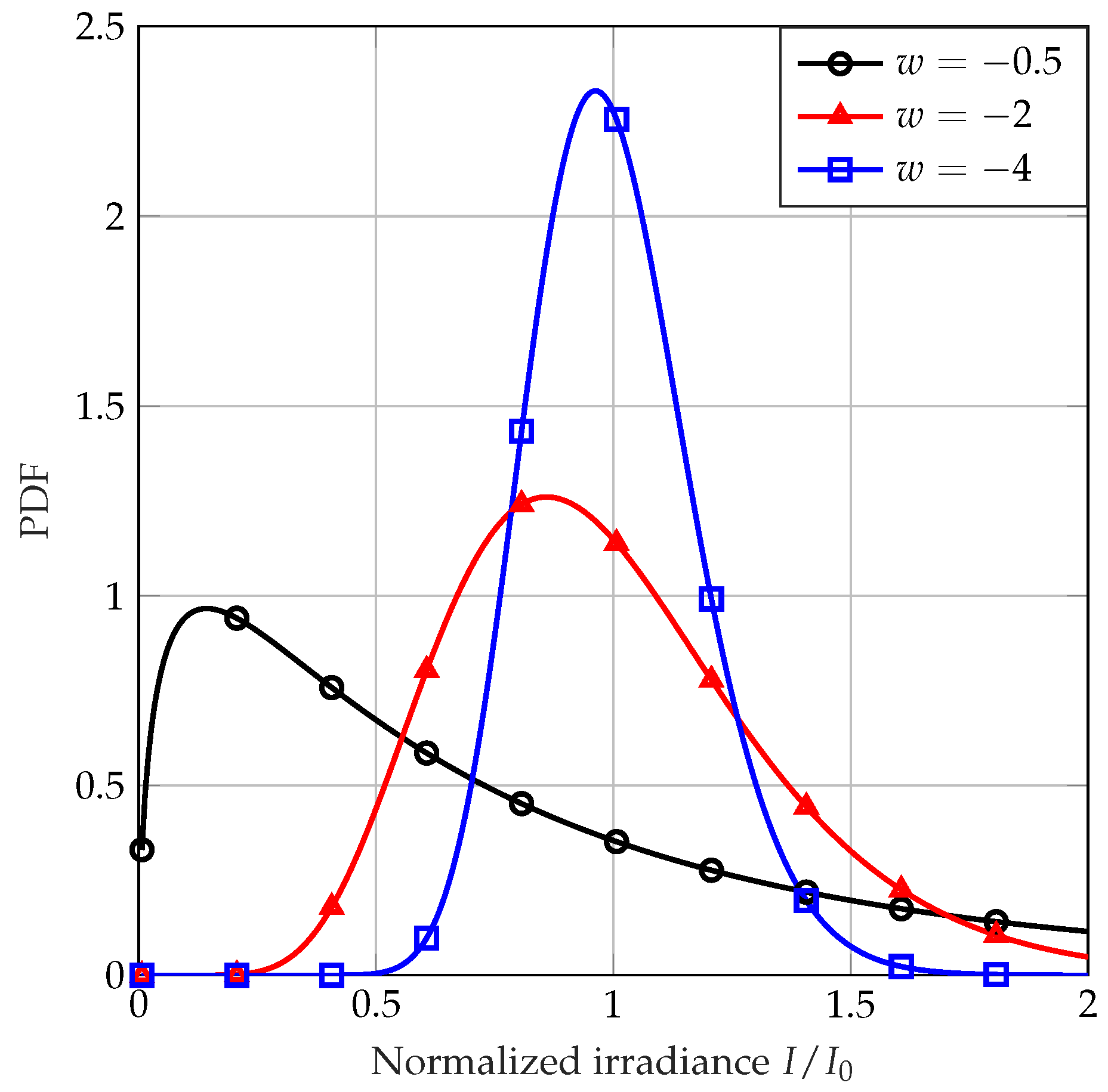
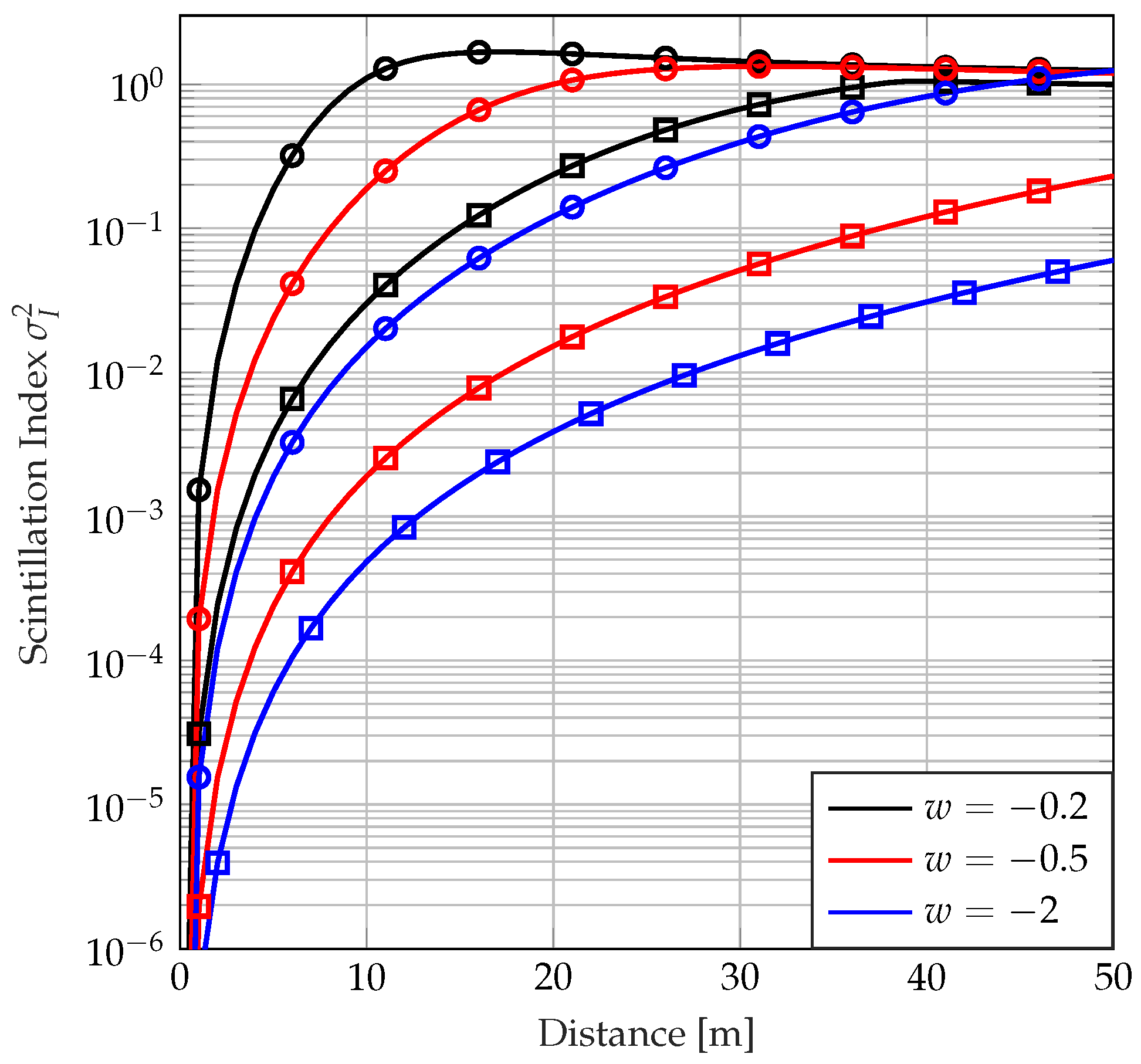
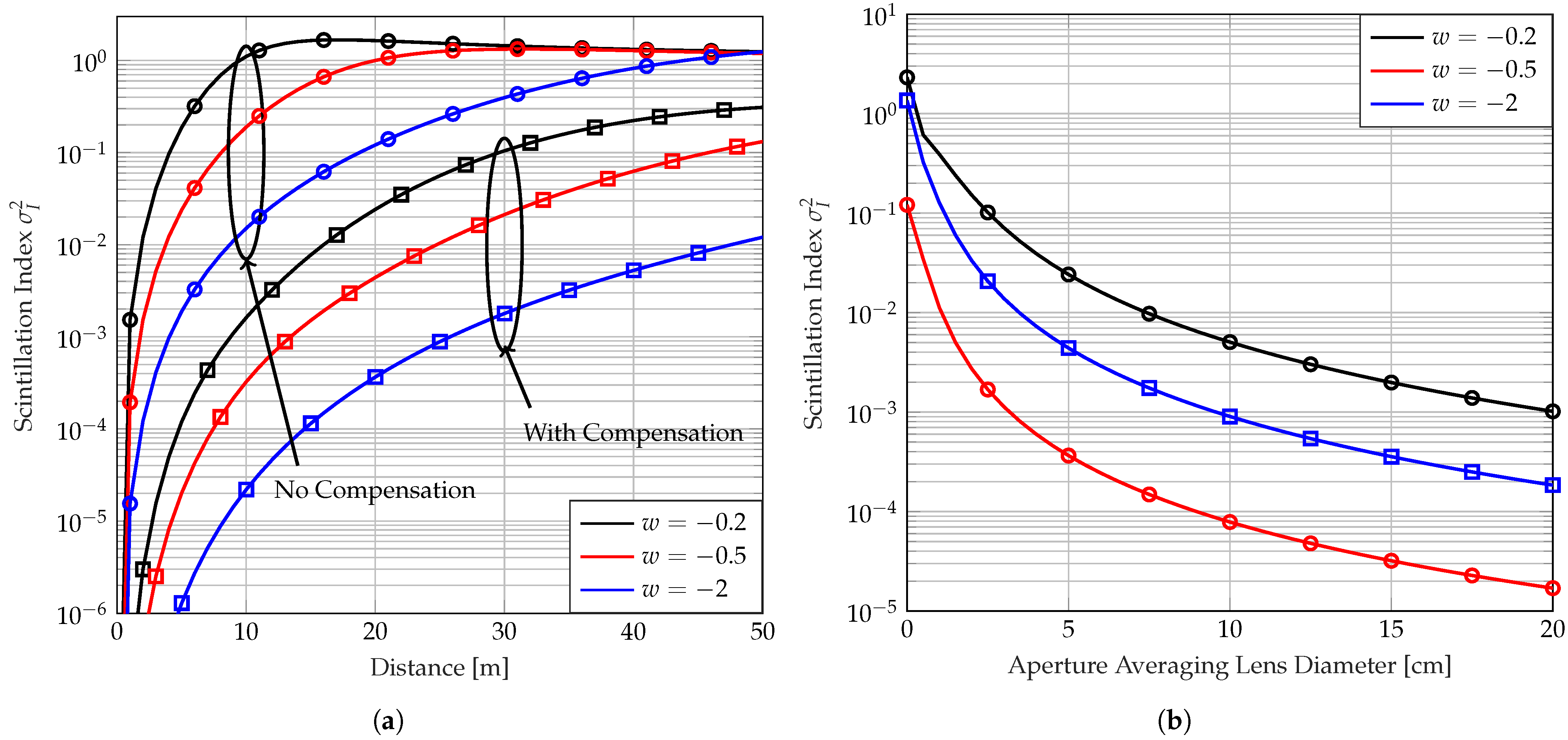
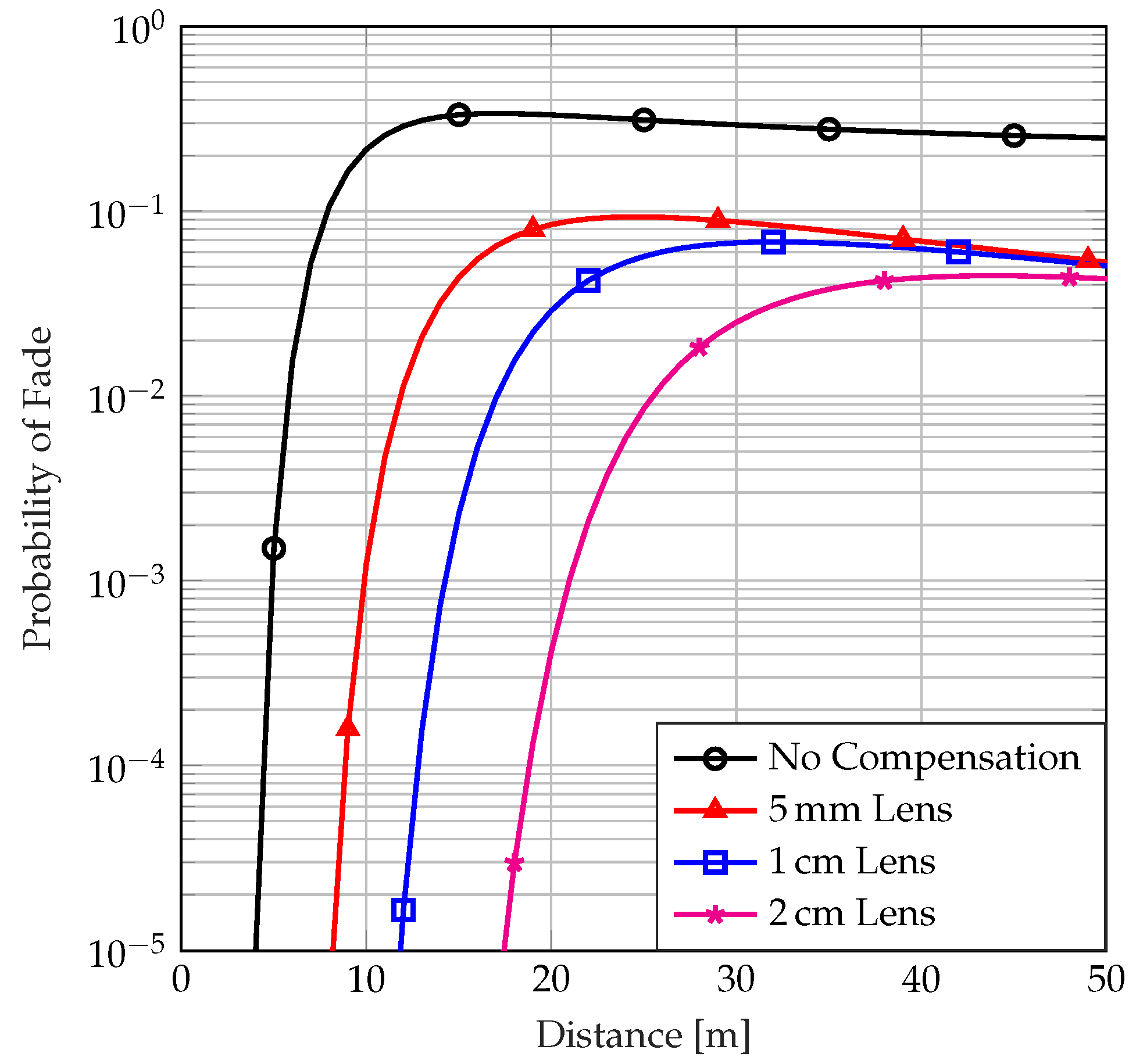
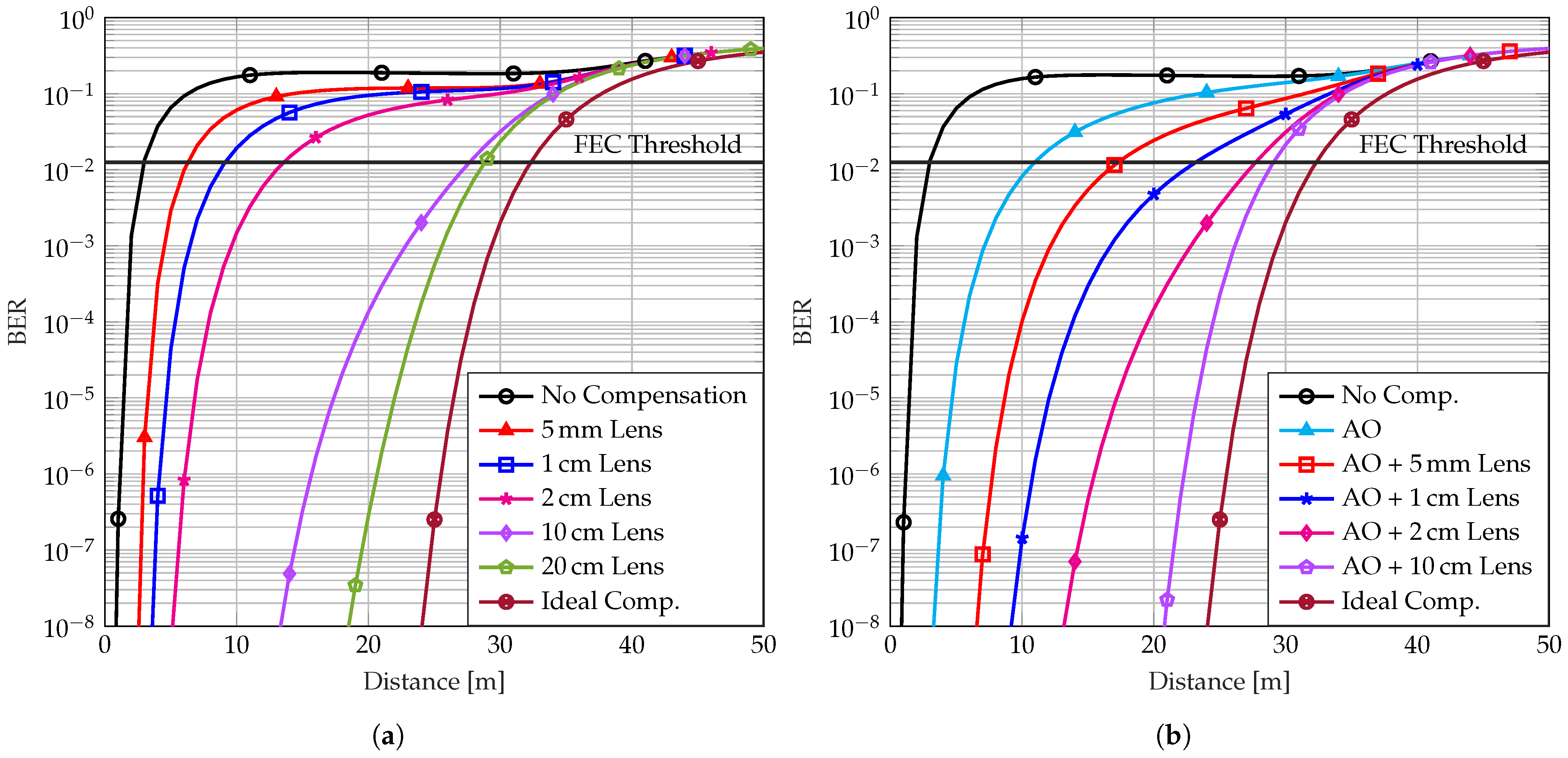
4. Numerical Results, Evaluations, and Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Hoeher, P.A.; Sticklus, J.; Harlakin, A. Underwater Optical Wireless Communications in Swarm Robotics: A Tutorial. IEEE Commun. Surv. Tutor. 2021, 23, 2630–2659. [Google Scholar] [CrossRef]
- Abdelfatah, R.; Alshaer, N.; Ismail, T. A review on pointing, acquisition, and tracking approaches in UAV-based FSO communication systems. Opt. Quantum Electron. 2022, 54, 571. [Google Scholar] [CrossRef]
- Kaymak, Y.; Rojas-Cessa, R.; Feng, J.; Ansari, N.; Zhou, M.; Zhang, T. A survey on acquisition, tracking, and pointing mechanisms for mobile free-space optical communications. IEEE Commun. Surv. Tutor. 2018, 20, 1104–1123. [Google Scholar] [CrossRef]
- Zhang, Q.; Yue, D.; Xu, X. Generalized transmit laser selection for vertical underwater wireless optical communications over Gamma-Gamma turbulence channels. Opt. Express 2023, 31, 37943–37958. [Google Scholar] [CrossRef]
- Palitharathna, K.W.S.; Suraweera, H.A.; Godaliyadda, R.I.; Herath, V.R.; Thompson, J.S. Average rate analysis of cooperative NOMA aided underwater optical wireless systems. IEEE Open J. Commun. Soc. 2021, 2, 2292–2310. [Google Scholar] [CrossRef]
- Kaushal, H.; Kaddoum, G. Underwater optical wireless communication. IEEE Access 2016, 4, 1518–1547. [Google Scholar] [CrossRef]
- Mobley, C. Light and Water; Academic Press: Cambridge, MA, USA; Elsevier Science: Amsterdam, The Netherlands, 1994. [Google Scholar]
- Derakhshandeh, A.; Pachnicke, S.; Hoeher, P.A. Underwater Wireless Laser-Based Communications Using Optical Phased Array Antennas. IEEE Photonics J. 2023, 15, 1–9. [Google Scholar] [CrossRef]
- Xu, L.; Li, K.; Zhang, G.; Yang, J.; Yin, Z.; Zhong, M.; Lu, H.; Deng, G.; Li, Y. Fully Electrically Driven Liquid Crystal Reconfigurable Intelligent Surface for Terahertz Beam Steering. IEEE Trans. Terahertz Sci. Technol. 2024, 14, 708–717. [Google Scholar] [CrossRef]
- Ndjiongue, A.R.; Ngatched, T.M.N.; Dobre, O.A.; Haas, H. Re-configurable intelligent surface-based VLC receivers using tunable liquid-crystals: The concept. J. Lightw. Technol. 2021, 39, 3193–3200. [Google Scholar] [CrossRef]
- Aboagye, S.; Ngatched, T.M.N.; Ndjiongue, A.R.; Dobre, O.A.; Shin, H. Liquid crystal-based RIS for VLC transmitters: Performance analysis, challenges, and opportunities. IEEE Wireless Commun. 2023, 31, 98–105. [Google Scholar] [CrossRef]
- Toselli, I.; Gladysz, S. Improving system performance by using adaptive optics and aperture averaging for laser communications in oceanic turbulence. Opt. Express 2020, 28, 17347–17361. [Google Scholar] [CrossRef] [PubMed]
- Zeng, Z.; Fu, S.; Zhang, H.; Dong, Y.; Cheng, J. A Survey of Underwater Optical Wireless Communications. IEEE Commun. Surv. Tutor. 2016, 19, 204–238. [Google Scholar] [CrossRef]
- Fletcher, A.S.; Hamilton, S.A.; Moores, J.D. Undersea laser communication with narrow beams. IEEE Commun. Mag. 2015, 53, 49–55. [Google Scholar] [CrossRef]
- Hill, R.J. Optical propagation in turbulent water. J. Opt. Soc. Am. 1978, 68, 1067–1072. [Google Scholar] [CrossRef]
- Nikishov, V.V.; Nikishov, V.I. Spectrum of turbulent fluctuations of the sea-water refraction index. Int. J. Fluid Mech. Res. 2000, 27, 1. [Google Scholar] [CrossRef]
- Korotkova, O.; Farwell, N.; Shchepakina, E. Light scintillation in oceanic turbulence. Waves Random Complex Media 2012, 22, 260–266. [Google Scholar] [CrossRef]
- Ata, Y.; Kiasaleh, K. Analysis of optical wireless communication links in turbulent underwater channels with wide range of water parameters. IEEE Trans. Veh. Technol. 2023, 72, 6363–6374. [Google Scholar] [CrossRef]
- Yao, J.-R.; Elamassie, M.; Korotkova, O. Spatial power spectrum of natural water turbulence with any average temperature, salinity concentration, and light wavelength. J. Opt. Soc. Am. A 2020, 37, 1614–1621. [Google Scholar] [CrossRef]
- Baykal, Y. Scintillation index in strong oceanic turbulence. Opt. Commun. 2016, 375, 15–18. [Google Scholar] [CrossRef]
- Luan, X.; Yue, P.; Yi, X. Scintillation index of an optical wave propagating through moderate-to-strong oceanic turbulence. J. Opt. Soc. Am. A 2019, 36, 2048–2059. [Google Scholar] [CrossRef]
- Deng, P.; Yuan, X.-H.; Huang, D. Scintillation of a laser beam propagation through non-Kolmogorov strong turbulence. Opt. Commun. 2012, 285, 880–887. [Google Scholar] [CrossRef]
- Andrews, L.C.; Phillips, R.L. Laser Beam Propagation Through Random Media, 2nd ed.; CRC Press: Boca Raton, FL, USA, 2005. [Google Scholar]
- Tyson, R.K.; Frazier, B.W. Principles of Adaptive Optics; CRC Press: Boca Raton, FL, USA, 2022. [Google Scholar]
- Andrews, L.C.; Phillips, R.L.; Hopen, C.Y.; Al-Habash, M.A. Theory of optical scintillation. J. Opt. Soc. Am. A 1999, 16, 1417–1429. [Google Scholar] [CrossRef]
- Sharma, A.; Straguzzi, J.N.; Xue, T.; Govdeli, A.; Chen, F.D.; Stalmashonak, A.; Sacher, W.D.; Poon, J.K. Crosstalk-Compensated Optical Phased Arrays for Wide-Angle Beam-Steering. In Proceedings of the Optical Fiber Communication Conference, San Diego, CA, USA, 24–28 March 2024. Th2A.3. [Google Scholar]
- Huang, A.; Tao, L.; Wang, C.; Zhang, L. Error performance of underwater wireless optical communications with spatial diversity under turbulence channels. Appl. Opt. 2018, 57, 7600–7608. [Google Scholar] [CrossRef] [PubMed]
- Peppas, K.P.; Boucouvalas, A.C.; Ghassemlooy, Z. Performance of underwater optical wireless communication with multi-pulse pulse-position modulation receivers and spatial diversity. IET Optoelectron. 2017, 11, 180–185. [Google Scholar] [CrossRef]
- Liu, J.; Li, Y.; Yang, R.; Pan, Z.; Zou, F.; Li, Z.; Geng, C.; Li, X. Performance optimization of spatial diversity antenna using hybrid combination for terrestrial optical wireless communication. Opt. Commun. 2024, 555, 130228. [Google Scholar] [CrossRef]
- Fu, Y.; Huang, C.; Du, Y. Effect of aperture averaging on mean bit error rate for UWOC system over moderate to strong oceanic turbulence. Opt. Commun. 2019, 451, 6–12. [Google Scholar] [CrossRef]
- Eso, E.; Ghassemlooy, Z.; Zvanovec, S.; Sathian, J.; Abadi, M.M.; Younus, O.I. Performance of vehicular visible light communications under the effects of atmospheric turbulence with aperture averaging. Sensors 2021, 21, 2751. [Google Scholar] [CrossRef]
- Vetelino, F.S.; Young, C.; Andrews, L.; Recolons, J. Aperture averaging effects on the probability density of irradiance fluctuations in moderate-to-strong turbulence. Appl. Opt. 2007, 46, 2099–2108. [Google Scholar]
- Shaffer, B.D.; Vorenberg, J.R.; Wilcox, C.C.; McDaniel, A.J. Generalizable turbulent flow forecasting for adaptive optics control. Appl. Opt. 2023, 62, G1–G11. [Google Scholar] [CrossRef]
- Soloviev, A.A.; Kotov, A.V.; Perevalov, S.E.; Esyunin, M.V.; Starodubtsev, M.V.; Alexandrov, A.G.; Galaktionov, I.V.; Samarkin, V.V.; Kudryashov, A.V.; Ginzburg, V.N.; et al. Adaptive system for wavefront correction of the PEARL laser facility. Quantum Electron. 2020, 50, 1115. [Google Scholar] [CrossRef]
- Galaktionov, I.; Sheldakova, J.; Samarkin, V.; Toporovsky, V.; Kudryashov, A. Atmospheric turbulence with Kolmogorov spectra: Software simulation, real-time reconstruction and compensation by means of adaptive optical system with bimorph and stacked-actuator deformable mirrors. Photonics 2023, 10, 1147. [Google Scholar] [CrossRef]
- Yoon, M.S.; Oh, K.-J.; Choo, H.-G.; Kim, J. A spatial light modulating LC device applicable to amplitude-modulated holographic mobile devices. In Proceedings of the 2015 IEEE 13th International Conference on Industrial Informatics (INDIN), Cambridge, UK, 22–24 July 2015; pp. 677–681. [Google Scholar] [CrossRef]
- Wang, M.; Zong, L.; Mao, L.; Marquez, A.; Ye, Y.; Zhao, H.; Vaquero Caballero, F.J. LCoS SLM study and its application in wavelength selective switch. Photonics 2017, 4, 22. [Google Scholar] [CrossRef]
- Kong, N.; Li, C.; Xia, M.; Li, D.; Qi, Y.; Xuan, L. Optimization of the open-loop liquid crystal adaptive optics retinal imaging system. J. Biomed. Opt. 2012, 17, 026001. [Google Scholar]
- Zhang, F.; Shen, H.; Sun, Y. Shack-Hartmann wavefront sensor based on a two-dimensional mixed aperture diffractive lens array. Opt. Lett. 2024, 49, 522–530. [Google Scholar] [CrossRef]
- Cai, D.; Ling, N.; Jiang, W. Performances of liquid crystal spatial light modulator (LC-SLM) as a wave-front corrector for atmospheric turbulence compensation. Proc. SPIE 2006, 6457, 64570P. [Google Scholar]
- Pivnenko, M.; Li, K.; Chu, D. Sub-millisecond switching of multi-level liquid crystal on silicon spatial light modulators for increased information bandwidth. Opt. Express 2021, 29, 24614–24627. [Google Scholar] [CrossRef]
- Bellone de Grecis, E.; Rouquette, P. Characterization of a spatial light modulator for MORFEO and HARMONI adaptive optics test devices. Proc. SPIE 2024, 13097, 130975D. [Google Scholar] [CrossRef]
- Liu, X.; Li, J.; Yang, Y. Reference-free calibration for liquid crystal spatial light modulators: High-resolution phase-only modulation. Opt. Express 2024, 32, 30724–30737. [Google Scholar]
- Daly, J.T.; Pezzaniti, J.L.; Riza, N.A. Wavefront control with a spatial light modulator containing dual-frequency liquid crystal. Proc. SPIE 2004, 5553, 1–8. [Google Scholar]
- Aghajani, A.; Kashani, F.D.; Yousefi, M. Laboratory study of aberration calculation in underwater turbulence using Shack-Hartmann wavefront sensor and Zernike polynomials. Opt. Express 2024, 32, 15978–15992. [Google Scholar] [CrossRef]
- Hu, L.; Hu, S.; Gong, W.; Si, K. Learning-based Shack-Hartmann wavefront sensor for high-order aberration detection. Opt. Express 2019, 27, 33504–33517. [Google Scholar] [CrossRef] [PubMed]
- Hu, L.; Hu, S.; Gong, W.; Si, K. Deep learning assisted Shack-Hartmann wavefront sensor for direct wavefront detection. Opt. Lett. 2020, 45, 3741–3744. [Google Scholar] [CrossRef] [PubMed]
- Wang, J.Y.; Markey, J.K. Modal compensation of atmospheric turbulence phase distortion. JOSA 1978, 68, 78–87. [Google Scholar] [CrossRef]
- Tyson, R.K. Bit-error rate for free-space adaptive optics laser communications. JOSA A 2002, 19, 753–758. [Google Scholar] [CrossRef]
- Andrews, L.C.; Phillips, R.L.; Hopen, C.Y. Aperture averaging of optical scintillations: Power fluctuations and the temporal spectrum. Waves Random Media 2000, 10, 53. [Google Scholar] [CrossRef]
- Andrews, L.C.; Phillips, R.L.; Yu, P.T. Optical scintillations and fade statistics for a satellite-communication system. Appl. Opt. 1995, 34, 7742–7751. [Google Scholar] [CrossRef]
- Ghassemlooy, Z.; Popoola, W.; Rajbhandari, S. Optical Wireless Communications: System and Channel Modelling with Matlab®; CRC Press: Boca Raton, FL, USA, 2019. [Google Scholar]
- Gökçe, M.C.; Baykal, Y.; Ata, Y. Adaptive optics effect on performance of BPSK-SIM oceanic optical wireless communication systems with aperture averaging in weak turbulence. J. Quant. Spectrosc. Radiat. Transf. 2020, 256, 107335. [Google Scholar] [CrossRef]


| Parameter | Value |
|---|---|
| Attenuation coefficient in clean ocean | |
| LC-SLM aperture diameter | |
| LC-SLM fitting error constant | |
| Rate of dissipation of turbulent kinetic energy | |
| Kolmogorov microscale | |
| Rate of dissipation of mean-square temperature | |
| Carrier frequency | |
| Laser launch power | |
| Insertion loss of MZM | |
| Insertion loss of OPA | |
| Number of OPA antenna elements | |
| Transmitter and receiver antenna directivity |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Derakhshandeh, A.; Hoeher, P.A.; Pachnicke, S. Underwater Coherent Optical Wireless Communications with Electronic Beam Steering and Turbulence Compensation Using Adaptive Optics and Aperture Averaging. Photonics 2025, 12, 268. https://doi.org/10.3390/photonics12030268
Derakhshandeh A, Hoeher PA, Pachnicke S. Underwater Coherent Optical Wireless Communications with Electronic Beam Steering and Turbulence Compensation Using Adaptive Optics and Aperture Averaging. Photonics. 2025; 12(3):268. https://doi.org/10.3390/photonics12030268
Chicago/Turabian StyleDerakhshandeh, Ali, Peter A. Hoeher, and Stephan Pachnicke. 2025. "Underwater Coherent Optical Wireless Communications with Electronic Beam Steering and Turbulence Compensation Using Adaptive Optics and Aperture Averaging" Photonics 12, no. 3: 268. https://doi.org/10.3390/photonics12030268
APA StyleDerakhshandeh, A., Hoeher, P. A., & Pachnicke, S. (2025). Underwater Coherent Optical Wireless Communications with Electronic Beam Steering and Turbulence Compensation Using Adaptive Optics and Aperture Averaging. Photonics, 12(3), 268. https://doi.org/10.3390/photonics12030268






