Abstract
Color shift keying is a modulation scheme for visible light communication that uses fixtures with three or more narrow-spectral light-emitting diodes to transmit data while fulfilling the primary function of illumination. When this modulation is used indoors, the reflectivity of the walls strongly affects the inter-channel interference and illumination quality. In this paper we present an indoor channel model that takes into account multi-wavelength propagation. This model is available as an open-source Python package. The model calculates the inter-channel interference, illuminance, correlated color temperature, and color rendering index at the receiver position. The Python package includes a module for estimating the symbol error rate. To validate the model, we computed the received power at each color photodetector for four different indoor scenarios. The model demonstrated a color rendering index of less than 15 when using IEEE-based color shift keying and non-uniform illumination on a horizontal plane. The simulation determined the required luminous flux to achieve a symbol error rate of less than when the photodetector is at the center of the indoor space and vertically below the light source. To maintain a symbol error rate less than , the luminous flux increases when the photodetector is displaced in a diagonal direction from the center of the plane.
1. Introduction
Visible light communication (VLC) is a wireless method for transmitting data via the modulation of visible light intensity. VLC offers several advantages over traditional radio frequency (RF) wireless technologies [1]. One of its primary benefits is the substantial bandwidth available within the visible portion of the electromagnetic spectrum. VLC is also a cost-effective wireless solution for two main reasons: first, the electronic components utilized for VLC are simpler and less expensive compared to the specialized circuits required for RF modulation; second, VLC can be implemented using commercial light-emitting diodes (LEDs) already deployed in lighting systems, obviating the need to develop new optical antenna devices. Additionally, VLC is immune to electromagnetic interference (EMI), as the visible spectrum is not impacted by such interference. Therefore, VLC can be effectively utilized in environments such as hospitals, where where RF technologies are restricted due to the potential for EMI to interfere with and disrupt monitoring instruments. The IEEE 802.15.7 standard [2] was introduced with the objective of standardizing the various schemes for communication with visible light and defining the modulation techniques. This standard presents three IM/DD modulation schemes: on–off keying (OOK), variable pulse position modulation (VPPM), and color shift keying (CSK). It should be noted that there are other techniques not presented in this document, including metameric modulation and orthogonal frequency division multiplexing (OFDM).
CSK employs three or more distinct wavelengths for data transmission, effectively leveraging spectral diversity to encode information. This modulation technique utilizes WDM alongside a constellation of symbols to represent bits of information [3]. The block diagram in Figure 1 illustrates a CSK modulator based on three LEDs and three photodetectors. The digital-to-analog converter (DAC), driver, and LEDs constitute the analog front-end on the transmitter side, while the photodetectors (PD), signal adapter, and analog-to-digital converter (ADC) form the analog front-end on the receiver side. Additionally, the color coding, color-to-intensity conversion, and channel estimation sequence represent the logical components required to implement the CSK modulation scheme. The channel depicted in this diagram highlights the potential interference that may arise among the three color bands.
The modulation process of CSK is carried out as follows. First, a bit stream at the input of the color coding block is mapped to a specific point in the CIE 1931 color space. In the CIE 1931 color space, a set of points represents symbols of the constellation, such as M -QAM or M-PSK. Each color point represents a combination of bits. This indicates that four symbols are needed to encode two bits per symbol, eight symbols to encode three bits, and sixteen symbols to encode four bits, with the number of symbols increasing correspondingly as the bit count per symbol increases. Figure 2 shows the CSK format for 4, 8, and 16 color points and their corresponding mapping rules according to the IEEE 802.15.7 standard [2]. As shown in the 4-CSK mapping image, the vertices of the triangle are the intrinsic color points of each band, that is, the intrinsic color point of each RGB-LED. The output of the color coding is the coordinate of the corresponding color that is mapped, which forms the input for the color-to-intensity coder block. Because the color point must be generated with a specific combination of the three -bands, this block encodes each value to the corresponding values, where represents the optical power of band i (red LED) to generate the d-color point, represents the optical power of band j (green LED), and represents the optical power of band k (blue LED). The relationship between the color coordinates and optical power values is expressed as follows:
where are the intrinsic color coordinates of band i, are the intrinsic color coordinates of band j and are the intrinsic color coordinates of band k. Based on this linear relation, the color-to-intensity encoder computes the optical power in each band to generate a specific color by including a constraint of constant total optical power, which can be expressed as
CSK is a promising modulation scheme within the realm of VLC, primarily due to its ability to enhance spectral efficiency by utilizing wavelength division multiplexing. This enables the transmission of more data within a given bandwidth, resulting in higher data rates, making CSK suitable for applications requiring substantial data throughput [4]. Regarding lighting performance, one of its key strengths lies in its capacity to modulate information by varying the intensity of multiple colored LEDs, typically red, green, and blue, without altering the overall luminous flux. This ensures non-flickering light, providing a seamless user experience for illumination while facilitating efficient data transmission. A distinct feature of CSK is its ability to deliver tunable perceived color by modifying the constellation design, which allows for adjustment of the light’s color temperature to meet various aesthetic or functional requirements in indoor environments. This flexibility in color tuning makes CSK particularly well suited for smart indoor lighting systems, where both communication and lighting quality are paramount. Furthermore, CSK schemes can achieve a color rendering index (CRI) greater than 80 [5], ensuring that the lighting accurately represents the colors of objects within the space. This is a critical factor in environments where high-quality lighting is essential, such as retail spaces, healthcare facilities, and art galleries.
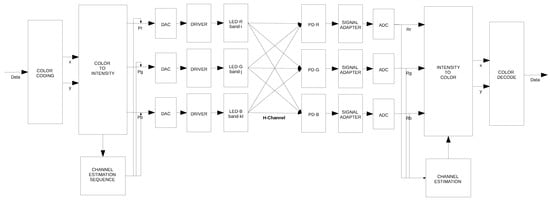
Figure 1.
Functional block diagram of the CSK modulation format.
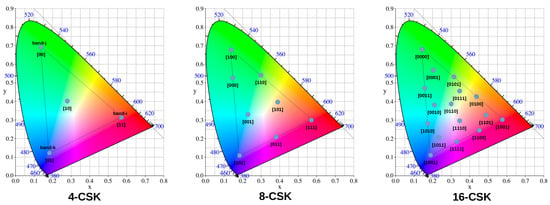
Figure 2.
Color point mapping for 4-CSK, 8-CSK, and 16-CSK.
For indoor VLC applications, the power received by the photodetector depends on both line-of-sight (LoS) and non-line-of-sight (NLoS) components. The spectral power distribution (SPD) of the NLoS component is modified according to the spectral reflectance of the objects and walls inside the indoor space. Due to the wide spectral emission of LEDs and the wide spectral response photodetectors, the power radiated by an LED at a central wavelength is detected by the photodetectors at different wavelengths. This effect is known as inter-channel interference, or cross-talk [6]. According to [2], the inter-channel interference in CSK can be modeled as a gain matrix, and determines the communication performance of the communication system; on the other hand, VLC systems for indoor applications must fulfill lighting quality requirements such as illumination level, color temperature, and color quality. These parameters also depend on the SPD of the light received from LoS and NLoS. Therefore, an adequate analytical estimation of cross-talk and lighting parameters for indoor CSK systems must consider both LoS and NLoS components.
Different channel models are widely used for indoor applications. More specialized channel models can compute the channel impulse response (CIR) function, which completely characterizes the channel performance. These models consider realistic geometries such as walls, objects, people, and furniture [7,8,9,10]. Simpler models only calculate some characteristics for empty rooms with rectangular, cylindrical, or spherical shapes [11,12,13,14,15,16]. Concerning the models used to study the CSK performance, several limitations of CSK channel models have been identified: (i) the models do not consider the spectral response of emitters, detectors, and walls when computing the received power; (ii) the models do not compute the photometric and colorimetric characteristics of the illumination; and (iii) there are no open-source computational tools to simulate these kinds of indoor WDM-VLC systems. To address these limitations, we implement a simple indoor channel model considering multi-wavelength propagation. This model was designed as a Python package and is available at PyPI. Using the recursive algorithm presented in [17], the steady-state gain for each color channel and the normalized interference gain matrix were computed for a rectangular empty room. The same model was used to compute the illuminance, correlated color temperature, and color rendering index at the receiver position. The model includes a module for estimating the symbol error rate based on the interference gain matrix and the dark current of the photodetector.
2. Recursive Channel Model
The comprehension of the diverse behaviors of light is derived from two fundamental principles: the manner in which light waves propagate through space, and the manner in which these waves interact with matter [18]. The geometric optic is a simplified model for the propagation of light. It is employed to describe the reflection and refraction of light by objects, mirrors, and lenses, assuming that the wavelength of light is much smaller than the scale of the objects with which light interacts. This model forms the foundation of the ray-tracing technique, which we employ to model indoor optical channels. The recursive channel model is founded upon the principles of geometric optics and offers a valuable methodology for simulating the propagation of light in indoor settings, including empty rectangular rooms. This method can help to simulate the effects of light transmission and reflection within the space, providing a framework for analyzing communication systems such as VLC.
The model presented in this work extends the original model introduced in [17], incorporating several key features essential for the analysis of CSK modulation. First, it estimates the power received by the detector across multiple central wavelengths. Second, the model simplifies the computation of received power at each wavelength, allowing for calculations up to ten orders of reflections. Third, based on the received power at each wavelength, the model estimates the spectrum received by the photodetector. Fourth, it evaluates inter-channel interference by analyzing the received spectrum and the spectral responsivity of the photodetectors. Fifth, photometric and colorimetric metrics such as the illuminance, colorimetric coordinates, correlated color temperature, and color rendering index are derived from the spectrum estimation. Sixth, the model accommodates custom CSK constellation designs to calculate the received spectrum and associated photometric and colorimetric metrics. Finally, the model estimates the symbol error rate as a function of the source luminous flux. These advancements represent the primary contributions of the current model compared to the original work.
The following section presents the underlying logic of the recursive model. The recursive model accounts for two types of responses when calculating the power received by the photodetector: the line-of-sight components between the light source and the photodetector (), and the non-line-of-sight components (). In Figure 3, the direct ray from the light source over a distance represents the LOS component. A ray emitted by the light source and reflected by a single reflective element before reaching the photodetector (with distances and ) is classified as a first-order NLOS component. If the ray reflects off two surfaces before reaching the photodetector, it becomes a second-order NLOS component. Thus, the CIR can be expressed as the superposition of the LoS and the infinity reflections:
where is the CIR of the components undergoing exactly k reflections, is the LoS response, and the sub-index n indicates that the CIR is computed for multiple wavelengths; thus, represents the CIR at the n-th central wavelength and the symbol t represents the variable representing time. is the following set of transmitter parameters:
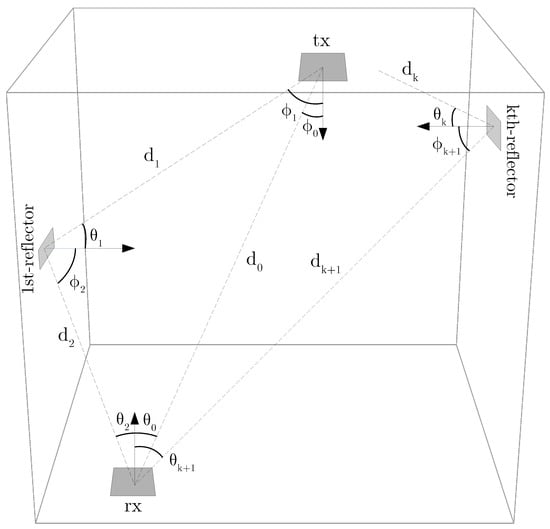
Figure 3.
Geometric notation for the indoor channel model: tx and rx represent the RGB LED and the three photodetectors, respectively, d represents the distance between the corresponding two points, denotes an output angle of a light ray at a specific point, and denotes the input angle of a light ray at that specific point.
- : Light source position vector
- : Normal vector tx position
- m: Mode number Lambertian emission
- : Luminous flux emitted by the light LED
- : Central wavelengths of LEDs
- : Full width at half-maximum
and is the set of receiver parameters:
- : Photodetector position vector
- : Normal vector receiver position
- : Sensitive area
- : Field of View
- : Spectral responsivity.
Figure 3 shows the geometry notation. The LoS and NLoS expressions are raised from this notation.
2.1. LED Source Model
VLC uses LEDs as the light source. The spatial distribution of the radiation intensity of the LED is modeled using the generalized Lambertian radiant intensity, defined as follows:
where m is Lambert’s mode number defining the directivity of the source. The order of the Lambertian emission m is related to the LED semi-angle at half-power :
2.2. Receiver Model
The receiver is modeled as an active area that collects optical radiation in incident angles smaller than the detector’s field-of-view (FOV).
2.3. LoS Propagation Model
The power received at the photodetector directly from the LED is , which is calculated according to Equation (7):
where represents the distance between the transmitter and the receiver. This equation assumes that the irradiance over the detector’s active area is constant, as is large compared to the detector’s size. The CRI of the LoS is an impulse function with time shifting and modified amplitude. The LoS response is equal for n wavelengths, as the right part of this equation does not depend on n.
2.4. NLoS Propagation Model
This recursive model computes the NLoS components by dividing the walls into smaller areas or cells , assuming a Lambertian scattering in each cell. Each of these smaller areas plays the role of an elemental receiver () and an elemental source (). It is crucial that these smaller areas be sufficiently small to ensure optimal model accuracy, although this refinement increases computational time. This method serves as an approximation of the actual propagation process, which involves an infinite number of rays traversing the space. One of these smaller areas is designated the LED source and another is designated as the photodetector, while the remaining segments represent reflective elements on each of the six walls. Figure 3 identifies the areas corresponding to the light source, photodetector, and reflective elements in yellow, blue, and gray, respectively. The channel impulse response for the reflection k can be calculated as
where is the number of cells and ∗ is the convolution operation. The convolution can be computed as a scalar multiplication, as and are impulse functions. The term can be replaced for the LED model as follows:
In accordance with [19], this definition can be expressed as follows:
where represents the reflectance factor at wavelength n of cell j () and its value. With as the total number of cells and k reflections, the number of elementary computations performed to calculate the CIR is equal to .
3. Channel Characterization Metrics
3.1. DC Gain Channel and Received Power
The DC channel gain represents the DC value of the frequency response CIR [20]. It can be expressed as
where represents the DC gain for each wavelength. The average power received by the photodetector can be computed using the DC gain and the average power transmitted by the light source , as illustrated by the relationship in Equation (15).
3.2. Inter-Channel Cross-Talk Matrix
VLC systems utilizing WDM techniques are subject to inter-channel interference, primarily due to the non-ideal spectral emissions of the LEDs and the spectral responsivity of the photodetectors (PDs). In the specific case of CSK modulation, the use of three distinct color channels in both the transmitter and receiver (typically red, green, and blue) introduces interference. For instance, when the green channel is activated to represent a particular symbol in the constellation, the receiver may not solely detect the signal in the green channel, as the red and blue channels may also capture part of the emitted radiation.
Estimating the inter-channel interference in WDM-based communication systems is essential for maintaining signal integrity, optimizing system performance, and reducing bit error rates. Accurate estimation allows for better channel separation, improved spectral efficiency, and enhanced modulation schemes such as CSK. Additionally, it enables the design of more advanced receivers capable of mitigating interference, helping to ensure reliable communication. In VLC systems where communication and illumination coexist, estimating the interference is crucial for balancing lighting quality and efficient data transmission. The system’s inter-channel cross-talk is determined by computing the inner product between the spectral power distribution received on the active area and the responsivity of the photodetector for each central wavelength, as follows:
where represents the optical-to-electrical conversion of the n-th LED radiation that arrives at the m-th photodetector. The interference cross-talk matrix is defined in Equation (17).
The spectral distribution of the received power from each LED is estimated by assuming a Gaussian shape:
where represents the full width at half-maximum, is the central wavelength of the LED, and is the received power at the central wavelength.
3.3. Illuminance
Illuminance is a photometric measure that quantifies the amount of luminous flux incident on a surface per unit area. It is expressed in lux (lx), where 1 lux equals one lumen per square meter. The illuminance represents the intensity of light perceived by the human eye on a given surface, which affecta visibility and visual comfort in different environments. In indoor lighting applications, appropriate levels of illuminance are essential for tasks requiring specific visibility conditions, contributing to both efficiency and occupant wellbeing. The total spectral power distribution received by the photodetector is computed as follows:
The illuminance E (photometric quantity) can be calculated as
where means the relative spectral luminous efficiency of the human vision as characterized by the photopic luminosity function and is a constant that establishes the relationship between the (physical) radiometric unit (Watts) and the (physiological) photometric unit (lumens).
3.4. Correlated Color Temperature
CCT refers to the color appearance of light, expressed in Kelvin (K), ranging from warm hues (lower CCT) to cool tones (higher CCT). In indoor applications, CCT is critical for optimizing visual comfort, task performance, and influencing psychological wellbeing. Appropriate CCT settings can create conducive lighting environments, improve productivity, and ensure accurate color representation, particularly in professional settings such as offices, retail spaces, and healthcare facilities. Additionally, tunable CCT in modern lighting systems supports energy efficiency and enhances user wellbeing. The correlated color temperature is calculated from the spectral power distribution received on the active area of the photodetector . The is represented in the CIExy 1931 color space using three coordinates [21]. The CCT is calculated using the method presented in [22].
3.5. Color Rendering Index
The CRI is an important colorimetric quantity that measures the fidelity with which a light source reproduces colors relative to an ideal light source of a given color temperature. By definition, a black body has a CRI of 100, making it an ideal light source. The color rendering index is determined based on the spectral power distribution received on the active area of the photodetector . The CRI is calculated using the method outlined in [23].
3.6. Symbol Error Rate
The SER is estimated according to the model for a CSK transmission shown in Equation (21). In this expression, represents the values of luminous flux at each color LED for the i-th symbol, is the value of the three currents at the photodetectors for the i-th symbol, H is the cross-talk interference matrix, and is the noise.
Following Equation (21), the model under consideration represents a noise communication channel concerning the optical-to-electrical conversion in each channel of the color detector. The thermal and shot noises are included in the received symbols. According to [24], these noises can be modeled by a normal distribution, with the standard deviation of the total noise expressed by Equation (22):
where represents the gain of the transimpedance amplifier commonly used to obtain a voltage signal from the photocurrent, is the standard deviation of the thermal noise, and is the standard deviation of the shot noise. The variance of the thermal noise depends on the temperature T, the bandwidth B, and the scaling factor , defined as follows:
where is Boltzmann’s constant. The variance of the shot noise depends on the corresponding color channel current and the dark current as follows:
4. Implementation of the Indoor Channel
The model was implemented as a Python package (version 1.0.0) Python package URL: https://github.com/jufgutierrezgo/python-vlc-rm.git, accessed on 8 October 2024. Figure 4 shows the corresponding block diagram, and the following subsections explain each block in detail.
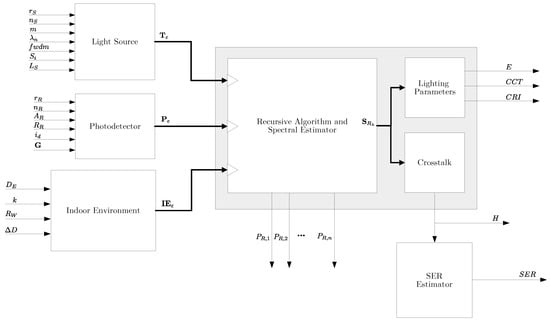
Figure 4.
Block diagram of the Python-based model.
4.1. Transmitter
This block represents the transmitter, defined by six input parameters: the position , the normal vector , Lambert’s number for the LED radiation m, the central wavelengths for each color LED, for each color LED, the specification of symbol constellation , and the luminous flux emitted by each symbol . The transmitter block provides functions that plot the spatial power distribution of the LED. Additionally, it computes the inverse luminous efficiency of the LEDs, that is, the average radiometric power emitted by each color LED according to the modulation. The encapsulation of the transmitter’s parameters is represented by in Figure 4.
4.2. Photodetector
This block represents the elements of the photodetector: its position , normal vector , active area , field-of-view , spectral responsivity , dark current , and gain . Similar to the transmitter block, the photodetector block uses multiple detectors tuned at different wavelengths. This block plots the spectral responsivity and prints the string representation of the input parameters defined by the user. The encapsulation of the photodetector’s parameters is represented by in Figure 4.
4.3. Indoor Environment
The indoor environment block represents the indoor space of the VLC system. This block is defined by the user from a set of input parameters: the size , number of reflections k, reflectance of each wall , and resolution . The resolution establishes the size of the smaller areas used to compute the NLoS propagation. An indoor environment-type object method was developed to create a grid of points on each wall. Each point is a 3D Cartesian coordinate representing the center of a smaller area. This block computes the pairwise parameters of the grid of points, including the Euclidean distance and the cosine of the two angles formed between two points. Figure 3 shows that the angles and are formed with respect to the normal vector at each point and the vector between two points. The indoor environment block computes the cosine of these angles. The encapsulation of the indoor environment’s parameters is represented by in Figure 4.
4.4. Recursive Model
The recursive model block represents the algorithms used to estimate the DC gain and received power at the different wavelengths along with the spectral power distribution, cross-talk matrix, illuminance, CRI, and CCT. The input parameters of this block consist of data encapsulated from a transmitter block, photodetector block, and indoor environment block. A description of these three sub-blocks is presented below.
4.4.1. Recursive Algorithm and Spectral Estimator
This block calculates the equations of the recursive model presented in Section 2. To do this, the differential power between cell i and cell j is calculated using Equation (25).
The result of is represented as a matrix. The response is determined by computing the LoS response between the transmitter and each of the cells, the LoS response between each of the cells and the detector, and the matrix of differential power between the cells. The model computes the function for each reflection order k using elementary computations for ; it uses bytes of memory for . The block returns the received power at different central wavelengths (). A second part of this block estimates the spectral power distribution. Because the model assumes that the received power at the detector has a roughly Gaussian shape, Equation (18) was implemented based on the input parameters of the transmitter block and the received power for each central wavelength. In Figure 4, the estimation of the spectral power distribution of the received power is represented as .
4.4.2. Cross-Talk Interference
The cross-talk block implements the discrete version of the Equation (16) to create the cross-talk interference matrix. The spectral resolution in the discrete version is equal to 1 nm in an interval of 380 nm and 780 nm.
4.4.3. Lighting Parameters
The lighting parameters block represents the three algorithms used to compute the illuminance, CCT, and CRI. The input parameters of this block consist of the previously estimated total SPD received on the detector. The Python library is employed to compute these lighting indexes [25].
4.5. SER Estimator
The SER estimator block represents the algorithm used to estimate the SER from the cross-talk interference matrix. The received symbols are estimated according to Equation (21). This block plots the SER against the flux in the transmitter and saves the results to a text file.
5. Results
The channel model implemented in Python was employed to characterize the received power of the four indoor scenarios presented in [17]. The results obtained with the Python package were compared with the results presented in [17] to validate the model. Additionally, the SER of a CSK modulation with sixteen symbols was estimated based on the cross-talk matrix, spectral responses of the LEDs, detectors, and reflectance of the walls over an AWGN channel.
5.1. Recursive Algorithm Validation
In [17], the authors simulated four configurations (A, B, C, and D) by varying the parameters of the room, the transmitter, and the detector. They reported the received power of the LoS and the first three reflection orders for configurations A and B. For configurations C and D, only the total received power was reported. Our Python-based model was used to simulate these same four scenarios; however, we kept the number of cells used to compute the recursive equations equal for all reflection orders. The results are presented in Table 1 together with the results from [17]. Table 2 shows the relative error between the results of the two models. The low relative error validates the correct operation of our recursive algorithm. Furthermore, because the Python-based model can compute the received power without exponentially increasing the amount of memory used, the received power of configurations A and B were simulated for ten reflections. Table 3 illustrates these results.

Table 1.
Simulation results of the received power of the four indoor configurations.

Table 2.
Relative power error between the model from [17] and our Python-based model.

Table 3.
Simulation with ten reflection orders for Configurations A and B using our Python model.
5.2. Cross-Talk and Lighting Characterization
Our Python model simulated an indoor environment for computing the received power, normalized cross-talk interference, and lighting parameters. Figure 5a shows the configuration for the indoor CSK-based VLC system. These parameters were simulated for six different positions of the photodetector on the receiver plane. In accordance with the specifications outlined in the IEEE standard for CSK modulation, the system employed a symbol constellation design based on a sixteen-point configuration [2]. The luminous flux per symbol was set at 5000 lm. The simulation considered the spectral power distribution of the LEDs, the spectral response of the photodetectors, the reflectance of the walls at the LEDs’ central wavelengths, and up to ten reflection orders to calculate the received power. Figure 5b shows the spectral response of the three LEDs, the spectral responsivity of the three color photodetectors, and the spectral response of two materials as presented in [7]. The walls and the floor of the rectangular room used these materials. The active area of each color detector was set at a value of 0.33 . Table 4 and Table 5 show the simulation results.
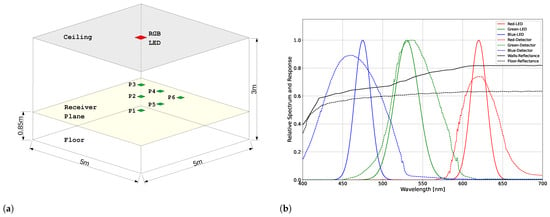
Figure 5.
Description of the indoor environment dimensions, receiver’s position, spectral response of the transmitter and photodetectors, and reflectance of the walls. (a) Indoor VLC environment with Configuration A. (b) Spectral response of RGB-LED and photodetectors and reflectance of the walls.

Table 4.
Characterization results of the DC gain and cross-talk for an indoor environment.

Table 5.
Characterization results of the indoor lighting parameters.
5.3. Symbol Error Rate Characterization
Based on the results of the received power and cross-talk interference, we estimated the SER with respect to the total luminous flux emitted by the RGB-LED at three photodetector positions. The Python package includes a module that performs a sweep of the luminous flux emitted by the LED source and then calculates the corresponding SER values. A simulation was conducted with a dark current of 1 pA for each color detector. In order to ensure that the received symbols fell within an appropriate operational range for analog–digital converters, the gain factor defined in the photodetector noise modeling (Equation (22)) was set to a value of 2 . The bandwidth was defined as 3.5 MHz under the rise time reported by the photodetector manufacturer. The estimation of the SER was conducted for CSK with sixteen symbols based on the IEEE 802.15.7 standard. Figure 6 shows the SER performance of the CSK-based VLC system in the indoor environment.
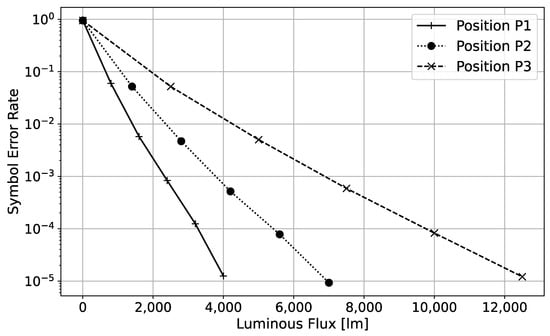
Figure 6.
SER of CSK modulation with sixteen symbols against the luminous flux emitted by the RGB-LED for three photodetector positions.
6. Discussion
According to Table 2, the received power calculated by our Python recursive algorithm presented a relative error of less than 3% for the four indoor configurations for the reference model presented in [17]. Based on these results, the recursive algorithm’s performance is considered to be validated. Additionally, the Python algorithm computed the received power with more than three reflection orders due to the reduced memory compared to [17]. The simulation with ten reflection orders for Configurations A and B revealed additional information and features that could not be elucidated in the simulation with three orders of reflection. In the case of environments with high-reflectance walls, such as Configuration A, the received power at the detector position increased by approximately 22% of the received power computed with three reflection orders. In Configuration B, however, there was an increase of only 2%. It is essential to consider high-order reflection (>3) for high-reflectance indoor environments, as the communication and illumination characteristics are strongly dependent on high-order NLoS components.
Concerning the characterization of cross-talk in the indoor Configuration A, Table 4 shows the numerical variation of the normalized cross-talk matrix when the photodetector position changes. If the cross-talk is compared between positions P1 and P3, the index changes by roughly 30% and the index changes by roughly 13%. The other photodetector positions also show that and increase if the detector is closer to the walls. Because the walls are more reflective at larger wavelengths and the received power from NLoS is greater near the walls, the photodetected current of the red and green channels increases in comparison with the blue channel. The index is always the greater value of the cross-talk matrix, as the radiometric power emitted by the blue color LED is the greatest. This occurs because one restriction of CSK modulation is that all transmitted symbols must produce the same luminous flux. The radiometric power of the blue LED for producing 1 lm is greater than the radiometric power of the red and green LEDs. This means that the luminous efficiency of the blue LED is the lowest; thus, the photo detected current generated by the blue color detector is the greatest. The inter-channel interference represented by the , , , , , and indexes is significantly low due to the narrow spectral responses of LEDs and effective alignment of these responses with those of the detectors. The importance of cross-talk characterization is that the optimization of the VLC must consider the cross-talk matrix in order to maximize the minimum Euclidean distance between the received symbols. The solved design of the CSK constellation depends on establishing certainty regarding the inter-channel interference and the DC channel gain. Until now, previous CSK optimizations have only considered a unique cross-talk matrix.
Table 4 shows the received power for every color channel when the detector’s position changes. The power reported for the receivers corresponds to a radiated power of 1 W at every color LED. The red channel presents the greatest power and the blue channel the lowest received power according to the spectral response of the wall’s reflectance. For Configuration A, as illustrated in Figure 5a, displacement of the photodetector by 1 meter with respect to the center of the receiver plane results in a reduction of received power by more than 20% across each color detector channel (red, green, and blue). The lighting parameters shown in Table 5 reveal three critical problems in the illumination quality: non-uniform illuminance over the receiver plane, low color rendering, and saturated perceived color. The non-uniform illuminance problem must be solved using more than one RGB-LED source; on the other hand, the problems regarding color rendering and perceived color depend on the CSK constellation design. These simulations were carried out using the constellation design proposed in IEEE 802.15.7. Consequently, with low luminous efficiency of the blue LED, users will perceive a saturated blue color with very low color rendering quality. The design of the CSK constellation must be studied as an optimization problem that improves the symbol error rate and ensures color rendering quality.
The communication performance of the VLC indoor system was analyzed by simulating an AWGN channel model while incorporating the effects of shot noise and thermal noise observed in the photodetector. A simulation was conducted to estimate the luminous flux required to achieve an SER of approximately for IEEE-based CSK modulation with sixteen symbols. With the receiver positioned vertically below the light source (position P1 in Figure 5a), a luminous flux of approximately 4000 lm is required to achieve an SER of approximately . At positions P2 and P3, the luminous flux increases to about 7000 lm and 12,500 lm, respectively. The final analysis demonstrates the degradation of communication quality as the light detector is moved away from the light source. The estimated luminous flux corresponds to the smaller active area of the photodetectors. Enhancing the optical power on the active area can be achieved using lenses or optical concentrators, which allow for managing reduced luminous flux at the transmitter while maintaining an appropriate SER. Additionally, the observed SER curves are based on the IEEE-standard constellation design; however, the Python package also supports customized constellation designs. Consequently, the performance of an optimal constellation design tailored to the indoor channel characteristics can be demonstrated using our Python-based model.
7. Conclusions
The primary contribution of this work is the development and validation of a novel open-source Python-based indoor channel model for CSK in visible light communication systems. The model successfully calculates the received power at each color photodetector, along with the inter-channel interference and lighting parameters within an empty rectangular room, assuming Lambertian reflective walls. Validation against a reference model demonstrated a relative error of less than 3% across four indoor configurations, with enhanced performance in handling high-order reflections (up to ten orders). Notably, for environments with high-reflectance walls, the model revealed that higher-order reflections substantially impact the received power, contributing to an increase in detected power of up to 22% in certain configurations, which emphasizes the need to account for these components in highly reflective environments.
The model also enables a detailed cross-talk analysis across different photodetector positions, showing significant variations in inter-channel interference, particularly in configurations where the photodetector was positioned near walls. These findings are essential for optimizing CSK constellations to minimize symbol error rates while maintaining acceptable illumination quality. Moreover, the model simulated the spectral responses of commercial LEDs and photodetectors, capturing key illumination challenges such as non-uniform illuminance, low color rendering index (CRI), and saturated perceived color when using the IEEE 802.15.7 standard constellation. Addressing these issues requires optimizing the CSK constellation design, particularly to improve color quality and communication performance.
In terms of communication performance, the model simulated an AWGN channel to estimate the symbol error rate (SER) under realistic noise conditions. The results showed that for a target SER of approximately , the required luminous flux increased significantly as the receiver was moved away from the light source, demonstrating the spatial sensitivity of the system. The findings also suggested that optimizing the receiver’s design through techniques such as optical concentration can reduce the required luminous flux while maintaining adequate communication quality. Additionally, the model’s flexibility allows for the simulation of custom constellation designs, offering a powerful tool for optimizing CSK systems to meet both communication and lighting performance goals in various indoor environments.
Author Contributions
Conceptualization, J.F.G. and J.M.Q.; methodology, J.F.G., D.S. and J.M.Q.; software, J.F.G. and D.S.; validation, J.F.G., D.S. and J.M.Q.; formal analysis, J.F.G.; investigation, J.F.G.; resources, J.M.Q.; data curation, J.F.G.; writing—original draft preparation, J.F.G.; writing—review and editing, J.F.G., D.S. and J.M.Q.; visualization, J.F.G.; supervision, D.S. and J.M.Q.; project administration, J.M.Q.; funding acquisition, J.M.Q. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Colombian Ministry of Science, Technology, and Innovation (Ministerio de Ciencia, Tecnología e Innovación—MINCIENCIAS) and the Universidad Nacional de Colombia, under the framework of the Bicentennial Doctoral Scholarship for Excellence, as defined in Article 45 of Law 1942 of 2018, Bogotá, Colombia.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
No new data were created or analyzed in this study. Data sharing is not applicable to this article.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Khan, L.U. Visible light communication: Applications, architecture, standardization and research challenges. Digit. Commun. Netw. 2017, 3, 78–88. [Google Scholar] [CrossRef]
- IEEE Std 802.15.7-2018; IEEE Standard for Local and Metropolitan Area Networks–Part 15.7: Short-Range Optical Wireless Communications. (Revision of IEEE Std 802.15.7-2011). IEEE: Piscataway, NJ, USA, 2019; pp. 1–407.
- King, L.R. IEEE 802.15.7 Visible Light Communication: Modulation Schemes and Dimming Support. Coll. Math. J. 2013, 44, 117–123. [Google Scholar] [CrossRef]
- Monteiro, E.; Hranilovic, S. Design and Implementation of Color-Shift Keying for Visible Light Communications. J. Light. Technol. 2014, 32, 2053–2060. [Google Scholar] [CrossRef]
- Liang, X.; Yuan, M.; Wang, J.; Ding, Z.; Jiang, M.; Zhao, C. Constellation design enhancement for color-shift keying modulation of quadrichromatic LEDs in visible light communications. J. Light. Technol. 2017, 35, 3650–3663. [Google Scholar] [CrossRef]
- Ramaswami, R.; Sivarajan, K.N.; Sasaki, G.H. Optical Networks—A Practical Perspective; Morgan Kaufmann: San Francisco, CA, USA, 2009; Volume 316, p. 400. [Google Scholar]
- Miramirkhani, F.; Uysal, M. Channel Modeling and Characterization for Visible Light Communications. IEEE Photonics J. 2015, 7, 1–16. [Google Scholar] [CrossRef]
- Miramirkhani, F.; Narmanlioglu, O.; Uysal, M.; Panayirci, E. A Mobile Channel Model for VLC and Application to Adaptive System Design. IEEE Commun. Lett. 2017, 21, 1035–1038. [Google Scholar] [CrossRef]
- Ramirez-Aguilera, A.M.; Luna-Rivera, J.M.; Guerra, V.; Rabadan, J.; Perez-Jimenez, R.; Lopez-Hernandez, F.J. A generalized multi-wavelength propagation model for VLC indoor channels using Monte Carlo simulation. Trans. Emerg. Telecommun. Technol. 2019, 30, 1–13. [Google Scholar] [CrossRef]
- Kalikulov, N.; Dautov, K.; Kizilirmak, R.C. Location estimation for DCO-OFDM based VLC in realistic indoor channel. In Proceedings of the 11th IEEE International Conference on Application of Information and Communication Technologies, AICT 2017-Proceedings, Moscow, Russia, 20–22 September 2017; pp. 1–4. [Google Scholar] [CrossRef]
- Zhang, M.; Zhang, Y.; Yuan, X.; Zhang, J. Mathematic models for a ray tracing method and its applications in wireless optical communications. Opt. Express 2010, 18, 18431. [Google Scholar] [CrossRef] [PubMed]
- Chun, H.; Chiang, C.J.; O’Brien, D.C. Visible light communication using OLEDs: Illumination and channel modeling. In Proceedings of the 2012 International Workshop on Optical Wireless Communications, IWOW 2012, Pisa, Italy, 22 October 2012; pp. 8–10. [Google Scholar] [CrossRef]
- Sarbazi, E.; Uysal, M. Ray Tracing Based Channel Modeling for Visible Light Communications. In Proceedings of the 2014 22nd Signal Processing and Communications Applications Conference (SIU), Trabzon, Turkey, 23–25 April 2014; pp. 702–705. [Google Scholar]
- Muhammad, S.S. Delay profiles for indoor diffused visible light communication. In Proceedings of the 13th International Conference on Telecommunications, ConTEL 2015, Graz, Austria, 13–15 July 2015; pp. 1–5. [Google Scholar] [CrossRef]
- Becerra, R.; Azurdia-Meza, C.A.; Palacios Játiva, P.; Soto, I.; Sandoval, J.; Ijaz, M.; Carrera, D.F. A Wavelength-Dependent Visible Light Communication Channel Model for Underground Environments and Its Performance Using a Color-Shift Keying Modulation Scheme. Electronics 2023, 12, 577. [Google Scholar] [CrossRef]
- Palacios Játiva, P.; Azurdia-Meza, C.A.; Sánchez, I.; Zabala-Blanco, D.; Dehghan Firoozabadi, A.; Soto, I.; Seguel, F. An Enhanced VLC Channel Model for Underground Mining Environments Considering a 3D Dust Particle Distribution Model. Sensors 2022, 22, 2483. [Google Scholar] [CrossRef] [PubMed]
- Barry, J.R.; Kahn, J.M.; Krause, W.J.; Lee, E.A.; Messerschmitt, D.G. Simulation of Multipath Impulse Response for Indoor Wireless Optical Channels. IEEE J. Sel. Areas Commun. 1993, 11, 367–379. [Google Scholar] [CrossRef]
- Dutre, P.; Bekaert, P.; Bala, K. Advanced Global Illumination; AK Peters/CRC Press: Natick, MA, USA, 2018. [Google Scholar]
- Lee, K.; Park, H.; Barry, J.R. Indoor channel characteristics for visible light communications. IEEE Commun. Lett. 2011, 15, 217–219. [Google Scholar] [CrossRef]
- Al-Kinani, A.A.A. Channel Modelling for Visible Light Communication Systems. Ph.D. Thesis, Heriot-Watt University, Edinburgh, EH, USA, 2018. [Google Scholar]
- Ohno, Y. CIE Fundamentals for Color Measurements. In Digital Printing Technologies; IS&T’s NIP16; IS&T: Vancouver, CA, USA, 2000; p. 1. Available online: https://tsapps.nist.gov/publication/get_pdf.cfm?pub_id=841491 (accessed on 8 October 2024).
- Ohno, Y. Practical use and calculation of CCT and Duv. Leukos 2014, 10, 47–55. [Google Scholar] [CrossRef]
- International Commission on Illumination. Colorimetry, 4th ed.; CIE Central Bureau: Vienna, Austria, 2018. [Google Scholar]
- Gutierrez, J.F.; Sandoval, D.; Quintero, J.M. An Analytical Performance Study of a Non-Line-of-Sight Optical Camera Communication System Based on Rolling Shutter and Color Shift Keying. In Proceedings of the 2023 IEEE Sustainable Smart Lighting World Conference & Expo (LS18), Mumbai, India, 8–10 June 2023; pp. 1–6. [Google Scholar] [CrossRef]
- Smet, K.A. Tutorial: The LuxPy Python toolbox for lighting and color science. Leukos 2020, 16, 179–201. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).