Abstract
Utilizing the phase-matching conditions of inter-modal four-wave mixing in an elliptical-core few-mode fiber supporting three non-degenerate modes, we experimentally demonstrate schemes for generating orbital-angular-momentum (OAM)-entangled photon pairs with high mode purity and for achieving highly mode-selective frequency conversion of beams in OAM-compatible (LP11a, LP11b) mode basis. These techniques expand the toolbox for using OAM modes in both classical and quantum communications and information processing.
1. Introduction
Spatial modes (e.g., those of multimode fibers and waveguides) represent an important degree of freedom for increasing the capacity of both classical and quantum communications [1,2]. For both communication types, using different spatial modes as separate communication channels yields the capacity increase proportional to the number of modes. Alternatively, in the quantum case, the use of entanglement in multiple degrees of freedom (e.g., in polarization [3], frequency [4], time-bin [5,6], and spatial modes) may enable new communication and networking protocols relying on quantum information encoding in high-dimensional Hilbert space. While polarization, frequency, and time-bin entanglement generation has already been implemented in an integrated platform compatible with low-loss transport over optical fiber, the spatial entanglement still relies on bulk-crystal-based setups, e.g., spatially- or orbital-angular-momentum- (OAM) entangled photons have been generated in crystal platforms and transported over hollow-core photonic crystal fiber [7], a few-mode fiber (FMF) [8], and vortex fiber [9]. On the other hand, the FMF itself has been recently gaining traction as a platform for nonlinear-optical signal processing based on inter-modal four-wave mixing (IM-FWM) [10]. This is because the mature and flexible fiber design and manufacturing employed in making the FMF provide wide options for mode- and dispersion-engineering, as well as for an excellent mode match to the FMFs used in low-loss transmission links. IM-FWM in FMF has been used for tunable wavelength conversion [11,12,13] and correlated photon-pair generation [14,15,16], but no attempts of spatial-mode entanglement have been made yet. We have recently described a novel scheme for the generation of spatial-mode-entangled photon pairs in LP01 and LP11 modes directly in the FMF using a combination of two IM-FWM processes [17,18,19]. In the present paper, we extend this scheme to LP11a and LP11b modes, which can enable the generation of OAM-entangled photon pairs. A brief preliminary report on this work was given in a conference paper [20].
Another requirement for communications with multiple spatial modes is the availability of dynamically reconfigurable spatial-mode demultiplexers. In classical communications, such a demultiplexer, in addition to separating individual spatial channels, can also undo the mode mixing taking place in the transmission fiber [21], which relaxes the requirements for electronic processing of the received signals. In quantum communications using high-dimensional Hilbert space for encoding, the same demultiplexer enables projective measurements that can alternate between mutually unbiased spatial-mode bases. In either case, the low loss and low crosstalk of the demultiplexer are important. Previously, we have proposed [22] and experimentally demonstrated such a demultiplexer in a two-mode LiNbO3 waveguide [23,24], where, by adjusting the spatial profile of a 1560-nm pump wave, we could selectively upconvert either mode TM00 or mode TM01, or any superposition of these two modes of a 1540-nm signal to TM01 mode at 775 nm, for both classical [23] and single-photon-level [24] signals. More recently, we have demonstrated a scheme of similar functionality (mode demultiplexing by mode-selective frequency conversion) in a χ(3) nonlinear medium by using a combination of two IM-FWM processes in an FMF [25,26,27,28,29,30]. Compared to the LiNbO3 platform, nonlinear FMFs can offer wider design options for mode- and dispersion-engineering and better mode match to the FMFs used in transmission links. The IM-FMF allows for the dynamic reconfigurability of the demultiplexer’s mode basis by controlling the spatial modes and wavelengths of the pumps and taking advantage of mode-selective phase-matching conditions of IM-FMF. Our results [25] have shown good crosstalk performance (mode selectivity) for each of the two required IM-FWM processes individually. In [26,27], we implemented both processes simultaneously and demonstrated their combined ability to handle any superposition of LP01 and LP11a modes in the two-mode signal space. In this paper, expanding on our brief preliminary report at a conference [31], we investigate the mode-selective frequency conversion in the OAM-compatible basis of LP11a and LP11b modes.
Hence, this paper presents the experimental investigation of nonlinear-optical signal processing in the FMF in the basis of LP11a and LP11b modes, which can be used to construct OAMl modes with orbital angular momentum l = ±1: OAM±1 = (LP11a ± i LP11b)/2½. The experimental progress toward OAM-entangled photon-pair generation is described in Section 2.1. Section 2.2 reports the experimental demonstration of spatial-mode-selective frequency conversion in this mode basis. In both Section 2.1 and 2.2, the demonstrations are performed with a classical signal. Section 3 presents the discussion and conclusions about this work.
2. Experimental Investigation of OAM-Compatible χ(3) Nonlinear Processes for Spatially-Entangled State Generation and Spatial-Mode-Selective Frequency Conversion in FMF
The use of nonlinear-optical devices for spatially-multimode classical and quantum information processing was pioneered by the demonstration of noiseless image amplification by a spatially-broadband phase-sensitive optical parametric amplifier [32]. After this early experiment, theoretical understanding has been developed for spatially-broadband parametric amplification [33,34] and frequency conversion [35] in bulk-crystal media. The theory development culminated in the derivation of the spatial modes of such bulk devices [36,37,38], which undergo independent evolutions without coupling to one another. These modes, closely related to the Schmidt modes used in the analysis of spontaneous parametric down-conversion, are obtained by a singular-value decomposition of the Green’s function describing the light propagation in the crystal, which is a technique previously used to analyze the quantum noise of solitons in optical fiber [39,40,41]. The understanding of complex spatial interactions in the bulk nonlinear-optical devices has soon led to the proposals of image amplifiers [22,42] and mode-selective frequency converters [22] based on multimode waveguides in χ(2) media. The latter have been subsequently experimentally demonstrated [23,24]. Given that FMFs provide great flexibility in mode- and dispersion-engineering, they are excellent candidates for achieving similar functionality in a χ(3) nonlinear medium. Hence, we have demonstrated the spatial-mode-selective frequency conversion [25,26,27,28,29,30] and key processes for spatially-entangled photon-pair generation [16,17,18,19,30] in the LP01 and LP11 mode basis in the FMF. Below we extend this approach to OAM-compatible LP11a and LP11b mode basis. The intra- and inter-modal Kerr nonlinearities [43], Raman interactions [44], and a few-mode parametric amplification [45] in FMFs have also been studied recently.
As the nonlinear medium for the IM-FWM in all our experiments, we have chosen a graded-index elliptical-core FMF [12], to be referred to as three-mode fiber (TMF) below, which supports three non-degenerate spatial modes: LP01, LP11a, and LP11b. The TMF’s key parameters are as follows [12]: The optical loss is about 0.2 dB/km for all of the modes; the 10% core ellipticity breaks the LP11 mode degeneracy and keeps the distributed crosstalk between any two modes below –27 dB; the calculated effective areas of the LP01 and the LP11a,b modes are 89 μm2 and 125 μm2 at 1550 nm, respectively, resulting in a rather modest value of the nonlinear constant γ01/11 = 0.7/W/km responsible for IM-FWM between LP01 and the LP11 modes and limiting the conversion efficiencies achievable with our available pump power.
2.1. Experiments Toward Generation of OAM-Entangled Photon Pairs
The spatial-mode entanglement scheme is realized by a combination of two IM-FWM processes, Processes 1 and 2, as shown in Figure 1a. The two employed IM-FWM processes are:
- IM-FWM process 1: With the assistance of pump 1 in mode LP11a and pump 2 in mode LP11b, a signal photon is created in mode LP11a at frequency νs, while the idler photon is created in the orthogonal mode LP11b at frequency νi.
- IM-FWM process 2: In the presence of pump 3 in mode LP11a and pump 4 in mode LP11b, a signal photon at frequency νs is created in mode LP11b, whereas the idler photon is created in the orthogonal mode LP11a at frequency νi.
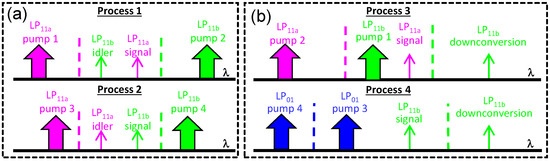
Figure 1.
(a) Two parametric processes, whose combination enables OAM-entangled photon-pair generation in the TMF. (b) Two parametric processes, whose combination enables OAM-compatible mode-selective frequency conversion in the TMF. The colored dashed line represents the location of the wavelength representing the average frequency of the two waves belonging to the same spatial mode of that color.
With all four pumps present, processes 1 and 2 take place simultaneously. Their photon pair generation probabilities can be equalized by adjusting relative powers of the two pump pairs, which results in the generation of the maximally-entangled state |LP11b⟩s|LP11a⟩i + eiφ|LP11a⟩s|LP11b⟩i, where phase φ can be changed by varying the phase difference Δφ = (φp1 + φp2) − (φp3 + φp4) between the two pairs of pumps. For φ = π, this state is equivalent to the OAM-entangled state |l = +1⟩s| l = −1⟩i − | l = −1⟩s| l = +1⟩i, where l is the orbital quantum number.
For each of the two processes in Figure 1a, both energy conservation and momentum conservation are required for the nonlinear interaction. Equation (1) describes the energy conservation relationship for the processes 1 and 2:
Here, νp1, νp2, νp3, and νp4 denote the frequencies of pumps 1, 2, 3, and 4, respectively. The momentum conservation is satisfied by the phase-matching condition for the four interacting waves. This condition for IM-FWM involving two spatial modes has been obtained in [10] and consists of two requirements:
- The number of photons in each spatial mode should be preserved (i.e., if the signal and idler are in two different spatial modes, then one pump should be in the signal’s spatial mode, and the other pump—in the idler’s mode);
- The group velocity at the average frequency of the two waves in one mode (LP11a in our case) should be equal to the group velocity at the average frequency of the two waves in the other mode (LP11b in our case).
These average frequencies, converted to wavelengths, are shown by the dashed lines in Figure 1a. Figure 2 shows measured relative inverse group velocities (RIGV) 1/vg of LP01, LP11a, and LP11b modes of our TMF. The curve of LP11b is approximately parallel to the curve of LP11a and is horizontally shifted by ~17 nm (Δν1 = 2.1 THz), i.e., the phase-matching is satisfied when the dashed lines in Figure 1a are separated by 17 nm. This phase-matching condition [10] can be expressed as the following equation:
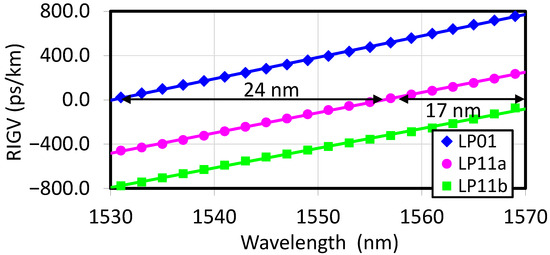
Figure 2.
Measured relative inverse group velocity (RIGV) data for the modes of our TMF.
Assuming known signal and idler frequencies, we can solve the system of Equations (1) and (2) for the four pump frequencies required for the OAM entanglement generation:
Thus, the energy conservation (1) and momentum conservation (2) impose 4 constraints on the frequencies of the 6 involved waves, shown by Equation (3), and any two frequencies that are not separated by Δν1 [i.e., are shown on different lines of Equation (3)] can be arbitrarily chosen. The remaining 4 frequencies are obtained from Equation (3).
In our experimental demonstration, the wavelengths of the signal and idler are chosen to be at 1564.8 nm and 1558.4 nm, respectively, which results in pumps 1, 2, 3, and 4 placed at 1541.3, 1582.4, 1547.3, and 1576.1 nm, respectively, as calculated by Equation (3). The experimental schematic is shown in Figure 3. The input signal and pumps (Ando AQ4321, Ando AQ8201-13E, and three Photonetics 3642 HE1550 tunable external cavity lasers) are carved by intensity modulators (standard telecom 10 GHz modulators from JDSU, Covega, and Fujitsu) into 10-ns-long flat-top pulses with a 10-MHz repetition rate (10% duty cycle). The optical pulses are amplified by telecom-grade C- and L-band erbium-doped fiber amplifiers (EDFAs) and coupled from fiber to free space using three fiber collimators.
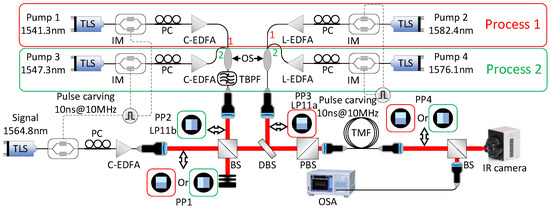
Figure 3.
Experimental setup for investigation of OAM entanglement generation. TLS: tunable laser source; PC: polarization controller; C-EDFA: C-band erbium-doped fiber amplifier; L-EDFA: L-band erbium-doped fiber amplifier; TBPF: tunable optical bandpass filter; OS: optical switch; IM: intensity modulator; PP: phase plate; BS: beam splitter; DBS: dichroic beam splitter; PBS: polarizing beam splitter; TMF: three-mode fiber; OSA: optical spectrum analyzer; IR: infrared.
In process 1, signal and pump 1 are combined by a beam splitter (BS) in free space, and their spatial modes are individually converted to LP11a by two corresponding phase plates (PPs), PP1 and PP2, respectively. One half of the glass-made PP is covered with a photoresist to introduce an additional π phase shift to the incident light wave, compared to the other half that is not covered by the photoresist. By placing the photoresist boundary at the center of the incident fundamental Gaussian beam (LP01 mode), we can convert it into LP11 mode. By rotating the PP, LP01 can be converted into LP11a, LP11b, or a superposition of these two modes. Pump 2 is converted to LP11b mode by a phase plate PP3 and combined with signal and pump 1 via a dichroic beam splitter (DBS). The three waves pass through a polarization beam splitter (PBS) to ensure their polarizations are aligned. After the PBS, the three waves are coupled into a 1-km-long TMF by a fiber collimator. The TMF output is coupled to free space by another fiber collimator, followed by a free-space BS, which sends half of the output light to an infrared camera, while the remaining half is coupled by a fiber collimator into a standard single-mode fiber (SSMF) connected to the optical spectrum analyzer (OSA). In this arrangement the OSA measures the LP01 mode output of the TMF, since only this mode can couple into the fundamental mode of the SSMF. By inserting phase plate PP4 prior to the SSMF coupling, the LP11a or LP11b mode output of TMF can be converted into LP01 mode, with its spectrum observed on the OSA. Thus, the OSA can independently measure the LP01, LP11a, and LP11b outputs (referred to as “output ports” below) of the TMF.
In this proof-of-concept experiment, we study the processes 1 and 2 separately. In process 2, pump 1 and pump 2 are replaced by pump 3 and pump 4, respectively, by an optical switch (OS). For this process, the signal’s spatial mode is changed from LP11a to LP11b mode by rotating PP1 by 90°. To maximize IM-FWM, we co-polarize all three input waves entering the TMF. In future experiments, the OS will be replaced by wavelength multiplexers to enable the combination of processes 1 and 2 by the simultaneous presence of all 4 pumps.
We characterize the idler mode purity by comparing the idler power in the target spatial mode and the idler power in the undesired spatial mode of the TMF. Therefore, the purity of process 1 is calculated by the ratio of the power between the idler in LP11b mode and the idler in LP11a mode, and the mode purity for process 2 is calculated by the ratio of powers between the idler in LP11a mode and the idler in LP11b mode.
To show that these two parametric processes are only sensitive to a specific spatial mode of the signal, we measure their spatial-mode selectivity by comparing the idler power generated in the desired process (idler mode LP11b with the input signal in the mode LP11a for process 1, idler mode LP11a with the input signal in the mode LP11b for process 2) and the idler power in the desired mode, but generated in the undesirable process, i.e., with the input signal of the same power as before, but in the wrong mode (signal mode LP11b for process 1, signal mode LP11a for process 2).
Figure 4 shows the spectra at the LP11a (blue traces) and LP11b (magenta traces) output ports of the TMF for processes (a) 1 and (b) 2. The significant difference in the idler powers of the two traces indicates high spatial-mode purity of the idler, which is better than 22 dB for process 1 and better than 31 dB for process 2 (after subtracting the background amplified spontaneous emission noise). The average powers inside the TMF are 0 dBm for the signal in all cases and 15, 9.5, 17, and 7.5 dBm for pumps 1, 2, 3, and 4, respectively.
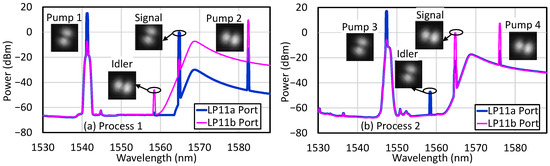
Figure 4.
Optical spectra, measured at the LP11a (blue traces) and LP11b (magenta traces) output ports of the TMF for processes (a) 1 (signal in LP11a mode) and (b) 2 (signal in LP11b mode).
The easily measurable signal-to-idler classical conversion efficiency (CE, measured as the ratio of the output idler and input signal powers) is given by CE = g − 1 = ⟨n⟩, where g is the phase-insensitive parametric gain, and ⟨n⟩ is the average number of generated spontaneous parametric photons per mode, also representing the probability of a single spontaneous signal-idler photon pair generation for our case of CE << 1. In the perfectly phase-matched regime CE = sinh2[2γ(P1(3)P2(4))1/2L] ≈ 4γ2P1(3)P2(4)L2 << 1, where L is the fiber length, Pi(j) is the power of the pump with index i = 1, 2 (for process 1) or j = 3, 4 (for process 2), and γ = n2ω/(cAeff) is the nonlinear constant, with Aeff being the effective area of the nonlinear interaction, equal to the inverse of the intensity overlap integral between the modes LP11a and LP11b. We require CE = ⟨n⟩ << 1 to ensure that the probability of simultaneous generation of two pairs ⟨n⟩2 is negligibly small.
In Figure 4, CEs are –46.0 dB and –47.0 dB for the processes 1 and 2, respectively. The CEs of the undesirable processes, separately measured by injecting the signal into the wrong mode (LP11b for process 1 and LP11a for process 2), are suppressed by more than 30.0 dB and 26.9 dB, compared to processes 1 and 2, respectively. This indicates high spatial-mode selectivity of our IM-FWM processes.
The presence of the TMF group velocity dispersion leads to gradual walk-off among the 4 interacting waves in each process. The largest group walk-off is between the signal and idler waves in process 1, which in our case amounts to ~430 ps at the end of the fiber. For 10-ns-long pump pulses used in our experiment, this is equivalent to a 4.3% reduction in the state fidelity (from 100% to 95.7%), which could be improved by using shorter fiber (custom-made highly nonlinear FMF) and higher pump power.
To summarize, we used a classical seed signal to experimentally verify the mode-selective properties of two IM-FWM parametric processes, in which a low-gain parametric amplifier in TMF couples the LP11a signal to the LP11b idler and the LP11b signal to the LP11a idler. In the spontaneous regime, the combination of these two processes with a particular relative phase difference Δφ between the two pump pairs would generate OAM-entangled signal-idler photon pairs. We have demonstrated the conversion efficiencies of at least –47 dB with mode selectivity of about 27 dB or better, producing the idler beam with mode purity of 22 dB or better. The demonstrated CEs are high enough for practical applications and can be further increased to CE~1% (higher CEs than that are not desirable due to a noticeable two-pair generation probability) by raising the four pump powers while still keeping the total power below 1W. The next step will be to optimize the pump multiplexing scheme, both to minimize the losses and to stabilize the pump phase difference Δφ. Spontaneous regime would, in addition, require strong suppression of the amplified spontaneous emission of the pump beams at signal and idler frequencies, as well as narrow bandpass filtering of the output to minimize the contribution of the Raman noise [24]. It is worth noting that the IM-FWM process permits modal phase-matching of signal/idler and pumps separated by more than one Raman Stokes shift [14], which can potentially mitigate any noise effects from the parasitic Raman interactions.
2.2. Experiments on OAM-Compatible Spatial-Mode-Selective Frequency Conversion
The spatial-mode-selective frequency conversion is realized by a combination of two IM-FWM processes, shown in Figure 1b:
- In the presence of pump 1 in mode LP11b and pump 2 in mode LP11a, process 3 transfers the signal in mode LP11a to a wavelength-converted beam in mode LP11b.
- In the presence of pumps 3 and 4 in mode LP01, process 4 transfers the signal in mode LP11b to the same wavelength-converted beam in mode LP11b.
When both processes occur simultaneously, any superposition of signal modes LP11a and LP11b, including the OAM modes (LP11a ± i LP11b)/21/2, can be selectively converted to the new frequency, while the orthogonal superposition is left untouched at the signal frequency. The relative mode weights in the selected superposition are chosen by the relative strengths of processes 3 and 4, which are, in turn, determined by the products of powers of pumps 1 and 2 (for process 3) and of pumps 3 and 4 (for process 4). The relative phase between the modes in the superposition is determined by the pump phase difference Δφ = (φp1 − φp2) − (φp3 − φp4). For example, Δφ = π/2 selects the mode with OAM l = ±1. Note that, if both pumps in either process are identically phase-modulated to suppress stimulated Brillouin scattering, this modulation does not disturb the relative phase Δφ and does not broaden the spectra of the signal and wavelength-converted beams. By adjusting Δφ and relative pump powers of processes 3 and 4, one can demultiplex any spatial mode from (LP11a, LP11b) mode space by converting it to a new wavelength. Unlike the linear-optics-based spatial-mode demultiplexers such as photonic lanterns or multi-plane light converters [46], this demultiplexer can be dynamically reconfigured to select another mode without introducing any extra loss in the signal path.
To calculate the phase-matching conditions for the processes 3 and 4, we need to use the horizontal shifts of ~17 nm (Δν1 = 2.1 THz) between the RIGV curves for LP11a and LP11b modes and ~24 nm (Δν2 = 3.0 THz) between the curves for LP01 and LP11a modes in Figure 2. The energy conservation and phase-matching conditions (momentum conservation) are shown, respectively, by Equations (4) and (5) below:
Here, the subscript “WC” denotes the frequency of the wavelength-converted beam. From Equations (4) and (5), we can find 4 constraints on the frequencies of the 6 waves involved:
Here, two frequencies, νs (or νp3) and νp1 (or νp2), can be arbitrarily chosen, whereas the frequencies of the four remaining waves are calculated from Equation (6).
In the experiment, the signal and converted-beam wavelengths are 1583.0 nm and 1601.1 nm, respectively, while the wavelengths of pumps 1, 2, 3, and 4 are 1558.3, 1541.1, 1560.1, and 1542.9 nm, respectively. Figure 5 shows the experimental setup for OAM-compatible spatial-mode-selective frequency conversion. All pumps and signals are carved into 10-ns-long flat-top pulses, and pumps are amplified with telecom-grade C-band EDFAs using an arrangement similar to that described in Section 2.1. Pump 2 is converted to LP11a mode by a phase plate PP1, combined with the signal in free space by a dichroic beam splitter DBS, and then combined with LP01-mode pumps 3 and 4 by a free-space beam-splitter BS1. Pump 1 is converted to LP11b mode by a phase plate PP2, combined with these 4 beams by BS2, and coupled into the 1-km-long TMF by a collimator preceded by a PBS. The TMF output is coupled to the free space via a fiber collimator and is split between an infrared camera and another fiber collimator that is connected to the optical spectrum analyzer OSA by SSMF. In this arrangement, the OSA measures the spectrum of the LP01 mode at the TMF output (the only mode that couples to the SSMF). We will refer to this as the measurement at “the LP01 output port” of the TMF. By inserting a phase plate PP4 or PP5 prior to the SSMF collimator, we can convert LP11a or LP11b mode, respectively, to the SSMF mode. That way, we can select any output mode (“output port”) of the TMF to be measured by the OSA. The spatial mode of the signal can be gradually varied from LP11a to LP11b by rotating the phase plate PP3 (when it is at 0°, it generates 100% LP11a mode, and when it is at 90°, it generates 100% LP11b mode; in the intermediate positions, it generates various two-mode superpositions). To maximize IM-FWM, we co-polarize all three input waves in each process with the help of the PBS.
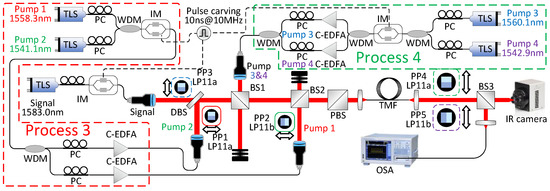
Figure 5.
Experimental setup for OAM-compatible spatial-mode-selective frequency conversion. TLS: tunable laser source; PC: polarization controller; WDM: wavelength-division multiplexer; C-EDFA: C-band erbium-doped fiber amplifier; IM: intensity modulator; PP: phase plate; BS: beam splitter; DBS: dichroic beam splitter; PBS: polarizing beam splitter; TMF: three-mode fiber; OSA: optical spectrum analyzer; IR: infrared.
The mode selectivity of each individual process is quantified by comparing the conversion efficiency (CE) for the “desired” signal mode (LP11a in process 3, LP11b in process 4) to the CE for the “undesirable” signal mode (LP11b in process 3, LP11a in process 4). The gray and blue traces in Figure 6 show the ratio of these two efficiencies (inverted crosstalk) for process 3 to be 23.8 dB (after subtracting the background amplified spontaneous emission noise). Inverted crosstalk for process 4 is 29.2 dB, as shown in Figure 7a. The “desired” CEs are –43.2 dB and –43.1 dB for the processes 3 and 4, respectively. The mode purity of the converted beam can be quantified by the ratio between its powers measured at the correct (LP11b) and wrong (LP11a) output ports [only the correct output port LP11b is shown in Figure 6 and Figure 7a], which is 31.1 dB for process 3 and 27.3 dB for process 4.
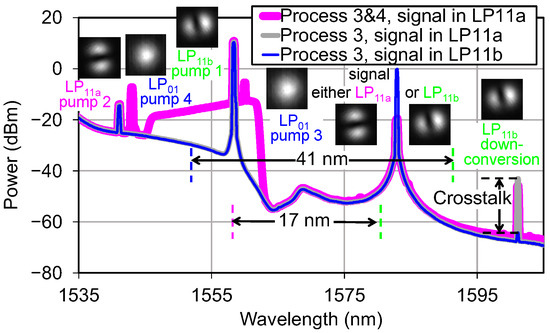
Figure 6.
Spectra at the LP11b output port for process 3 alone (gray, blue) and processes 3 and 4 combined (magenta).
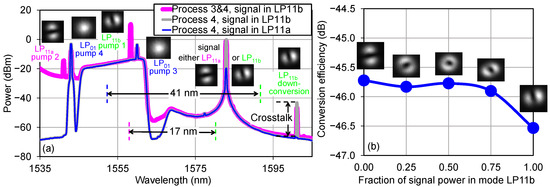
Figure 7.
(a) Spectra at the LP11b output port for process 4 alone (gray, blue) and processes 3 and 4 combined (magenta). (b) Conversion efficiencies (CEs) for various signal mode superpositions.
Figure 6 and Figure 7a also show the spectra of the LP11b output port for processes 3 and 4 taking place simultaneously (i.e., when all 4 pumps are present) by the magenta traces. Average powers inside the TMF are 0 dBm for the signal and 10.5, 5.5, 9, and 7 dBm for pumps 1, 2, 3, and 4, respectively. At these powers, the CEs for processes 3 and 4 are nearly equal. If we had stable phase Δφ = (φp1 − φp2) − (φp3 − φp4), we would have been able to select for wavelength conversion a superposition of LP11a and LP11b signal modes with a specific relative phase, e.g., an OAM mode. Since the phase Δφ is also responsible for the direction of ωp1 + ωp4 = ωp2 + ωp3 phase-sensitive parametric amplification process among the 4 pumps (this process may require coupling a small fraction of pump 1 into the LP11a mode to meet the IM-FWM selection rules), it can be stabilized with a single phase-locking loop by monitoring one of the pump waves. However, such stabilization, typically relying on mutually coherent pumps derived from an optical frequency comb, is out of the scope for this paper, and our Δφ fluctuates randomly on a 0.1–1 µs scale. This means that we can observe mode-independent wavelength conversion of the signal, as both LP11a and LP11b components of any signal superposition are independently converted to LP11b mode at the new frequency and then added incoherently. This is illustrated in Figure 7b, which shows nearly the same CEs (within a 0.8 dB range from one another), measured for various signal superpositions with a weight of the LP11b component ranging from 0 to 100%.
To summarize, we have proposed and experimentally implemented two simultaneous IM-FWM processes enabling OAM-compatible mode-selective frequency conversion. We have achieved the mode-selective wavelength conversion efficiencies of about –43 dB with better than –23 dB crosstalk for modes LP11a and LP11b. For various superpositions of these modes, the results show that, in the absence of the pump phase stabilization, our scheme produces mode-independent signal frequency conversion in OAM-compatible (LP11a, LP11b) mode space. Since the data symbol duration should be longer than the larger of the intra-modal and inter-modal group delays between the original and converted signals (335 ps in our case), the use of a shorter FMF with higher nonlinearity is desirable for future optical communication applications. Such a customized, highly nonlinear FMF with a reduced core size, along with a high-power EDFA used for the pumps, would also help to increase the CEs to practically important levels.
3. Discussion and Conclusions
This work extends the nonlinear-optical signal processing to classical and quantum communication applications involving OAM modes. It employs IM-FWM processes in few-mode fibers, which enable both spatial-mode and wavelength selectivity in wavelength converters and parametric photon-pair generators. These features are important for increasing the capacity of both classical and quantum communication links by employing multiple OAM spatial modes.
For the OAM-entangled photon-pair generation, we have designed and experimentally demonstrated with a classical seed signal two mode-selective IM-FWM processes that couple signal and idler photons in the orthogonal modes of the OAM-compatible (LP11a, LP11b) mode space. We have measured the conversion efficiencies of at least −47 dB with high mode selectivity of about 27 dB or better, producing the idler beam with mode purity of 22 dB or better. At our pulse repetition rate, this corresponds to a ~200 pairs per second generation rate for the spontaneous (unseeded) regime.
For the mode-selective wavelength conversion, we have designed and experimentally demonstrated a combination of two simultaneous mode-selective IM-FWM processes that can potentially selectively wavelength-convert any signal mode superposition in the OAM-compatible (LP11a, LP11b) mode space without perturbing the orthogonal mode superposition. For each process separately, we have achieved the mode-selective wavelength conversion efficiency of about −43 dB with low crosstalk of less than −23 dB. For both processes running simultaneously, in the absence of active stabilization of the pump phase, we have achieved mode-independent signal frequency conversion in the OAM-compatible (LP11a, LP11b) mode space. The mode-selective wavelength conversion can be used for projective measurements at the receiver side of quantum communication links, as well as for spatial-mode de-multiplexing in classical communication systems and networks. In the latter case, in contrast to wavelength conversion in conventional highly-nonlinear fibers, IM-FWM in FMF uses modal phase-matching and does not require operation in the vicinity of zero-dispersion wavelength, which mitigates inter-channel nonlinearities (four-wave mixing, cross-phase modulation) that are otherwise capable of degrading the performance of WDM communication systems.
In the future work, the key relative phase between the pump pairs needs to be stabilized, and the loss in pump multiplexing arrangement needs to be reduced. The former can be achieved by deriving the pump waves from different components of an optical frequency comb and controlling one of their phases by a relatively slow feedback loop driven by a particular IM-FWM product among the pumps. The use of a frequency comb generated either electro-optically or nonlinear-optically [47] would eliminate the issues with frequency stability and linewidths of 4 independent pump lasers, which could otherwise require a complex combination of frequency-locking and fast phase-locking loops. The spatial mode multiplexing of the pumps can be facilitated by either a photonic lantern with low insertion loss and high crosstalk or a multi-plane light conversion [46] with higher insertion loss and lower crosstalk, depending on the overall loss budget of the system.
Author Contributions
M.V.: concept; M.V. and X.L.: overall architecture and methodology; A.S. and C.G.: experimental setup design and measurements; F.P.: three-mode fiber and its dispersion characterization; C.G. and A.S.: writing the first draft; C.G., A.S. and M.V.: preparing the figures; M.V.; project supervision; all authors: review and editing of the manuscript. All authors have read and agreed to the published version of the manuscript.
Funding
This work has been supported in part by the National Science Foundation grants ECCS-1937860, ECCS-1842680, and OMA-2231388.
Data Availability Statement
The data that support the findings of this study are available from the corresponding author upon reasonable request.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Puttnam, B.J.; Rademacher, G.; Luís, R.S. Space-division multiplexing for optical fiber communications. Optica 2021, 8, 1186–1203. [Google Scholar] [CrossRef]
- Xavier, G.B.; Lima, G. Quantum information processing with space-division multiplexing optical fibres. Commun. Phys. 2020, 3, 9. [Google Scholar] [CrossRef]
- Bittermann, J.A.; Bulla, L.; Ecker, S.; Neumann, S.P.; Fink, M.; Bohmann, M.; Friis, N.; Huber, M.; Ursin, R. Photonic entanglement during a zero-g flight. Quantum 2024, 8, 1256. [Google Scholar] [CrossRef]
- Rübeling, P.; Heine, J.; Johanning, R.; Kues, M. Quantum and coherent signal transmission on a single-frequency channel via the electro-optic serrodyne technique. Sci. Adv. 2024, 10, eadn8907. [Google Scholar] [CrossRef]
- Chang, K.C.; Cheng, X.; Sarihan, M.C.; Vinod, A.K.; Lee, Y.S.; Zhong, T.; Gong, Y.X.; Xie, Z.; Shapiro, J.H.; Wong, F.N.; et al. 648 Hilbert-space dimensionality in a biphoton frequency comb: Entanglement of formation and Schmidt mode decomposition. npj Quan. Inf. 2021, 7, 48. [Google Scholar] [CrossRef]
- Chang, K.C.; Sarihan, M.C.; Cheng, X.; Zhang, Z.; Wong, C.W. Large-alphabet time-bin quantum key distribution and Einstein–Podolsky–Rosen steering via dispersive optics. Quan. Sci. Technol. 2024, 9, 015018. [Google Scholar] [CrossRef]
- Löffler, W.; Euser, T.G.; Eliel, E.R.; Scharrer, M.; Russell, P.S.J.; Woerdman, J.P. Fiber transport of spatially entangled photons. Phys. Rev. Lett. 2011, 106, 240505. [Google Scholar] [CrossRef]
- Kang, Y.; Ko, J.; Lee, S.M.; Choi, S.K.; Kim, B.Y.; Park, H.S. Measurement of the entanglement between photonic spatial modes in optical fibers. Phys. Rev. Lett. 2012, 109, 020502. [Google Scholar] [CrossRef]
- Cozzolino, D.; Polino, E.; Valeri, M.; Carvacho, G.; Bacco, D.; Spagnolo, N.; Oxenløwe, L.K.K.; Sciarrino, F. Air-core fiber distribution of hybrid vector vortex-polarization entangled states. Adv. Photonics 2019, 1, 046005. [Google Scholar] [CrossRef]
- Essiambre, R.J.; Mestre, M.A.; Ryf, R.; Gnauck, A.H.; Tkach, R.W.; Chraplyvy, A.R.; Sun, Y.; Jiang, X.; Lingle, R. Experimental investigation of inter-modal four-wave mixing in few-mode fibers. IEEE Photonics Technol. Lett. 2013, 25, 539–542. [Google Scholar] [CrossRef]
- Anjum, O.F.; Guasoni, M.; Horak, P.; Jung, Y.; Petropoulos, P.; Richardson, D.J.; Parmigiani, F. Polarization-insensitive four-wave-mixing-based wavelength conversion in few-mode optical fibers. J. Light. Technol. 2018, 36, 3678–3683. [Google Scholar] [CrossRef]
- Parmigiani, F.; Horak, P.; Jung, Y.; Grüner-Nielsen, L.; Geisler, T.; Petropoulos, P.; Richardson, D.J. All-optical mode and wavelength converter based on parametric processes in a three-mode fiber. Opt. Express 2017, 25, 33602–33609. [Google Scholar] [CrossRef]
- Anjum, O.F.; Guasoni, M.; Horak, P.; Jung, Y.; Suzuki, M.; Hasegawa, T.; Bottrill, K.; Richardson, D.J.; Parmigiani, F.; Petropoulos, P. Selective wavelength conversion in a few-mode fiber. Opt. Express 2019, 27, 24072–24081. [Google Scholar] [CrossRef] [PubMed]
- Rottwitt, K.; Koefoed, J.G.; Christensen, E.N. Photon-pair sources based on intermodal four-wave mixing in few-mode fibers. Fibers 2018, 6, 32. [Google Scholar] [CrossRef]
- Guo, C.; Su, J.; Zhang, Z.; Cui, L.; Li, X. Generation of telecom-band correlated photon pairs in different spatial modes using few-mode fibers. Opt. Lett. 2019, 44, 235–238. [Google Scholar] [CrossRef]
- Li, X.; Cui, L.; Guo, X.; Ou, Z.Y.; Vasilyev, M. Fiber-based sources of quantum light for quantum information processing. In Proceedings of the Asia Communications and Photonics Conference (ACP), Shanghai, China, 24–27 October 2021. paper M4A.1. [Google Scholar]
- Shamsshooli, A.; Guo, C.; Parmigiani, F.; Li, X.; Vasilyev, M. Toward generation of spatially-entangled photon pairs in a few-mode fiber. In Proceedings of the Conference on Lasers and Electro-Optics (CLEO), Washington DC, USA, 10–15 May 2020. paper JTh2A.27. [Google Scholar]
- Shamsshooli, A.; Guo, C.; Parmigiani, F.; Li, X.; Vasilyev, M. Progress Toward Generation of Spatially-Entangled Photon Pairs in a Few-Mode Fiber. In Proceedings of the IEEE Photonics Conference (IPC), Vancouver, BC, Canada, 28 September–1 October 2020. paper MI2.2. [Google Scholar]
- Shamsshooli, A.; Guo, C.; Parmigiani, F.; Li, X.; Vasilyev, M. Progress Toward Spatially-Entangled Photon-Pair Generation in a Few-Mode Fiber. IEEE Photonics Technol. Lett. 2021, 33, 864–867. [Google Scholar] [CrossRef]
- Shamsshooli, A.; Guo, C.; Parmigiani, F.; Li, X.; Vasilyev, M. Toward generation of orbital-angular-momentum-entangled photon pairs in a few-mode fiber. In Proceedings of the Frontiers in Optics conference, Washington DC, USA, 14–17 September 2020. paper FM1D.2. [Google Scholar]
- Shibahara, K.; Mizuno, T.; Ono, H.; Nakajima, K.; Miyamoto, Y. Long-haul DMD-unmanaged 6-mode-multiplexed transmission employing cyclic mode-group permutation. In Proceedings of the Optical Fiber Communication (OFC) conference, San Diego, CA, USA, 8–12 March 2020. paper Th3H.3. [Google Scholar]
- Kwon, Y.B.; Vasilyev, M. Mode-selective frequency up-conversion in a χ(2) waveguide. Proc. SPIE 2014, 8964, 89640N. [Google Scholar]
- Kwon, Y.B.; Giribabu, M.; Li, L.; Samudrala, S.C.; Langrock, C.; Fejer, M.M.; Vasilyev, M. Experimental demonstration of spatial-mode-selective frequency up-conversion in a multimode χ(2) waveguide. In Proceedings of the Conference on Lasers and Electro-Optics (CLEO), San Jose, CA, USA, 5–10 June 2016. paper STh3P.4. [Google Scholar]
- Kwon, Y.B.; Giribabu, M.; Langrock, C.; Fejer, M.M.; Vasilyev, M. Single-photon-level spatial-mode-selective frequency up-conversion in a multimode χ(2) waveguide. In Proceedings of the Conference on Lasers and Electro-Optics (CLEO), San Jose, CA, USA, 14–19 May 2017. paper FF2E.1. [Google Scholar]
- Shamsshooli, A.; Guo, C.; Parmigiani, F.; Li, X.; Vasilyev, M. Mode-Selective Frequency Conversion in a Three-Mode Fiber. In Proceedings of the Conference on Lasers and Electro-Optics (CLEO), San Jose, CA, USA, 10–15 May 2020. paper SM3P.3. [Google Scholar]
- Shamsshooli, A.; Guo, C.; Vasilyev, M.; Parmigiani, F.; Li, X. Reconfigurable mode-selective frequency conversion in a three-mode fiber. In Proceedings of the IEEE Photonics Conference (IPC), Vancouver, BC, Canada, 28 September–1 October 2020. paper ThF1.2. [Google Scholar]
- Shamsshooli, A.; Guo, C.; Parmigiani, F.; Li, X.; Vasilyev, M. Reconfigurable Spatial-Mode-Selective Frequency Conversion in a Three-Mode Fiber. IEEE Photonics Technol. Lett. 2021, 33, 860–863. [Google Scholar] [CrossRef]
- Shamsshooli, A.; Kwon, Y.B.; Guo, C.; Parmigiani, F.; Li, X.; Langrock, C.; Fejer, M.M.; Vasilyev, M. Spatial-Mode-Selective Frequency Conversion. In Proceedings of the Photonics in Switching and Computing Conference, Washington, DC, USA, 27–29 September 2021. paper Tu4A.1. [Google Scholar]
- Shamsshooli, A.; Guo, C.; Vasilyev, M.; Parmigiani, F.; Li, X.; Akasaka, Y.; Palacharla, P. Emerging applications of wavelength conversion. In Proceedings of the IEEE Photonics Conference (IPC), Vancouver, BC, Canada, 17–21 October 2021. paper ThE2.1. [Google Scholar]
- Shamsshooli, A.; Kwon, Y.B.; Guo, C.; Vasilyev, M. Devices for quantum communication over mode-division-multiplexing systems. Proc. SPIE 2023, 12446, 124460E. [Google Scholar]
- Shamsshooli, A.; Guo, C.; Parmigiani, F.; Li, X.; Vasilyev, M. Toward OAM-selective frequency conversion in a three-mode fiber. In Proceedings of the Conference on Lasers and Electro-Optics (CLEO), San Jose, CA, USA, 11–13 May 2021. paper SM1F.5. [Google Scholar]
- Choi, S.-K.; Vasilyev, M.; Kumar, P. Noiseless Optical Amplification of Images. Phys. Rev. Lett. 1999, 83, 1938–1941, Erratum in Phys. Rev. Lett. 2000, 84, 1361. [Google Scholar] [CrossRef]
- Vasilyev, M.; Stelmakh, N.; Kumar, P. Phase-sensitive image amplification with elliptical Gaussian pump. Opt. Express 2009, 17, 11415–11425. [Google Scholar] [CrossRef] [PubMed]
- Vasilyev, M.; Stelmakh, N.; Kumar, P. Estimation of the spatial bandwidth of an optical parametric amplifier with plane-wave pump. J. Mod. Opt. 2009, 56, 2029–2033. [Google Scholar] [CrossRef]
- Vasilyev, M.; Kumar, P. Frequency up-conversion of quantum images. Opt. Express 2012, 20, 6644–6656. [Google Scholar] [CrossRef] [PubMed]
- Vasilyev, M.; Annamalai, M.; Stelmakh, N.; Kumar, P. Quantum properties of a spatially-broadband traveling-wave phase-sensitive optical parametric amplifier. J. Mod. Opt. 2010, 57, 1908–1915. [Google Scholar] [CrossRef]
- Annamalai, M.; Stelmakh, N.; Vasilyev, M.; Kumar, P. Spatial modes of phase-sensitive parametric image amplifiers with circular and elliptical Gaussian pumps. Opt. Express 2011, 19, 26710–26724. [Google Scholar] [CrossRef]
- Annamalai, M.; Stelmakh, N.; Kumar, P.; Vasilyev, M. Compact representation of the spatial modes of a phase-sensitive image amplifier. Opt. Express 2013, 21, 28134–28153. [Google Scholar] [CrossRef]
- Levandovsky, D.; Vasilyev, M.; Kumar, P. Perturbation theory of quantum solitons: Continuum evolution and optimum squeezing by spectral filtering. Opt. Lett. 1999, 24, 43–45. [Google Scholar] [CrossRef]
- Levandovsky, D.; Vasilyev, M.; Kumar, P. Soliton squeezing in a highly transmissive nonlinear optical loop mirror. Opt. Lett. 1999, 24, 89–91, Erratum in Opt. Lett. 1999, 24, 423. [Google Scholar] [CrossRef]
- Levandovsky, D. Quantum Noise Suppression in Optical Fibers. Ph.D. Thesis, Northwestern University, Evanston, IL, USA, 1999. [Google Scholar]
- Annamalai, M.; Vasilyev, M. Phase-sensitive multimode parametric amplification in a parabolic-index waveguide. IEEE Photonics Technol. Lett. 2012, 24, 1949–1952. [Google Scholar] [CrossRef]
- Cui, L.; Liu, X.; Guo, C.; Zhang, Z.; Zhao, N.; Vasilyev, M.; Li, X. Measurement of effective nonlinear coefficients in few-mode fibers. Opt. Lett. 2019, 44, 5768–5771. [Google Scholar] [CrossRef]
- Zhang, Z.; Cheng, H.; Guo, C.; Cui, L.; Zhang, Y.; Mo, Q.; Yu, H.; Vasilyev, M.; Li, X. Investigation of Spontaneous Raman Scattering in Few-Mode Fibers: Dependence on Polarization and Spatial Modes. J. Light. Technol. 2021, 39, 6281–6287. [Google Scholar] [CrossRef]
- Huo, N.; Cheng, H.; Zhu, S.; Guo, C.; Zhang, Y.; Mo, Q.; Cui, L.; Vasilyev, M.; Li, X. Gain-equalizable few-mode fiber optical parametric amplifier in telecom band. Opt. Comm. 2022, 508, 127735. [Google Scholar] [CrossRef]
- Fontaine, N.K.; Ryf, R.; Chen, H.; Neilson, D.; Carpenter, J. Design of high order mode-multiplexers using multiplane light conversion. In Proceedings of the European Conference on Optical Communications (ECOC), Gothenburg, Sweden, 17–21 September 2017. [Google Scholar]
- Ataie, V.; Myslivets, E.; Kuo, B.P.-P.; Alic, N.; Radic, S. Spectrally Equalized Frequency Comb Generation in Multistage Parametric Mixer With Nonlinear Pulse Shaping. J. Light. Technol. 2014, 32, 840–846. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).