Thermal Stability and Optical Behavior of Porous Silicon and Porous Quartz Photonic Crystals for High-Temperature Applications
Abstract
1. Introduction
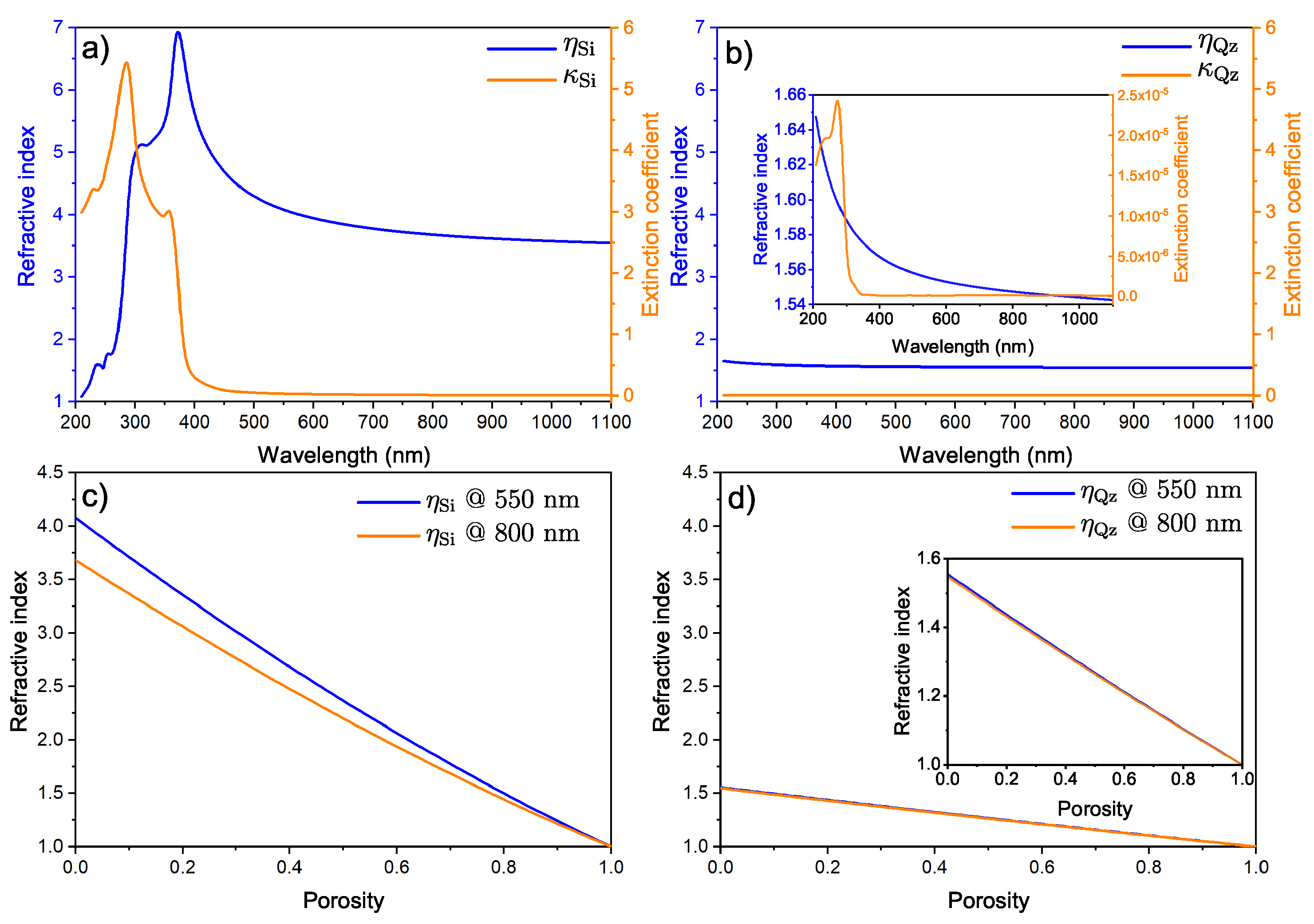
2. Optical Properties of Raw Materials
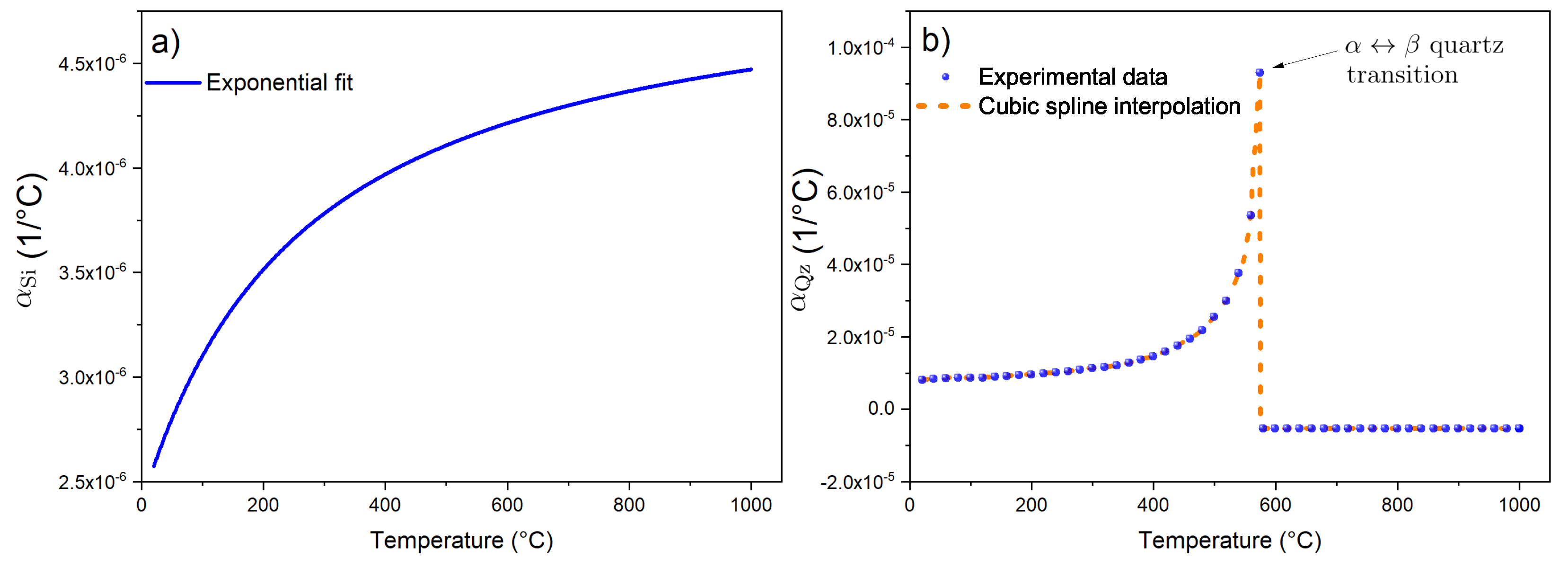
3. Theoretical Models
4. Simulation Design
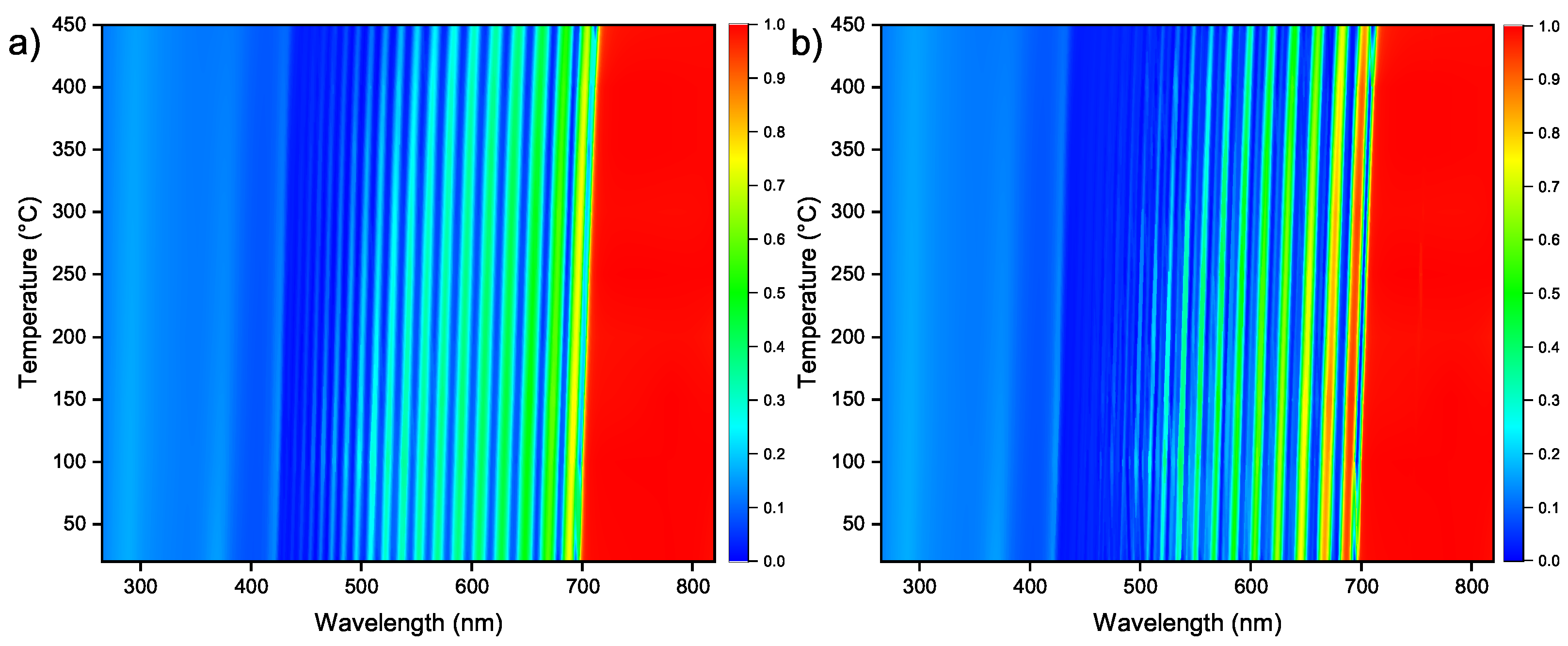
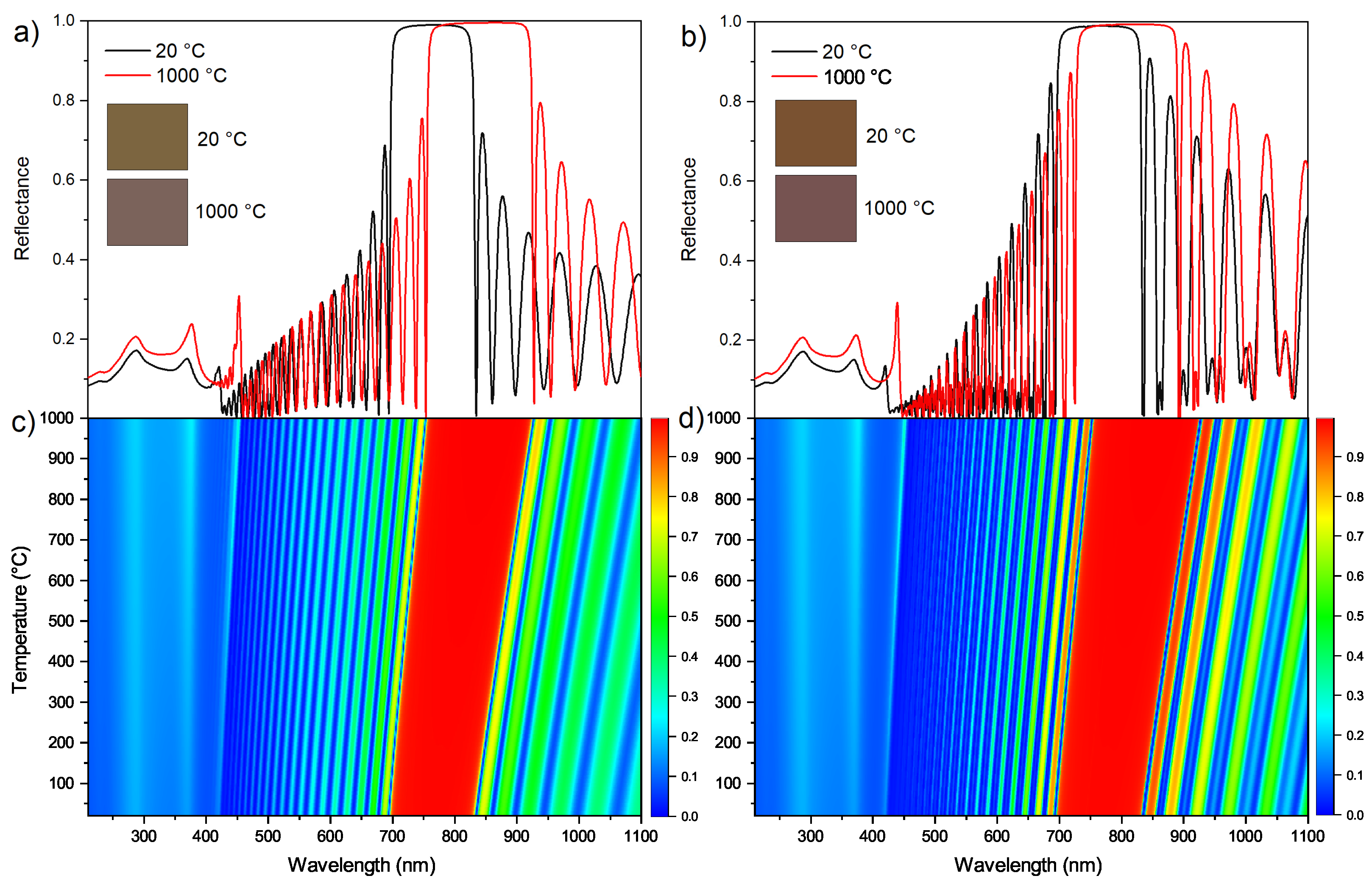
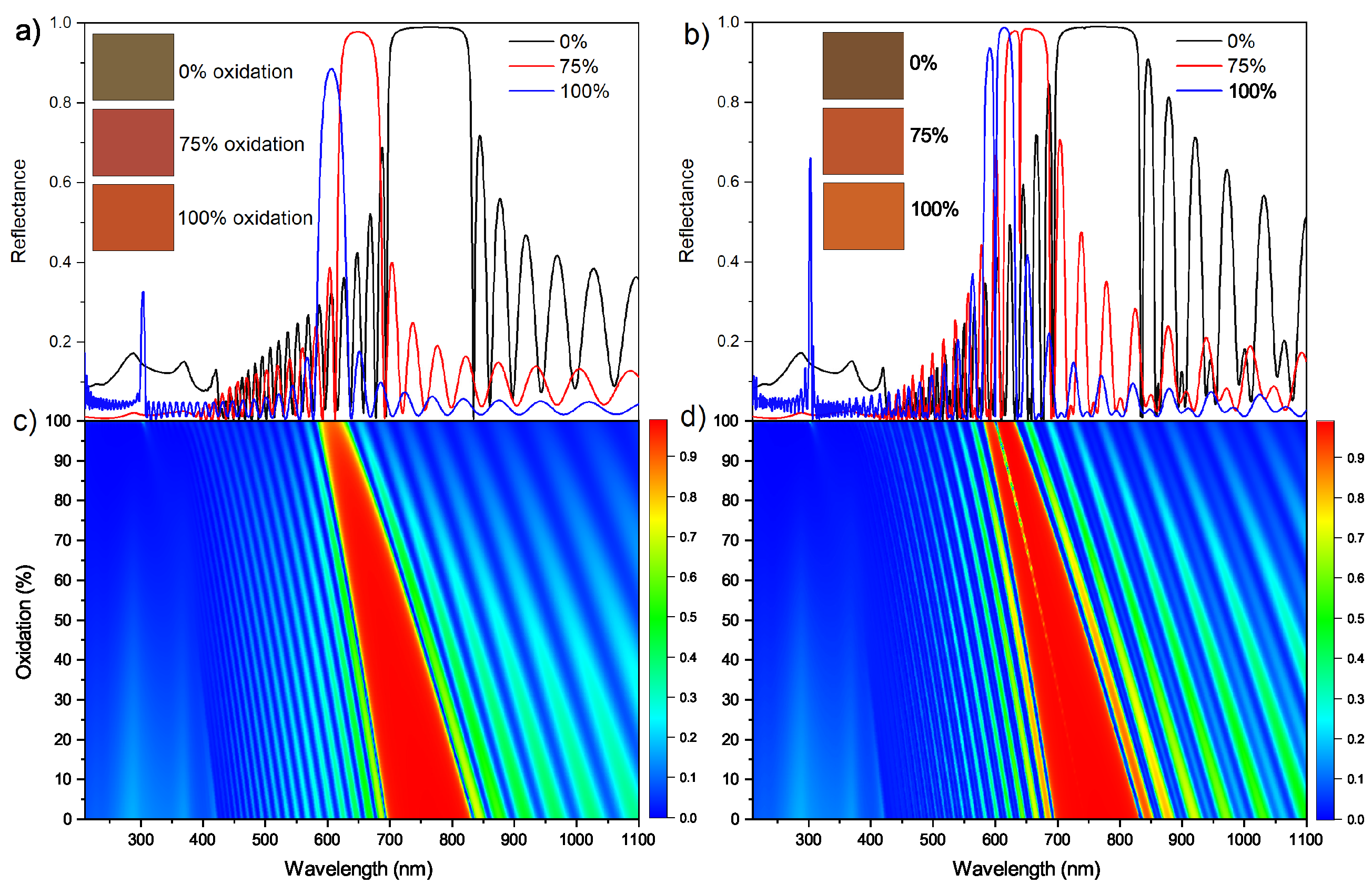
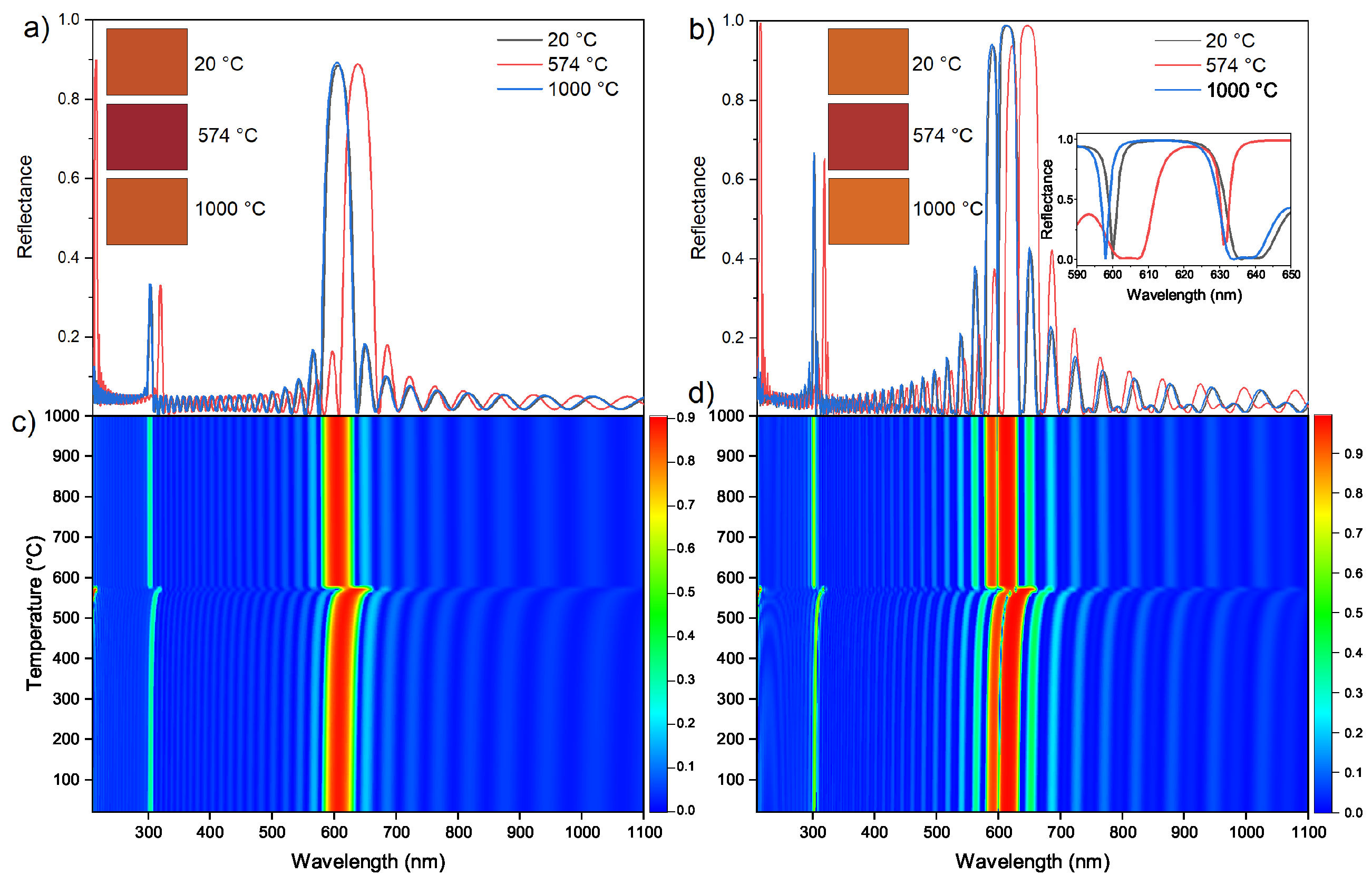
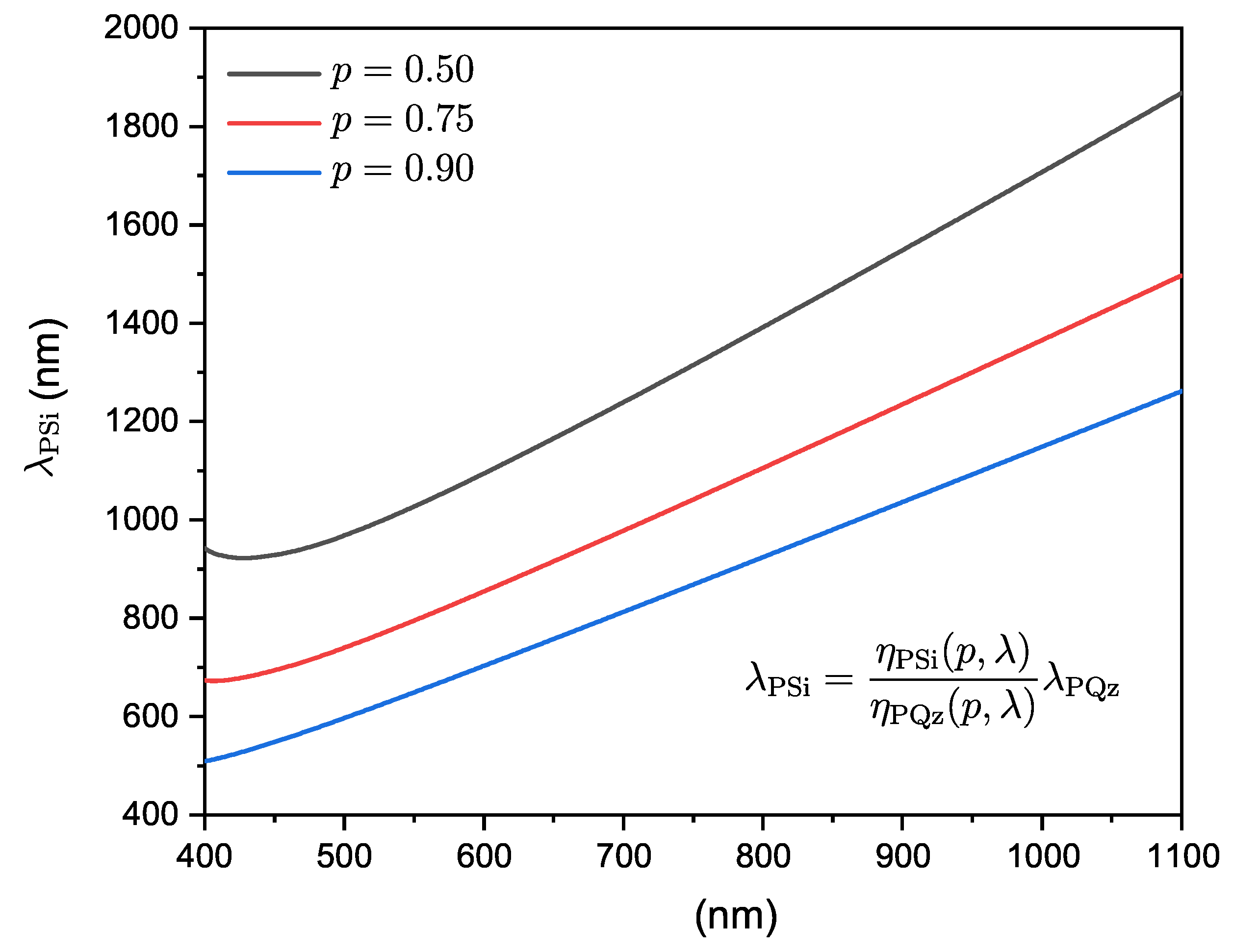
5. Numerical Results and Discussion
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Joannopoulos, J.D.; Villeneuve, P.R.; Fan, S. Photonic crystals: Putting a new twist on light. Nature 1997, 386, 143–149. [Google Scholar] [CrossRef]
- Joannopoulos, J.; Villeneuve, P.R.; Fan, S. Photonic crystals. Solid State Commun. 1997, 102, 165–173. [Google Scholar] [CrossRef]
- Yablonovitch, E. Inhibited Spontaneous Emission in Solid-State Physics and Electronics. Phys. Rev. Lett. 1987, 58, 2059–2062. [Google Scholar] [CrossRef]
- Yablonovitch, E. Photonic band-gap structures. J. Opt. Soc. Am. B 1993, 10, 283–295. [Google Scholar] [CrossRef]
- Yablonovitch, E. Photonic Crystals. J. Mod. Opt. 1994, 41, 173–194. [Google Scholar] [CrossRef]
- Mizeikis, V.; Juodkazis, S.; Marcinkevičius, A.; Matsuo, S.; Misawa, H. Tailoring and characterization of photonic crystals. J. Photochem. Photobiol. C Photochem. Rev. 2001, 2, 35–69. [Google Scholar] [CrossRef]
- Butt, M.; Khonina, S.; Kazanskiy, N. Recent advances in photonic crystal optical devices: A review. Opt. Laser Technol. 2021, 142, 107265. [Google Scholar] [CrossRef]
- Fu, L.; Lin, M.; Liang, Z.; Wang, Q.; Zheng, Y.; Ouyang, Z. The Transmission Properties of One-Dimensional Photonic Crystals with Gradient Materials. Materials 2022, 15, 8049. [Google Scholar] [CrossRef] [PubMed]
- Zhang, S.; Huang, B.; Bian, Y.; Han, C.; Tian, D.; Chen, X.; Qiu, J.; Zhu, A.; Yang, A.; Shao, J. Two-dimensional photonic crystals as selective filters for thermophotovoltaic applications. Opt. Express 2023, 31, 9186–9195. [Google Scholar] [CrossRef]
- Ren, H.; Jiang, C.; Hu, W.; Gao, M.; Wang, J. Photonic crystal channel drop filter with a wavelength-selective reflection micro-cavity. Opt. Express 2006, 14, 2446–2458. [Google Scholar] [CrossRef]
- Zimmermann, J.; Kamp, M.; Forchel, A.; März, R. Photonic crystal waveguide directional couplers as wavelength selective optical filters. Opt. Commun. 2004, 230, 387–392. [Google Scholar] [CrossRef]
- Gevorgyan, A.H.; Vanyushkin, N.A.; Rafayelyan, M.S. Light localization in 1D chirped photonic crystals. Eur. Phys. J. Plus 2022, 137, 719. [Google Scholar] [CrossRef]
- Wilson, M. A photonic crystal localizes light in two dimensions. Phys. Today 2007, 60, 22–23. [Google Scholar] [CrossRef]
- Deych, L.; Lisyansky, A. Localization of light in one-dimensional disordered photonic crystals: Statistics of resonant transmission in the band gap region. In Proceedings of the Frontiers in Optics; Optica Publishing Group: Washington, DC, USA, 2003; p. WB1. [Google Scholar] [CrossRef]
- Tanaue, H.B.; Reyes-Gómez, E.; Bruno-Alfonso, A. Light localization in one-dimensional photonic crystal heterostructures. Photonics Nanostruct. Fundam. Appl. 2021, 47, 100958. [Google Scholar] [CrossRef]
- Kang, L.; Fei, H.; Lin, H.; Wu, M.; Wang, X.; Zhang, M.; Liu, X.; Sun, F.; Chen, Z. Thermal tunable silicon valley photonic crystal ring resonators at the telecommunication wavelength. Opt. Express 2023, 31, 2807–2815. [Google Scholar] [CrossRef] [PubMed]
- Singh, J.J.; Dhawan, D.; Gupta, N. All-optical photonic crystal logic gates for optical computing: An extensive review. Opt. Eng. 2020, 59, 110901. [Google Scholar] [CrossRef]
- Rao, D.G.S.; Palacharla, V.; Swarnakar, S.; Kumar, S. Design of all-optical D flip-flop using photonic crystal waveguides for optical computing and networking. Appl. Opt. 2020, 59, 7139–7143. [Google Scholar] [CrossRef] [PubMed]
- Rao, D.G.S.; Swarnakar, S.; Kumar, S. Performance analysis of all-optical NAND, NOR, and XNOR logic gates using photonic crystal waveguide for optical computing applications. Opt. Eng. 2020, 59, 057101. [Google Scholar] [CrossRef]
- Sayed, F.A.; Elsayed, H.A.; Mehaney, A.; Eissa, M.F.; Aly, A.H. A doped-polymer based porous silicon photonic crystal sensor for the detection of gamma-ray radiation. RSC Adv. 2023, 13, 3123–3138. [Google Scholar] [CrossRef] [PubMed]
- Zaky, Z.A.; Al-Dossari, M.; Sharma, A.; Aly, A.H. Effective pressure sensor using the parity-time symmetric photonic crystal. Phys. Scr. 2023, 98, 035522. [Google Scholar] [CrossRef]
- Pacholski, C. Photonic Crystal Sensors Based on Porous Silicon. Sensors 2013, 13, 4694–4713. [Google Scholar] [CrossRef] [PubMed]
- Exner, A.T.; Pavlichenko, I.; Lotsch, B.V.; Scarpa, G.; Lugli, P. Low-Cost Thermo-Optic Imaging Sensors: A Detection Principle Based on Tunable One-Dimensional Photonic Crystals. ACS Appl. Mater. Interfaces 2013, 5, 1575–1582. [Google Scholar] [CrossRef] [PubMed]
- Carroll, L.; Lee, J.S.; Scarcella, C.; Gradkowski, K.; Duperron, M.; Lu, H.; Zhao, Y.; Eason, C.; Morrissey, P.; Rensing, M.; et al. Photonic Packaging: Transforming Silicon Photonic Integrated Circuits into Photonic Devices. Appl. Sci. 2016, 6, 426. [Google Scholar] [CrossRef]
- Dong, P.; Chen, Y.K.; Duan, G.H.; Neilson, D.T. Silicon photonic devices and integrated circuits. Nanophotonics 2014, 3, 215–228. [Google Scholar] [CrossRef]
- Guo, X.; Ji, X.; Yao, B.; Tan, T.; Chu, A.; Westreich, O.; Dutt, A.; Wong, C.; Su, Y. Ultra-wideband integrated photonic devices on silicon platform: From visible to mid-IR. Nanophotonics 2023, 12, 167–196. [Google Scholar] [CrossRef] [PubMed]
- Isaza, C.; Lujan-Cabrera, I.A.; Anaya Rivera, E.K.; Rizzo Sierra, J.A.; Zavala De Paz, J.P.; Ramirez-Gutierrez, C.F. Generation of a Synthetic Database for the Optical Response of One-Dimensional Photonic Crystals Using Genetic Algorithms. Mathematics 2022, 10, 4484. [Google Scholar] [CrossRef]
- Yablonovitch, E. Photonic crystals: Semiconductors of light. Sci. Am. 2001, 285, 46–55. [Google Scholar] [CrossRef]
- Kamp, M.; Happ, T.; Mahnkopf, S.; Duan, G.; Anand, S.; Forchel, A. Semiconductor photonic crystals for optoelectronics. Phys. E Low-Dimens. Syst. Nanostruct. 2004, 21, 802–808. [Google Scholar] [CrossRef]
- Benisty, H.; Lourtioz, J.M.; Chelnokov, A.; Combrie, S.; Checoury, X. Recent Advances Toward Optical Devices in Semiconductor-Based Photonic Crystals. Proc. IEEE 2006, 94, 997–1023. [Google Scholar] [CrossRef]
- El-Kady, I.; Sigalas, M.M.; Biswas, R.; Ho, K.M.; Soukoulis, C.M. Metallic photonic crystals at optical wavelengths. Phys. Rev. B 2000, 62, 15299–15302. [Google Scholar] [CrossRef]
- Vasilantonakis, N.; Terzaki, K.; Sakellari, I.; Purlys, V.; Gray, D.; Soukoulis, C.M.; Vamvakaki, M.; Kafesaki, M.; Farsari, M. Three-Dimensional Metallic Photonic Crystals with Optical Bandgaps. Adv. Mater. 2012, 24, 1101–1105. [Google Scholar] [CrossRef] [PubMed]
- Romanato, F.; Businaro, L.; Vaccari, L.; Cabrini, S.; Candeloro, P.; De Vittorio, M.; Passaseo, A.; Todaro, M.; Cingolani, R.; Cattaruzza, E.; et al. Fabrication of 3D metallic photonic crystals by X-ray lithography. Microelectron. Eng. 2003, 67–68, 479–486. [Google Scholar] [CrossRef]
- Qian, L.; Hu, Y.; Chen, Z.; Zhao, D.; Dong, J.; Chen, X. Temperature Dependence of Optical Bistability in Superconductor–Semiconductor Photonic Crystals Embedded with Graphene. Crystals 2023, 13, 545. [Google Scholar] [CrossRef]
- Aly, A.H.; Sabra, W. Superconductor-Semiconductor Metamaterial Photonic Crystals. J. Supercond. Nov. Magn. 2016, 29, 1981–1986. [Google Scholar] [CrossRef]
- Segovia-Chaves, F.; Vinck-Posada, H. Dependence of the defect mode with temperature, pressure and angle of incidence in a 1D semiconductor-superconductor photonic crystal. Phys. C Supercond. Its Appl. 2018, 553, 1–7. [Google Scholar] [CrossRef]
- Kitzerow, H.S.; Lorenz, A.; Matthias, H. Tuneable photonic crystals obtained by liquid crystal infiltration. Phys. Status Solidi (a) 2007, 204, 3754–3767. [Google Scholar] [CrossRef]
- Ozaki, M.; Matsuhisa, Y.; Yoshida, H.; Ozaki, R.; Fujii, A. Photonic crystals based on chiral liquid crystal. Phys. Status Solidi (a) 2007, 204, 3777–3789. [Google Scholar] [CrossRef]
- Ramirez-Gutierrez, C.F.; Martinez-Hernandez, H.D.; Lujan-Cabrera, I.A.; Rodriguez-García, M.E. Design, fabrication, and optical characterization of one-dimensional photonic crystals based on porous silicon assisted by in-situ photoacoustics. Sci. Rep. 2019, 9, 14732. [Google Scholar] [CrossRef] [PubMed]
- Calvo, M.E.; Colodrero, S.; Hidalgo, N.; Lozano, G.; López-López, C.; Sánchez-Sobrado, O.; Míguez, H. Porous one dimensional photonic crystals: Novel multifunctional materials for environmental and energy applications. Energy Environ. Sci. 2011, 4, 4800–4812. [Google Scholar] [CrossRef]
- Ortiz-Vazquez, E.; Lujan-Cabrera, I.; Isaza, C.; Rizzo-Sierra, J.; Ramirez-Gutierrez, C. Design of broadband modulated one-dimensional photonic crystals based on porous silicon using evolutionary search. Optik 2022, 260, 169002. [Google Scholar] [CrossRef]
- Dias, M.R.S.; Gong, T.; Duncan, M.A.; Ness, S.C.; McCormack, S.J.; Leite, M.S.; Munday, J.N. Photonics roadmap for ultra-high-temperature thermophotovoltaics. Joule 2023, 7, 2209–2227. [Google Scholar] [CrossRef]
- Kim, J.H.; Jung, S.M.; Shin, M.W. High-temperature degradation of one-dimensional metallodielectric (W/SiO2) photonic crystal as selective thermal emitter for thermophotovoltaic system. Opt. Mater. 2017, 72, 45–51. [Google Scholar] [CrossRef]
- Du, Q. High energy radiation damage on silicon photonic devices: A review. Opt. Mater. Express 2023, 13, 403–412. [Google Scholar] [CrossRef]
- Rinnerbauer, V.; Ndao, S.; Yeng, Y.X.; Chan, W.R.; Senkevich, J.J.; Joannopoulos, J.D.; Soljačić, M.; Celanovic, I. Recent developments in high-temperature photonic crystals for energy conversion. Energy Environ. Sci. 2012, 5, 8815–8823. [Google Scholar] [CrossRef]
- Tan, C. Review and analysis of refractive index temperature dependence in amorphous SiO2. J. Non-Cryst. Solids 1998, 238, 30–36. [Google Scholar] [CrossRef]
- Tan, C.Z. Dependence of the refractive index on density, temperature, and the wavelength of the incident light. Eur. Phys. J. B 2021, 94, 139. [Google Scholar] [CrossRef]
- Waxler, R.M.; Weir, C.E. Effect of Hydrostatic Pressure on the Refractive Indices of Some Solids. J. Res. Natl. Bur. Stand A Phys. Chem. 1965, 69A, 325–333. [Google Scholar] [CrossRef]
- Fan, S. Thermal Photonics and Energy Applications. Joule 2017, 1, 264–273. [Google Scholar] [CrossRef]
- Yoo, M.J.; Pyun, K.R.; Jung, Y.; Lee, M.; Lee, J.; Ko, S.H. Switchable radiative cooling and solar heating for sustainable thermal management. Nanophotonics 2024, 13, 543–561. [Google Scholar] [CrossRef]
- Bahramipour, S.S.; Askarpour, A.N. One-dimensional photonic crystal with tilted termination and its angular filtering properties for radiative cooling. Opt. Express 2024, 32, 5191–5205. [Google Scholar] [CrossRef] [PubMed]
- Li, W.; Liu, T.; Zhu, J. Thermal photonics for sustainability. Nanophotonics 2024, 13, 539–541. [Google Scholar] [CrossRef]
- Ramirez-Gutierrez, C.F.; Lujan-Cabrera, I.A.; Isaza, C.; Anaya Rivera, E.K.; Rodriguez-Garcia, M.E. In Situ Photoacoustic Study of Optical Properties of P-Type (111) Porous Silicon Thin Films. Nanomaterials 2021, 11, 1314. [Google Scholar] [CrossRef] [PubMed]
- Sierra-Moreno, R.F.; Lujan-Cabrera, I.A.; Cabrera-Teran, J.M.; Ortiz-Vazquez, E.; Rodriguez-Garcia, M.E.; Ramirez-Gutierrez, C.F. Study of the optical response of oxidized porous silicon structures by thermal oxidation in air. J. Mater. Sci. 2022, 57, 11226–11241. [Google Scholar] [CrossRef]
- Jiménez-Vivanco, M.R.; Herrera, R.; Martínez, L.; Morales, F.; Misaghian, K.; Toledo-Solano, M.; Lugo, J.E. Theoretical and Experimental Study of Optical Losses in a Periodic/Quasiperiodic Structure Based on Porous Si-SiO2. Photonics 2023, 10, 1009. [Google Scholar] [CrossRef]
- Castillo-Gallardo, V.; Puente-Díaz, L.E.; Mochán Backal, W.L.; Agarwal, V. Porous silica based controllable reversible freestanding Bragg structures: From omnidirectional mirrors to transparency. Ceram. Int. 2024; in proof. [Google Scholar] [CrossRef]
- Schubert, E.F.; Kim, J.K.; Xi, J.Q. Low-refractive-index materials: A new class of optical thin-film materials. Phys. Status Solidi (b) 2007, 244, 3002–3008. [Google Scholar] [CrossRef]
- Rajan, S.P.; Keloth Paduvilan, J.; Velayudhan, P.; Krishnageham Sidharthan, S.; Simon, S.M.; Thomas, S. Progress in 2D/3D nanomaterials incorporated polymer thin films for refractive index engineering: A critical review. J. Polym. Res. 2024, 31, 124. [Google Scholar] [CrossRef]
- Niklasson, G.A.; Granqvist, C.G.; Hunderi, O. Effective medium models for the optical properties of inhomogeneous materials. Appl. Opt. 1981, 20, 26–30. [Google Scholar] [CrossRef]
- Ramirez-Gutierrez, C.F.; Castaño-Yepes, J.D.; Rodriguez-García, M.E. In situ photoacoustic characterization for porous silicon growing: Detection principles. J. Appl. Phys. 2016, 119, 185103. [Google Scholar] [CrossRef]
- Kuntyi, O.; Zozulya, G.; Shepida, M. Porous Silicon Formation by Electrochemical Etching. Adv. Mater. Sci. Eng. 2022, 2022, 1482877. [Google Scholar] [CrossRef]
- Bardet, B.; De Sousa Meneses, D.; Defforge, T.; Billoué, J.; Gautier, G. In situ investigation of mesoporous silicon oxidation kinetics using infrared emittance spectroscopy. Phys. Chem. Chem. Phys. 2016, 18, 18201–18208. [Google Scholar] [CrossRef]
- Green, M.A. Self-consistent optical parameters of intrinsic silicon at 300K including temperature coefficients. Sol. Energy Mater. Sol. Cells 2008, 92, 1305–1310. [Google Scholar] [CrossRef]
- Khashan, M.; Nassif, A. Dispersion of the optical constants of quartz and polymethyl methacrylate glasses in a wide spectral range: 0.2–3 μm. Opt. Commun. 2001, 188, 129–139. [Google Scholar] [CrossRef]
- Choy, T.C. Effective Medium Theory: Principles and Applications; Oxford University Press: Oxford, UK, 2015; Volume 165. [Google Scholar]
- Missoni, L.L.; Ortiz, G.P.; Martínez Ricci, M.L.; Toranzos, V.J.; Mochán, W.L. Rough 1D photonic crystals: A transfer matrix approach. Opt. Mater. 2020, 109, 110012. [Google Scholar] [CrossRef]
- Mitsas, C.L.; Siapkas, D.I. Generalized matrix method for analysis of coherent and incoherent reflectance and transmittance of multilayer structures with rough surfaces, interfaces, and finite substrates. Appl. Opt. 1995, 34, 1678–1683. [Google Scholar] [CrossRef]
- Rego, G. Temperature Dependence of the Thermo-Optic Coefficient of SiO2 Glass. Sensors 2023, 23, 6023. [Google Scholar] [CrossRef]
- Watanabe, H.; Yamada, N.; Okaji, M. Linear Thermal Expansion Coefficient of Silicon from 293 to 1000 K. Int. J. Thermophys. 2004, 25, 221–236. [Google Scholar] [CrossRef]
- Okada, Y.; Tokumaru, Y. Precise determination of lattice parameter and thermal expansion coefficient of silicon between 300 and 1500 K. J. Appl. Phys. 1984, 56, 314–320. [Google Scholar] [CrossRef]
- Polyakova, I.G. 4. The Main Silica Phases and Some of Their Properties. In Glass; Schmelzer, J.W.P., Ed.; De Gruyter: Berlin, Germany; Boston, MA, USA, 2014; pp. 197–268. [Google Scholar] [CrossRef]
- Johnson, S.E.; Song, W.J.; Cook, A.C.; Vel, S.S.; Gerbi, C.C. The quartz α↔β phase transition: Does it drive damage and reaction in continental crust? Earth Planet. Sci. Lett. 2021, 553, 116622. [Google Scholar] [CrossRef]
- Vuye, G.; Fisson, S.; Nguyen Van, V.; Wang, Y.; Rivory, J.; Abelès, F. Temperature dependence of the dielectric function of silicon using in situ spectroscopic ellipsometry. Thin Solid Film. 1993, 233, 166–170. [Google Scholar] [CrossRef]


| Photonic Structure | DBR | FPM |
|---|---|---|
| Structure | ||
| 0.75 | 0.75 | |
| 0.91 | 0.91 | |
| 0.75 | 0.75 | |
| (nm) | 160 | 160 |
| (nm) | 120 | 120 |
| (nm) | - | 100 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lujan-Cabrera, I.A.; Anaya Rivera, E.K.; Rizzo Sierra, J.A.; De Paz, J.P.Z.; Isaza, C.; Ramirez-Gutierrez, C.F. Thermal Stability and Optical Behavior of Porous Silicon and Porous Quartz Photonic Crystals for High-Temperature Applications. Photonics 2025, 12, 94. https://doi.org/10.3390/photonics12020094
Lujan-Cabrera IA, Anaya Rivera EK, Rizzo Sierra JA, De Paz JPZ, Isaza C, Ramirez-Gutierrez CF. Thermal Stability and Optical Behavior of Porous Silicon and Porous Quartz Photonic Crystals for High-Temperature Applications. Photonics. 2025; 12(2):94. https://doi.org/10.3390/photonics12020094
Chicago/Turabian StyleLujan-Cabrera, Ivan Alonso, Ely Karina Anaya Rivera, Jose Amilcar Rizzo Sierra, Jonny Paul Zavala De Paz, Cesar Isaza, and Cristian Felipe Ramirez-Gutierrez. 2025. "Thermal Stability and Optical Behavior of Porous Silicon and Porous Quartz Photonic Crystals for High-Temperature Applications" Photonics 12, no. 2: 94. https://doi.org/10.3390/photonics12020094
APA StyleLujan-Cabrera, I. A., Anaya Rivera, E. K., Rizzo Sierra, J. A., De Paz, J. P. Z., Isaza, C., & Ramirez-Gutierrez, C. F. (2025). Thermal Stability and Optical Behavior of Porous Silicon and Porous Quartz Photonic Crystals for High-Temperature Applications. Photonics, 12(2), 94. https://doi.org/10.3390/photonics12020094







