Portable Filter-Free Lens-Free Incoherent Digital Holography System
Abstract
1. Introduction
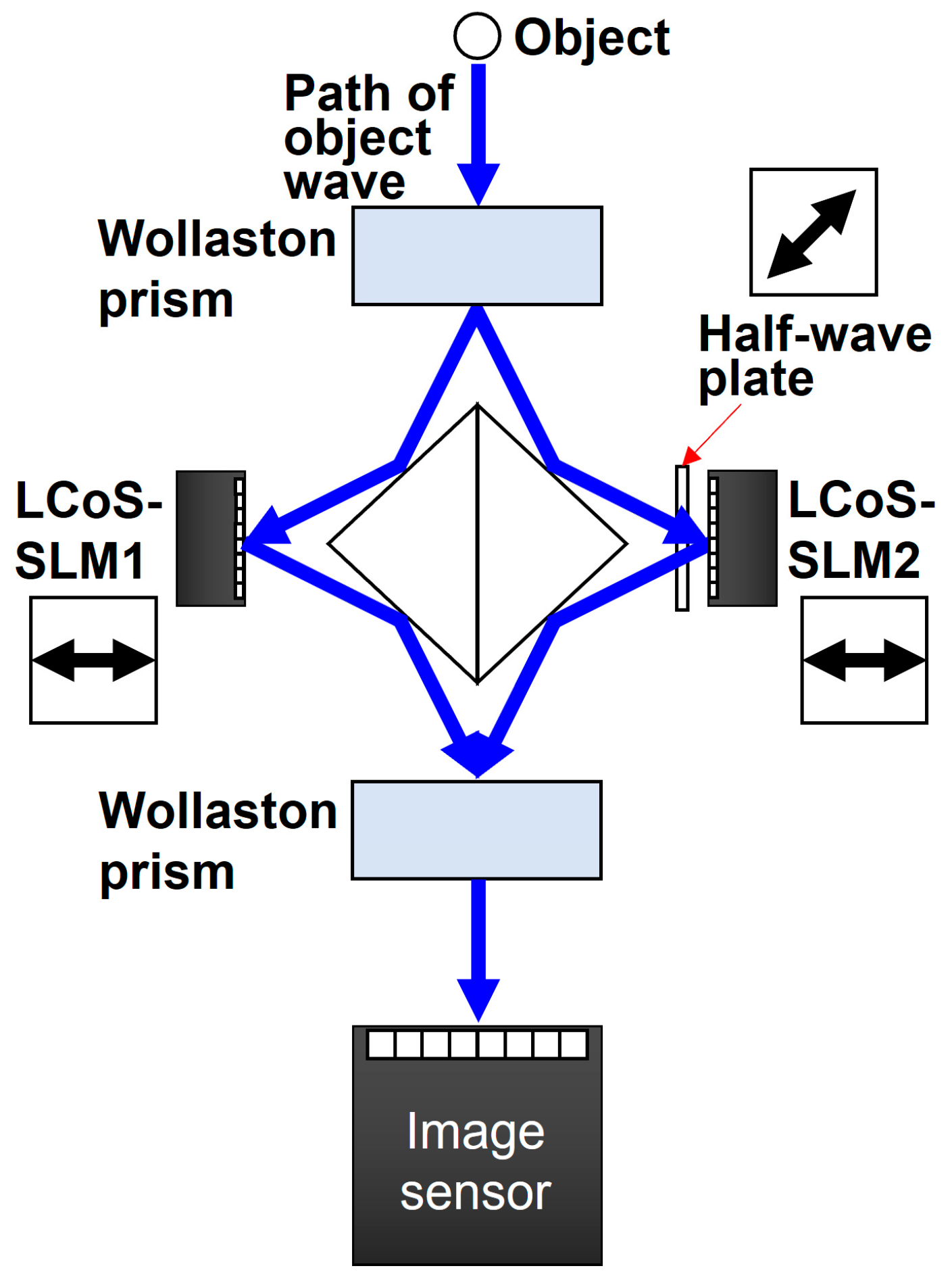
2. Developed Incoherent Digital Holography System
3. Experimental Results
4. Discussion and Conclusions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Gabor, D. A new microscopic principle. Nature 1948, 161, 777–778. [Google Scholar] [CrossRef] [PubMed]
- Leith, E.N.; Upatnieks, J. Reconstructed wavefronts and communication theory. J. Opt. Soc. Am. 1962, 52, 1123–1128. [Google Scholar] [CrossRef]
- Lohmann, A.W. Reconstruction of vectorial wavefronts. Appl. Opt. 1965, 4, 1667. [Google Scholar] [CrossRef]
- Hariharan, P. Optical Holography: Principles, Techniques and Applications; Cambridge University Press: New York, NY, USA, 1996. [Google Scholar]
- Kubota, T.; Komai, K.; Yamagiwa, M.; Awatsuji, Y. Moving picture recording and observation of three-dimensional image of femtosecond light pulse propagation. Opt. Express 2007, 15, 14348. [Google Scholar] [CrossRef]
- Enloe, L.; Murphy, J.; Rubinstein, C. Bstj briefs hologram transmission via television. Bell Syst. Tech. J. 1966, 45, 335. [Google Scholar] [CrossRef]
- Goodman, J.W.; Lawrence, R.W. Digital image formation from electronically detected holograms. Appl. Phys. Lett. 1967, 11, 77–79. [Google Scholar] [CrossRef]
- Poon, T.-C. Digital Holography and Three-Dimensional Display; Springer: Berlin, Germany, 2006. [Google Scholar]
- Kim, M.K. Digital Holographic Microscopy: Principles, Techniques, and Applications; Springer: New York, NY, USA, 2011. [Google Scholar]
- Picart, P.; Li, J.-C. Digital Holography; Wiley: Hoboken, NJ, USA, 2013. [Google Scholar]
- Poon, T.-C.; Liu, J.-P. Introduction to Modern Digital Holography with MATLAB®; Cambridge University Press: Cambridge, UK, 2014. [Google Scholar]
- Shimobaba, T.; Ito, T. Hardware Acceleration of Computational Holography; Springer: Singapore, 2023. [Google Scholar]
- Zhang, Y.; Poon, T.-C. Modern Information Optics wit MATLAB; Cambridge University Press: Cambridge, UK, 2023. [Google Scholar]
- Cotte, Y.; Toy, F.; Jourdain, P.; Pavillon, N.; Boss, D.; Magistretti, P.; Marquet, P.; Depeursinge, C. Marker-free phase microscopy. Nat. Photon. 2013, 7, 113–117. [Google Scholar] [CrossRef]
- Kakue, T.; Yonesaka, R.; Tahara, T.; Awatsuji, Y.; Nishio, K.; Ura, S.; Kubota, T.; Matoba, O. High-speed phase imaging by parallel phase-shifting digital holography. Opt. Lett. 2011, 36, 4131–4133. [Google Scholar] [CrossRef]
- Xia, P.; Awatsuji, Y.; Nishio, K.; Matoba, O. One million fps digital holography. Electron. Lett. 2014, 50, 1693–1695. [Google Scholar] [CrossRef]
- Lohmann, A.W. Wavefront reconstruction for incoherent objects. J. Opt. Soc. Am. 1965, 55, 1555. [Google Scholar] [CrossRef]
- Peters, P.J. Incoherent holograms with mercury light source. Appl. Phys. Lett. 1966, 8, 209–210. [Google Scholar] [CrossRef]
- Sirat, G.; Psaltis, D. Conoscopic holography. Opt. Lett. 1985, 10, 4–6. [Google Scholar] [CrossRef]
- Liu, J.-P.; Tahara, T.; Hayasaki, Y.; Poon, T.-C. Incoherent digital holography: A review. Appl. Sci. 2018, 1, 143. [Google Scholar] [CrossRef]
- Rosen, J.; Vijayakumar, A.; Kumar, M.; Rai, M.R.; Kelner, R.; Kashter, Y.; Bulbul, A.; Mukherjee, S. Recent advances in selfinterference incoherent digital holography. Adv. Opt. Photon. 2019, 11, 1–66. [Google Scholar] [CrossRef]
- Rosen, J.; Alford, S.; Anand, V.; Art, J.; Bouchal, P.; Bouchal, Z.; Erdenebat, M.-U.; Huang, L.; Ishii, A.; Juodkazis, S.; et al. Roadmap on Recent Progress in FINCH Technology. J. Imaging 2021, 7, 197. [Google Scholar] [CrossRef] [PubMed]
- Tahara, T.; Zhang, Y.; Rosen, J.; Anand, V.; Cao, L.; Wu, J.; Koujin, T.; Matsuda, A.; Ishii, A.; Kozawa, Y.; et al. Roadmap of incoherent digital holography. Appl. Phys. B 2022, 128, 193. [Google Scholar] [CrossRef]
- Rosen, J.; Alford, S.; Allan, B.; Anand, V.; Arnon, S.; Arockiaraj, F.G.; Art, J.; Bai, B.; Balasubramaniam, G.M.; Birnbaum, T.; et al. Roadmap on computational methods in optical imaging and holography. Appl. Phys. B 2024, 130, 166. [Google Scholar] [CrossRef]
- Tahara, T.; Shimobaba, T.; Kozawa, Y. Review on imaging and sensing with holography. J. Opt. 2025, in press. [Google Scholar] [CrossRef]
- Schilling, B.W.; Poon, T.-C.; Indebetouw, G.; Storrie, B.; Shinoda, K.; Suzuki, Y.; Wu, M.H. Three-dimensional holographic fluorescence microscopy. Opt. Lett. 1997, 22, 1506–1508. [Google Scholar] [CrossRef] [PubMed]
- Rosen, J.; Brooker, G. Non-scanning motionless fluorescence three-dimensional holographic microscopy. Nat. Photon. 2008, 2, 190–195. [Google Scholar] [CrossRef]
- Bon, P.; Linarès-Loyez, J.; Feyeux, M.; Alessandri, K.; Lounis, B.; Nassoy, P.; Cognet, L. Self-interference 3D superresolution microscopy for deep tissue investigations. Nat. Methods 2018, 15, 449. [Google Scholar] [CrossRef] [PubMed]
- Liebel, M.; Pazos-Perez, N.; van Hulst, N.F.; Alvarez-Puebla, R.A. Surface-enhanced Raman Scattering Holography. Nat. Nanotechnol. 2020, 15, 1005–1011. [Google Scholar] [CrossRef] [PubMed]
- Kim, M.K. Full color natural light holographic camera. Opt. Express 2013, 21, 9636–9642. [Google Scholar] [CrossRef] [PubMed]
- Itoh, K.; Inoue, T.; Yoshida, T.; Ichioka, Y. Interferometric supermultispectral imaging. Appl. Opt. 1990, 29, 1625. [Google Scholar] [CrossRef] [PubMed]
- Yoshimori, K. Interferometric spectral imaging for three-dimensional objects illuminated by a natural light source. J. Opt. Soc. Am. A 2001, 18, 765. [Google Scholar] [CrossRef]
- Rosen, J.; Brooker, G. Fluorescence incoherent color holography. Opt. Express 2007, 15, 2244–2250. [Google Scholar] [CrossRef] [PubMed]
- Naik, D.N.; Pedrini, G.; Takeda, M.; Osten, W. Spectrally resolved incoherent holography: 3D spatial and spectral imaging using a Mach-Zehnder radial-shearing interferometer. Opt. Lett. 2014, 39, 1857–1860. [Google Scholar] [CrossRef] [PubMed]
- Rosen, J.; Brooker, G. Digital spatially incoherent Fresnel holography. Opt. Lett. 2007, 32, 912–914. [Google Scholar] [CrossRef]
- Katz, B.; Rosen, J. Super-resolution in incoherent optical imaging using synthetic aperture with Fresnel elements. Opt. Express 2010, 18, 962–964. [Google Scholar] [CrossRef] [PubMed]
- Tahara, T. Polarization-filterless polarization-sensitive polarization-multiplexed phase-shifting incoherent digital holography (P4IDH). Opt. Lett. 2023, 48, 3881–3884. [Google Scholar] [CrossRef]
- Tahara, T. Incoherent digital holography with two polarization-sensitive phase-only spatial light modulators and reduced number of exposures. Appl. Opt. 2024, 63, B24–B31. [Google Scholar] [CrossRef] [PubMed]
- Tahara, T. Filter-free lens-free polarimetric incoherent digital holography. J. Opt. 2024, 26, 075707. [Google Scholar] [CrossRef]
- Bruning, J.H.; Herriott, D.R.; Gallagher, J.E.; Rosenfeld, D.P.; White, A.D.; Brangaccio, D.J. Digital Wavefront Measuring Interferometer for Testing Optical Surfaces and Lenses. Appl. Opt. 1974, 13, 2693–2703. [Google Scholar] [CrossRef]
- Yamaguchi, I.; Zhang, T. Phase-shifting digital holography. Opt. Lett. 1997, 22, 1268–1270. [Google Scholar] [CrossRef] [PubMed]
- Tahara, T.; Mori, R.; Kikunaga, S.; Arai, Y.; Takaki, Y. Dual-wavelength phase-shifting digital holography selectively extracting wavelength information from wavelength-multiplexed holograms. Opt. Lett. 2015, 40, 2810–2813. [Google Scholar] [CrossRef] [PubMed]
- Tahara, T.; Mori, R.; Arai, Y.; Takaki, Y. Four-step phase-shifting digital holography simultaneously sensing du-al-wavelength information using a monochromatic image sensor. J. Opt. 2015, 17, 125707. [Google Scholar] [CrossRef]
- Isomae, Y.; Sugawara, N.; Iwasaki, N.; Honda, T.; Amari, K. Phase-Only Spatial Light Modulator Having High Reflectance, High-Definition Pixels And High Photo-Durability. In Proceedings of the Digital Optical Technologies 2021, Online, 21–25 June 2021; Volume 11788, pp. 191–196. [Google Scholar]
- Kelner, R.; Katz, B.; Rosen, J. Optical sectioning using a digital Fresnel incoherent-holography-based confocal imaging system. Optica 2014, 1, 70–74. [Google Scholar] [CrossRef]
- Vijayakumar, A.; Kashter, Y.; Kelner, R.; Rosen, J. Coded aperture correlation holography system with improved performance [Invited]. Appl. Opt. 2017, 56, F67–F77. [Google Scholar] [CrossRef] [PubMed]
- Choi, K.; Yim, J.; Min, S. Optical defocus noise suppressing by using a pinhole-polarizer in Fresnel incoherent correlation holography. Appl. Opt. 2017, 56, F121–F127. [Google Scholar] [CrossRef] [PubMed]
- Tahara, T.; Ishii, A.; Ito, T.; Ichihashi, Y.; Oi, R. Single-shot wavelength-multiplexed digital holography for 3D fluorescent microscopy and other imaging modalities. Appl. Phys. Lett. 2020, 117, 031102. [Google Scholar] [CrossRef]
- Zhu, B.; Ueda, K. Real-time wavefront measurement based on diffraction grating holography. Opt. Commun. 2003, 225, 1–6. [Google Scholar] [CrossRef]
- Nobukawa, T.; Muroi, T.; Katano, Y.; Kinoshita, N.; Ishii, N. Single-shot phase-shifting incoherent digital holography with multiplexed checkerboard phase gratings. Opt. Lett. 2018, 43, 1698–1701. [Google Scholar] [CrossRef] [PubMed]
- Sakamaki, S.; Yoneda, N.; Nomura, T. Single-shot in-line Fresnel incoherent holography using a dual-focus checkerboard lens. Appl. Opt. 2020, 59, 6612–6618. [Google Scholar] [CrossRef]
- Kelner, R.; Rosen, J. Spatially incoherent single channel digital Fourier holography. Opt. Lett. 2012, 37, 3723–3725. [Google Scholar] [CrossRef] [PubMed]
- Kelner, R.; Rosen, J.; Brooker, G. Enhanced resolution in Fourier incoherent single channel holography (FISCH) with reduced optical path difference. Opt. Express 2013, 21, 20131–20144. [Google Scholar] [CrossRef] [PubMed]
- Tahara, T. Self-reference digital holography unit adaptable to optical microscope with light-emitting diode. Opt. Express 2024, 32, 46090–46102. [Google Scholar] [CrossRef]




| Left Region (50 × 50 Pixels) | Center Region (50 × 50 Pixels) | Right Region (50 × 50 Pixels) | |
|---|---|---|---|
| IDH with four-step PSI | 5.64 | 5.58 | 5.99 |
| IDH with three-step PSI | 6.83 | 7.20 | 7.38 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tahara, T. Portable Filter-Free Lens-Free Incoherent Digital Holography System. Photonics 2025, 12, 167. https://doi.org/10.3390/photonics12020167
Tahara T. Portable Filter-Free Lens-Free Incoherent Digital Holography System. Photonics. 2025; 12(2):167. https://doi.org/10.3390/photonics12020167
Chicago/Turabian StyleTahara, Tatsuki. 2025. "Portable Filter-Free Lens-Free Incoherent Digital Holography System" Photonics 12, no. 2: 167. https://doi.org/10.3390/photonics12020167
APA StyleTahara, T. (2025). Portable Filter-Free Lens-Free Incoherent Digital Holography System. Photonics, 12(2), 167. https://doi.org/10.3390/photonics12020167





