Macroscopic Fourier Ptychographic Imaging Based on Deep Learning
Abstract
1. Introduction
2. Theory of Fourier Ptychographic Imaging
2.1. Imaging Model of FP
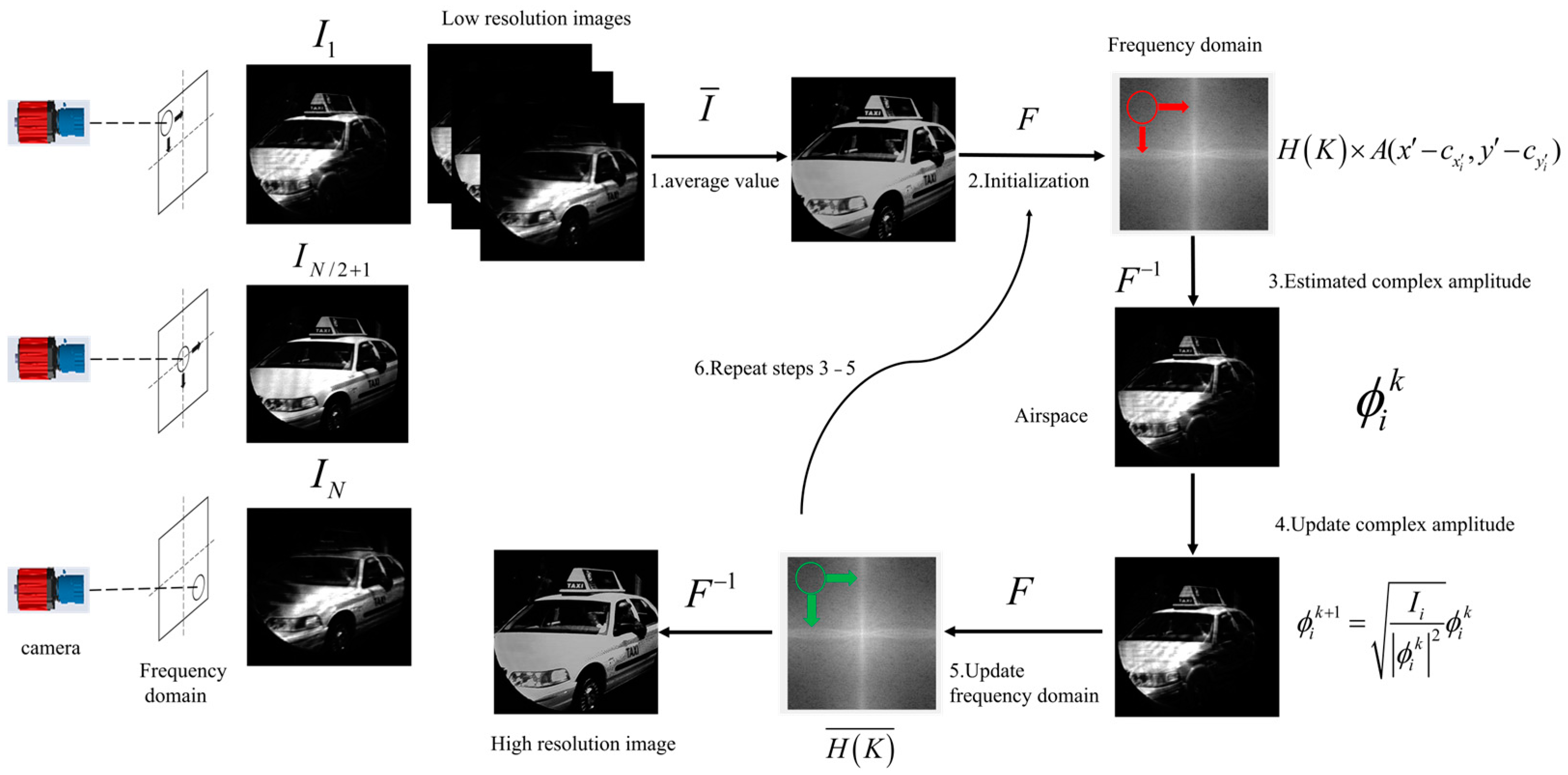
2.2. Imaging Process of FP
2.3. Simulation Results
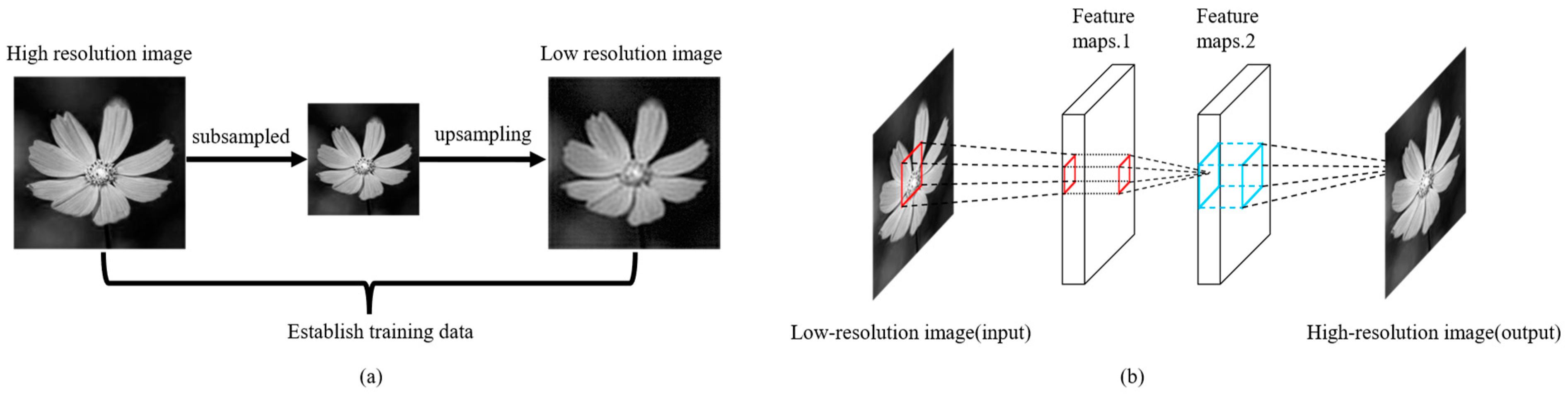
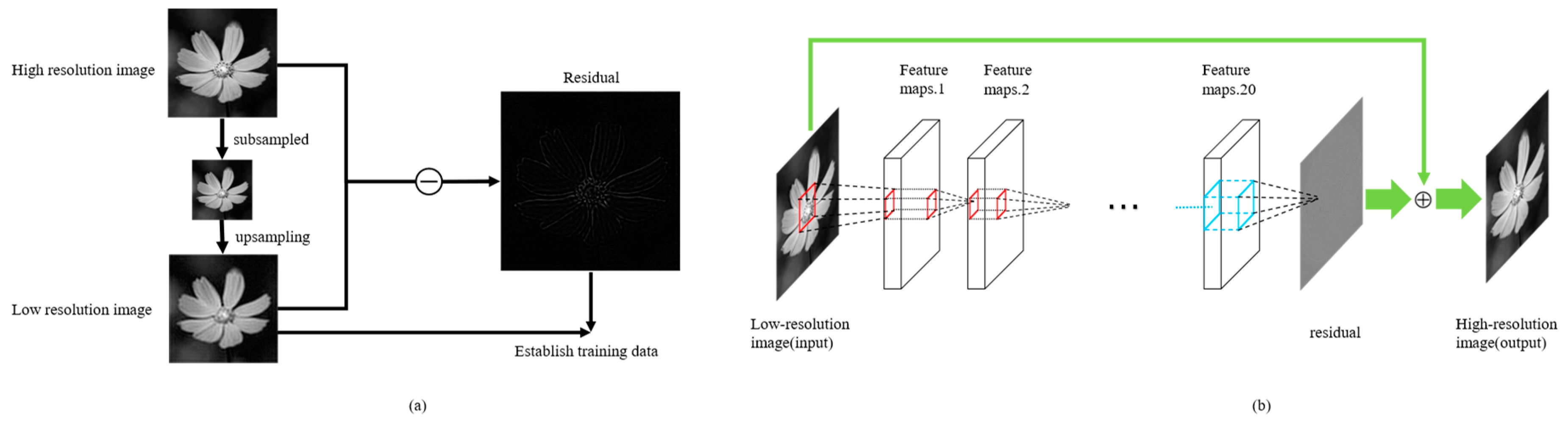
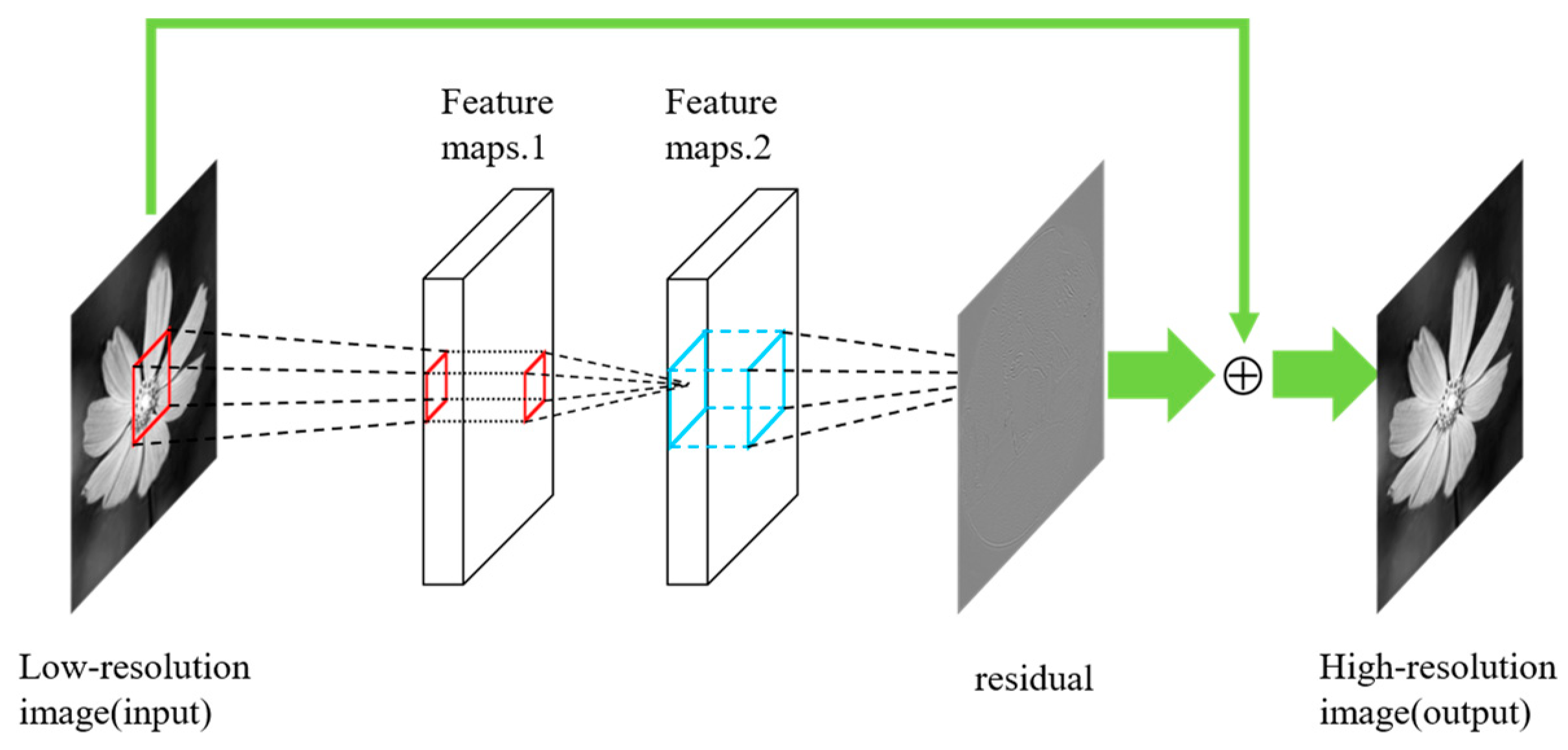
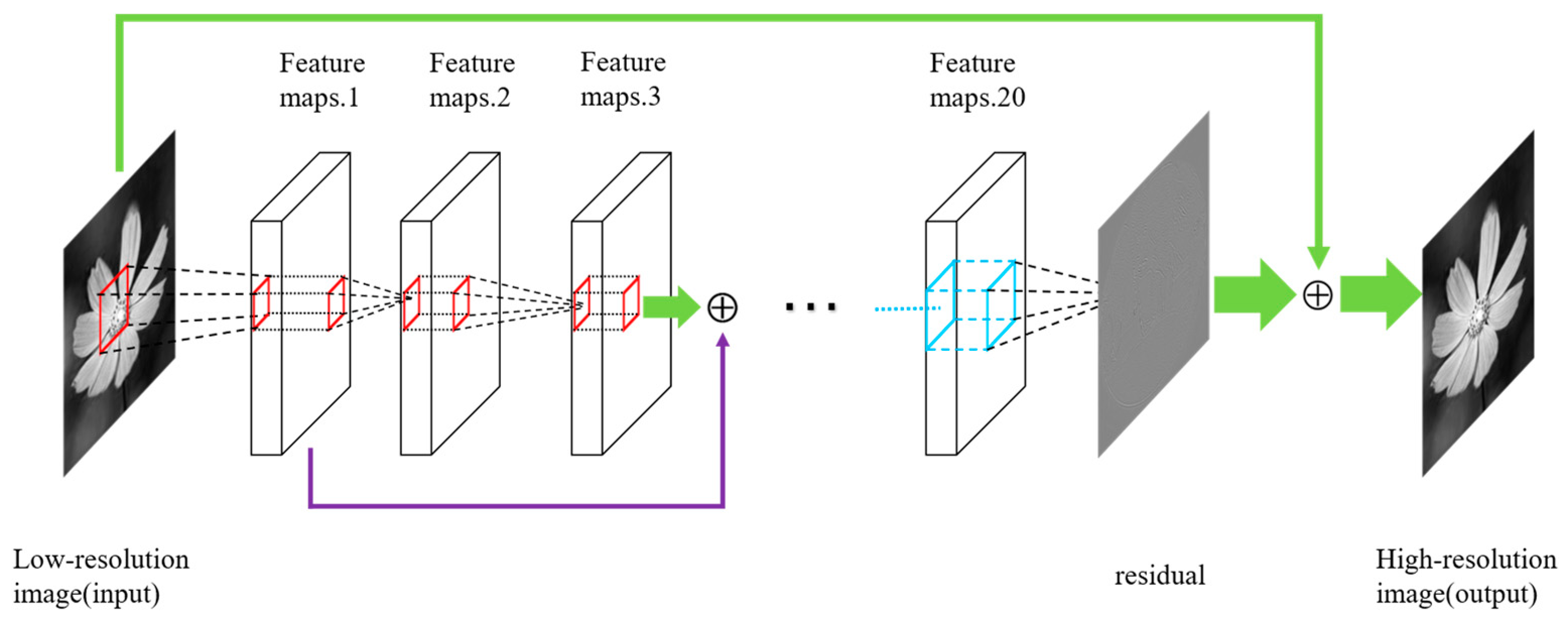
3. Deep Learning Network Architectures
4. Imaging Quality Evaluation Criteria
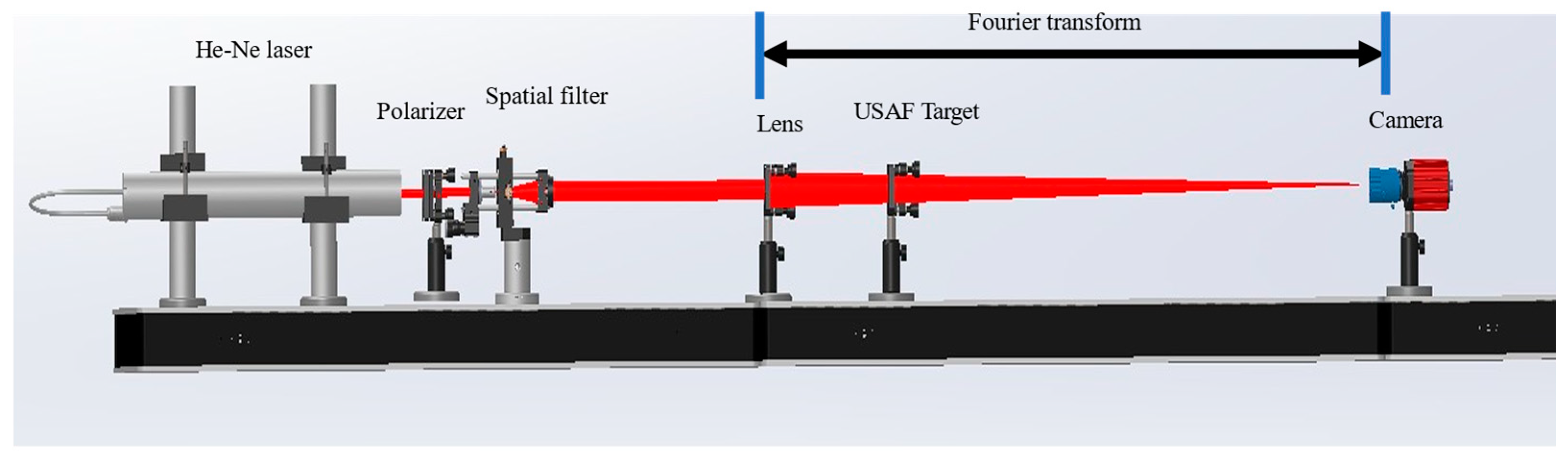
5. Macroscopic FP Experiment Based on Deep Learning
6. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| FP | Fourier ptychography |
| SRCNN | Super-resolution convolutional neural network |
| ResNet | Residual neural network |
| VDSR | Very deep super-resolution |
| FPM | Fourier ptychographic microscopy |
| CNN | Convolutional neural network |
| IAPR | International Association of Pattern Recognition |
| TC-12 | Technical Committee 12 |
| SR | Super-resolution |
| SSIM | Structural similarity index measurement |
| PSNR | Peak signal-to-noise ratio |
| SAR | Synthetic aperture ratio |
References
- Zheng, G.A.; Horstmeyer, R.; Yang, C.H. Wide-field, high-resolution Fourier ptychographic microscopy. Nat. Photonics 2013, 7, 739–745. [Google Scholar] [CrossRef] [PubMed]
- Zheng, G.A.; Shen, C.; Jiang, S.W.; Song, P.M.; Yang, C.H.E. Concept, implementations and applications of Fourier ptychography. Nat. Rev. Phys. 2021, 3, 207–223. [Google Scholar] [CrossRef]
- Sun, J.S.; Zuo, C.; Zhang, L.; Chen, Q. Resolution-enhanced Fourier ptychographic microscopy based on high-numerical-aperture illuminations. Sci. Rep. 2017, 7, 1187. [Google Scholar] [CrossRef] [PubMed]
- Tadesse, G.K.; Eschen, W.; Klas, R.; Tschernajew, M.; Tuitje, F.; Steinert, M.; Zilk, M.; Schuster, V.; Zürch, M.; Pertsch, T.; et al. Wavelength-scale ptychographic coherent diffractive imaging using a high-order harmonic source. Sci. Rep. 2019, 9, 1735. [Google Scholar] [CrossRef]
- Wang, A.Y.; Zhang, Z.Q.; Wang, S.Q.; Pan, A.; Ma, C.W.; Yao, B.L. Fourier Ptychographic Microscopy via Alternating Direction Method of Multipliers. Cells 2022, 11, 1512. [Google Scholar] [CrossRef]
- Dong, S.Y.; Horstmeyer, R.; Shiradkar, R.; Guo, K.K.; Ou, X.Z.; Bian, Z.C.; Xin, H.L.; Zheng, G.A. Aperture-scanning Fourier ptychography for 3D refocusing and super-resolution macroscopic imaging. Opt. Express 2014, 22, 13586–13599. [Google Scholar] [CrossRef]
- Holloway, J.; Asif, M.S.; Sharma, M.K.; Matsuda, N.; Horstmeyer, R.; Cossairt, O.; Veeraraghavan, A. Toward long-distance subdiffraction imaging using coherent camera arrays. IEEE Trans. Comput. Imaging 2016, 2, 251–265. [Google Scholar] [CrossRef]
- Holloway, J.; Wu, Y.C.; Sharma, M.K.; Cossairt, O.; Veeraraghavan, A. SAVI: Synthetic apertures for long-range, subdiffraction-limited visible imaging using Fourier ptychography. Sci. Adv. 2017, 3, e1602564. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Y.B.; Song, P.M.; Zhang, J.; Dai, Q.H. Fourier ptychographic microscopy with sparse representation. Sci. Rep. 2017, 7, 8664. [Google Scholar] [CrossRef]
- Yang, M.Y.; Fan, X.W.; Wang, Y.M.; Zhao, H. Experimental Study on the Exploration of Camera Scanning Reflective Fourier Ptychography Technology for Far-Field Imaging. Remote Sens. 2022, 14, 2264. [Google Scholar] [CrossRef]
- Bian, L.H.; Suo, J.L.; Chung, J.; Ou, X.Z.; Yang, C.H.; Chen, F.; Dai, Q.H. Fourier ptychographic reconstruction using Poisson maximum likelihood and truncated Wirtinger gradient. Sci. Rep. 2016, 6, 27384. [Google Scholar] [CrossRef] [PubMed]
- Cui, B.Q.; Zhang, S.H.; Wang, Y.C.; Hu, Y.; Hao, Q. Pose correction scheme for camera-scanning Fourier ptychography based on camera calibration and homography transform. Opt. Express 2022, 30, 20697–20711. [Google Scholar] [CrossRef] [PubMed]
- Yang, M.Y.; Fan, X.W.; Wang, Y.M.; Zhao, H. Analysis, Simulations, and Experiments for Far-Field Fourier Ptychography Imaging Using Active Coherent Synthetic-Aperture. Appl. Sci. 2022, 12, 2197. [Google Scholar] [CrossRef]
- Wang, B.W.; Li, S.; Chen, Q.; Zuo, C. Learning-based single-shot long-range synthetic aperture Fourier ptychographic imaging with a camera array. Opt. Lett. 2023, 48, 263–266. [Google Scholar] [CrossRef]
- Jiang, R.B.; Shi, D.F.; Wang, Y.J. Long-range fourier ptychographic imaging of the object in multidimensional motion. Opt. Commun. 2025, 575, 131307. [Google Scholar] [CrossRef]
- Zhang, Q.; Lu, Y.R.; Guo, Y.H.; Shang, Y.J.; Pu, M.B.; Fan, Y.L.; Zhou, R.; Li, X.Y.; Pan, A.; Zhang, F.; et al. 200 mm optical synthetic aperture imaging over 120 meters distance via macroscopic Fourier ptychography. Opt. Express 2024, 32, 44252–44264. [Google Scholar] [CrossRef]
- Yu, J.; Li, J.; Wang, X.; Zhang, J.; Liu, L.; Jin, Y. Microscopy image reconstruction method based on convolution network feature fusion. In Proceedings of the 2021 International Conference on Electronic Information Engineering and Computer Science (EIECS), Changchun, China, 23–26 September 2021; pp. 214–218. [Google Scholar]
- Jiang, S.W.; Guo, K.K.; Liao, J.; Zheng, G.A. Solving Fourier ptychographic imaging problems via neural network modeling and TensorFlow. Biomed. Opt. Express 2018, 9, 3306–3319. [Google Scholar] [CrossRef]
- Wu, Z.L.; Kang, I.K.; Yao, Y.D.; Jiang, Y.; Deng, J.J.; Klug, J.; Vogt, S.; Barbastathis, G. Three-dimensional nanoscale reduced-angle ptycho-tomographic imaging with deep learning (RAPID). eLight 2023, 3, 7. [Google Scholar] [CrossRef]
- Grubinger, M.; Clough, P.; Müller, H.; Deselaers, T. The IAPR TC12 Benchmark: A New Evaluation Resource for Visual Information Systems. Workshop Ontoimage 2006, 2, 13–55. [Google Scholar]
- Yang, J.; Wright, J.; Huang, T.S.; Ma, Y. Image super-resolution via sparse representation. IEEE Trans. Image Process. 2010, 19, 2861–2873. [Google Scholar] [CrossRef]
- Dong, C.; Loy, C.C.; He, K.; Tang, X. Image super-resolution using deep convolutional networks. IEEE Trans. Pattern Anal. Mach. Intell. 2015, 38, 295–307. [Google Scholar]
- Kim, J.; Lee, J.K.; Lee, K.M. Accurate Image Super-Resolution Using Very Deep Convolutional Networks. In Proceedings of the 2016 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Las Vegas, NV, USA, 27–30 June 2016; pp. 1646–1654. [Google Scholar]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Delving Deep into Rectifiers: Surpassing Human-Level Performance on ImageNet Classification. In Proceedings of the 2015 IEEE International Conference on Computer Vision (ICCV), Santiago, Chile, 7–13 December 2015; pp. 1026–1034. [Google Scholar]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep Residual Learning for Image Recognition. In Proceedings of the 2016 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Las Vegas, NV, USA, 27–30 June 2016; pp. 770–778. [Google Scholar]
- Kappeler, A.; Ghosh, S.; Holloway, J.; Cossairt, O.; Katsaggelos, A. Ptychnet: CNN based fourier ptychography. In Proceedings of the 2017 IEEE International Conference on Image Processing (ICIP), Beijing, China, 17–20 September 2017; pp. 1712–1716. [Google Scholar]







Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, J.; Sun, W.; Wu, F.; Shan, H.; Xie, X. Macroscopic Fourier Ptychographic Imaging Based on Deep Learning. Photonics 2025, 12, 170. https://doi.org/10.3390/photonics12020170
Liu J, Sun W, Wu F, Shan H, Xie X. Macroscopic Fourier Ptychographic Imaging Based on Deep Learning. Photonics. 2025; 12(2):170. https://doi.org/10.3390/photonics12020170
Chicago/Turabian StyleLiu, Junyuan, Wei Sun, Fangxun Wu, Haoming Shan, and Xiangsheng Xie. 2025. "Macroscopic Fourier Ptychographic Imaging Based on Deep Learning" Photonics 12, no. 2: 170. https://doi.org/10.3390/photonics12020170
APA StyleLiu, J., Sun, W., Wu, F., Shan, H., & Xie, X. (2025). Macroscopic Fourier Ptychographic Imaging Based on Deep Learning. Photonics, 12(2), 170. https://doi.org/10.3390/photonics12020170




