Analysis of Dissipation Mechanisms for Cesium Rydberg Atoms in Magic-Wavelength Optical Trap
Abstract
1. Introduction
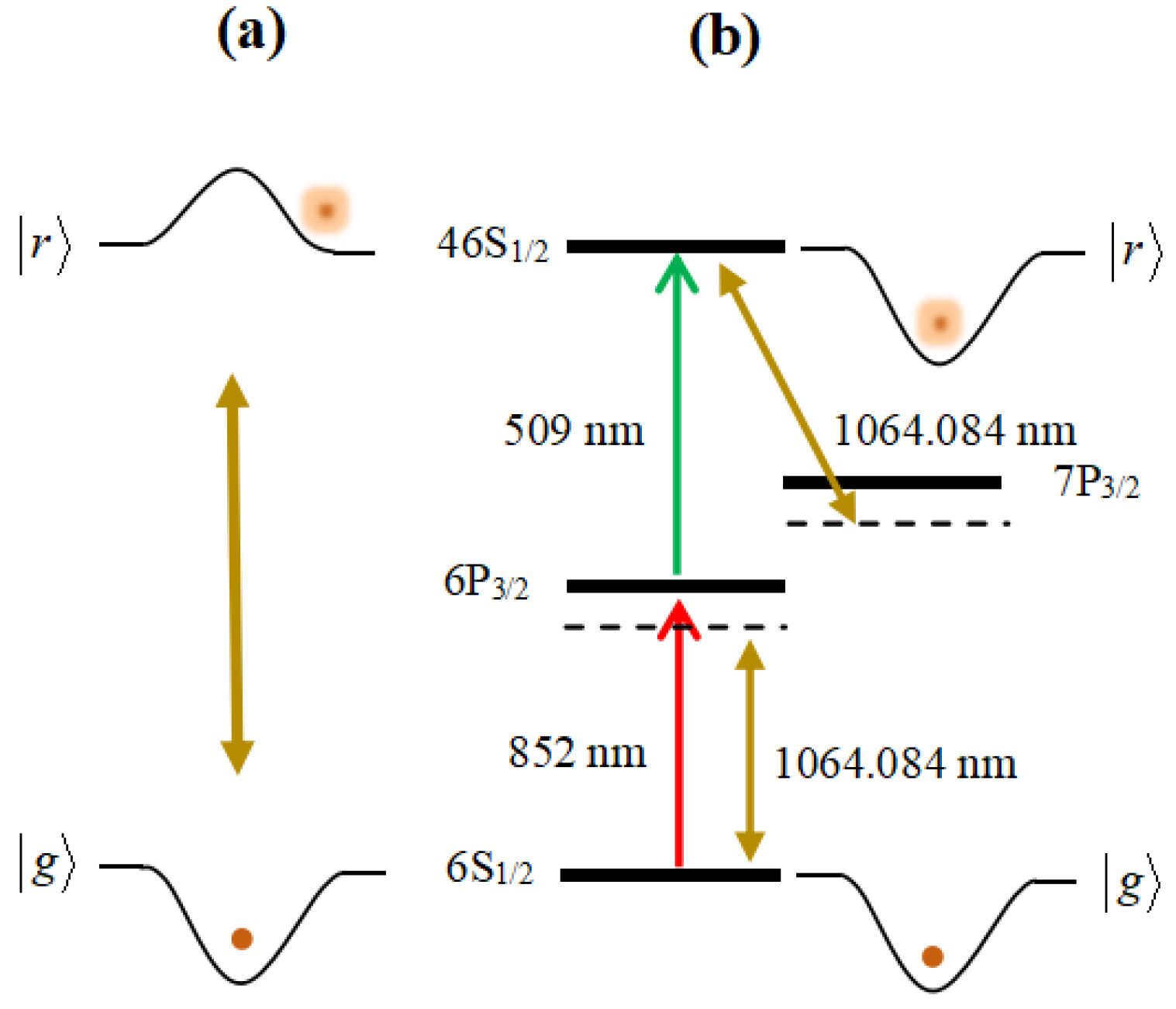
2. Trapping Principle
3. Magic Trapping of Ground and Rydberg States
3.1. Magic Condition for 6S1/2 and 46S1/2 States
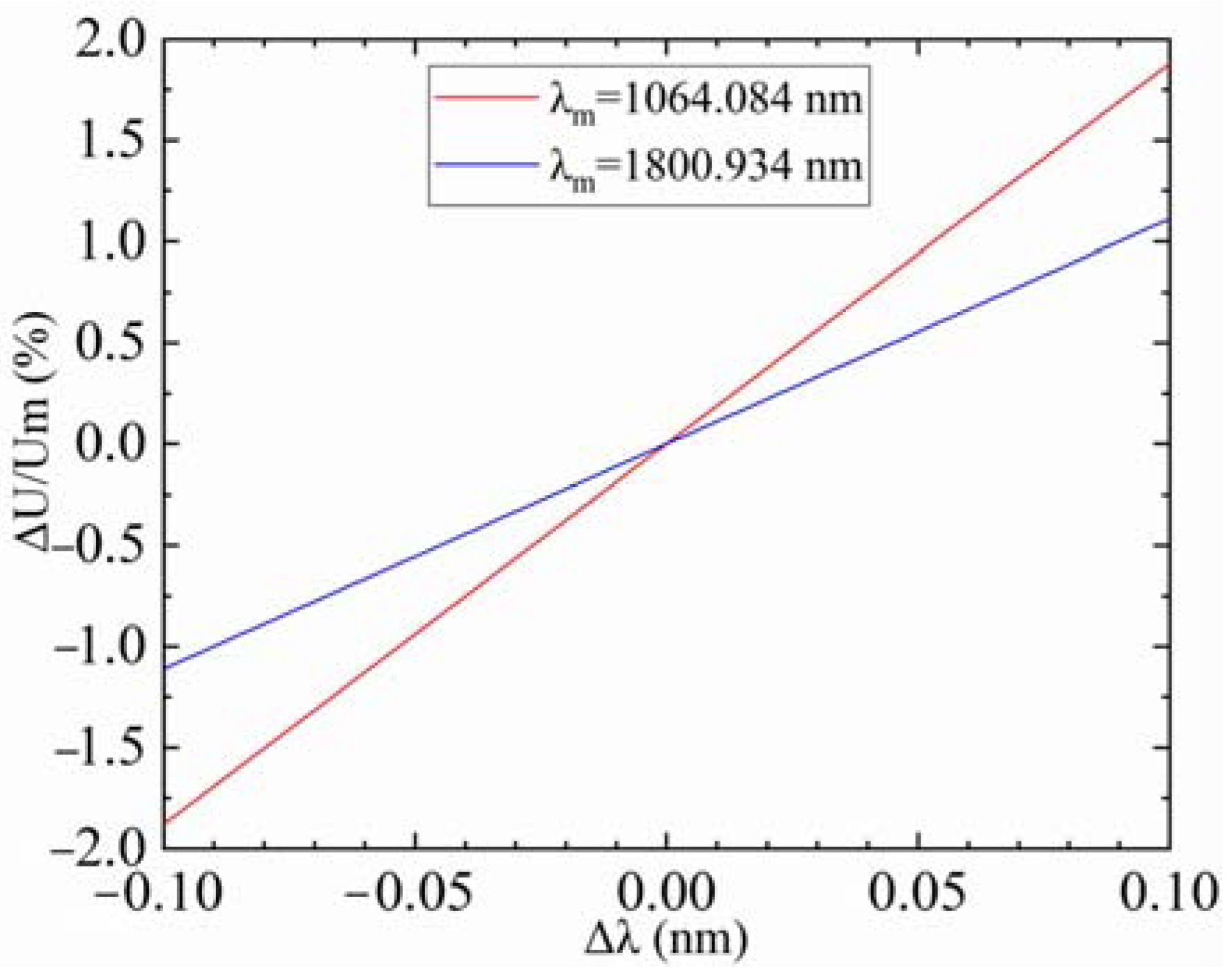
3.2. The Robustness of the Magic ODT
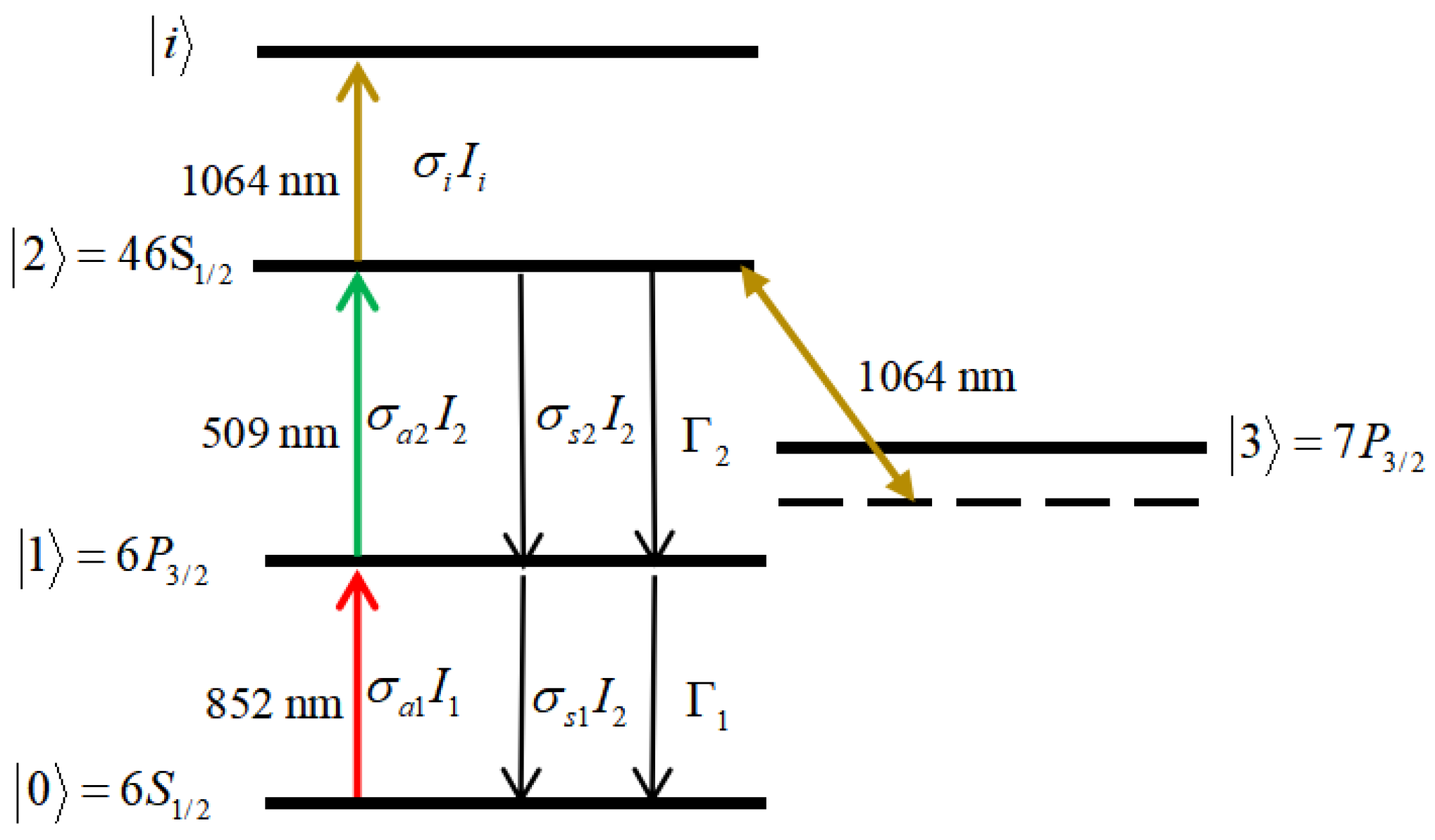
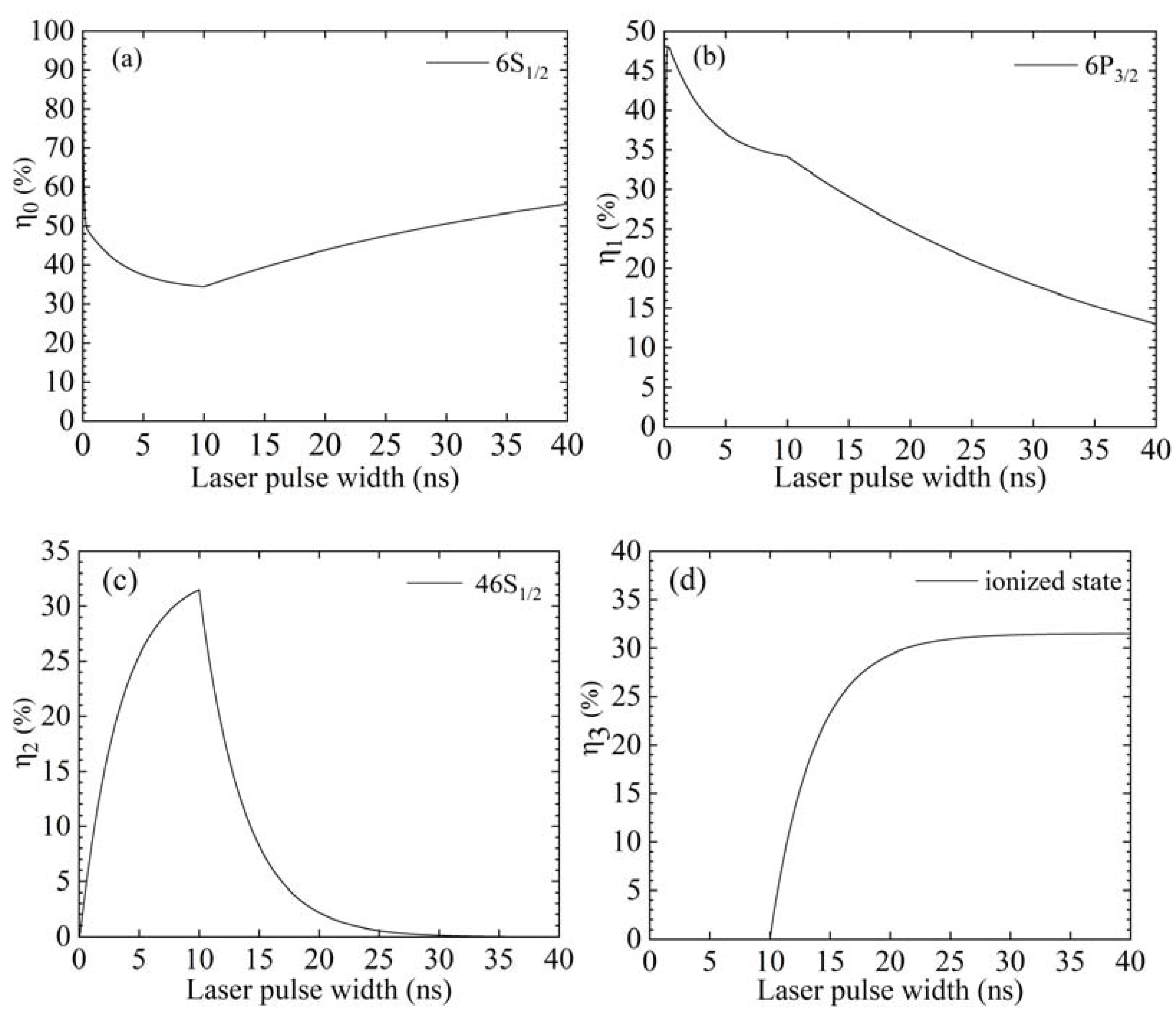
4. Trapping Lifetime of Cs Rydberg State in Magic ODT
4.1. Spontaneous Radiation and Blackbody Radiation
4.2. Photon Scattering
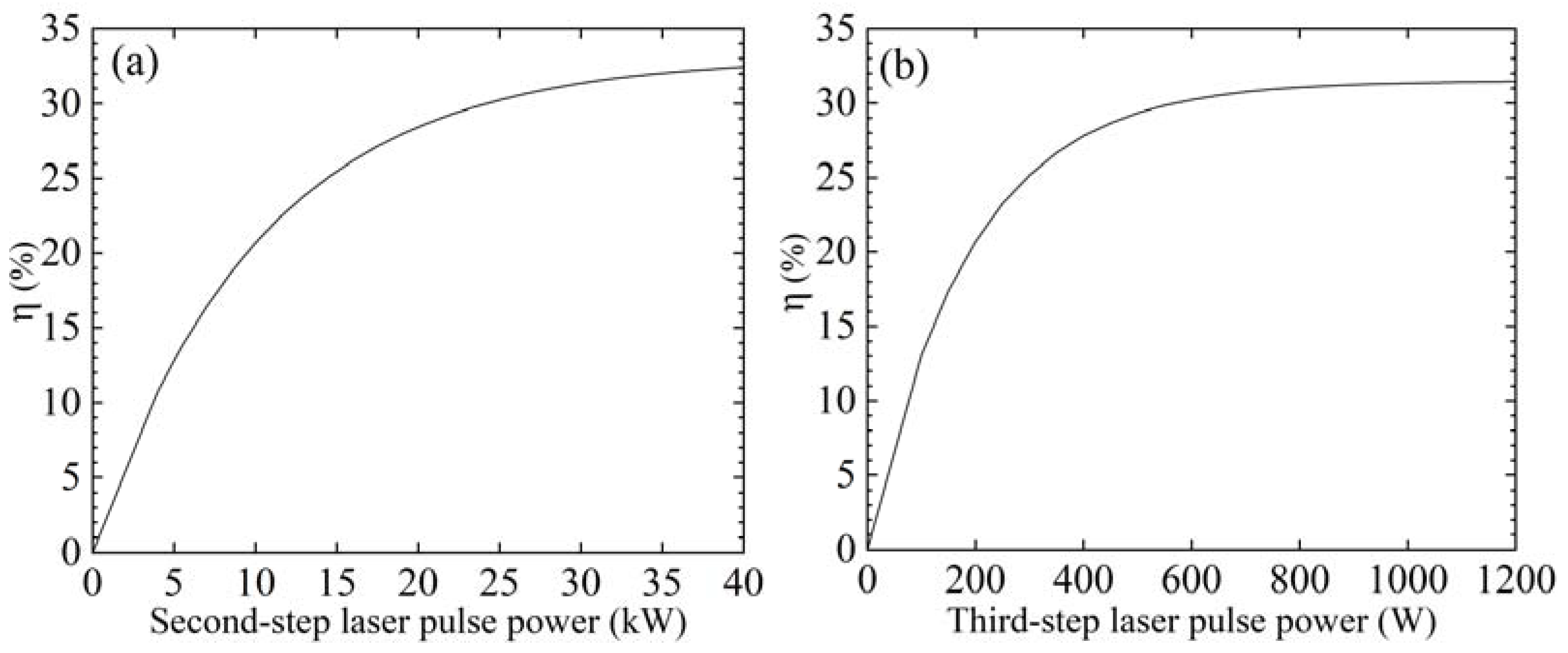
4.3. Photoionization
- (1)
- For 0 < t < t1,
- (2)
- For t1 < t < t2,
- (1)
- For 0 < t < t1,
- (2)
- For t1 < t < t2,
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Saffman, M.; Walker, T.G.; Mølmer, K. Quantum information with Rydberg atoms. Rev. Mod. Phys. 2010, 82, 2313–2363. [Google Scholar] [CrossRef]
- Deiglmayr, J. Long-range interactions between Rydberg atoms. Phys. Scr. 2016, 91, 104007. [Google Scholar] [CrossRef]
- Adams, C.S.; Pritchard, J.D.; Shaffer, J.P. Rydberg atom quantum technologies. J. Phys. B At. Mol. Opt. Phys. 2020, 53, 012002. [Google Scholar] [CrossRef]
- Zhang, Z.-Y.; Zhang, T.-Y.; Liu, Z.-K.; Ding, D.-S.; Shi, B.-S. Research progress of Rydberg many-body interaction. Acta Phys. Sin. 2020, 69, 180301. [Google Scholar] [CrossRef]
- Lesanovsky, I. Many-Body Spin Interactions and the Ground State of a Dense Rydberg Lattice Gas. Phys. Rev. Lett. 2011, 106, 025301. [Google Scholar] [CrossRef]
- Nguyen, H.; Lampen, J.; Berman, P.R.; Kuzmich, A. Differential nuclear-spin-dependent light shifts and state mixing of Rydberg atoms. Phys. Rev. A 2019, 100, 033412. [Google Scholar] [CrossRef]
- Saffman, M.; Walker, T.G. Analysis of a quantum logic device based on dipole-dipole interactions of optically trapped Rydberg atoms. Phys. Rev. A 2005, 72, 352–362. [Google Scholar] [CrossRef]
- Choi, J.-H.; Guest, J.R.; Povilus, A.P.; Hansis, E.; Raithel, G. Magnetic Trapping of Long-Lived Cold Rydberg Atoms. Phys. Rev. Lett. 2005, 95, 243001. [Google Scholar] [CrossRef]
- Hyafil, P.; Mozley, J.; Perrin, A.; Tailleur, J.; Nogues, G.; Brune, M.; Raimond, J.M.; Haroche, S. Coherence-Preserving Trap Architecture for Long-Term Control of Giant Ryberg Atoms. Phys. Rev. Lett. 2004, 93, 103001. [Google Scholar] [CrossRef]
- Grimm, R.; Weidemüller, M.; Ovchinnikov, Y.B. Optical dipole traps for neutral atoms. In Advances in Atomic, Molecular, and Optical Physics; Elsevier: Amsterdam, The Netherlands, 2000; Volume 42, pp. 95–170. [Google Scholar]
- Hankin, A.M.; Jau, Y.-Y.; Parazzoli, L.P.; Chou, C.W.; Armstrong, D.J.; Landahl, A.J.; Biedermann, G.W. Two-atom Rydberg blockade using direct 6S to n P excitation. Phys. Rev. A 2014, 89, 033416. [Google Scholar] [CrossRef]
- Lampen, J.; Nguyen, H.; Li, L.; Berman, P.R.; Kuzmich, A. Long-lived coherence between ground and Rydberg levels in a magic-wavelength lattice. Phys. Rev. A 2018, 98, 033411. [Google Scholar] [CrossRef]
- Levine, H.; Keesling, A.; Omran, A.; Bernien, H.; Schwartz, S.; Zibrov, A.S.; Endres, M.; Greiner, M.; Vuletić, V.; Lukin, M.D. High-Fidelity Control and Entanglement of Rydberg-Atom Qubits. Phys. Rev. Lett. 2018, 121, 123603. [Google Scholar] [CrossRef] [PubMed]
- Liu, Y.; Sun, Y.; Fu, Z.; Xu, P.; Wang, X.; He, X.; Wang, J.; Zhan, M. Infidelity Induced by Ground-Rydberg Decoherence of the Control Qubit in a Two-Qubit Rydberg-Blockade Gate. Phys. Rev. Appl. 2021, 15, 054020. [Google Scholar] [CrossRef]
- Suarez, E.; Wolf, P.; Weiss, P.; Slama, S. Superradiance decoherence caused by long-range Rydberg-atom pair interactions. Phys. Rev. A 2022, 105, 041302. [Google Scholar] [CrossRef]
- Steane, A.M.; Lucas, D.M. Quantum Computing with Trapped Ions, Atoms and Light. Fortschritte Der Phys. 2000, 48, 839–858. [Google Scholar] [CrossRef]
- Ye, J.; Kimble, H.J.; Katori, H. Quantum State Engineering and Precision Metrology Using State-Insensitive Light Traps. Science 2008, 320, 1734–1738. [Google Scholar] [CrossRef]
- Katori, H.; Ido, T.; Kuwata-Gonokami, M. Optimal Design of Dipole Potentials for Efficient Loading of Sr Atoms. J. Phys. Soc. Jpn. 1999, 68, 2479–2482. [Google Scholar] [CrossRef]
- Hogan, S.D.; Merkt, F. Demonstration of Three-Dimensional Electrostatic Trapping of State-Selected Rydberg Atoms. Phys. Rev. Lett. 2008, 100, 043001. [Google Scholar] [CrossRef]
- Anderson, S.E.; Younge, K.C.; Raithel, G. Trapping Rydberg Atoms in an Optical Lattice. Phys. Rev. Lett. 2011, 107, 263001. [Google Scholar] [CrossRef]
- Barredo, D.; Lienhard, V.; Scholl, P.; de Léséleuc, S.; Boulier, T.; Browaeys, A.; Lahaye, T. Three-Dimensional Trapping of Individual Rydberg Atoms in Ponderomotive Bottle Beam Traps. Phys. Rev. Lett. 2020, 124, 023201. [Google Scholar] [CrossRef]
- Bai, J.-D.; Liu, S.; He, J.; Wang, J. Towards implementation of a magic optical-dipole trap for confining ground-state and Rydberg-state Cs cold atoms. J. Phys. B At. Mol. Opt. Phys. 2020, 53, 155302. [Google Scholar]
- Bai, J.-D.; Wang, X.; Hou, X.; Liu, W.; Wang, J. Angle-Dependent Magic Optical Trap for the 6S1/2—nP3/2 Rydberg Transition of Cs Atoms. Photonics 2022, 9, 303. [Google Scholar] [CrossRef]
- Bai, J.-D.; Liu, S.; Liu, W.-Y.; Jie, Q.; Wang, J.-M. Theoretical analysis of polarization-angle-dependent magic-wavelength optical dipole trap of Cs atoms. Acta Phys. Sin. 2023, 72, 063102. [Google Scholar] [CrossRef]
- Bai, J.; Liu, Y.; Fan, S.; Liu, S.; Liu, W.; Jie, Q.; Li, Y.; Wang, J. Magic wavelengths for the 6S-7P transition of cesium atoms. Results Phys. 2023, 52, 106853. [Google Scholar] [CrossRef]
- Le Kien, F.; Schneeweiss, P.; Rauschenbeutel, A. Dynamical polarizability of atoms in arbitrary light fields: General theory and application to Cs. Eur. Phys. J. D 2013, 67, 92. [Google Scholar] [CrossRef]
- Manakov, N.; Ovsiannikov, V.; Rapoport, L. Atoms in a laser field. Phys. Rep. 1986, 141, 320–433. [Google Scholar] [CrossRef]
- Beloy, K. Theory of the ac Stark Effect on the Atomic Hyperfine Structure and Applications to Microwave Atomic Clocks. Ph.D. Thesis, University of Nevada, Reno, NV, USA, 2009. [Google Scholar]
- Šibalić, N.; Pritchard, J.D.; Adams, C.S.; Weatherill, K.J. ARC: An open-source library for calculating properties of alkali Rydberg atoms. Comput. Phys. Commun. 2017, 220, 319–331. [Google Scholar] [CrossRef]
- Robertson, E.J.; Šibalić, N.; Potvliege, R.M.; Jones, M.P.A. ARC 3.0: An expanded Python toolbox for atomic physics calculations. Comput. Phys. Commun. 2021, 261, 107814. [Google Scholar] [CrossRef]
- Yerokhin, V.A.; Buhmann, S.Y.; Fritzsche, S.; Surzhykovet, A. Electric dipole polarizabilities of Rydberg states of alkali-metal atoms. Phys. Rev. A 2016, 94, 032503. [Google Scholar] [CrossRef]
- Ovsiannikov, V.D.; Glukhov, I.L.; Nekipelov, E.A. Ionization cross sections and contributions of continuum to optical characteristics of Rydberg states. J. Phys. B At. Mol. Opt. Phys. 2012, 45, 095003. [Google Scholar] [CrossRef]
- Mitroy, J.; Safronova, M.S.; Clark, C.W. Theory and applications of atomic and ionic polarizabilities. J. Phys. B At. Mol. Opt. Phys. 2010, 43, 202001. [Google Scholar] [CrossRef]
- Gallagher, T.F. Rydberg Atoms; Cambridge University Press: Cambridge, UK, 2005. [Google Scholar]
- Saffman, M.; Walker, T.G. Publisher’s Note: Entangling single- and N-atom qubits for fast quantum state detection and transmission. Phys. Rev. A 2005, 72, 042302. [Google Scholar]
- Weber, K.H.; Sansonetti, C.J. Accurate energies of nS, nP, nD, nF, and nG levels of neutral Cs. Phys. Rev. A 1987, 35, 4650–4660. [Google Scholar] [CrossRef] [PubMed]
- Notermans, R.P.M.J.W.; Rengelink, R.J.; van Leeuwen, K.A.H.; Vassen, W. Magic wavelengths for the 23S→21S transition in helium. Phys. Rev. A 2014, 90, 052508. [Google Scholar] [CrossRef]
- Gillespie, D.T. Approximate accelerated stochastic simulation of chemically reacting systems. J. Chem. Phys. 2001, 115, 1716–1733. [Google Scholar] [CrossRef]
- Qi, X.-Q.; Wang, F.; Dai, C.-J. Photoexcitation and photoionization of alkali atoms. Acta Phys. Sin. 2015, 64, 133201. [Google Scholar]
- Sang, C.-C.; Wan, J.-J.; Dong, C.-Z.; Ding, X.-B.; Jiang, J. Relaxation effect in photoionization process of lithium. Acta Phys. Sin. 2008, 57, 2152–2160. [Google Scholar] [CrossRef]
- Vacchini, B.; Breuer, H.-P. Exact master equations for the non-Markovian decay of a qubit. Phys. Rev. A 2010, 81, 042103. [Google Scholar] [CrossRef]
- Shen, H.Z.; Wang, Q.; Yi, X.X. Dispersive Readout Non-Markovian Environments. Phys. Rev. A 2022, 105, 023707. [Google Scholar] [CrossRef]
- Breuer, H.-P.; Laine, E.-M.; Piilo, J. Measure for the Degree of Non-Markovian Behavior of Quantum Processes in Open Systems. Phys. Rev. Lett. 2009, 103, 210401. [Google Scholar] [CrossRef]
- Romans, K.L.; Acharya, B.P.; Silva, A.D.; Foster, K.; Russ, O.; Fischer, D. Photoionization of Rydberg atoms out of an optical dipole trap. arXiv 2023, arXiv:2304.09767. [Google Scholar]


| Transition | Transition Wavelength (nm) | Magic Wavelength (nm) | Polarizability (a.u.) | Magic Detuning (GHz) |
|---|---|---|---|---|
| 46S1/2 ↔ 7P1/2 | 1043.980 | 1043.974 | 1125.554 | 1.6515 |
| 46S1/2 ↔ 7P3/2 | 1064.090 | 1064.084 | 1049.664 | 1.5897 |
| 46S1/2 ↔ 8P1/2 | 1774.540 | 1774.523 | 502.563 | 1.6196 |
| 46S1/2 ↔ 8P3/2 | 1800.960 | 1800.934 | 498.655 | 2.4049 |
| Transition | Transition Wavelength (nm) | Reduced Matrix Element (ea0) | Einstein A Coefficient (s−1) | Frequency Detuning (GHz) | Photon Scattering Rate (s−1) |
|---|---|---|---|---|---|
| 46S1/2 ↔ 7P3/2 | 1064.09 | 0.039 | 3.89 × 103 | 1.5897 | 262.89 |
| 46S1/2 ↔ 7P1/2 | 1043.98 | 0.029 | 4.36 × 103 | −5429.197 | 2.3 × 10−5 |
| Cs at M = 132.9 g/mol, T = 944.15 K | ||||||
|---|---|---|---|---|---|---|
| Laser | Excitation Path | ν0 (Hz) | A (s−1) | λ (nm) | P (W) | δ (cm2) |
| First laser | 6S1/2 ↔ 6P3/2 | 351.72571 × 1012 | 3.226 × 107 | 852 | 100 | 0.03 |
| Second laser | 6P3/2 ↔ 46S1/2 | 587.94712 × 1012 | 2.246 × 104 | 509 | 3 × 104 | 0.03 |
| Third laser | 46S1/2 ↔|i> | 1064 | 1000 | 0.03 | ||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fan, S.; Liu, Y.; Liu, W.; Zhao, Y.; Li, Y.; Bai, J. Analysis of Dissipation Mechanisms for Cesium Rydberg Atoms in Magic-Wavelength Optical Trap. Photonics 2025, 12, 138. https://doi.org/10.3390/photonics12020138
Fan S, Liu Y, Liu W, Zhao Y, Li Y, Bai J. Analysis of Dissipation Mechanisms for Cesium Rydberg Atoms in Magic-Wavelength Optical Trap. Photonics. 2025; 12(2):138. https://doi.org/10.3390/photonics12020138
Chicago/Turabian StyleFan, Shaofeng, Yang Liu, Wenyuan Liu, Yang Zhao, Yijun Li, and Jiandong Bai. 2025. "Analysis of Dissipation Mechanisms for Cesium Rydberg Atoms in Magic-Wavelength Optical Trap" Photonics 12, no. 2: 138. https://doi.org/10.3390/photonics12020138
APA StyleFan, S., Liu, Y., Liu, W., Zhao, Y., Li, Y., & Bai, J. (2025). Analysis of Dissipation Mechanisms for Cesium Rydberg Atoms in Magic-Wavelength Optical Trap. Photonics, 12(2), 138. https://doi.org/10.3390/photonics12020138





