Temporal Faraday and Other Magneto-Optic Effects
Abstract
1. Introduction
2. Single Temporal Interface
3. Restored Frequency
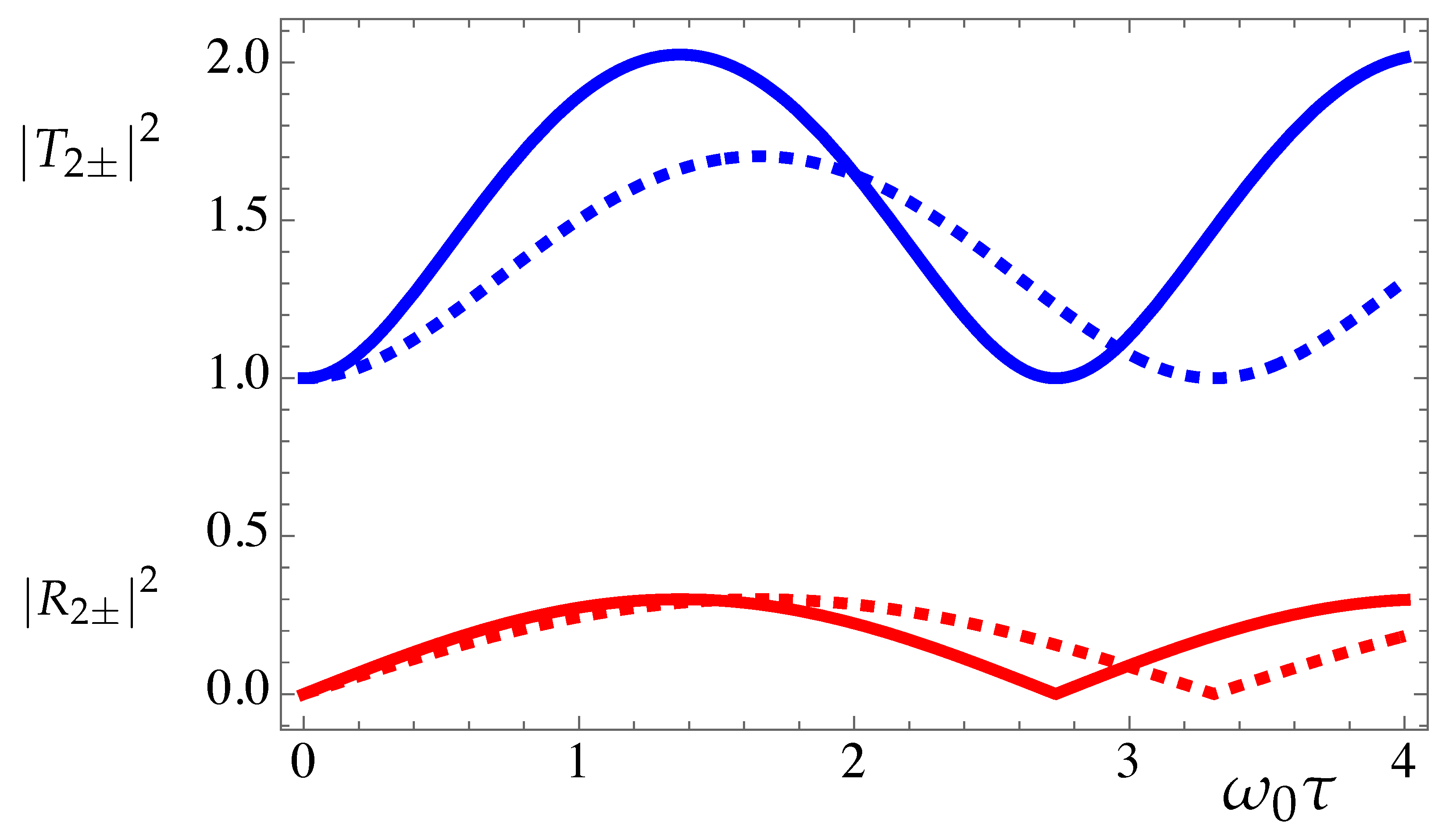
4. Specific Examples
4.1. Magnetized Plasmas
4.2. Nonlinear Kerr Medium
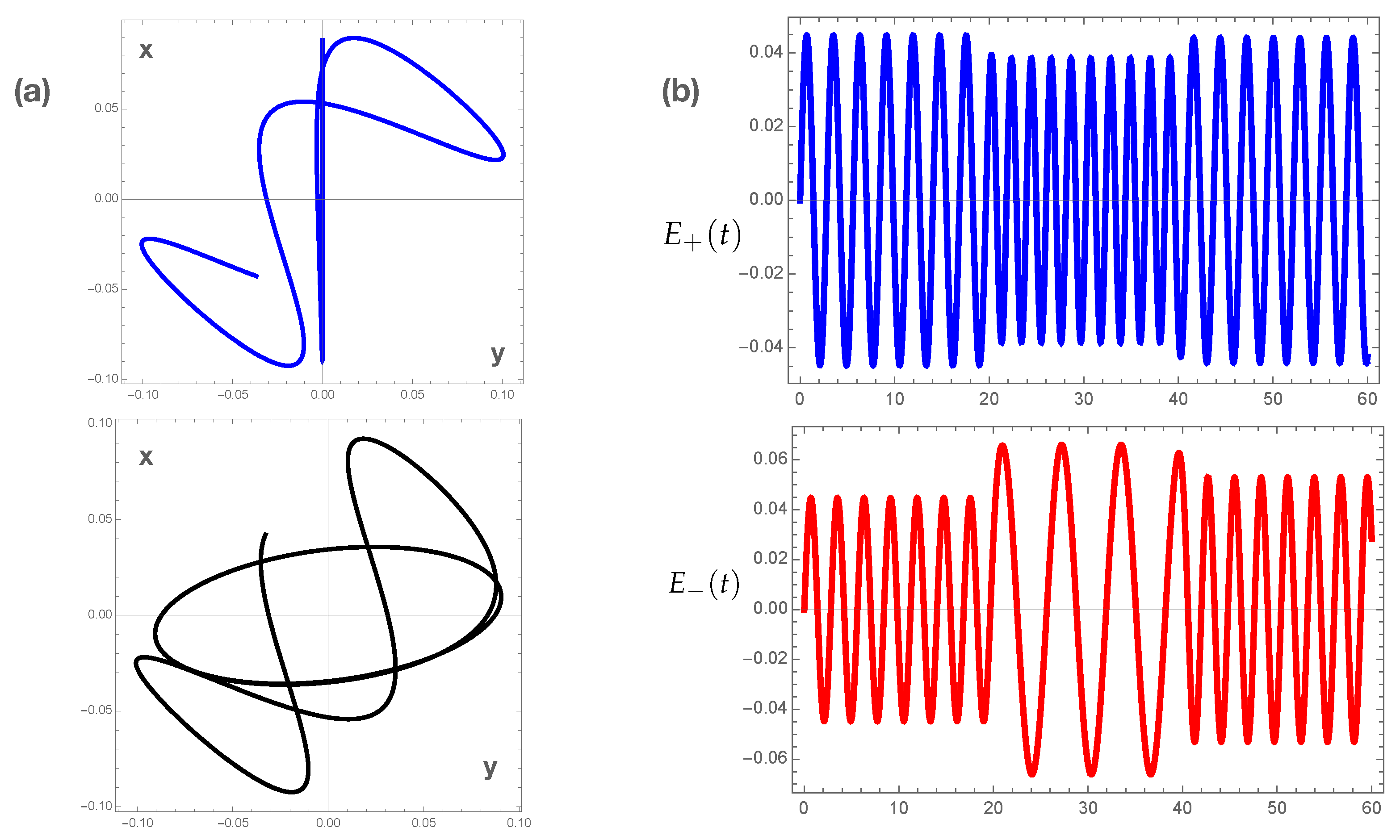
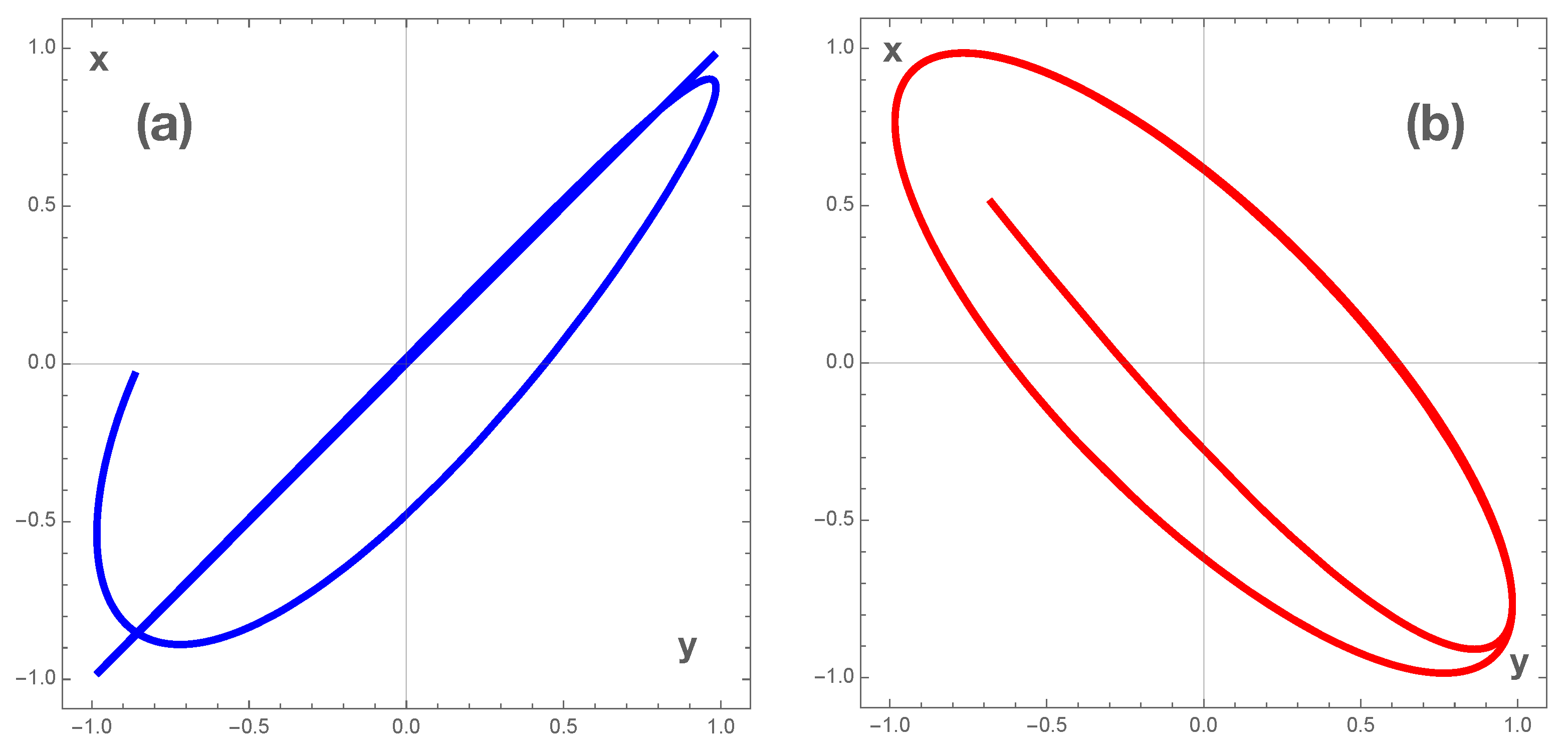
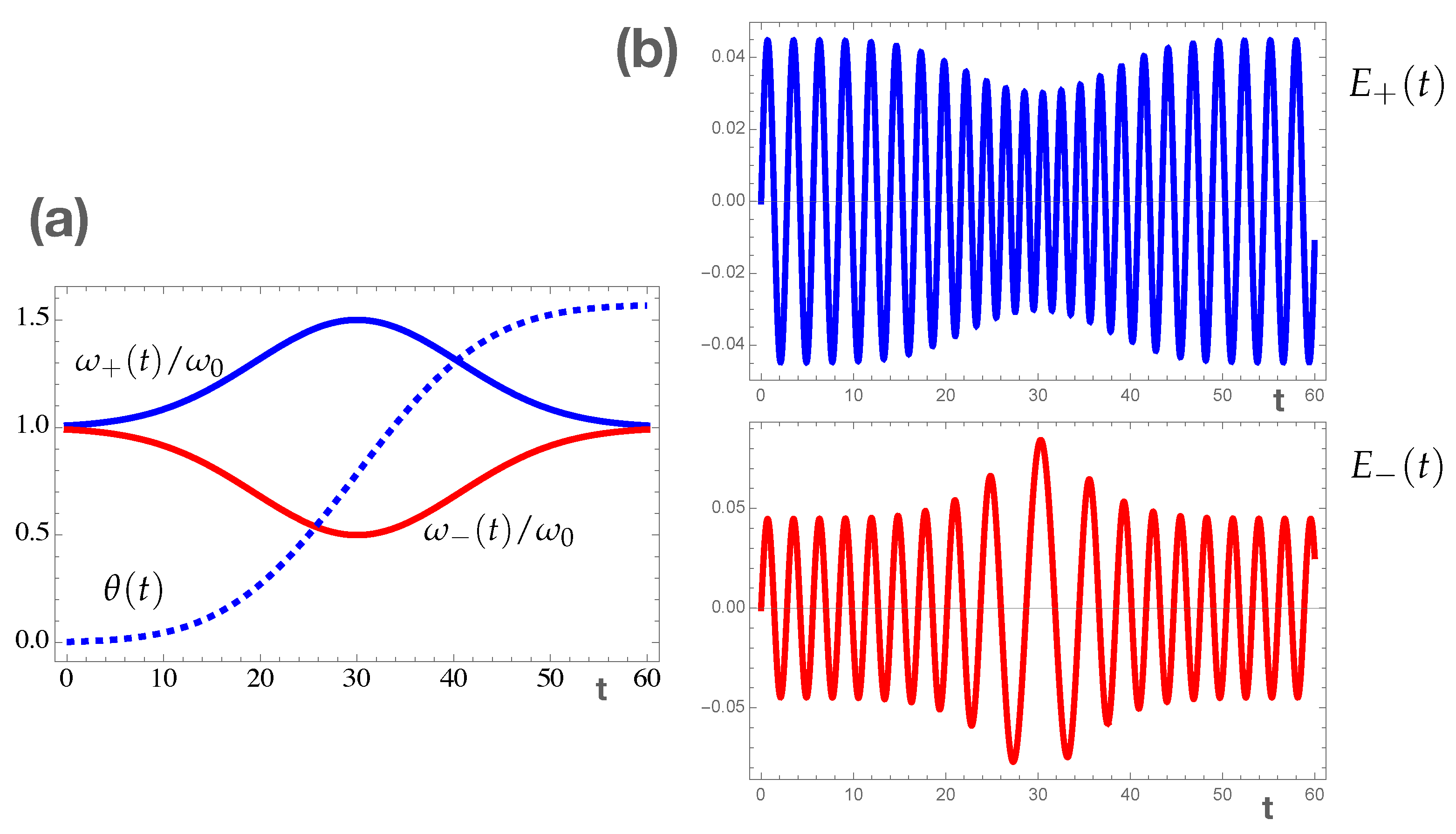
5. Slow Time Variations
6. Conclusions
Funding
Data Availability Statement
Conflicts of Interest
References
- Plansinis, B.W.; Donaldson, W.R.; Agrawal, G.P. What is the Temporal Analog of Reflection and Refraction of Optical Beams? Phys. Rev. Lett. 2015, 115, 183901. [Google Scholar] [CrossRef]
- Biancalana, F.; Amann, A.; Uskov, A.V.; O’Reilly, E.P. Dynamics of Light Propagation in Spatiotemporal Dielectric Structures. Phys. Rev. E 2007, 75, 046607. [Google Scholar] [CrossRef]
- Mendonça, J.T.; Shukla, P.K. Time Refraction and Time Reflection: Two Basic Concepts. Phys. Scr. 2002, 65, 160. [Google Scholar] [CrossRef]
- Galiffi, E.; Tirole, R.; Yin, S.; Li, H.; Vezzoli, S.; Huidobro, P.A.; Silveirinha, M.G.; Sapienza, R.; AlùA; Pendry, J.B. Photonics of Time-Varying Media. Adv. Photonics 2022, 4, 014002. [Google Scholar] [CrossRef]
- Mendonça, J.T. Time Refraction and Spacetime Optics. Symmetry 2024, 16, 1548. [Google Scholar] [CrossRef]
- Moussa, H.; Xu, G.; Yin, S.; Galiffi, E.; Radi, Y.; Alú, A. Observation of Temporal reflection and Broadband Frequency Translation at Photonic Time Interfaces. Nat. Phys. 2023, 19, 863. [Google Scholar] [CrossRef]
- Lustig, E.; Segal, O.; Saha, S.; Bordo, E.; Chowdhury, S.N.; Sharabi, Y.; Fleischer, A.; Boltasseva, A.; Cohen, O.; Shalaev, V.M.; et al. Time-refraction optics with single cycle modulation. Nanophotonics 2023, 12, 2221. [Google Scholar] [CrossRef] [PubMed]
- Mendonça, J.T.; Martins, A.M.; Guerreiro, A. Temporal Beam Splitter and Temporal Interference. Phys. Rev. A 2003, 68, 043801. [Google Scholar] [CrossRef]
- Rizza, C.; Castaldi, G.; Galdi, V. Short-Pulsed Metamaterials. Phys. Rev. Lett. 2022, 128, 257402. [Google Scholar] [CrossRef] [PubMed]
- Sandberg, R.T.; Thomas, A.G.R. Photon Acceleration from Optical to XUV. Phys. Rev. Lett. 2023, 130, 085001. [Google Scholar] [CrossRef]
- Shcherbakov, M.R.; Werner, K.; Fan, Z.; Talisa, N.; Chowdhury, E.; Shvets, G. Photon Acceleration and Tunable Broadband Harmonics Generation in Nonlinear Time-dependent Metasurfaces. Nat. Commun. 2019, 10, 1345. [Google Scholar] [CrossRef] [PubMed]
- Zhang, J.; Donaldson, W.R.; Agrawal, G.P. Spatiotemporal Bragg gratings forming inside a nonlinear dispersive medium. Opt. Lett. 2024, 49, 5854. [Google Scholar] [CrossRef] [PubMed]
- Lustig, E.; Segal, O.; Saha, S.; Fruhling, C.; Shalaev, V.M.; Boltasseva, A.; Segev, M. Photonic time-crystals—Fundamental concepts. Opt. Express 2023, 31, 9165. [Google Scholar] [CrossRef] [PubMed]
- Wang, X.; Mirmoosa, M.S.; Asadchy, V.S.; Rockstuhl, C.; Fan, S.; Tretyakov, S. Metasurface-based realization of photonic time crystals. Sci. Adv. 2023, 9, eadg7541. [Google Scholar] [CrossRef]
- Sacha, K.; Zakrzewski, J. Time Crystals: A review. Rep. Prog. Phys. 2018, 81, 016401. [Google Scholar] [CrossRef]
- Lyubarov, M.; Lumer, Y.; Dikopoltsev, A.; Lustig, E.; Sharabi, Y.; Segev, M. Amplified Emission and Lasing in Photonic Time Crystals. Science 2022, 377, 425. [Google Scholar] [CrossRef] [PubMed]
- Horsley, S.A.R.; Pendry, J.B. Traveling Wave Amplification in Stationary Gratings. Phys. Rev. Lett. 2024, 133, 156903. [Google Scholar] [CrossRef] [PubMed]
- Svidzinsky, A. Time Reflection of Light from a Quantum Perspective and Vacuum Entanglement. Opt. Express 2024, 32, 15623. [Google Scholar] [CrossRef]
- Prain, A.; Vezzoli, S.; Westerberg, N.; Roger, T.; Faccio, D. Spontaneous Photon Production in Time-dependent Epsilon-near-zero Materials. Phys. Rev. Lett. 2017, 118, 133904. [Google Scholar] [CrossRef] [PubMed]
- Mendonça, J.T.; Guerreiro, A.; Martins, A.M. Quantum Theory of Time Refraction. Phys. Rev. A 2000, 62, 033805. [Google Scholar] [CrossRef]
- Dodonov, V.V.; Klimov, A.B.; Nikonov, D.E. Quantum Phenomena in Nonstationary Media. Phys. Rev. A 1993, 47, 4422. [Google Scholar] [CrossRef]
- Ok, F.; Bahrami, A.; Caloz, C. Electron Scattering at a Potential Temporal Step Discontinuity. Sci. Rep. 2024, 14, 5559. [Google Scholar] [CrossRef] [PubMed]
- Engheta, N. Four-dimensional optics using time-varying metamaterials. Science 2023, 379, 1190. [Google Scholar] [CrossRef] [PubMed]
- Yuan, L.; Fan, S. Temporal Modulation Brings Metamaterials Into New Era. Light Sci. Appl. 2022, 11, 173. [Google Scholar] [CrossRef] [PubMed]
- Caloz, C.; Deck-Léger, Z.-L. Spacetime metamaterials. IEEE Trans. Antennas Propag. 2019, 67, 1569. [Google Scholar]
- Bruno, V.; DeVault, C.; Vezzoli, S.; Kudyshev, Z.; Kudyshev, Z.; Huq, T.; Mignuzzi, S.; Jacassi, A.; Saha, S.; Shah, Y.D.; et al. Negative Refraction in Time-Varying Strongly Coupled Plasmonic-Antenna Epsilon Near-Zero Systems. Phys. Rev. Lett. 2020, 124, 043902. [Google Scholar] [CrossRef] [PubMed]
- Zhou, Y.; Alam, M.Z.; Karimi, M.; Upham, J.; Reshef, O.; Liu, C.; Willner, A.E.; Boyd, R.W. Broadband Frequency Translation Through Time Refraction in an Epsilon-Near-Zero Material. Nat. Commun. 2020, 11, 2180. [Google Scholar] [CrossRef] [PubMed]
- Li, H.; Yin, S.; Alú, A. Nonreciprocity and Faraday Rotation at Time Interfaces. Phys. Rev. Lett. 2022, 128, 173901. [Google Scholar] [CrossRef]
- Zhang, G.P.; Hübner, W.; Lefkidis, G.; Bai, Y.; George, T.F. Paradigm of the Time-resolved Magneto-optical Kerr Effect for Femtosecond Magnetism. Nat. Phys. 2009, 5, 499. [Google Scholar] [CrossRef]
- Ino, Y.; Shimano, R.; Svirko, Y.; Kuwata-Gonokami, M. Terahertz Time Domain Magneto-optical Ellipsometry in Reflection Geometry. Phys. Rev. B 2004, 70, 155101. [Google Scholar] [CrossRef]
- Ding, J.; Jin, W.; Chen, Q.; Hou, C.; Yu, Y.; Du, L.; Li, C.; Zeng, F.; Wu, A. Optical Properties, Magnetooptical Properties and Terahertz Time-domain Spectrum of Tb3Sc2Al3O12 Crystals grown by Optical Floating Zone Methods. Opt. Mat. Express 2018, 8, 2880. [Google Scholar] [CrossRef]
- Swanson, D.G. Plasma Waves, 2nd ed.; Institute of Physics Publishing: Bristol, UK, 2003. [Google Scholar]
- Landau, L.D.; Lifshitz, E.M.; Pitaevskii, L.P. Electrodynamics of Continuous Media, 2nd ed.; Butterworth-Heinemann: Oxford, UK, 1984; Volume 8. [Google Scholar]
- Mendonça, T.T.; Guerreiro, A. Time refraction and the quantum properties of vacuum. Phys. Rev. A 2005, 72, 063805. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mendonça, J.T. Temporal Faraday and Other Magneto-Optic Effects. Photonics 2025, 12, 139. https://doi.org/10.3390/photonics12020139
Mendonça JT. Temporal Faraday and Other Magneto-Optic Effects. Photonics. 2025; 12(2):139. https://doi.org/10.3390/photonics12020139
Chicago/Turabian StyleMendonça, José Tito. 2025. "Temporal Faraday and Other Magneto-Optic Effects" Photonics 12, no. 2: 139. https://doi.org/10.3390/photonics12020139
APA StyleMendonça, J. T. (2025). Temporal Faraday and Other Magneto-Optic Effects. Photonics, 12(2), 139. https://doi.org/10.3390/photonics12020139




