Ultra-Compact Inverse-Designed Integrated Photonic Matrix Compute Core

Abstract

Leveraging our developed Global–Local Integrated Topology inverse design algorithm, we designed an efficient, compact, and symmetrical power splitter on a silicon-on-insulator platform. This device achieves a low insertion loss of 0.18 dB and a power imbalance of <0.0002 dB between its output ports within an ultra-compact footprint of 5.5 µm × 2.5 µm. The splitter, combined with an ultra-compact 0–π phase shifter measuring only 4.5 µm × 0.9 µm on the silicon-on-insulator platform, forms an ultra-compact inverse-designed integrated photonic matrix compute core, thus enabling the function of matrix operations in optical neural networks. Through a networked cascade of power splitters and phase shifters, this silicon-based photonic matrix compute core achieves an integration density of ~26,000 computational units/mm². Moreover, it attained 99.05% accuracy in handwritten digit recognition (0–9) and exhibited strong robustness against fabrication errors, maintaining >80% accuracy with >0.9 probability under simulated random fabrication errors.

1. Introduction

The rapid advancement of semiconductor technology has enabled artificial neural networks (ANNs) to achieve remarkable success in domains including object classification [1], computer vision [2], real-time translation [3], and autonomous driving [4]. However, conventional ANNs exhibit computational speed limitations intrinsic to the von Neumann architecture [5]. Within this context, optical neural networks (ONNs) have emerged as promising alternatives to traditional ANNs owing to their inherent advantages: ultra-wide-bandwidth, high computational speed, and massive parallelism [6,7,8]. Existing ONN implementations include Mach–Zehnder interferometer (MZI) cascades [6,9,10,11], integrated diffractive optical neural networks (DONNs) [12,13,14,15], compact multi-mode interference convolutional processors [16], and neural networks implemented using phase-change materials (PCMs) [17]. Among these approaches, ONNs based on the multistage interference principle, such as MZI-based ONNs, have been widely adopted by researchers due to their high scalability and excellent classification accuracy [18]. However, these methods remain constrained by low integration density (<10³ units/mm², typically ~10² units/mm²). Constructing highly-integrated photonic platforms remains a significant challenge for multistage interference-based ONNs.

In recent years, inverse design methodologies have emerged as powerful tools for developing ultra-compact integrated photonic devices [19,20,21,22,23,24,25,26], significantly enhancing the integration density of photonic platforms. In our previous work, we developed the Global–Local Integrated Topology (GLINT) inverse design algorithm [27]—a global–local co-optimization framework that enables direct optimization of binary waveguide-silica structures. Leveraging the GLINT algorithm, we designed an ultra-compact, symmetric power splitter (5.5 µm × 2.5 µm) that achieves an insertion loss of 0.18 dB and a power imbalance below 0.0002 dB. Through network-level cascading of power splitters and novel compact phase shifters (4.5 µm × 0.9 µm), we constructed an ultra-compact inverse-designed integrated photonic matrix compute core (PMCC, 132 µm × 16 µm). The proposed PMCC, capable of performing matrix operations for ONNs, was evaluated on the Modified National Institute of Standards and Technology (MNIST) handwritten digit classification task, achieving a classification accuracy of 99.05%. Notably, our PMCC achieves an integration density of 2.6 × 10⁴ computational units/mm²—adopting a multistage interferometric architecture similar to that of MZI-based ONNs, yet yielding a significantly higher integration density.

Furthermore, to evaluate fabrication-error tolerance, we developed a stochastic fabrication-error model that incorporates over-etching, under-etching, and etch-induced deformations in inversely designed geometries. These errors were introduced as normally distributed random parameters. Using this model, we constructed 1000 PMCC structures, each with random fabrication errors, and evaluated each structure on 10,000 MNIST test images. Statistical analysis revealed that more than 90% of the simulation test results maintained greater than 80% recognition accuracy, demonstrating exceptional process robustness in our PMCC.

In the following sections, we first introduce the fundamental principles of the PMCC in Section 2, presenting its general architecture. Subsequently, Section 3 and Section 4 detail the essential components of the PMCC: the compact symmetric power splitter and the compact phase shifter, respectively. Following this, Section 5 demonstrates an application example of the PMCC for handwritten digit recognition (0–9). Finally, Section 6 establishes a unique stochastic fabrication-error simulation model to validate the robustness of the system.

2. Introduction to the Principles of the PMCC

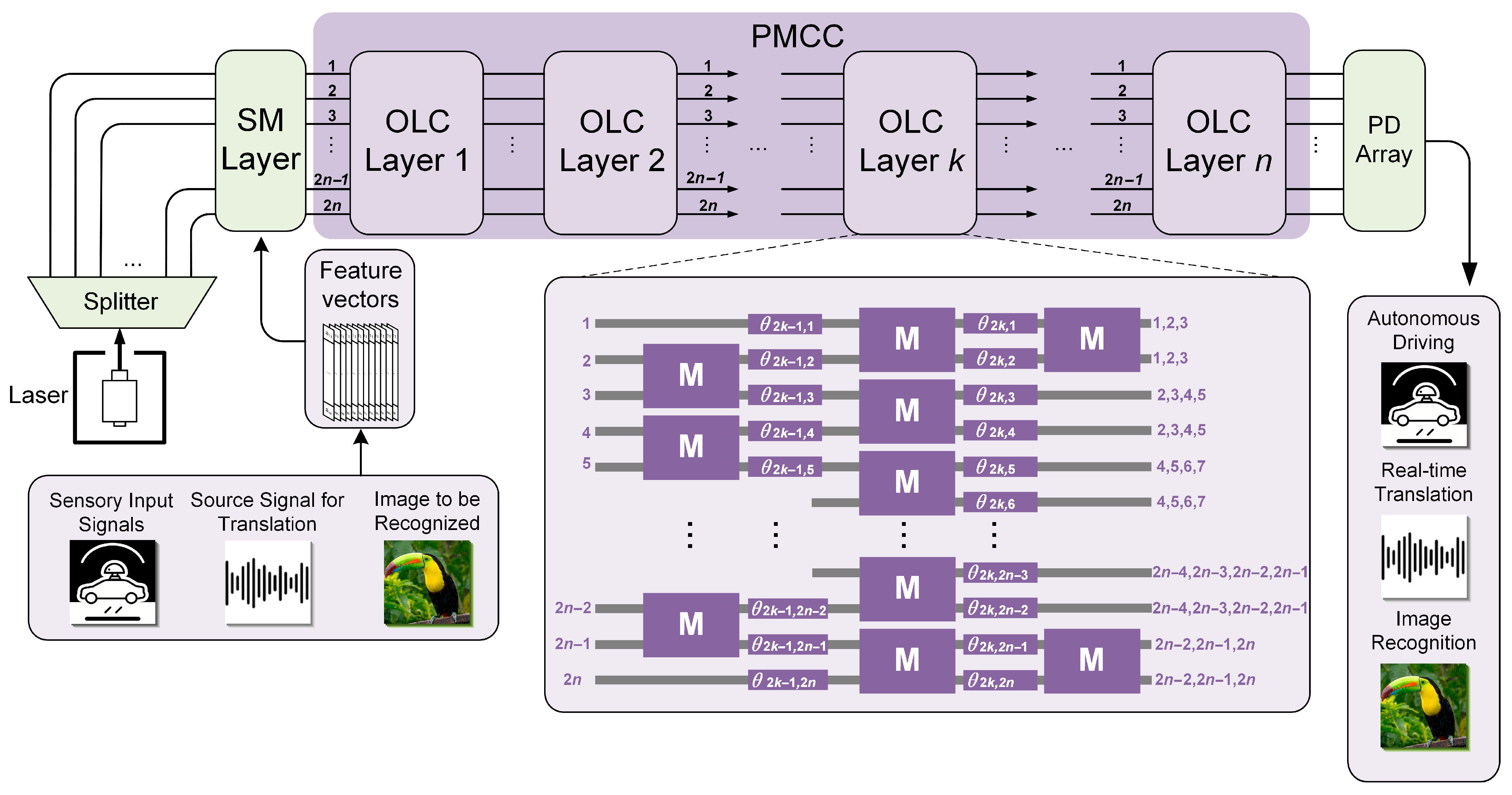
This section provides a concise introduction to the fundamental principles of the PMCC. Figure 1 illustrates the basic architecture of a PMCC with 2n input and output ports, which includes general optical locally-connected (OLC) layers, and provides a schematic overview of the operational process of the PMCC. Specifically, upon acquisition by edge devices, multimodal data such as video, audio, and images undergo feature preprocessing and are subsequently processed by the signal modulation layer (SM layer), which encodes the information onto the incident optical carriers before introducing them into the system. After the information-carrying light passes through n OLC layers—where complex all-optical matrix operations are performed on the feature vectors—the output signals are captured by a photodiode array (PD array), enabling functionalities such as real-time translation, autonomous driving, and image recognition.

The specific network connectivity of this OLC layer is shown in Figure 1. The function of the OLC layer is to establish partial connectivity between input and output ports and to impart an independent phase shift to the signal from each input port. Specifically, output ports 1, 2 and output ports 2n − 1, 2n can be connected to input ports 1, 2, 3 and input ports 2n − 2, 2n − 1, 2n, respectively. For output ports 2j − 1 and 2j (1 < j < n), both can be connected to input ports 2j − 2, 2j − 1, 2j, and 2j + 1, thereby achieving partial interconnection between input and output ports. The PMCC is constructed by cascading n OLC layers, each consisting of 2n + 1 2 × 2 power splitters M and 4n phase shifters ${\theta }_{s,t}$ (s, t = 1, 2, …, 2n). The input information is modulated in parallel onto 2n continuous-wave laser fields from the same laser source, which are then injected into the 2n input ports of the PMCC. After processing by the PMCC, the resulting 2n output optical fields can either be directed to subsequent optical processing modules or be demodulated and converted into electronic signals via photodetectors to retrieve the processed information. The transfer function of the phase shifter ${\theta }_{s,t}$ is given by $e^{i{\theta }_{s,t}}$, and that of the power splitter M is expressed as:

$$\begin{array}{c}\mathbf{A}=\left[\begin{array}{cc}{ A}_{11} & A_{12} \\ { A}_{21} & A_{22} \end{array}\right]\end{array}$$

(1)

Under ideal conditions where the insertion loss of the power splitters is negligible, A is strictly a unitary matrix. According to the input-output connectivity rules of the OLC layer, after cascading through n OLC layers, the signal at each of the final 2n output ports corresponds to a weighted sum of the signals from the initial 2n input ports. To ensure that the energy from each input port is distributed as uniformly as possible across the different output ports, M should be a 50:50 power splitter satisfying:

$$\begin{array}{c}\left|A_{pq}\right|={\displaystyle \frac{1}{\sqrt{2}}}\end{array}$$

(2)

where p, q = 1, 2. Furthermore, assume that T₁, T₂, T₃, P_k (k = 1, 2, …, 2n) are all 2n × 2n matrices satisfying the following conditions:

$$\begin{array}{c}{\mathbf{T}}_1=\left[\begin{array}{ccc}\begin{array}{cc}1& 0\\ 0& \mathbf{A}\end{array}& \begin{array}{c}\dots \\ \dots \end{array}& \begin{array}{cc}0& 0\\ 0& 0\end{array}\\ \begin{array}{cc}⋮& ⋮\end{array}& \ddots & \begin{array}{cc}⋮& ⋮\end{array}\\ \begin{array}{cc}0& 0\\ 0& 0\end{array}& \begin{array}{c}\dots \\ \dots \end{array}& \begin{array}{cc}\mathbf{A}& 0\\ 0& 1\end{array}\end{array}\right]\end{array}$$

(3)

$$\begin{array}{c}{\mathbf{T}}_2=\left[\begin{array}{ccc}\begin{array}{cc}\mathbf{A}& 0\\ 0& \mathbf{A}\end{array}& \begin{array}{c}\dots \\ \dots \end{array}& \begin{array}{cc}0& 0\\ 0& 0\end{array}\\ \begin{array}{cc}⋮& ⋮\end{array}& \ddots & \begin{array}{cc}⋮& ⋮\end{array}\\ \begin{array}{cc}0& 0\\ 0& 0\end{array}& \begin{array}{c}\dots \\ \dots \end{array}& \begin{array}{cc}\mathbf{A}& 0\\ 0& \mathbf{A}\end{array}\end{array}\right]\end{array}$$

(4)

$$\begin{array}{c}{\mathbf{T}}_3=\left[\begin{array}{ccc}\begin{array}{cc}\mathbf{A}& 0\\ 0& 1\end{array}& \begin{array}{c}\dots \\ \dots \end{array}& \begin{array}{cc}0& 0\\ 0& 0\end{array}\\ \begin{array}{cc}⋮& ⋮\end{array}& \ddots & \begin{array}{cc}⋮& ⋮\end{array}\\ \begin{array}{cc}0& 0\\ 0& 0\end{array}& \begin{array}{c}\dots \\ \dots \end{array}& \begin{array}{cc}1& 0\\ 0& \mathbf{A}\end{array}\end{array}\right]\end{array}$$

(5)

$$\begin{array}{c}{\mathbf{P}}_k=\left[\begin{array}{ccc}\begin{array}{cc}{e}^{i{\theta }_{k,1}}& 0\\ 0& e^{i{\theta }_{k,2}}\end{array}& \begin{array}{c}\dots \\ \dots \end{array}& \begin{array}{cc}0 & 0\\ 0 & 0\end{array}\\ \begin{array}{cc}⋮ & ⋮\end{array}& \ddots & \begin{array}{cc}⋮ & ⋮\end{array}\\ \begin{array}{cc}0 & 0\\ 0 & 0\end{array}& \begin{array}{c}\dots \\ \dots \end{array}& \begin{array}{cc}{e}^{i{\theta }_{k,2n-1}}& 0\\ 0 & e^{i{\theta }_{k,2n}}\end{array}\end{array}\right]\end{array}$$

(6)

Then the transfer function of the entire PMCC is given by:

$$\begin{array}{c}{\mathbf{T}}_{\mathrm{P}\mathrm{M}\mathrm{C}\mathrm{C}}={\displaystyle \prod _{k=n}^1}{\mathbf{T}}_3{\mathbf{P}}_{2k}{\mathbf{T}}_2{\mathbf{P}}_{2k-1}{\mathbf{T}}_1\end{array}$$

(7)

Based on the unitarity of A, it follows that ${\mathbf{T}}_1$, ${\mathbf{T}}_2$, ${\mathbf{T}}_3$ are also unitary matrices, and thus ${\mathbf{T}}_{\mathrm{P}\mathrm{M}\mathrm{C}\mathrm{C}}$ is likewise unitary. If the phase shift of each phase shifter is regarded as an independent variable of ${\mathbf{T}}_{\mathrm{P}\mathrm{M}\mathrm{C}\mathrm{C}}$, then ${\mathbf{T}}_{\mathrm{P}\mathrm{M}\mathrm{C}\mathrm{C}}$ possesses 4n² independent variables, enabling its application in complex quantum computations and theoretical physics simulations [28].

3. Compact Symmetric Power Splitter

Compact power splitters represent the first essential component of the PMCC, designed using our GLINT inverse design algorithm. We first provide a concise overview of the GLINT algorithm [27] employed in designing this device. This algorithm employs a trajectory-based optimization strategy and iteratively modifies the structure by flipping material states within waveguide-substrate regions, enabling direct optimization of binary photonic structures. The GLINT algorithm comprises two distinct phases: global search and local refinement. The global search phase identifies performance-critical regions using large-scale global search regions, while local refinement utilizes small-scale local optimization regions to optimize features, thus achieving a 20 nm × 20 nm pixel size for optimization while maintaining computational efficiency. Device performance is quantified by a Figure of Merit (FOM, 0 ≤ FOM ≤ 1), where lower values indicate superior performance. All simulation results during algorithm iterations were obtained via the three-dimensional finite-difference time-domain (3D-FDTD) method with a spatial resolution of 20 nm × 20 nm and with perfectly matched layer (PML) boundary conditions.

In the original global–local optimization framework, the center points for both global and local optimization regions are randomly selected within the optimization region. To reduce computational cost, we introduced a symmetry constraint module, which confines candidate center points for global optimization and local refinement to the upper half-region of the optimization region. During each waveguide-substrate material inversion operation, synchronized inversion is performed in the geometrically symmetric lower region, ensuring structural symmetry preservation throughout all optimization iterations.

Figure 2a shows the initial structure of the compact power splitter designed on a 220-nm silicon-on-insulator (SOI) platform with dimensions of 5.5 µm × 2.5 µm, where silicon is represented in white and silica in blue, featuring two input ports on the left and two output ports on the right. The width of the input and output waveguides is 0.5 μm, with 1.6 μm spacing between the upper and lower ports. In the absence of the symmetry constraint, simulations must be conducted separately for signals input through each of the two ports during every step of the optimization iteration. By incorporating the symmetry module, however, the simulation results for the upper input port can be symmetrically mapped to deduce that of the lower input port, thereby reducing the computational cost by half. Figure 2c presents the schematic of the optimized power splitter after inverse design. This symmetric compact device operates at 1550 nm wavelength. Figure 2b,d show the simulated electric field distributions in the initial and optimized structures, respectively, with a 1550 nm signal applied at the upper input port. To satisfy Equation (2), the FOM is defined as:

$$\begin{array}{c}FOM=1-\left(1-\left|0.5-t_{11}\right|\right)\times \left(1-\left|0.5-t_{12}\right|\right)\end{array}$$

(8)

here, t₁₁ denotes the transmission at the upper output port when a 1550 nm signal is applied to the upper input port, and t₁₂ represents the transmission at the lower output port under the same input conditions.

The initial structure employs a coupled-waveguide design principle, which utilizes evanescent field coupling between two closely spaced curved waveguides to achieve energy exchange. While achieving a 1:1 splitting ratio solely through coupling typically requires coupling lengths of tens to hundreds of microns, the GLINT algorithm optimizes the coupling region, enabling it to achieve the same functionality at a length of just 5.5 μm. Although this initial structure does not achieve the precise 1:1 splitting ratio—instead producing an approximate 1:10 ratio (Figure 2b)—its coupling characteristics establish the foundation for subsequent optimization. By optimizing the geometry of the optimization region, the GLINT algorithm enables precise control of the splitting ratio, which fulfills the target performance specifications of the power splitter. Figure 2e presents the transmission spectrum of the optimized structure under upper input port excitation, with blue/red curves representing transmission at the upper and lower output ports, respectively. The device exhibits 0.18 dB insertion loss at 1550 nm, where both output ports achieve approximately −3.19 dB transmission. The power imbalance (<0.0002 dB) at this wavelength is negligible—a finding consistent with the symmetric electric field distribution shown in Figure 2d. Furthermore, as indicated by the transmission curves in Figure 2e, the power imbalance of the splitter remains below 0.15 dB over an input wavelength range of 1550 ± 5 nm.

The electric field transmission matrix (transfer function) of the optimized structure can be expressed as:

$$\begin{array}{c}{\mathbf{A}}_{\mathbf{E}}=\left[\begin{array}{cc}-0.657+0.219i& -0.211-0.660i\\ -0.211-0.660i& -0.657+0.219i\end{array}\right]\end{array}$$

(9)

Herein, the input/output ports are sequentially numbered from top to bottom as port 1 and 2. For the complex matrix ${\mathbf{A}}_{\mathbf{E}}$, the element $A_E(i,j)$ represents the electric field transmission ratio from input port j to output port i (i, j = 1, 2) under 1550 nm wavelength. The power transmission matrix ${\mathbf{A}}_{\mathbf{P}}$ is obtained by taking the squared modulus of each element in ${\mathbf{A}}_{\mathbf{E}}$:

$$\begin{array}{c}{\mathbf{A}}_{\mathbf{P}}=\left[\begin{array}{cc}0.480057& 0.480038\\ 0.480038& 0.480057\end{array}\right]\end{array}$$

(10)

The $A_P(i,j)$ represents the transmission ratio from input port j to output port i (i, j = 1, 2) under 1550 nm wavelength. As evidenced by ${\mathbf{A}}_{\mathbf{P}}$, the differential transmission between output ports is 0.0019%—approaching zero. This indicates exceptional power-splitting symmetry where optical power is equally divided between dual outputs with high precision. The high-performance design provides a buffering effect against fabrication errors, which significantly improves the PMCC’s robustness.

Finally, the impact of temperature variations on the power splitter was evaluated. The thermo-optic coefficients of Si and SiO₂ at the operating wavelength are approximately 1.86 × 10⁻⁴ K⁻¹ and 1.0 × 10⁻⁵ K⁻¹, respectively. Based on 3D-FDTD simulations, a temperature variation of ±5 °C results in a power variation of less than 0.6% and a phase shift below 6.4 × 10⁻⁴π at the output ports, demonstrating the robustness of the device against temperature fluctuations.

4. Compact Phase Shifter

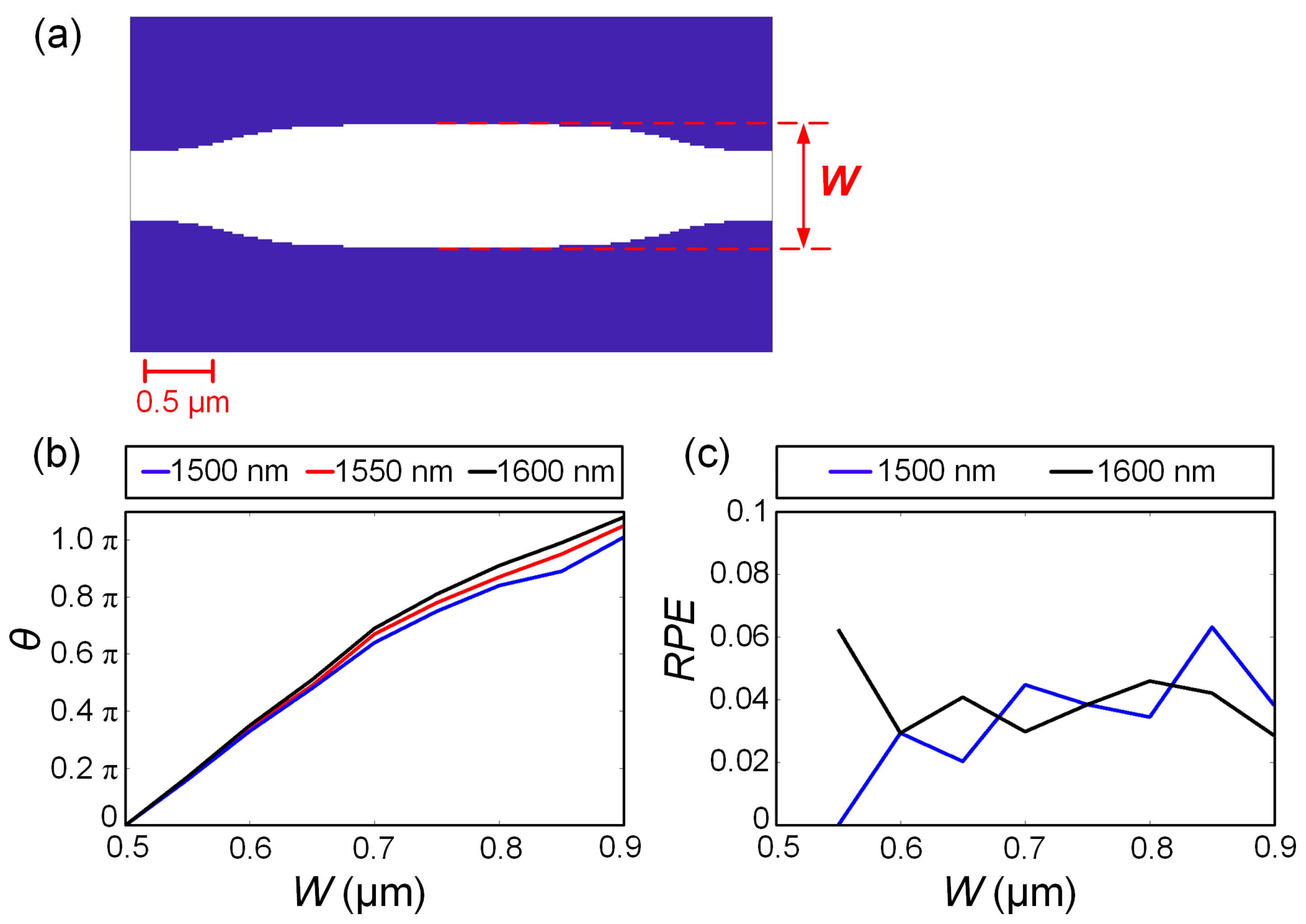
In addition to power splitters, phase shifters represent another essential component for realizing multistage interference in PMCC. We further propose a compact phase shifter that offers a 0–π modulation range achieved by varying the width (W) of the structure.

Figure 3a shows the design structure of the phase shifter, with a maximum footprint of 4.5 µm × 0.9 µm. The core component of the phase shifter is a tunable region with a variable W, ranging from 0.5 µm to 0.9 µm. The widths of both the input and output waveguides are fixed at 0.5 µm. When the width W of the tunable region is 0.5 µm, the structure is equivalent to a straight waveguide. By adjusting the width W, the effective index within the modulation region can be modified, thereby achieving phase modulation. The electric field phase difference between the output and input ports for the straight waveguide case (W = 0.5 µm) is recorded as θ₀. After adjusting the width W, the simulated electric field phase difference between the output and input ports is recorded as θ_W. The phase shift θ introduced by the phase shifter is defined as:

$$\begin{array}{c}\theta = {\theta }_W- {\theta }_0\end{array}$$

(11)

In essence, θ represents the additional phase shift introduced by the phase shifter relative to a straight waveguide of identical length.

Figure 3b depicts the relationship between the structure width W and the phase shift θ. Simulation results demonstrate that for W ranging from 0.5 µm to 0.9 µm under 1550 nm optical input, the structure achieves a maximum phase shift of π with virtually negligible insertion losses (<5.8 × 10⁻³ dB). A quasi-linear relationship exists between θ and W, which enables straightforward determination of the required W value for a target phase shift through simple calculation, thereby significantly streamlining the device design process. To evaluate the wavelength sensitivity of the structure, the relationship between θ and W was further calculated at input wavelengths of 1500 nm and 1600 nm, with the corresponding data represented by the blue and black curves in Figure 3b. Here, we introduce the concept of relative phase error (RPE)—defined as the relative error in phase shift when the input wavelength deviates from the design wavelength—to quantitatively evaluate wavelength sensitivity:

$$\begin{array}{c}RPE= \left|{\displaystyle \frac{{\theta }_{\lambda }-{\theta }_{1550}}{{\theta }_{1550}}}\right|\end{array}$$

(12)

where ${\theta }_{\lambda }$ denotes the phase shift θ at an input wavelength of λ (with λ = 1500 nm and 1600 nm corresponding to the blue and black curves in Figure 3b, respectively), and θ₁₅₅₀ represents the phase shift θ at the design wavelength of 1550 nm (red curve in Figure 3b). Figure 3c demonstrates that the percentage deviation in phase shift is less than 7% under a wavelength deviation of ±50 nm from the design wavelength. Furthermore, in the error analysis (Section 6), even after introducing both a maximum phase deviation of π/20 (corresponding to a mean RPE of 16%) in the phase shifters and the etching errors in the power splitters, our PMCC maintained strong performance in the handwritten digit recognition task, achieving over 80% accuracy in more than 90% of the trials. This robust performance indirectly demonstrates the limited impact of a ±50 nm wavelength deviation on the system.

Furthermore, we evaluated the impact of temperature variations on the phase shifter. Based on 3D-FDTD simulations, a temperature variation of ±5 °C induces a phase shift of less than 0.0019π radians, demonstrating the robustness of the device against temperature fluctuations.

5. Constructing the Compact Optical Neural Network

In this subsection, to accomplish the task of recognizing handwritten digits (0–9), we constructed a PMCC by network-level cascading of 55 power splitters and 100 phase shifters (Figure 4a). The resulting network comprises 10 input ports and 10 output ports, establishing full signal connectivity from all inputs to all outputs. This architecture enables arbitrary weight tuning for neural networks through phase adjustment in individual phase shifters. The proposed network is capable of performing 10 × 10 matrix operations. To calculate the integration density, the structure comprising one power splitter and two compact phase shifters (Figure 4b) is defined as a compact computational unit (CCU, 10 µm × 3 µm). Based on this definition, the implemented PMCC, with a footprint of 132 μm × 16 μm, achieves an integration density of approximately 26,000 units per mm².

Furthermore, to validate the layout feasibility of the designed ultra-compact PMCC, we performed 3D-FDTD simulations (with a resolution of 20 nm × 20 nm) on adjacent power splitters and phase shifters to quantify the crosstalk between adjacent devices. In the PMCC, the center-to-center spacing between vertically adjacent power splitters is 3.2 μm, the minimum input/output waveguide spacing is 1.6 μm, and the minimum spacing between adjacent phase shifters is only 0.7 μm. Simulation results demonstrate that the crosstalk between adjacent power splitters remains below −57 dB, while that between adjacent phase shifters is below −68 dB, both being extremely low and thereby confirming the rationality of the PMCC layout.

Herein, we employ the complex MNIST dataset to validate the functionality of the constructed PMCC (Figure 4c). This dataset comprises 60,000 training images and 10,000 test images, each being a 28 × 28-pixel grayscale image labeled across 10 digits classes (0–9). For each training image, the 28 × 28 pixels matrix is converted into a 10 × 1 feature vector via conventional neural network techniques. This feature vector is subsequently fed into the ten input ports on the left side of the PMCC. Training involves adjusting the phases of 100 phase shifters within the PMCC.

Prior to the initiation of training, the gradient of the loss function with respect to ${\theta }_{s,t}$ is computed. Within the general framework illustrated in Figure 1, the input electric field vector of the PMCC is defined as X = [X₁, X₂, …, X_2n]ᵀ (the 10 × 1 feature vector in this subsection), while the output electric field vector is denoted as Y = [Y₁, Y₂, …, Y_2n]ᵀ. After photodetection, the output is given by F = [F₁, F₂, …, F_2n]ᵀ, where Fₖ = |Yₖ|² for k = 1, 2, …, 2n. Denoting the loss function of the deep learning network as L(F), the gradient of the loss function with respect to the phase shift parameter ${\theta }_{s,t}$ of the PMCC can be expressed as follows:

$$\begin{array}{c}{\displaystyle \frac{\partial L}{\partial {\theta }_{s,t}}}= 2Re\left[i{e}^{i{\theta }_{s,t}}{\displaystyle \sum _k}{\displaystyle \frac{\partial L}{\partial F_k}}{R}_{k,t}^s{Y}_k^{*}{\displaystyle \sum _l}{Q}_{t,l}^s{X}_l\right]\end{array}$$

(13)

where:

$$\begin{array}{c}{\mathbf{R}}^s=\left\{\begin{array}{c}\left({\displaystyle \prod _{k=n}^{\frac{s}{2}+1}}{\mathbf{T}}_3{\mathbf{P}}_{2k}{\mathbf{T}}_2{\mathbf{P}}_{2k-1}{\mathbf{T}}_1\right){\mathbf{T}}_3, \mathrm{mod}\left(s,2\right)=0\\ \left({\displaystyle \prod _{k=n}^{\frac{\left(s+3\right)}{2}}}{\mathbf{T}}_3{\mathbf{P}}_{2k}{\mathbf{T}}_2{\mathbf{P}}_{2k-1}{\mathbf{T}}_1\right){\mathbf{T}}_3{\mathbf{P}}_{s+1}{\mathbf{T}}_2, \mathrm{mod}\left(s,2\right)=1\end{array}\right. \end{array}$$

(14)

$$\begin{array}{c}{\mathbf{Q}}^s=\left\{\begin{array}{c}{\mathbf{T}}_2{\mathbf{P}}_{s-1}{\mathbf{T}}_1\left({\displaystyle \prod _{k=\frac{s}{2}-1}^1}{\mathbf{T}}_3{\mathbf{P}}_{2k}{\mathbf{T}}_2{\mathbf{P}}_{2k-1}{\mathbf{T}}_1\right), \mathrm{mod}\left(s,2\right)=0\\ {\mathbf{T}}_1\left({\displaystyle \prod _{k=\frac{\left(s-3\right)}{2}}^1}{\mathbf{T}}_3{\mathbf{P}}_{2k}{\mathbf{T}}_2{\mathbf{P}}_{2k-1}{\mathbf{T}}_1\right), \mathrm{mod}\left(s,2\right)=1\end{array}\right. \end{array}$$

(15)

Using Equation (13) and the backpropagation algorithm, the phase shift parameters ${\theta }_{s,t}$ can be optimized to determine the specific phase shift values for each phase shifter within the PMCC.

In this subsection, the training was performed on a single GPU, requiring approximately 3.5 h to converge with about 1 × 10⁵ iterations. Following network training, we conducted classification simulations on the 10,000 test images, achieving a recognition accuracy of 99.05% with the confusion matrix shown in Figure 4d, thereby verifying the feasibility of this PMCC.

The PMCC architecture depicted in Figure 4a is specifically designed for the 0–9 handwritten digit classification task. For other task objectives, the architecture illustrated in Figure 1 can be adapted by modifying both the number of input/output ports (2n) and the corresponding count of OLC layers (n) to accommodate them. Notably, as n increases, the PMCC system constructed with the splitters and phase shifters designed in Section 3 and Section 4 exhibits an approximately linear increase in insertion loss (∼0.4n dB), a quadratic increase in training complexity, and a near-exponential rise in power consumption.

6. Stochastic Fabrication-Error Simulation Model

We have established a simulation-verified efficient PMCC achieving 99.05% accuracy under ideal conditions. We next turn to detailed analysis of potential error sources within this system and construct a stochastic error simulation framework to validate the PMCC’s robustness.

The first device that affects the output of the PMCC is the power splitter. For the compact fully-symmetric power splitter designed using the GLINT algorithm, potential fabrication errors primarily originate from the loss of numerous small-scale isolated island/hole structures during the etching process. As demonstrated in our previous work, the presence of a high density of hole/island structures in the designed layout poses significant challenges to manufacturability. During the global search and local refinement steps of the GLINT algorithm, overlapping regions between individual circular search areas may lead to the formation of such small-scale isolated islands or holes.

To simulate fabrication errors in the power splitter, we introduced the following modifications to the design: removing all isolated islands and holes smaller than 40 nm, merging features separated by gaps narrower than 40 nm, and smoothing structural boundaries to emulate the worst-case fabricated device morphology. Ultimately, the resulting structure, shown in Figure 5b, is deemed to represent the power splitter geometry under conditions of maximum fabrication error. The electric field transmission matrix (transfer function) of this structure is defined as ${\mathbf{B}}_{\mathbf{E}}$:

$$\begin{array}{c}{\mathbf{B}}_{\mathbf{E}}=\left[\begin{array}{cc}-0.675+0.064i& -0.064-0.675i\\ -0.064-0.675i& -0.675+0.064i\end{array}\right]\end{array}$$

(16)

${\mathbf{B}}_{\mathbf{E}}$ represents the electric field transmission matrix under conditions of maximum fabrication error, where each element in ${\mathbf{B}}_{\mathbf{E}}$ exhibits a significant deviation in both magnitude and phase compared to the original matrix ${\mathbf{A}}_{\mathbf{E}}$. Here, we define the phase matrix of the electric field transmission matrix ${\mathsf{\Gamma }}_{\mathbf{E}}$ as ${\mathsf{\theta }}_{\mathsf{\Gamma }\mathbf{E}}$:

$$\begin{array}{c}{\theta }_{\Gamma E}\left(i,j\right) =arg\left({\Gamma }_E\left(i,j\right)\right) \end{array}$$

(17)

where 0 ≤ ${\theta }_{\Gamma E}\left(i,j\right)$ < 2π; i, j = 1, 2; $\Gamma =A,B$. Building on this, a stochastic electric field transmission matrix $\tilde{\mathbf{A}}$ is generated by introducing Gaussian-distributed random variables ${\zeta }_{ij}$ and ${\eta }_{ij}$, ${\zeta }_{ij},{\eta }_{ij}~N\left(0,{\displaystyle \frac{1}{9}}\right)$:

$$\begin{array}{c}\tilde{A}\left(i,j\right)=\left(\left|A_E\left(i,j\right)\right|+\left|{\zeta }_{ij}\right|\left(\left|B_E\left(i,j\right)\right|-\left|A_E\left(i,j\right)\right|\right)\right)e^{i\left({\theta }_{AE}\left(i,j\right)+\left|{\eta }_{ij}\right|\left({\theta }_{BE}\left(i,j\right)-{\theta }_{AE}\left(i,j\right)\right)\right)}\end{array}$$

(18)

The magnitude and phase of each element in $\tilde{\mathbf{A}}$ are defined as $\left|\tilde{A}\left(i,j\right)\right|$ and ${\theta }_{\tilde{A}}\left(i,j\right)$, respectively. In matrices ${\mathbf{A}}_{\mathbf{E}}$ and ${\mathbf{B}}_{\mathbf{E}}$, the squared modulus ${\left|A_E\left(i,j\right)\right|}^2$ and ${\left|B_E\left(i,j\right)\right|}^2$ represent the ideal transmission and the transmission under maximum fabrication error, respectively, while the phases ${\theta }_{AE}\left(i,j\right)$ and ${\theta }_{BE}\left(i,j\right)$ correspond to the ideal phase shift and the phase shift under maximum fabrication error of the electric field, respectively.

According to the 3σ rule of Gaussian distribution, the probabilities that $0\le \left|{\zeta }_{ij}\right|<1$ and $0\le \left|{\eta }_{ij}\right|<1$ are both 99.74%. Therefore, according to Equation (18), the probability that both $\left|A_E(i,j)\right|\le \left|\tilde{A}\left(i,j\right)\right|<\left|B_E\left(i,j\right)\right|$ and ${\theta }_{AE}(i,j)\le {\theta }_{\tilde{A}}\left(i,j\right)<{\theta }_{BE}\left(i,j\right)$ is 99.74%, thus effectively emulating the impact of stochastic fabrication errors on the electric field transmission matrix of the power splitter.

The second device that impacts the output of the PMCC is the phase shifter. Owing to its relatively regular structure, this compact phase shifter incorporates no challenging-to-fabricate features—such as holes, isolated islands, or narrow gaps—thus avoiding fabrication-induced loss of critical structures caused by complex geometries. The dominant source of error in this device stems from fabrication deviations in waveguide width, specifically over-etching or under-etching. Here, we set the maximum etching error of the phase shifter to ± 20 nm, corresponding to a phase deviation of π/20. Similarly, the designed phase θ is perturbed via a Gaussian random variable $\xi$, $\xi ~N\left(0,{\displaystyle \frac{1}{9}}\right)$ to generate a stochastic phase $\tilde{\theta }$:

$$\begin{array}{c}\tilde{\theta }= \theta +{\displaystyle \frac{\pi }{20}}\times \xi \end{array}$$

(19)

The probability that $\theta -\mathsf{\pi }/20<\tilde{\theta }<\theta +\mathsf{\pi }/20$ is 99.74%.

At this stage, we obtained the stochastic electric field transmission matrix $\tilde{\mathbf{A}}$ for the power splitters and the stochastic phase $\tilde{\theta }$ for the phase shifters. To validate the system robustness, 55 power splitter electric field transmission matrices ${\mathbf{A}}_{\mathbf{E}}$ in the trained PMCC were replaced with ${\tilde{\mathbf{A}}}_u$ (u = 1, 2, …, 55), and all phase shifter values ${\theta }_{s,t}$ were substituted with ${\tilde{\theta }}_{s,t}$ (s,t = 1, 2, …, 10). After random assignment of 55 ${\tilde{\mathbf{A}}}_u$ matrices and 100 ${\tilde{\theta }}_{s,t}$ phase shifter values, a PMCC structure with random fabrication errors was obtained. We constructed 1000 PMCC structures with independent fabrication errors and evaluated the recognition accuracy for each PMCC using 10,000 test images, thereby obtaining the error-affected accuracy (absolute recognition accuracy) for 1000 individual PMCC with different fabrication errors. This procedure is equivalent to performing 1000 Monte Carlo trials.

Here, we use probability to represent the results of 1000 independent simulations of error-affected accuracy (Figure 6). The results show that the probability of the error-affected accuracy exceeds 90% is 0.689, and the probability that it exceeds 80% reaches 0.912. This indicates that, despite performance fluctuations induced by fabrication errors, the system maintains functional recognition capability with high probability. It is particularly noteworthy that even under the worst-case fabrication conditions—where the power splitter electric field transmission matrices approach ${\mathbf{B}}_{\mathbf{E}}$ and each phase shifter exhibits the maximum etching error of ±20 nm—the system still achieves recognition accuracy greater than 50%, demonstrating strong robustness of the PMCC against fabrication errors.

7. Conclusions

In summary, we have constructed an ultra-compact inverse-designed integrated PMCC on an SOI platform, which is capable of facilitating sophisticated functional matrix operations. In this work, the PMCC achieved a recognition accuracy of 99.05% on the 0–9 handwritten digit classification task. The proposed architecture comprises a networked cascade of power splitters designed with the GLINT algorithm and compact phase shifters, enabling matrix output modulation through multistage interference control, and achieves an integration density of 2.6 × 10⁴ computational units per mm²—far exceeding that of conventional multistage interferometric architectures such as MZI-based ONNs.

To validate the fabrication robustness of the PMCC, we developed a unique stochastic fabrication-error framework and performed 1000 PMCC structures with different fabrication errors by introducing random perturbations into the trained model, with their error-affected accuracy subsequently evaluated. Simulation results indicate that over 90% of the results maintain a recognition accuracy above 80%, and even under worst-case fabrication conditions where all fabrication errors are maximized, the accuracy remains above 50%, demonstrating the robustness of the PMCC.

Currently, the integration density of our PMCC is primarily constrained by the sizes of the power splitters and phase shifters. In the future, we will further optimize the GLINT algorithm to design even smaller and more manufacturable compact power splitters and phase shifters, thereby further increasing the integration density. We anticipate that with continued advances in etching and integration technologies, our PMCC framework will play an increasingly important role in the near future, particularly in edge AI applications such as real-time translation and autonomous driving.