Simultaneously Achieving SBS Suppression and PGC Demodulation Using a Phase Modulator in a Remote Interferometric Fiber Sensing System

Abstract

Stimulated Brillouin scattering (SBS) suppression and phase demodulation are two fundamental issues in remote interferometric fiber sensing systems. A method is proposed for achieving simultaneous SBS suppression and phase-generated carrier (PGC) demodulation in remote interferometric fiber sensing systems, with only the use of an electro-optic phase modulator (PM). A single-frequency laser is phase-modulated by a PM to generate multi-sideband light, which can suppress SBS in long-haul fibers and generate PGC combined with the optical fiber interferometer. Then, the phase signal of the optical fiber interferometer can be demodulated by the PGC demodulation method. A detailed theoretical analysis and the experimental results are presented to confirm the feasibility of the method. The results show that the proposed method can achieve high-performance PGC demodulation with much higher bandwidth and larger dynamic range than the conventional method. Meanwhile, the SBS and its induced phase noise can be suppressed effectively. This work presents a simple setup for SBS suppression and PGC demodulation in a remote interferometric fiber sensing system. The proposed method shows great potential for application in remote and large-scale interferometric fiber sensing systems.

1. Introduction

Remote interferometric fiber sensing systems have been widely used in various fields, such as resource exploration, acoustic signal detection, and earthquake monitoring, because of their advantages in offering continuous real-time, large-area monitoring [1,2,3,4]. However, long-haul transmissions lead to serious power loss in these systems. One intuitive solution is to increase the optical power injected into the fibers. But various optical nonlinear effects, including stimulated Brillouin scattering (SBS), four-wave mixing, modulation instability, self-phase modulation, and cross-phase modulation, limit the maximum input power [5]. Among those nonlinear effects, SBS has the lowest threshold (4–5 mW) in the long-haul (over 50 km) optical fiber [6]. Therefore, the suppression of SBS is the priority issue in the remote interferometric fiber sensing system. Though many SBS suppression methods have been extensively studied in other optical fiber systems [7,8,9,10], SBS suppression in remote interferometric fiber sensing systems still require specific attention. Expensive and complicated methods, such as increasing the core diameter, applying inhomogeneous doping, or applying temperature/strain gradient modulation, are not applicable in the long-haul subsea environment. Laser-frequency modulation [11] and phase modulation [12] are widely used in remote interferometric fiber sensing systems due to their advantages: simplicity and low cost.

Moreover, it is important that the SBS suppression method applied in remote interferometric fiber sensing systems is compatible with the phase demodulation method used. As is well known, phase demodulation is a fundamental feature of interferometric fiber sensing systems, bringing a significant advantage: high sensitivity [13]. High-performance phase demodulation and SBS suppression must be considered simultaneously in remote interferometric fiber sensing systems.

The laser frequency modulation method was found to simultaneously achieve SBS suppression and PGC phase demodulation [14]. But the method needs expensive, fast-modulated laser; moreover, unwanted laser-intensity variation (LIV) may lead to deterioration in performance. The phase-modulation-based SBS suppression method has been studied in detail in a remote interferometric fiber sensing system [5,15]. In existing studies, phase modulation only plays the role of SBS suppression. The phase demodulation process is achieved by other phase-demodulation methods, leading to system complexity and, potentially, excess phase noise [5]. Though the excess phase noise can be suppressed effectively by the method presented in [15], the strict matching condition between the modulation frequency and the optical delay difference brings practical difficulties in large-scale arrays.

In this paper, we propose a method for simultaneously achieving SBS suppression and PGC demodulation in remote interferometric fiber sensing systems through using an electro-optic phase modulator. The single-frequency laser is modulated by a PM to generate multi-sideband light. Then, the phase-modulated light is injected into the long-haul fiber, which can effectively suppress SBS. After long-haul transmission, the phase modulated light is injected into an optical fiber interferometer and the PGC can be generated. The quadrature signals (sin and cos) for PGC demodulation can be obtained by the first and second sidebands of the multi-sideband light, respectively. The phase information of the optical fiber interferometer can be demodulated by the typical PGC demodulation process. Detailed theoretical and experimental analyses are presented to confirm the feasibility of the method. The results show that the proposed method can effectively suppress SBS and simultaneously achieve PGC demodulation. Compared to the laser frequency modulation method, the proposed method does not need expensive, fast-modulated laser, so the unwanted LIV can be avoided. Moreover, the proposed method has the advantage of wide bandwidth and large dynamic range. Compared to existing phase-modulation methods, the proposed method avoids the strict matching condition present in [15]. In summary, the present paper presents a simple and practical method for achieving simultaneous SBS suppression and PGC demodulation in remote interferometric fiber sensing systems.

2. Theory

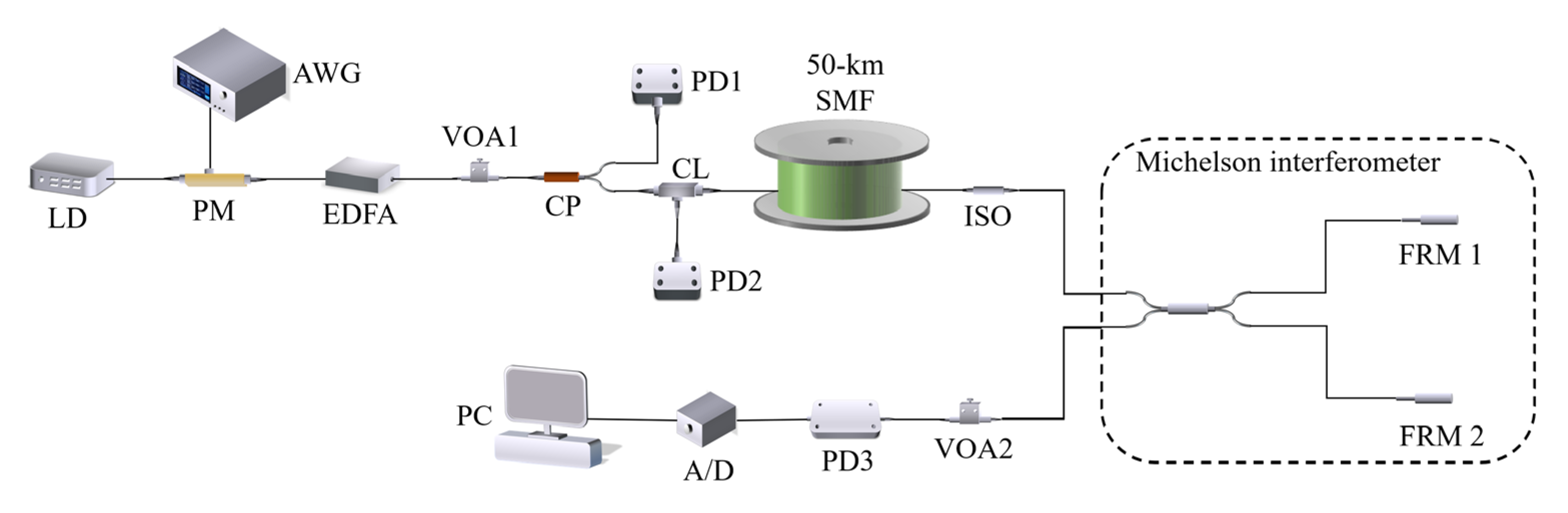
The system is schematically shown in Figure 1. The single-frequency light from a 1550 nm laser diode (LD) is modulated by an electro-optic phase modulator (PM). Then, the modulated light is amplified by an Erbium-doped fiber amplifier (EDFA). The amplified light undergoes attenuation by a variable optical attenuator (VOA1) and then injects into a 50 km single-mode fiber (SMF) via a coupler (CP) and a circulator. The fractional ratio of the CP is 1:99. Of the injected light, 1% is monitored by a photodetector (PD1). Another photodetector (PD2) is used to measure the backscattering power at circular port 3. An isolator (ISO) is used to suppress the Rayleigh scattering induced phase noise [16]. After 50 km transmission, the modulated light is injected into a Michelson interferometer (MI). The MI is encapsulated in a box to suppress the environmental noise. Two Faraday rotation mirrors (FRM1/2) are used to suppress the polarization-fading-induced phase noise. Another variable optical attenuator (VOA2) is placed at the output port of the MI to keep the optical power into the photodetector (PD3) constant. The detected light signal is converted to digital form by an analog-to-digital convertor (A/D) for PGC-Arctan demodulation in the computer (PC).

The single-frequency light with cosinusoidal phase modulation can be expressed as follows:

$$E=E_0\cos ({\omega }_{0}t+M\cos ({\omega }_{m}t+\theta )+\varphi ),$$

(1)

where $E_0$ and ${\omega }_0$ represent the amplitude and angular frequency of the light, respectively. $M$ is the phase modulation index and ${\omega }_m$ represents the phase modulation angular frequency. $\varphi$ is the phase of light. $\theta$ is the carrier phase delay, which is caused by the time delay of optical path, circuit transmission, and photoelectric conversion [17].

The output of the MI can be expressed as [18]:

$$I=\sigma \left[\cos \left({\omega }_0\Delta t+2M\sin ({\displaystyle \frac{{\omega }_m\Delta t}{2}})\sin ({\omega }_{m}t+{\displaystyle \frac{{\omega }_m\Delta t}{2}}+\theta )+\Delta \varphi \right)\right]$$

(2)

where $\sigma$ represents the responsivity of the detector, $\Delta t=\Delta L\cdot 2n/c$, $\Delta L$ is the arm difference of MI, $n$ is refractive index of the fiber, and $c$ is the speed of light. $\Delta t$ and $\Delta \varphi$ represent the time delay difference and phase difference between the two arms, respectively. We set

$$C=2M\sin ({\omega }_m\Delta t/2).$$

(3)

and

$${\phi }_m=\theta +{\omega }_m\Delta t/2.$$

(4)

Equation (2) can be expanded in terms of the Bessel functions as:

$$\begin{array}{c}I=\sigma \left(\left[J_0(C)+2{\displaystyle \sum _1^{\infty }{J}_{2n}(C)\cos \left(2n({\omega }_{m}t+{\phi }_m)\right)}\right]\cos (\Delta \varphi )\right.\\ \left.-2{\displaystyle \sum _0^{\infty }{J}_{2n+1}(C)\sin }\left((2n+1)({\omega }_{m}t+{\phi }_m)\right)\sin (\Delta \varphi )\right)+const.\end{array}$$

(5)

It can be seen that Equation (5) is a typical expression of the PGC demodulation scheme [15]. $C$ and ${\phi }_m$ represent the carrier phase modulation depth and carrier phase delay, respectively. Compared to the conventional PGC demodulation scheme, the method has an excess phase delay, ${\omega }_m\Delta t/2$. $C$ and ${\phi }_m$ can be calculated accurately as shown in [17]. Multiplexing Equation (5) with the reference signals $R_1=\sin ({\omega }_{m}t+{\phi }_m)$ and $R_2=\cos (2{\omega }_{m}t+2{\phi }_m)$, the results after low-pass filtering can be obtained as:

$$\left\{\begin{array}{c}{Y}_1=\sigma J_1(C)\sin (\Delta \varphi ),\\ Y_2=\sigma J_2(C)\cos (\Delta \varphi ).\end{array}\right.$$

(6)

$\Delta \varphi$ can be obtained as:

$$\Delta \varphi =\arctan \left({\displaystyle \frac{Y_1/J_1(C)}{Y_2/J_2(C)}}\right).$$

(7)

Typically, $C$ can be set as 2.63 to make $J_1(C)=J_2(C)$. Equation (7) can be expressed as:

$$\Delta \varphi =\arctan \left({\displaystyle \frac{Y_1}{Y_2}}\right).$$

(8)

Finally, $\Delta \varphi$, which contains the signal, is obtained. It should be noted that the value of $C$ is not strictly limited to 2.63. When $C$ deviates from 2.63, $\Delta \varphi$ can still be obtained accurately by calculating $C$ [17]. This brings significant flexibility in the parameter setting of $M$, $\Delta t$ (or $\Delta L$, because of $\Delta t=\Delta L\cdot 2n/c$), and ${\omega }_m$. The strict parameter-matching condition between modulation frequency and optical delay difference (${\omega }_m\Delta t=2k\pi ,$ where $k$ is an integral) that is encountered in [15] can be avoided. In [15], when the strict matching condition is not satisfied, the system noise increases significantly. For the proposed method, even if the selection of parameters $M$, $\Delta t$ (or $\Delta L$), and ${\omega }_m$ does not yield a $C$ of 2.63, the system can still correctly demodulate the phase without compromising the signal-to-noise ratio (SNR). The significant flexibility in the parameter settings makes the proposed method suitable in large-scale remote interferometric fiber sensing systems, where the arm length difference ($\Delta L$) of the interferometer is susceptible to alterations induced by environmental variations.

In principle, the demodulation bandwidth and maximum demodulation signal amplitude of the PGC demodulation scheme are mainly limited by the modulation frequency. The demodulation bandwidth is 0~$f_m/2$ and the maximum detectable signal amplitude is [19]:

$$D_{\max }<{\displaystyle \frac{f_m}{2f_s}}-1$$

(9)

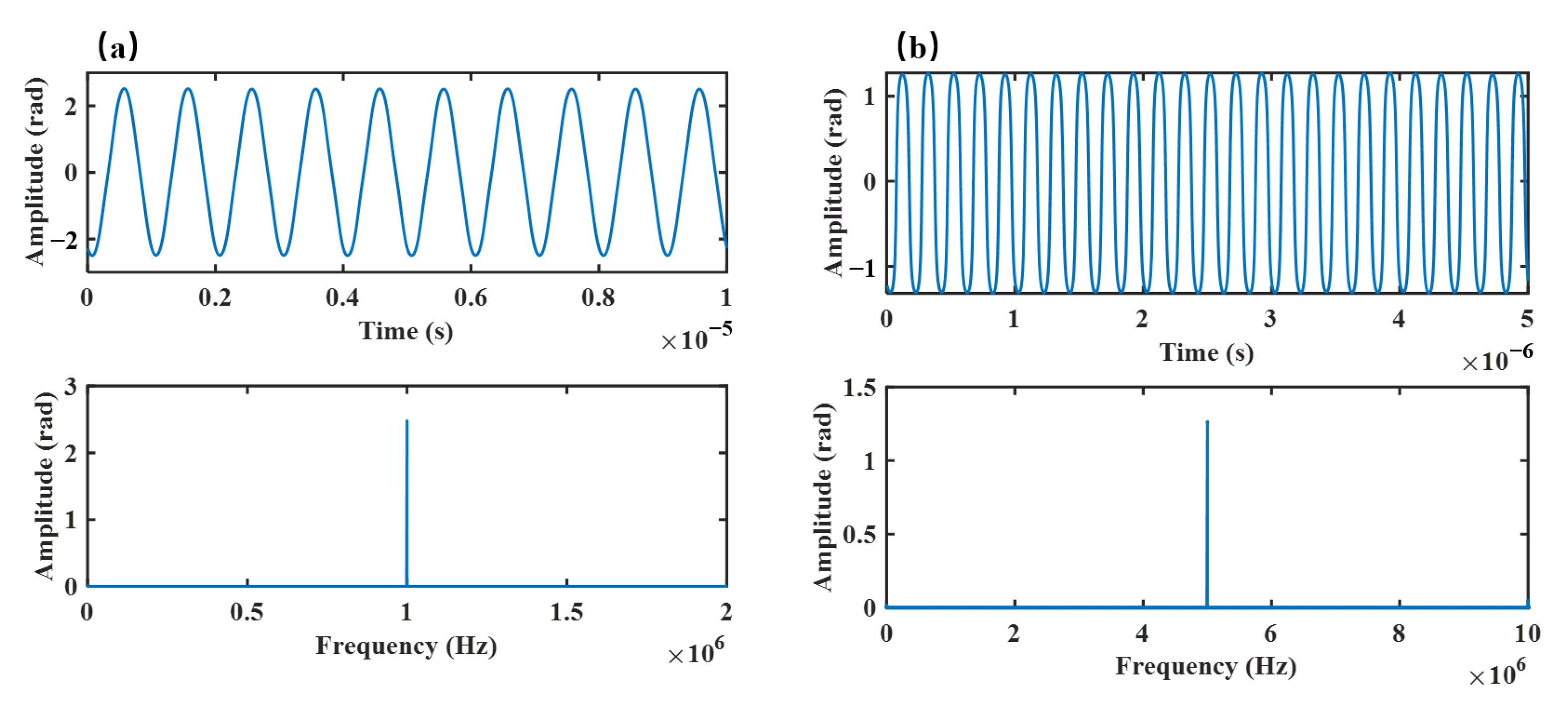
where $f_m$ and $f_s$ represent the PGC frequency and signal frequency, respectively. Thanks to the high bandwidth (typical value: ~GHzs) of the PM, the proposed method can achieve a much higher carrier frequency than the laser-frequency-modulation-based PGC method, the carrier frequency of which is lower than 100 kHz (limited by the laser performance) [20]. This means that the proposed method exhibits a much higher frequency bandwidth and larger dynamic range than the frequency-modulation-based PGC method. For a 1 kHz signal, the maximum achievable demodulated signal amplitude of conventional PGC does not exceed 50 rad according to Equation (9), whereas the proposed method achieves a maximum achievable demodulated signal amplitude of up to 100,000 rad. For the frequency-modulation-based PGC method, a 1 MHz signal cannot be demodulated, as its frequency significantly exceeds that of the carrier signal (lower than 100 kHzs). For the proposed method, when the carrier frequency is 62.5 MHz, the maximum achievable demodulated amplitude of 1 MHz signal reaches 30 rad according to Equation (9). The simulation results corresponding to this scenario are presented in Figure 2.

Next, we analyze the SBS suppression performance of the proposed method. Equation (1) can be expanded in terms of the Bessel functions as:

$$\begin{array}{l}E=E_0\{J_0(M)\cos ({\omega }_{0}t+\theta )\\ +{\displaystyle \sum _{n=1}^{+\infty }{(-1)}^n{J}_{2n}(M)(\cos [2n({\omega }_{m}t+\theta )+{\omega }_{0}t+\varphi ]}+\cos [{\omega }_{0}t+\varphi -2n({\omega }_{m}t+\theta )])\\ -{\displaystyle \sum _{n=1}^{+\infty }{(-1)}^n{J}_{2n+1}(M)}(\sin [(2n+1)({\omega }_{m}t+\theta )+{\omega }_{0}t+\varphi ]+\sin [{\omega }_{0}t+\varphi -(2n+1)({\omega }_{m}t+\theta )])\},\end{array}$$

(10)

where $J_n(M)$ is the n-th order Bessel function. It can be seen that the modulated light is a multi-frequency light with a frequency interval of ${\omega }_m$. The energy of the single-frequency light is distributed over multiple sidebands after modulation, by which SBS can be effectively suppressed. The SBS threshold can be expressed as [21,22]:

$$P_{th}^{SBS}=21{\displaystyle \frac{K{A}_{eff}}{g_p{L}_{eff}}}(1+{\displaystyle \frac{\Delta \upsilon }{\Delta {\upsilon }_B}}),$$

(11)

where $L_{eff}=[1-\exp (-\alpha L)]/\alpha$, $L$ is the fiber length, $\alpha$ is the attenuation coefficient of the fiber, $K$ is the polarization factor, $A_{eff}$ is the effective area of the fiber core, $g_p$ is the peak value of the Brillouin gain, $\Delta \upsilon$ is the linewidth of the light source, and $\Delta {\upsilon }_B$ is the spontaneous Brillouin bandwidth. For the narrow-linewidth laser, $\Delta \upsilon$ is quite small compared with $\Delta {\upsilon }_B$; thus, the second term in the bracket can be ignored.

For single-frequency light, the natural Brillouin gain can be expressed as [6]:

$$g(\upsilon )={\displaystyle \frac{{(\Delta {\upsilon }_B/2)}^2}{{[\upsilon -({\upsilon }_0-{\upsilon }_B)]}^2+{(\Delta {\upsilon }_B/2)}^2}}{g}_P,$$

(12)

where ${\upsilon }_B$ is the Brillouin frequency shift and ${\upsilon }_0$ is the center frequency of the pump light. For multi-frequency laser generated by phase modulation, the Brillouin gain spectrum is the sum of the Brillouin gain of each side band:

$$g_m(\upsilon )={\displaystyle \sum _0^n{[J_k(M)]}^2{g}_P\frac{{(\Delta {\upsilon }_B/2)}^2}{{[\upsilon -({\upsilon }_0+k{\upsilon }_p-{\upsilon }_B)]}^2+{(\Delta {\upsilon }_B/2)}^2}},$$

(13)

where ${\upsilon }_p$ is the modulation frequency. According to Equations (11) and (13), the SBS threshold can be expressed as:

$$P_{th}^{SBS}=21{\displaystyle \frac{K{A}_{eff}}{g_B({\upsilon }_{\max })L_{eff}}},$$

(14)

where $g_B({\upsilon }_{\max })$ is the peak value of effective Brillouin gain under phase modulation.

To suppress SBS effectively, the phase modulation frequency must be comparable or higher than the Brillouin gain bandwidth [15]. In this paper, we typically set the modulation frequency as 62.5 MHz. For simplicity, $C$ is typically set as 2.63. Under this condition (because of $C=2M\sin ({\omega }_m\Delta t/2)$), there is a corresponding relationship between $M$ and $\Delta L$($\Delta t=\Delta L\cdot 2n/c$).

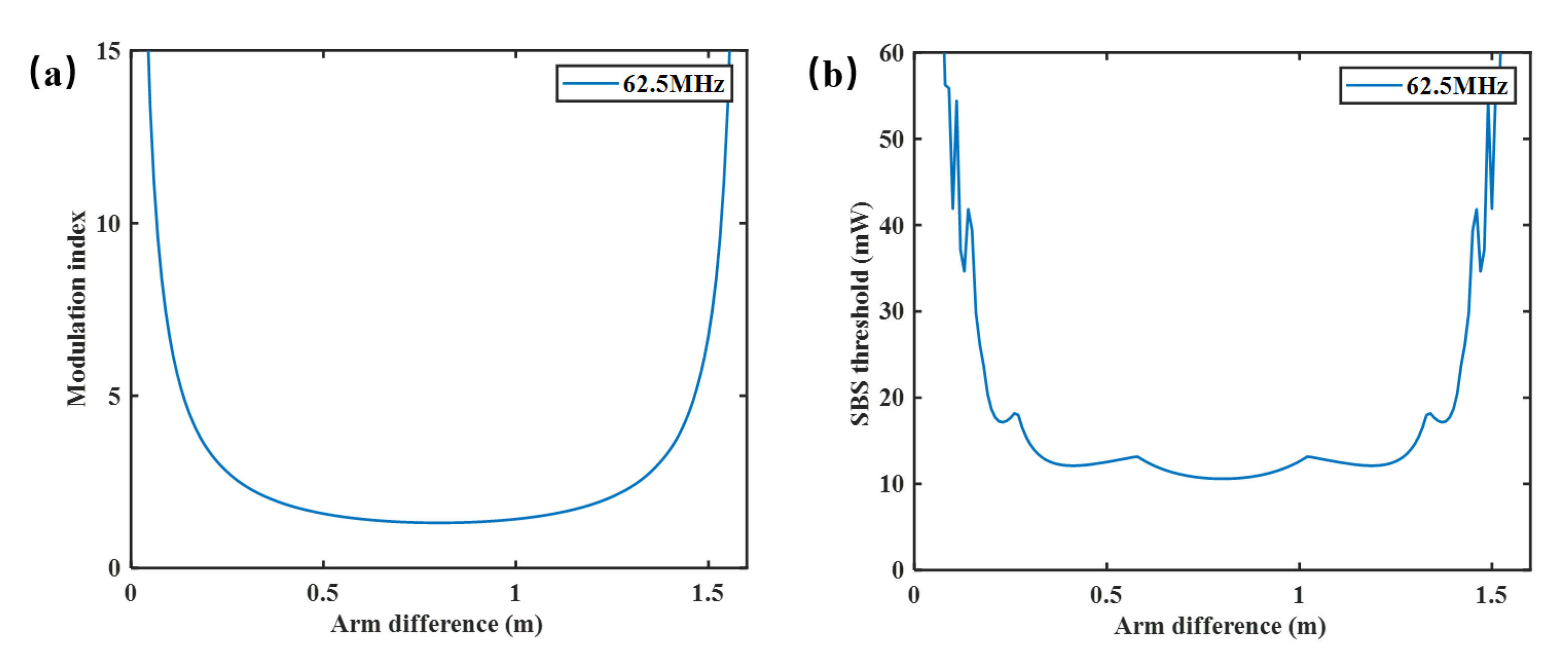
Figure 3 shows modulation index $M$ and the SBS threshold versus the arm difference $\Delta L$, when the modulation frequencies of 62.5 MHz and $C$ are both 2.63, respectively. The two curves are derived from Equations (3) and (14). The modulation index $M$ decreases first and then increases with the increase in the arm difference. According to the authors of [23], the smaller the arm difference, the lower the phase noise of the system. According to Equation (14), the higher the $M$, the higher SBS threshold can be obtained. Therefore, shorter $\Delta L$ and higher $M$ should be chosen to achieve lower phase noise and higher SBS threshold. Theoretically, when the arm difference is set as 0.14 m, the modulation index is 4.84, the SBS threshold can be increased to 41.8 mW. The results show the method can significantly increase the SBS threshold.

3. Experimental Results

Experiments were conducted to confirm the feasibility of the proposed method. The arm difference of the interferometer was set as a typical value, 1 m. The modulation frequency was set as 62.5 MHz. The phase modulation index $M$ was set as 1.42 to make $C=2.63$.

Firstly, an experiment was conducted to confirm the feasibility of the phase demodulation. A piezoelectric (PZT) wrapped by optical fiber was inserted in one arm of the optical fiber interferometer. The single frequency signals of 1 MHz and 5 MHz were applied to the PZT to generate sinusoidal signals. The proposed method was used to demodulate the applied signal. The demodulated results are shown in Figure 4. The demodulated signals agree well with the sinusoidal signals. The results confirm that the method can accurately achieve both phase demodulation and wide bandwidth performance.

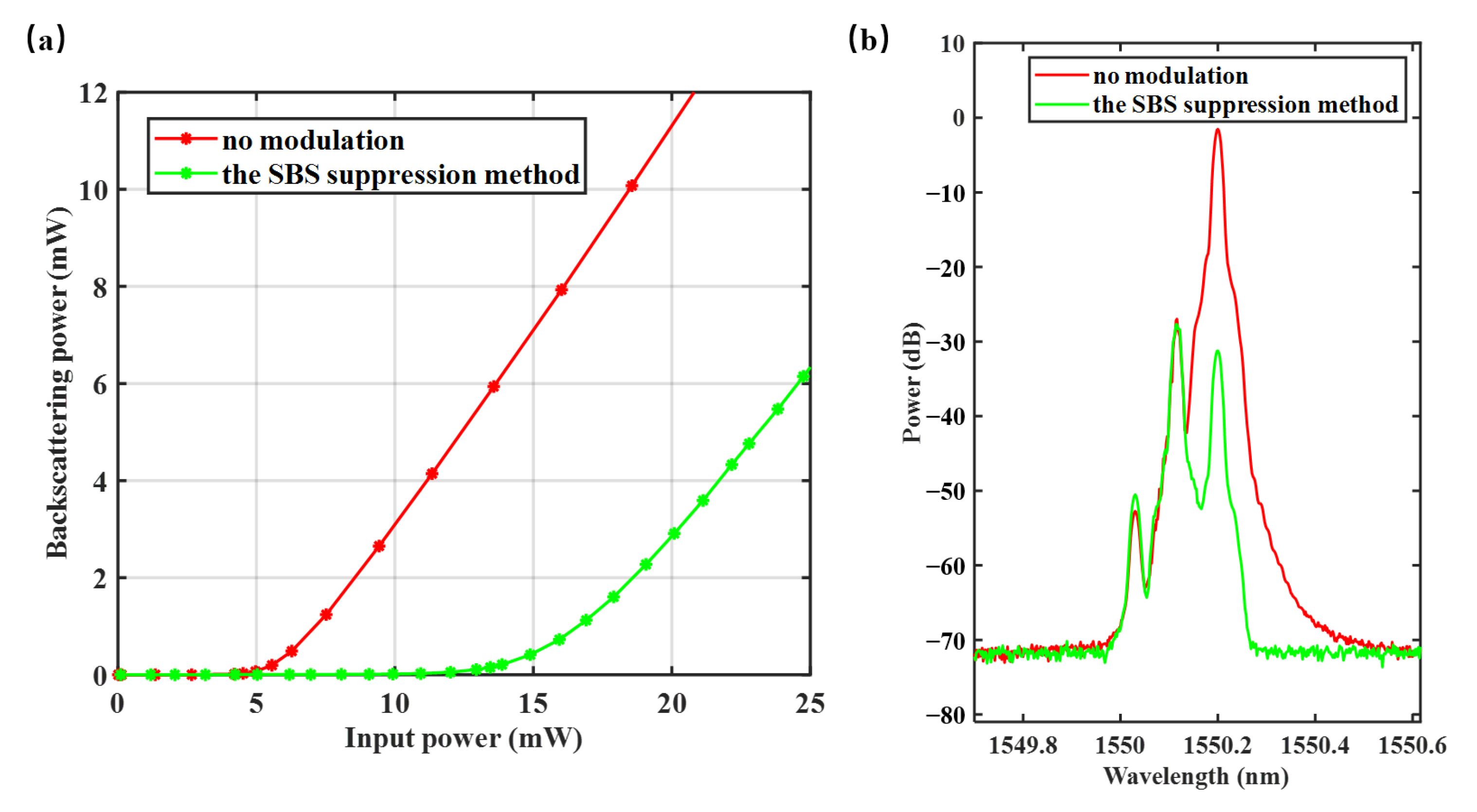
Next, an experiment was conducted to study the effect of the method on the SBS threshold. Figure 5a shows the backscattering power versus the input power with and without phase modulation. The input power when the backscattering power is equal to 1% of the input power was defined as the SBS threshold. When the phase modulation was not applied, the SBS threshold was about 4.7 mW. The SBS threshold was about 13.2 mW when phase modulation was applied; this result is consistent with the theoretical SBS threshold, 13.1 mW, shown in Equation (14) and Figure 3.

Figure 5b shows the optical spectrum of the backscattering light without phase modulation and with the phase modulation when the input power is 10 mW. The three peaks from left to right in the figures are, respectively, the anti-stokes light, the pump light, and the stokes light, respectively. When the input power is 10 mW, the stokes light is much higher than the pump light without phase modulation, which means that there has been significant occurrence of SBS. When the proposed method is applied, the stokes light is suppressed effectively. The results above show that this method can effectively suppress SBS.

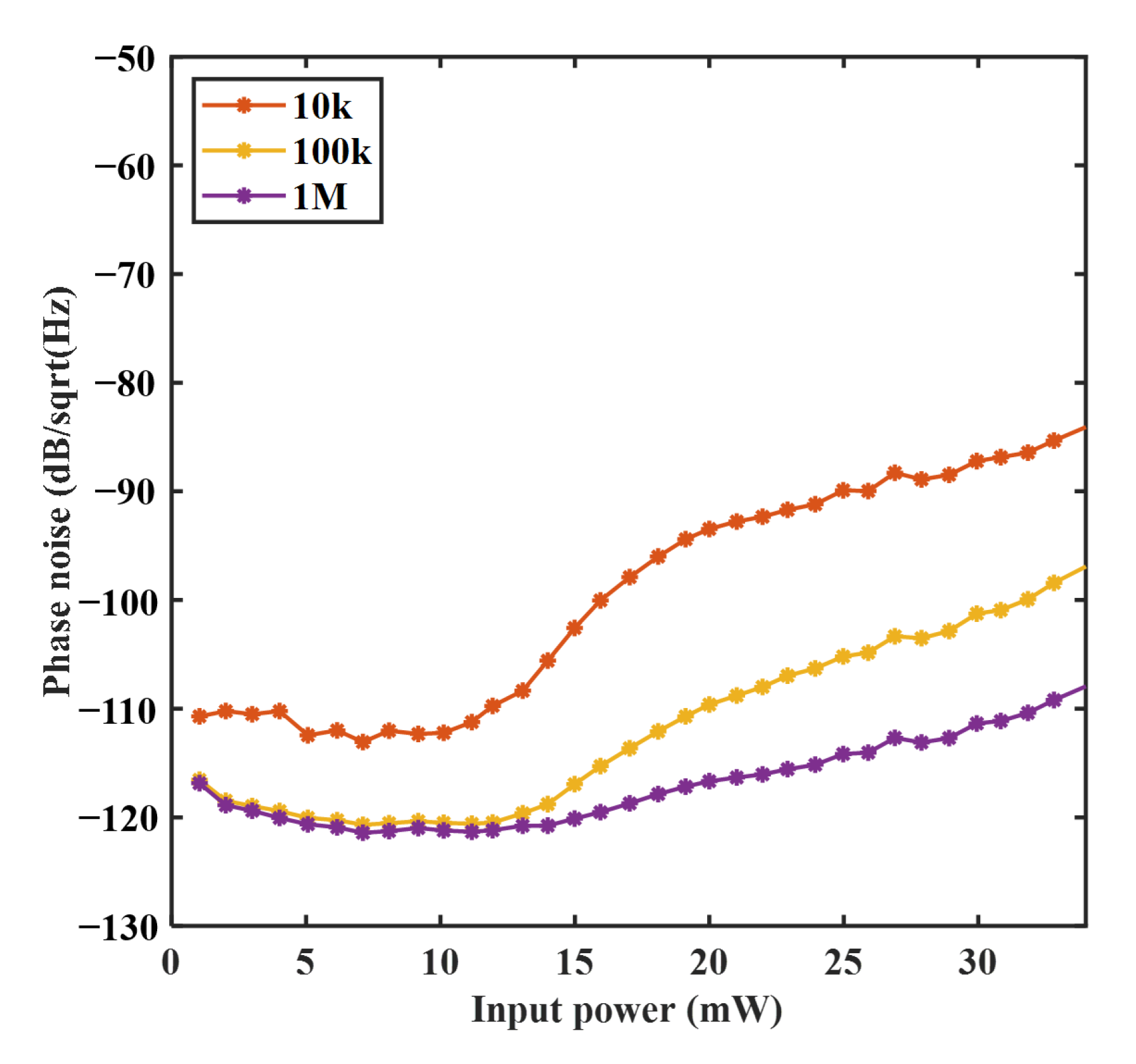
Phase noise is a key parameter that determines the detection sensitivity of the remote interferometric fiber sensing system. The proposed method is used to achieve phase demodulation; then, the phase noise can be obtained. Figure 6 shows the phase noise versus the input power at different frequencies (10 kHz, 100 kHz, and 1 MHz are shown typically) when the proposed method is used. The results show the phase noises at different frequencies remain at low level (below −110 dB/√Hz) when the input power is below 13 mW. When the input power exceeds the SBS threshold (~13 mW), the phase noise increases sharply. As shown in Figure 5a, the SBS threshold is about 13.2 mW when the proposed method is used. The input power at which the phase noise starts increasing is nearly equal to the SBS threshold (~13.2 mW). The results show the proposed method can suppress SBS and its induced phase noise, simultaneously. Moreover, the phase noise of a conventional PGC system operating below the SBS threshold is slightly above −110 dB/√Hz [14], whereas the phase noise of our system remains below −110 dB/√Hz under the same conditions. This indicates that the proposed method not only introduces no significant excess noise but also outperforms traditional PGC demodulation.

4. Discussion and Conclusions

The paper presents a proof-of-concept for the method. The results show that the proposed method can effectively suppress SBS and simultaneously achieve high-performance PGC demodulation. In the experimental results, the SBS threshold was found to be between 4.7 mW and 13.2 mW, while the phase noise remains at a low level. Compared to the SBS threshold of the laser frequency modulation method (about 15 mW) [14], the experimental results of our method are similar; meanwhile, the theoretical threshold is significantly higher. According to Figure 3, the SBS threshold can be further increased, optimizing the parameters. Theoretically, the SBS threshold can be increased to 41.8 mW when the arm difference is 0.14 m and the modulation index is 4.84. Since the $C$ is not fixed at 2.63 and can be calculated, the parameter selection no longer needs to adhere to strict matching conditions, such as those used in [15]. Furthermore, the flexibility in selecting $C$ expands the range of selectable system parameters, which enables us to optimize the system performance. The SBS threshold can be further increased (above 41.8 mW) by raising the modulation index. Meanwhile, the shorter arm difference leads to lower phase noise [23]. The experimental results demonstrate that, when operating below the SBS threshold, the proposed method not only introduces no significant excess noise but also exhibits superior noise performance compared to conventional PGC demodulation. The proposed method eliminates the need for modulated lasers or specialized sensors, which not only reduces system cost and avoids unwanted LIV but also enables deployment in harsh environments such as deep-sea acoustic detection. The proposed method also exhibits higher frequency bandwidth and larger dynamic range than conventional frequency-modulation-based PGC demodulation methods. Since PM can achieve a bandwidth in the GHz range, while the carrier frequency of laser frequency modulation is limited to below 100 kHz, the maximum demodulation signal amplitude of the proposed method can reach more than 10,000 times that of laser frequency modulation for signals at the same frequency. Moreover, the proposed method can detect signals up to tens of MHz, which enables its application in fields such as ultrasonic detection and high-frequency acoustic communication. This paper shows only the proof-of-concept results; ongoing work will be conducted to achieve further suppression of the nonlinear effect and phase noise.

In summary, we propose a method for simultaneously achieving effective SBS suppression and high-performance PGC demodulation using only an electro-optic phase modulator in a remote interferometric fiber sensing system. The theoretical and experimental results confirm the feasibility of the proposed method. This work presents a simple, flexible, and practical setup for SBS suppression and PGC demodulation for remote interferometric fiber sensing systems. The proposed method shows great potential for application in remote, large-scale interferometric fiber sensing systems.