Cooling of Optically Levitated Particles: Principles, Implementations, and Applications
Abstract
1. Introduction
2. Capture and Manipulation of Particles
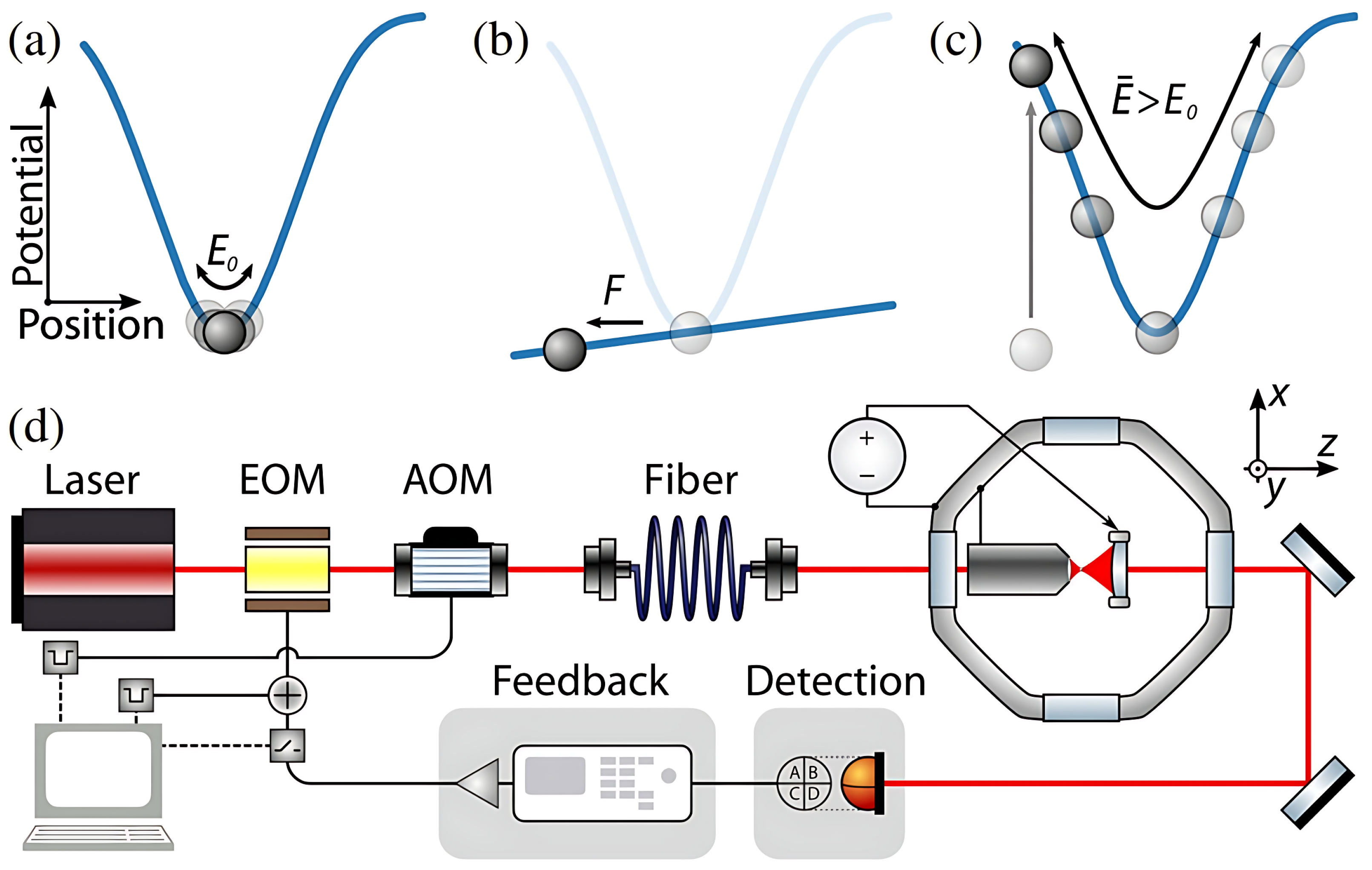
2.1. Principles of Levitation
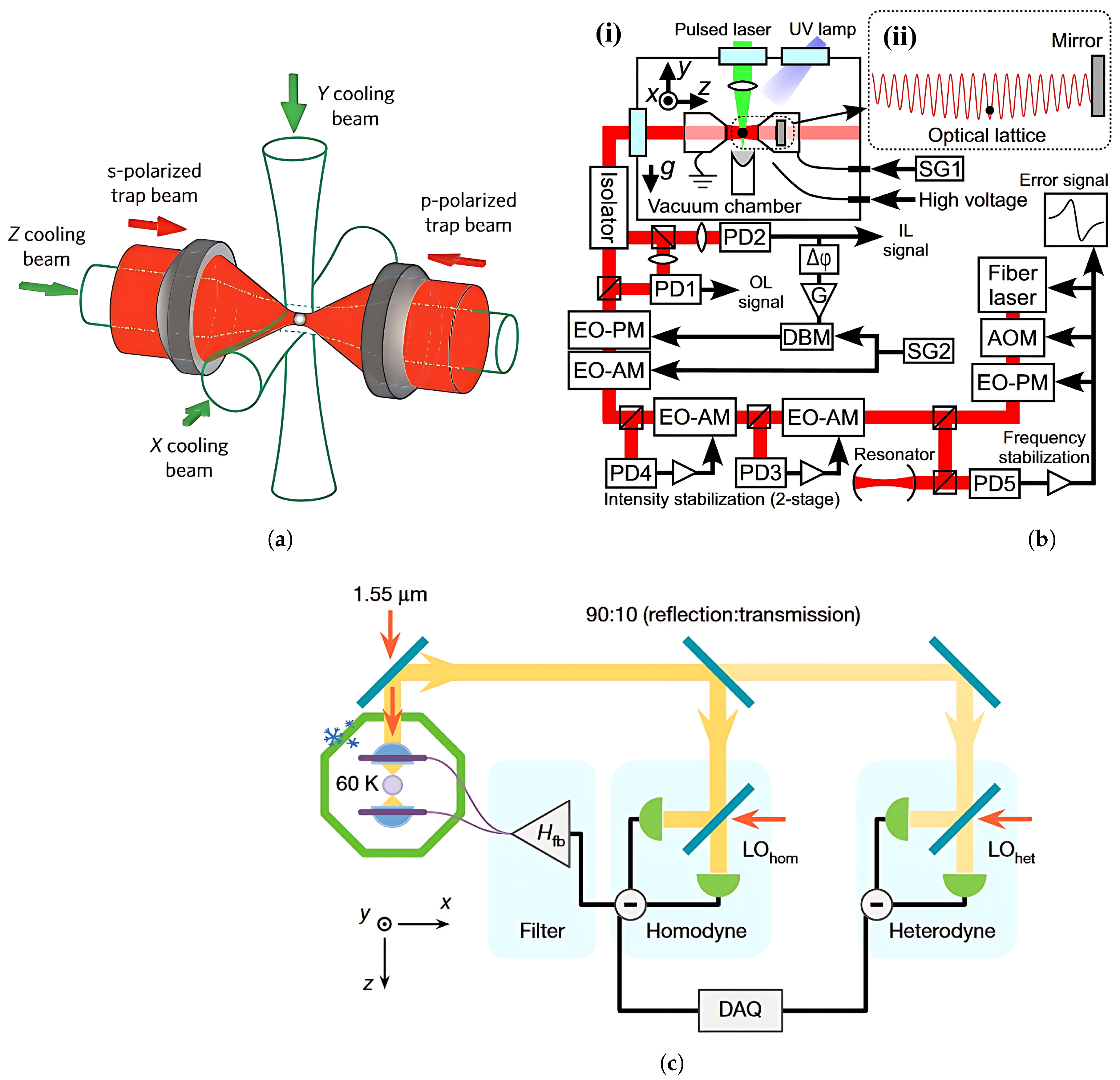
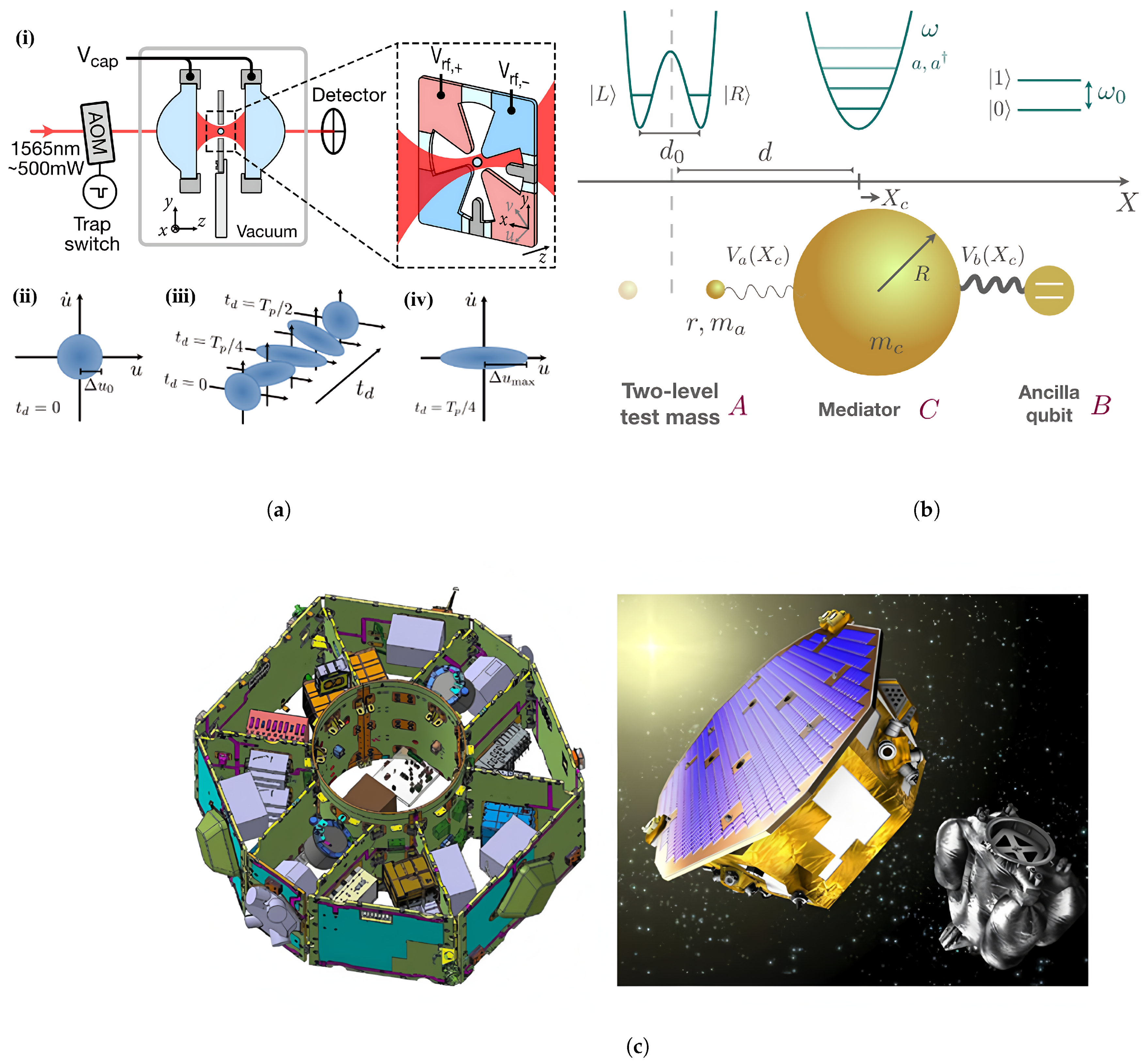
2.2. Loading Technique
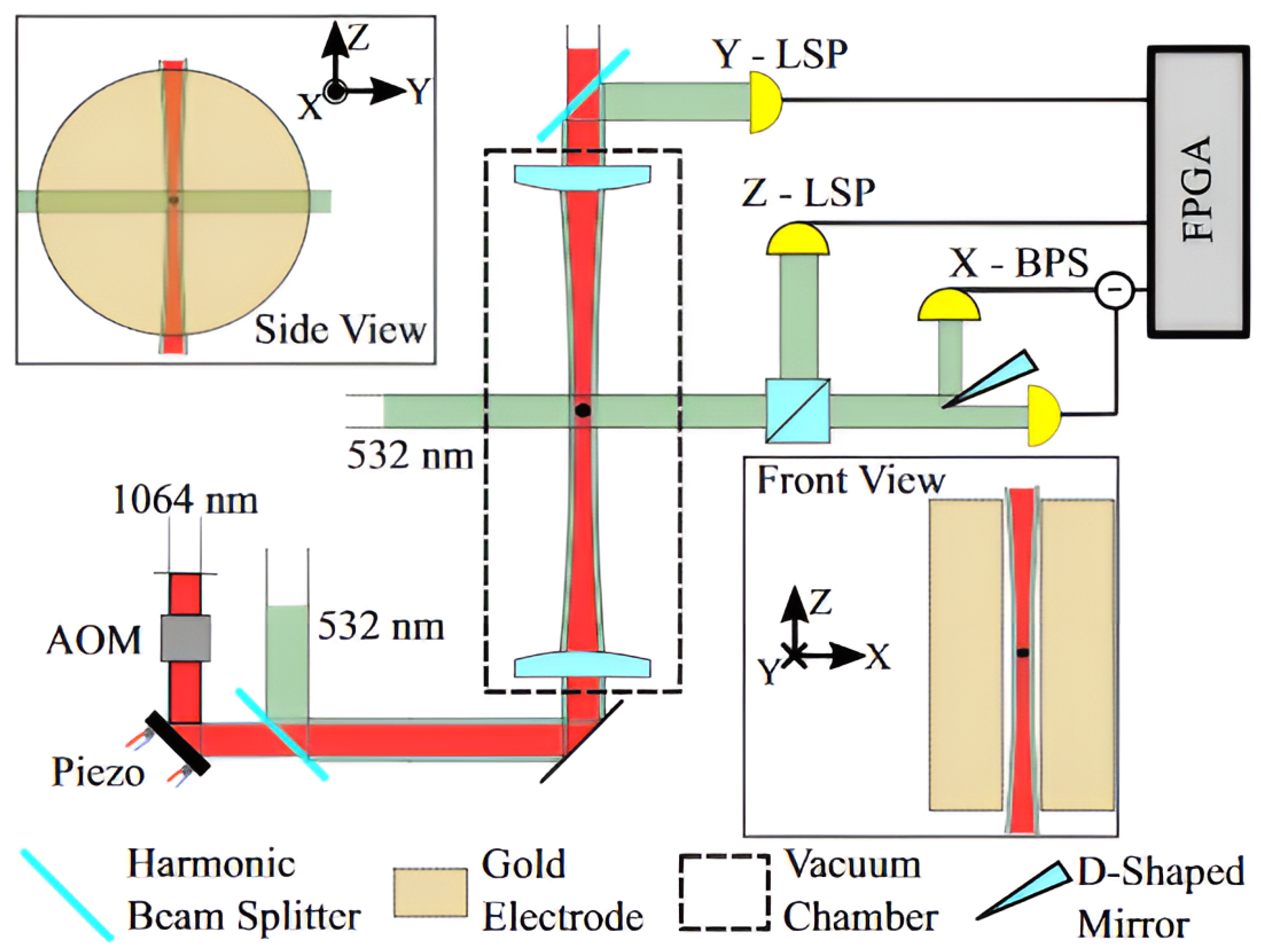
2.3. Motion Detection Technique
2.4. Noise Analysis
2.4.1. Thermal Noise
2.4.2. Quantum Noise
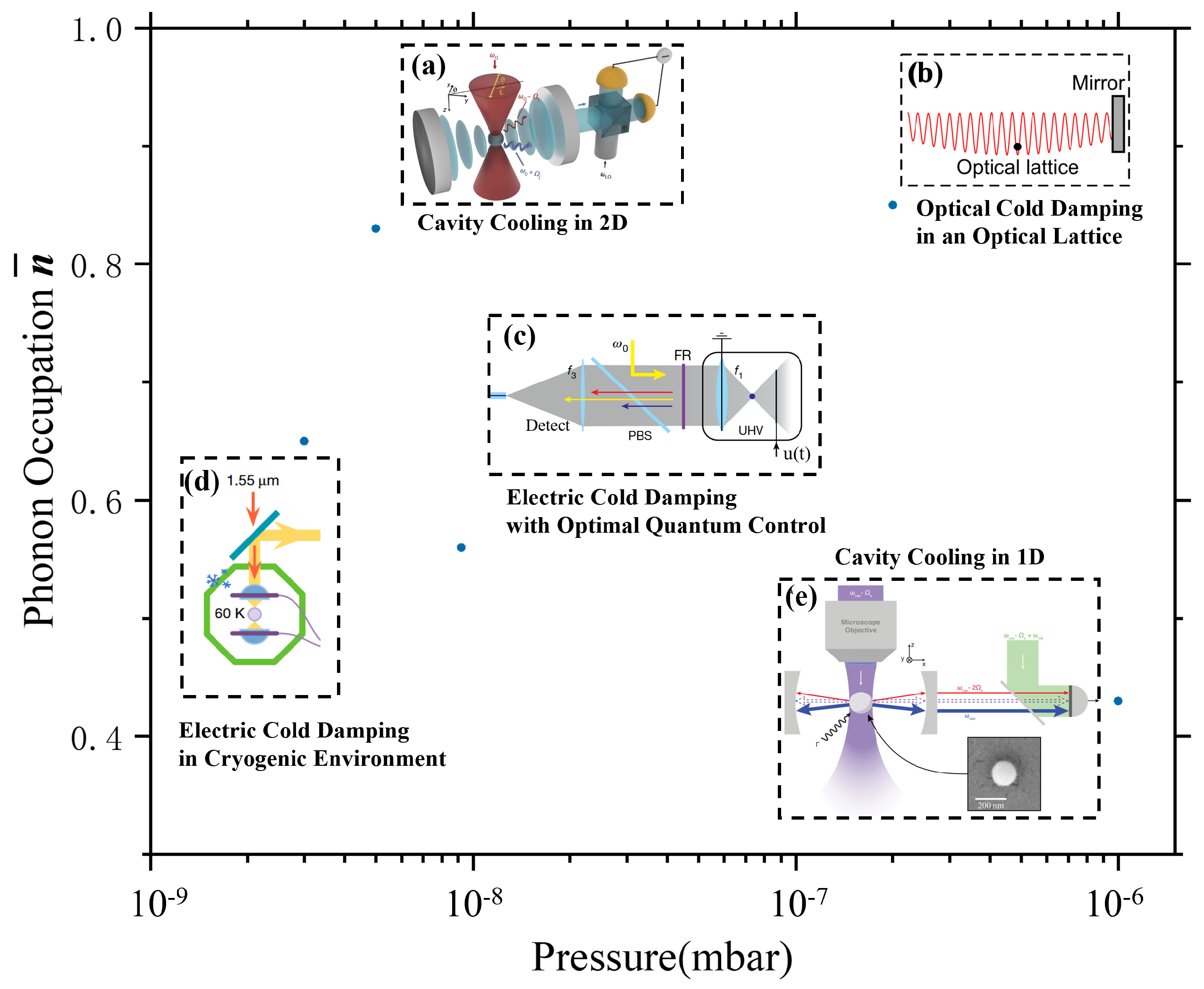
3. Methods of Cooling
3.1. Active Feedback Cooling
3.1.1. Velocity Feedback Cooling
3.1.2. Parametric Feedback Cooling
3.2. Passive Feedback Cooling
3.2.1. Dispersive Coupling Scheme
3.2.2. Coherent Scattering Scheme
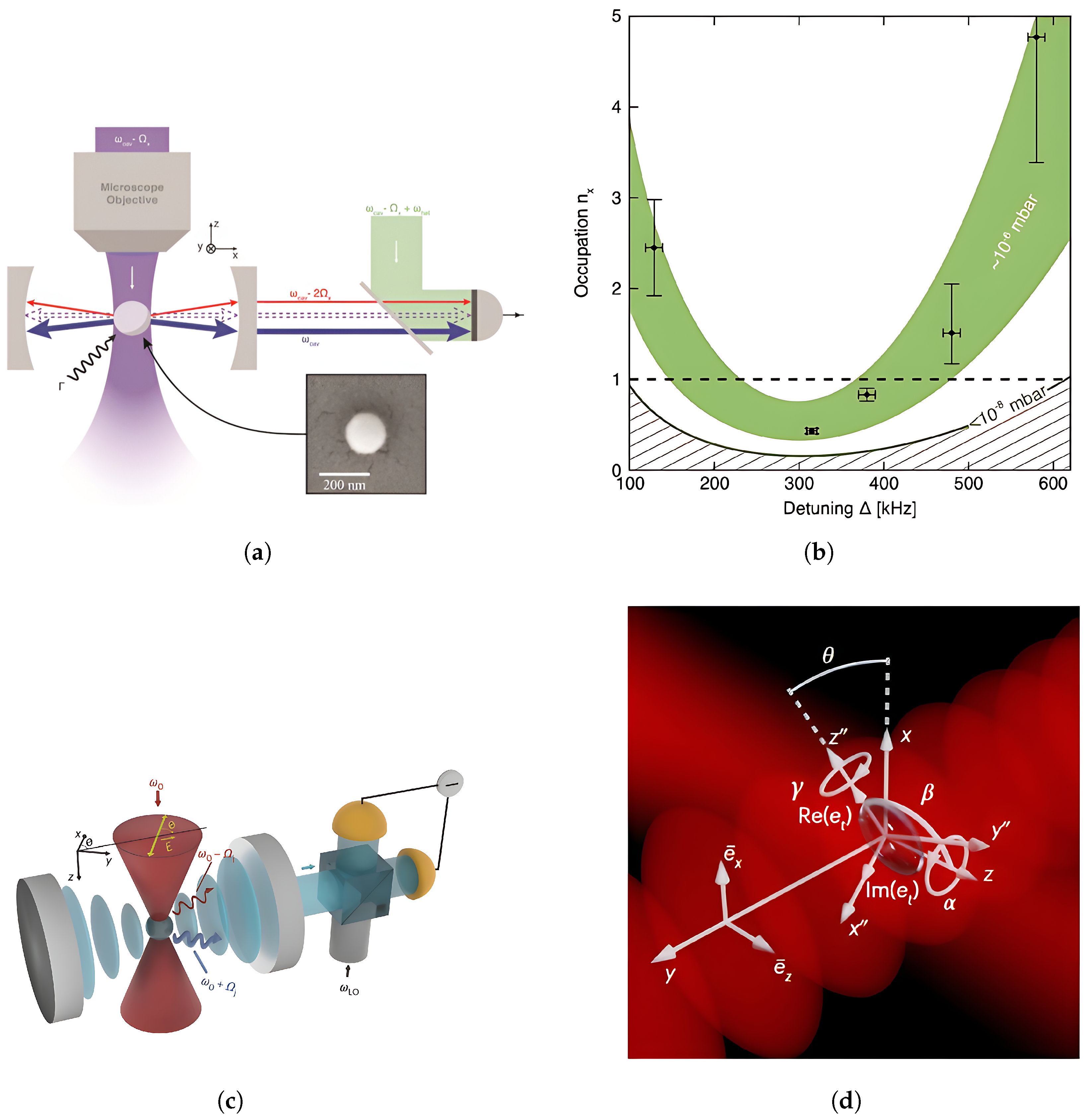
4. Applications
4.1. Precision Sensing
4.1.1. Force
4.1.2. Acceleration
4.1.3. Rotation and Torque
4.2. Fundamental Physics
4.2.1. New Physics
4.2.2. Macroscopic Quantum Physics
5. Outlook
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Kepler, J. De Cometis Libelli Tres, Typis Andreæ Apergeri, Sumptibus 601 Sebastiani Mylii Bibliopolæ Augustani. 1619. Available online: https://books.google.com/books?id=rs0MIosWD-4C&printsec=frontcover&source=gbs_atb#v=onepage&q&f=false (accessed on 24 August 2025).
- Hansch, T.; Schawlow, A. Cooling of Gases by Laser Radiation. Opt. Commun. 1975, 13, 68–69. [Google Scholar] [CrossRef]
- Neuhauser, W.; Hohenstatt, M.; Toschek, P.; Dehmelt, H. Optical-Sideband Cooling of Visible Atom Cloud Confined in Parabolic Well. Phys. Rev. Lett. 1978, 41, 233–236. [Google Scholar] [CrossRef]
- Chu, S.; Bjorkholm, J.E.; Ashkin, A.; Cable, A. Experimental Observation of Optically Trapped Atoms. Phys. Rev. Lett. 1986, 57, 314–317. [Google Scholar] [CrossRef]
- Balykin, V.O.; Letokhov, V.S.; Sidorov, A.I. Intense stationary flow of cold atoms formed by laser deceleration of atomic beam. Opt. Commun. 1984, 49, 248–252. [Google Scholar] [CrossRef]
- Monroe, C.; Swann, W.; Robinson, H.; Wieman, C. Very cold trapped atoms in a vapor cell. Phys. Rev. Lett. 1990, 65, 1571–1574. [Google Scholar] [CrossRef]
- Anderson, M.H.; Ensher, J.R.; Matthews, M.R.; Wieman, C.E.; Cornell, E.A. Observation of Bose-Einstein Condensation in a Dilute Atomic Vapor. Science 1995, 269, 198–201. [Google Scholar] [CrossRef]
- Boulder Atomic Clock Optical Network (BACON) Collaboration. Frequency ratio measurements at 18-digit accuracy using an optical clock network. Nature 2021, 591, 564–569. [Google Scholar] [CrossRef]
- Monroe, C.; Meekhof, D.M.; King, B.E.; Itano, W.M.; Wineland, D.J. Demonstration of a Fundamental Quantum Logic Gate. Phys. Rev. Lett. 1995, 75, 4714–4717. [Google Scholar] [CrossRef] [PubMed]
- Endres, M.; Bernien, H.; Keesling, A.; Levine, H.; Anschuetz, E.R. Atom-by-atom assembly of defect-free one-dimensional cold atom arrays. Science 2016, 354, 1024–1027. [Google Scholar] [CrossRef]
- Cohadon, P.F.; Heidmann, A.; Pinard, M. Cooling of a Mirror by Radiation Pressure. Phy. Rev. Lett. 1999, 83, 3174–3177. [Google Scholar] [CrossRef]
- Metzger, C.H.; Karrai, K. Cavity cooling of a microlever. Nature 2004, 432, 1002–1005. [Google Scholar] [CrossRef] [PubMed]
- Kleckner, D.; Bouwmeester, D. Sub-kelvin optical cooling of a micromechanical resonator. Nature 2006, 444, 75–78. [Google Scholar] [CrossRef] [PubMed]
- Usami, K.; Naesby, A.; Bagci, T.; Melholt Nielsen, B.; Liu, J. Optical cavity cooling of mechanical modes of a semiconductor nanomembrane. Nature Phys. 2012, 8, 168–172. [Google Scholar] [CrossRef]
- Ashkin, A. Acceleration and Trapping of Particles by Radiation Pressure. Phy. Rev. Lett. 1970, 24, 156–159. [Google Scholar] [CrossRef]
- Ashkin, A.; Dziedzic, J.M. Feedback stabilization of optically levitated particles. Appl. Phys. Lett. 1977, 30, 202–204. [Google Scholar] [CrossRef]
- Ashkin, A. History of optical trapping and manipulation of small-neutral particle, atoms, and molecules. IEEE J. Sel. Top. Quantum Electron. 2000, 6, 841–856. [Google Scholar] [CrossRef]
- Li, T.; Kheifets, S.; Medellin, D.; Raizen, M.G. Measurement of the Instantaneous Velocity of a Brownian Particle. Science 2010, 328, 1673–1675. [Google Scholar] [CrossRef]
- Li, T.; Kheifets, S.; Raizen, M.G. Millikelvin cooling of an optically trapped microsphere in vacuum. Nat. Phys. 2011, 7, 527–530. [Google Scholar] [CrossRef]
- Gieseler, J.; Deutsch, B.; Quidant, R.; Novotny, L. Subkelvin Parametric Feedback Cooling of a Laser-Trapped Nanoparticle. Phy. Rev. Lett. 2012, 109, 103603. [Google Scholar] [CrossRef]
- Conangla, G.P.; Ricci, F.; Cuairan, M.T.; Schell, A.W.; Meyer, N.; Quidant, R. Optimal Feedback Cooling of a Charged Levitated Nanoparticle with Adaptive Control. Phy. Rev. Lett. 2019, 122, 223602. [Google Scholar] [CrossRef]
- Asenbaum, P.; Kuhn, S.; Nimmrichter, S.; Sezer, U.; Arndt, M. Cavity cooling of free silicon nanoparticles in high vacuum. Nat. Commun. 2013, 4, 2743. [Google Scholar] [CrossRef]
- Delić, U.; Reisenbauer, M.; Dare, K.; Grass, D.; Vuletić, V.; Kiesel, N.; Aspelmeyer, M. Cooling of a levitated nanoparticle to the motional quantum ground state. Science 2020, 367, 892–895. [Google Scholar] [CrossRef] [PubMed]
- Magrini, L.; Rosenzweig, P.; Bach, C.; Deutschmann-Olek, A.; Hofer, S.G. Real-time optimal quantum control of mechanical motion at room temperature. Nature 2021, 595, 373–377. [Google Scholar] [CrossRef] [PubMed]
- Tebbenjohanns, F.; Mattana, M.L.; Rossi, M.; Frimmer, M.; Novotny, L. Quantum control of a nanoparticle optically levitated in cryogenic free space. Nature 2021, 595, 378–382. [Google Scholar] [CrossRef] [PubMed]
- Kamba, M.; Shimizu, R.; Aikawa, K. Optical cold damping of neutral nanoparticles near the ground state in an optical lattice. Opt. Express 2022, 30, 26716–26727. [Google Scholar] [CrossRef]
- Pedernales, J.S.; Streltsov, K.; Plenio, M.B. Enhancing Gravitational Interaction between Quantum Systems by a Massive Mediator. Phy. Rev. Lett. 2022, 128, 110401. [Google Scholar] [CrossRef]
- Braccini, L.; Schut, M.; Serafini, A.; Mazumdar, A.; Bose, S. Large Spin Stern-Gerlach Interferometry for Gravitational Entanglement. arXiv 2023, arXiv:2312.05170. [Google Scholar] [CrossRef]
- Bonvin, E.; Devaud, L.; Rossi, M.; Militaru, A.; Dania, L. State Expansion of a Levitated Nanoparticle in a Dark Harmonic Potential. Phy. Rev. Lett. 2024, 132, 253602. [Google Scholar] [CrossRef]
- Direkci, S.; Winkler, K.; Gut, C.; Hammerer, K.; Aspelmeyer, M.; Chen, Y. Macroscopic quantum entanglement between an optomechanical cavity and a continuous field in presence of non-Markovian noise. Phys. Rev. Res. 2024, 6, 013175. [Google Scholar] [CrossRef]
- Liang, T.; Zhu, S.; He, P.; Chen, Z.; Wang, Y.; Li, C.; Fu, Z.; Gao, X.; Chen, X.; Li, N.; et al. Yoctonewton force detection based on optically levitated oscillator. Fundam. Res. 2023, 3, 57–62. [Google Scholar] [CrossRef]
- Lee, J.G.; Adelberger, E.G.; Cook, T.S.; Fleischer, S.M.; Heckel, B.R. New Test of the Gravitational 1/r2 Law at Separations down to 52 μm. Phy. Rev. Lett. 2020, 124, 101101. [Google Scholar] [CrossRef] [PubMed]
- LSD Collaboration; Winstone, G.; Wang, Z.; Klomp, S.; Felsted, R.G. Optical Trapping of High-Aspect-Ratio NaYF Hexagonal Prisms for kHz-MHz Gravitational Wave Detectors. Phy. Rev. Lett. 2022, 129, 053604. [Google Scholar] [CrossRef] [PubMed]
- Moore, D.C.; Rider, A.D.; Gratta, G. Search for Millicharged Particles Using Optically Levitated Microspheres. Phy. Rev. Lett. 2014, 113, 251801. [Google Scholar] [CrossRef]
- Bateman, J.; McHardy, I.; Merle, A.; Morris, T.R.; Ulbricht, H. On the Existence of Low-Mass Dark Matter and its Direct Detection. Sci. Rep. 2015, 5, 8058. [Google Scholar] [CrossRef] [PubMed]
- Mancini, S.; Vitali, D.; Tombesi, P. Optomechanical Cooling of a Macroscopic Oscillator by Homodyne Feedback. Phy. Rev. Lett. 1998, 80, 688–691. [Google Scholar] [CrossRef]
- Ranjit, G.; Atherton, D.P.; Stutz, J.H.; Cunningham, M.; Geraci, A.A. Attonewton force detection using microspheres in a dual-beam optical trap in high vacuum. Phys. Rev. A 2015, 91, 051805. [Google Scholar] [CrossRef]
- Hempston, D.; Vovrosh, J.; Toroš, M.; Winstone, G.; Rashid, M.; Ulbricht, H. Force sensing with an optically levitated charged nanoparticle. Appl. Phys. Lett. 2017, 111, 133111. [Google Scholar] [CrossRef]
- Hebestreit, E.; Frimmer, M.; Reimann, R.; Novotny, L. Sensing Static Forces with Free-Falling Nanoparticles. Phy. Rev. Lett. 2018, 121, 063602. [Google Scholar] [CrossRef]
- Monteiro, F.; Li, W.; Afek, G.; Li, C.l.; Mossman, M.; Moore, D.C. Force and acceleration sensing with optically levitated nanogram masses at microkelvin temperatures. Phys. Rev. A 2020, 101, 053835. [Google Scholar] [CrossRef]
- Fu, Z.; Zhu, S.; Dong, Y.; Chen, X.; Gao, X.; Hu, H. Force detection sensitivity spectrum calibration of levitated nanomechanical sensor using harmonic coulomb force. Opt. Lasers Eng. 2022, 152, 106957. [Google Scholar] [CrossRef]
- Piotrowski, J.; Windey, D.; Vijayan, J.; Gonzalez-Ballestero, C.; Sommer, A.d.l.R. Simultaneous ground-state cooling of two mechanical modes of a levitated nanoparticle. Nat. Phys. 2023, 19, 1009–1013. [Google Scholar] [CrossRef]
- Horak, P.; Hechenblaikner, G.; Gheri, K.M.; Stecher, H.; Ritsch, H. Cavity-Induced Atom Cooling in the Strong Coupling Regime. Phy. Rev. Lett. 1997, 79, 4974–4977. [Google Scholar] [CrossRef]
- Vuletić, V.; Chu, S. Laser Cooling of Atoms, Ions, or Molecules by Coherent Scattering. Phy. Rev. Lett. 2000, 84, 3787–3790. [Google Scholar] [CrossRef] [PubMed]
- Vuletić, V.; Chan, H.W.; Black, A.T. Three-dimensional cavity Doppler cooling and cavity sideband cooling by coherent scattering. Phys. Rev. A 2001, 64, 033405. [Google Scholar] [CrossRef]
- Barker, P.F.; Shneider, M.N. Cavity cooling of an optically trapped nanoparticle. Phys. Rev. A 2010, 81, 023826. [Google Scholar] [CrossRef]
- Kiesel, N.; Blaser, F.; Delić, U.; Grass, D.; Kaltenbaek, R.; Aspelmeyer, M. Cavity cooling of an optically levitated submicron particle. Proc. Natl. Acad. Sci. USA 2013, 110, 14180–14185. [Google Scholar] [CrossRef]
- Millen, J.; Fonseca, P.Z.G.; Mavrogordatos, T.; Monteiro, T.S.; Barker, P.F. Cavity Cooling a Single Charged Levitated Nanosphere. Phy. Rev. Lett. 2015, 114, 123602. [Google Scholar] [CrossRef]
- Fonseca, P.; Aranas, E.; Millen, J.; Monteiro, T.; Barker, P. Nonlinear dynamics and strong cavity cooling of levitated nanoparticles. Phy. Rev. Lett. 2016, 117, 173602. [Google Scholar] [CrossRef]
- Delić, U.; Reisenbauer, M.; Grass, D.; Kiesel, N.; Vuletić, V.; Aspelmeyer, M. Cavity Cooling of a Levitated Nanosphere by Coherent Scattering. Phy. Rev. Lett. 2019, 122, 123602. [Google Scholar] [CrossRef]
- Pontin, A.; Fu, H.; Toroš, M.; Monteiro, T.S.; Barker, P.F. Simultaneous cavity cooling of all six degrees of freedom of a levitated nanoparticle. Nat. Phys. 2023, 19, 1003–1008. [Google Scholar] [CrossRef]
- Li, N.; Zhu, X.m.; Li, W.q.; Fu, Z.h.; Hu, M.z.; Hu, H.z. Review of optical tweezers in vacuum. Front. Inf. Technol. Electron. Eng. 2019, 20, 655–673. [Google Scholar] [CrossRef]
- Pesce, G.; Jones, P.H.; Maragò, O.M.; Volpe, G. Optical tweezers: Theory and practice. Eur. Phys. J. Plus 2020, 135, 949. [Google Scholar] [CrossRef]
- Aspelmeyer, M.; Kippenberg, T.J.; Marquardt, F. Cavity optomechanics. Rev. Mod. Phys. 2014, 86, 1391–1452. [Google Scholar] [CrossRef]
- Wen, P.; Wang, M.; Long, G.L. Ground-state cooling in cavity optomechanical systems. Front. Phys. 2023, 11, 1218010. [Google Scholar] [CrossRef]
- Gonzalez-Ballestero, C.; Aspelmeyer, M.; Novotny, L.; Quidant, R.; Romero-Isart, O. Levitodynamics: Levitation and control of microscopic objects in vacuum. Science 2021, 374, eabg3027. [Google Scholar] [CrossRef] [PubMed]
- Winstone, G.; Bhattacharya, M.; Geraci, A.A.; Li, T.; Pauzauskie, P.J.; Vamivakas, N. Levitated optomechanics: A tutorial and perspective. arXiv 2023, arXiv:2307.11858. [Google Scholar] [CrossRef]
- Harada, Y.; Asakura, T. Radiation forces on a dielectric sphere in the Rayleigh scattering regime. Opt. Commun. 1996, 124, 529–541. [Google Scholar] [CrossRef]
- Bui, A.A.M.; Stilgoe, A.B.; Lenton, I.C.D.; Gibson, L.J.; Kashchuk, A.V. Theory and practice of simulation of optical tweezers. J. Quant. Spectrosc. Radiat. Transf. 2017, 195, 66–75. [Google Scholar] [CrossRef]
- Callegari, A.; Mijalkov, M.; Gököz, A.B.; Volpe, G. Computational toolbox for optical tweezers in geometrical optics. JOSA B 2015, 32, B11–B19. [Google Scholar] [CrossRef]
- Kubo, R. The fluctuation-dissipation theorem. Rep. Prog. Phys. 1966, 29, 255. [Google Scholar] [CrossRef]
- Nagornykh, P.; Coppock, J.E.; Kane, B.E. Cooling of levitated graphene nanoplatelets in high vacuum. Appl. Phys. Lett. 2015, 106, 244102. [Google Scholar] [CrossRef]
- Kamba, M.; Kiuchi, H.; Yotsuya, T.; Aikawa, K. Recoil-limited feedback cooling of single nanoparticles near the ground state in an optical lattice. Phys. Rev. A 2021, 103, L051701. [Google Scholar] [CrossRef]
- Calamai, M.; Ranfagni, A.; Marin, F. Transfer of a levitating nanoparticle between optical tweezers. AIP Adv. 2021, 11, 025246. [Google Scholar] [CrossRef]
- Lindner, S.; Juschitz, P.; Rieser, J.; Fein, Y.Y.; Debiossac, M. Hollow-core fiber loading of nanoparticles into ultra-high vacuum. Appl. Phys. Lett. 2024, 124, 143501. [Google Scholar] [CrossRef]
- Tebbenjohanns, F.; Frimmer, M.; Novotny, L. Optimal position detection of a dipolar scatterer in a focused field. Phys. Rev. A 2019, 100, 043821. [Google Scholar] [CrossRef]
- Jain, V.; Tebbenjohanns, F.; Novotny, L. Microkelvin Control of an Optically Levitated Nanoparticle. In Proceedings of the Frontiers in Optics, Rochester, NY, USA, 17–21 October 2016; p. FF5B.2. [Google Scholar]
- Jain, V. Direct Measurement of Photon Recoil from a Levitated Nanoparticle. Phy. Rev. Lett. 2016, 116. [Google Scholar] [CrossRef]
- Kamba, M.; Shimizu, R.; Aikawa, K. Nanoscale feedback control of six degrees of freedom of a near-sphere. Nat. Commun. 2023, 14, 7943. [Google Scholar] [CrossRef]
- Ashkin, A.; Dziedzic, J.M. Optical levitation in high vacuum. Appl. Phys. Lett. 1976, 28, 333–335. [Google Scholar] [CrossRef]
- Goldwater, D.; Stickler, B.A.; Martinetz, L.; Northup, T.E.; Hornberger, K.; Millen, J. Levitated electromechanics: All-electrical cooling of charged nano- and micro-particles. Quantum Sci. Technol. 2019, 4, 024003. [Google Scholar] [CrossRef]
- Iwasaki, M.; Yotsuya, T.; Naruki, T.; Matsuda, Y.; Yoneda, M.; Aikawa, K. Electric feedback cooling of single charged nanoparticles in an optical trap. Phys. Rev. A 2019, 99, 051401. [Google Scholar] [CrossRef]
- Tebbenjohanns, F.; Frimmer, M.; Militaru, A.; Jain, V.; Novotny, L. Cold Damping of an Optically Levitated Nanoparticle to Microkelvin Temperatures. Phy. Rev. Lett. 2019, 122, 223601. [Google Scholar] [CrossRef] [PubMed]
- Vovrosh, J.; Rashid, M.; Hempston, D.; Bateman, J.; Paternostro, M.; Ulbricht, H. Parametric feedback cooling of levitated optomechanics in a parabolic mirror trap. JOSA B 2017, 34, 1421–1428. [Google Scholar] [CrossRef]
- Zheng, Y.; Guo, G.C.; Sun, F.W. Cooling of a levitated nanoparticle with digital parametric feedback. Appl. Phys. Lett. 2019, 115, 101105. [Google Scholar] [CrossRef]
- Manikandan, S.K.; Qvarfort, S. Optimal quantum parametric feedback cooling. Phys. Rev. A 2023, 107, 023516. [Google Scholar] [CrossRef]
- Ghosh, A.; Kumar, P.; Sommer, C.; Jimenez, F.G.; Sudhir, V.; Genes, C. Theory of phase-adaptive parametric cooling. Phys. Rev. A 2023, 107, 053521. [Google Scholar] [CrossRef]
- Penny, T.W.; Pontin, A.; Barker, P.F. Performance and limits of feedback cooling methods for levitated oscillators: A direct comparison. Phys. Rev. A 2021, 104, 023502. [Google Scholar] [CrossRef]
- Hechenblaikner, G.; Gangl, M.; Horak, P.; Ritsch, H. Cooling an atom in a weakly driven high-Q cavity. Phys. Rev. A 1998, 58, 3030–3042. [Google Scholar] [CrossRef]
- Chan, H.W.; Black, A.T.; Vuletić, V. Observation of Collective-Emission-Induced Cooling of Atoms in an Optical Cavity. Phy. Rev. Lett. 2003, 90, 063003. [Google Scholar] [CrossRef]
- Maunz, P.; Puppe, T.; Schuster, I.; Syassen, N.; Pinkse, P.W.H.; Rempe, G. Cavity cooling of a single atom. Nature 2004, 428, 50–52. [Google Scholar] [CrossRef]
- Nußmann, S.; Murr, K.; Hijlkema, M.; Weber, B.; Kuhn, A.; Rempe, G. Vacuum-stimulated cooling of single atoms in three dimensions. Nat. Phys. 2005, 1, 122–125. [Google Scholar] [CrossRef][Green Version]
- Arcizet, O.; Cohadon, P.F.; Briant, T.; Pinard, M.; Heidmann, A. Radiation-pressure cooling and optomechanical instability of a micromirror. Nature 2006, 444, 71–74. [Google Scholar] [CrossRef] [PubMed]
- Gigan, S.; Böhm, H.R.; Paternostro, M.; Blaser, F.; Langer, G. Self-cooling of a micromirror by radiation pressure. Nature 2006, 444, 67–70. [Google Scholar] [CrossRef] [PubMed]
- Wilson-Rae, I.; Nooshi, N.; Zwerger, W.; Kippenberg, T.J. Theory of Ground State Cooling of a Mechanical Oscillator Using Dynamical Backaction. Phy. Rev. Lett. 2007, 99, 093901. [Google Scholar] [CrossRef] [PubMed]
- Jayich, A.M.; Sankey, J.C.; Børkje, K.; Lee, D.; Yang, C. Cryogenic optomechanics with a Si3N4 membrane and classical laser noise. New J. Phys. 2012, 14, 115018. [Google Scholar] [CrossRef]
- Safavi-Naeini, A.H.; Chan, J.; Hill, J.T.; Gröblacher, S.; Miao, H. Laser noise in cavity-optomechanical cooling and thermometry. New J. Phys. 2013, 15, 035007. [Google Scholar] [CrossRef]
- Dania, L.; Kremer, O.S.; Piotrowski, J.; Candoli, D.; Vijayan, J.; Romero-Isart, O.; Gonzalez-Ballestero, C.; Novotny, L.; Frimmer, M. High-purity quantum optomechanics at room temperature. Nat. Phys. 2025. [Google Scholar] [CrossRef]
- Xu, Y.; Liu, Y.H.; Liu, C.; Liao, J.Q. Simultaneous ground-state cooling of two levitated nanoparticles by coherent scattering. Phys. Rev. A 2024, 109, 053521. [Google Scholar] [CrossRef]
- Ranjit, G.; Cunningham, M.; Casey, K.; Geraci, A.A. Zeptonewton force sensing with nanospheres in an optical lattice. Phys. Rev. A 2016, 93, 053801. [Google Scholar] [CrossRef]
- Hoang, T.M.; Ma, Y.; Ahn, J.; Bang, J.; Robicheaux, F.; Yin, Z.Q.; Li, T. Torsional Optomechanics of a Levitated Nonspherical Nanoparticle. Phy. Rev. Lett. 2016, 117, 123604. [Google Scholar] [CrossRef]
- Reimann, R.; Doderer, M.; Hebestreit, E.; Diehl, R.; Frimmer, M. GHz Rotation of an Optically Trapped Nanoparticle in Vacuum. Phy. Rev. Lett. 2018, 121, 033602. [Google Scholar] [CrossRef]
- Ahn, J.; Xu, Z.; Bang, J.; Ju, P.; Gao, X.; Li, T. Ultrasensitive torque detection with an optically levitated nanorotor. Nature Nanotechnol. 2020, 15, 89–93. [Google Scholar] [CrossRef]
- Geraci, A.A.; Papp, S.B.; Kitching, J. Short-Range Force Detection Using Optically Cooled Levitated Microspheres. Phy. Rev. Lett. 2010, 105, 101101. [Google Scholar] [CrossRef] [PubMed]
- Geraci, A.; Goldman, H. Sensing short range forces with a nanosphere matter-wave interferometer. Phys. Rev. D 2015, 92, 062002. [Google Scholar] [CrossRef]
- Peters, A.; Chung, K.Y.; Chu, S. Measurement of gravitational acceleration by dropping atoms. Nature 1999, 400, 849–852. [Google Scholar] [CrossRef]
- Panda, C.D.; Tao, M.J.; Ceja, M.; Khoury, J.; Tino, G.M.; Müller, H. Measuring gravitational attraction with a lattice atom interferometer. Nature 2024, 631, 515–520. [Google Scholar] [CrossRef]
- Rider, A.D.; Blakemore, C.P.; Gratta, G.; Moore, D.C. Single-beam dielectric-microsphere trapping with optical heterodyne detection. Phys. Rev. A 2018, 97, 013842. [Google Scholar] [CrossRef]
- Monteiro, F.; Ghosh, S.; Fine, A.G.; Moore, D.C. Optical levitation of 10-ng spheres with nano-$g$ acceleration sensitivity. Phys. Rev. A 2017, 96, 063841. [Google Scholar] [CrossRef]
- Ahn, J.; Xu, Z.; Bang, J.; Deng, Y.H.; Hoang, T.M. Optically Levitated Nanodumbbell Torsion Balance and GHz Nanomechanical Rotor. Phy. Rev. Lett. 2018, 121, 033603. [Google Scholar] [CrossRef]
- Arita, Y.; Mazilu, M.; Dholakia, K. Laser-induced rotation and cooling of a trapped microgyroscope in vacuum. Nat. Commun. 2013, 4, 2374. [Google Scholar] [CrossRef]
- Kim, P.H.; Hauer, B.D.; Doolin, C.; Souris, F.; Davis, J.P. Approaching the standard quantum limit of mechanical torque sensing. Nature Commun. 2016, 7, 13165. [Google Scholar] [CrossRef]
- Rudolph, H.; Delić, U.; Aspelmeyer, M.; Hornberger, K.; Stickler, B.A. Force-Gradient Sensing and Entanglement via Feedback Cooling of Interacting Nanoparticles. Phy. Rev. Lett. 2022, 129, 193602. [Google Scholar] [CrossRef]
- Das, D.; Home, D.; Ulbricht, H.; Bose, S. Mass-Independent Scheme to Test the Quantumness of a Massive Object. Phy. Rev. Lett. 2024, 132, 030202. [Google Scholar] [CrossRef] [PubMed]
- Rider, A.D.; Moore, D.C.; Blakemore, C.P.; Louis, M.; Lu, M.; Gratta, G. Search for Screened Interactions Associated with Dark Energy below the 100 μm Length Scale. Phy. Rev. Lett. 2016, 117, 101101. [Google Scholar] [CrossRef] [PubMed]
- Aggarwal, N.; Winstone, G.P.; Teo, M.; Baryakhtar, M.; Larson, S.L.; Kalogera, V.; Geraci, A.A. Searching for New Physics with a Levitated-Sensor-Based Gravitational-Wave Detector. Phy. Rev. Lett. 2022, 128, 111101. [Google Scholar] [CrossRef]
- Monteiro, F.; Afek, G.; Carney, D.; Krnjaic, G.; Wang, J.; Moore, D.C. Search for Composite Dark Matter with Optically Levitated Sensors. Phy. Rev. Lett. 2020, 125, 181102. [Google Scholar] [CrossRef]
- Carney, D.; Krnjaic, G.; Moore, D.C.; Regal, C.A.; Afek, G. Mechanical quantum sensing in the search for dark matter. Quantum Sci. Technol. 2021, 6, 024002. [Google Scholar] [CrossRef]
- LIGO Scientific Collaboration and Virgo Collaboration; Abbott, B.P.; Abbott, R.; Abbott, T.D.; Abernathy, M.R. GW150914: The Advanced LIGO Detectors in the Era of First Discoveries. Phy. Rev. Lett. 2016, 116, 131103. [Google Scholar] [CrossRef]
- Romero-Isart, O.; Pflanzer, A.C.; Blaser, F.; Kaltenbaek, R.; Kiesel, N.; Aspelmeyer, M.; Cirac, J.I. Large Quantum Superpositions and Interference of Massive Nanometer-Sized Objects. Phy. Rev. Lett. 2011, 107, 020405. [Google Scholar] [CrossRef]
- Fuchs, T.M.; Uitenbroek, D.G.; Plugge, J.; van Halteren, N.; van Soest, J.P.; Vinante, A.; Ulbricht, H.; Oosterkamp, T.H. Measuring gravity with milligram levitated masses. Sci. Adv. 2024, 10, eadk2949. [Google Scholar] [CrossRef]





Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, J.; Lin, Y.; Cai, H.; Chen, X.; Li, N.; Hu, H.; Liu, C. Cooling of Optically Levitated Particles: Principles, Implementations, and Applications. Photonics 2025, 12, 953. https://doi.org/10.3390/photonics12100953
Liu J, Lin Y, Cai H, Chen X, Li N, Hu H, Liu C. Cooling of Optically Levitated Particles: Principles, Implementations, and Applications. Photonics. 2025; 12(10):953. https://doi.org/10.3390/photonics12100953
Chicago/Turabian StyleLiu, Jiaming, Yizhe Lin, Han Cai, Xingfan Chen, Nan Li, Huizhu Hu, and Cheng Liu. 2025. "Cooling of Optically Levitated Particles: Principles, Implementations, and Applications" Photonics 12, no. 10: 953. https://doi.org/10.3390/photonics12100953
APA StyleLiu, J., Lin, Y., Cai, H., Chen, X., Li, N., Hu, H., & Liu, C. (2025). Cooling of Optically Levitated Particles: Principles, Implementations, and Applications. Photonics, 12(10), 953. https://doi.org/10.3390/photonics12100953






